Abstract
Wood density is a critical control on tree biomass, so poor understanding of its spatial variation can lead to large and systematic errors in forest biomass estimates and carbon maps. The need to understand how and why wood density varies is especially critical in tropical America where forests have exceptional species diversity and spatial turnover in composition. As tree identity and forest composition are challenging to estimate remotely, ground surveys are essential to know the wood density of trees, whether measured directly or inferred from their identity. Here, we assemble an extensive dataset of variation in wood density across the most forested and tree-diverse continent, examine how it relates to spatial and environmental variables, and use these relationships to predict spatial variation in wood density over tropical and sub-tropical South America. Our analysis refines previously identified east-west Amazon gradients in wood density, improves them by revealing fine-scale variation, and extends predictions into Andean, dry, and Atlantic forests. The results halve biomass prediction errors compared to a naïve scenario with no knowledge of spatial variation in wood density. Our findings will help improve remote sensing-based estimates of aboveground biomass carbon stocks across tropical South America.
Similar content being viewed by others
Introduction
Understanding spatial and temporal variation in forest biomass carbon stocks is critical for numerous applications and research questions, including national carbon stock inventories [e.g. ref. 1], assessments of forest responses and recovery from disturbance2,3,4, and investigation of climate feedbacks [e.g. ref. 5]. However, quantifying the distribution of aboveground live carbon stocks across the tropical forest biome remains challenging. Despite decades of fieldwork6 and investment in satellite and airborne remote sensing to measure canopy structure with Lidar or vegetation volume through radar scattering1,7, there is still considerable uncertainty about the amount and distribution of aboveground carbon in tropical forests. Indeed, marked differences among recent global maps of biomass carbon8,9,10 reflect the challenge of large-scale calibration and validation across tropical forests.
The challenge partly arises because remote-sensing approaches, which allow large-scale and spatially continuous measurements, cannot provide all the information available from ground-based surveys. Wood density is a fundamental determinant of tree biomass11,12,13, and estimating it requires skilled botanical surveys to identify trees. Airborne and satellite remote-sensing methods provide measurements that allow estimates of tree height or volume, but not their identity or wood density14. While some inferences about taxonomic composition can be made from hyperspectral imagery [e.g. refs. 15, 16], this remains limited compared to what can be obtained by a ground-based botanical survey. Lack of wood density information can lead to marked discrepancies between remote sensed and ground-based estimates of aboveground biomass17, including spatial biases in aboveground biomass estimates of around 30% even within a single country18.
Future improvements in remote-sensing-based forest biomass maps therefore require improved knowledge of spatial variation in tree wood density. The need to tackle this huge challenge is especially important in South America. Not only are tropical rain forests here the most extensive in the world, but they also include many of the most productive and carbon-rich forests on Earth19,20 and large carbon sinks and fluxes [e.g. 21,22,23]. The nature of the challenge is also most profound in South America, as ~40% of Earth’s 73,000 tree species are found in forests here24. Amazonia alone is home to at least 15,00025, and beyond the Amazon marked differences in species composition pertain across South America’s diverse forest ecosystems26,27,28.
While the proximate driver of spatial variation in wood density is turnover in species composition, it may ultimately relate to environmental gradients, as wood density is an important ecological trait mediating species responses to the environment. High wood density trees experience lower mortality risks29,30, but as dense wood is costly to produce there is a trade-off between producing less dense wood and growing faster, and producing denser wood and having lower mortality risk31. This lower mortality risk may arise through resistance to mechanical breakage32, the dominant cause of tree death in Southern and Western Amazonia30,33, although resistance to breakage may be offset by greater flexibility of low wood density species34. Wood density is also linked to drought sensitivity, as higher wood density predicts lower vulnerability to cavitation35,36 and resilience of growth to drought37, although these relationships are influenced by the allocation of xylem space to different tissues38. Species with high wood density are therefore likely to tend to be more tolerant of environmental stresses such as drought, while the growth advantage of low wood density species may be most marked in competitive environments (e.g. with high soil fertility) and in frequently-disturbed forests where rapid colonisation of gaps is key (e.g. unstable soils). There is some empirical evidence to support these theoretical predictions. For example, Chave et al.32 found that wood density varied across North and South America with gradients of temperature and precipitation, while Quesada et al.39 found that wood density was lower on more fertile and more poorly structured soils, as well as tending to be higher where precipitation was lower and temperatures were higher (i.e. greater potential for drought stress). These studies highlight the potential for improved prediction of spatial variation in wood density by incorporating relationships with environmental variables. However, it is unknown how such different drivers acting at multiple spatial scales combine to influence variation in wood density across tropical South American forests.
We leverage our extensive collective effort to measure and identify trees in forests across South America to describe spatial variation in community wood density, and use relationships with environmental variables to map estimated wood density at 1km resolution across tropical and sub-tropical South American forests. This builds on early descriptions of spatial variation in wood density [e.g. 17,40] by utilising newly available forest plot data, and expands the analysis to include non-Amazonian forests, providing a resource to support remote-sensing analyses quantifying aboveground biomass.
Results
Variation in wood density
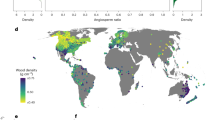
Basal-area weighted wood density varied two-fold across tropical and sub-tropical South American forests (mean = 0.63 g cm-3, Fig. 1). Wood density varied significantly between regions (linear model, F7,973 = 71.6, P < 0.001, R2 = 0.34). Within Amazonia, forests in East-Central Amazon and the Guiana Shield had the highest wood density on average, followed by the Brazilian Shield, with the lowest wood density in western areas (Fig. 1b). Wood density in the Atlantic Forest was similar to that in the Brazilian Shield. Dry forests tended to have high wood density, but there was a cluster of plots (distributed across dry forest areas) with some of the lowest wood density in the dataset. Montane forests had the lowest average wood density (Fig. 1b).
a Location of forest inventory plots where wood density was quantified. b Variation in basal-area weighted wood density between regions. Colours in a relate to regions in (b). N = 981 plots (Lowland-NW = 182 plots, Lowland-SW = 168, East-central Amazon = 205, Guiana Shield = 123, Brazilian Shield = 119, Atlantic forest = 69, Andes = 71, Dry forests = 44). Black points show mean values in each region estimated by a linear model with wood density as the response variable and region as the explanatory variable; lines show 95% confidence intervals from that model.
Spatial patterns in wood density
To understand this variation, models (generalised additive models [GAMs] and random forests) were constructed with three sets of explanatory variables; (1) latitude and longitude only, (2) environmental (climate, soil and topography, see Table 1) variables only, and (3) both environmental and spatial variables. Longitude was the most important explanatory variable across all models it was included in (Fig. 2), with a west-to-east gradient in increasing wood density (Fig. S1). Latitude, soil texture and soil chemistry (cation exchange capacity and pH) were the next most important variables (Fig. 2), although there were differences between models, with greater importance of pH and soil texture in GAM models compared to random forests (Fig. 2). Wood density decreased with cation exchange capacity in the GAM and random forest models without spatial covariates (Fig S1), but these relationships were weaker when latitude and longitude were included (Fig. 2, Fig. S1). While climate variables were generally less important than soil variables, their importance varied between models. Mean annual temperature was the most important climate variable when spatial covariates were not included, while cloud frequency and maximum cumulative water deficit were more important climate variables in the GAM with spatial covariates (Fig. 2). GAMs modelled positive relationships with wind speed and negative relationships with lightning frequency, but these relationships were less evident in random forest models (Fig. S1). Topography, height above nearest drainage and rock depth had limited effects in all models (Fig. 2).
Global Shapley additive explanations (SHAP values) have been calculated for random forest (RF, blue) and generalised additive models (GAM, green) fitted with either just environmental or spatial variables (env/ spatial, open circles) or to both environmental and spatial variables (both, filled circles). Higher SHAP values indicate a greater contribution of a feature to model predictions. Variables are ordered on the x-axis based on their mean SHAP value across models.
The west-to-east gradient in Amazonia of increasing wood density was evident in predictions of spatial patterns in wood density from all models, with the highest predicted values along the East and Central Amazon basin and in the Guiana Shield (Fig. 3). Some differences were evident between models (Fig.S2, S3), for example the GAM trained on environmental explanatory variables predicted a region of high wood density in the south-east of Brazil’s Amazonas state (Fig. S2). All models predicted high wood density in seasonally dry tropical forests to the south and east of the Amazon Basin, but lower values were predicted in northern South America. As well as capturing broad-scale gradients, models predicted substantial local-scale variation in wood density, which are likely to reflect local variation in soil characteristics (Fig S4). However, when comparing observed and predicted wood density values in plots, it was notable that models predicted a more restricted range of wood density values (Fig S5). Uncertainty in predictions between models varied spatially, with greater uncertainty in Andean montane forests, southern Venezuela, and the south-east fringes of the Amazon basin, and strong agreement between models in part of Western Amazonia and the Guiana Shield (Fig. S3).
Ensemble predictions averaging the six input models are shown. Predictions for individual models are presented in Fig. S2, with inter-model uncertainty in Fig. S3. Forested areas outside the area of applicability of model predictions are shown in grey – see Fig. S2 for model predictions without this exclusion, and Fig. S7 for alternative definitions of areas of model applicability.
Performance of models
When tested using cross-validation, predicted values of wood density were positively correlated with observed values for all modelling methods (r = 0.62 – 0.75, coefficient of determination = 0.37–0.57 Table 2), with mean prediction errors (i.e. the difference between observed and predicted stand-level wood density values) of 0.049-0.057 g cm−3 (Table 2). These prediction errors were lower than would be obtained by comparing the overall mean wood density in our dataset with observed values (prediction error = 0.105 g cm−3). When model predictions were tested on independent spatial clusters (e.g. fitting models without dry forests, and testing predictions on dry forests), correlations with observed values were lower but remained positive on average (r = 0.272 for ensemble, Table 2), and prediction errors were larger (0.068 g cm-3 for ensemble, Table 2) but on average were still lower than if an overall mean had been used (Table 2). However, negative coefficients of determination for models tested on independent clusters (Table 2) indicates that differences between model predictions and observed values were larger than if the mean for that region was used.
Using the database mean value for wood density to estimate plot-level carbon stocks led to a median error of 8.4% (interquartile range = 4.0 – 14.0%), while using the observed plot-level mean wood density value resulted in a median error of 0.8% (interquartile range = 0.4 – 1.7%). Using the ensemble mean of model predictions resulted in a median error of 4.5% (interquartile range = 2.2-8.7%), with individual models having median errors between 4.5% and 5.4%. Our model predictions therefore lie close to midway between the naïve scenario with no knowledge of spatial variation in wood density and the best-case scenario with perfect locally-based knowledge of spatial variation in wood density.
Discussion
We assembled an unprecedented dataset of variation in wood density within and across the biomes of Earth’s most forested and tree-diverse continent, and employ multiple methods to relate wood density to environmental and spatial variables to produce predictions of wood density and associate error estimates in mature forests across tropical and sub-tropical South America. These provide important new products for the remote sensing community, approximately halving errors in carbon stock estimates compared to having a single mean value of wood density. Additionally, our work advances the understanding of spatial variation in wood density by (1) mapping fine-scale variation, which field data shows is substantial11,18 but which is not captured in previous analyses using spatial interpolation of plot data17,40, (2) extending predictions of wood density across Andean, seasonally dry and Atlantic forests, and (3) establishing that previously described gradients in wood density across Amazonia [e.g. 41] largely hold in this substantially larger dataset.
Patterns and drivers of spatial variation in wood density
Previous studies have described a gradient in wood density across Amazonia, with the highest wood density in forests in the Guiana Shield, and lower values in western Amazonia17,40,41. While our results largely support this pattern we find that wood density in parts of Eastern and Central Amazonia are similar or higher to the Guiana Shield. Our results are also consistent with previous studies reporting lower wood density in montane forests18,42, and indicate that while seasonally dry tropical forests on average have high wood density, dry forests can have amongst the highest or very lowest wood densities of all South American forests.
Despite the generally higher observed and predicted wood density in seasonally dry tropical forests, we did not find strong relationships between dry season water availability, temperature or cloud cover and wood density, so do not find clear support for the hypothesised effects of water limitation leading to higher wood density. This contrasts to previous studies which found negative relationships between wood density and precipitation within Amazonia39 and amongst tree species across the Americas32. It is possible that some effects of these climate variables have been attributed to latitude and longitude in our models, but this does not explain the lack of clear relationships in models without spatial variables. Furthermore, by simply considering observed wood density values, it is evident that species in forests experiencing substantial water limitation can have very high or very low wood density (Fig. S1), possibly reflecting the diversity of strategies trees have for coping with water limitation, which can result in high wood density (high vessel density) or low wood density (water storage in tissues)43. Wood density tends to decrease with succession in dry forests, with high wood density species facilitating the establishment of other species44. While all our plots were in mature forest, plots are subject to natural disturbance events which is expected to lead to substantial variation in wood density.
There was some support for wood density being correlated with factors associated with more frequent disturbances. Soil texture was identified by models (especially GAMs) as important for predicting wood density, which is consistent with the mechanism proposed by Quesada et al.39 whereby less stable soils lead to more frequent disturbances which promote low wood density species. We note that the measures of soil properties available in gridded datasets are imperfect, and that evaluation using in situ soil data would add stronger support for this hypothesis, as well as for the relationships with soil chemistry variables (CEC and pH) identified here. Wood density also tended to be lower where lightning was more frequent, which would be consistent with lightning disturbances promoting forest turnover, but more observations are needed from forests experiencing frequent lightning, especially as this negative effect of lightning was sensitive to subsampling data (Fig. S6).
Performance and applicability of model predictions
Despite the size of our dataset, it still represents a small fraction of the forested extent of tropical South America. We assessed the area we could validly make predictions to in three ways. Firstly, we identified areas where model predictions were especially sensitive to subsampling data. Secondly, we identified areas with explanatory variable values outside the range seen in our data. Thirdly, we calculated a multivariate dissimilarity index describing environmental and spatial variables, and calculated the area of applicability45 of our models based on the dissimilarity index values of our different training and testing datasets (Fig. S7). These mostly indicate that our models are applicable to the majority of tropical South American forests, but should be more cautiously applied to higher-elevation Andean forests. However, some dry forest areas and parts of lowland Amazonia had dissimilarity indices higher than typically observed between non-spatial cross-validation folds, meaning that non-spatial cross-validation metrics should be seen as an upper bound rather than central estimate of model performance in these areas (Fig. S7).
Model performance was substantially lower when tested using spatial cross-validation (i.e. leaving a region out of model training, and using that for model testing). Indeed, while correlation coefficients remained positive, negative coefficient of variation values indicate that models were systematically over or underpredicting wood density, leading to greater prediction errors than if the true regional mean was used (although there were still substantial improvements over using the dataset mean). This spatial cross-validation is expected to represent a lower bound of model performance46 as it requires predictions to be extrapolated beyond the range of training data, whereas 97% of tropical South American forests had dissimilarity index values of one or less (indicating that the dissimilarity to the most similar training data point is less than or equal to the mean dissimilarity of points within the training dataset).
While models substantially improved predictions of wood density compared to just using a mean value across the dataset, improvements in models with environmental explanatory variables compared to those with just spatial explanatory variables was limited. Spatially structured explanatory variables can show good predictive skill despite having no causal effect47, and both GAMs and random forests were capable of fitting complex relationships between wood density and latitude and longitude. When environmental variables were also included, the complexity of relationships with spatial variables reduced (Fig. S1). This indicates that spatial-only models captured environmental variation that was taken up by environmental variables when both types were included in models. In models with both environmental and spatial variables, latitude and longitude could still capture gradients caused by unmodelled environmental variables (e.g. soil phosphorus, which was not available as a fine-scale gridded variable), or capture gradients due to biogeographic history. In the former case, relationships may not extrapolate as spatial coordinates may not prove a reliable proxy beyond the range of the training data, while in the latter case spatial coordinates are more closely tied to a causal mechanism. The relative superiority of models with both spatial and environmental variables compared to those with spatial variables alone was greater when evaluating models on spatially distinct training data (Table 2), which would be consistent with environmental variables better capturing causal mechanisms.
Previous studies have modelled relationships between environmental variables and wood density at larger (all Americas32,) or smaller (Amazonia alone39,) scales than this study. Larger spatial extents, and hence larger environmental gradients, means it is more likely that environmental response curves are fully characterised48 but increases the chances of spatial nonstationary and therefore missing regional relationships49. We explored this by training models separately for each spatial region, and comparing predictions to models trained to the whole dataset. Predictions of regionally and dataset-wide trained models were similar (Fig. S5), which indicates that our models were sufficiently flexible to capture regional patterns.
We used gridded climate and soil data, which would have much greater measurement error than in situ values. This is expected to lead to regression dilution48,49, where relationships with climate and soil variables are weaker than they would be if measured in situ. Comparisons of relationships with soil variables with previous studies using the smaller number of plots with in situ soil measurements39 should therefore be made cautiously. It is also important to note that analyses relate to wood density treating wood density as a species-level attribute. However, wood density also varies within species along environmental gradients50,51 and with stand characteristics52. In situ measurements of wood density are sparse, so treating it as a species-level variable was the only feasible approach for a study of this scale, but patterns could be further refined by consideration of intra-specific variation.
It is important to note that our predictions are for mature, closed canopy forests, so should not be used for secondary forests. Wood density is expected to be lower in secondary forests2, although in some seasonally dry and montane forests wood density can decline with succession44,53. These differences in trajectories of wood density between forest types may be explained by differing successional mechanisms44, so we may expect large-scale spatial patterns in secondary forests to differ from the old-growth forest patterns described here.
We provide ensemble averaged predictions (Fig. 3) alongside predictions of individual models (Fig. S2), inter-model uncertainty (Fig. S3) and their spatial applicability (Fig. S7). Using these estimates of spatial variation in wood density is anticipated to approximately halve errors in carbon stock estimates compared to a naïve scenario where only the mean wood density is known. While there is potential to improve models further to reduce prediction errors, some errors will remain even with perfect knowledge of spatial variation in wood density, as it would still not be known which trees within a plot have higher or lower wood density. These remaining errors represent data that can only be obtained with ground-based field surveys to identify and measure every tree in a plot. In all, while our analysis reveals some of the challenges of high-fidelity biomass mapping in species rich forests it substantially advances the spatial extent, granularity and environmental range of tropical American forest wood density measurement and prediction. Our findings and maps will contribute to better remote sensing-based estimates of biomass carbon stocks across tropical South America.
Methods
Plot selection and field sampling
We identified and measured trees in forest inventory plots in tropical and sub-tropical South America. These plots were established and maintained by networks of researchers (RAINFOR, DBTV, COL-TREE, TROBIT, DRYFLOR, ATDN, PPBIO, FATE, RAS, MonANPeru, Nordeste, sANDES, SECO, BDFFP) using shared protocols54, and are curated and stored in the online ForestPlots.net database6,55. These networks and ForestPlots.net aim to promote equitable research collaborations in tropical ecology, and the development of this study followed the ForestPlots code of conduct (https://forestplots.net/en/join-forestplots/code-of-conduct). Plots for this study were selected based on being in mature, structurally intact and closed canopy forests (i.e. excluding secondary forests, forests with a known history of logging or burning, and savannah formations). While no restrictions in terms of soil type, edaphic factors or elevation were applied, plots were filtered to exclude those in which fewer than 80% of stems were identified to genus level, giving a dataset of 981 plots (Fig. 1). For multi-census plots, we use data for the first census for comparability with single-census plots and because a higher proportion of stems were identified to species in this census in >80% of instances. Plots were predominantly established following standardised RAINFOR protocols54 although plots varied in area (0.04 to 25 ha, mean area = 0.76 ha). In each, the diameter of all stems ≥10cm were measured at breast height (1.3m) or above buttresses or other deformities. Stems were identified by botanists to species level where possible (85.1% of stems identified to species and 95.4% to genus).
Wood density metrics
The wood density of each stem in our dataset was estimated by cross-referencing the taxonomic identify of each tree with a database of wood density values56. We note that this approach does not capture intra-specific variation in wood density57, and that even mean wood density is missing for many species56. Stems were matched to the mean species-level value where possible (46.4% of stems), followed by genus-level (38.6%), family-level (11.0%) and plot-level mean values (4.0%), with taxonomic matches performed using the getWoodDensity function in the BIOMASS R package58.
Stand-level wood density can be summarised from these tree-level values in a variety of different ways, each requiring increasing amount of information about the composition of the stand. Firstly, wood density can be calculated as the mean value across all taxa present in a stand (WD1). For this, we took the arithmetic mean of wood density for each taxonomic entity (i.e. the set of fully identified species, genera with indeterminate species identifications, families with indeterminate genus, and fully unidentified stems, with taxon-level wood density obtained as described above). This discounts information about taxon abundance, simply considering which taxa are present. Secondly, wood density can be calculated as the abundance weighted mean of taxa present in the stand (i.e. the mean wood density of all stems in the stand, WD2). For this, we took the arithmetic mean of wood density across all stems in the plot. This includes information about abundance, but discounts information about stem size. Thirdly, the basal-area weighted mean wood density can be calculated, which gives more weight to stems that account for a larger proportion of stand basal area (WD3). For this, we took the basal-area weighted mean of wood density of all stems in the plot. This therefore includes information about the size of stems as well as their abundance. We calculated all three metrics but only present results for WD3 (basal-area weighted wood density). This incorporates the most information about stand composition and is the most directly linked to aboveground biomass; all three metrics were strongly correlated (Fig. S8).
Environmental variables
We obtained climate and soil variables that were hypothesised to relate to spatial variation in wood density (Table 1) at 1km resolution. Mean annual temperature and total annual precipitation were obtained from Worldclim version 259. To represent seasonal drought stress, we calculated maximum cumulative water deficit (MCWD) as the cumulative balance between monthly precipitation (from Worldclim59) and potential evapotranspiration (from TerraClimate60,). For each plot, we calculated the balance between precipitation and potential evapotranspiration in the wettest month, and then calculated the water balance in subsequent months as the difference between precipitation and potential evapotranspiration in that month plus the cumulative water balance, if negative, in the preceding month. The minimum value of this metric across the year, representing the greatest cumulative water deficit, was obtained for each plot. Cloud variables were obtained from Wilson and Jetz61, and represent the proportion of Modis passes at each ___location where cloud was present. Soil variables were obtained from the SoilGrids database62. In situ soil data would be preferable for quantifying relationships between wood density and soil variables [e.g.39], but could not be used because of the need for a dataset with complete spatial coverage for extrapolating wood density values. We used soil cation exchange capacity (CEC) as a measure of soil fertility and extracted soil pH, depth to rock horizon, and the percentage of sand, silt and clay. The latter three variables were simplified into two variables as Texture1 = ln(Sand/Clay) and Texture2 = ln(Silt/Clay). CEC was chosen as a measure of soil fertility as it is available across the study area, but we note that it is not a perfect proxy as it includes saturation with H and Al. We included an interaction between CEC and pH to account for this (see data analysis), and also explored the sensitivity of our results to using an Amazon-only soil base cation concentration dataset63; predicted wood density using CEC and soil base cation concentration were strongly correlated (r = 0.97-0.99 across models). Topography was quantified from the hole-filled 90m resolution SRTM64 as mean slope in a 200m diameter buffer around plot locations and rugosity as the standard deviation of elevations in this buffer. Height above nearest drainage (HAND) was obtained from65. Topography metrics were processed in Google Earth Engine66, other metrics were processed in Rv4.2.267.
Data analysis
Statistical analysis was motivated by the goal of prediction68. We constructed models with three sets of explanatory variables. Firstly, wood density was modelled as a function of just longitude and latitude, providing a spatial interpolation of the data. Secondly, wood density was modelled as a function of environmental variables alone. These variables have potential causal effects on wood density, but may also capture variation due to unmodelled spatial gradients. Finally, we modelled wood density as a function of both environmental variables and spatial coordinates. This latter approach potentially allows spatial gradients not included in the environmental explanatory variable set to be captured by the spatial variables, and was chosen over methods that account for non-independence of model residuals, which may be preferable if our goal was inference, as our approach allows spatial effects to be included in model predictions.
We related wood density to these explanatory variables using random forests and generalised additive models, with both approaches chosen as they can capture complex non-linear relationships between response and explanatory variables. We checked for collinearity between explanatory variables prior to training models, and found strong corelations (|r | >0.7) between slope and rugosity, slope and HAND, and between mean annual precipitation and MCWD, and therefore discarded one of each pair (slope and mean annual precipitation) from subsequent analysis. Following removal of these variables, variance inflation factors for environmental variables were all less than four.
Random forests were constructed using the randomForest R package69. Hyperparameters for the number of trees to construct and the number of variables to sample at each split were selected by trying each combination of hyperparameter pairs (2-8 variables to try, and 100 to 1000 trees in increments of 100), and selecting the combination with the lowest mean square error (800 trees, three variables tried at each split).
Generalised additive models (GAMs) were constructed using the mgcv R package70. The complexity of non-linear relationships in GAMs was selected using restricted maximum likelihood. The basis dimension, which sets the maximum complexity of smooth terms, was set to nine for environmental variables. While this allows more complex non-linear relationships than might be theoretically expected, it ensures the function space in the realm of ecologically expected relationships (e.g, unimodal) is not overly constrained. Latitude and longitude were modelled as a single interacting smooth term with a basis dimension of 50. GAMs were also fitted with a penalty term that selects variables out of the model71, but these performed worse at predicting wood density than models without the penalty term, so were not used further. Residual spatial autocorrelation was not evident in any of the models (Fig. S9). Variable importance was assessed using approximate Shapley additive explanations values, which provide additive contributions of each feature to each observation72. Values were calculated using the fastshap R package73 and summarised across the dataset to give the global importance of each variable.
We assessed model performance using both spatial and non-spatial cross-validation. These are expected to provide lower and upper bounds of predictive performance respectively46. For non-spatial cross-validation, data were divided into ten approximately equal sized sets, with each set left out of model training in turn and used as independent test data. A problem with this validation method is that calibration and validation data, while different, may not be truly independent because of spatial autocorrelation, so model predictive performance may be overestimated. We therefore also applied a more stringent validation procedure where data were split into spatial clusters, and one cluster left out in turn from model fitting to be used for validation. We assigned plots to one of six biogeographic regions (adapted from67,68). These were North-west lowland forests, South-west lowland forests, East-central Amazon, Guiana Shield, Brazilian Shield, with remaining plots (Atlantic Forest, montane forests > 1200 m asl, seasonally dry forests with < 1000 mm precipitation per year) grouped together into a sixth region. This method ensures that test data are truly independent of training data but is likely to be overly harsh as it truncates environmental gradients meaning that models are forced to extrapolate into novel environmental space. Model performance was assessed using three metrics; the square-root of the mean-square error between predicted and observed values (RMSE), the correlation coefficient between predicted and observed values, and the coefficient of determination (1-(residual sum of squares/ total sum of squares)). These were calculated for each model, and compared to a null scenario where predicted wood density values were randomly drawn from the distribution of observed values.
To assess the consequences of imperfect wood density estimates for estimates of carbon stocks, we estimated aboveground carbon stocks in each plot using (1) taxonomically matched wood density of each stem (i.e. the data available from field surveys), (2) the observed mean wood density for the plot (i.e. the data that would be available if spatial variation in stand wood density could be estimated perfectly), (3) predicted mean wood density from the different models, and (4) the dataset mean wood density (i.e. a naïve position with no knowledge of spatial variation in wood density). The aboveground biomass of each stem was estimated using the Chave et al.13 allometric equation applied to measured diameters, the aforementioned wood density values, with height estimated based on relationships between environmental stress and height-diameter allometries13. Calculations were conducted using the BIOMASS R package58. Aboveground biomass estimates were converted to carbon using a carbon fraction of 0.45674.
Mapping wood density
GAM and random forest models were used to predict wood density based on the environmental conditions and latitude and longitude of 1 km2 grid-cells in tropical South America. Predictions were masked to areas indicated as forest in GLC 200075. Environmental variables for each grid-cell were obtained as described above (e.g. for MCWD, we extracted monthly precipitation and evapotranspiration in each 1km grid-cell, and then calculated the cumulative water balance from the wettest month as described above), except for rugosity which was obtained at 1 km resolution from GTOPO3076.
We evaluated the spatial applicability of model predictions in three ways (Fig. S7). Firstly, we took 1000 samples (without replacement) of half the dataset, refitted models, and predicted wood density for the entire dataset. We could therefore calculate the standard deviation for each observation in our data. We then related this standard deviation to each explanatory variable using locally-weighted polynomial regression. Taking a standard deviation of 0.05 as an arbitrary threshold for indicating high uncertainty, this allowed us to map areas where predictions were less well constrained (i.e. explanatory variables had values where they were sensitive to subsampling). Secondly, we identified areas with explanatory variables outside the range seen in our training data (i.e. where models are extrapolating to novel absolute conditions). Thirdly, we calculated a multivariate dissimilarity index (DI) following45. This method firstly calculates the Euclidean distance between pairs of locations based on their explanatory variables (which have first been scaled for comparability); we did not weight variables by their importance as we wanted the metric to be applicable across different models. The DI is then calculated as the minimum distance to an observation in the training data, divided by the mean distance between training data points. Values of more than one thus indicate points that are more dissimilar to the nearest training data point than the average dissimilarity amongst training data points. We followed Meyer and Pebsma’s45 method for defining binary threshold to denote the area of applicability (i.e. the zone where model validation metrics are expected to give a true measure of performance), noting that the threshold definition is somewhat arbitrary. This approach calculates the DI between each data point and the nearest data point that is not in the same cross-validation fold, and then uses 1.5 times the interquartile range as the upper threshold DI value. This was calculated for both the spatial and non-spatial cross validation approaches.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
The wood density data generated in the study and used to build models of spatial variation in wood density are deposited in https://doi.org/10.5521/forestplots.net/2024_4. Predictions of wood density along with measures of uncertainty and areas of applicability are deposited in https://doi.org/10.6084/m9.figshare.27118437. Data sources for climate, soil and topography variables used in analyses are listed in Table 1, and extracted values for each plot deposited in https://doi.org/10.5521/forestplots.net/2024_4. Forest cover data are from the Global Land Cover 2000 database [82, https://forobs.jrc.ec.europa.eu/glc2000]. Source data are provided with this paper.
Code availability
The analysis code is available at https://doi.org/10.5521/forestplots.net/2024_4.
References
Marvin, D. C. & Asner, G. P. Spatially explicit analysis of field inventories for national forest carbon monitoring. Carbon Balance Manag. 11, 9 (2016).
Berenguer, E. et al. Seeing the woods through the saplings: Using wood density to assess the recovery of human-modified Amazonian forests. J. Ecol. 106, 2190–2203 (2018).
Poorter, L. et al. Functional recovery of secondary tropical forests. Proc. Natl Acad. Sci. 118, e2003405118 (2021).
Bustamante, M. M. C. et al. Toward an integrated monitoring framework to assess the effects of tropical forest degradation and recovery on carbon stocks and biodiversity. Glob. Change Biol. 22, 92–109 (2016).
Hubau, W. et al. Asynchronous carbon sink saturation in African and Amazonian tropical forests. Nature 579, 80–87 (2020).
ForestPlots.net et al. Taking the pulse of Earth’s tropical forests using networks of highly distributed plots. Biol. Conserv. 260, 108849 (2021).
Duncanson, L. et al. Aboveground biomass density models for NASA’s Global Ecosystem Dynamics Investigation (GEDI) lidar mission. Remote Sens. Environ. 270, 112845 (2022).
Avitabile, V. et al. An integrated pan-tropical biomass map using multiple reference datasets. Glob. Change Biol. 22, 1406–1420 (2016).
Santoro, M. et al. The global forest above-ground biomass pool for 2010 estimated from high-resolution satellite observations. Earth Syst. Sci. Data, 13, 3927–3950 (2021).
Araza, A. et al. A comprehensive framework for assessing the accuracy and uncertainty of global above-ground biomass maps. Remote Sens. Environ. 272, 112917 (2022).
Phillips, O. L. et al. Species Matter: Wood Density Influences Tropical Forest Biomass at Multiple Scales. Surv. Geophys. 40, 913–935 (2019).
Baker, T. R. et al. Maximising Synergy among Tropical Plant Systematists, Ecologists, and Evolutionary Biologists. Trends Ecol. Evol. 32, 258–267 (2017).
Chave, J. et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 20, 3177–3190 (2014).
Jucker, T. et al. Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Glob. Change Biol. 23, 177–190 (2017).
Draper, F. C. et al. Imaging spectroscopy predicts variable distance decay across contrasting Amazonian tree communities. J. Ecol. 107, 696–710 (2019).
Wagner, F. H. et al. Using the U-net convolutional network to map forest types and disturbance in the Atlantic rainforest with very high resolution images. Remote Sens. Ecol. Conserv. 5, 360–375 (2019).
Mitchard, E. T. A. et al. Markedly divergent estimates of Amazon forest carbon density from ground plots and satellites. Glob. Ecol. Biogeogr. 23, 935–946 (2014).
Sæbø, J. S. et al. Ignoring variation in wood density drives substantial bias in biomass estimates across spatial scales. Environ. Res. Lett. 17, 054002 (2022).
Sullivan, M. J. P. et al. Diversity and carbon storage across the tropical forest biome. Sci. Rep. 7, 39102 (2017).
Duque, A. et al. Mature Andean forests as globally important carbon sinks and future carbon refuges. Nature. Communications 12, 2138 (2021).
Pan, Y. et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 333, 988–993 (2011).
Brienen, R. J. W. et al. Long-term decline of the Amazon carbon sink. Nature 519, 344–348 (2015).
Gatti, L. V. et al. Amazonia as a carbon source linked to deforestation and climate change. Nature 595, 388–393 (2021).
Cazzolla Gatti, R. et al. The number of tree species on Earth. Proc. Natl Acad. Sci. 119, e2115329119 (2022).
Ter Steege, H. et al. Biased-corrected richness estimates for the Amazonian tree flora. Sci. Rep. 10, 10130 (2020).
Oliveira-Filho, A. T. et al. On the floristic identity of Amazonian vegetation types. Biotropica 53, 767–777 (2021).
Silva-Souza, K. J. P. & Souza, A. F. Woody plant subregions of the Amazon forest. J. Ecol. 108, 2321–2335 (2020).
Dryflor et al. Plant diversity patterns in neotropical dry forests and their conservation implications. Science 353, 1383–1387 (2016).
Chao, K.-J. et al. Growth and wood density predict tree mortality in Amazon forests. J. Ecol. 96, 281–292 (2008).
Esquivel-Muelbert, A. et al. Tree mode of death and mortality risk factors across Amazon forests. Nature. Communications 11, 5515 (2020).
King, D. A. et al. The role of wood density and stem support costs in the growth and mortality of tropical trees. J. Ecol. 94, 670–680 (2006).
Chave, J. et al. Towards a worldwide wood economics spectrum. Ecol. Lett. 12, 351–366 (2009).
Reis, S. M. et al. Climate and crown damage drive tree mortality in southern Amazonian edge forests. J. Ecol. 110, 876–888 (2022).
Larjavaara, M. & Muller-Landau, H. C. Still rethinking the value of high wood density. Am. J. Bot. 99, 165–168 (2012).
Liang, X. et al. Wood density predicts mortality threshold for diverse trees. N. Phytol. 229, 3053–3057 (2021).
Markesteijn, L. et al. Ecological differentiation in xylem cavitation resistance is associated with stem and leaf structural traits. Plant. Cell Environ. 34, 137–148 (2011).
Serra-Maluquer, X. et al. Wood density and hydraulic traits influence species’ growth response to drought across biomes. Global Change Biology, 2022.
Janssen, T. A. J. et al. Wood allocation trade-offs between fiber wall, fiber lumen, and axial parenchyma drive drought resistance in neotropical trees. Plant, Cell Environ. 43, 965–980 (2020).
Quesada, C. A. et al. Basin-wide variations in Amazon forest structure and function are mediated by both soils and climate. Biogeosciences 9, 2203–2246 (2012).
Ter Steege, H. et al. Continental-scale patterns of canopy tree composition and function across Amazonia. Nature 443, 444–447 (2006).
Baker, T. R. et al. Variation in wood density determines spatial patterns inAmazonian forest biomass. Glob. Change Biol. 10, 545–562 (2004).
Blundo, C. et al. Forest biomass stocks and dynamics across the subtropical Andes. Biotropica 53, 170–178 (2021).
De Lima, A. L. A. et al. Do the phenology and functional stem attributes of woody species allow for the identification of functional groups in the semiarid region of Brazil? Trees 26, 1605–1616 (2012).
Poorter, L. et al. Wet and dry tropical forests show opposite successional pathways in wood density but converge over time. Nat. Ecol. Evol. 3, 928–934 (2019).
Meyer, H. & Pebesma, E. Predicting into unknown space? Estimating the area of applicability of spatial prediction models. Methods Ecol. Evol. 12, 1620–1633 (2021).
Wadoux, A. M. J. C. et al. Spatial cross-validation is not the right way to evaluate map accuracy. Ecol. Model. 457, 109692 (2021).
Fourcade, Y. & Besnard, A. G. and J. Secondi, Paintings predict the distribution of species, or the challenge of selecting environmental predictors and evaluation statistics. Glob. Ecol. Biogeogr. 27, 245–256 (2018).
Barbet-Massin, M., Thuiller, W. & Jiguet, F. How much do we overestimate future local extinction rates when restricting the range of occurrence data in climate suitability models? Ecography 33, 878–886 (2010).
Pease, B. S., Pacifici, K. & Kays, R. Exploring spatial nonstationarity for four mammal species reveals regional variation in environmental relationships. Ecosphere 13, e4166 (2022).
Damgaard, C. Measurement Uncertainty in Ecological and Environmental Models. Trends Ecol. Evol. 35, 871–873 (2020).
McInerny, G. J. & Purves, D. W. Fine‐scale environmental variation in species distribution modelling: regression dilution, latent variables and neighbourly advice. Methods Ecol. Evol. 2, 248–257 (2011).
De Oliveira Ivanka, R. et al. Effect of tree spacing on growth and wood density of 38-year-old Cariniana legalis trees in Brazil. South. Forests: a J. For. Sci. 80, 311–318 (2018).
Castillo-Figueroa, D., González-Melo, A. & Posada, J. M. Wood density is related to aboveground biomass and productivity along a successional gradient in upper Andean tropical forests. Front Plant Sci. 14, 1276424 (2023).
Phillips, O. et al. RAINFOR field manual for plot establishment and remeasurement. The Royal Society, Leeds, UK, 2016.
Lopez-Gonzalez, G. et al. ForestPlots.net Database. www.forestplots.net. Date of extraction 23/03/2023. 2009.
Zanne, A. E. et al. Towards a worldwide wood economics spectrum. Dryad Digital Repository. Dryad Digital Repository: Global wood density database, 2009.
Muller-Landau, H. C. Interspecific and Inter-site Variation in Wood Specific Gravity of Tropical Trees. Biotropica 36, 20–32 (2004).
Réjou‐Méchain, M. et al. biomass: an r package for estimating above‐ground biomass and its uncertainty in tropical forests. Methods Ecol. Evol. 8, 1163–1167 (2017).
Fick, S. E. & Hijmans, R. J. WorldClim 2: new 1‐km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 37, 4302–4315 (2017).
Abatzoglou, J. T. et al. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958–2015. Sci. Data 5, 170191 (2018).
Wilson, A. M. & Jetz, W. Remotely sensed high-resolution global cloud dynamics for predicting ecosystem and biodiversity distributions. PLoS Biol. 14, e1002415 (2016).
Hengl, T. et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS one 12, e0169748 (2017).
Zuquim, G. et al. Introducing a map of soil base cation concentration, an ecologically relevant GIS-layer for Amazonian forests. Geoderma Regional 33, e00645 (2023).
Jarvis, A. et al. Hole-filled SRTM for the globe Version 4. available from the CGIAR-CSI SRTM 90m Database http://srtm.csi.cgiar.org.
Donchyts, G. et al. Global 30m height above the nearest drainage. Proceedings of the EGU General Assembly, 2016.
Gorelick, N. et al. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 202, 18–27 (2017).
R. Core Team, R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/ 2022.
Tredennick, A. T. et al. A practical guide to selecting models for exploration, inference, and prediction in ecology. Ecology 102, e03336 (2021).
Liaw, A. & Wiener, M. Classification and regression by randomForest. R. N. 2, 18–22 (2002).
Wood, S., Generalized Additive Models: An Introduction with R. 2nd Edition ed. 2017: Chapman and Hall.
Marra, G. & Wood, S. N. Practical variable selection for generalized additive models. Comput. Stat. Data Anal. 55, 2372–2387 (2011).
Štrumbelj, E. & Kononenko, I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst. 41, 647–665 (2014).
Greenwell, B., fastshap: Fast Approximate Shapley Values (R package version 0.0. 7). 2021.
Martin, A. R., Doraisami, M. & Thomas, S. C. Global patterns in wood carbon concentration across the world’s trees and forests. Nat. Geosci. 11, 915–920 (2018).
Bartholomé, E. & Belward, A. S. GLC2000: a new approach to global land cover mapping from Earth observation data. Int. J. Remote Sens. 26, 1959–1977 (2005).
Earth Resources Observation and Science Center, U.S. Geological Survey, and U.S.D.o.t. Interior, USGS 30 ARC-second Global Elevation Data, GTOPO30. 1997, Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory: Boulder, CO.
Reis, C. R. et al. Forest disturbance and growth processes are reflected in the geographical distribution of large canopy gaps across the Brazilian Amazon. J. Ecol. 110, 2971–2983 (2022).
Gora, E. M. et al. Effects of lightning on trees: A predictive model based on in situ electrical resistivity. Ecol. Evol. 7, 8523–8534 (2017).
Albrecht, R. I. et al. Where Are the Lightning Hotspots on Earth? Bull. Am. Meteorol. Soc. 97, 2051–2068 (2016).
Acknowledgements
This paper is a product of the multiple forest plot networks and their combined records collected over decades and curated at ForestPlots.net. As well as investigators and field leaders included here, we gratefully acknowledge the efforts of several hundred additional botanists, technicians and field assistants who contributed to installation, measurement and identification of trees across South American forests. RAINFOR, PPBio and ForestPlots.net have been supported by numerous people and grants since their inception. For their important contributions to developing the RAINFOR network and its antecedents we are also indebted to Jon Lloyd and Manuel Gloor as well as our late, esteemed colleagues Elisbán Armas, Terry Erwin, Thomas Lovejoy, Alwyn Gentry, Sandra Patiño, Antonio Peña Cruz and Jean-Pierre Veillon. For supporting the networks, we thank the European Research Council (ERC Advanced Grant 291585 – ‘T-FORCES’), the Gordon and Betty Moore Foundation (#1656 ‘RAINFOR’, and ‘MonANPeru’), the European Union’s Fifth, Sixth and Seventh Framework Programme (EVK2-CT-1999-00023 – ‘CARBONSINK-LBA’, 283080 – ‘GEOCARBON’, 282664 – ‘AMAZALERT), the Natural Environment Research Council (NE/ D005590/1 – ‘TROBIT’, NE/F005806/1 – ‘AMAZONICA’, E/M0022021/1 - ‘PPFOR’), several NERC Urgency and New Investigators Grants, the NERC/State of São Paulo Research Foundation (FAPESP) consortium grants ‘BIO-RED’ (NE/N012542/1), ‘ECOFOR’ (NE/K016431/1, 2012/51872-5, 2012/51509-8), ‘ARBOLES’ (NE/S011811/1, FAPESP 2018/15001-6), ‘SEOSAW’ (NE/P008755/1), ‘SECO’ (NE/T01279X/1), Brazilian National Research Council (PELD/CNPq 403710/2012-0), the Royal Society (University Research Fellowships and Global challenges Awards) (ICA/R1/180100 - ‘FORAMA’), the National Geographic Society, US National Science Foundation (DEB 1754647) and Colombia’s Colciencias. We thank the National Council for Science and Technology Development of Brazil (CNPq) for support to the Cerrado/Amazonia Transition Long-Term Ecology Project (PELD/441244/2016-5), the PPBio Phytogeography of Amazonia/Cerrado Transition Project (CNPq/PPBio/457602/2012-0), PELD-RAS (CNPq, Process 441659/2016-0), RESFLORA (Process 420254/2018-8), Synergize (Process 442354/2019-3), the Empresa Brasileira de Pesquisa Agropecuária – Embrapa (SEG: 02.08.06.005.00), the Fundação de Amparo à Pesquisa do Estado de São Paulo – FAPESP (2012/51509-8 and 2012/51872-5), the Goiás Research Foundation (FAPEG/PELD: 2017/10267000329) the EcoSpace Project (CNPq 459941/2014-3), PELD 441572/2020-0, the FATE project (03/12595-7) and several PVE and Productivity Grants. We also thank the “Investissement d’Avenir” program (CEBA, ref. ANR-10LABX-25-01), the São Paulo Research Foundation (FAPESP 03/12595-7, 2016/21043-8) and the Sustainable Landscapes Brazil Project (through Brazilian Agricultural Research Corporation (EMBRAPA), the US Forest Service, USAID, and the US Department of State) for supporting plot inventories in the Atlantic Forest sites in Sao Paulo, Brazil. We thank to the National Council for Technological and Scientific Development (CNPq) for the financial support of the PELD project (441244/2016-5, 441572/2020-0) and FAPEMAT (0346321/2021). We thank Reserva Particular do Patrimônio Natural Serra das Almas for supporting our research at the reserve. This paper also includes plots where recensuses and data assimilation were funded by SECO (NE/T01279X/1), and plots established by Darwin Initiative funded project 20-021, NERC-Newton-FAPESP project Nordeste (NE/N01247X/1; NE/N012550/1) and the USAID funded Partnerships for Enhanced Engagement in Research project. This manuscript is an output of ForestPlots.net Research Project 75A. “Mapping LATAM Forest Wood Density”, which is part of the NERC-FAPESP funded project ARBOLES (NE/S011811/1). ForestPlots.net is a meta-network and cyber-initiative developed at the University of Leeds that unites permanent plot records and supports tropical forest scientists. We acknowledge the contributions of the ForestPlots.net Collaboration and Data Request Committee (B.S.M., E.N.H.C., O.L.P., T.R.B., B. Sonké, C. Ewango, J. Muledi, S.L.L., L. Qie) for facilitating this project and associated data management. The development of ForestPlots.net and curation of data has been funded by several grants including NE/B503384/1, NE/N012542/1 - ‘BIO-RED’, ERC Advanced Grant 291585 - ‘T-FORCES’, NE/F005806/1 - ‘AMAZONICA’, NE/N004655/1 - ‘TREMOR’, NERC New Investigators Awards, the Gordon and Betty Moore Foundation (‘RAINFOR’, ‘MonANPeru’), ERC Starter Grant 758873 -‘TreeMort’, EU Framework 6, a Royal Society University Research Fellowship, and a Leverhulme Trust Research Fellowship. For supporting M.S. we thank NERC (NE/N012542/1 and NE/W003872/1) and the Royal Society (a Royal Society Global Challenges grant “Sensitivity of Tropical Forest Ecosystem Services to Climate Changes”). F.E. was supported by BJT-FAPESPA Program (Process No. 2021/658588) and the Serrapilheira Institute fellowship/FAPESPA (grant number – R-2401–46863), T.F.D. received support from the Brazilian National Council for Scientific and Technological Development (CNPq - 312589/2022-0 Research Productivity Grant) and FAPESP grant 2015/50488-5, G.W.F was supported by APQ 00031-19 FAPEMIG/Renova and J.P. was supported by a CNPq productivity scholarship (312571/2021-6).
Author information
Authors and Affiliations
Contributions
M.J.P.S., O.L.P. and D.G. designed research, M.J.P.S., O.L.P., D.G., E.A., E.A.O., J.A., E.A.D., L.F.A., A.A., L.A., A.A.-M., E.A., L.A., O.A.M.C., F.B., T.B., O.B., C.B., J.B. Jo.B., E.B., L.B., C.B., D.B., F.B. K.M.B., R.J.W.B., I.S.B., B.B., G.C., J.L.C., D.C., M.A.C., W.C., H.C.dL., L.C., S.C.R., S.C., P.R., V.C.M., J.C., F.C., J.A.C., G.C.V., F.l.C., I.C., Ld.C., M.Bd.M., Jd.A.P., G.D., K.D., M.D., M.Md.E.S., T.F.D., A.D., A.Du., C.D.R., F.E., M.M.E.S., A.E.M., W.F.-R., S.F., T.F., G.W.F., J.F., Y.R.F.N., J.C.G.F., K.G.C., R.G., L.H., R.H., E.N.H.C., W.H.H., M.I., C.A.J., M.K., T.K., J.K., B.K., S.G.L., W.F.L., A.L., S.L.L., M.L.D., G.L.G., W.M., Y.M., L.M.A.M., A.G.M., J.L.M.P., B.S.M., B.H.M.J., J.A.M.V., S.M.R., T.M., W.M., A.M.M., P.M., P.S.M., P.M., S.C.M., M.N., D.N., A.D.L., P.N.V., W.L.O., W.P., N.C.P.C., A.P.G., G.P.M., K.Pd.A., M.P.C., P.J.F.P.R., T.P., G.C.P., J.P., N.C.A.P., M.P., A.P.L., L.P., N.C.Ca.S., H.R.-.A., M.R.M., C.R.R., G.R.-T., P.M.S.R., Ds.J.R., T.R.dS., J.R.R.P., G.M.R.M., K.R., Kru., C.R., N.S.R., R.S., R.M.S., T.S., A.S., R.S.B., J.S., M.S.dJ., J.S., M.S., R.C.S., C.S.V., J.O.S., M.S., M.F.S., Y.C.S.-S., P.S., R.M.S.S., T.S., J.T., Ht.S., J.T., R.T., M.T., A.T.-L., W.T., Pvd.H., Md.D.M.V., S.A.V., E.V., J.M.V.C., D.M.Vi., L.J.V., V.A.V., V.W., F.Y.I., P.A.Z., J.A.Z. perfomed research by contributing plot data. M.J.P.S., O.L.P., A.L. and G.C.P. contributed analysis tools. M.J.P.S. analysed data. M.J.P.S. and O.L.P. wrote the first draft, all authors reviewed and edited the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Ze-Xin Fan and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sullivan, M.J.P., Phillips, O.L., Galbraith, D. et al. Variation in wood density across South American tropical forests. Nat Commun 16, 2351 (2025). https://doi.org/10.1038/s41467-025-56175-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-56175-4