Al₂O₃/Al hybrid nanolaminates with superior toughness, strength and ductility

At the turn of the millennium, smaller is stronger was the mainstream motto in the field of mechanical behavior of materials^1,2. Decreasing specimen dimensions in the form of nanowires, thin films and nanoribbons and/or decreasing internal structure sizes through grain and phase size reduction were the roads towards extreme hardness. The core principle was to confine plasticity mechanisms whether controlled by dislocations or twins in crystalline materials or by shear banding activity in amorphous systems^1,2,3,4. Nevertheless, a high strength, as quantified by yield stress σ_y, was almost systematically associated to a low ductility, as quantified by true fracture strain ε_f or uniform elongation ε_u^3,5,6. Many strategies emerged to restore ductility while preserving strength, including bimodal grain size distributions, nanotwins, hybridizing of soft and hard layers^3,6,7,8. The underlying principle often relates to increasing the strain hardening and rate sensitivity to enhance the uniform elongation and to decreasing the presence of defects and weak/brittle interfaces to delay damage nucleation and enhance the fracture strain³.

However, high strength-ductility balance does not necessarily mean high fracture toughness^3,9. Fracture toughness quantifies the resistance to initiation of a pre-existing crack, in terms of critical stress intensity factor K_Ic or critical energy release rate G_Ic for mode I. G_Ic represents the energy per unit area spent in the fracture process zone (FPZ) in which damage and failure mechanisms occur adjacent to the crack tip. One reason for a low G_Ic in materials with high σ_y–ε_f balance is the transition into another failure mechanism in the presence of a sharp crack tip¹⁰. But another major reason is that G_Ic scales as \({\sigma }_{c}\times {h}_{0}\times {\epsilon }_{f}^{*}\) where σ_c is the local fracture stress, \({\epsilon }_{f}^{*}\) is the local fracture strain in the FPZ and h₀ is a characteristic length setting the size of the FPZ (see Supplementary Note 1). For perfect cleavage, σ_c is the theoretical fracture strength, ~10–50 GPa for typical inorganic materials while h₀ is set by atomic spacing ~0.3 nm and \({\epsilon }_{f}^{*}\) is ~0.1–0.3 leading to G_Ic ≈ 0.5–3 J.m⁻², i.e., about two times the surface energy. But, when dissipative mechanisms take place, σ_c is dictated by plasticity mechanisms with σ_c ~ 3σ_y¹¹ while \({\epsilon }_{f}^{*}\) can vary a lot between 0.05 and 1. The length h₀ depends on microstructure and damage mechanisms, ranging anywhere between nm to mm. Hence, one may have large σ_c and ϵ_f in tension but low h₀ (combined to potentially low \({\epsilon }_{f}^{*}\) at crack tip) leading to a modest fracture toughness.

In the context of thin coatings, with thickness typically smaller than a few micrometers, superior resistance to wear, scratch, erosion and abrasion requires not only a high strength/hardness, but sufficient ductility and a high fracture toughness to avoid cracking. A combination of high σ_y, G_Ic, and ε_f is thus heavily needed for advanced protective coatings. Compared to bulk materials, enhancing fracture toughness of coatings involves the additional difficulty that the small thickness intrinsically limits the material volume in which dissipation can occur, constraining h₀ to submicron sizes. Furthermore, a thickness dependence of G_Ic is found for materials with dissipation from the micro-¹² to the macro-scale¹³. Hence, again, high σ_y–ε_f balance does not necessarily mean high G_Ic. The grand objective of this research is to create novel coatings with superior balance of these three properties. Here we show that alumina layers below 100 nm thickness when stacked with aluminum interlayers exhibit exceptional performances including toughness equal to 300 J.m⁻² determined by on chip nanomechanics. This is almost two orders of magnitude higher than bulk alumina and higher than any other thin hard coatings. In addition, a hardness above 8 GPa combines with a fracture strain above 5%. The origin of this set of properties is unravelled via in situ TEM and mechanical models.

Working principles for making tough, strong and ductile coatings

A first strategy to raise G_Ic is the activation of dissipative mechanisms, to impact h₀ and ε_f*, such as through delaying/mitigating damage accumulation towards more extensive plastic dissipation, and/or by favouring crack blunting after arrest, pinning, deflection and multiplication^3,9,14,15. A second strategy involves crack shielding mechanisms through e.g., crack bridging, crack front undulation, plane stress conditions and/or multi-crack patterning^3,9,14. Nature has been a source of inspiration for a number of successful toughening strategies^16,17,18. Among many options, lamination has proven effective to raise G_Ic^19,20. Through-thickness cracks are arrested by well-tuned interfaces, in so-called “crack arrestor” mode, while transverse cracks, in so-called “crack divider” mode, take benefit from the presence of a dissipative layer in the stack, from limiting the effect/propagation of microflaws inside weak layers and/or from partial delamination effects. A nanolaminate structure thus potentially activates these crack toughening mechanisms while also exhibiting high strength owing to multiple interfaces and small scale^21,22, and, sometimes, ductility by a smart selection of constituents and thicknesses^3,7,23,24. However, nanolamination used for simultaneously combining strength, fracture toughness and ductility has rarely been explored in particular in the context of thin coatings. The challenge is extreme to find working principles that can trigger ductilization mechanisms in systems with high density of interfaces while not creating new sources of damage and/or loosing strength. This is also challenging in terms of methods to determine properties and characterize mechanisms at submicron scale, allowed today by progress in nanomechanical testing and in situ HRTEM methods^6,25,26.

We elaborated the following innovative strategy starting with amorphous alumina as main building block (often abbreviated “a-Al₂O₃” but simply denoted Al₂O₃ here). The logic was that Al₂O₃ has remarkable functional properties for instance as insulator²⁷ but also intrinsically large strength and resistance to oxidation. Furthermore, a high ductility potential has recently been demonstrated by Frankberg et al.²⁸ with 15% fracture strain in freestanding films with thickness below 50 nm promoted by statistically low occurrence of flaws in the volume and by a reduced potential for catastrophic avalanche-type shear localization owing to the small thickness constraint. In a follow-up study, Frankberg and co-workers also found that uniaxially compressed amorphous alumina micropillars with radius up to 5.5 µm exhibit high ductility (15 to 40% fracture strain in compression) when these pillars are free of processing-induced flaws²⁹. Finding a way to maintain this high ductility for thicker coatings in the presence of pre-existing flaws when deformed now in uniaxial tension would significantly enlarge the range of applications of Al₂O₃. The natural solution to take benefit of the excellent properties of very thin alumina layers is to stack thin Al₂O₃ films with thin “glue” interlayers. Nanolamination with Al appears as the natural choice for such interlayers owing to excellent interface compatibility^30,31. Thin Al layers are also extremely ductile depending on purity^32,33 and can reach yield stress in the 1 GPa range below 100 nm thickness^34,35, being potentially able to trigger different dissipative and shielding mechanisms, while not cutting too much on hardness if sufficiently diluted. Al/Al₂O₃ multilayers have already been explored in the literature, showing good performances^20,30,36,37, but the fracture toughness has not been investigated or optimized nor the combination of strength, ductility, and fracture toughness, nor the link to tribological properties essential for coating applications. We prove here, using a combination of advanced nanomechanical and characterization methods, supplemented by finite element simulations, never attained performance levels of Al/Al₂O₃ nanolaminates with Al₂O₃ thickness below 100 nm and Al layers in the 10–20 nm range.

Microstructure of Al₂O₃/Al nanolaminates

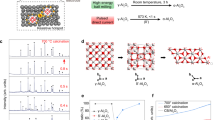
Nanolaminates (NLs) with thickness of Al₂O₃ and Al layers ranging between 5 and 250 nm and 5 and 500 nm, respectively, have been processed by sputtering, see Fig. 1a, as described in “Methods” and Supplementary Note 2. The NL constituent thicknesses are labeled by thickness Al₂O₃/thickness Al in nm (e.g., “50/10” means alternating 50 nm Al₂O₃ and 10 nm Al). Figure 1b shows the initial microstructure of 50/10 NL. The Al layers exhibit a morphological texture with columnar grains and lateral dimension typically 2 to 3 times the Al layer thickness. The interface roughness is controlled and does not exceed R_a ≈ 3 nm for 50/10 NL (see Supplementary Note 2). The HRTEM micrograph proves the excellent Al₂O₃/Al interface coherency and the amorphous nature of Al₂O₃ layers, with a stoichiometry measured by XPS (see Supplementary Note 3).

a Principle of deposition method via DC magnetron sputtering; b bright-field TEM image of 50/10 NL specimen. The inset shows a high-resolution TEM image of the Al/Al₂O₃/Al interface together with Fast Fourier Transforms (FFTs) from the yellow squares. The coloured EELS map shows layers of aluminum (yellow) alternating with amorphous alumina (oxygen in blue). The Al₂O₃ layers are fully amorphous. Note also the good coherency of the Al/Al₂O₃ interfaces with limited undulations.

Full size image

Mechanical behavior of Al₂O₃/Al nanolaminates under contact

The variations of indentation elastic modulus E’_f and hardness H determined by nanoindentation are displayed in Fig. 2a, b as a function of the Al₂O₃ content. These properties were extracted at indentation depth large enough to provide a response representative of the laminate. The elastic modulus varies close to a Reuss “iso-stress” type behavior when changing Al₂O₃ content, although the values are about 10% lower than the theoretical bound. The hardness increases with increasing Al₂O₃ content, but not linearly, up to a value of 8 GPa for 95% Al₂O₃, only 20% softer than pure Al₂O₃. TEM analysis of cross-sections taken below indents as in Fig. 2e indicate that the Al layer increasingly accommodates deformation by shear flow as thickness gets reduced. This increases the plastic zone size at similar indentation depth³⁸ and explains why hardness is below the rule of mixture. Figure 2e also reveals the remarkably large plastic deformation of Al₂O₃ without any signs of cracking or delamination below the indent. Indentation tests performed at different strain rates, see Supplementary Note 4, give a rate sensitivity exponent around 0.05 which is sufficiently high to have a significant impact on delaying plastic localization^3,7,39. The origin of this stable ductile behavior as well as more detailed analysis of the (visco-)plastic indentation response, are addressed in Supplementary Note 4 supported by finite element simulations.

Determination via nanoindentation of a the elastic modulus, the dashed line represents the Voigt “iso-strain” rule of mixture, the blue curve represents the analytical Reuss “iso-stress” rule of mixture and b nanohardness as a function of  the volume fraction of Al₂O₃ (with precise NL constituent thicknesses indicated on the plot), the dashed line represents the linear evolution of hardness from pure Al to pure Al₂O₃; c, d SEM top view micrographs of indents for a NL with thick layers and with thin layers respectively (with Al₂O₃ in blue and Al in yellow); e focused ion beam cross-section below an indent imaged by HAADF-STEM superimposed by EELS map, showing the extreme deformation of the NL layers without failure; f–h SEM top view micrographs of nanoscratch tracks.

Full size image

Figure 2c, d shows SEM top views of indents in two NLs. While systems with thick Al₂O₃ (and thick Al) exhibit radial cracks, the ones with Al₂O₃ thickness below 100 nm are immune of cracks. This is a direct remarkable evidence of toughening and ductilization, which is further confirmed by the analysis of wear tracks produced by nanoscratch (see “Methods”) shown in Fig. 2f–h for three different NLs. The failure mode differs among the NLs with two main deformation mechanisms. Large cracks develop at the vicinity of the track for 200 nm thick Al₂O₃ while the deformation is smooth for thinner layers, with an optimum response at 50 nm thickness. The Al₂O₃ layers literally slide over highly plastically deformed Al layers, in agreement with the indentation analysis above, and appear thus mechanically isolated above a threshold stress corresponding to the shear strength of aluminum. TEM micrographs extracted along the wear track confirm this scenario, see Supplementary Note 5.

The mechanical behavior of NLs with Al₂O₃ thickness <100 nm and Al <50 nm combines thus superior ductility, hardness and cracking resistance. Nanoscratch test is a good indicator of the wear resistance⁴⁰, proving a high tribology potential of these NLs. Nevertheless, a deeper analysis and quantitative comparison of performances with other systems require to go a step further with the determination of intrinsic properties on freestanding specimens as presented next.

Mechanical properties from freestanding specimens

Figure 3a provides the true stress–true strain response extracted from uniaxial tension tests performed in situ on NL specimens 100/10, 50/10, and 150/100 (only trilayered) with the push-to-pull (PTP) frame⁴¹ shown in Fig. 3b within a TEM, see “Methods”. These tests confirm that the excellent ductility of very thin Al₂O₃ single layers found by Frankberg et al.²⁸ is partly conserved by NLs with ε_f around 0.07 (we performed test on single 65-nm-thick Al₂O₃ layer and found also total elongation close to 15 %, see Supplementary Note 6). Note that the interaction with the electron beam can artificially ductilize the response of thin films⁴². Hence, only beam-off conditions that avoid irradiation effects are presented and discussed here. The strength of the Al₂O₃ rich multilayers is above 3 GPa, in agreement with the rule of thumb σ_y = H/3. Figure 3c shows for 50/10 NL broken specimens multiple cracks in the Al₂O₃, arrested by the very ductile Al layers, which thus act as a toughening agent⁴³. Note that some defective regions are sometimes present in the undeformed (as-deposited) layers, becoming favorable loci for crack nucleation, see Supplementary Note 6.

a True stress true strain uniaxial tension response of the three systems 50/10,100/10 and 150/100 Al₂O₃/Al NLs; b push to pull (PTP) frame with BF-TEM magnifications on the three tested NLs; c higher magnification of the undeformed 50/10 NL on the left and after fracture on the right, with transverse cracks in Al₂O₃ indicated by yellow arrows, arrested by the Al interlayers.

Full size image

The recently established on chip cracking method⁴³ shown in Fig. 4 (see “Methods”) has been used to determine G_Ic for 50/10 and 50/20 NLs with 5 layers each. Figure 4a shows a symmetric double cantilever beam configuration with a central elliptical notch. When the test structure is released from the substrate, the actuating arms pull on the test specimen with the initiation of a crack at notch root, propagation and arrest, see zoom in Fig. 4b. Figure 4c shows the estimated K_Ic as a function of the crack advance Δa for the different 5-layers NLs (50/20 and 50/10) that led to successful cracking tests. There is no clear trend for an increase of fracture toughness with crack propagation, indicating limited to no R-effect (see Supplementary Note 7). The mean fracture toughness K_Ic is equal to 6.6 ± 0.5 MPa.m^1/2. This means G_Ic is around 300 J.m⁻², assuming an overall Young’s modulus of 145 GPa (which was the value used in the FE simulations to extract the K value). The fracture toughness of bulk Al₂O₃ is equal to ~1.5 MPa.m^1/2, or G_Ic around 12 J.m⁻² Crack-on-chip tests performed on freestanding 42-nm-thick Al₂O₃ films give a K_Ic of about 3.3 MPa.m^1/2, meaning G_Ic near 55 J.m⁻² (see Supplementary Note 7). In addition, Frankberg et al.²⁸ reported a K_Ic for a 40 nm thick Al₂O₃ film of 3.1 MPa.m^1/2. These results confirm the toughening of Al₂O₃ below 100 nm when nanolaminated with thin Al interlayers. A G_Ic equal to ~300 J.m⁻² for a 100-nm-thick freestanding material is an exceptionally high fracture energy as discussed next.

a Global view showing the SiN actuator beams pulling after release on the long central NL structure containing an elliptical hole (the structure includes two springs on both side to release the residual stresses in the crack propagation direction to avoid any T-stress); b zoom of the cracks initiated at the notch roots and arrested at some distance further from which the fracture toughness is determined by finite element simulations; c variation of K_Ic with crack advance (one point is one specimen) for the 50/20/50 symmetric and asymmetric test structures, and one 50/10/50 asymmetric test structure.

Full size image

Origins of the high fracture toughness combined to high strength-ductility balance

Before discussing fracture toughness, the results above prove that Al₂O₃/Al NLs have excellent hardness close to 10 GPa if the presence of Al is minimized and used only as a “glue” to stack thin Al₂O₃ layers. In parallel, the NLs exhibit good ductility in tension coming from the intrinsic high fracture strain of very thin Al₂O₃ films (Supplementary Note 7) as well as from the crack arrest potential of the Al layers that prevent flaws to grow to a critical size. Indeed, for K_Ic = 6.6 MPa.m^1/2 (although this is a value measured for a crack divider mode, while the PTP test induces crack arrestor mode) and a fracture stress of 3–4 GPa, the critical crack size is around 1 μm. The moderate rate sensitivity exponent of 0.05 is also a positive factor to delay plastic localization.

In order to further assess the exceptional combined performances with K_Ic ≈ 6.6 MPa.m^1/2, σ_y ≈ 3 to 4 GPa and ε_f ≈ 7%, an in-depth literature survey has been made to collect data on the strength, ductility and fracture toughness of thin coating systems, involving both single layers and nanolaminates. The database and corresponding references are presented in Supplementary Note 8. Now, systematic testing of strength, ductility and fracture toughness as performed here are rare and some assumption had to be made to convert measurements, these are detailed in Note 8. Figure 5a is a map plotting σ_y versus K_Ic. Contour lines of equal critical crack lengths are added. The best NLs investigated here have the largest fracture toughness ever when considering systems with strength above 1 GPa which is a realistic requirement to mitigate plastic deformation under contact.

The error bars are extracted directly from the referenced sources. Measurement data on the deposition sputtered single layer Al₂O₃ film and the Al₂O₃-Al-Al₂O₃ laminate film produced in this work are included with star symbols. The dashed lines are contours of equal critical crack length a_c, defined in the supplementary Note 8. The dotted line divides the map into two fracture mode regimes; the hatched region highlights a strength-toughness regime for which no representative material system could be identified.

Full size image

To explain the extreme fracture energy of ~300 J.m⁻², a local fracture stress in FPZ σ_c ≈ 3σ_y ≈ 10 GPa is assumed¹¹ and h₀ is set by the thickness of the NL (here 190 nm), which leads to a local ε_f* around 0.15. This is a large value for ε_f*, larger than measured in uniaxial tension, even though a lower fracture strain of the FPZ is expected due to higher stress triaxiality at the crack tip. First note that in uniaxial tension, the specimen is large and the fracture strain is partly conditioned by the presence of defects and heterogeneities while the FPZ volume in cracked specimens is orders of magnitudes smaller. Second, the plastic zone size assuming plane stress conditions r_p = 1/π (K_Ic²/σ_y²) is around 1.5 μm, significantly larger than the thickness. Hence, the cracked specimens undergo near plane stress conditions which involves much lower stress triaxiality at crack tip and favors larger local deformations before failure^12,13. This is presumably for the same reason that the very thin 42 nm thick single Al₂O₃ layers (see Supplementary Note 7) exhibit a higher fracture toughness than bulk, although still half the one of the NLs. Third, the high value may reflect the absence of easy damage mechanism giving a good capacity to accommodate large deformations by crack tip plasticity. Finally, an additional toughening principle can be invoked to further justify the large K_Ic in the NLs compared to the single Al₂O₃ layers. The TEM observations of the crack tips found in the scratch tracks, see Supplementary Note 5, show indeed partial interface delamination. Such a delamination is an effective toughening mechanism in laminates for divider crack configuration^44,45. This mechanism might cooperate with crack front undulation due to crack propagating more slowly in Al layers, although this cannot be confirmed by TEM, with an associated shielding effect⁴⁶. Further investigations will aim at determining more precisely the sources of toughening and at testing thicker NLs to determine if G_Ic keeps increasing with thickness as expected.

To connect to the very good tribological resistance, the high G_Ic in the crack-divider mode is certainly a key reason for the remarkable resistance to cracking under mechanical contacts (Fig. 2d, e). In this case, cracking initiation also involves the crack arrestor configuration with the crack propagating through the thickness as well as channeling further in divider mode. The literature indicates that soft interlayers should ideally have a thickness equal to the plastic zone size and a yield stress lower or equal to 20% of the hard layer to optimally reduce the crack driving force in arrestor mode⁴⁵. Here, σ_yAl/σ_yAl2O3 is in the range 0.1–0.2 depending on Al thickness, in agreement with the criterion. However, an Al layer below 50 nm is much smaller than the ~1.5 μm plastic zone size. The easy sliding/shear flow in the Al very thin layers provides an additional ductilization/shielding mechanism that spreads plasticity, not accounted in the reference above, that raises the potential for crack tip blunting and that decreases the local stress concentration. This “greasy” Al effect is similar to mechanisms found in nacre¹⁸ and resembles the low friction in Au/Ni nanolaminates triggered by shear induced mixing⁴⁷ which is also activated for layer thickness below 100 nm. The difficulty when designing toughening and ductilization principles is that one needs several mechanisms to counteract any possible weakest link scenario. This is the case here with the combination of crack arrest, super shear, and intrinsic ductility when using Al₂O₃ thickness below 100 nm and Al layers in the range 10–20 nm.

Amorphous Al₂O₃ is ductile below 100 nm with extensive plasticity before failure, and tougher than in bulk form as well. In order to benefit from these superior properties for applications requiring thicker coating/materials, thin Al₂O₃ layers can be stacked with very thin Al layers acting as a “gluing & toughening” agent. Synergetic effects lead to exceptional fracture toughness of nanolaminates around 300 J.m⁻² for 50 nm Al₂O₃ and 10 or 20 nm Al which is totally unique for thin coatings, while maintaining a strength above 3 GPa. This directly reflects into a very good wear resistance. This set of properties results from combination of mechanisms including confined stable plasticity, crack arrest and super shear in the Al layer which add/cooperate with the good properties of the thin oxide layer. This unprecedented performance makes Al₂O₃/Al NLs an appealing system for coating applications requiring high tribological performances, including corrosion.

Processing

The Al₂O₃/Al NLs have been deposited using DC magnetron sputtering from a 99.9995% Al target. Sputtering was performed at ambient temperature and at 1.5 mTorr under a current of 300 mA. The laminate structure is produced by varying the gas mixture from pure Ar (25 sccm) for Al layers to Ar/O₂ mixture (22/3 sccm) for the Al₂O₃ layers. The sputtering rate was measured prior to deposition to adapt the deposition time for each sample configuration. For Al₂O₃ deposition, the selected O₂ partial pressure was the highest accessible to ensure stoichiometry of the Al₂O₃ before the voltage drop which indicates poisoning of the Al target. Two types of stacks have been produced: thick stacks approaching 1 µm for the indentation and tribological tests and elementary 3- or 5 layer stacks for in situ TEM and on chip testing (see further). The full set of NLs is given in Supplementary Note 2.

Ex situ composition microstructure characterization

Cross-sectional foils were prepared using a dual-beam focused ion beam (FIB) instrument (ThermoFisher Scientific Helios Nanolab 650) for ex situ high-resolution TEM, STEM, STEM-EDX and ED analysis. A Pt protection layer was deposited in two steps—by an electron beam, then by an ion beam—in order to avoid FIB damage of sample surface. The FIB foils were thinned to a thickness <50 nm. An ion beam of 2 kV/0.2 nA was employed to achieve the final thinning of the specimen and to minimize irradiation damage generated during high‐voltage FIB thinning. A state-of-the-art spherical aberration-corrected ThermoFisher Scientific Titan X-Ant-EM transmission electron microscope equipped with a D-Corr probe aberration corrector and highly efficient SuperX system was used for HAADF-STEM imaging. HAADF-STEM images were acquired at 300 kV using a convergence semi-angle α of 21 mrad, 50 pA probe current. EELS data were recorded on GIF Enfinium spectrometer in dual-EELS mode for recording zero-loss and core-loss spectra quasi simultaneously. The EELS data were acquired with 0.2 s/pixel and 0.1 eV/pixel dispersion.

In situ TEM characterization

For in situ PTP experiments, a cross-sectional thick FIB specimen with dimensions of about 10 × 2 × 4 μm³ was cut and mounted into the PTP device using an Omniprobe micromanipulator. The in situ specimen was thus thinned directly on the PTP device. The central region of the specimen was thinned to a thickness of about 150 nm, and at the final stage, the Pt protective layer and the substrate were cut off to obtain a freestanding Al/Al₂O₃/Al multilayer film. The in situ uniaxial tensile experiments were conducted in a ThermoFisher Scientific Tecnai Osiris microscope operating at 200 kV in bright-field TEM mode in beam-off mode (beam was blanked during the in situ experiment). A 100 µm conductive diamond flat punch indenter of the single‐tilt PI 95 TEM PicoIndenter (Bruker.Inc) was used. Tensile experiments were performed in load control mode with loading rate equal to 0.1 μN/s. The applied force was determined by removing the contribution of the spring stiffness from the raw force. The true stress was calculated by dividing the force on the specimen by the current cross‐sectional area. Sample thickness was measured in high-resolution mode of SEM with a resolution of ~3 nm while sample width and length were measured on the BF-TEM images. Videos with rate of 5 frames/s were recorded and post-processed using home-made MATLAB scripts. The engineering strain was extracted by measuring the displacement on the movies using digital image correlation.

Nanoindentation and nanoscratch

Nanoindentation experiments have been performed with a nanoindenter G200 (KLA Tencor) using the Dynamic Contact Module (DCM V2®) head to generate accurate measurements at low loads and displacements. A diamond Berkovich tip with a low tip defect height (h₀ = 5 nm) was used. Coated silicon wafers were glued to the sample holders using a thermoplastic glue (heating during 1 min at 150 °C). The hardness and elastic modulus were calculated using the Oliver and Pharr model together with the Hay model for substrate effect correction and taken at 10% of the coating thickness. More details and references are given in Supplementary Note 4. The scratch experiments were performed in the same nanoindentor with a XP head equipped with a lateral force module. A diamond cono-spherical tip of radius 5 µm and equivalent cone angle of 90° was used. For each nanolaminate a set of 6 scratches was performed. From this experiment, the coefficient of friction, the elastic recovery and the critical load are extracted, together with valuable observations of coating failure mechanisms. Details of the nanoindentation and nanoscratch procedures and results are given in Supplementary Notes 4 and 5.

On chip testing

The on-chip cracking test structures shown in Fig. 4 are fabricated within the UCLouvain WINFAB cleanrooms following microelectronics/MEMS based processes. The key steps of the process include: (i) deposition on a 380-μm-thick Si wafer of 32-nm-thick SiN layer by low pressure chemical vapor deposition with about 1 GPa residual stress (precise value systematically measured by Stoney method combined to other test structures, see details in ref. ⁴³); (ii) patterning of SiN layer into slightly tapered beams with length varying between 100 and 300 μm through positive lithography using photoresist AZMIR 701 followed by reactive ion etching in CHF₃ and O₂ gas; (iii) pre-patterning through negative lithography using photoresist AZ nLof 5510 of symmetric or asymmetric test configurations with notches of 2 μm initial opening, overlapping with the SiN beams—note also on Fig. 4 the presence of springs at the end of the test specimens to relax the longitudinal residual stress⁴⁸; (iv) deposition of 50/10 and 50/20 5-layer NL as explained above; (v) release of the full test structure “notched 5-layer attached to SiN” by XeF₂ etching of the Si; (vi) during release the SiN beams progressively contract, pulling on the notched 5-layer. If the imposed displacement is large enough, a crack initiates at the notch tip, propagates and arrests due to the decrease of the imposed energy release rate G. The final crack length is measured and detailed finite element calculations are performed to accurately determine the corresponding G value which provide the toughness G_Ic (see details of data reduction scheme in refs. ^43,48 and finite element calculation procedure in the Supplementary Note 7). 26 “50/20” and 1 “50/10” structures lead to successful tests out of which a G_Ic value could be extracted equal to 300 ± 30 J m⁻².