Introduction

The spin Hall effect of light (SHEL) refers to the microscopic, transverse, and spin-dependent displacement of light during refraction and reflection at optical interfaces that alter its propagation direction1. This microscopic effect is driven by the transversality of light and the geometric phase arising from vector rotation in three-dimensional space2. A notable example of SHEL is the splitting of obliquely injected linearly polarized light into two circular polarizations, left and right circular polarizations (LCP and RCP, respectively) (Fig. 1a)2,3,4,5,6,7,8,9,10,11,12,13. Since the amount of the displacement, or spin Hall shift, is generally much smaller than the wavelength, the split beams spatially overlap and cannot be distinguished by direct observation. Consequently, there have been intensive studies on enhancing the spin Hall shift14,15 by using artificially designed interfaces16,17, such as metamaterials18,19,20,21 and metasurfaces22,23.

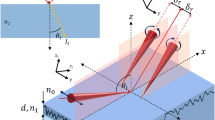
Fig. 1: Comparison between conventional weak measurement and metasurface-implemented single-shot weak measurement for observing the spin Hall effect of light (SHEL).
figure 1

a Illustration of the SHEL. (b) Conventional weak measurement setup and (c) its multistep procedure. HWP: half wave plate, LP: linear polarizer, L: lens. (d) Replacement of LP2 with a polarization beamsplitter metasurface. The metasurface splits the incidence into two orthogonal linear polarizations, \({{\bf{e}}}_{1}\) and \({{\bf{e}}}_{2}\), and deflects them in different directions. (e) Single-shot procedure and expected image using the metasurface.

Full size image

Meanwhile, the SHEL can be measured with high precision via an optical technique known as weak measurement24,25,26,27,28. This method amplifies the spin Hall shift by several orders of magnitude at the expense of reduced intensity through processes called preselection and postselection29,30. Such signal amplification enables the measurement of displacement on the scale of a few hundred micrometers or beyond, in contrast to its nanoscale nature, showcasing the potential of SHEL as a promising tool for high-precision, nondestructive investigation of unknown interfaces31. Therefore, SHEL has been utilized to sensitively identify various parameters at a given interface, such as electric and magnetic properties32, refractive index33,34, film thickness35, conductivity36, temperature37, humidity38, geometric fluctuations39, and more40,41,42,43,44.

However, this measurement technique is limited to a multistep process. A single captured image provides the beam position only at a specific postselection angle, which is insufficient for evaluating the beam displacement. Therefore, an additional measurement for the unperturbed case or the opposite postselection angle is required to obtain a single spin Hall shift. As a result, most previous experiments have been restricted to static situations, even though the measurement targets are sometimes dynamic variables that change over time41. This limitation has been a significant obstacle that hinders the implementation of SHEL-based precision measurement into practical applications to this date, despite its high precision. While there have been a few attempts to leverage SHEL for real-time detection37,45, they require a prior step of measuring the undisturbed beam position before conducting the measurements. Therefore, a single-shot measurement of SHEL that remains effective even when the unperturbed beam position changes over time is still not achievable.

The multistep requirement can be relaxed by utilizing the multifunctionality of a metasurface, an artificially engineered nanoantenna array designed to manipulate light. In this work, we propose a single-shot weak measurement of the SHEL by replacing the postselection polarizer with a metasurface that functions as a polarization beamsplitter. In contrast to previous work, in which metasurfaces have been used as interfaces to generate and tailor the SHEL12,18,19,20,21,22,23, we utilize the metasurface as an optical component in a setup to measure the effect at two distinct postselection angles simultaneously. The metasurface spatially splits the incidence into two orthogonal, linearly polarized beams by deflecting them in different directions, with each beam experiencing either an amplified or reduced spin Hall shift. Consequently, the metasurface-implemented weak measurement setup allows us to read out the spin Hall shift from a single captured image without requiring calibration, in contrast to conventional multistep weak measurements. Additionally, the amplification and precision of this setup can be adjusted by rotating the metasurface, similar to the way commercial linear polarizers are used. As proof of concept, we first experimentally observe the SHEL at an air-prism interface in a single shot and then measure the SHEL through a tilted polarizer while varying its angle in real time. The experimental results agree well with theoretical predictions and simulations for both measurements, demonstrating the validity of our approach. The metasurface-enabled single-shot weak measurement is expected to expand the applicability of SHEL to various scenarios that requires high precision and instantaneous detection, such as chemical, biological, and medical monitoring.

Results

Concept and principle

Initially proposed in the quantum context46, weak measurement is a technique that amplifies a small change through preselection and postselection47. The weak measurement devised to measure the SHEL consists of a pair of lenses (L1 and L2), with focal lengths f1 and f2, respectively, and linear polarizers24 (LP1 and LP2), as shown in Fig. 1b. LP1 sets the initial polarization state of the incidence. The linearly polarized incidence then undergoes SHEL at the surface of a prism and becomes a superposition of two circularly polarized beams with different center positions, (x,  y) = (0,   ± δ), where δ represents the spin Hall shift at the air-prism interface and can be determined by averaging the intensity over y (Fig. 1a). Here, the incident plane is the zx-plane. The splitting along the x-axis may also occur48 but is neglected here (see Supplementary Note 1 for the rationale behind this omission). The behavior of δ for the reflected light is described by25

$${\delta }_{H}^{\pm }=\mp \frac{\cot {\theta }_{i}}{{k}_{0}}\,{\mbox{Re}}\,(1+{r}_{s}/{r}_{p}),$$
(1)
$${\delta }_{V}^{\pm }=\mp \frac{\cot {\theta }_{i}}{{k}_{0}}\,{\mbox{Re}}\,(1+{r}_{p}/{r}_{s}),$$
(2)

where subscripts H and V indicate horizontal and vertical incident polarizations, respectively, superscripts + and − denote LCP and RCP components of the reflected, respectively, rs and rp are Fresnel reflection coefficients under s and p polarizations, respectively, θi is the incident angle, k0 = 2π/λ is the wave number, and λ is the wavelength. Eqs. (1) and (2) hold when the spin Hall shift is sufficiently smaller than the beam waist (w0), i.e., ∣δ∣ ≪ w0. This condition is satisfied within this study.

Filtering the reflected beam using LP2 alters the intensity profile and relocates the beam center. The spatial distribution of the postselected beam is then captured by the camera. The preselection and postselection processes amplify the displacement as29

$$W=A\delta=\delta F\cot \alpha,$$
(3)

where W is the displacement of the postselected beam along the transverse axis (see Fig. 1c), obtained by averaging the y position of the intensity profile, and corresponds to the measurement variable of the weak setup, i.e., weak value, \(A=F\cot \alpha\) is the amplification factor, F = f2/zR is the propagation factor, zR is the Rayleigh length of the beam between L1 and L2, and α is the postselection angle, the relative angle between the postselection polarization and the orthogonal axis of the preselection (insets in Fig. 1c).

Classical optics demonstrates that the amplitude follows a \(\sin \alpha\) curve, leading to a measurable intensity that diminishes as \({\sin }^{2}\alpha\) (Supplementary Note 2) but simultaneously, the displacement is amplified following the cotangent curve (Eq. (3))24,29. In particular, for α being small (≤1°), i.e., where the optical axis of LP2 is nearly orthogonal to LP1, this amplification generally reaches several orders of magnitude (103−105). This allows us to estimate δ with a resolution of d/A, where d is the pixel size of a position-sensitive detector. Given that commercially available cameras have pixel sizes on the order of a few micrometers, the resolution of δ can be reduced to a few nanometers or even the subnanometer scale24 through weak measurement. However, a single intensity distribution is insufficient to determine δ because the y center position of the unperturbed beam, corresponding to y = 0 in Fig. 1c, is unknown.

Traditional methods can be categorized into two distinct approaches. In the first approach, the position of the unperturbed beam is recorded separately from that of the spin Hall shifted beams. This process is referred to as calibration hereafter and is required independently of the angular alignment of the polarizer. If this calibration is performed beforehand, a single frame in the subsequent measurements provides δ. In the second approach, the weak measurement is conducted multiple times by rotating LP2 across a small angular range (Fig. 1c). Then, δ at each postselection angle is derived by combining the data from the various frames. The minimum number of frames required is two. For instance, W at α is determined by measuring the distance along the y-axis between the postselected beams at  ± α and dividing it by 2 (ref. 24). In both cases, LP2 has only one function, i.e., projecting light along its optical axis, and the resultant postselected image at the instantaneous α is captured by the detector. As a result, a single snapshot does not provide sufficient information to determine δ; therefore, it is obtained by recording two or more images at different times. This multistep requirement hinders the observation of SHEL in dynamic situations, in which the beam position fluctuates, for instance, when light reflects at the surface of a film swelling in response to humidity49.

To compress the multistep processes into a single step, we replace LP2 with a metasurface that splits the incidence into two orthogonal, linearly polarized beams, \({{\bf{e}}}_{1}={(\cos \alpha,\sin \alpha )}^{T}\) and \({{\bf{e}}}_{2}={(-\sin \alpha,\cos \alpha )}^{T}\), and spatially separate them by steering each with small, opposite deflection angles ±θ along the x-axis (Fig. 1c–e). This metasurface can be considered as a polarization beamsplitter that has functions of two linear polarizers and a beamsplitter simultaneously (Fig. 1d). Given that the postselection angles are π/2 + α for \({{\bf{e}}}_{1}\) and α for \({{\bf{e}}}_{2}\) (see Fig. 1e, inset), the two beams experience shifts of \({W}_{1}=-\delta F\tan \alpha\) and \({W}_{2}=\delta F\cot \alpha\), respectively, as per Eq. (3), and are captured simultaneously at different positions on the detector (Fig. 1e). In other words, the spin Hall shifted beam, originally a superposition of LCP centered at (0, δ) and RCP at (0,  −δ), is split into nonoverlapping beams, one being \({{\bf{e}}}_{1}\) centered at \((-{d}_{x}/2,\,-\delta F\tan \alpha )\) and the other being \({{\bf{e}}}_{2}\) centered at \(({d}_{x}/2,\,\delta F\cot \alpha )\), where dx is the displacement between the two separated beams along the x-axis. Therefore, the relative y position difference between these two beams can be measured via a single measurement as

$$Y\equiv {W}_{2}-{W}_{1}=\frac{2\delta F}{\sin 2\alpha },$$
(4)

which also has a linear relation with δ. Accordingly, the spin Hall shift can be determined as \(\delta=Y\sin 2\alpha /2F\) from this single-shot measurement. Additionally, the weak values of each postselected beam can be deduced as \({W}_{1}=-Y{\sin }^{2}\alpha\) and \({W}_{2}=Y{\cos }^{2}\alpha\). This indicates that the amplification factor of this single-shot setup corresponds to \(1/{\cos }^{2}\alpha\) of that of the conventional setup, which is even higher than the previous amplification. See Supplementary Note 3 for the amplification factor when the linear relation between the weak value and spin Hall shift (Eq. (3)) breaks down. While the two weak signals in Fig. 1e are illustrated on the similar intensity scale, they differ by \({\cot }^{2}\alpha\) (Supplementary Note 2) but can be matched to similar scales by adding a polarizer. Here, we discuss the metasurface deflecting the postselected beams along the x-axis, but this choice can be arbitrary as long as the two beams do not spatially overlap.

Polarization beamsplitting metasurface

To realize a metasurface that spatially separates the spin Hall shifted beam into two orthogonal linear polarization states, \({{\bf{e}}}_{1}\) and \({{\bf{e}}}_{2}\), (Fig. 2a), the phases ϕ1 and ϕ2 acquired by \({{\bf{e}}}_{1}\) and \({{\bf{e}}}_{2}\) while passing through the metasurface are defined as equal in magnitude but opposite in sign, with a linearly varying profile. The unit structure of the metasurface, or meta-atom, is chosen as a horizontally aligned rectangular nanorod50 arranged on a 45°-rotated square lattice (Fig. 2b; Supplementary Note 4). Under periodic boundary conditions, the meta-atom possesses a Jones matrix given by \({{{\mathcal{J}}}}=\,{\mbox{diag}}\,({t}_{x},\,{t}_{y})\). The Jones matrix of the metasurface, when rotated by an angle β, can be obtained through pointwise coordinate rotation: \({{{{\mathcal{J}}}}}_{\beta }=R(-\beta )\,{\mbox{diag}}\,({t}_{1},\,{t}_{2})R(\beta )\) where R(β) is the rotation matrix by β and t1 and t2 are transmission coefficients map obtained by rotating two-dimensional spatial map of tx and ty by β, i.e., \({t}_{1,2}({x}^{{\prime} },\,{y}^{{\prime} })={t}_{x,y}(x,\,y)\) where \({({x}^{{\prime} },{y}^{{\prime} })}^{T}=R(\beta ){(x,y)}^{T}\). The eigenvectors of \({{{{\mathcal{J}}}}}_{\beta }\) are \({(\cos \beta,\sin \beta )}^{T}\) and \({(-\sin \beta,\cos \beta )}^{T}\) with t1 and t2 being the corresponding eigenvalues. This indicates that by designing the unrotated metasurface to have \({t}_{x}=\exp (i{\phi }_{x})\) and \({t}_{y}=\exp (i{\phi }_{y})\) and then rotating it by α, i.e., letting β = α, the metasurface can assign independent phase gains, ϕ1 = arg(t1) and ϕ2 = arg(t2), to the polarization states \({{\bf{e}}}_{1}\) and \({{\bf{e}}}_{2}\). This transformation differs from the rotation of meta-atoms on a fixed lattice51,52, as in our case, both the eigenpolarization states and the phase maps rotate simultaneously (Supplementary Note 4). By rotating the metasurface after fabrication, we can arbitrarily choose α, thereby controlling the amplification of our measurement.

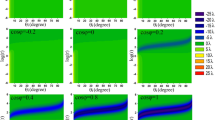
Fig. 2: Metasurface as a polarization beamsplitter.
figure 2

a Illustration of the polarization beamsplitting of the spin Hall shifted beam using the metasurface. b Schematic of a unit cell of the metasurface and (c) scanning electron microscopy image of the fabricated sample. d The two phase maps (ϕx and ϕy) of the metasurface. e Transmittance and phase profiles of the x-polarized light through the metasurface near the center. Black: ideal, blue: metasurface. The ideal phase profile is discretized by the unit cell period. f Normalized intensity of the two split beams and (g) their ratio. h Intensity distribution when the incident polarization angle is 38°.

Full size image

The amplification of the SHEL achieved through this linear polarization splitting fails when the basis of the splitting transitions to circular polarization. Therefore, geometric phase metasurfaces designed to manipulate light in the circular basis are incompatible with the requirements of our work (Supplementary Note 5). Meanwhile, although the spin Hall shifted beam is normally incident on the metasurface, the deflection induced by the metasurface generates a second SHEL22, independent of the effect at the air-prism interface. This second spin Hall shift is not amplified through our weak measurement technique and has the circular polarization basis. Thus, the splitting cancels out, leaving W, determined by the separation of linearly polarized postselected beams, unaffected.

To determine the dimensions of the meta-atoms, the Jones matrix elements (tx and ty) of the meta-atom, made of hydrogenated amorphous silicon (a-Si:H) on a glass substrate with a fixed period of p = 420 nm and height h = 416 nm, are calculated numerically by varying the length and width (Supplementary Note 4). The minimal feature size of 100 nm and the gap size of 150 nm are used to address the fabrication resolution. A 1.5 mm by 1.5 mm metasurface is then fabricated using electron beam lithography (Fig. 2c; see Methods). The phase gradient along the 45° direction (\({\phi }_{x}=-{\phi }_{y}={k}_{0}(x+y)\sin \theta /\sqrt{2}\)) is used in the fabricated sample (Fig. 2d) with a deflection angle of θ = 2. 3° to ensure that both spots are captured by our detector (sensor size: 5.0 × 3.7 mm2). The phase of the designed metasurface closely reproduces the ideal phase profile (Fig. 2e). The transmittance is not ideal and exhibits fluctuations, mainly attributed to the relatively low fabrication resolution, but can be improved by reducing the minimal feature and gap size. Still, the performance degradation due to the nonuniform transmittance profile is insignificant (see Fig. 3b). The linear phase profile diminishes as the incident angle increases but retains a similar trend up to small incident angles (Supplementary Note 6).

Fig. 3: Single-shot observation of the SHEL at an air-prism interface.
figure 3

a Schematic of the metasurface-implemented weak measurement setup. b Weak signals observed under various α. c–e Intensity distributions obtained from (c) conventional weak measurement, (d) metasurface-implemented weak measurement, and (e) simulation for α = 0.5°. The black lines in (d, e) represent a gradient of \(\tan (\pi /4-\alpha )\) and intersect the postselected beam on the right. f–h Same as (c–e) for α = 2.5°.

Full size image

The polarization beamsplitting by the metasurface is examined under the direct incidence, without the preselection and postselection, by varying the incident polarization angle (Fig. 2f and g; see Methods for details). The intensity profiles of the two spots follow \({\sin }^{2}\theta\) and \({\cos }^{2}\theta\) curves (Fig. 2f), resulting in an intensity ratio of \({\cot }^{2}\theta\) (Fig. 2g). The extinction ratio of the metasurface, obtained from the measured results, is 259.4:1 and 57.2:1 for the x- and y-polarized incidences, respectively. These values are relatively low compared to commercial polarizers, yet the measured results closely follow the theory. The captured intensity distribution when the polarization angle is 38° shows that the two separated beams align along the curve y = x (Fig. 2h). Higher-order beams are also observed but only the first-order beams (highlighted within the boxes in Fig. 2h) are used. The unexpected central beam, not predicted numerically, is attributed to fabrication imperfections and nonlocality (Supplementary Note 7). While these imperfections reduce the splitting efficiency, they do not affect the splitting process itself, as confirmed by the results in Fig. 2f and g.

Single-shot observation

The fabricated metasurface is integrated into the weak measurement setup (Fig. 3a; see Methods). To match the output intensity scale of the two postselected beams, a film polarizer (yellow) is placed after the metasurface. The optical axis of the film polarizer is oriented perpendicularly to the polarization angle of the reflected beam. Since each of the postselected beams has a uniform polarization state, only their intensity changes through the polarizer whereas their distribution and center positions are preserved. We examine the SHEL at the interface of a BK-7 prism (refractive index: 1.515). Incident polarization is horizontal, the laser diameter is 680 μm, and other parameters are set as: λ = 632.8 nm, θi = 45°, f1 = 60 mm, and f2 = 50 mm. These focal lengths are not favorable for high precision (\(A\propto F\propto {f}_{2}/{f}_{1}^{2},\,F=7.97\)) but are chosen to ensure that the spin Hall shifted beam after passing through the L2 (diameter ≈ 571 μm) is entirely covered by the metasurface. The resolution of δ in our single-shot setup is 5.44 nm. However, higher amplification and, consequently, better resolution can be achieved by fabricating a larger metasurface and using a shorter f1 and/or a longer f2. (Supplementary Note 8).

Theoretically predicted, numerically simulated, and experimentally measured W values are displayed in Fig. 3b (see Methods for the numerical simulation). At this static interface, δ = 225.0 nm (Eq. (1)) and W follows a cotangent curve as α changes (Eq. (3)). The linear relation between W and δ begins to deviate26 and becomes nonlinear as \(W=\delta F\cot \alpha /(1+{(\delta {w}_{0}^{-1}\cot \alpha )}^{2})\) as α approaches zero (compare black solid and dotted curves) and reduces to zero after reaching its maximum value, \({w}_{0}\sqrt{1+{F}^{2}}/2\approx 142.8\) μm (black solid). The simulated W using the ideal phase map (blue dashed) and the realistic metasurface design (red dashed) closely match the theoretical predictions and are nearly indistinguishable in Fig. 3b. In the conventional weak measurement setup (Fig. 1b) conducted for comparison, the postselected beam is captured by varying α from  − 2.5° to 2.5°. The measured W values are obtained after finding the center position of the incidence (y = 0) when the entire process is completed. The experimental results agree with the theory (black square). A single capture, however, does not provide the weak values.

In contrast, the metasurface-implemented weak measurement does not require such a multistep or calibration process. Before starting this measurement, the metasurface is mounted on a rotation stage and positioned so that the splitting direction under direct incidence is 45°. This process is intended to align the metasurface horizontally, corresponding to α = 0, akin to aligning the optical axis of a commercial polarizer prior to measurements, and is not a calibration. We conduct the measurement by rotating the metasurface (Fig. 3a) and acquire a single image that includes two postselected beams simultaneously. The rotation of the metasurface not only determines the postselection angle but also alters the deflecting direction from π/4 to π/4 − α (Fig. 3d and g, black line). The difference in the y position averages between the two postselected beams is obtained from the single image as \(Y=\bigtriangleup Y-\tan (\pi /4-\alpha )\bigtriangleup X\) where \(\bigtriangleup\) X, Y are the center position differences of the two beams along the x- and y-axes, respectively (see Supplementary Note 9). The weak signals are then determined using \({W}_{2}=Y{\cos }^{2}\alpha\) and are shown as red circles in Fig. 3b. These results are in excellent agreement with theoretical and simulated results.

Furthermore, the experimentally measured intensity distributions from both conventional and metasurface-implemented weak measurements at two selected α, 0.5° and 2.5°, along with numerically simulated distributions using the metasurface, are shown in Fig. 3c–h. Raw images at other angles are available in Supplementary Note 9. While conventional weak measurement provides only one weak signal per measurement step (Fig. 3c and f), the metasurface approach allows for the observation of two signals in a single measurement (Fig. 3d and g). In addition, the postselected beams nicely reproduce the theoretically predicted distributions, a distorted shape with an upward shift for small α (Fig. 3d) and a less distorted shape for large α (Fig. 3g). The reversed relative intensity between the measured and simulated distributions can be explained by imperfect orthogonality between the incident polarization and the optical axis of the film polarizer and does not affect W (Supplementary Note 10). The distance between the beams along the x-axis is larger in experiments (Fig. 3d and g) compared to simulations (Fig. 3e and h) due to the longer propagation distance from the metasurface to the detector, but does not affect the overall results (Supplementary Note 11). As observed in the splitting measurement, the central beam, which is absent in the numerical simulations, appears in the experimental results but is not included in the calculation of the weak value. Our metasurface is designed for the single wavelength and thus should be redesigned to work at different wavelengths (Supplementary Note 12). In contrast to the conventional weak measurements, in which the order of the linear polarizer and lens in both preselection and postselection can be switched24, the metasurface and lens in the postselection cannot change their order in our setup due to the angular splitting.

While we use the prism for simplicity, by switching it to a coated prism or multilayer structure, this setup can be used to deduce unknown parameters such as layer thickness35 and index33,34, etc. Whereas this static demonstration can also be reproduced in a conventional multistep setup by measuring the beam position of the unperturbed case, which serves as y = 0, by setting α = π/2, this conventional approach cannot be applied if the reference line changes over time due to dynamics at the interface.

Real-time observation

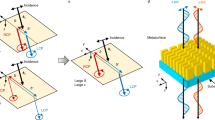
We then construct a refractive type setup to demonstrate real-time observation of the SHEL under varying conditions (Fig. 4a). A film polarizer (gray) serves as an interface to generate the SHEL53, with its tilted angle (ϕ) along the vertical axis as a variable in our experiment. Both the incident polarization and the optical axis of the film polarizer are set vertically. The optical axis of the second film polarizer, positioned after the metasurface (yellow), is horizontally aligned. The focal lengths of both lenses remain unchanged from the previous setup. The SHEL at this isotropic-anisotropic interface follows the relation53 \(\delta=-\cot \theta /{k}_{0}\), which is equivalent to Eq. (2) except that θ = π/2 − ϕ is the relative angle between the light propagation direction (red arrow in Fig. 4a, inset) and the polarizer’s absorption axis (purple). The film polarizer is rotated by ϕ within the range of 30° to 40° according to a predefined function (Fig. 4b) using a motorized stage. This change in ϕ over time induces time-varying behavior in δ and consequently in W. Unlike the dynamic response of the postselected beam, the position of the unperturbed beam remains still, making the entire process measurable via the conventional weak setup, provided the calibration process to measure the position of the unperturbed beam precedes.

Fig. 4: Real-time observation of the SHEL through a tilted polarizer.
figure 4

a The metasurface-implemented weak measurement setup with a schematic that illustrates the rotation of the film polarizer. b The variation in the rotation angle of the film polarizer over time. c Experimentally measured weak values (red) with theoretical predictions (black solid and dotted) and simulation results (blue and red dashed). The red shaded area indicates the standard deviation across nine consecutive measurements.

Full size image

Before initiating the measurements, we set α = 3° when ϕ = 35°. The amplification factor in this setup is 152.08. Then, nine consecutive measurement cycles are repeated with 100 captures each, taking approximately 196 seconds per cycle. The average time step can be further reduced, with the minimum limited by the camera’s frame rate. The measured results (Fig. 4c, red solid) show good agreement with both theoretical (black) and simulation results (red and blue dashed), particularly near ϕ = 35°, where α is defined. Discrepancies in other angular ranges are attributed to a slight shift in α during the rotation of the film polarizer; similar tendency are observed in conventional weak measurement setups using a commercial linear polarizer for postselection (Supplementary Note 10). This angle shift causes the actual α to be smaller (larger) than our initial setting of 3° at ϕ < 35° (ϕ > 35°), resulting in overestimated (underestimated) W. The same tendency is observed in Fig. 4c, explaining the deviation between the experimental results and theory. Note that theoretical and simulation results are mostly overlapping and nearly indistinguishable. Raw images at several selected times are shown in Supplementary Note 9.

The time evolution of ϕ can be deduced from the measured W in a single shot. Sensitivity and resolution are not discussed in detail here, as they depend on the specific applications of the metasurface-assisted setup. The resolution of δ in this real-time demonstration is 22.69 nm, which is less precise compared to previous metasurface-free setups24. This lower precision is due to suboptimal setup parameters, such as the limited size of the metasurface and the relatively large α, and is not a limitation of our proposal; precision can be improved by several orders of magnitude as discussed in the previous section.

Discussion

In conclusion, we have integrated a metasurface into the weak measurement setup and enabled instantaneous observation of the SHEL. Unlike previous techniques that required multiple steps to evaluate a single spin Hall shift, our approach uses the metasurface to spatially separate the two spin Hall shifted beams into different spots based on their polarization states, allowing for a single-shot readout of the SHEL. This theoretical proposal is experimentally validated in both static and dynamic cases by measuring the SHEL first at an air-prism interface for various amplifications and then through a polarizer by varying its tilted angle over time for a fixed amplification. While we adjust the tilted angle of the anisotropic plate as a proof of concept, our single-shot measurement setup can be extended to monitor real-world phenomena with high precision and combined with previous static measurements to simplify the measurement process. This advancement facilitates real-time measurement of SHEL in dynamic scenarios, even when the original beam position changes over time. One potential direction for future research is the real-time monitoring of molecular concentrations in biological samples or the tracking of chemical reaction rates using our proposed scheme.

Compared to commercially available polarizers used for the postselection, our metasurface has a low extinction ratio and slightly distorts the spatial distribution of the beams, which may lead to less accurate results. This limitation is not an inherent flaw of our approach but can be addressed by improving the polarizer performance of the metasurface, for example, by fabricating it with higher resolution and/or designing it with uniform amplitudes and reduced nonlocality. In our demonstration, we use a metasurface with horizontally aligned meta-atoms and rotate it to dynamically control amplification and precision. However, a metasurface in which meta-atoms have a predefined rotation angle and/or a linear phase along the x-axis (\({\phi }_{1}=-{\phi }_{2}={k}_{0}x\sin \theta\)) can also be a great option, especially when the amplification factor does not need to be changed (Supplementary Note 13). In addition, this metasurface works not only under horizontal or vertical polarization but also under any other linear polarizations (Supplementary Note 14). For further improvement, while the film polarizer is added in our study to match the intensity scale of the two postselected beams, metasurfaces that can independently control both phase and amplitude54,55 could be used for intensity matching and thus to remove the film polarizer (Supplementary Note 15). Finally, applying the multifunctionality of metasurfaces to other weak measurement techniques, such as those used for measuring angular shifts56,57, could be a potential direction for future work.

Methods

Numerical simulations

To numerically predict the postselected beam distribution, the two-dimensional electric field profile of the spin Hall shifted beam was used as the incidence8. The output field from the metasurface was obtained by pointwise multiplying the Jones vector of the incidence with the Jones matrix of the metasurface: \({{\bf{E}}}_{o}(x,\,y)={{{\mathcal{J}}}}(x,\,y){{\bf{E}}}_{i}(x,\,y)\), where subscripts i and o denote the input and output, respectively. Rayleigh-Sommerfeld diffraction was then applied with a propagation distance of zp = 30 mm. The distance between the two postselected beams, dx, is related to the deflection angle ±θ by \({d}_{x}=2{z}_{p}\tan \theta\).

Metasurface fabrication

A 416 nm-thick a-Si:H film was deposited on a glass substrate using plasma-enhanced chemical vapor deposition (PECVD, BMR Technology, HiDep-SC) with flow rates of 10 and 75 sccm for silane (SiH4) and hydrogen (H2), respectively. The operating temperature and chamber pressure were 300°C and 25 mTorr, respectively. The designed metasurface pattern was transferred to positive-tone electron beam resist (Zeon Corporation, ZEP520A) through an electron-beam lithography process (ELIONIX, ELS-BODEN; acceleration voltage: 50 kV, beam current: 10 nA). After developing exposed patterns using a developer (Zeon Corporation, ZED-N50), a 40 nm-thick chromium (Cr) mask was deposited using an electron beam evaporator (KVT, KVE-ENS4004), followed by a lift-off process of dipping in dimethylacetamide for 1 min at 20°C and a sonication process of 45 Hz for 1 min. Finally, Cr mask patterns were transferred onto the a-Si:H film using a dry etching process (TTL, FABstar), followed by the remover of Cr mask using Cr etchant (CR-7).

Optical measurements

In the splitting measurement, the incident light passed sequentially through a half-wave plate, the metasurface, and a lens (f = 100 mm) before being captured by the detector. The polarization angle was adjusted using the half-wave plate. The intensities of the two separated beams were normalized to have a minimum of zero and a maximum of unity.

For the conventional weak measurement setup, weak values were determined by averaging the y position of the intensity distribution as: ∬yI(x,  y)dxdy/∬I(x,  y)dxdy. In the single-shot measurement, the integration was performed over a small region (300 × 300 pixel2 = 1035 × 1035 μm2) around each beam and calculated the y average within each region. The center position was updated iteratively until the error became smaller than the size of a single pixel. This process took an average of 0.12 s to complete. A sample script that computes the weak value from the captured image is publicly available. In the weak measurement setup using the tilted polarizer, the film polarizer (Thorlabs, LPVISE2X2) was mounted on a motorized rotation stage (Thorlabs, KPRM1E/M), which was controlled by a servo motor controller (Thorlabs, KDC101). An artificial time pause was introduced to ensure that the motorized stage reaches the designated angle. The actual elapsed time (average time step: 1.96 s, standard deviation: 0.11 s) was recorded at each capture. A polarized helium-neon laser (Thorlabs, HNL100LB) was used as the light source and a color complementary metal-oxide-semiconductor camera (Thorlabs, CS165CU/M; pixel size: 3.45 μm) served as the detector.