Introduction

Tunable electronic1, magnetic2, and ferroelectric3 properties in two-dimensional materials, e.g., as a function of electric field, electrostatic doping, pressure, number of layers, or relative twist angle, not only facilitate studying the fundamentals of phase transitions in the two-dimensional limit but also unveil their potential for applications. In this context, two-dimensional moiré materials4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20, including twisted bilayer graphene4,5,6,7,8,9,10 and twisted transition metal dichalcogenides11,12,13,14,15,16, have garnered significant recent attention due to the tunability of their physical response as a function of the twist angle and electrostatic gating, which leads to a myriad of ground states including topological phases like the Chern insulators17, integer10 and fractional quantum anomalous Hall effects20 and strongly correlated ones such as Mott insulators5,11, Wigner crystals11, magnetism9, and unconventional superconductivity6. Here, we unveil the remarkable tunability of the electronic and superconducting properties of a seemingly simple topological metal: atomically thin 1T’-WS2. We reversibly tune this system into a regime that simultaneously displays an anomalous Hall effect, usually the hallmark of intrinsic broken time-reversal symmetry and superconductivity, suggesting an unconventional superconducting pairing symmetry.

At ambient pressure, 1T’-WS2 already stands as a promising candidate for topological superconductivity21,22,23,24,25 since, as we discuss below, its band structure is characterized by topologically non-trivial indices. Its close relative, 2M-WS2, which has undergone more extensive studies, harbors topological surface states26,27 as well as Majorana-bound states within its vortex cores28,29. Additionally, 2M-WS2 was identified as an exotic spin-orbit-parity coupled superconductor25, responsible for features such as a two-fold symmetric superconducting state and an exceptionally high upper critical magnetic field, i.e., that surpasses the Pauli paramagnetic limit. These unique attributes have spurred immense interest in transition metal dichalcogenides at the intersection of topology and superconductivity21,22. However, 1T’-WS2 poses a unique challenge due to its metallic nature characterized by a high carrier density21,22. The large carrier density makes the precise control of its electronic state via electrostatic gating quite challenging. In contrast, we find that the mechanical manipulation of its lattice parameters provides a fruitful avenue for reversibly tuning the electronic properties without introducing impurities in 1T’-WS2. In this study, we harness hydrostatic pressure as a means for tuning the lattice parameters of 1T’-WS2 and hence, its electronic band structure. Through systematic pressure-dependent electrical transport experiments, we observe the emergence of the anomalous Hall effect upon increasing the pressure, which coincides with the suppression of the superconducting state observed at ambient pressure. Intriguingly, as we continue to increase pressure, while remaining within the metallic state characterized by the anomalous Hall effect, we observe the emergence of a pressure-induced reentrant superconducting phase displaying very high upper critical fields, i.e., 2.5 times larger than the weak coupling Pauli limiting field value.

Results

To conduct transport measurements under various hydrostatic pressures, we fabricated Hall bar devices using mechanically exfoliated few-layer (twelve-layers) 1T’-WS2 (see Fig. 1a–d and “Methods” Section I) and positioned the sample within a piston-cylinder pressure cell, using Daphne oil as the pressure medium. The highlight of our experiment is illustrated in Fig. 1e–g displaying the superconducting phase diagram as a function of the hydrostatic pressure based on data collected from three distinct samples. Figure 1e portrays the critical temperature (Tc) of the superconducting transition plotted against the external hydrostatic pressure (P). Initially, Tc exhibits a gradual decline with increasing P, followed by its abrupt vanishing at \(P=1.15\) GPa, implying the suppression of superconductivity (referred to as SC1). Upon further increasing P, a second superconducting dome (noted as SC2) emerges at \(P=1.8\) GPa, which is characterized by a lower Tc with respect to SC1. Next, we investigate the upper critical magnetic fields, which we define as the field at which the sample resistance drops to half of its value in the normal state just above the transition. When comparing SC2 to SC1, we find that the out-of-plane superconducting upper critical magnetic fields (\({\mu }_{0}{H}_{c2\perp {bc}}\)), for fields perpendicular to the bc-plane, and the ratio \({\mu }_{0}{H}_{c2\perp {bc}}/{T}_{c}\) are markedly smaller (Fig. 1f) than the values measured for SC1. Surprisingly, the in-plane upper critical magnetic fields (\({\mu }_{0}{H}_{c2{||bc}}\)) for the SC2 phase for fields oriented along the c-axis exhibit similar magnitudes relative to those of the SC1 state, leading to a twofold increase in the ratio \({\mu }_{0}{H}_{c2{||c}}/{T}_{c}\) for the SC2 state (Fig. 1g). This distinct behavior for the in-plane and out-of-plane upper critical fields reveal a substantial increase in the superconducting anisotropy \(\gamma\), defined as the ratio \(\gamma=\frac{{H}_{c2{||bc}}}{{H}_{c2\perp {bc}}}={\zeta }_{{||bc}}/{{\rm{\zeta }}}_{\perp {bc}}\), where \({\zeta }_{{||bc}}\) and \({{\rm{\zeta }}}_{\perp {bc}}\) represent the coherence lengths along and perpendicular to the bc-plane, respectively. This remarkable increase in anisotropy indicates that the superconducting properties of the SC2 state differ from those of SC1 (see also Supplementary Fig. 2), i.e., characterized by a larger in-plane coherence length versus a decreased inter-planar one.

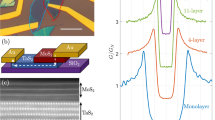
Fig. 1: Observation of a tunable superconducting state in atomically thin 1T’-WS2.
figure 1

a Crystal structure and the unit cell of 1 T’-WS2 crystal. b Optical microscopy image of an atomically thin 1T’-WS2 flake, obtained through mechanically exfoliation from the crystal’s bc plane and subsequently encapsulated with hBN. The flake, comprising approximately twelve atomic layers, is demarcated by white dashed lines. Current (I+ and I−) and voltage (V+ and V−) probes for four-terminal electrical transport measurements are also marked. c Atomic force microscopy (AFM) image of a 1 T’-WS2 flake with the same optical contrast as the flake in (b). d AFM height (h) profile collected along the green line in (c) (the arrow indicates the directions of the scan), revealing a thickness of \(h\simeq 6.4\) nm that aligns with the expected thickness for twelve atomic layers of 1T’-WS2. e Critical temperature (Tc) of the superconducting transition plotted against the external hydrostatic pressure (P). Initially, Tc decreases with increasing pressure, leading to the disappearance of the superconducting state SC1 (pink-shaded region), at \(P=1.15\) GPa. However, at \(P=1.8\) GPa, a new superconducting state (SC2; purple shaded region) emerges with a smaller Tc relative to SC1. f Out-of-plane upper critical magnetic field (\({\mu }_{0}{H}_{c2\perp {bc}}\)) plotted against pressure. Akin to Tc, \({\mu }_{0}{H}_{c2\perp {bc}}\) decreases with increasing P in the SC1 state and then resuscitates with a smaller value in the SC2 state. The inset shows the P dependence of \({\mu }_{0}{H}_{c2\perp {bc}}\) normalized by Tc, with \({\mu }_{0}{H}_{c2\perp {bc}}/{T}_{c}\) being smaller in the SC2 state. g Pressure-dependence of the in-plane upper critical magnetic field (\({\mu }_{0}{H}_{c2{||bc}}\)). Like Tc and \({\mu }_{0}{H}_{c2\perp {bc}}\), \({\mu }_{0}{H}_{c2{||bc}}\) decreases with increasing P in the SC1 state. However, \({\mu }_{0}{H}_{c2{||bc}}\) in the SC2 state becomes similar in magnitude to that of the SC1 state, despite the comparatively much smaller Tc and \({\mu }_{0}{H}_{c2\perp {bc}}\). The inset illustrates the P dependence of \({\mu }_{0}{H}_{c2{||bc}}\) normalized by Tc, revealing a nearly two-fold larger \({\mu }_{0}{H}_{c2{||bc}}/{T}_{c}\) in the SC2 state. Data in (e-g) were obtained from three samples with identical thicknesses, and are represented by the purple, green, and orange data points. Source data are provided as a Source Data file.

Full size image

Figure 2 provides illustrative examples of the raw electrical transport data, from which we constructed the phase diagrams depicted in Fig. 1e-g. The temperature (T) dependence of the four-probe resistance (R) of a 1T’-WS2 sample reveals a metallic response under all pressures (shown in Fig. 2a). At ambient pressure (\(P\cong 0\)), the R as a function of T plot demonstrates a discernible superconducting transition. With increasing pressure, this transition steadily shifts to lower temperatures, a trend that becomes evident by comparing the traces corresponding to pressures of 0.1, 0.5, and 1.0 GPa (as shown in Fig. 2a), until it vanishes at \(P=1.15\) GPa. The analysis of the magnetic-field dependence, conducted for fields aligned both perpendicular to the bc-plane and along the c-axis, reveals a consistent pattern: the superconducting transition shifts to lower fields within the SC1 state as pressure increases (Fig. 2b, c). In an intermediate pressure range, exemplified by the traces collected under \(P=1.15\), 1.5, and 1.63 GPa in Fig. 2a, b, no superconducting transition is observed. Remarkably, at \(P=1.8\) GPa, the superconducting transition resurfaces with a notably lower transition temperature (Fig. 2a) and reduced upper critical magnetic field for fields perpendicular to the bc-plane (Fig. 2b). However, for fields parallel to the bc-plane, the transition displays similar upper critical fields relative those of the SC1 state. For instance, the trace at \(P=2.3\) GPa (Fig. 2c) illustrates this occurrence, resulting in substantial values for the ratios \({\mu }_{0}{H}_{c2{||bc}}/{T}_{c}\). Notice that our transport results are reproducible upon depressurization, indicating a return to the original crystallographic structure. Supplementary Fig. 3 presents transport data at 0.1 GPa, showing measurements taken as pressure increased from 0 to 0.1 GPa and then decreased from 2.3 GPa to 0.1 GPa. Both measurements display the same transport behavior, demonstrating reversibility.

Fig. 2: Transport measurements under several pressures reveal two superconducting states.
figure 2

a Temperature (T) dependence of the four-probe resistance (R) for the 1T’-WS2 device measured at different hydrostatic pressures (P). The sample exhibits metallic behavior at all pressures. At \(P=0\), R as a function of T shows a superconducting transition, which shifts to lower temperatures with increasing pressure before vanishing at \(P=1.15\) GPa. However, superconductivity reappears at 1.8 GPa in the reentrant state SC2, occurring at notably lower temperatures relative to the first superconducting state, SC1. b Magnetoresistance of the 1T’-WS2 device when the magnetic field is oriented perpendicular to the bc-plane, plotted for different pressures. The superconducting transition shifts to lower fields upon increasing pressure, disappearing at \(P=1.15\) GPa and reappearing at 1.8 GPa, with a lower critical field when compared to SC1. c Magnetoresistance of the 1T’-WS2 device when the magnetic field is oriented along the c-axis of the crystal, shown for different pressures. Akin to the data in (b), the superconducting transition shifts to lower fields with increasing pressure in SC1 state. However, in contrast to the behavior observed for fields perpendicular to the bc plane, the superconducting transition in the SC2 state occurs at a similar temperature when compared to the SC1 state for fields oriented along the bc-plane. All data in (b and c) were collected at \(T=0.3\) K. Source data are provided as a Source Data file.

Full size image

After uncovering the superconducting phase diagram of 1T’-WS2, we turn to investigate its normal state. To achieve this, we conducted Hall effect measurements (depicted for \(T=10\) K in Fig. 3 and Supplementary Fig. 3) for various pressures. These measurements provide crucial insights into the distinctions between the SC1 and SC2 states, by shedding light on the normal state from which superconductivity nucleates. When examining the Hall resistance within the pressure range where the SC1 state is observed, a linear response as a function of the field is observed (Fig. 3a, b for \(P=0\) and 1.0 GPa, respectively). This is consistent with prior findings under vacuum21,22. Upon further increasing pressure, a noteworthy development occurs—precisely at \(P=1.15\) GPa, where the superconducting state vanishes, an anomalous Hall component emerges (Supplementary Fig. 4a,b). The anomalous Hall effect is also present at pressures \(P \, > \, 1.15\) GPa, as evident in the \(P=1.63\) GPa data (Fig. 3c, d). Surprisingly, even at higher pressures where SC2 is observed the normal state continues to exhibit an anomalous Hall effect, albeit less pronounced; refer to Fig. 3e, f (\(P=2.3\) GPa) and Supplementary Fig. 3c, d (\(P=1.8\) GPa), where the anomalous Hall effect is evident but less prominent relative to the signal observed in the range \(1.15 \, < \, P \, < \, 1.8\,\)GPa. It is worth noting that no hysteresis is observed in these experiments.

Fig. 3: Emergence of the anomalous Hall effect upon the disappearance of the first superconducting state and its coexistence within the reentrant superconducting state.
figure 3

Hall resistance (Rxy) at different pressures: \(P=0\) GPa (a), 1.0 GPa (b), 1.63 GPa (c), and 2.3 GPa (e), plotted as a function of the magnetic field with fields oriented perpendicularly to the bc-plane. In (a, b), Rxy shows a linear response as a function of the field, displaying no anomalous Hall effect. However, at \(P=1.63\) GPa (c) and 2.3 GPa (e), along with a reasonably linear Hall effect, an anomalous component emerges at low fields. Anomalous Hall resistance, \({R}_{{xy}}^{{AHE}}\), obtained after subtracting the linear-in-field component of Rxy, plotted as a function of magnetic field for \(P=1.63\) GPa (d) and 2.3 GPa (f). Superconductivity is absent at \(P=1.63\) GPa where the anomalous Hall effect is more pronounced. Conversely, in the reentrant superconducting state at 2.3 GPa, superconductivity coexists with the relatively subdued anomalous Hall effect. All the data were acquired at \(T=10\) K. Source data are provided as a Source Data file.

Full size image

Lastly, we examine the temperature dependence of the anomalous Hall effect. Figure 4 showcases the key data, where we provide two examples: one at \(P=1.63\) GPa, a pressure where no superconductivity is observed at low temperatures, and the other at \(P=2.3\) GPa, where the reentrant superconductivity becomes prominent. In both instances, a strong temperature dependence is observed for the anomalous component, while the linear-in-field component exhibits minimal sensitivity to temperature. Notably, at \(P=1.63\) GPa, where the anomalous Hall effect is more pronounced, this effect significantly diminishes at a temperature of \(T=28\) K (Fig. 4a, b). Conversely, at \(P=2.3\) GPa, the anomalous Hall effect vanishes entirely by \(T=25\) K (Fig. 4c, d). This temperature-dependent behavior provides an indicative energy scale for the destabilization of the underlying magnetic order. Notably, the R as a function of T data (Supplementary Fig. 5) reveals a weak anomaly near \(T=30\) K, which nearly coincides with the disappearance of the anomalous Hall effect. A clear understanding of what this anomaly represents and whether it signals a phase-transition would require structural analysis under high pressures and therefore will be left for future research.

Fig. 4: Temperature dependence of the anomalous Hall effect.
figure 4

a Hall resistance (Rxy) at \(P=1.63\) GPa, as a function of the magnetic field perpendicular to the bc-plane, for different temperatures. An anomalous Hall component is evident, and this component weakens as the temperature increases. b Anomalous Hall resistance, obtained by subtracting the linear-in-field component of Rxy, as a function of the magnetic field at \(P=1.63\) GPa, and for different temperatures. The anomalous Hall effect diminishes with rising the temperature, and becomes almost entirely suppressed at \(T=28\) K. c Rxy at \(P=2.3\) GPa, where the reentrant superconductivity is present, as a function of the magnetic field perpendicular to the bc-plane, for different temperatures. The anomalous Hall component also weakens with increasing temperature. d Anomalous Hall resistance, \({R}_{{xy}}^{{AHE}}\), obtained by subtracting the linear-in-field contribution from Rxy, as a function of magnetic field at \(P=2.3\) GPa, and for different temperatures. The anomalous Hall effect diminishes as the temperature rises and eventually becomes negligible at \(T=25\) K. Parts of the curves for H < 0.5 T and T < 2 K in (c, d) are blocked by the superconducting state. Notably, the value of saturated \({R}_{{xy}}^{{AHE}}\) at \(P=2.3\) GPa in high magnetic fields (above Hc2) and below Tc appears to slightly decrease when compared to its immediate higher-temperature value. This behavior contrasts with the one observed at \(P=1.63\,\)GPa, where the sample is no longer superconducting, and the saturated value of \({R}_{{xy}}^{{AHE}}\) continues to increase as the temperature is lowered. This observation suggests a possible competition between superconductivity and the anomalous Hall effect in the reentrant superconducting state at \(P=2.3\) GPa. Insets of (b and d) illustrate the temperature dependence of RxyAHE (3T). Source data are provided as a Source Data file.

Full size image

Examining the temperature-dependent anomalous Hall effect (\({R}_{{xy}}^{{AHE}}\)) data at these two pressures hints at a potential competition between the anomalous Hall effect phase and superconductivity. First, at a given temperature, the saturated value of \({R}_{{xy}}^{{AHE}}\) at \(P=2.3\) GPa (where the reentrant superconducting state is present) is lower than the one measured at \(P=1.63\) GPa, where the sample does not exhibit superconductivity. Second, at \(P=2.3\) GPa, and below Tc, the saturated value of \({R}_{{xy}}^{{AHE}}\) appears to decrease slightly compared to its immediate higher-temperature value. This contrasts with the behavior measured at \(P=1.63\) GPa, where the saturated value of \({R}_{{xy}}^{{AHE}}\) consistently increases as the temperature is lowered. These observations indicate a possible competition between superconductivity and the anomalous Hall effect. The reentrant superconducting state manifests when \({R}_{{xy}}^{{AHE}}\) is suppressed at low temperatures.

The wealth of pressure-tunable electronic states in 1T’-WS2, as depicted in Figs. 1–4, prompts us to elucidate the dependence of the low-energy electronic structure on the applied pressure (see Supplementary Figs. 6, 7 and Supplementary Table 4, 5 for details). To this end, we performed first-principles calculations of the electronic band structure as a function of pressure, which allows us to track changes occurring around the Fermi energy as a function of pressure, as well as identify possible topological phase transitions (Fig. 5a, d–f). For our calculations, we assume that 1T’-WS2 remains structurally stable under pressure. This assumption is supported by two key observations: (i) our transport measurements reveal a reversible pressure evolution (Supplementary Fig. 3), and (ii) our phonon calculations show no signs of phononic instability within the studied pressure range (Supplementary Fig. 8). We observe that the system undergoes a topological phase transition upon increasing pressure, where the topological indices are defined with respect to the direct gap above the band leading to electron-hole compensation: at P = 0 GPa, the system realizes a topological crystalline insulator followed, at P ~ 1.0 GPa, by a phase transition as a result of a band inversion at the point Y, which drives the system into a strong topological phase. We performed a slab calculation at P = 2.3 GPa (Fig. 5c), therefore in the strong topological phase, finding that the surface perpendicular to the stacking direction exhibits a cone at \(\underline{{\Gamma }}\). located 50 meV above the Fermi level. Since these boundary modes reside at higher energies, they are not expected to influence the low-energy transport properties of the system but may be accessed by other experimental probes.

Fig. 5: Pressure-tuned topological and Lifshitz transitions revealed from electronic band structure and susceptibility calculations.
figure 5

a Band structure as obtained from first principles calculation at two values of pressure P = 0 GPa, and 2.3 GPa, marked by solid and dashed lines, respectively. The band structure is shown along a path in the reciprocal space (see Supplementary Table 5), and the color of the bands denotes the band inversion driving the change of topology (symmetry indicators z2w1 = 1, z2w2 = 1, z2w3 = 0, z4 = 0 P = 0 GPa and z2w1 = 0, z2w2 = 0, z2w3 = 0, z4 = 3 for P = 2.3 GPa). b Leading eigenvalue of the random phase approximation (RPA) susceptibility evaluated along the same path in momentum space as in (a) for P = 2.3 GPa and a Hubbard interaction of U = 6.5 eV. The leading divergence discussed in the main text arises along the Y1-Γ line. c Surface spectral function for a slab at P = 2.3 GPa, with a surface cone arising at \(\underline{{\Gamma }}\) located at ~ 50 meV. The coordinates of \(\underline{{Z}}\), \(\underline{{\Gamma }}\) and \(\underline{{R}}\) in terms of the basis vectors of the reciprocal cell in the semi-infinite slab geometry are (0,1/2), (0,0), and (1/2,1/2), respectively. Fermi surface as obtained from the first principles calculations at d, P = 0 GPa, e, P = 1.63 GPa, and f, P = 2.3 GPa in the first Brillouin zone. Blue (purple) Fermi surface sheets mark the electron-like (hole-like) pockets. In (e and f), the Lifshitz transition fusing electron-like pockets and extending over Brillouin zone boundaries, respectively, is visible. Additionally, in (f), a hole in the hole-like pocket along qx emerges.

Full size image

The change in topology, however, has a profound effect on the orbital makeup of the bands at the Fermi surface. In the low-pressure phase, these bands exhibit a mixed d- and p-orbital nature around Y, whereas in the strong topological phase, their character changes to predominantly p-orbital. It would be interesting to further explore how this orbital transformation is linked to the breakdown of superconductivity. At lower energies, we find the emergence of a markedly three-dimensional topography for the Fermi surface, despite the layered nature of the material. At P = 0 GPa (Fig. 5d), the Fermi level is fixed at perfect electron-hole compensation, which is in line with our Hall transport measurements, revealing linear behavior as a function of the magnetic field at low temperatures, despite the presence of both types of carriers. With increasing pressure, we first observe a Lifshitz transition merging both electron-like Fermi surfaces (Fig. 5e). Subsequently, at yet higher values of pressure, we observe merged Fermi surface sheets to cross the Brillouin zone boundaries in addition to the appearance of a hole in the Fermi sheet around the Y point (Fig. 5f). Lifshitz transitions are connected to van Hove singularities in two dimensions, which are singularities in the density of states, and can introduce new possible pairing momenta, thus marking potential ‘hot spots’ on the Fermi surface for nucleating superconductivity.

Discussion

Having elucidated the electronic structure of 1T’-WS2 under pressure, we discuss the plausible explanations for the experimental observations. A possible origin for the emergence of the anomalous Hall effect, particularly in strongly spin-orbit coupled systems such as 1T’-WS2, is magnetic order. However, a sizable anomalous Hall effect has also been observed in paramagnetic systems, such as ZnO/MnZnO30, or Kagome metals where some form of fluctuating, or weak magnetism is debated, but conclusive evidence for long-range magnetic order is lacking31. Another possible origin for such an anomalous Hall effect is skew scattering on localized magnetic moments. However, S is not magnetic while W is known to be paramagnetic. Furthermore, anomalous Hall is not observed at lower pressures, indicating the absence of magnetic impurities. Still, the significant temperature dependence of the anomalous Hall signal, with a near-complete attenuation of the anomalous Hall effect around \(T=30\) K, hints towards an itinerant nature of the magnetic order relating to electron-electron interactions. To elucidate this possibility theoretically, we derived Wannierized tight-binding models at fixed values of pressure P = 0 GPa and P = 2.3 GPa and used the random phase approximation (RPA) method to evaluate the susceptibility in the system (Fig. 5b). The RPA results allow us to identify possible charge and spin instabilities of the Fermi liquid. Specifically, we obtain a leading divergence of the susceptibility at a star of incommensurate wave vectors (Fig. 5b), which can either lead to a single-q or multi-q ordered state. In addition, this leading divergence is magnetic in nature. Therefore, it may lead to an incommensurate spin density wave. Such a magnetic tendency, and associated magnetic fluctuations, offer a plausible explanation for the observed anomalous Hall response32. Therefore, our discovery of the anomalous Hall effect in 1T’-WS2 encourages further investigations into magnetic order using complementary experimental techniques, such as muon spin relaxation experiments.

Upon delineating the plausible origins of the observed anomalous Hall effect, it is worth discussing how it may influence the reentrant superconducting state. In fact, our experimental findings clearly indicate a correlation between the superconductivity and the anomalous Hall effect. First, the SC1 state disappears when the anomalous Hall effect emerges. The anomalous Hall effect is prominent in the pressure range where superconductivity is absent and becomes relatively subdued in the pressure range where the reentrant superconducting state (SC2) emerges. Conversely, Tc is higher in the SC1 state where the anomalous Hall effect is not observed, while it is lower in the SC2 state where the anomalous Hall effect is observed. These observations also raise the possibility of an unconventional, perhaps a spin-triplet paired, superconducting state in phase SC2, which prompts us to discuss plausible order parameters for the superconducting phases within 1T’-WS2, leveraging a symmetry analysis. The low symmetry inherent to the 1T’ structure limits the potential irreducible representations for the superconducting order parameter to four: Ag, Bg, Au, and Bu, as dictated by the C2h point group symmetry. This group is generated by inversion symmetry and a (nonsymmorphic) C2 symmetry or—equivalently—to an in-plane mirror symmetry. Among these representations, Ag and Bg (Au and Bu) are characterized as even (odd) under inversion, whereas Ag and Bu (Au and Bg) belong to mirror-even (mirror-odd) categories. Notably, all these irreducible representations are one-dimensional. This framework leads us to discount the likelihood of spontaneous time-reversal symmetry breaking stemming from the superconducting order in 1T’-WS2—a mechanism seen in chiral p-wave superconductors. Nonetheless, it is plausible for superconductivity to emerge in a phase, where time-reversal symmetry is broken by an alternative mechanism. Neglecting multiorbital effects, we can associate Ag and Bg with singlet pairing and Au and Bu with triplet pairing. Should we assume that the ambient pressure scenario realizes the Ag phase (fully gapped), and that the reentrant superconducting phase unveiled in this study is distinct, three potential candidates remain for its order parameter: Au, Bg, and Bu. Among these, both Bg and Au exhibit nodal characteristics, featuring line nodes in three dimensions and point nodes in two dimensions. Their symmetry character manifests as dxy and px, respectively. In contrast, Bu may potentially be nodeless. In a time-reversal symmetry-broken environment, suggested by the anomalous Hall effect observed with SC2, we can speculate that the triplet phases Au and Bu might be more inherently compatible with this reentrant superconducting state. The possibility of an unconventional superconducting phase at re-entrance would be consistent with our first-principles calculations, which point to a progressive weakening of the electron-phonon coupling with the concomitant increase in the spin susceptibility as the hydrostatic pressure increases (Supplementary Figs. 8–10).

Superconducting phases in WS2 were previously studied under hydrostatic pressure. For example, in the 2M-WS2 phase, the superconducting state gradually weakens upon increasing pressure33, while in the 3R-WS2 phase, superconductivity only emerges at pressures exceeding 45 GPa34. Insofar, there are no reports on the effect of pressure on the superconductivity of the 1T’ phase of WS2. The 1T’ phase we examine here under hydrostatic pressure features subtle differences in unit cell parameters (see Supplementary Information) with respect to the other previously studied WS2 phases. These structural differences are likely to contribute to significant differences in the observed high-pressure behavior with respect to the other phases, as exposed by our experiments.

In conclusion, we have discovered pressure-induced reentrant superconductivity coexisting with the anomalous Hall effect in atomically thin 1T’-WS2. The system undergoes a series of phase transitions under increasing pressure, as depicted schematically in Supplementary Fig. 11. The superconducting state gradually weakens with increasing pressure, indicated by diminishing Tc and Hc2 values. This transition progresses with the suppression of Tc at 1.15 GPa coinciding with the onset of the anomalous Hall effect. Interestingly, at \(P=1.8\) GPa, superconductivity reemerges, albeit with a lower Tc and an increased superconducting anisotropy while still coexisting with a less pronounced anomalous Hall effect. This suggests an interplay between two distinct electronic orders, i.e., superconductivity with magnetism. The reentrant superconducting state exhibits substantially elevated \({\mu }_{0}{H}_{c2{||bc}}/{T}_{c}\) values, while \({\mu }_{0}{H}_{c2\perp {bc}}/{T}_{c}\) decreases, indicating a superconducting state that is distinct from the one at low pressures, possibly of an unconventional nature. This discovery represents clear evidence for the pressure tuning of the electronic properties of atomically thin 1T’-WS2, manifesting as pressure-induced anomalous transport and potentially, an unconventional superconducting phase. Furthermore, with our findings, 1T’-WS2 joins a rare but growing number of materials (for instance, the AV3Sb5 Kagomes; A\(\equiv\) K, Rb, Cs)31, in which superconductivity nucleates in a phase exhibiting signatures of broken time-reversal-symmetry in the form of an anomalous Hall-effect. However, the consequences of time-reversal-symmetry breaking for the superconducting pairing symmetry in 1T’-WS2 remains unclear and as an open question for future research.

Methods

Synthesis of 1T’-WS2 single crystals

Initially, K2WO4 and S powders with a molar ratio of 1:4 were meticulously mixed and ground in a mortar with a total weight of 1.0 g. The resulting homogeneous mixture was then sealed in an evacuated quartz ampoule, which was then heated in a box furnace. The temperature was gradually elevated to 500 °C in ~6 h, and then maintained for another 90 h. The precursors were obtained after the furnace was turned off and naturally cooled down to room temperature. Next, 500 mg of the prepared precursor was placed into an alumina crucible within a quartz tube, which was cleaned and purged with H2/Ar mixed gas (20% H2/80% Ar) for 15 min three times. The crucible was then placed into the preheated furnace at 750 °C for further reaction. The reaction was maintained for 10 h before rapidly cooling the quartz tube to room temperature. After that, the resulting product was thoroughly washed with Milli-Q water until the pH value of the suspension reached 7–8, and it was subsequently stored in Milli-Q water for 24 h. To remove any remaining potassium residue, the crystals were transferred to an I2 acetonitrile solution for another 24 h. Finally, the 1 T’-WS2 crystals were obtained after twice washing with Milli-Q water followed by drying in a vacuum oven at room temperature.

We follow the nomenclature used in ref. 21. by classifying our crystals as 1T’-WS2 (crystal structure is shown in Fig. 1a). We refer the reader to the supplementary Information for a detailed structural study of our 1T’-WS2 crystals.

Device fabrication and characterization

We utilized a polydimethylsiloxane (PDMS) stamp-based mechanical exfoliation technique to fabricate atomically thin 1T’-WS2 devices. The sample contacts on the silicon substrates were patterned with a 280 nm layer of thermal oxide using electron beam lithography, followed by chemical development and metal deposition (5 nm Cr/35 nm Au). The freshly exfoliated 1T’-WS2 flakes were obtained from bulk single crystals and placed on PDMS stamps. To ensure uniformly thick samples with good geometry, we examined them under optical microscope before transferring them onto SiO2/Si substrates with pre-patterned Cr/Au electrodes. Note that, we identified the thickness of the flakes by optical contrast, which is a commonly used method for the sensitive samples, see, e.g., ref. 35. As widely known in the field of two-dimensional materials, samples with various thicknesses show different optical contrast36. Therefore, we characterized the thickness of the samples using atomic force microscopy and established the corresponding relationship between optical contrast and thickness beforehand. To preserve the intrinsic properties of the compound and minimize environmental effects, we encapsulated the samples with hexagonal boron nitride (h-BN) thin films, with thicknesses ranging from ~10 to ~30 nm. This encapsulation ensured that the samples on the devices were protected from direct exposure to air. All sample fabrication processes were performed in a glovebox with a gas purification system maintaining the environment at low levels of O2 and H2O (<1 ppm). For imaging, we used an Olympus BX 53M microscope to capture optical images, and AFM images were taken with a Bruker Dimension Icon3 in tapping mode.

Pressure-dependent magnetotransport measurements

Measurements at variable pressure were conducted using a standard oil-based piston pressure cell. The 1T’-WS2 devices were securely mounted to the pressure cell using electrically insulating epoxy. To create hydrostatic pressure, the pressure cell was filled with Daphne 7575 oil, a suitable hydrostatic fluid. Once assembled, the pressure cell was placed in a hydraulic press, and pressure was applied by a piston fed through a hole in the threaded top screw of the cell. When the desired pressure was achieved, the top screw was clamped to lock in the pressure. For pressure measurements at low temperatures (around \(T=10\) K), a small ruby chip fixed to the tip of a fiber optic was utilized. The low-temperature and variable pressure magnetotransport measurements were carried out in a 3He variable temperature insert at a base temperature of 0.3 K, with magnetic fields up to 18 T. These measurements were conducted at the National High Magnetic Field Laboratory in Tallahassee, Florida, USA. As pressure can only be varied at room temperature, the samples underwent different thermal cycles during the measurements at different pressures. To ensure the reliability of the results, multiple devices were prepared and measured.