Abstract
Moiré superlattices in van der Waals materials have emerged as a promising platform for studying the correlated states in condensed matter physics. These correlated states have substantial effects on the emission coherence, an important parameter for quantum light applications. However, the effect of correlated states on the excitonic emission coherence is largely unexplored. Here, we show that the coherence of moiré interlayer exciton emission in tungsten diselenide (WSe2)/molybdenum disulfide (MoS2) heterobilayers is sensitive to the correlated insulating states in this material. We demonstrate that the emission linewidth of interlayer exciton shows a dip at a particular power range, which we attributed to the excitonic (bosonic) interaction. Moreover, such linewidth minima also appear in the doping dependence of the photoluminescence spectrum at the integer electronic filling factor, fel = 1, demonstrating the effect of the electronic (fermionic) correlated insulating state on the interlayer exciton emission coherence. Our results demonstrate the richness of exciton-exciton and exciton-electron interactions in moiré semiconductors and pave the way for engineering emission coherence by controlling such interactions.
Similar content being viewed by others
Introduction
Understanding the impact of correlated states of particles on material properties is a crucial step in advancing solid-state devices1,2. Correlated states occur when the behaviours and properties of multiple particles, including fermions (e.g., electrons) and bosons (e.g., excitons (bound electron-hole pairs)), are interdependent. These states are related to many fascinating phenomena, including superconductivity3,4 and correlated insulators5,6.
One notable consequence of particle correlation is that their emission will be correlated or synchronized. This behaviour modifies the overall coherence of the total emission from the material7,8. Hence, by examining the coherence of the emitted light9,10,11,12, we can directly probe the particle correlation unambiguously. Coherence is also an important figure of merit for many applications, including laser and quantum light sources. Hence, it is crucial to understand the connection between coherence and correlated state in solid-state physics.
One of the promising platforms for performing such a study is the semiconductor two-dimensional (2D) moiré superlattice based on transition metal dichalcogenide (TMD)13,14,15,16,17. The in-plane moiré superlattice is formed by the interference pattern resulting from the interaction between two or more stacked monolayer TMD materials. The localization induced by this superlattice can result in flat bands18,19,20, enhancing the effect of the particle correlation on the material behavior21,22. Moreover, the doping and electric field in the 2D material can be controlled precisely using electrical gating23, enabling the study of correlated behaviour in a large range of particle density and electric field24,25,26,27. This versatility makes it a promising tool for the quantum simulation of correlated states, including the effect of correlated states on emission coherence.
Here, by performing excitation power, temperature, and doping dependence study, we experimentally demonstrate the effect of correlated state on the coherence of interlayer exciton (IX, i.e., bound electron-hole pair with electron and hole located in different layers) photoluminescence (PL) emission in WSe2/MoS2 heterobilayer. From the power-dependent PL spectrum and coherence time measurement, we find that the IX PL spectrum linewidth decreases while its coherence time increases within a particular power range, indicating the effect of excitonic interaction28,29,30,31. The observed linewidth dip persists until a temperature of 50 K, above which the phonon-induced scattering suppresses the linewidth reduction. The linewidth reduction is also observed when the carrier doping, instead of excitation power, is increased until the linewidth reaches the minimum value at the filling factor fel = 1, i.e., one electron has been added to each moiré cell. These findings demonstrate the effect of excitonic and electronic correlation on the IX emission coherence.
Results
Device structure and conceptual overview
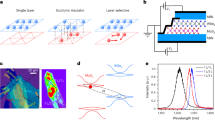
The device structure is shown in Fig. 1a, while the optical image of the fabricated device (Device 1) is shown in Fig. 1b (see Methods for the fabrication detail). We adopt the dual capacitor structure, allowing carrier doping control by gate voltages. The heterobilayer consists of monolayer WSe2 stacked on monolayer MoS2. The MoS2 and WSe2 are connected to a common electrical ground. The second harmonic generation (SHG) signal (Supplementary Fig. S1a) in the heterostructure region is suppressed, indicating that the stacking is closer to AB (i.e., a 60o twist angle) stacking32. By performing polarization-resolved SHG (Supplementary Fig. S1b), we determine that the twist angle is close to AB stacking within ±1o. The heterobilayer is placed between two dielectric hexagonal boron nitride (hBN) layers, each with a thickness of around 11 to 12 nm (Supplementary Fig. S1c). The top and bottom graphite electrodes sandwich the hBN layers, completing the capacitor structure. One voltage source (Vg) is connected to both electrodes for controlling carrier doping.
Due to the different lattice constant between MoS2 and WSe2, a moiré superlattice is created even well-aligned19,33. The superlattice potential induces not only electron localization but also exciton localization34, creating multiple moiré IX energy levels (Fig. 1c)35,36,37,38. The interaction between the moiré IX and the moiré-induced quasiparticle lattice (i.e., either electron or exciton lattice) can affect the moiré IX PL emission29,30,31,39,40,41, such as the coherence (Fig. 1d, e). Our particular interest is the effect of the superlattice on the high energy moiré IXs. These moiré IXs are less confined compared to the low-energy IX. Hence, they are more affected by the surrounding environment. Thus, their emission properties, including the linewidth and coherence, are expected to be sensitive to correlated states involving multiple particles.
a Device structure. The black, blue, purple, and green layers indicate graphite electrodes, hBN, WSe2, and MoS2, respectively. One voltage source (Vg) is connected to both electrodes to control the carrier doping. b Optical image of the fabricated device (Device 1). The solid line illustrates the heterostructure region. The dotted lines illustrate the graphite region as top gate, bottom gate and ground. The scale bar is 10 μm. c Illustration of interaction between moiré interlayer exciton (IX) and moiré-induced quasiparticle lattice. The linewidth of the high-energy moiré IX can be affected by the interaction. d, e A schematic of moiré IX emissions in low coherence (d) and high coherence (e). The temporal coherence of the moiré IX is affected by the correlated states. The different coloured arrows illustrate the IX emissions at different energies.
Enhanced IX coherence via IX-IX interaction
We then study the evolution of the PL spectrum when the excitation power is varied (Fig. 2a). At high enough excitation power (above 8 μW), we observed the emergence of the high-energy IX peak (labelled as P2), whose emission dominates the PL signal at higher power (above 34 μW). Similar results are obtained from another bilayer sample (Supplementary Fig. S2a). Power dependence of the PL spectrum under different excitation wavelengths also shows a similar behaviour (Supplementary Fig. S3). More discussion on the origin of the P2 emission is given in Supplementary Note 1.
In this study, we focus on the high-energy P2 emission. Figure 2b shows the power-dependent linewidth of the P2 emission obtained from two-peak Gaussian fitting of the PL spectra (see inset of Fig. 2b for the fitting result at 34 μW). The P2 linewidth decreases from 19.3 meV at ~34 μW to 17.6 meV at ~110 μW, resulting in a linewidth dip at the 100 to 150 μW power range. Such behaviour is also observed from a different excitation ___location (Supplementary Fig. S4) as well as from another sample (Supplementary Fig. S2b). To confirm the linewidth narrowing of the P2 emission, we measured the coherence time of the P2 emission (coming from the high-energy moiré IX decay) using a Mach-Zehnder interferometer setup with an installed delay line in one of the arms (see inset of Fig. 2c). Optical filters were applied before the interferometer to select the P2 emission (see Methods for measurement setup detail). We recorded the intensity as a function of the time delay and extracted the coherence time for various excitation powers (Supplementary Fig. S5). As shown in Fig. 2c, we observed a peak in the power-dependent coherence time at the power range where the linewidth narrowing happens. Considering that the coherence time is inversely proportional to the linewidth, such observation confirms the linewidth narrowing at this power range.
The observation of the linewidth dip above can be understood by considering the power dependence of the spectrum broadening. The linewidth of the PL emission (wPL) results from inhomogeneous and homogeneous broadening42,43. Considering the IX long lifetime of ~4 ns (see Supplementary Fig. S6a for the time-resolved PL intensity), the IX homogeneous linewidth is mainly affected by dephasing43,44 instead of lifetime. Hence, wPL can be expressed as
where \({w}_{{{\rm{dep}}}}\) is the linewidth due to the dephasing process and \({w}_{{{\rm{inh}}}}\) is the inhomogeneous linewidth.
a Power-dependent IX photoluminescence (PL) spectrum from Device 1. The low- and high-energy moiré IXs are labelled as P1 and P2, respectively. b Linewidth vs excitation power for P2 emission. Inset: fitted PL spectrum under 730 nm 34 μW excitation. c Coherence time vs excitation power of the P2 emission. Inset: temporal coherence measurement setup. The arrowed lines show the two paths taken by the light. In (b, c), the symbols are the measured values, and the shaded area represents the coherence time uncertainty. The line is the guide for the eye. d Schematic of inhomogeneous broadening reduction by IX-IX repulsion. The dashed grey and solid black lines are the disorder potential at zero and finite IX density, respectively. The disorder potential is screened by the increasing IX density at a higher power. The red and white circles labelled as ‘e’ and ‘h’ represent the electron and hole, respectively.
Figure 2d illustrates the effect of IX density on the inhomogeneous broadening. The disorder potential induces a spatial variation of the IX energy, resulting in inhomogeneous broadening of the PL emission linewidth. As the power increases, the exciton population will accumulate at the local minimum of the disorder potential. Considering IX-IX repulsion, such accumulation results in a larger blue shift at the disorder minima ___location than the average blueshift. Consequently, the linewidth becomes narrower with increasing power45,46,47. However, the IX-IX repulsion also results in excitation-induced dephasing44. This dephasing results in linear-in-density linewidth broadening, which compete with the linewidth narrowing effect described before. The combination of these two mechanisms results in the linewidth dip observed in the experiment.
Temperature and power effects on IX linewidth
To further check the validity of this reasoning, we conducted a temperature dependence study and compared the result with the theoretical model. Figure 3a shows the PL spectra at constant excitation power ( ~ 100 μW) and temperatures varying from 5 K to 72 K. The PL spectrum shows a redshift, which can be attributed to the temperature-induced bandgap change. Figure 3b shows that the linewidth dip gets smaller with increasing temperature and eventually disappears at 50 K. This phenomenon can be understood by considering that the inhomogeneous linewidth reduction mechanism relies on the IX accumulation at the disorder potential minimum, which depends on IX density and mobility. For the 5 K – 72 K temperature range, the IX density does not change much with temperature, as shown by the relatively similar PL intensity and the power saturation curve in this temperature range (Supplementary Fig. S7). Hence, the primary mechanism behind the temperature dependence is IX mobility reduction with increasing temperature47. We developed a theoretical model considering the temperature dependence of the moiré IX mobility (Supplementary Note 2). As shown in Fig. 3b, the model fits the data well, further supporting the physical picture.
a Temperature dependence of the PL spectrum from Device 1. The excitation power used is ~100 μW. b P2 linewidth vs power at various temperatures. The dots and lines are the data and the fitting with the theoretical model, respectively. The shaded area represents the linewidth uncertainty obtained from the two-peak Gaussian fitting of the PL spectrum.
Enhanced IX coherence at correlated electronic state
Finally, we performed a gate (doping) dependence experiment to study the effect of electron population on the IX linewidth, focusing on electron doping case. The gate dependence of the PL spectrum is shown in Fig. 4a. We then extracted the peak energy and the linewidth of the P2 emission from these PL spectra. As shown in Fig. 4b, the linewidth shows a dip, while the peak energy shows a peak at fel = 1 (see Supplementary Note 3 for discussion on charge density and filling factor). The linewidth reduction at the integer filling factor suggests that the correlated electrons affect the IX-IX interaction. This phenomenon can be understood by considering the increase in IX PL intensity at integer filling factors (see Supplementary Fig. S8). The intensified PL signal can be attributed to a longer IX lifetime41, which in turn leads to a higher IX density even at a constant excitation power. Considering the IX-IX interaction, the increased IX density at fel = 1 results in a reduction in inhomogeneous broadening and also contributes to IX energy blueshift. From the PL measurement, we found that the P2 emission intensity is enhanced by around 3 times at fel = 1. Based on the theoretical calculation, this enhancement reduces the linewidth from 18.4 meV to 14.1 meV, which agrees well with the experimental results shown in Fig. 4b. A similar phenomenon is also observed in other integer electron filling factors (see Supplementary Note 4). More discussion on the doping dependence of the PL spectrum and linewidth, including the contribution of the change in dielectric constant14,48 and charge fluctuation, is given in Supplementary Note 1 and 2.
a PL spectra at various gate voltages at 21.7 μW excitation power from Device 1. b P2 peak energy and linewidth vs gate voltage. At fel = 1, the PL linewidth shows a dip while its energy shows a peak behaviour. The symbols are the measurement results, and the shaded area represents the parameter uncertainty obtained from two-peak Gaussian fitting of the PL spectrum. The lines are guides for the eye. c Schematic of inhomogeneous broadening reduction by correlated electronic state. The longer lifetime of IX at fel = 1 results in increased IX density, which in turn reduces the inhomogeneous broadening.
Discussion
In summary, we have demonstrated the effect of excitation power and electrical doping on the IX PL emission linewidth. By studying the IX PL linewidth evolution, we have shown that the IX-IX interaction is affected by both excitonic interaction and electronic correlation. These results could be used to design nonlinear excitonic devices which can be controlled by both excitation power and electrical gating. We show that it is possible to reduce the IX linewidth by utilizing correlated states. Reducing the linewidth can reduce the coupling strength required to reach lasing49,50 or the strong-coupling regime between IXs and other quasiparticles (including other excitons and photons)51, where strong nonlinear behaviour can be observed. Furthermore, the gate tunability of the linewidth shows the possibility of controlling the cross-over from linear to nonlinear regime using gate voltages (see also Supplementary Fig. S10).
Our demonstration of the long-range IX-IX interaction effect on the high-energy moiré IX opens possible optical manipulation of the higher-energy moiré band. We note that the high-energy moiré IX becomes the lowest IX energy level at electron full filling (see Fig. 4a). Our work shows that the disorder effect on this IX can be minimized, which is beneficial in realizing many-body excitonic state52,53,54, such as exciton Bose-Einstein condensate. Additionally, compared to the low-energy IX, the high-energy moiré IX is affected more by the higher-energy moiré bands. Hence, utilizing the IX-electron interaction involving the higher-energy moiré bands and the optical addressability of this IX, it could be possible to detect and manipulate the topological properties of the higher-energy moiré band optically. Such properties play a crucial role, for example, concerning the non-Abelian anyon in moiré superlattices55.
Finally, our result of electrically tunable linewidth demonstrates that exciton coherence in the high-energy moiré band is strongly influenced by the correlated electrons in the lower-energy moiré band. The interaction between multiple moiré IX and electronic bands can lead to novel correlated states involving exciton and electron, including quantum interference between these quasiparticles. While here we focus on the PL linewidth, the rich exciton-exciton and exciton-electron interaction can also affect the lineshape. For example, it could be possible to electrically drive two different excitonic states into a resonance condition, resulting in asymmetric Fano-like PL lineshape56 (see Supplementary Note 1 for more discussion). Our finding shows that the coherence of IX emission is an indispensable tool to uncover phenomena related to correlated excitonic (bosonic) and electronic (fermionic) states in the 2D heterostructure.
Methods
Sample fabrication
Monolayers WSe2 and MoS2, few-layer graphite (FLG), and thin hBN were first mechanically exfoliated from their bulk crystal. Subsequently, we used a layer-by-layer dry-transfer technique to prepare MoS2/WSe2 heterostructures onto the SiO2/Si substrate with ultralow doping Si. FLG was used to contact the heterostructure (as ground) and top/bottom gates, and thin hBN (around 11 to 12 nm thick, see Supplementary Fig. S1c) was used as the dielectric layers. The crystal orientation of monolayer WSe2 and MoS2 was determined by the sharp edge of samples57. We then annealed the samples under an ultrahigh vacuum (around 10−7 mbar) at 200 °C for 3 hours.
CW and time-resolved PL measurements
All PL spectra under CW excitation and time-resolved PL measurements were performed in a home-built confocal optical microscope in the reflection geometry. The PL spectra were obtained by using a spectrometer (Princeton) with a liquid nitrogen-cooled charge-coupled device (CCD) InGaAs photodetector (range: 800 nm–1600 nm). A 50× long-work distance infrared objective lens (LCPLN50XIR) with a spot size of around 1 µm [numerical aperture (NA) = 0.65] was used. The sample temperature was cooled/controlled using a cryostat (Montana Instruments and Attocube, Attodry 2100). A 726 nm pulse laser (source FWHM < 80 ps with a maximum repetition rate of 80 MHz) was used for time-resolved IX PL measurement, and a 730 nm CW laser was used for obtaining PL spectra. An infrared superconducting single-photon detector (SSPD, range: up to 1550 nm) was used as a photodetector for time-resolved PL and photon count measurement. For energy- and time-resolved PL measurement, a 950 nm long pass filter combined with 1200 nm short pass (for P1 emission measurement) or 1200 nm long pass filters (for P2 emission measurement) were used to cut the signal.
Time-coherence measurement
The time coherence measurements were performed in a home-built coherence system. An SSPD with a range of up to 1550 nm was used as a photodetector.
SHG measurement
The SHG measurements were performed at room temperature. A pulse laser from a Ti:Sapphire oscillator (Spectra Physics, Tsunami) with a peak at around 880 nm, a repetition rate of 80 MHz, and a pulse duration of 100 fs was used as the excitation source. The laser power was around 0.8 mW.
Data availability
Relevant data supporting the key findings of this study are available within the article and the Supplementary Information file. All raw data generated during the current study are available from the corresponding authors upon request.
References
Basov, D. N., Averitt, R. D., van der Marel, D., Dressel, M. & Haule, K. Electrodynamics of correlated electron materials. Rev. Mod. Phys. 83, 471–541 (2011).
Quintanilla, J. & Hooley, C. The strong-correlations puzzle. Phys. World 22, 32 (2009).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Bednorz, J. G. & Müller, K. A. Possible highTc superconductivity in the Ba−La−Cu−O system. Z. Phys. B 64, 189–193 (1986).
Boer, J. H. D. & Verwey, E. J. W. Semi-conductors with partially and with completely filled 3d-lattice bands. Proc. Phys. Soc. 49, 59 (1937).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Dicke, R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99–110 (1954).
Laikhtman, B. & Rapaport, R. Exciton correlations in coupled quantum wells and their luminescence blue shift. Phys. Rev. B 80, 195313 (2009).
Richard, M. et al. Experimental evidence for nonequilibrium Bose condensation of exciton polaritons. Phys. Rev. B 72, 201301 (2005).
Anankine, R. et al. Temporal coherence of spatially indirect excitons across Bose–Einstein condensation: the role of free carriers. New J. Phys. 20, 073049 (2018).
Lagoin, C., Suffit, S., Baldwin, K., Pfeiffer, L. & Dubin, F. Mott insulator of strongly interacting two-dimensional semiconductor excitons. Nat. Phys 18, 149–153 (2022).
Sigl, L. et al. Signatures of a degenerate many-body state of interlayer excitons in a van der Waals heterostack. Phys. Rev. Res 2, 042044 (2020).
Tang, Y. et al. Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 579, 353–358 (2020).
Xu, Y. et al. Correlated insulating states at fractional fillings of moiré superlattices. Nature 587, 214–218 (2020).
Regan, E. C. et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020).
Wang, L. et al. Correlated electronic phases in twisted bilayer transition metal dichalcogenides. Nat. Mater. 19, 861–866 (2020).
Chu, Z. et al. Nanoscale conductivity imaging of correlated electronic states in WSe2/WS2 moiré superlattices. Phys. Rev. Lett. 125, 186803 (2020).
Zhang, Z. et al. Flat bands in twisted bilayer transition metal dichalcogenides. Nat. Phys. 16, 1093–1096 (2020).
Pan, Y. et al. Quantum-confined electronic states arising from the moiré pattern of MoS2–WSe2 heterobilayers. Nano Lett 18, 1849–1855 (2018).
Li, H. et al. Imaging moiré flat bands in three-dimensional reconstructed WSe2/WS2 superlattices. Nat. Mater. 20, 945–950 (2021).
Wu, F., Lovorn, T., Tutuc, E. & MacDonald, A. H. Hubbard model physics in transition metal dichalcogenide moiré bands. Phys. Rev. Lett 121, 026402 (2018).
Li, W., Lu, X., Dubey, S., Devenica, L. & Srivastava, A. Dipolar interactions between localized interlayer excitons in van der Waals heterostructures. Nat. Mater. 19, 624–629 (2020).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Li, T. et al. Continuous Mott transition in semiconductor moiré superlattices. Nature 597, 350–354 (2021).
Ghiotto, A. et al. Quantum criticality in twisted transition metal dichalcogenides. Nature 597, 345–349 (2021).
Gu, J. et al. Dipolar excitonic insulator in a moiré lattice. Nat. Phys. 18, 395–400 (2022).
Zhang, Z. et al. Correlated interlayer exciton insulator in heterostructures of monolayer WSe2 and moiré WS2/WSe2. Nat. Phys. 18, 1214–1220 (2022).
Brem, S. & Malic, E. Bosonic delocalization of dipolar moiré excitons. Nano Lett 23, 4627–4633 (2023).
Xiong, R. et al. Correlated insulator of excitons in WSe2/WS2 moiré superlattices. Science 380, 860–864 (2023).
Gao, B. et al. Excitonic Mott insulator in a Bose-Fermi-Hubbard system of moiré WS2/WSe2 heterobilayer. Nat. Commun. 15, 2305 (2024).
Park, H. et al. Dipole ladders with large Hubbard interaction in a moiré exciton lattice. Nat. Phys. 19, 1286–1292 (2023).
Hsu, W.-T. et al. Second harmonic generation from artificially stacked transition metal dichalcogenide twisted bilayers. ACS Nano 8, 2951–2958 (2014).
Zhang, C. et al. Interlayer couplings, moiré patterns, and 2D electronic superlattices in MoS2/WSe2 hetero-bilayers. Sci. Adv 3, e1601459 (2017).
Karni, O. et al. Structure of the moiré exciton captured by imaging its electron and hole. Nature 603, 247–252 (2022).
Tran, K. et al. Evidence for moiré excitons in van der Waals heterostructures. Nature 567, 71–75 (2019).
Wu, F., Lovorn, T. & MacDonald, A. H. Theory of optical absorption by interlayer excitons in transition metal dichalcogenide heterobilayers. Phys. Rev. B 97, 035306 (2018).
Brem, S., Linderälv, C., Erhart, P. & Malic, E. Tunable phases of moiré excitons in van der Waals heterostructures. Nano Lett 20, 8534–8540 (2020).
Tan, Q., Rasmita, A., Zhang, Z., Novoselov, K. S. & Gao, W.-B. Signature of cascade transitions between interlayer excitons in a moiré superlattice. Phys. Rev. Lett 129, 247401 (2022).
Miao, S. et al. Strong interaction between interlayer excitons and correlated electrons in WSe2/WS2 moiré superlattice. Nat. Commun 12, 3608 (2021).
Liu, E. et al. Excitonic and valley-polarization signatures of fractional correlated electronic phases in a WSe2/WS2 moiré superlattice. Phys. Rev. Lett. 127, 037402 (2021).
Tan, Q. et al. Layer-dependent correlated phases in WSe2/MoS2 moiré superlattice. Nat. Mater 22, 605–611 (2023).
Moody, G. et al. Intrinsic homogeneous linewidth and broadening mechanisms of excitons in monolayer transition metal dichalcogenides. Nat. Commun. 6, 8315 (2015).
Ovesen, S. et al. Interlayer exciton dynamics in van der Waals heterostructures. Commun. Phys 2, 23 (2019).
Erkensten, D., Brem, S. & Malic, E. Exciton-exciton interaction in transition metal dichalcogenide monolayers and van der Waals heterostructures. Phys. Rev. B 103, 045426 (2021).
High, A. A. et al. Indirect excitons in elevated traps. Nano Lett. 9, 2094–2098 (2009).
Alloing, M., Lemaître, A. & Dubin, F. Quantum signature blurred by disorder in indirect exciton gases. Europhys. Lett. 93, 17007 (2011).
Ivanov, A. L. Quantum diffusion of dipole-oriented indirect excitons in coupled quantum wells. Europhys. Lett 59, 586 (2002).
Xu, Y. et al. Creation of moiré bands in a monolayer semiconductor by spatially periodic dielectric screening. Nat. Mater 20, 645–649 (2021).
Liu, Y. et al. Room temperature nanocavity laser with interlayer excitons in 2D heterostructures. Sci. Adv. 5, eaav4506 (2019).
Paik, E. Y. et al. Interlayer exciton laser of extended spatial coherence in atomically thin heterostructures. Nature 576, 80–84 (2019).
Zhang, L. et al. Van der Waals heterostructure polaritons with moiré-induced nonlinearity. Nature 591, 61–65 (2021).
Butov, L. V., Gossard, A. C. & Chemla, D. S. Macroscopically ordered state in an exciton system. Nature 418, 751–754 (2002).
Leonard, J. R. et al. Moiré pattern of interference dislocations in condensate of indirect excitons. Nat. Commun 12, 1175 (2021).
Anton-Solanas, C. et al. Bosonic condensation of exciton–polaritons in an atomically thin crystal. Nat. Mater. 20, 1233–1239 (2021).
Kang, K. et al. Evidence of the fractional quantum spin Hall effect in moiré MoTe2. Nature 628, 522–526 (2024).
Fano, U. Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 124, 1866–1878 (1961).
Tan, Q. et al. Layer-engineered interlayer excitons. Sci. Adv 7, eabh0863 (2021).
Acknowledgements
This work is supported by the Singapore ASTAR (M21K2c0116, M24M8b0004), National Research Foundation through its Competitive Research Program (CRP Award No. NRF-CRP22-2019-0004, NRF-CRP30-2023-0003, NRF2023-ITC004-001 and NRF-MSG-2023-0002) and Singapore Ministry of Education (MOE-T2EP50221-0005, MOE-T2EP50222-0018). We thank Leonid Butov for discussion regarding the experimental results.
Author information
Authors and Affiliations
Contributions
W.-b.G. and Q.T. conceived and designed the experiments, Q.T. fabricated the devices, and performed the experiments with the help of Z.Z., X.C. and X.D., K.W. and T.T. provided high-quality BN, A.R. performed the theoretical analysis, A.R. and Q.T. analyzed the data., A.R., Q.T., R.H., H.C. and W.-b.G. wrote the manuscript with inputs from all authors. W-b.G. supervised the project. All authors contributed to the discussion of the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Tan, Q., Rasmita, A., Zhang, Z. et al. Enhanced coherence from correlated states in WSe2/MoS2 moiré heterobilayer. Nat Commun 16, 4518 (2025). https://doi.org/10.1038/s41467-025-57391-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-57391-8