Introduction

Heterogeneous catalysts are always subjected to specific working conditions, such as temperature, pH, and electrode potential, and interact with environmental species1,2. This can result in changes ranging from a single atomic layer to several atomic layers, and may even lead to alterations in bulk composition (Fig. 1) e.g., the coverage effect of adsorbates on the surface3,4,5,6,7, the subsurface incorporation of O, H, and other heteroatoms8,9,10, and the degradation process11,12,13. The resulting surface states and overall structures of catalysts under specific conditions are considered the active phases in catalytic reactions14,15,16. They are typically dynamic and may undergo transitions as conditions change, which are intimately tied to the mechanistic insights and material design within this field17.

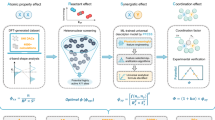
Fig. 1: The overview of the persistent homology-based sampling algorithm (PH-SA) and overall framework for active phase discovery.
figure 1

a The PH-SA involves decomposing material structures into small atomic aggregates, followed using persistent homology to identify the potential interaction sites within each unit. By combining the sites identified by all the aggregates, the potential active sites for species within the entire material structure can be obtained. b After identifying the sites, a combinatorial enumeration is used to generate a set of structures. c The machine learning force field (MLFF) is trained by transfer learning to enhance computational efficiency. d The Pourbaix diagram under specific external conditions is constructed to facilitate catalytic mechanism analysis.

Full size image

The determination of active phase under ambient condition is, therefore, the very fundamental issue of heterocatalysis and essentially involves identifying the distribution of environmental species. Experimental methods for investigating the active phase are expensive and intricate, rendering it challenging to cover a broad range of experimental conditions2,18. To obtain atomic-scale insights into operando active phases, the field frequently relies on computational simulations. A basic approach involves using chemical intuition to hypothesize possible microscopic structures and employing density functional theory (DFT) to perform energetic calculations19,20, constructing phase diagrams under specific reaction environments. Nevertheless, human intuition cannot ensure adequate exploration of the phase space to identify the most thermodynamically favorable structures. Furthermore, the rapid escalation in the number of configurations to be explored will render DFT calculations computationally prohibitive. Machine learning force fields (MLFF), while maintaining accuracy, are significantly faster than DFT calculations and thus are increasingly becoming the preferred tools for exploring active phases2,21,22,23,24,25,26. However, MLFF requires precise fitting of the potential energy surface, which necessitates exploring enough possible configurations22,27. In this regard, developing efficient sampling algorithms that do not rely on chemical intuition has become a top priority, which not only facilitates the exploration of more potential configurations but also enables their rapid evaluation via effectively training MLFF.

Global optimization-based approaches such as basin hopping28,29,30,31, evolutionary algorithms32 and random structure search33 offer principled approaches to comprehensively navigating the ambiguity of active phase. However, these methods usually rely on skillful parameter adjustments and predefined conditions, and face challenges in exploring the entire configuration space and dealing with amorphous structures. The graph theory-based algorithms34,35,36,37, which can enumerate configurations for a specific adsorbate coverage on the surface with graph isomorphism algorithms, even on an asymmetric one. Nevertheless, these methods can only study the adsorbate coverage effect on the surface because the graph representation is insensitive to three-dimensional information, making it unable to consider subsurface and bulk structure sampling. Other geometric-based methods38,39 also have been developed for determining surface adsorption sites but still face difficulties when dealing with non-uniform materials or embedding sites in subsurface.

Topology, independent of metrics or coordinates, presents a novel approach that could potentially offer a comprehensive traversal of structural complexity. Persistent homology, an emerging technique in the field of topological data analysis, bridges the topology and real geometry by capturing geometric structures over various spatial scales through filtration and persistence40. Through embedding geometric information into topological invariants, which are the properties of topological spaces that remain unchanged under specific continuous deformations, it allows the monitoring of the “birth,” “death,” and “persistence” of isolated components, loops, and cavities across all geometric scales using topological measurements. Topological persistence is usually represented by persistent barcodes, where different horizontal line segments or bars denote homology generators41. Persistent homology has been successfully employed to the feature representation for machine learning42,43, molecular science44,45, materials science46,47,48,49,50,51,52,53,54,55, and computational biology56,57. The successful application motivates us to explore its potential as a sampling algorithm due to its capability of characterizing material structures multidimensionally.

In this work, we introduce a topology-based automatic active phase exploration framework, enabling the thorough configuration sampling and efficient computation via MLFF. The core of this framework is a sampling algorithm (PH-SA) in which the persistent homology analysis is leveraged to detect the possible adsorption/embedding sites in space via a bottom-up approach. The PH-SA enables the exploration of interactions between surface, subsurface and even bulk phases with active species, without being limited by morphology and thus can be applied to periodical and amorphous structures. MLFF are then trained through transfer learning to enable rapid structural optimization of sampled configurations. Based on the energetic information, Pourbaix diagram is constructed to describe the response of active phase to external environmental conditions. We validated the effectiveness of the framework with two examples: the formation of Pd hydrides with slab models and the oxidation of Pt clusters in electrochemical conditions. The structure evolution process of these two systems was elucidated by screening 50,000 and 100,000 possible configurations, respectively. The predicted phase diagrams with varying external potentials and their intricate roles in shaping the mechanisms of CO2 electroreduction and oxygen reduction reaction were discussed, demonstrating close alignment with experimental observations. Our algorithm can be easily applied to other heterogeneous catalytic structures of interest and pave the way for the realization of automatic active phase analysis under realistic conditions.

Results

The overview of PH-SA and the overall framework

The Fig. 1 is the overview of the topology-based automatic active phase exploration framework. In order to determine the active phase of the catalysts, the first step is to identify the sites in the material that can accommodate active species, which can range from the surface to the bulk. We leverage the persistent homology, an advanced algorithm in topology data analysis, to achieve this goal, namely PH-SA algorithm. The technical details of PH-SA are presented in the method section. Here, we briefly introduce its logic (Fig. 1a). Initially, we decompose a material structure into combinations of atom aggregates, consisting of two, three, and more atoms, with the underlying physical implication that active species typically interact with only a few surrounding atoms. The geometric characteristics of the atom aggregate (points cloud) can be capture over various spatial scales through a manipulation, namely filtration. Specifically, each point synchronously expands in the space with the filtration parameters being atomic diameter. The filtration process will generate the persistent barcodes with the evolution of different Betti numbers. For a given structure aggregate, the number of independent components, loops and cavities are topological invariants and they are referred to as β0, β1, and β2, respectively. The “birth,” “death,” and “persistence” of β0, β1, and β2 are recorded in the persistent barcodes. The “death” of the Betti numbers corresponds to a contact mode of spheres centered on points, and this contact point may represent a possible local adsorption or embedding site where active species may interact. This is because its approximately equidistant positioning relative to surrounding atoms effectively minimizes repulsive interactions, facilitating the formation of energetically favorable bonding configurations. The geometric coordinates of the contact point can be readily determined through fitting constrained by the topological information of the death points. By iterating over atom aggregates of varying sizes within the material structure, one can automatically identify plausible sites capable of accommodating active species.

The Fig. 2 illustrates the interaction sites determination of an octahedron, which can represent a typical local unit in the FCC crystal structure. The octahedron is firstly decomposed to the possible atom aggregates with two, three until six atoms. For each aggregate, persistent homology analysis is performed. Taking the six atoms one as an example (Fig. 2a), the behaviors of β0, β1 and β2 are separately plotted with the horizontal axis being the filtration parameter ϵ (atomic diameter) from top to bottom. In the early stage, there are six bars in the β0 subfigure, indicating the six isolated atoms. When the filtration parameter ϵ reaches ~2.5 Å, each ball, growing from the initially isolated atoms, overlaps with its closest four balls. Consequently, six bars of β0 turn into one bar in β2 subfigure, representing the emergence of an independent noncontractible quadrilateral structure (cavity). The contact point of two ball is actually the bridge site between two neighboring atoms and can be readily obtain from the record of barcodes. When the filtration parameter reaches ~3.75 Å, the β2 bar disappears, leaving only a β0 bar persistent due to six atoms fully contact and fuse into one large sphere. From this changing moment, the 6-fold site in the center can then be determined. In real material structures, sites are prone to deformation due to dynamic effects. In Fig. 2b, we use a deformed octahedron to illustrate the versatility of the PH-SA method. During the evolution of the barcode, the β0 disappears successively, which is significantly different from the simultaneous disappearance of the undeformed octahedron. The bridge sites can still be derived from the position where each β0 disappears, and the disappearance of the β2 also corresponds to the possible site in the center. Unlike the regular octahedron, the deformed octahedron exhibits β1 barcodes as the points expand, indicating the presence of loop microstructures at certain stages during the filtration process. Owing to its abstract nature, the filtration method can be applied to atom aggerates with any morphology. The analysis results of the square planar and its distorted derivative, which are simpler with only β0 and β1 barcodes but represent a typical local structure on the FCC (100) surface, are shown in Figure S1. Notably, while each Betti number’s death point can correspond to a potential active site, in practice, we focus solely on the last death point (excluding the persistent β0) for each aggregate to avoid redundant computations. This shift stems from our methodology, which initiates with two atoms and progressively applies persistent homology to larger aggregates. Consequently, the structural information from earlier death points of larger aggregates is generally already captured in smaller aggregates with fewer atoms. Using the octahedral structure as an example (Fig. 2a), the bridge sites corresponding to the β0 death points were already identified during the two-atom combination analysis. Instead of performing persistent homology directly on the entire structure, we adopt this bottom-up approach to avoid interactions within the whole system that might obscure topological features in the barcodes and the loss of corresponding interaction sites (Figure S2). By doing so, this strategy can achieve a balance between computational efficiency and identifying as many potential active sites as possible.

Fig. 2: The illustration of persistent homology-based sampling algorithm (PH-SA).
figure 2

The determination of possible interactions sites by PH-SA with (a) regular octahedron and (b) deformed octahedron unit structure as examples. The blue balls are the atoms and red balls indicate the possible interaction sites. The barcodes of β0, β1 and β2 record the persistent homology process. Each bar of β0 corresponds to an isolated atom (point). The β1 corresponds to the existence of loop. The β2 corresponds to the existence of cavity.

Full size image

After the determination of all the adsorption/embedding sites of the material structure with persistent homology, we can then sample the possible configurations of the active phase (Fig. 1b). For the active species embedded in the bulk lattice, their initial positions can be directly placed on the identified interaction sites. For the interaction sites on the surface, the active species will adopt an adsorbed state with their positions determined by the hard sphere model. The close contacts of atoms in this enumeration process corresponding to very high repulsive energies will be rejected based on hard-sphere cut-offs based on their summation of covalent radius (Fig. 2). Graph isomorphism algorithm is applied to eliminate structures with the same graph connectivity to avoid repeated enumeration34. Following the construction of structure ensembles, the MLFF is established to accelerate the structure optimization by transfer learning based on the DPA pre-trained model58(Fig. 1c). Lastly, the energy variation trends and phase diagrams connected to external environmental conditions can be readily obtained to analyze the physicochemical properties of the system and facilitate comparisons with experimental results (Fig. 1d). The overall procedure is also summarized by flowchart in Figure S3.

Simulating complex heterogeneous catalytic systems with the framework

To demonstrate the general applicability of the PH-SA method for diverse material morphologies, we selected two of the most commonly used catalyst structural models, slab and cluster, for illustration59. The periodic slab model is widely employed in theoretical studies of heterogeneous catalysis to examine the properties of specific exposed surfaces of catalysts60,61. Its distinguishing feature lies in the fixed lattice parameters, which prevent deformation of the slab in the xy-plane during interactions with environmental species. The cluster model is another commonly used atomic structure, characterized by its amorphous nature62,63. The interaction of the cluster with environmental species can induce structural deformation, which in turn increases the complexity of subsequent interactions with the surrounding species. Below, we will demonstrate the PH-SA and the overall framework in two specific systems, followed by the detailed discussion of the results.

The PdHx system with slab model

The formation of palladium hydride is taken as the first example to demonstrate the PH-SA and the overall framework. The research on metal hydrides has attracted widespread attentions due to their potential applications in catalysis, energy storage, superconductivity and so on64,65. In an electrochemical environment, Pd exhibits a remarkable tendency to intercalate hydrogen, leading to the formation of active PdHx phase that extends seamlessly from the surface to several atomic layers beneath(Fig. 3a), which can significantly affect the performance of electrocatalytic reactions10,66,67,68,69.

Fig. 3: The PdHx system with different H concentrations (x = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1).
figure 3

a Schematic diagram of the PdHx atomic model. Comparison between (b) energies and (c) forces predicted by the machine learning force field (MLFF) model and those calculated by density functional theory (DFT). The EDFT and FDFT are energy and force calculated by DFT. The EMLFF and FMLFF are energy and force calculated by MLFF. Root Mean Square Error (RMSE) and R-squared (R²) are used as performance evaluation metrics for MLFF training. Color code: silver: Pd; yellow: H.

Full size image

The 4 × 4 Pd (100) surface has been chosen as the model system to investigate the hydrogen phase diagram of Pd (Fig. 3a). Initially, the persistent homology is applied to Pd (100). By using the PH-SA, we identified a total of 1064 possible hydrogen adsorption/intercalation sites. The large number of sites indicates that the configurational space for hydrogen adsorption/insertion is vast. Subsequently, possible adsorption configurations were enumerated across ten gradients with H:Pd ratios of 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1, with 5000 configurations for each gradient. We then extracted 50 structures each of the H:Pd ratio from 0.1 to 1, and subjected them to structure relaxation by DFT calculations. These structural data were integrated with the pre-trained DPA model58 to construct a machine learning force field for PdHx systems. The fine-tuned machine learning force field achieved an energy accuracy of 0.001 eV per atom and a force accuracy of 0.045 eV Å−1 (Fig. 3b, c, more details in Methods).

We leveraged the constructed machine learning force field to optimize the structures of all 50,000 configurations and calculated the average hydrogen adsorption energy. Interestingly, the lowest adsorption energy of each concentration gradient does not vary monotonically, exhibiting a trend of first rising (H:Pd = 0.1 − 0.4), then falling(H:Pd = 0.5), and finally rising again(H:Pd = 0.6 − 1) (Figure S4). We further calculated the mixing energy of PdHx using energy of pure Pd (100) and the most stable configuration of PdH1 as references. It can be observed that at PdH0.5, the structure indeed possesses the minimum mixing energy (Fig. 4a). At low hydrogen concentrations, the atoms preferentially occupy the surface sites. As hydrogens begin to infiltrate the bulk, they primarily settle between the second and third Pd layers rather than the sublayer, which can alleviate the atomic repulsion between internal and interfacial hydrogens and foster a smoother integration process of adsorption energy (Fig. 4b). Interestingly, with the increase of hydrogen concentration, the surface of Pd (100) gradually changes from the 4-fold hollow sites arrangement to the mixed arrangement of 3-fold hollow sites, similar to the atomic arrangement of the (111) crystal plane, and 4-fold hollow sites with the coordination number of surface Pd increasing at around H: Pd = 0.5 (Fig. 4c and Figure S5). The slight enhancement in adsorption strength at this juncture may stem from the inherent stability of the (111) crystal plane over the (100) crystal plane, offsetting the instability arising from interatomic repulsion. Nevertheless, as the H concentration further surges, the repulsive forces among hydrogen atoms inevitably undermine the adsorption intensity. When the H: Pd ratio reaches 1, the surface is completely converted into 3-fold hollow sites (Fig. 4c and Figure S5). This phenomenon is widely reported as the “hex” reconstruction in the FCC (100) crystal plane70,71,72,73, and hydrogen can be a driving force in the electrochemical environment according to our results.

Fig. 4: Results analysis of the PdHx system with different H concentrations (x = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1).
figure 4

a The mixing energy of PdHx with different H concentrations. The mixing energy of each structure is calculated by referencing to the energy of the Pd slab and PdH1 with the lowest adsorption energy. Therefore, only one sample in H concentrations of 0 and 1, while each other concentration contains 5000 samples. b The occupation ratio of H in different layers of Pd along with the total H concentration. The Pd slab consists of four layers of Pd atoms, providing five possible adsorption/embedding layers for H. The black, red, and blue lines represent H adsorption on the top and bottom surfaces of Pd, the second and fourth adsorption layers, and the third adsorption layer, respectively. Due to the symmetry of the slab model, the black and red lines correspond to two equivalent layers. c The average Pd-Pd coordination numbers of surface Pd atoms, calculated for the lowest energy configurations at each concentration gradient. The structures of pure Pd, PdH0.5, and PdH1 are shown. The red dot, error bars and violin plot show the average coordination number, the standard deviation of the average coordination number and the distribution of different Pd atom coordination numbers, respectively. d The concentration of hydrogen in Pd as a function of potentials. The dashed line shows the potential at −0.1 V vs RHE, corresponding to the PdH0.6 structure. e The adsorption energies of *COOH and *CO on the lowest energy PdHx structures at different hydrogen concentrations. f The free energy diagram of CO2 reduction to CO with pure Pd and PdH0.6. The insets show the *CO adsorption configurations on Pd and PdH0.6 substrates. The free energy curves are obtained using the computational hydrogen electrode model. The hydrogen concentration in (a–e) is expressed as the unitless ratio of the number of hydrogen atoms to the number of Pd atoms. Color code: silver: Pd; yellow: H; red: O; black: C.

Full size image

The formation of PdHx active phases is believed to significantly promote the electroreduction of CO2 to CO66,67,68,69. We selected the configurations with the lowest adsorption energy of hydrogen from each gradient to perform free energy calculations, aiming to investigate the phase diagram of the PdHx system under external pH and potential conditions. At pH = 7.3, Pd tends to accommodate 60% hydrogen at -0.1 V vs RHE, which is consistent with experimental findings in CO2 electroreduction condition(Fig. 4d and Figure S6)69. We have calculated the effects of different hydrogen concentrations on the adsorption energies of *COOH and *CO, observing an overall decrease in the adsorption energies of both *COOH and *CO as the H concentration rises (Fig. 4e). This trend can be attributed to hydrogen drawing away some electrons, thereby diminishing Pd’s capability to donate electrons to carbon-containing species and to bind them strongly. Since Pd is a catalyst that is susceptible to CO poisoning, weakening the adsorption of CO is expected to effectively enhance the reduction performance of CO2, as evidenced by the free energy diagram calculations (Fig. 4f), exemplified by the case of PdH0.6.

The PtOx system with cluster model

Platinum nanoparticles (Pt NPs) hold paramount significance across a broad spectrum of electrocatalytic processes, encompassing the oxidation of small molecules74, plasma-assisted catalysis75, the oxygen evolution reaction76, and the oxygen reduction reaction77,78. In electrochemical environment, the Pt NPs are performed under oxygen-rich conditions, leading to the platinum surface and interior can be oxidized, which can significantly impact catalytic activity under ambient conditions79. The evolution mechanism of Pt NPs oxidation process entails sufficient sampling and analysis of Pt-O active phases.

The icosahedral Pt55 cluster with diameter at ~1 nm has been chosen as the model system to investigate the oxidization of Pt NPs (Fig. 5a). At begins, the persistent homology is applied to Pt55. From the evolution of barcodes, we identified a total of 392 possible oxygen adsorption/intercalation sites. Given the amorphous nature of Pt NPs, we enumerated 10,000 possible PtOx (x = 0.1 − 1 with the increasement of 0.1) configurations per gradient level, evaluated their energies via MLFF calculations, and selected the lowest 5% as seeds for subsequent gradient iterations. Persistent homology was used to pinpoint updated interaction sites in this process. This operation effectively accounts for the deformation of Pt NPs induced by O adsorption/intercalation, thereby providing a more realistic representation of the gradual oxidation process of Pt NPs under electrochemical conditions. It can be observed that as oxygens are inserted into the Pt cluster, the resulting PtOx obviously generates more potential interaction sites (Fig. 5b) to accommodate oxygen atoms due to the significant change and expansion in the shape of the cluster, as we will discuss below. The utilization of persistent homology to determine the updated interaction sites further enhances the accuracy and robustness of the simulations, as it allows for a dynamic tracking of structural changes and interactions during the oxidation process. Ab-initio molecular dynamics were performed to generate data for fine-tuning the DPA pre-trained model (details in method sections). The fine-tuned MLFF achieves an energy accuracy of 0.008 eV per atom and a force accuracy of 0.21 eV Å−1 (Fig. 5c, d, more details in Methods).

Fig. 5: The PtOx system with different O concentrations (x = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1).
figure 5

a Schematic diagram of the PtOx atomic model. b The potential interaction sites for oxygen against with the oxygen concentration in Pt cluster. The oxygen concentration is expressed as the unitless ratio of the number of oxygen atoms to the number of Pt atoms. Comparison between (c) energies and (d) forces predicted by the machine learning force field (MLFF) model and those calculated by density functional theory (DFT). The EDFT and FDFT are energy and force calculated by DFT. The EMLFF and FMLFF are energy and force calculated by MLFF. Root mean square error (RMSE) and R-squared (R²) are used as performance evaluation metrics for MLFF training. Color code: silver: Pt; red: O.

Full size image

The overall change of oxygen adsorption energy shows a continuous increase with the increase of oxygen concentration, with a relatively drastic change at the beginning and then a relatively gentle change (Fig. 6a). Initially, oxygens tend to adsorb on the surface. As the increase of oxygen content, oxygen begins to embed into the interior of Pt particles with O: Pd=0.4. These internal oxygen atoms directly emerge near the mass centroid rather than in the vicinity of the surface region (Fig. 6b). This phenomenon is analogous to the PdHx system and is readily comprehensible from a thermodynamic perspective. The mass centroid is farthest from the surface, thus can effectively avoid the energy penalty associated with the increasing O-O interatomic repulsion. Concurrently, the particles undergo a remarkable volumetric expansion, embracing the emergence of Pt-O components within their bulk (Figure S7). This expansion may also explain why the surge in adsorption energy plateaus at higher oxygen levels. With the escalation of oxygen concentration, the augmentation of Pt-O coordination number is obvious. Pt55 attains Pt sites with 4-6 oxygen coordination, akin to the structural motifs found in Pt3O4 or PtO2, at 60% oxygen content (Fig. 6c). Since higher oxidation states of Pt generally correspond to poorer oxygen reduction reaction performance80,81,82, it can be predicted that the emergence of such basic units will seriously damage the catalytic activity of clusters. We further constructed the Pourbaix diagram to study the phase transition process under actual electrochemical conditions by correcting the zero-point energy and entropy of the lowest energy configuration at each gradient (Fig. 6d). The findings reveal that, under typical acidic oxygen reduction reaction conditions (pH = 1), Pt55 attains full oxygen incorporation at approximately 0.6 V, implying diminished catalytic activity, given that oxygen reduction reaction typically thrives at elevated potentials, such as 0.9 V. This does align with experimental results, which suggested that ultra-small Pt clusters (< 2 nm) impede the oxygen reduction reaction83.It is noted that we focused only on thermodynamic stability and kinetic processes can be considered for a complete picture of oxygen embedding.

Fig. 6: Results analysis of the PtOx system with different O concentrations (x = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1).
figure 6

a The oxygen adsorption energy of PtOx at different oxygen concentrations. For each oxygen concentration gradient, 10,000 structures were sampled. b The distribution of distances between the mass center of the entire cluster and each oxygen atom, analyzed for the lowest energy configurations at each oxygen concentration gradient. The oxygen index on the x-axis refers to numbering the oxygen atoms in the system based on their distance from the center of mass, arranged from smallest to largest. c The proportion of Pt atoms with different oxygen coordination numbers as a function of total oxygen concentration, analyzed for the lowest energy configurations at each oxygen concentration gradient. d The Pourbaix diagram for the PtOx system. Each color represents the stable PtOx phase under the given potential and pH conditions. Notably, PtO0.9 is not in the figure because its thermodynamic stability is lower than that of PtO1, and therefore PtO0.8 tends to directly transition to the PtO1 structure. The oxygen concentration in (a, c) is expressed as the unitless ratio of the number of oxygen atoms to the number of Pt atoms.

Full size image

Discussion

The core concept underlying our persistent homology-driven sampling approach rests on the premise that the interplay between active species and material structure is intimately tied to a select few neighboring atoms. As such, we embark on a bottom-up strategy to perform persistent homology analysis on microscopic structural units. From a mathematical perspective, the “barcode death” point represents a critical spatial ___location associated with the scale at which a topological feature, such as a ring or void, disappears during the thickening process. This point reflects a balance in distances to surrounding points, capturing the intrinsic geometry of the structure. This methodical process offers a robust and intuitive approach that not only elucidates the spatial arrangements of these motifs but also elegantly determines the plausible interaction sites. Owing to the abstract mathematical nature of the persistent homology method, it can analyze materials of any morphology. Upon the generation of potential interaction sites, one can easily generate a myriad of potential adsorption/intercalation configurations, guided solely by the basic constraint of hard-sphere radii. This strategy is advantageous for the traversal of local minima and the exploration of the global potential energy landscape, while circumventing the daunting task of navigating the vast, Cartesian-based grand canonical sampling space. Furthermore, the entire process can be highly automated, requiring minimal human intervention and manipulation.

We compared the PH-SA with the classical basin hopping algorithm2,29,30,84 for the PdHx and PtOx systems. The generally lower average adsorption energy achieved by PH-SA highlights its superior ability to identify more stable structures (Figures S8, S9). Fundamentally, the PH-SA and the basin hopping method represent two distinct technical approaches. The PH-SA excels in rapidly identifying and enumerating potential interaction sites across materials with diverse morphologies, ensuring that the identified sites are geometrically plausible. This approach allows for an initial exploration of configuration distributions, followed by the selective refinement of configurations of interest through structural optimization. In contrast, the basin hopping method integrates configuration generation with structural optimization in a sequential manner. New configurations are generated by applying perturbations to the current optimized configurations, requiring each step to undergo optimization before proceeding. Without the optimization step, the reliance on random perturbations would easily generate invalid, high-energy configurations, making the process less efficient and less directed. The difference in logic also endows the PH-SA method with greater potential for computational efficiency, as verified in the Pd-H and Pt-O systems (Figure S10). In addition, when considering only the surface adsorption sites, the number of sites identified by the PH-SA method is consistent with that determined by previous graph-theory-based methods36 in both systems (Figure S11), thereby demonstrating the robustness of the PH-SA method.

In complex systems, persistent homology can swiftly identify key structural features, while basin hopping may necessitate repeated global structural transformations and numerous iterations to explore the underlying state space. In this regard, the persistent homology approach minimizes heuristic bias since it remains largely data-driven, reducing dependency on initial configurations and optimization pathways. Furthermore, basin hopping relies heavily on stochastic processes with less explicit mathematical foundations. Whereas persistent homology is firmly rooted in well-defined mathematical principles, offering systematic and interpretable insights into structural arrangements. It is capable of handling complex structures of arbitrary dimensions and can adapt to amorphous, distorted, and deformed site distributions.

The primary objective of this work is to demonstrate the feasibility of the persistent homology algorithm for structural sampling of materials with arbitrary morphologies. The slab model was utilized to illustrate the scenario where the lattice is fixed, primarily suited for theoretical simulations in the field of heterocatalysis. Furthermore, the cluster model was employed to demonstrate cases where material structures undergo expansion and deformation. The hydrogen adsorption under reduction environment and oxygen adsorption under oxidation environment were selected as model process. The two catalyst structures and reaction process we demonstrated are both representative, providing strong evidence for the general applicability of the method. The number of atoms and involved elements in the adopted models are kept relatively small and simple. Exploring large-scale systems and multi-species interaction systems, such as the CO adsorption phase diagram on CuOx in CO2 electroreduction85,86,87 and the lithium storage process of SiOx in the electrochemical energy storages88, two important and ongoing controversial issues in their respective fields, are also entirely feasible by leveraging the power of machine-learned force fields (MLFFs). Grand canonical Monte Carlo (GCMC) can be readily integrated into the overall framework to further optimize the construction of active phase diagrams38. In fact, in the PtOx system, our approach of using the top 5% lowest-energy configurations from each gradient to generate configurations for the next gradient like the typical operations in GCMC for enumerating configurations, albeit without the employment of the Metropolis criterion. Lastly, we employed transfer learning to construct the machine learning force field, given that we mainly focus on the trend analysis of energy distribution. For more complex multi-element systems and kinetic analysis, active learning can be integrated with our sampling algorithm to construct high-accuracy force fields on-the-fly.

In summary, we present a framework for automatic active phase exploration grounded in topological data analysis, empowering comprehensive configuration sampling and facilitating efficient computations harnessing the power of MLFF in periodical and amorphous structures. At the heart of this framework lies a sampling algorithm, PH-SA, which treats the material structure as points cloud and employs persistent homology analysis to discern potential adsorption/embedding sites through a methodical bottom-up approach. MLFF are then trained through transfer learning to enable rapid structural optimization of sampled configurations. Based on the energetic information, Pourbaix diagram is constructed to delineate the response of the active phase to varying external environmental conditions. The formation of Pd hydrides with slab models and the oxidation of Pt clusters under electrochemical conditions are elucidated and show excellent agreements with experimental observations in both material reconstruction and catalytic reaction activity tuning. Our algorithm can be easily generalized to diverse structures of interest, thereby pioneering the path towards the realization of automated active phase analysis under practical, real-world conditions.

Methods

Persistent homology and interaction sites determination

Persistent homology is used to identify potential active sites in atomic structures. We primarily utilize the filtration process to obtain the barcodes of atomic aggregates constituting the material structure, from which filtering parameters are extracted to locate the spatial coordinates of potential active sites. The mathematical foundation of persistent homology is provided in the supplementary information. The implementation of the persistent homology relies on the open-source package GUDHI89. Here, we focus on describing the practical operational process.

Step one: enumerating atomic aggregates within the material structure. We start by selecting a central atom and constructing atomic aggregates consisting of two to ten atoms within a 5 Å radius via combinatorial enumeration. Each atom in the structure is used as the central atom in turn. The atomic indices and three-dimensional coordinates of each aggregate are recorded in this process, and duplicates (aggregates with the same atomic indices) are removed to avoid redundancy. The effect of threshold variation on site determination is tested in S12.

Step two: obtaining filtering parameters of the atomic aggregates. For each atomic aggregate, persistent homology is applied to generate persistent barcodes, containing β0, β1, and β2 with their respective birth, death, and persistence times. These Betti numbers correspond to topological invariants of independent components, loops, and cavities. Intuitively, each death point in the barcode represents a potential active site in space, as shown in Fig. 2. Here, we focus on the last death point (excluding the persistent β0) for each aggregate, as it typically marks the disappearance of the largest void or cavity formed by most of the atoms in the aggregate. In material structures, foreign atoms (e.g., hydrogen or oxygen) typically occupy these interstitial sites. Since our calculation begins with pairs of atoms, the structural information from earlier death points of larger aggregates is generally already captured in smaller aggregates with fewer atoms. For instance, the bridge sites on each edge of an octahedron are determined during the persistent homology analysis of two atoms (Fig. 2). Although this conclusion has not been rigorously proven, this approach can strike a balance between computational efficiency and the identification of as many potential active sites as possible. When performing persistent homology, it is also necessary to specify the type of complex used. For atomic aggregates consisting of four or fewer atoms, we employ the Alpha complex, while for aggregates with more than four atoms, we utilize the Vietoris-Rips complex. The advantages of this combined strategy are discussed in Figs. S13, S14.

Step three: determining the three-dimensional coordinates of potential active sites. We can obtain the filtering parameters of the last death point from persistent homology, but the corresponding spatial coordinates of the interaction sites cannot be directly acquired, even though their positions are intuitive, as illustrated in Fig. 2. This requires a simple fitting step as presented in Eqs. (1) and (2):

$$\mathop{\min }\limits_{\text{x}}\mathop{\sum }\limits_{\text{i}=1}^{\text{n}}{\text{w}}_{\text{i}}{({||}{\text{p}}_{\text{i}}-\text{x}{||}-\text{d})}^{2}$$
(1)
$${\text{w}}_{\text{i}}=\frac{{\text{r}}_{\text{i}}}{{\sum }_{\text{j}=1}^{\text{n}}{\text{r}}_{\text{j}}}$$
(2)

Here, p represents the three-dimensional coordinates of each atom within the atomic aggregate, recorded during enumeration. The w is the radius weight of different elements composing the atomic aggregate, r is the radius of each atom, i and j are the atom indices, x denotes the coordinates of interaction site to be determined, and d is the filtration parameter derived from the last death point in persistent homology. The underlying rationale of this formulation is as follows: the death point in persistent homology reflects the critical scale at which a ring and/or cavity is filled during the thickening process. This corresponding filtration parameter d can be interpreted as the maximum distance that the “expanding” spheres (centered at the points in the cloud) must travel from their origins to reach and fill this cavity. The d serves as a guiding value in our fitting formula, which aims to determine a geometric point x such that its distance to all surrounding atoms closely approximates d. By minimizing the cumulative squared error in the objective function, we can determine the spatial coordinates of the interaction site. In this process, we also considered that when the material structure contains different elements, the spatial coordinates of the potential sites should be adjusted based on the radii ratio of the different elements, in order to enhance their physical plausibility. By leveraging this interpretation, the fitting process geometrically approximates the topological information provided by the death point, establishing a connection between the topological scale and spatial geometry. While it is possible to directly optimize the function for each atomic aggregate to identify coordinate without using persistent homology, this approach would transform the optimization into a two-parameter problem. As a result, the computational time would increase significantly, as demonstrated in Figure S15. Therefore, using persistent homology to obtain the filtration parameters is crucial for improving computational efficiency and ensuring the identification of potential active sites in a more systematic and scalable manner.

The DFT calculations

The DFT calculations were performed using VASP (Vienna Ab-initio Simulation Package) with the projector-augmented-wave (PAW) scheme90. The Perdew-Burke-Ernzerhof (PBE) functional was utilized to describe electron exchange-correlation interactions. Empirical Grimme’s D3 scheme was employed to account for van-der-Waals interactions91. For the PdHx system, the structure optimization was performed for the construction of MLFF and the free energy diagram calculations. The cut-off energy set to 400 eV, and the convergence criteria for electronic structure 0.05 eV/Å with the 2 × 2 × 1 Monkhorst-Pack k-point grid. For the PtOx system, the ab initio molecule simulation was performed to generate the data for the construction of MLFF due to its amorphous nature. The AIMD was carried out using a canonical system synthesis (NVT) and a Nosé-Hoover thermostat at a temperature of 300 K with Gamma-point. The free energy diagrams of CO2 electroreduction process on Pd and Pd0.6 were calculated by the well-known computational hydrogen electrode method92 with Eq. (3):

$$\text{G}={\text{E}}_{\text{DFT}}+{\text{E}}_{\text{ZPE}}-\text{TS}$$
(3)

where \({E}_{\text{DFT}}\) is the ground state energy calculated by DFT. The vibrational frequencies of adsorbed species were calculated to consider entropies (TS) and zero-point energies (\({E}_{\text{ZPE}}\)) in the Gibbs free energy within the harmonic approximations using the finite difference method.

The graph isomorphism to remove duplicate configurations

In the process of configuration enumeration, there may be enumerated configurations with the same chemical environment. Taking Pd as an example, there are many bridge sites on the surface of Pd, and the configurations generated by adsorbing an H on these bridge sites have similar chemical environments, and the energy differences will be very small. In order to avoid enumerating these configurations with repeated chemical environments, we use graph isomorphism to remove duplicates from the enumerated configurations. Specifically, the generated configuration is converted into an atomic graph by atomic connectivity based on atomic radii, and each graph is transformed three times by the Weisfeiler-Lehman (WL) transformation using the WL algorithm to obtain a WL graph93. Finally, the isomorphism algorithm of networkx is used to determine whether the WL graph is isomorphic or not, so as to obtain the unique configuration under the current gradient.

The construction of MLFF based on DPA

DPA, a deep potential model with a gated attention mechanism, is a pre-trained machine learning force field based on the OC20 database, covering 56 elements and millions of atomic configurations58. Fine-tuning DPA for specific tasks enables high-accuracy force fields more efficiently than training MLFF from scratch. The fine-tuning process for MLFFs leverages pre-trained weights and adapts them to target systems using high-quality DFT data. After featurizing the DFT data into a compatible format, a loss function based on discrepancies in predicted energies and forces is minimized through backpropagation. We employed global fine-tuning, updating all model parameters without freezing any components. The hyperparameter settings used in the fine-tuning process are detailed below. For both PdHx and PtOx systems, the same hyperparameters were used (Table S1), except for the number of training steps. Next, we present the DFT datasets and the results of force field fine-tuning for the PdHx and PtOx systems, respectively.

The construction of MLFF for Pd-H system. A Pd unit cell was cut in the (100) plane to form a 4\(\times\)4 supercell with four layers and a vacuum spacing of 13 Å was added to the end of the slab. A total of 1064 adsorption sites including the upper and lower surfaces as well as the inner part of the slab were generated by the persistent homology approach. For each of the 10 gradients from H: Pd=0.1 to 1, 5000 unique configurations were generated. We randomly selected fifty structures for each H: Pd concentration gradient from all structures to perform DFT structural optimization, resulting in 9,128 frames of structure-energy data. The Pd-H MLFF were constructed by fine tuning the DPA model with above DFT calculations and the pre-training weights using DPA-1-OC2M. The training, validation, and test sets were divided in the ratio of 85%:5%:10%. The fine-tuned process carried out in 100,000 steps. Using DPA-1-OC2M weights on the test set before fine-tuning, a root mean square error (RMSE) of 0.33 eV per atom for energy and 0.14 eV Å−1 for force was obtained. After fine-tuning, the RMSE of energy comes to 0.001 eV per atom, and the RMSE of force is 0.045 eV Å−1. The stability of the model is demonstrated by a 5-fold cross-validation.

The construction of MLFF for Pt-O system. Icosahedral Pt13 and Pt55 NPs were used to fine tune the DPA pre-trained model to construct the Pt-O MLFF. We randomly selected five configurations for each of the systems with O:Pt ratios of 0.1, 0.3, 0.5, 0.7, and 0.9, and conducted AIMD simulations with a 1 fs time step. In general, even relatively short AIMD simulation durations can provide an initial training dataset for MLFF, as we primarily focus on the structural-energy/force pairs at DFT accuracy obtained from each ionic step, which serve as input data for training the MLFF model25,94,95,96. For the five Pt13 structures, each structure was run for 2000 frames, and for the Pt55 structures, each was run for 10000 frames, resulting in a total of 60,000 frames of structures. The Pt-O dataset was then used to fine-tune the DPA model. The dataset was divided into 85%:5%:10% for training, validation, and test. A 5-fold cross-validation was performed to confirm the robustness of the model. Before fine-tuning, these pre-trained weights were used to go for data testing, yielding an RMSE of 0.47 eV per atom for energy and 0.87 eV Å−1 for force. After 200000 steps of fine tuning, the RMSE of energy is obtained as 0.008 eV per atom as well as the RMSE of force 0.21 eV Å−1. The accuracy is similar with previous work24. In this study, the MLFF is trained to rapidly optimize sampled configurations for trend analysis of energy distribution. For a more detailed investigation of the system’s dynamic processes, additional sampling can be incorporated into the training set. By combining this with active learning, the MLFF can be retrained from scratch to achieve a more generalized and accurate force field.

Energy hull, Phase diagram and free energy diagram

High-throughput calculations based on the MLFF are carried out to obtain the average adsorption energy with different concentration of active species according to equation as Eq. (4):

$${E}_{\text{ad}}({\text{Pd}}_{64}{\text{H}}_{x})=\frac{E({\text{Pd}}_{64}{\text{H}}_{x})}{x}-\frac{E({\text{Pd}}_{64})}{x}-\frac{1}{2}E({\text{H}}_{2})$$
(4)

Where the \(E({\text{Pd}}_{64}{\text{H}}_{x})\), \(E({\text{Pd}}_{64})\) and\(\,E({\text{H}}_{2})\) are electronic energy of \({\text{Pd}}_{64}{\text{H}}_{x}\), pure Pd and H2, respectively. The energy hull of PtOx system is calculated in similar way with the energy of oxygen reference to H2O and H292. For PdHx system, we have also calculated the mixing energy to better exhibit the evolution trend as Eq. (5):

$${E}_{\text{Mixing}}=E({\text{Pd}}_{64}{\text{H}}_{x})-{xE}({\text{Pd}}_{64}{\text{H}}_{64})-(1-x)E({\text{Pd}}_{64})$$
(5)

Where the \(E({\text{Pd}}_{64}{\text{H}}_{x})\), \(E\,({\text{Pd}}_{64}{\text{H}}_{64})\) and \(E({\text{Pd}}_{64})\) are electronic energy of \({\text{Pd}}_{64}{\text{H}}_{x}\), \({\text{Pd}}_{64}{\text{H}}_{64}\) with lowest adsorption energy and pure Pd, respectively.

After the obtaining of energy hull of the \(\text{Pd}{\text{H}}_{x}\) system and the \(\text{Pt}{\text{O}}_{x}\) system, we constructed the Pourbaix diagram for analysis the phase diagram under different environment conditions, specifically, the pH and potential. The computational hydrogen electrode scheme92 was used to build the Pourbaix diagram. The lowest adsorption energy case was used for the Gibbs free energy calculation with entropy and zero-point energy correction.

For \(\text{Pd}{\text{H}}_{x}\) system, the free energy difference (ΔG) is calculated according to Eqs. (6) and (7) as follows:

$${\text{Pd}}_{64}{\text{H}}_{64}\leftrightarrow {\text{Pd}}_{64}{\text{H}}_{x}+(64-x)({\text{H}}^{+}+{\text{e}}^{-})$$
(6)
$$\Delta G={G}_{{\text{Pd}}_{64}{\text{H}}_{x}}-{G}_{{\text{Pd}}_{64}{\text{H}}_{64}}+\frac{(64-x)}{2}{G}_{{\text{H}}_{2}}-(64-x)(\text{e}U\text{+}0.059\text{pH})$$
(7)

The \({G}_{{\text{Pd}}_{64}{\text{H}}_{x}}\) and \({G}_{{\text{Pd}}_{64}{\text{H}}_{64}}\) are the free energy of \({\text{Pd}}_{64}{\text{H}}_{x}\) and \({\text{Pd}}_{64}{\text{H}}_{64}\), respectively. The pH was set to 7.3. U is the applied potential.

For the PtOx system, the free energy difference (ΔG) is calculated according to Eqs. (8) and (9) as follows:

$$\text{Pt}+x{\text{H}}_{2}\text{O}-2x({\text{H}}^{+}+{\text{e}}^{-})\leftrightarrow \text{Pt}{\text{O}}_{x}$$
(8)
$$\Delta G\,={G}_{{\text{PtO}}_{x}}-{G}_{\text{Pt}}-2x(\text{e}U\text{+}0.059\text{pH})-x({G}_{{\text{H}}_{2}\text{O}}-{G}_{{\text{H}}_{2}})$$
(9)

The \({G}_{{\text{PtO}}_{x}}\) and the \({G}_{\text{Pt}}\) are the free energy of \(\text{Pt}\)Ox and \(\text{Pt}\), respectively. pH and U are the pH value and applied potential, respectively.