Protein sequence modelling with Bayesian flow networks

Atkinson, Timothy; Barrett, Thomas D.; Cameron, Scott; Guloglu, Bora; Greenig, Matthew; Tan, Charlie B.; Robinson, Louis; Graves, Alex; Copoiu, Liviu; Laterre, Alexandre

doi:10.1038/s41467-025-58250-2

Download PDF

Article
Open access
Published: 03 April 2025

Protein sequence modelling with Bayesian flow networks

Nature Communications volume 16, Article number: 3197 (2025) Cite this article

5727 Accesses
20 Altmetric
Metrics details

Subjects

Abstract

Exploring the vast and largely uncharted territory of amino acid sequences is crucial for understanding complex protein functions and the engineering of novel therapeutic proteins. Whilst generative machine learning has advanced protein sequence modelling, no existing approach is proficient in both unconditional and conditional generation. In this work, we propose that Bayesian Flow Networks (BFNs), a recently introduced framework for generative modelling, can address these challenges. We present ProtBFN, a 650M parameter model trained on protein sequences curated from UniProtKB, which generates natural-like, diverse, structurally coherent, and novel protein sequences, significantly outperforming leading autoregressive and discrete diffusion models. Further, we fine-tune ProtBFN on heavy chains from the Observed Antibody Space to obtain an antibody-specific model, AbBFN, which we use to evaluate zero-shot conditional generation capabilities. AbBFN is found to be competitive with or better than antibody-specific BERT-style models when applied to predicting individual framework or complimentary determining regions.

Computational scoring and experimental evaluation of enzymes generated by neural networks

Article Open access 23 April 2024

Protein structure generation via folding diffusion

Article Open access 05 February 2024

Opportunities and challenges in design and optimization of protein function

Article 02 April 2024

Introduction

Proteins drive nearly every process in biological systems, in both health and disease. Despite this, only a small fraction of the possible protein-sequence space—characterised by the vast combinatorial complexity of possible amino acid sequences—has been explored with vast regions of the theoretical space not yet having been observed in natural proteins^1,2. This represents not only a gap in our fundamental knowledge of biological processes but also potentially untapped opportunities for developing novel functional and therapeutic proteins^3,4.

In recent years, machine learning (ML) has emerged as a powerful tool to bridge this gap, becoming an integral part of computational biology. Techniques initially developed for natural language processing (NLP) have proven particularly impactful. Drawing on parallels between modelling sequences of words and amino acids (the ‘language of proteins’), these self-supervised models learn to generate novel sequences from corpora of unlabelled data. For example, BERT-style models—such as the Evolutionary Scale Modelling (ESM) series^5,6,7—are trained to predict masked amino acids based on the context of the rest of the sequence. However, whilst being trained to conditionally generate missing parts of a sequence; BERT models are ill-suited for the generation of entirely new protein sequences. Instead, they are primarily used to generate embeddings used for various downstream tasks such as folding⁶, inverse folding⁸, contact prediction⁹ and various other applications^10,11,12.

As generative pre-trained transformer (GPT) models have emerged as the dominant paradigm in NLP^13,14, equivalent autoregressive protein language models—such as ProtGPT2¹⁵, ProtGen¹⁶ and RITA¹⁷—have been explored for de novo protein-sequence generation. These autoregressive models build sequences from left to right, with each amino acid conditioned only on the preceding partial sequence. Since protein function depends on 3D shape, important regions are often spread throughout the sequence and are not just located at termini. This makes GPT models less effective for many practical design tasks. Indeed, the complex and long-range interactions between different parts of the protein sequence raise doubts about whether an autoregressive approach is the best choice for generating proteins.

Given the limitations of treating protein sequences strictly as linguistic constructs, recent efforts have explored generative techniques from other domains. Notably, diffusion models^18,19, which excel in image generation²⁰, have shown promise in structural protein modelling through adaptations like RFDiffusion²¹ and AlphaFold3²². However, diffusion models are tailored for continuous variables and do not naturally transfer to modelling discrete-data, such as amino acid sequences. Whilst the development of so-called “discrete diffusion" methods is a promising area of research^{23,24,25,26,27}—for example, by defining forward processes over discrete spaces with noise added from a finite set of corruptions²³—practically, none have yet been proved effective at both de novo unconditional generation and arbitrary conditional generation of novel protein sequences.

Here, we propose that recently developed Bayesian Flow Networks (BFNs)²⁸ can address the above-mentioned challenges. BFNs are generative models that do not enforce a specific decomposition of the joint distribution over all variables. Moreover, rather than modelling the data directly, BFNs model the continuous parameters of a distribution over the data. As such, they naturally handle non-continuous data modalities, including discrete variables, as a first-class citizen while remaining conceptually aligned with diffusion models²⁹. Intuitively, rather than “learning the data", BFNs “learn beliefs about the data". As they have only recently been proposed, BFNs have not been tested across the same range of tasks as the aforementioned generative approaches.

In this work, we demonstrate that BFNs can effectively handle the complexity of protein-sequence modelling whilst unifying unconditional and conditional generation. Specifically, we present ProtBFN, a 650 M parameter model trained for de novo generation of protein sequences. The generated proteins match the known natural distribution in terms of direct metrics such as amino acid propensity and sequence length and computed properties; whilst being globally coherent, globular sequences. Compared to state-of-the-art autoregressive and discrete diffusion models, we find ProtBFN’s samples are more natural whilst covering more of the known protein-sequence space. ProtBFN is also capable of exploring unseen regions of the protein space. It is able to generate novel sequences with low identity to known proteins but retains a high structural similarity to the natural motifs found in databases such as CATH³⁰. Finally, we fine-tune ProtBFN to yield an antibody-specific model, AbBFN. Consistent with our findings for ProtBFN, AbBFN is able to unconditionally generate highly plausible heavy-chain candidates. To validate the conditional generation capabilities of our model, we then apply AbBFN to the task of inpainting individual complementarity-determining regions (CDR) and framework regions of existing VH chains. Despite having only been trained for unconditional generation, AbBFN recovers the underlying distribution of amino acid usage and matches the performance of leading BERT-style transformer models trained specifically for this task. Moreover, the flexible conditional generation of BFNs allows AbBFN to retain strong amino acid recovery rates and outperform the BERT models when the masking region is increased to include all framework regions.

Results

A Bayesian flow network for protein sequences

Generative models aim to capture the joint distribution p(x) of a dataset, where each sample comprises N variables denoted as x = [x₁, …, x_N]. Typically, these models are trained to reconstruct the original data from noised or corrupted samples. Traditional sequence modelling techniques, such as GPT and BERT, manipulate subsets of these variables to create noised training targets. Specifically, GPT models the distribution autoregressively ($p({{{\bf{x}}}})={\prod }_{i=1}^{N}p({x}_{i}| {x}_{j < i})$), while BERT generates data conditionally based on non-masked variables (p(x_i,j,…∣x_k∉i,j,…)).

In contrast, BFNs uniformly apply noise across all variables, similar to variational diffusion models. The generation of a new sample unfolds as a continuous-time denoising process, initiating from a random prior and concluding with a well-defined sample. Unlike traditional diffusion techniques that directly model the data, x, BFNs adjust the parameters of the data’s distribution, θ = [θ₁, …, θ_N], where p(x_i∣θ_i) governs the distribution over the i^th variable. This distinction is crucial, especially for handling discrete-data where variables are categorically correct or incorrect. This lack of intermediate gradations makes defining a smooth denoising process over the data (i.e., with the data becoming monotonically more accurate) a significant challenge in the application of traditional diffusion methods.

Training

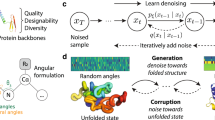
The denoising process used to generate samples can be viewed as a communication protocol (see Fig. 1), where Alice describes a ground-truth data point (e.g., a sequence of amino acids) to Bob by sending a series of noisy observations, y^(1: i) ≡ {y⁽¹⁾, …y⁽ⁱ⁾}, that become increasingly more informative. Training a BFN is then equivalent to Bob learning a model that, given a series of observations with known noise, predicts a data distribution that best matches the next observations, y⁽ⁱ⁺¹⁾. Concretely, this training process at step i applied to protein sequences is as follows.

1.
Alice sends a noisy observation (y⁽ⁱ⁾) of a protein (x) from the sender distribution (${p}_{{{{\rm{s}}}}}^{(i)}$) to Bob.
2.
Bob summarises all noisy observations, y^(1: i), on a per-amino-acid basis via Bayesian inference, to obtain the parameters of an input distribution θ⁽ⁱ⁾.
3.
These parameters are input into a neural network Φ, which predicts an output distribution (${p}_{o}^{i}$). This step models the joint distribution of amino acids, refining the single-variable Bayesian inferences.
4.
To obtain Bob’s belief over the form of the next noisy observation, (y⁽ⁱ⁺¹⁾), the output distribution is noised in an equivalent manner to the ground-truth data, to obtain the receiver distribution (${p}_{{{{\rm{r}}}}}^{(i+1)}$).

Minimising the difference between the predicted and true distribution over the next data samples in an N step generation process is then given by the training objective;

$${{{{\mathcal{L}}}}}^{N}={\sum }_{i=1}^{N}{D}_{{{{\rm{KL}}}}}\left({p}_{{{{\rm{s}}}}}^{(i)}\parallel {p}_{{{{\rm{r}}}}}^{(i)}\right).$$

(1)

It is possible to derive a continuous-time loss function ${{{{\mathcal{L}}}}}^{\infty }$ in the limit of N → ∞²⁸ which is used in practice (see “Methods” for details).

**Fig. 1: Application of a Bayesian Flow Network (BFN) to protein-sequence modelling.**

Inference

When sampling full protein sequences from the model unconditionally, there is no fixed ground-truth. Instead, Bob effectively hallucinates Alice with the previous step’s receiver distribution taking on the role of the sender distribution (${p}_{{{{\rm{s}}}}}^{(i)}\leftarrow {p}_{{{{\rm{r}}}}}^{(i-1)}$). Repeating this process N times generates samples from the learned distribution.

Whilst a naive approach for conditional generation is to use the sender distribution for variables with ground truth and the receiver distribution elsewhere, we found that this does not converge to the true conditional distribution. Instead, we combine this approach with sequential Monte Carlo (SMC) sampling; which ensures that the sampled variables are consistent with fixed variables under the learned joint distribution. Full details on the sampling methodology are found in the “Methods”.

ProtBFN: A foundational generative model for protein sequences

Using the described method, we trained a 650 M parameter model, ProtBFN, on a curated dataset of sequences that span the known protein space. This dataset considers non-hypothetical protein sequences in UniProtKB³¹ and we refer to this curated and clustered dataset as UniProtCC. In assessing the capabilities of ProtBFN, we compare against leading autoregressive and discrete diffusion models for protein-sequence generation—ProtGPT2¹⁵ and EvoDiff³², respectively. We note that both ProtGPT2 and EvoDiff are trained on the UniRef50 dataset, which, unlike UniProtCC, includes proteins of hypothetical or unknown existence. A summary comparing the training data, model sizes, and training costs of these models to ProtBFN can be found in Supplementary Table 3. By training ProtBFN exclusively on high-confidence sequences from UniRef50, where evidence supports the existence of these proteins, we ensure it remains focused on the biologically relevant manifold of possible proteins. Our evaluation analyses 10,000 protein sequences generated by each model and compares these to randomly selected subsets of 10,000 sequences from the UniProtCC and UniRef50 datasets. Extended details of the data curation, training and sampling procedures are provided in the “Methods”.

Learning to generate natural protein sequences

A primary goal of ProtBFN is to learn the distribution of natural proteins. Although no single metric can definitively assess the naturalness of generated protein samples, various statistical and biophysical properties can be computed and compared against the expected natural distributions. To this end, Fig. 2 presents a selection of such experiments from which we can infer that ProtBFN not only matches the natural distribution on which it was trained but does so more faithfully than the autoregressive and discrete diffusion baselines on their respective training dataset.

**Fig. 2: ProtBFN is an effective de novo generator of protein sequences; generating novel protein sequences that in distribution under both local and global metrics.**

A direct test of the plausibility of ProtBFN’s generated set of protein sequences is to examine the frequency with which amino acids and oligomers occur, as these are strongly related to the robustness of the genetic code³³. These measures (Fig. 2a, b) are well aligned with the UniProtCC distribution. However, whilst these frequency metrics are indicative, they do not alone confirm the coherence of individual samples, therefore, we also compute per-sample metrics. ProtBFN’s generated sequences have a natural-like distribution of lengths (Fig. 2c), which is another indicator of our ability to model the underlying distribution. In contrast, ProtGPT2 significantly diverges from the UniRef50 distribution under this metric, while EvoDiff artificially matches the target distribution because sequence length is pre-selected before generation. Additional results comparing the biophysical properties of the generated sequences are detailed in Supplementary Note 1.

For structural analysis, we first leverage NetSurfP-3.0³⁴ (a secondary structure and relative solvent accessibility prediction method) to annotate each residue in the sequences with structural information. We again find that ProtBFN matches the natural distribution on these metrics, even when considering how these properties vary as a function of position in the sequence (Fig. 2e and Supplementary Note 1). To evaluate the overall structural properties, we use the mean predicted local distance difference test (pLDDT) of ESMFold⁷ as a measure of confidence in the predicted structure (Fig. 2d). Interactions between residues far apart within protein sequence are critical in determining overall structure. Higher pLDDT scores, therefore, indicate that ESMFold can identify interactions that are similar to those found in its training data. Indeed, we observe that ProtBFN consistently produces sequences that obtain high pLDDT scores, closely matching those of naturally occurring proteins. The sensitivity of this metric to the global coherence of a protein is evidenced by ProtGPT2 and EvoDiff’s divergence from their training distribution, even when accounting for the greater number of lower-scored proteins in UniRef compared to UniProtCC.

Finally, to confirm that ProtBFN is generating novel proteins rather than memorising training data, we search for the nearest match for each generated sequence within the UniProtCC training data (Fig. 2f). Results show that generated sequences are highly likely to be novel, with 4444 (8851 and 9489) of the generated samples having a sequence identity to the nearest match of less than 50% (80% and 95%), respectively.

ProtBFN effectively covers the known proteome

Broad coverage of the proteome ensures that a model has learned the diversity of protein sequences, and thus could be used to develop a wide array of functional proteins. Having confirmed the naturalness and novelty of the sequences generated by ProtBFN, we next assess the proteome coverage provided by these sequences. To do so, we first use mmseqs2³⁵ to align generated sequences with UniRef50 (Table 1), as UniRef50 represents a non-redundant set of protein clusters spanning known protein diversity.

Table 1 ProtBFN generates more natural and diverse proteins than baseline methods

Full size table

69.7% of ProtBFN’s of sequences are found to align (≥50% sequence identity) with a known UniRef50 cluster. This is a significantly higher proportion than ProtGPT2 and EvoDiff, despite the fact that these models are trained uniformly on the UniRef50 clusters. As the number of sampled sequences (10,000) is far smaller than the number of UniRef50 clusters (~65 M), we measure coverage as the ratio of observed to expected unique clusters hit if drawing 10,000 samples from a model’s training distribution. Calculation details of this proposed coverage score are provided in the “Methods” and empirically, we find that ProtBFN provides substantially better coverage of the protein space than the baseline methods. This result, paired with Fig. 2f reinforces the idea that ProtBFN creates novel sequences that still cover the functional protein space present in UniProtKB.

To visualise the distribution coverage, we compute the embeddings of the protein sequences using a state-of-the-art protein language model and project these into two dimensions (Fig. 3). The close match between ProtBFN and UniProtCC’s visualised distributions highlights that the generated sequences provide broad coverage of the natural distribution, even in this biologically meaningful representation space. Additional measures supporting ProtBFN’s extensive coverage of the protein space are detailed in Supplementary Note 2.

**Fig. 3: ProtBFN sequences show broad coverage of the training distribution in embedding space of a protein language model.**

ProtBFN generates globular structural motifs with novel sequences

Protein function is closely tied to structure^36,37. Therefore, to characterise de novo protein sequences, which may differ substantially from those observed in nature, we analyse their correspondence with empirically determined protein conformations. The CATH S40 database³⁰ contains approximately 30,000 non-redundant, experimentally solved protein domains that provide broad coverage of known structural diversity. We compare the structural similarity of 2000 sequences sampled from each model against CATH S40 domains using template modelling (TM) scores. The TM1 and TM2 scores are normalised against the length of the generated protein and the length of the CATH S40 ___domain, respectively. A TM score above 0.5 is generally recognised as being indicative of the same fold³⁸. To avoid matching only fragments of CATH domains to generated proteins, or vice versa, a positive match requires both TM1 and TM2 scores to exceed 0.5.

ProtBFN achieves a CATH hit-rate of 65.7%, surpassing ProtGPT2 (25.3%) and EvoDiff (12.0%). Moreover, these hits are of higher quality, with 68.0% of ProtBFN hits having sequential structure alignment programme (SSAP) scores^39,40 above 80. This corresponds to the highest level of similarity (homologous superfamily) in CATH’s classification, compared to 38.0% and 19.2% for ProtGPT2 and EvoDiff, respectively (Fig. 4c). Furthermore, the proportion of near-complete hits, where both TM scores approach 1 (Fig. 4a), shows that ProtBFN generates longer sequences that fold into known domains more frequently. This is supported by the fact that ProtBFN samples retain high SSAP scores across all sampled protein lengths (see Supplementary Fig. 4). However, despite high structural correspondence, ProtBFN’s sequences exhibit low sequence similarity to their CATH S40 targets—80.4% of hits have under 50% sequence similarity (Fig. 4b). This capability to produce recognisable globular folds with novel sequences is a prerequisite for the use of ProtBFN for rational protein design, and suggests a meaningful capability to go beyond training data and explore the uncharted proteome.

**Fig. 4: ProtBFN generates sequences that fold into naturally occurring structural motifs.**

It is important to consider once again the diversity of the generated samples and, as illustrated in Fig. 4d, ProtBFN also excels in generating a structurally diverse array of functionally complex protein domains. The model spans the breadth of classes catalogued in CATH, including alpha-helical (samples 7972, 5245, 16618, 12773, 3599), beta-sheet (15753, 16197, 18606), alpha-beta (19532, 4791, 18747, 16313), and irregular domains (13525). ProtBFN also effectively models various functional types, such as transmembrane proteins, including porins (15753) and transporters (16618), along with enzymes (2773, 13161). Additionally, the generated globular proteins span small (18606, 7972, 18747) and large (16197, 5245, 4791) structural domains, irrespective of CATH class.

Lastly, we used Merizo⁴¹, a tool for ___domain segmentation, to understand the ___domain distributions of ProtBFN samples (Fig. 4e). Close to half of the tested samples have two domains, 26.9% have single domains, and 22.7% have three or more domains. Interestingly, the multi-___domain constructs typically exhibit ___domain-___domain interfaces, characterised by different types of interactions, rather than being simply connected by disordered loops (Supplementary Note 3). This highlights that ProtBFN is able to generate proteins with globally coherent interactions, even when the interacting residues are separate in sequence space and belong to different folds. More broadly, this analysis demonstrates the structural and functional depth of ProtBFN’s learned distribution, highlighting the potential applicability of BFN generation across a diverse range of biological and biotechnological applications.

AbBFN: A foundational sequence model tuned specifically for antibodies

The design of antibodies, a class of proteins that identifies and neutralises pathogens, is central to protein engineering applications such as monoclonal antibody-based cancer therapies⁴². To adapt our foundational generative model, ProtBFN, for specialised domains, we developed AbBFN, an antibody-specific model, by fine-tuning on variable heavy (VH) chains from the Observed Antibody Space (OAS) database⁴³. We consider two validation sets in our analysis: 20,000 VH samples uniformly drawn from OAS and heavy-chain sequences from the SAbDab benchmark⁴⁴. To ensure no data leakage, our training set is filtered to remove sequences similar to those in either validation set, leaving 195 M training examples. Full details on the training data and process are provided in “Methods”.

Unconditional generation of antibody chains

Analogous to our investigation of ProtBFN, we validate the unconditional generation of AbBFN by comparing various metrics between the generated and training (OAS) distribution. Detailed results in Supplementary Note 6 confirm that AbBFN accurately captures the natural distribution of VH chains.

Zero-shot inpainting of antibody chains

Antibody VH chains are segmented into three complementary determining regions (CDRs) and four framework (FR) regions. The former primarily determines the binding specificity. The latter provides a scaffold for the CDRs^45,46, contributes to properties of the molecule such as stability, antibody pairing and antibody expression^47,48,49,50, and also contributes to binding⁵¹. A common task for antibody sequence models is to conditionally generate subsets of these regions based on a given partial sequence (inpainting), with performance measured in terms of the amino acid recovery (AAR) rate. Although AbBFN is only trained on the unconditional joint distribution of amino acids, it is possible to arbitrarily sample conditioned on any subset of variables as described in “Methods”. This allows AbBFN to be applied in a zero-shot manner to any in-painting task, such as inpainting of specific regions of antibody chains, despite the fact that it was never trained on this specific conditional generation task.

We compare AbBFN to leading antibody-specific language models AntiBERTy⁵² and AbLang2⁵³, which were trained for BERT-style conditional generation. As both of these methods were trained on the entire OAS, they have been exposed to both our validation datasets, potentially causing data leakage. Despite this, AbBFN is able to recover individual FR and CDR regions as well as these specialist models on the OAS validation set (Table 2), whilst demonstrating AAR rates consistent with the known increased variability of CDRs, particularly CDR-H3. Notably, AbBFN significantly outperforms the baseline models in predicting all FR regions simultaneously. We attribute this to the larger masked region being out-of-distribution for BERT-style methods, which does not afflict the more flexible generation of a BFN.

Table 2 AbBFN can inpaint antibody heavy-chain regions with zero-shot conditional generation

Full size table

On the SAbDab benchmark (Table 3), AbBFN retains strong performance. It significantly outperforms baseline methods that have not been trained on this data, including those that can condition the generation of additional structural data^44,54. We attribute the increased gap between AbBFN and the language model methods to the removal of sequences similar to the SAbDab benchmark from our training data. To address this, we report the performance of AbBFN+, which underwent rapid fine-tuning (1000 adaptation steps) on the nine training folds for each test fold (see Methods). AbBFN+ outperforms all methods on CDR-H1 and CDR-H2 and significantly closes the gap on CDR-H3.

Table 3 AbBFN baseline performance can be further improved with rapid fine-tuning

Full size table

We hypothesise that the antibody-specific models AbLang2 and AntiBERTy outperform AbBFN on the CDR-H3 recovery task partly because of the unique way CDR-H3 sequences are generated in vivo. Unlike CDR-H1 and CDR-H2 sequences, which are entirely encoded by the V-gene of the heavy chain, CDR-H3 sequences are encoded by a combination of V-, D-, and J-genes. This combination leads to significant diversity at the junctions where these gene segments join. Additionally, during the somatic recombination events that create naive CDR-H3 sequences, extra nucleotides are randomly added at these junctions without a template–a process known as non-templated nucleotide addition. Consequently, the possible variations for CDR-H3 loops are extraordinarily vast⁵⁵. Recent large-scale sequencing studies have confirmed this theoretical diversity of CDR-H3 sequences^56,57.

This exceptional diversity–greater than that of general proteins⁵⁸ and other CDR loops⁵⁹–also results in significant structural variability in the CDR-H3 regions^58,60,61. Due to this diversity and randomness, we expect CDR-H3 sequences to exhibit high information entropy (i.e., low predictability), as discussed by Olsen et al.⁵³. We argue that the observed discrepancy in performance between different CDR loops can be attributed to two main factors: (i) the overlap between the SAbDab benchmark and the training data of AbLang2 (trained on OAS data clustered to cover every unique CDR-H3 sequence) and AntiBERTy (trained on a much larger corpus than AbBFN), and (ii) the lower predictability of CDR-H3 sequences. Furthermore, we propose that the unique sequence dynamics of the CDR-H3 loop–driven by V(D)J recombination and non-templated nucleotide addition–may not be effectively captured by the general protein model ProtBFN, which forms the basis of AbBFN. This could contribute to its lower CDR-H3 recovery rates compared to antibody-specific models.

Discussion

In this work, we have demonstrated that BFNs have significant advantages in terms of both performance and flexibility compared to traditional methods for protein-sequence modelling. ProtBFN generates plausible, diverse and novel protein sequences more effectively than leading autoregressive and discrete diffusion models. Additionally, AbBFN highlights that these models can be fine-tuned for ___domain-specific capabilities, achieving or surpassing the conditional generation performance of BERT models that were trained specifically for sequence inpainting tasks. These capabilities underscore the potential of BFNs for the exploration of uncharted regions of the proteome and rational protein design.

Given the promise shown in protein generation, it appears reasonable to extend the application of BFNs to other biological sequence modelling tasks, such as RNA and DNA. More broadly, the ability of BFNs to handle different data modalities within a unified framework suggests the possibility of building multimodal models, for example, that integrate sequences and structural data^62,63. Combined with the arbitrary zero-shot conditional generation we demonstrate in this paper, such multimodal BFN’s could provide unparalleled generative flexibility, further enhancing our ability to design and understand complex biological systems.

Nevertheless, it is important to acknowledge that BFNs are still an emerging technology with considerable fundamental questions remaining unexplored. In this direction, recent insights connecting BFNs with diffusion models through stochastic differential equations²⁹, may facilitate the incorporation of the plethora of advanced sampling methods, e.g., refs. ^64,65,66, for diffusion, thereby providing even stronger performance.

Methods

Bayesian flow networks for discrete-data

Overview

Let p(x) be a distribution over D discrete variables that we wish to approximate. For some x~p(⋅) we have that x = [x₁, …, x_D] ∈ V^D, where V = [v₁…v_K] is a vocabulary with ∣V∣ = K. The BFN approximation to p(x) is constructed through the iterative revealing of information about x through a sequence of noisy observations y^(1: i) = {y⁽¹⁾…y⁽ⁱ⁾}.

A noisy observation at step i, ${{{{\bf{y}}}}}^{(i)}=[{y}_{1}^{(i)},\ldots,{y}_{D}^{(i)}]\in {{\mathbb{R}}}^{D\times K}$ is drawn from the sender distribution as a normally distributed vector for each variable,

$${p}_{s}\left({y}_{j}^{(i)}| {{{\bf{x}}}};{\alpha }_{i}\right)={{{\mathcal{N}}}}\left({\alpha }_{i}(K{{{\bf{e}}}}{({{{\bf{x}}}})}_{j}-1),{\alpha }_{i}K{{{\bf{I}}}}\right),$$

(2)

$${p}_{s}\left({{{{\bf{y}}}}}^{(i)}| {{{\bf{x}}}};{\alpha }_{i}\right)=\mathop{\prod }_{j=1}^{D}{p}_{s}\left({y}_{j}^{(i)}| {{{\bf{x}}}};{\alpha }_{i}\right),$$

(3)

where ${\alpha }_{i}\in {{\mathbb{R}}}^{+}$ is the accuracy at step i, such that a higher α_i reveals more information about the true value of x, and ${{{\bf{e}}}}({{{\bf{x}}}})\in {{\mathbb{R}}}^{D\times K}$ is a one-hot encoding of x,

$${{{\bf{e}}}}{({{{\bf{x}}}})}_{i,j}=\left\{\begin{array}{ll}1,&\,{{\mbox{if}}}\,\,{x}_{i}={v}_{j}\\ 0,&\,{\mbox{otherwise}}\,\end{array}\right\}.$$

(4)

By starting from some prior distribution θ⁽⁰⁾ over the value of x and taking into account all observations so far, the input distribution is derived, providing the optimal estimation of the likelihood of each variable x_j independently,

$${{{{\boldsymbol{\theta }}}}}_{j,k}^{(i)} =p({x}_{j}={v}_{k} \, | \, {{{{\bf{y}}}}}_{j}^{(1:i)})\\ =\frac{{{{{\boldsymbol{\theta }}}}}_{j,k}^{(i-1)}\cdot \exp {y}_{j,k}^{(i)}}{{\sum }_{q=1}^{K}{{{{\boldsymbol{\theta }}}}}_{j,q}^{(i-1)}\cdot \exp {y}_{j,q}^{(i)}}\\ =\frac{{{{{\boldsymbol{\theta }}}}}_{j,k}^{(0)}\cdot \exp {\sum }_{p=1}^{i}{y}_{j,k}^{(p)}}{\mathop{\sum }_{q=1}^{K}{{{{\boldsymbol{\theta }}}}}_{j,q}^{(0)}\cdot \exp \mathop{\sum }_{p=1}^{i}{y}_{j,q}^{(p)}}$$

(5)

As θ⁽ⁱ⁾ is constructed based on an independent assumption about x₁…x_D, it is clearly suboptimal whenever these variables are interdependent. The neural network ϕ is the output distribution, which aims to provide a better estimation by taking into account the interdependency between variables. Specifically,

$$\phi {\left({{{{\boldsymbol{\theta }}}}}^{(i)}\right)}_{j,k}\approx p({x}_{j}={v}_{k} \, | \, {{{{\bf{y}}}}}^{(1:i)})$$

(6)

This approximation implies an equivalent approximation of the distribution of the next noisy observation y⁽ⁱ⁺¹⁾. This approximation, referred to as the receiver distribution, is a mixture of Gaussians for each variable,

$${p}_{r}\left({y}_{j}^{(i+1)}\,|\, \phi \left({{{{\boldsymbol{\theta }}}}}^{(i)}\right);{\alpha }_{i+1}\right)=\mathop{\sum }_{k=1}^{K}\phi {\left({{{{\boldsymbol{\theta }}}}}^{(i)}\right)}_{j,k}\cdot {{{\mathcal{N}}}}\left({\alpha }_{i+1}(K{{{\bf{e}}}}({v}_{k})-1),{\alpha }_{i+1}K{{{\bf{I}}}}\right),$$

(7)

$${p}_{r}\left({{{{\bf{y}}}}}^{(i+1)}\,|\, \phi \left({{{{\boldsymbol{\theta }}}}}^{(i)}\right);{\alpha }_{i+1}\right)=\mathop{\prod }_{j=1}^{D}{p}_{r}\left({y}_{j}^{(i+1)}\,|\, \phi \left({{{{\boldsymbol{\theta }}}}}^{(i)}\right);{\alpha }_{i+1}\right),$$

(8)

The error in ϕ is measured through the KL-divergence between p_s and p_r at each step. For N steps,

$${L}^{N}={\sum }_{i=1}^{N}{D}_{{{{\rm{KL}}}}}\left({p}_{{{{\rm{s}}}}}(\cdot \,|\, {{{\bf{x}}}};{\alpha }_{i})\parallel {p}_{{{{\rm{r}}}}}(\cdot | \phi \left({{{{\boldsymbol{\theta }}}}}^{(i-1)}\right);{\alpha }_{i})\right).$$

(9)

In practice, it is possible to derive a continuous-time loss L^∞ where N → ∞. Under the assumption of a uniform prior θ⁽⁰⁾, the loss becomes remarkably simple and easy to approximate through Monte Carlo integration,

$${L}^{\infty }={{\mathbb{E}}}_{t \sim U(0,1)}\left[{{\mathbb{E}}}_{{{{{\bf{y}}}}}^{(t)} \sim {p}_{s}(\cdot \, | \, {{{\bf{x}}}};\beta (t))}\left[\frac{\alpha (t)}{2}{\left| \left| {{{\bf{e}}}}({{{\bf{x}}}})-\phi \left({{{{\boldsymbol{\theta }}}}}^{(t)}\right)\right| \right| }^{2}\right]\right].$$

(10)

This loss function reflects the transition from an N-step process to a continuous-time process, where t moves from 0 to 1. The sequence of accuracies α₁…α_N is replaced with the monotonically increasing accuracy schedule,

$$\beta (t)={\beta }_{1}{t}^{2},$$

(11)

where ${\beta }_{1}\in {{\mathbb{R}}}^{+}$ is the final accuracy at t = 1, and its derivative scales the loss through time,

$$\alpha (t)=\frac{d}{dt}\beta (t)=2{\beta }_{1}t.$$

(12)

The continuous-time loss corresponds to a negative variational lower bound²⁸, and therefore by optimising the parameters of ϕ to minimise it, we arrive at an approximation of the true distribution p(x) from which x was drawn. To train our models, we follow the general procedure outlined in ref. ²⁸. Specifically, the computation of the loss is described in Box 1.

Entropy encoding

In ref. ²⁸, the current time t is presented to the output network alongside the input distribution θ^(t). During initial sampling experiments, we discovered that, during the sampling process, the entropy of the input was noticeably higher at a given time t in comparison to that observed during training. We believe that this phenomenon occurs as the input distribution θ^(t) contains additional entropy from uncertainty in the output distribution $\phi ({{{{\boldsymbol{\theta }}}}}^{(t)})$. When time t is presented as an additional input to the network, this mismatch is, essentially, out of distribution for the output network, hampering performance. To resolve this, we replace the conventional Fourier encoding of time t used in²⁸ with a Fourier encoding of the entropy of each variable, appended to its corresponding input distribution before being passed into the network. This effectively makes the model invariant to t, and such an approach mirrors similar techniques used in diffusion models^22,67. In general, the use of entropy encoding is a design choice, and alternative representations of progress through the sampling process could suffice.

Sampling

We explored a variety of alternative sampling methods that reduce the overall temperature of sample generation from ProtBFN. In the conventional discrete-data sampling method described in²⁸, restricting ourselves to the logit space, the discrete sample generation process moves from y^(t) at time t to y^(s) at time s according to the equation,

$${{{{\bf{y}}}}}^{(s)}={{{{\bf{y}}}}}^{(t)}+{\alpha }_{s}\left(K\phi \left({{{{\boldsymbol{\theta }}}}}^{(t)}\right)-1\right)+\sqrt{{\alpha }_{s}K}{{{{\bf{z}}}}}^{(t)},$$

(13)

where ${{{{\boldsymbol{\theta }}}}}^{(t)}={\mathtt{softmax}}({{{{\bf{y}}}}}_{t})$, ${{{{\bf{z}}}}}^{(t)} \sim {{{\mathcal{N}}}}({{{\bf{0}}}},{{{\bf{I}}}})$ is isotropic noise and α_s = β(s) − β(t) is the change in accuracy. By the additivity of normally distributed variables and with y⁽⁰⁾ = 0, the distribution of y^(s) given preceding steps at times i = 0, …t is,

$${{{{\bf{y}}}}}^{(s)} \sim {{{\mathcal{N}}}}\left({\sum}_{i}{\alpha }_{i}\left(K\phi \left({{{{\boldsymbol{\theta }}}}}^{(i)}\right)-1\right),K\beta (s)\right),$$

(14)

or equivalently,

$${{{{\bf{y}}}}}^{(s)}=\left({\sum}_{i}{\alpha }_{i}\left(K\phi \left({{{{\boldsymbol{\theta }}}}}^{(i)}\right)-1\right)\right)+\sqrt{K\beta (s)}{{{\bf{z}}}},$$

(15)

where z ~ N(0, I) is a fixed isotropic noise. Sampling according to Equation (15) would yield an ODE similar to that described in²⁹. However, we observed that simply by replacing the summation of previous predictions with the most recent prediction, e.g.,

$${{{{\bf{y}}}}}^{(s)}=\beta (s)\left(K\phi \left({{{{\boldsymbol{\theta }}}}}^{(t)}\right)-1\right)+\sqrt{K\beta (s)}{{{\bf{z}}}},$$

(16)

substantially reduced the perplexity of generated samples. Effectively, this method is equivalent to taking our most recent prediction $\phi ({{{{\boldsymbol{\theta }}}}}^{(t)})$ and supposing that we had predicted it at every step 0…s. This method is further motivated under the assumption that the most recent prediction from the model is the ‘best guess’ for the centre of the input distribution; by reconstructing the input distribution at that point, we more closely match the flow distribution seen during sampling. We note the similarity of our method to the sampling method proposed in ref. ⁶³, where at each step, the input distribution is reconstructed from the most recent prediction. The main distinction between the two methods is that the sampler proposed in ref. ⁶³ resampled the underlying isotropic noise at each step (SDE-like), whereas our method uses a fixed isotropic noise throughout the process (ODE-like). Our overall sampling method is described in Box 2, which we refer to as Reconstructed ODE (R-ODE). As the choice of sampling method can dramatically change performance, we include an empirical comparison of various sampling methods in Supplementary Note 4.

Box 1 Continuous-time loss

1: Input: Φ, x

2: Output: L

3: t ~ U [0, 1]

4: β(t) ← β₁t²

5: α(t) ← 2β₁t

6: ${{{{\bf{y}}}}}^{(t)} \sim {{{\mathcal{N}}}}(\beta (t)\,\left(K{{{\bf{e}}}}\,({{{\bf{x}}}})-1\right),K\,\beta (t)\,{{{\bf{I}}}})$

7: ${{{{\boldsymbol{\theta }}}}}^{(t)}\leftarrow {\mathtt{softmax}}\,({{{{\bf{y}}}}}^{(t)})$

8: ${L}^{\infty }\leftarrow \frac{\alpha (t)}{2}{\left| \left| {{{\bf{e}}}}({{{\bf{x}}}})-\phi \left({{{{\boldsymbol{\theta }}}}}^{(t)}\right)\right| \right| }^{2}$

9: return L^∞

Box 2 Reconstructed ODE sampling

1: Input: N steps, output network $\phi$

2: Output: generated sample x

3: z ~ N (0, I)

4: y⁽⁰⁾ ← 0

5: fori = 0…N do

6: $t\leftarrow \frac{i}{N}$

7: $s\leftarrow \frac{i+1}{N}$

8: ${{{{\boldsymbol{\theta }}}}}^{(t)}\leftarrow {\mathtt{softmax}}\,({{{{\bf{y}}}}}^{(t)})$

9: β(s) ← β₁s²

10: ${{{{\bf{y}}}}}^{(s)}\leftarrow \beta (s)\left(K\phi \left({{{{\boldsymbol{\theta }}}}}^{(t)}\right)-1\right)+\sqrt{K\beta (s)}{{{\bf{z}}}}$

11: end for

12: ${{{{\boldsymbol{\theta }}}}}^{(1)}\leftarrow {\mathtt{softmax}}({{{{\bf{y}}}}}^{(1)})$

13: ${{{\bf{x}}}} \sim \phi \left({{{{\boldsymbol{\theta }}}}}^{(1)}\right)$

14: return x

Inpainting

Consider the task of inpainting some sequence x according to a binary mask m ∈ [0, 1]^D where m_i = 0 indicates that the ith element of x should be used as conditioning information, and m_i = 1 indicates that the ith element of x should be inpainted. Inspired by SMCDiff⁶⁸, we treat conditional generation of the inpainted regions as a sequential Monte Carlo problem which we may solve with particle filtering^69,70. Given an output network ϕ and input distribution θ^(t) at time t, the KL divergence of the sender and receiver distributions, with accuracy α, for the conditioning subset x_m is,

$${D}_{KL}\left({p}_{s}^{{{{\bf{m}}}}}(\cdot \,|\, {{{\bf{x}}}};\alpha )\,| |\, {p}_{r}^{{{{\bf{m}}}}}\left(\cdot | \phi \left({{{{\boldsymbol{\theta }}}}}^{(t)}\right);\alpha \right)\right)={\sum }_{i=1}^{D}{m}_{i}\frac{{\alpha }_{t}K}{2}{\left| \left| {{{\bf{e}}}}{({{{\bf{x}}}})}_{i}-\phi {\left({{{{\boldsymbol{\theta }}}}}^{(t)}\right)}_{i}\right| \right| }^{2},$$

(17)

which we will denote D(x, m, θ^(t), α). Given q particles at time t with input distributions ${{{{\boldsymbol{\theta }}}}}_{1}^{(t)}\ldots {{{{\boldsymbol{\theta }}}}}_{q}^{(t)}$, we resample each particle with probability proportional to ${e}^{D({{{\bf{x}}}},{{{\bf{m}}}},{{{{\boldsymbol{\theta }}}}}_{i}^{(t)},\alpha )}$. Combining SMC with our sampling method, we arrive at the algorithm detailed in Box 3.

Box 3 Greedy SMC inpainting

1: Input: N steps, output network $\phi$, q particles, conditioning information x_m

2: Output: conditionally generated sample x

3: ${\{{{{{\bf{z}}}}}_{i}\leftarrow \sim {{{\mathcal{N}}}}({{{\bf{0}}}},{{{\bf{I}}}})\}}_{i=1}^{q}$

4: ${\left\{{{{{\bf{y}}}}}_{i}^{(0)}\leftarrow {{{\bf{0}}}}\right\}}_{i=1}^{q}$

5: for i = 0…N do

6: $t\leftarrow \frac{i}{N}$

7: $s\leftarrow \frac{i+1}{N}$

8: β(t) ← β₁t²

9: β(s) ← β₁s²

10: α ← β(s) − β(t)

11: ${\left\{{{{{\boldsymbol{\theta }}}}}_{i}^{(t)}\leftarrow {\mathtt{softmax}}\left({{{{\bf{y}}}}}_{i}^{(t)}\right)\right\}}_{i=1}^{q}$

12: ${\left\{{l}_{i}\leftarrow D\left({{{\bf{x}}}},{{{\bf{m}}}},{{{{\boldsymbol{\theta }}}}}_{i}^{(t)},\alpha \right)\right\}}_{i=1}^{q}$

13: ${\left\{u(i) \sim {\mathtt{softmax}}\left({\left\{{l}_{i}\right\}}_{i=1}^{q}\right)\right\}}_{i=1}^{q}$

14: ${\left\{{{{{\bf{y}}}}}_{i}^{(s)}\leftarrow \beta (s)\left(K\phi \left({{{{\boldsymbol{\theta }}}}}_{u(i)}^{(t)}\right)-1\right)+\sqrt{K\beta (s)}{{{{\bf{z}}}}}_{i}\right\}}_{i=1}^{q}$

15: end for

16: ${{{{\boldsymbol{\theta }}}}}_{1}^{(1)}\leftarrow {\mathtt{softmax}}({{{{\bf{y}}}}}_{1}^{(1)})$

17: ${{{\bf{x}}}} \sim \phi \left({{{{\boldsymbol{\theta }}}}}_{1}^{(1)}\right)$

18: return x

Pre-training ProtBFN

Model

ProtBFN is based on the 650-million parameter architecture used in ref. ⁶, which is a BERT-style encoder-only transformer⁷¹ with rotary positional embeddings⁷². The architecture consists of 33 layers, each consisting of 20-head multi-head self-attention⁷³ in 1280-dimensional space followed by a single-layer MLP with GeLU activation⁷⁴ and a hidden dimension of 5120. The only substantial difference between ProtBFN’s architecture and that used in ref. ⁶ is that the initial token embedding is replaced with a linear projection, as our network’s input θ^(t) is a distribution over possible token values.

Data

ProtBFN is trained on data obtained from the January 2024 release of UniProtKB³¹. The data is filtered according to the Protein Existence (PE) property, including only those proteins that are inferred from homology (PE = 3), have evidence at the transcript level (PE = 2) or have evidence at the protein level (PE = 1). By removing those proteins which are known to be hypothetical (PE = 4) or are of unknown existence (PE = 5), ProtBFN is restricted to model the distribution of proteins that are very likely to exist, meaning that greater confidence can be placed in the sequences it generates. Additionally, we found that it was substantially faster to train a model when removing hypothetical proteins, indicating that they introduce substantial amounts of additional entropy, which may imply their generally lower quality. Additionally, ProtBFN is trained only on those sequences with length l < 512, with the final token used to encode an end-of-sequence (EOS) token. After filtering by PE and length, the final training set contains 71 million sequences. Where clusters are used to reweight and debias the data, the clusters are obtained from UniRef50⁷⁵. Each sequence is represented by its amino acids followed by an end-of-sequence (EOS) token. All other tokens after EOS are PAD tokens, which are treated as normal tokens for the purposes of noisy observations, predictions and loss. As this dataset is a (C)urated and (C)lustered subset of UniProt, we will refer to it for the rest of the text as UniProtCC. As the choice of data is essential to the overall performance of any generative model, we provide a robust ablation of UniProtCC against UniRef50 in Supplementary Note 5.

Training

ProtBFN is first pre-trained for 250,000 training-steps with a batch size of 8192. We observed that a large batch size was necessary to obtain stable gradient estimates. Adam⁷⁶ is used with β₁ = 0.9 and β₂ = 0.98 as in ref. ²⁸. The learning rate is initialised to 0 and linearly increased to 10⁻⁴ at step 10,000, after which it is held constant. Throughout training, the norm of the gradient is clipped to 500. A copy of the network’s parameters is maintained with an exponential moving average of the weights with decay rate 0.999. During this first phase of training, samples are drawn uniformly at random from all training data.

Next, the model is trained for a further 250,000 steps with clustered data. Specifically, each cluster is constructed by taking all samples within the corresponding UniRef50 cluster, which passes through both the PE and the length filters. During this training phase, each cluster is sampled with probability proportional to the square root of its size, so that ProtBFN is debiased away from those proteins most heavily studied by humans, but not overly focused on very data-sparse 1-member clusters as would happen when uniformly sampling clusters or training only on the UniRef50 cluster centres as done in¹⁵. Once a cluster has been sampled, any sequence contained within it is chosen uniformly at random. During this second phase of training, the optimiser is completely reset and again, the learning rate is linearly increased from 0 to 10⁻⁵ over the first 10, 000 steps. The main focus of this article is providing evidence BFNs can be used in the protein space. For more in-depth analysis concerning biases present in protein data please refer to refs. ^53,77 and ⁷⁸.

The training curve of ProtBFN is shown in Fig. 5. The loss decreases monotonically over the first 250,000 steps. At the point at which the cluster sample weighting is introduced, the loss increases significantly, reflecting the distribution shift of the underlying training data. The loss continues to monotonically decrease over the next 250,000 steps, although overall loss remains higher than during the initial training stage, indicating that the introduction of the weighted cluster sampling leads to a substantially higher underlying entropy of training data.

**Fig. 5: Training curve for the pre-training of ProtBFN.**

Sampling and filtering

To generate the 10,000 samples used for ProtBFN de novo generation results, we use the sampling algorithm described in Box 2 with N = 10,000, e.g., 10,000 sampling steps, and with the weights of the model obtained from the exponential moving average. We found that the lower-temperature sampling method occasionally produced pathological sequences that are highly repetitive. To remedy this, we counted the number of sequential repeats of any given amino acid and considered any amino acid repetitive if it repeats more than 3 times. For any given sequence, the repetitive score was calculated as the total number of repetitive amino acids divided by the sequence length. We discarded any sequence within the top 20th percentile with respect to their repetitive score. Additionally, we found that the sampling method occasionally generated sequences with very high perplexity. We, therefore, discarded any sequence within the top 30th percentile with respect to their perplexity. This process rejected approximately 44% of generated samples.

Coverage score

For a given number of sequences, we can estimate the expected number of unique clusters to which the sequences would be assigned to. This estimate assumes that a given sequence can be assigned to multiple clusters, which is the case when clustering according to 50% sequence identity. If we sample n sequences randomly and independently from a set of clusters with normalised weighting ω_i, the expected number of unique clusters sampled can be calculated as

$${\mathbb{E}}\left[{N}_{{{{\rm{hits}}}}}\right]={\sum}_{i}\left(1-{(1-{\omega }_{i})}^{n}\right).$$

(18)

For ProtGPT2 and EvoDiff we use an equal weight for each cluster, since that corresponds to the UniRef50 dataset, while for ProtBFN we use cluster weights inversely proportional to the cluster size, as that corresponds to our training data. For our diversity score, we divide the number of unique clusters hit by the expected number of cluster hits as calculated above. This estimate does over-count the expected number of unique clusters since it treats the clusters independently; however, we compensate for that by normalising the diversity scores by the equivalent metric calculated on a large subsample of our training data.

Fine-tuning AbBFN

Data

We downloaded the heavy-chain unpaired OAS dataset⁴³ on 21st February 2024. We filtered the data with a similar procedure to ref. ⁷⁹, which is as follows:

1.
Filter out the studies: Bonsignori et al.⁸⁰, Halliley et al.⁸¹, Thornqvist et al.⁸².
2.
Filter out studies originating from immature B cells (BType is “Immature-B-Cells" or “Pre-B-Cells").
3.
Filter out studies originating from B cell cancers (Disease is “Light Chain Amyloidosis" or “CLL").

Then for each remaining study, filter the sequences as follows:

1.
Filter if: sequence contains a stop codon; sequence is non-productive; V and J regions are out of frame; Framework region 2 is missing; Framework region 3 is missing; CDR3 is longer than 37 amino acids; J region identity is less than 50%; CDR edge is missing an amino acid; locus does not match chain type.
2.
Remove sequences if they only appear once in a study, then make them unique.
3.
Filter if the conserved cysteine residue is not present, or misnumbered in the ANARCI numbering.
4.
Create the near-full-length sequence IMGT positions 21 through 128 (127 for light chains and for heavy chains from rabbits and camels). Filter if framework 1 region is <21 amino acids.
5.
Remove duplicate near-full-length sequences and tally up the counts, filter out sequences which only appeared once dropped on the grounds of insufficient evidence of genuine biological sequence as opposed to sequencing errors, following⁷⁹.
6.
Filter out sequences which contain any amino acids which are not the standard 20.
7.
We use the sequence from the full ANARCI⁸³ numbering, not the near-full-length sequence as in ref. ⁷⁹.

This corresponds to all of the filters/preprocessing described in ref. ⁷⁹ but using full variable ___domain sequence (insofar as it was present in the original sequence) instead of the near-full-length sequence. We applied one additional filter, which removed any sequences that had an ANARCI numbering with an empty region.

To create the SAbDab test set, we used SAbDab data downloaded on 29th February 2024, specifically the summary table, to select only the paired chains, ensuring we exclude single-___domain antibodies; most of these are of camelid origin and, therefore, belong to germline genes which were not present in our training set. We also removed single-chain fragment variable (scFv) antibodies. We then parse SEQRES attributes from the original SAbDab PDB files and ran ANARCI⁸³ on these using the IMGT numbering scheme to obtain the final variable ___domain sequences as ANARCI retains only the subset of the sequence that could be numbered, thereby removing additions such as purification tags.

To ensure that the training data is dis-similar to the testing data, we split the separated OAS and SAbDab data into heavy and light chains. We then uniformly selected and set aside 20,000 heavy-chain sequences from the OAS data at random and added all heavy chains from SAbDab to construct the test dataset. Next, we used MMSeqs2³⁵ to query this combined dataset against the remainder of the OAS dataset with default sensitivity of 5.7, minimum sequence identity of 0.95, coverage of 0.8 and coverage mode 0. We removed any hits from the training data. Due to the presence of heavily engineered antibodies, the test data originating from SAbDab is more out-of-distribution when compared to the test data originating from OAS, and filtering out the similar sequences still retained 99% of the data, whereas filtering out sequences that are similar to the 20,000 uniformly-sampled test set sequences from OAS retained 79% of the OAS data. Filtering out these similar sequences produced 195M training examples, compared to 248M before sequence similarity filtering.

Training

AbBFN is fine-tuned from the ProtBFN model on the filtered OAS data. For computational efficiency, the maximum sequence length is reduced to 256. It is trained for 100,000 steps with a batch size of 8192. Adam⁷⁶ is used with β₁ = 0.9 and β₂ = 0.98 as in ref. ²⁸. The learning rate is initialised to 0 and linearly increased to 10⁻⁵ at step 10, 000, after which it is held constant. Throughout the training, the norm of the gradient is clipped to 500. A copy of the network’s parameters is maintained with an exponential moving average of the weights with a decay rate of 0.999. The training curve of AbBFN is shown in Fig. 6.

Fine-tuning AbBFN+

To assess if AbBFN is able to learn the distribution of heavy-chain sequences in SAbDab, we further fine-tune the model on each of the 9 train folds from the 10-fold cross-validation splits used by ref. ⁴⁴, using the remaining test fold for evaluation. The model is fine-tuned for 1000 training-steps with a batch size of 512. Adam⁷⁶ is used with β₁ = 0.9 and β₂ = 0.98, and the learning rate is linearly increased from 0 to 10⁻⁵ over the 1000 training-steps. Throughout the training, the norm of the gradient is clipped to 500. A copy of the network’s parameters is maintained with an exponential moving average of the weights with a decay rate of 0.995. The exponential moving average parameters are used for inpainting results.

Sampling AbBFN

To generate the 10,000 samples used for AbBFN de novo generation results, we use the sampling algorithm described in Box 2 with N = 10,000, e.g., 10,000 sampling steps, and with the weights of the model obtained from the exponential moving average. We did not find that it was necessary to filter samples by repetitiveness or perplexity, possibly due to the increased simplicity of the OAS ___domain in comparison to UniProtCC by virtue of the common immunoglobulin fold.

Inpainting

To inpaint OAS and SAbDab test sequences, we use the algorithm described in Box 3. We use p = 1024 particles for each sequence and N = 100 sampling steps. For both AbBFN and AbBFN+, we use the weights of the model obtained from the exponential moving average during training.

Computational resources

ProtBFN was trained on 128 TPU v4 chips for approximately 2 weeks. AbBFN was further trained for approximately 3 days on 64 TPU v4 chips.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

All training data used in this work is available from publicly available servers—UniProt (www.uniprot.org) and the Observed Antibody Space (opig.stats.ox.ac.uk/webapps/oas). The curated UniProtCC training data are available via Zenodo⁸⁴ (https://doi.org/10.5281/zenodo.14678318). Source Data is available with this work as a Source Data file. Source data are provided in this paper.

Code availability

Source code for this work is available via Zenodo⁸⁵ (https://doi.org/10.5281/zenodo.14962052), with the open-source repository also available at https://github.com/instadeepai/protein-sequence-bfn. ProtBFN and AbBFN models can be found on Hugging Face at https://huggingface.co/InstaDeepAI/protein-sequence-bfn.

References

Packer, M. S. & Liu, D. R. Methods for the directed evolution of proteins. Nat. Rev. Genet. 16, 379 (2015).
Article CAS PubMed MATH Google Scholar
Bordin, N., Lau, A. M. & Orengo, C. Large-scale clustering of AlphaFold2 3d models shines light on the structure and function of proteins. Mol. Cell 83, 3950 (2023).
Article CAS PubMed Google Scholar
Dryden, D. T., Thomson, A. R. & White, J. H. How much of protein sequence space has been explored by life on earth? J. R. Soc. Interface 5, 953 (2008).
Article CAS PubMed PubMed Central Google Scholar
Copp, J. N., Akiva, E., Babbitt, P. C. & Tokuriki, N. Revealing unexplored sequence-function space using sequence similarity networks. Biochemistry 57, 4651 (2018).
Article CAS PubMed Google Scholar
Rives, A. et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc. Natl Acad. Sci. USA 118, e2016239 (2019).
Lin, Z. et al. Language models of protein sequences at the scale of evolution enable accurate structure prediction. bioRxiv https://doi.org/10.1101/2022.07.20.500902 (2022).
Lin, Z. et al. Evolutionary-scale prediction of atomic-level protein structure with a language model. Science 379, 1123 (2023).
Article ADS MathSciNet CAS PubMed MATH Google Scholar
Hsu, C. et al. Learning Inverse Folding from Millions of Predicted Structures. 8946 (ICML, 2022).
Rao, R., Meier, J., Sercu, T., Ovchinnikov, S. & Rives, A. Transformer protein language models are unsupervised structure learners. bioRxiv https://www.biorxiv.org/content/10.1101/2020.12.15.422761v1 (2020).
Capel, H. et al. ProteinGLUE multi-task benchmark suite for self-supervised protein modeling. Sci. Rep. 12, 16047 (2022).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Michael, R. et al. Assessing the performance of protein regression models. bioRxiv https://www.biorxiv.org/content/10.1101/2023.06.18.545472v1 (2023).
Robinson, L. et al. Contrasting sequence with structure: pre-training graph representations with PLMs. bioRxiv https://www.biorxiv.org/content/10.1101/2023.12.01.569611v1 (2023).
Floridi, L. & Chiriatti, M. GPT-3: Its nature, scope, limits, and consequences. Minds Mach. 30, 681 (2020).
Article MATH Google Scholar
Touvron, H. et al. Llama 2: Open foundation and fine-tuned chat models. https://arxiv.org/abs/2307.09288 (2023).
Ferruz, N., Schmidt, S. & Höcker, B. ProtGPT2 is a deep unsupervised language model for protein design. Nat. Commun. 13, 4348 (2022).
Article ADS CAS PubMed PubMed Central Google Scholar
Nijkamp, E., Ruffolo, J. A., Weinstein, E. N., Naik, N. & Madani, A. ProGen2: exploring the boundaries of protein language models. Cell Syst. 14, 968 (2023).
Article CAS PubMed Google Scholar
Hesslow, D., Zanichelli, N., Notin, P., Poli, I. & Marks, D. RITA: a study on scaling up generative protein sequence models. https://arxiv.org/abs/2205.05789 (2022).
Ho, J., Jain, A. & Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 33, 6840 (2020).
Google Scholar
Kingma, D., Salimans, T., Poole, B. & Ho, J. Variational diffusion models. Adv. Neural Inf. Process. Syst. 34, 21696 (2021).
MATH Google Scholar
Dhariwal, P. & Nichol, A. Diffusion models beat gans on image synthesis. Adv. Neural Inf. Process. Syst. 34, 8780 (2021).
MATH Google Scholar
Watson, J. L. et al. De novo design of protein structure and function with rfdiffusion. Nature 620, 1089 (2023).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Abramson, J. et al. Accurate structure prediction of biomolecular interactions with AlphaFold 3. Nature 630, 493–500 (2024).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Austin, J., Johnson, D. D., Ho, J., Tarlow, D. & Van Den Berg, R. Structured denoising diffusion models in discrete state-spaces. Adv. Neural Inf. Process. Syst. 34, 17981 (2021).
Google Scholar
Lou, A., Meng, C. & Ermon, S. Discrete diffusion modeling by estimating the ratios of the data distribution. Proceedings of the 41st International Conference on Machine Learning, vol. 235, 32819–32848 (PMLR, 2024).
Hoogeboom, E., Nielsen, D., Jaini, P., Forré, P. & Welling, M. Argmax flows and multinomial diffusion: Learning categorical distributions. Adv. Neural Inf. Process. Syst. 34, 12454 (2021).
Google Scholar
Hoogeboom, E. et al. Autoregressive diffusion models. The Tenth International Conference on Learning Representations, https://openreview.net/forum?id=Lm8T39vLDTE (OpenReview.net, 2022).
Johnson, D. D., Austin, J., Berg, R. v. D. & Tarlow, D. Beyond in-place corruption: insertion and deletion in denoising probabilistic models. https://arxiv.org/abs/2107.07675 (2021).
Graves, A., Srivastava, R. K., Atkinson, T. & Gomez, F. Bayesian flow networks. https://arxiv.org/abs/2308.07037 (2023).
Xue, K. et al. Unifying bayesian flow networks and diffusion models through stochastic differential equations. https://arxiv.org/abs/2404.15766 (2024a).
Sillitoe, I. et al. CATH: increased structural coverage of functional space. Nucleic Acids Res. 49, D266 (2021).
Article CAS PubMed MATH Google Scholar
UniProt Consortium. Uniprot: the universal protein knowledgebase in 2023. Nucleic Acids Res. 51, D523 (2023).
Alamdari, S. et al. Protein generation with evolutionary diffusion: sequence is all you need. bioRxiv https://www.biorxiv.org/content/10.1101/2023.09.11.556673v1 (2023).
Gilis, D., Massar, S., Cerf, N. J. & Rooman, M. Optimality of the genetic code with respect to protein stability and amino-acid frequencies. Genome Biol. 2, 1 (2001).
Article MATH Google Scholar
Høie, M. H. et al. NetSurfP-3.0: accurate and fast prediction of protein structural features by protein language models and deep learning. Nucleic Acids Res. 50, W510 (2022).
Article PubMed PubMed Central MATH Google Scholar
Steinegger, M. & Söding, J. MMseqs2 enables sensitive protein sequence searching for the analysis of massive data sets. Nat. Biotechnol. 35, 1026 (2017).
Article CAS PubMed MATH Google Scholar
Wright, P. E. & Dyson, H. J. Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm. J. Mol. Biol. 293, 321 (1999).
Article CAS PubMed MATH Google Scholar
Alberts, B. et al. in Molecular Biology of the Cell. 4th edn (Garland Science, 2002).
Zhang, Y. & Skolnick, J. Tm-align: a protein structure alignment algorithm based on the tm-score. Nucleic Acids Res. 33, 2302 (2005).
Article CAS PubMed PubMed Central MATH Google Scholar
Taylor, W. R. & Orengo, C. A. Protein structure alignment. J. Mol. Biol. 208, 1 (1989).
Article CAS PubMed MATH Google Scholar
Orengo, C. A. & Taylor, W. R. in Methods in Enzymology. Vol. 266, 617–635 (Elsevier, 1996).
Lau, A. M., Kandathil, S. M. & Jones, D. T. Merizo: a rapid and accurate protein ___domain segmentation method using invariant point attention. Nat. Commun. 14, 8445 (2023).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Zahavi, D. & Weiner, L. Monoclonal antibodies in cancer therapy. Antibodies 9, 34 (2020).
Article CAS PubMed PubMed Central MATH Google Scholar
Olsen, T. H., Boyles, F. & Deane, C. M. Observed antibody space: a diverse database of cleaned annotated, and translated unpaired and paired antibody sequences. Protein Sci. 31, 141 (2022).
Article CAS PubMed MATH Google Scholar
Kong, X., Huang, W., & Liu, Y. Conditional antibody design as 3D equivariant graph translation. https://arxiv.org/abs/2208.06073 (2022).
Amzel, L. M. & Poljak, R. J. Three-dimensional structure of immunoglobulins. Annu. Rev. Biochem. 48, 961 (1979).
Article CAS PubMed MATH Google Scholar
Davies, D. R. & Metzger, H. Structural basis of antibody function. Annu. Rev. Immunol. 1, 87 (1983).
Article CAS PubMed MATH Google Scholar
Chiu, M. L., Goulet, D. R., Teplyakov, A. & Gilliland, G. L. Antibody structure and function: the basis for engineering therapeutics. Antibodies 8, 55 (2019).
Article CAS PubMed PubMed Central Google Scholar
Lombana, T. N., Dillon, M., Bevers III, J. & Spiess, C. Optimizing antibody expression by using the naturally occurring framework diversity in a live bacterial antibody display system. Sci. Rep. 5, 17488 (2015).
Article ADS PubMed PubMed Central Google Scholar
Su, C. T.-T., Ling, W.-L., Lua, W.-H., Poh, J.-J. & Gan, S. K.-E. The role of antibody vκ framework 3 region towards antigen binding: Effects on recombinant production and protein l binding. Sci. Rep. 7, 3766 (2017).
Article ADS PubMed PubMed Central MATH Google Scholar
Mak, T. W. & Saunders, M. E. in The Immune Response (eds Mak, T. W. & Saunders, M. E.) 93–120 (Academic Press, Burlington, 2006).
Ovchinnikov, V., Louveau, J. E., Barton, J. P., Karplus, M. & Chakraborty, A. K. Role of framework mutations and antibody flexibility in the evolution of broadly neutralizing antibodies. Elife 7, e33038 (2018).
Article PubMed PubMed Central Google Scholar
Ruffolo, J. A., Gray, J. J. & Sulam, J. Deciphering antibody affinity maturation with language models and weakly supervised learning. https://arxiv.org/abs/2112.07782 (2021).
Olsen, T. H., Moal, I. H. & Deane, C. Addressing the antibody germline bias and its effect on language models for improved antibody design. bioRxiv https://www.biorxiv.org/content/10.1101/2024.02.02.578678v1 (2024).
Jin, W., Wohlwend, J., Barzilay, R. & Jaakkola, T. Iterative refinement graph neural network for antibody sequence-structure co-design. https://arxiv.org/abs/2110.04624 (2021).
Schroeder, H. W., Zemlin, M., Khass, M., Nguyen, H. H. & Schelonka, R. L. Genetic control of dh reading frame and its effect on b-cell development and antigen-specifc antibody production. Crit. Rev. Immunol. 30, 327 (2010).
Article CAS PubMed PubMed Central Google Scholar
Briney, B. S., Inderbitzin, A., Joyce, C. & Burton, D. R. Commonality despite exceptional diversity in the baseline human antibody repertoire. Nature 566, 393 (2018).
Article ADS Google Scholar
Olsen, T. H., Boyles, F. & Deane, C. M. Observed antibody space: a diverse database of cleaned, annotated, and translated unpaired and paired antibody sequences. Protein Sci. Publ. Protein Soc. 31, 141 (2021).
Article MATH Google Scholar
Regep, C., Georges, G., Shi, J., Popovic, B. & Deane, C. M. The h3 loop of antibodies shows unique structural characteristics. Proteins 85, 1311 (2017).
Article CAS PubMed PubMed Central Google Scholar
Wong, W. K., Leem, J. & Deane, C. M. Comparative analysis of the cdr loops of antigen receptors. Front. Immunol. 10, 2454 (2019).
Weitzner, B. D., Dunbrack, R. L. & Gray, J. J. The origin of cdr h3 structural diversity. Structure 23, 302 (2015).
Article CAS PubMed PubMed Central MATH Google Scholar
Bahrami Dizicheh, Z., Chen, I.-L. & Koenig, P. Vhh cdr-h3 conformation is determined by vh germline usage. Commun. Biol. 6, 864 (2023).
Article CAS PubMed PubMed Central Google Scholar
Song, Y. et al. Unified generative modeling of 3d molecules with bayesian flow networks. in The Twelfth International Conference on Learning Representations. https://openreview.net/forum?id=NSVtmmzeRB (OpenReview.net, 2024).
Qu, Y. et al. MolCRAFT: Structure-based drug design in continuous parameter space. https://arxiv.org/abs/2404.12141 (2024).
Ho, J. & Salimans, T. Classifier-free diffusion guidance. https://arxiv.org/abs/2207.12598 (2022).
Gonzalez, M. et al. SEEDS: Exponential SDE solvers for fast high-quality sampling from diffusion models. Adv. Neural Inf. Process. Syst. 36 https://arxiv.org/abs/2305.14267 (2024).
Xue, S. et al. SA-Solver: Stochastic adams solver for fast sampling of diffusion models. Adv. Neural Inf. Process. Syst. 36 https://arxiv.org/abs/2309.05019 (2024b).
Karras, T., Aittala, M., Aila, T. & Laine, S. Elucidating the design space of diffusion-based generative models. Adv. Neural Inf. Process. Syst. 35, 26565 (2022).
Google Scholar
Trippe, B. L. et al. Diffusion probabilistic modeling of protein backbones in 3D for the motif-scaffolding problem. https://arxiv.org/abs/2206.04119 (2022).
Doucet, A. et al. Sequential Monte Carlo Methods in Practice, Vol. 1 (Springer, 2001).
Doucet, A. et al. A tutorial on particle filtering and smoothing: fifteen years later. Handb. nonlinear Filter. 12, 3 (2009).
MATH Google Scholar
Devlin, J., Chang, M.-W., Lee, K., Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. https://arxiv.org/abs/1810.04805 (2018).
Su, J. et al. Roformer: Enhanced transformer with rotary position embedding. Neurocomputing 568, 127063 (2024).
Article Google Scholar
Vaswani, A. et al. Attention is all you need. Adv. Neural Inf. Process. Syst. 30 http://arxiv.org/abs/1706.03762 (2017).
Hendrycks, D. & Gimpel, K. Gaussian error linear units (GELUs). https://arxiv.org/abs/1606.08415 (2016).
Suzek, B. E. et al. UniRef clusters: a comprehensive and scalable alternative for improving sequence similarity searches. Bioinformatics 31, 926 (2015).
Article CAS PubMed MATH Google Scholar
Kingma, D. P. & Ba, J. Adam: A method for stochastic optimization. https://arxiv.org/abs/1412.6980 (2014).
Shaw, A. Y. et al. Removing bias in sequence models of protein fitness. bioRxiv https://www.biorxiv.org/content/10.1101/2023.09.28.560044v1 (2023).
Ding, F. & Steinhardt, J. N. Protein language models are biased by unequal sequence sampling across the tree of life. bioRxiv https://www.biorxiv.org/content/10.1101/2024.03.07.584001v1 (2024).
Bachas, S. et al. Antibody optimization enabled by artificial intelligence predictions of binding affinity and naturalness. bioRxiv https://www.biorxiv.org/content/10.1101/2022.08.16.504181v1 (2022).
Bonsignori, M. et al. Maturation Pathway from Germline to Broad HIV-1 Neutralizer of a CD4-Mimic Antibody. Cell 165, 449–463 (2016).
Halliley, J. L. Long-Lived Plasma Cells Are Contained within the CD19−CD38hiCD138+ Subset in Human Bone Marrow. Immunity 43, 132–145 (2015).
Thörnqvist, L. & Ohlin, M. Critical steps for computational inference of the 3'-end of novel alleles of immunoglobulin heavy chain variable genes - illustrated by an allele of IGHV3-7. Mol. Immunol. 103, 1–6 (2018).
Dunbar, J. & Deane, C. M. Anarci: antigen receptor numbering and receptor classification. Bioinformatics 32, 298 (2016).
Article CAS PubMed Google Scholar
Atkinson, T. et al. Uniprotcc—protbfn training data. https://doi.org/10.5281/zenodo.14678318 (2025a).
Atkinson, T. et al. instadeepai/protein-sequence-bfn: Publication code https://doi.org/10.5281/zenodo.14962052 (2025b).
Saka, K. et al. Antibody design using LSTM based deep generative model from phage display library for affinity maturation. Sci. Rep. 11, 5852 (2021).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
McInnes, L., Healy, J. & Melville, J. UMAP: Uniform manifold approximation and projection for dimension reduction. https://arxiv.org/abs/1802.03426 (2018).

Download references

Acknowledgements

This research was supported with Cloud TPUs from Google’s TPU Research Cloud (TRC).

Author information

These authors contributed equally: Timothy Atkinson, Thomas D. Barrett.

Authors and Affiliations

InstaDeep, 5 Merchant Square, London, W2 1AY, England
Timothy Atkinson, Thomas D. Barrett, Scott Cameron, Bora Guloglu, Matthew Greenig, Charlie B. Tan, Louis Robinson, Alex Graves, Liviu Copoiu & Alexandre Laterre

Authors

Timothy Atkinson
View author publications
Search author on:PubMed Google Scholar
Thomas D. Barrett
View author publications
Search author on:PubMed Google Scholar
Scott Cameron
View author publications
Search author on:PubMed Google Scholar
Bora Guloglu
View author publications
Search author on:PubMed Google Scholar
Matthew Greenig
View author publications
Search author on:PubMed Google Scholar
Charlie B. Tan
View author publications
Search author on:PubMed Google Scholar
Louis Robinson
View author publications
Search author on:PubMed Google Scholar
Alex Graves
View author publications
Search author on:PubMed Google Scholar
Liviu Copoiu
View author publications
Search author on:PubMed Google Scholar
Alexandre Laterre
View author publications
Search author on:PubMed Google Scholar

Contributions

T.B. oversaw the project and, along with T.A., conceived the research, wrote the code, performed experiments and co-wrote the manuscript. S.C. supported the validation of ProtBFN. B.G. and M.G. supported the validation of A.b.B.F.N. C.T. assisted with the design and evaluation of sampling methods. L.R. curated and implemented custom training and validation datasets. A.G. supported the work with Bayesian Flow Networks and developed modified sampling methods for conditional generation. L.C. assisted with the design and implementation of biological validation and in writing the manuscript. A.L. supported interpreting results and assisted in the preparation of the manuscript.

Corresponding author

Correspondence to Thomas D. Barrett.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Jaap Heringa and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Reporting Summary

Transparent Peer Review file

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Atkinson, T., Barrett, T.D., Cameron, S. et al. Protein sequence modelling with Bayesian flow networks. Nat Commun 16, 3197 (2025). https://doi.org/10.1038/s41467-025-58250-2

Download citation

Received: 15 July 2024
Accepted: 11 March 2025
Published: 03 April 2025
DOI: https://doi.org/10.1038/s41467-025-58250-2

Subjects

Abstract

Similar content being viewed by others

Computational scoring and experimental evaluation of enzymes generated by neural networks

Protein structure generation via folding diffusion

Opportunities and challenges in design and optimization of protein function

Introduction

Results

A Bayesian flow network for protein sequences

Training

Inference

ProtBFN: A foundational generative model for protein sequences

Learning to generate natural protein sequences

ProtBFN effectively covers the known proteome

ProtBFN generates globular structural motifs with novel sequences

AbBFN: A foundational sequence model tuned specifically for antibodies

Unconditional generation of antibody chains

Zero-shot inpainting of antibody chains

Discussion

Methods

Bayesian flow networks for discrete-data

Overview

Entropy encoding

Sampling

Inpainting

Pre-training ProtBFN

Model

Data

Training

Sampling and filtering

Coverage score

Fine-tuning AbBFN

Data

Training

Fine-tuning AbBFN+

Sampling AbBFN

Inpainting

Computational resources

Reporting summary

Data availability

Code availability

References

Acknowledgements

Author information

Authors and Affiliations

Contributions

Corresponding author

Ethics declarations

Competing interests

Peer review

Peer review information

Additional information

Supplementary information

Supplementary Information

Reporting Summary

Transparent Peer Review file

Source data

Source Data

Rights and permissions

About this article

Cite this article

Share this article

Search

Quick links