Abstract
Chirality, or handedness, is ubiquitous in science, from cell biology to physics, and in condensed matter can underlie exotic phases such as chiral charge density waves and chiral superconductivity. However, detecting subtle broken symmetries that define such states is challenging, leading to debate and controversy. Here, using second-order optical response, we reveal the broken symmetries of a chiral charge density wave in the Kagome lattice KV3Sb5. Polarization-dependent mid-infrared photocurrent microscopy uncovers a longitudinal, helicity-dependent photocurrent associated with the charge order, indicating broken inversion and mirror symmetries. These findings, supported by theoretical analysis, directly establish the intrinsic chiral nature of the ordered state. Moreover, the absence of a circular photogalvanic effect perpendicular to the incident light imposes stringent constraints on the point-group symmetries. Our study not only visualizes the chiral nature of the Kagome charge order, but also highlights the nonlinear photogalvanic effect as a sensitive probe for detecting subtle symmetry breakings.
Similar content being viewed by others
Introduction
In the framework of Ginzburg–Landau theory, the phase transitions result from symmetry breaking of the ground state and associated order parameters1. Therefore, scrutinizing the broken symmetries in the post-transition state is imperative for comprehending the mechanism driving the phase transition, particularly in systems where multiple interaction pathways are involved. For instance, charge density wave (CDW) like instabilities, where the electron density spontaneously undergoes periodic modulations, have been found to be widely present in high-temperature superconductors and strongly intertwined with the superconductivity2,3,4. The microscopic structure of the intertwined charge orders in strongly correlated systems, including the symmetry and anisotropy, provides invaluable insight in the interactions between charge, lattice and spin degrees of freedom and therefore has been attracting significant research attention5,6,7.
Recently, Kagome materials AV3Sb5 (A = K, Rb, Cs) have become a major focus of research endeavors, in which intertwined CDW and superconducting orders emerge at low temperatures8,9,10. Below the CDW transition temperature (Tc = 79 K – 102 K), the vanadium atoms form a star-of-David pattern in the Kagome plane and the in-plane wave (Q) vectors connecting the van-Hove singularities at different M points, induce a strong electronic band reconstruction11,12. Intriguingly, scanning tunneling microscopy (STM)13, muon spin relaxation14, optical Kerr15, and electrical transport measurements16 provided evidence for the spontaneous time-reversal symmetry breaking of the charge-ordered phase and the long-thought loop current state, although contradicting results were also reported17,18,19. In parallel, scanning birefringence microscopy15 and STM17 studies revealed the broken six-fold rotation symmetry and the presence of nematicity in the charge order state, which are challenged by the recent thermodynamic measurements20. The CDW was further demonstrated to be coexisting with superconductivity at lower temperatures21 and forms an electronic smectic state. However, despite intensive research, the exact symmetry of the highly unconventional charge-ordered states and the associated crystal structure is still under strong debate and remains elusive, partially due to the weak lattice distortion and the abundance of energy degenerate CDW configurations.
The circular photogalvanic effect (CPGE), which measures the change of second-order photocurrent response under light with opposite circular polarizations, have become a powerful tool for detecting broken symmetries22,23 and Berry curvature distributions24,25,26. The corresponding response tensor inherits the symmetry of the system, and the CPGE with long-wavelength probing light (such as mid to far infrared) can directly reveal the microscopic symmetry breaking of the wavefunctions of the low-energy states22,27.
In this study, we leverage the nonlinear photogalvanic effect to thoroughly examine the symmetries of the enigmatic charge order in KV3Sb5. Notably, we observe the emergence of longitudinal CPGE upon the onset of the CDW order. The intrinsic CPGE directly exposes the broken mirror and inversion symmetries within the charge order. The absence of CPGE in the horizontal direction further imposes constraints on the rotational and point group symmetries of the charge order at low temperatures. Consequently, our study illuminates the symmetries of the unconventional CDW order in KV3Sb5 and lays the foundations for further understanding of the order parameter in charge-ordered phases.
Results
We employed a mid-infrared (10.6 μm wavelength, ~120 meV photon energy) scanning photocurrent microscope to investigate the polarization-dependent photogalvanic response in KV3Sb5. The experimental setup is schematically illustrated in Fig. 1a, where the polarization of the mid-infrared laser beam is modulated using a quarter-wave plate prior to being directed perpendicularly to the sample surface. To measure the longitudinal (sample’s out-of-plane) photocurrent, we fabricated a sandwich structure consisting of graphite (as an electrode), KV3Sb5, and metal electrodes, as shown in Fig. 1b. The current generated across the top graphite electrode and the bottom metallic electrode was measured. The optical microscopy image of the device, including multiple electrodes, is presented in Fig. 1c.
a Overview of the mid-IR photocurrent microscope setup. b Schematic illustrating the device configuration for measuring the out-of-plane photocurrent (Iz). c Optical microscopy image of the device. The electrodes are labeled as A-E. d Spatial mapping of the Iz photocurrent, with the largest signal observed at the intersection between graphite and KV3Sb5. e Polarization dependence of Iz when the beam spot is positioned at the marked star in (d). The pump light polarization evolves from left-circular (LC) to horizontal (LH) to right-circular (RC) to horizontal (LH) and back to left-circular (LC) as the QWP angle changes from 45 to 225 degrees. f Decomposition of the photocurrent into four different channels, where A-D denote the fitting parameters in Eq. (1). The error bars are based on the combination of one standard deviation of the fitting parameters and the measurement uncertainties.
We begin our investigation by measuring spatially resolved photocurrent at \(T=10\) K to identify the regions where the photocurrent is generated. The resulting map, depicted in Fig. 1d, reveals a prominent positive photocurrent source at the intersection region between graphite and KV3Sb5. Additionally, a small negative photocurrent appears at the interface between exposed KV3Sb5 and the bottom electrode. This uneven and bipolar distribution of photocurrent suggests the presence of out-of-plane photo-thermoelectric currents stemming from the variation in the Seebeck coefficient at the contacts25,28. Such a distribution allows us to differentiate the contribution of CPGE from those associated with photo-thermoelectric currents in real space, as we will discuss further. Next, we focused the beam at the center of the positive photocurrent area (marked by the green star in Fig. 1d) and recorded the out-of-plane photocurrent (\({I}_{z}\)) as a function of the azimuthal angle of the quarter-wave plate. Remarkably, we find that the photocurrent generated under left-circular-polarized pump light is greater than that under right-circular-polarized light. This difference is the hallmark of the CPGE. To dissect the different components contributing to the photocurrent, we employed a fitting procedure using the following function29:
where \(\phi\) represents the quarter-wave plate angle. The fitting results presented in Fig. 1f reveal the presence of both the CPGE (A term, exhibiting a periodicity of 180 degrees) and linear photogalvanic effect (LPGE) contributions (B and C terms, exhibiting a periodicity of 90 degrees). Additionally, a polarization-independent contribution from photo-thermoelectric currents is observed.
To elucidate the origins of the different photocurrent contributions, we investigated their temperature dependence. Figure 2a presents a series of polarization-dependent measurements acquired at the same ___location but at different temperatures. At low temperatures, and as discussed earlier, a distinct CPGE signal emerges, allowing us to define ICPGE as half of the signal difference between left-circular-polarized and right-circular-polarized light. As the temperature increases, ICPGE gradually becomes less prominent before sharply diminishing above \(T=100\) K. To quantitatively analyze the temperature dependence, we extracted the value of this nontrivial component at each temperature by fitting the data using Eq. (1). The results are summarized in Fig. 2b for the CPGE component and Fig. 2c for the LPGE component. We find that ICPGE follows a power-law behavior below a critical temperature (T*\(\simeq 95\pm 10\) K, close to the CDW transition temperature) and saturates at low temperatures with a magnitude of 3 nA. On the other hand, the helicity-independent component (\(\sqrt{{B}^{2}+{C}^{2}}\)) exhibits a gradual decrease with rising temperatures, likely due to the increasing resistivity of the system. This is consistent with the trend expected for the photo-thermoelectric effect and does not show any obvious anomaly near T*30. The stark disparity in the temperature dependencies strongly supports a non-thermal origin for the CPGE (see also Supplementary Fig. 1). Instead, it suggests the emergence of an electronic order characterized by spontaneously broken symmetries, which accounts for the observed CPGE effect at lower temperatures.
a Polarization dependence of Iz at different temperatures. The curves are normalized and offset for better comparison. At 10 K, a nonzero circular photogalvanic effect (CPGE) component, ICPGE, manifests as the half-difference between Iz acquired with left-circular and right-circular polarized light. At 120 K, the ICPGE diminishes. b Temperature dependence of the ICPGE. The blue dashed line represents the fitting result with the scaling function \(f\left(T\right)={({T}^{*}-T)}^{\alpha }\theta ({T}^{*}-T)\), where \(\theta\) denotes the unit step function and \(\alpha=\left(0.3\pm 0.1\right)\). c Temperature dependence of the linear photogalvanic effect (LPGE) component ILPGE. It is worth noting that the ICPGE nearly vanishes above \(T=100\) K, while the ILPGE shows no distinguishable change across the charge density wave transition (TCDW). TCDW is extracted from measurements of the resistivity as a function of the temperature (see Supplementary Fig. 2) performed in a bulk KV3Sb5 crystal. The error bars in panels (b, c) are based on the combination of one standard deviation of the fitting parameters and the measurement uncertainties.
Having observed the CPGE associated with the charge order, we investigate its underlying mechanisms. To this end, we conducted a series of experiments to explore its correlation with the laser power, cooling conditions, contact geometry, and spatial distribution. The linear power dependence of the CPGE, as demonstrated in Supplementary Fig. 6, is consistent with its characterization as a second-order effect; see additional discussion in Supplementary Note 4. We further cooled the device from \(T=120\) K to 20 K using either right-circular-polarized or left-circular-polarized light with an illumination power of 2.9 mW. Subsequently, we measured the polarization dependence of \({I}_{z}\) at the same ___location. The results are depicted in Fig. 3a, where the two curves exhibit close quantitative alignment. Importantly, \({I}_{z}\) shows no apparent dependence on the “induction process,” distinguishing itself from the previously observed chiral induction and gyrotropic charge density wave phase in 1T-TiSe222. Furthermore, we investigated the in-plane photocurrent at \(T=10\) K and found no detectable polarization dependence (Fig. 3b). This observation suggests that the CPGE predominantly manifests along the longitudinal direction when subjected to the normal incidence of light. Such direction sensitivity rules out extrinsic influences such as fabrication-related anomalies or variations in input power with the azimuthal angle of the quarter-wave plate rotation as potential sources of the observed CPGE. Lastly, we examined the spatial variability of the CPGE by analyzing the half-difference between the \({I}_{z}\) measured under right-circular-polarized and left-circular-polarized light as we scanned the beam across the device (Fig. 3c, d). Interestingly, the CPGE signal measured at \(T=10\) K is primarily localized in the region where the top graphite, KV3Sb5, and the bottom gold contact overlap, in contrast to the spatial mapping of \({I}_{z}\) (Fig. 1d). At \(T=120\) K, the CPGE signal becomes nearly undetectable across the entire sample. This distinct spatial distribution of the CPGE current further discredits the thermal effect as the underlying generation mechanism31. Collectively, these experiments shed light on the CPGE’s behavior and rule out potential extrinsic factors, providing compelling evidence for an intrinsic origin of the observed CPGE in the graphite-KV3Sb5 device.
a Polarization dependence of the normalized out-of-plane photocurrent measured on the same device which was cooled down with either right-circular (blue points) or left-circular polarized (orange points) light. b Out-of-plane (blue) and in-plane (red) photocurrent as a function of light polarization. The measurement was performed at \(T=10\) K. For the in-plane photocurrent measurement, all contacts except contacts C and B (as labeled in Fig. 1c) are grounded. c CPGE distribution measured as a function of the beam spot ___location at \(T=\,\)10 K. The major contribution of CPGE appears circular, consistent with prior reports of CPGE from other materials22,31, and occurs at the overlap region between graphite, KV3Sb5, and the bottom contact (the blue dashed line). d CPGE distribution measured as a function of the beam spot ___location at \(T=\) 120 K.
Having discussed our experimental observations, we turn to explore the plausible mechanisms and symmetry prerequisites underlying the intriguing longitudinal CPGE in KV3Sb5. As the spin-orbit coupling in KV3Sb5 is weak8 and long-range magnetic order is absent32, the spin photogalvanic effect is expected to be minimal in KV3Sb5. Therefore, the observed helicity-dependent photocurrent is mainly driven by the orbital excitations, which in turn inherit the global symmetry of the electronic structure.
The photocurrent contributed from a k-point in the momentum space is determined by the CPGE tensor \({\widetilde{\beta }}_{{ij}}\left({{\bf{k}}}\right)\), where i represents the current direction and j denotes the laser propagating direction. \({\widetilde{\beta }}_{{ij}}\left({{\bf{k}}}\right)\) is proportional to the product of the Fermi velocity \({v}_{i}\left({{\bf{k}}}\right)\) and the Berry curvature \({\varOmega }_{j}\left({{\bf{k}}}\right)\)33. Initially, we focus on the impact of inversion symmetry on the CPGE. For a generic momentum point \({{\bf{k}}}\) and its partner \(-{{\bf{k}}}\) linked by inversion symmetry, the Fermi velocities will change the signs \({v}_{i}\left(-{{\bf{k}}}\right)={-v}_{i}\left({{\bf{k}}}\right)\), while the Berry curvatures remain unchanged \({\varOmega }_{j}\left(-{{\bf{k}}}\right)={\varOmega }_{j}\left({{\bf{k}}}\right)\). Consequently, the resulting photocurrents from each pair of inversion partner cancel each other out, with \({\widetilde{\beta }}_{{ij}}\left(-{{\bf{k}}}\right)={-\widetilde{\beta }}_{{ij}}\left({{\bf{k}}}\right)\) indicating that breaking inversion symmetry is essential for KV3Sb5 to exhibit a nonzero CPGE.
Next, we examine the influence of mirror planes M on the CPGE within KV3Sb5, starting with Mx, which transforms \({{\bf{k}}}=\) (kx, ky, kz) into Mx\({{\bf{k}}}\,\)= (-kx, ky, kz). This operation only alters the sign of kx, leading to a sign change in the x-component of the velocity while leaving the others unaffected: \({v}_{x}\)(Mx\({{\bf{k}}}\)) \({=-v}_{x}\left({{\bf{k}}}\right)\), \({v}_{y}\)(Mx\({{\bf{k}}}\)) \({=v}_{y}\left({{\boldsymbol{k}}}\right),\) \({v}_{z}\)(Mx\({{\bf{k}}}\)) \({=v}_{z}\left({{\bf{k}}}\right)\)(Fig. 4b, left-top). On the other hand, Berry curvature, being a pseudovector, only maintains its components perpendicular to the mirror plane, resulting in \({\varOmega }_{x}\)(Mx\({{\bf{k}}}\)) = \({\varOmega }_{x}\left({{\bf{k}}}\right)\), \({\varOmega }_{y}\)(Mx\({{\bf{k}}}\)) = \({-\varOmega }_{y}\left({{\bf{k}}}\right)\), \({\varOmega }_{z}\)(Mx\({{\bf{k}}}\)) = \({-\varOmega }_{z}\left({{\bf{k}}}\right)\) (Fig. 4b, left-bottom). In scenarios where the laser propagates along the z-axis and the current is measured in the same direction, the presence of a mirror plane Mx results in a null net current, as \({\widetilde{\beta }}_{{zz}}\)(Mx\({{\bf{k}}}\)) = \({v}_{z}\)\(({{\bf{k}}}){{\boldsymbol{\times }}}\) [\({-\varOmega }_{z}\)(\({{\bf{k}}}\))] = \(-{\widetilde{\beta }}_{{zz}}\)(\({{\bf{k}}}\)). A similar rationale concludes that mirror plane My (or Mz) also eliminates \({\widetilde{\beta }}_{{zz}}\), as illustrated in Fig. 4b (right). Therefore, to observe the nonzero photocurrents reported in our study \({\widetilde{\beta }}_{{zz}}\), all mirror planes must be broken in the correlated phases of KV3Sb5.
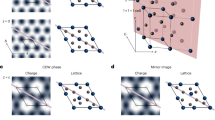
a Pristine phase of KV3Sb5, preserving inversion and mirror symmetries (Mx, My, and Mz). b Illustration of the effects of mirror symmetries on velocity \({v}_{i}\) and Berry curvature \({\varOmega }_{i}\). c Top and bottom patterns depicting structures with opposite chirality. The combination of two different chiral structures in a crystal yields an achiral structure with Mz mirror symmetry. d Calculated angle-resolved X-ray diffraction of high temperature (HT) and low temperature (LT) phase for TaTe2. Significant differences in the peaks' intensities within the region encircled by the red-dashed box are observable, signaling the presence of strong structural deformations across the CDW phase transition in TaTe2. e Calculated angle-resolved X-ray diffraction of the pristine phase and CDW phases of KV3Sb5.
Taking all the above into consideration, we experimentally demonstrated that all the inversion and mirror symmetries are broken in KV3Sb5 at low temperatures. Subsequently, we turn to determining the potential point groups of chiral KV3Sb5. Our measurements, as illustrated in Fig. 3, revealed a polarization-dependent in-plane CPGE of zero, indicating that, \({\widetilde{\beta }}_{{xz}}\) and \({\widetilde{\beta }}_{{yz}}\) are both zero. This outcome stems from the rotational symmetries along the z-axis present in KV3Sb5. Specifically, any of the following rotational symmetries along the z-axis would nullify the in-plane CPGE: C2z, S2z, C3z, S3z, C6z, and S6z (see Supplementary Note 1 and Supplementary Fig. 3). Therefore, based on our measurements, we can infer that the possible point groups for the CDW phase of KV3Sb5 are C2, D2; C3, D3; C6; D6. Considering the evidence of a two-fold rotation charge distribution on the surface in previous studies13,17, C2 and D2 are the most possible point groups. However, we cannot completely rule out the possibility that the bulk of chiral KV3Sb5 still preserves higher-fold screw rotations S3z and or/and S6z, which may not be detectable using surface-sensitive techniques.
Discussion
We would like to further address the challenges of pinning down the structural chirality in KV3Sb5. Previous STM measurements observed a rotating surface charge distribution at low temperatures, suggesting a chiral charge order in KV3Sb513. However, this rotating surface charge distribution only confirms the breaking of Mx and My. For instance, by applying the Mz operation, we can map a left-handed crystal into a right-handed crystal while the in-plane rotation direction remains the same (Fig. 4c). After the combination of the two opposite chiral crystals, the in-plane rotation remains unchanged, but the crystal is now an achiral structure with Mz. In other words, surface-sensitive experiments cannot fully rule out the existence of Mz. In another recent electronic magneto-chiral anisotropy measurement, the author also concluded that they can only confirm the breaking of Mx and My but not Mz16. In the current experiment, the long penetration depth of the 10 \(\mu m\) incident light (~20 nm) and the thickness of the device (~100 nm) ensures that the symmetry of the bulk crystal is probed, while the asymmetry induced by the interfaces is likely confined to a few layers at the interface and therefore is expected to be dominated by the bulk response. We note that the small atomic displacement in KV3Sb5 is the main reason challenging the experimental determination of the structure of KV3Sb5. Here, we compare KV3Sb5 with another CDW material TaTe234. The average displacement is around 0.15 \(\mathring{\rm A}\) in TaTe2, while the displacement in KV3Sb5 is only around 0.033 \(\mathring{\rm A}\). This difference can be visualized in our simulated X-ray diffraction (XRD) patterns. Detectable alterations can be observed between the high-temperature and low-temperature structures of TaTe2 (Fig. 4d). In contrast, the XRD patterns of the two phases of KV3Sb5 are nearly identical (Fig. 4e). Our systematic photocurrent study thus provides strong constraints on the symmetries of the chiral charge order in KV3Sb5.
Our experimental observations of longitudinal CPGE in KV3Sb5 associated with its charge order provide direct evidence for broken inversion and mirror symmetries, indicating that the bulk CDW order is chiral, namely the electronic state is not superimposable on its mirror image. Although the atomic displacements in the charge-ordered state are small (Fig. 4d), the electron-phonon coupling may contribute to the symmetry breaking observed in KV3Sb5. Our phonon calculations for the pristine phase of KV3Sb5 reveal softened phonon modes along the path from M to L (Supplementary Fig. 7). This indicates that electron-phonon interactions could be a driving force behind the CDW phase transition in KV3Sb5, aligning with the findings from previous studies35,36. Conversely, the detection of saddle points and quasi-nested electron and hole pockets on the Fermi surface points to inherent Fermi-surface instabilities11. The high tunability of this intriguing CDW phase further underscores the potential role of electron-electron interactions, suggesting that they are also critical in the formation of the chiral CDW instability13,16,37,38. Therefore, the CDW phase in AV3Sb5 (A = K, Rb, Cs) may result from a complex interplay between electron-phonon and electron-electron interactions. While this study provides a thorough investigation of the CPGE response in KV3Sb5, comparing it with other members of the metallic Kagome family, such as CsV3Sb5 and RbV3Sb5, remains an important direction for future research. This is particularly relevant given the differences in chiral transport properties observed across the family39. Furthermore, our approach utilizing non-linear photocurrent response can serve as a powerful tool for detecting subtle intrinsic symmetry breakings that lead to chiral electronic orders not only in other Kagome compounds but also in a broader range of quantum materials.
Methods
Single crystal synthesis
KV3Sb5 single crystals were grown by the flux method. K (99.95%), V (99.999%), and Sb (99.9999%) with the K/V/Sb=7: 3: 14 molar ratio were fully mixed. The mixture was then placed into an alumina crucible, sealed in a quartz tube with 10−3 Pa of Ar pressure, heated up to 1000 °C in 200 h, kept at 1000 °C for 12 h, and subsequently cooled to 200 °C over 230 h. After the stove had come down to room temperature, the flux was removed by putting the mixtures into deionized water. Finally, the high-quality single crystals of KV3Sb5 were harvested.
Device fabrication
We utilized a polydimethylsiloxane (PDMS) stamp-based mechanical exfoliation technique to fabricate KV3Sb5 devices. We patterned the electrical contacts onto the sample exfoliated onto the silicon substrates with a 280 nm layer of thermal oxide using electron beam lithography, followed by chemical development and metal deposition (5 nm Cr/35 nm Au). The fresh KV3Sb5 crystals were mechanically exfoliated from bulk single crystals on PDMS stamps. Prior to transferring them onto the SiO2/Si substrates with pre-patterned Cr/Au electrodes, we visually inspected the crystals under optical microscopy to select samples with favorable geometries. Note that the KV3Sb5 flake was transferred on the top of the pre-patterned contacts labeled B-E in Fig. 1c. The in-plane photocurrent (vertical to the light incidence) of the KV3Sb5 device was measured between electrodes B-E. To measure the photocurrent perpendicular to the sample plane (along the incident light), a few-layer graphene (graphite) was introduced as a top contact to connect the electrode A and the KV3Sb5 flake. The entire sample fabrication process was conducted within a glovebox equipped with a gas purification system, maintaining an environment with low levels of oxygen and water vapor (<1 ppm).
Photocurrent measurements
The probing light for our experiments was generated from a CO2 laser (Access Laser) and modulated using a mechanical chopper (Thorlabs) operating at a frequency of 167 Hz. To focus the laser onto the sample, we employed a ZnSe lens with a focal length of 50 mm, resulting in a beamspot size of ~25 μm at full width at half maximum. The input power on the sample surface was maintained at 2.9 mW. To detect the current signal, we employed a current preamplifier (SR570) for initial amplification, followed by the measurements using a lock-in amplifier (SR830). This setup ensured accurate and sensitive current detection. The device under investigation was cooled down using a customized cryostat (Oxford MicroHires) specifically designed for our experimental requirements. To ensure the reliability and consistency of our measurements, we repeated the experiments on multiple devices and performed multiple measurements for each device to ensure the reproducibility of the results.
First-principles calculations based on X-ray diffraction
The structures of the pristine phase and 2 × 2 × 2 CDW phase of KV3Sb5 are based on previous experimental work8 and theoretical predictions40, respectively. To minimize structural disparities between experimental data and theoretical calculations, we performed structural relaxations using identical parameters. Our ab-initio calculations were performed within the framework of density functional theory (DFT), employing the Vienna Ab initio Simulation Package (VASP) with the Perdew−Burke−Ernzerhof exchange−correlation functional41,42,43. The structural file (.cif) is provided as a Supplementary Data file. The valence electrons for K, V, and Sb were treated as 4s1, 3d34s2, and 5s25p3, respectively. In our calculations, we used a kinetic energy cutoff of 520 eV and a k-spacing parameter of 0.2 to ensure energy convergence within 1 meV/atom. An energy threshold of 10−6 eV and a force threshold of 3 × 10−3 eV/Å were applied. To account for van der Waals interactions, we included the zero-damping DFT-D3 method44 in our calculations. The simulated angle-resolved X-ray diffraction (XRD) data for the pristine phase and 2 × 2 × 2 CDW phase in the KV3Sb5 system were generated with an X-ray wavelength of 0.1671 Å9. For the TaTe2 system, both the high-temperature and low-temperature phase structures were experimentally determined and directly used for simulating X-ray diffraction data, with an X-ray wavelength of 0.1173 Å45.
Data availability
All data needed to evaluate the conclusions in the paper are present in the paper. Additional data are available from the corresponding authors upon request.
References
Landau, L. The theory of phase transitions. Nature 138, 840–841 (1936).
Tranquada, J. M., Sternlieb, B. J., Axe, J. D., Nakamura, Y. & Uchida, S. Evidence for stripe correlations of spins and holes in copper oxide superconductors. Nature 375, 561–563 (1995).
Hoffman, J. E. et al. A four unit cell periodic pattern of quasi-particle states surrounding vortex cores in Bi2Sr2CaCu2O8+δ. Science 295, 466–469 (2002).
Comin, R. et al. Charge order driven by fermi-arc instability in Bi2Sr2−xLax CuO6+δ. Science 343, 390–392 (2014).
Comin, R. et al. Symmetry of charge order in cuprates. Nat. Mater. 14, 796–800 (2015).
Teng, X. et al. Discovery of charge density wave in a kagome lattice antiferromagnet. Nature 609, 490–495 (2022).
Jiang, Y. et al. Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 573, 91–95 (2019).
Ortiz, B. R. et al. New kagome prototype materials: discovery of KV3Sb5, RbV3Sb5, and CsV3Sb5. Phys. Rev. Mater. 3, 094407 (2019).
Ortiz, B. R. et al. CsV3Sb5: A Z2 topological kagome metal with a superconducting ground state. Phys. Rev. Lett. 125, 247002 (2020).
Yang, S.-Y. et al. Giant, unconventional anomalous Hall effect in the metallic frustrated magnet candidate, KV3Sb5. Sci. Adv. 6, eabb6003 (2020).
Kang, M. et al. Twofold van Hove singularity and origin of charge order in topological kagome superconductor CsV3Sb5. Nat. Phys. 18, 301–308 (2022).
Hu, Y. et al. Rich nature of Van Hove singularities in Kagome superconductor CsV3Sb5. Nat. Commun. 13, 2220 (2022).
Jiang, Y.-X. et al. Unconventional chiral charge order in kagome superconductor KV3Sb5. Nat. Mater. 20, 1353–1357 (2021).
Mielke, C. et al. Time-reversal symmetry-breaking charge order in a kagome superconductor. Nature 602, 245–250 (2022).
Xu, Y. et al. Three-state nematicity and magneto-optical Kerr effect in the charge density waves in kagome superconductors. Nat. Phys. 18, 1470–1475 (2022).
Guo, C. et al. Switchable chiral transport in charge-ordered kagome metal CsV3Sb5. Nature 611, 461–466 (2022).
Li, H. et al. Rotation symmetry breaking in the normal state of a kagome superconductor KV3Sb5. Nat. Phys. 18, 265–270 (2022).
Farhang, C., Wang, J., Ortiz, B. R., Wilson, S. D. & Xia, J. Unconventional specular optical rotation in the charge ordered state of Kagome metal CsV3Sb5. Nat. Commun. 14, 5326 (2023).
Saykin, D. R. et al. High resolution polar kerr effect studies of CsV3Sb5: tests for time-reversal symmetry breaking below the charge-order transition. Phys. Rev. Lett. 131, 016901 (2023).
Frachet, M. et al. Colossal c -axis response and lack of rotational symmetry breaking within the kagome planes of the CsV3Sb5 superconductor. Phys. Rev. Lett. 132, 186001 (2024).
Chen, H. et al. Roton pair density wave in a strong-coupling kagome superconductor. Nature 599, 222–228 (2021).
Xu, S.-Y. et al. Spontaneous gyrotropic electronic order in a transition-metal dichalcogenide. Nature 578, 545–549 (2020).
Jog, H., Harnagea, L., Mele, E. J. & Agarwal, R. Exchange coupling–mediated broken symmetries in Ta2NiSe5 revealed from quadrupolar circular photogalvanic effect. Sci. Adv. 8, eabl9020 (2022).
Ma, J. et al. Nonlinear photoresponse of type-II Weyl semimetals. Nat. Mater. 18, 476–481 (2019).
Ma, Q. et al. Direct optical detection of Weyl fermion chirality in a topological semimetal. Nat. Phys. 13, 842–847 (2017).
Hosur, P. Circular photogalvanic effect on topological insulator surfaces: berry-curvature-dependent response. Phys. Rev. B 83, 035309 (2011).
Ma, Q., Grushin, A. G. & Burch, K. S. Topology and geometry under the nonlinear electromagnetic spotlight. Nat. Mater. 20, 1601–1614 (2021).
Dong, Y. et al. Giant bulk piezophotovoltaic effect in 3R-MoS2. Nat. Nanotechnol. 18, 36–41 (2023).
McIver, J. W., Hsieh, D., Steinberg, H., Jarillo-Herrero, P. & Gedik, N. Control over topological insulator photocurrents with light polarization. Nat. Nanotechnol. 7, 96–100 (2012).
Zeng, X. L. et al. Temperature dependence of photogalvanic effect in GaAs/AlGaAs two-dimensional electron gas at interband and intersubband excitation. J. Appl. Phys. 121, 193901 (2017).
Ma, J. et al. Unveiling Weyl-related optical responses in semiconducting tellurium by mid-infrared circular photogalvanic effect. Nat. Commun. 13, 5425 (2022).
Kenney, E. M., Ortiz, B. R., Wang, C., Wilson, S. D. & Graf, M. J. Absence of local moments in the kagome metal KV3Sb5 as determined by muon spin spectroscopy. J. Phys.: Condens. Matter 33, 235801 (2021).
Chang, G. et al. Unconventional photocurrents from surface fermi arcs in topological chiral semimetals. Phys. Rev. Lett. 124, 166404 (2020).
El Baggari, I. et al. Direct Visualization of Trimerized States in 1T’− TaTe2. Phys. Rev. Lett. 125, 165302 (2020).
Xie, Y. et al. Electron-phonon coupling in the charge density wave state of CsV3Sb5. Phys. Rev. B 105, L140501 (2022).
Luo, H. et al. Electronic nature of charge density wave and electron-phonon coupling in kagome superconductor KV3Sb5. Nat. Commun. 13, 273 (2022).
Li, H. et al. Observation of unconventional charge density wave without acoustic phonon anomaly in kagome superconductors AV3Sb5 (A =Rb, Cs). Phys. Rev. X 11, 031050 (2021).
Li, H., Liu, X., Kim, Y. B. & Kee, H.-Y. Origin of π -shifted three-dimensional charge density waves in the kagomé metal AV3Sb5 (A = Cs, Rb, K). Phys. Rev. B 108, 075102 (2023).
Guo, C. et al. Distinct switching of chiral transport in the kagome metals KV3Sb5 and CsV3Sb5. npj Quantum Mater. 9, 20 (2024).
Tan, H., Liu, Y., Wang, Z. & Yan, B. Charge density waves and electronic properties of superconducting kagome metals. Phys. Rev. Lett. 127, 046401 (2021).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Petkov, V., Chapagain, K., Yang, J., Shastri, S. & Ren, Y. Exotic bonding interactions and coexistence of chemically distinct periodic lattice distortions in the charge density wave compound TaTe2. Phys. Rev. B 102, 024111 (2020).
Acknowledgements
We acknowledge illuminating discussions with Titus Neupert. M.Z.H.'s group acknowledges primary support from the US Department of Energy, Office of Science, National Quantum Information Science Research Centers, Quantum Science Center (at ORNL) and Princeton University; STM Instrumentation support from the Gordon and Betty Moore Foundation (GBMF9461) and the theory work; and support from the US DOE under the Basic Energy Sciences program (grant number DOE/BES DE-FG-02-05ER46200) for the theory and sample characterization work including ARPES. MZH acknowledges partial support from the US DOE under the Basic Energy Sciences program (grant number DOE/BES DE-FG-02-05ER46200) for the sample characterization based on advanced spectroscopy work. Work at Nanyang Technological University was supported by the National Research Foundation, Singapore, under its Fellowship Award (NRF-NRFF13-2021-0010), the Agency for Science, Technology and Research (A*STAR) under its Manufacturing, Trade and Connectivity (MTC) Individual Research Grant (IRG) (Grant No.: M23M6c0100), the Singapore Ministry of Education (MOE) Academic Research Fund Tier 3 grant (MOE-MOET32023-0003), Singapore Ministry of Education (MOE) AcRF Tier 2 grant (MOE-T2EP50222-0014) and the Nanyang Assistant Professorship grant (NTU-SUG). The sample growth was supported by the National Key Research and Development Program of China (grant nos 2020YFA0308800 and 2022YFA1403400), the National Science Foundation of China (grant no 92065109), and the Beijing Natural Science Foundation (grant nos Z210006). Z.W. thanks the Analysis and Testing Center at BIT for assistance in facility support. L.B. is supported by the US-DoE, Basic Energy Sciences program through award DE-SC0002613. The National High Magnetic Field Laboratory is supported by the US-NSF Divisions of Materials Research and Chemistry through DMR-2128556 and the State of Florida.
Author information
Authors and Affiliations
Contributions
Photocurrent measurements were conducted by Z.-J.C., M.S.H., and Q.Z. First-principles calculations and symmetry analysis were carried out by S.S., Y.Z., M.Y., and G.C., in consultation with Z.-J.C. and M.S.H. Crystals were synthesized by J.L., Y.L., Y.Y., and Z.W. Transport experiments were performed by M.S.H. and Q.Z., in consultation with L.B. Figure development and manuscript writing were led by M.S.H., Z.-J.C., G.C., and M.Z.H. M.Z.H. supervised the project. Y.-X.J., J.-X.Y., T.A.C., M.L., X.Y., B.K., and J.Z. contributed in data interpretation. All authors discussed the results, interpretations, and conclusions.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Chunyu Guo, Jing Xia and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Cheng, ZJ., Hossain, M.S., Zhang, Q. et al. Broken symmetries associated with a Kagome chiral charge order. Nat Commun 16, 3782 (2025). https://doi.org/10.1038/s41467-025-58262-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-58262-y