Introduction

Many minerals and high-entropy oxides (HEOs) are known for their improved hardness, thermal stability, and oxidative, corrosive1, and wear resistance2,3. Because of these properties, multicomponent oxides show promise as durable thermal/environmental barrier coatings for extreme temperature applications, such as in turbine engines4, and demonstrate potential as platforms in catalytic reactions5,6. Like other phononically dominated materials, the spectrum of vibrational carriers and phonon scattering impacts the thermal transport in multi-cation oxides. Thus, it is critical to understand the fundamental mechanisms that govern the vibrational thermal transport properties to further realize the emergent thermophysical properties of this class of oxides.

Phonon scattering in alloys is enhanced by the presence of atomic species with different masses, sizes, and interatomic bonding, leading to reductions in thermal conductivity. This process has been studied analytically dating back to seminal works by Abeles and Klemens7,8. In these formalisms, the acoustic phonon spectrum transfers the energy, and these phonons are then elastically scattered based on the local perturbations in the host lattice arising from the chemical heterogeneity. These relatively simple approaches have proven surprisingly powerful in predicting the reductions in thermal conductivity of solid solutions with multiple elements, including multi-cation ceramics9,10,11,12. However, the assumed scattering rates are often fitted parameters and are needed to account for the strength of the phonon scattering rates (e.g., the degree of local lattice distortion). Additionally, realistic phonon dispersions in chemically disordered materials must often be approximated with Debye assumptions. These assumptions regarding the phonon spectrum and energies and concomitant scattering rate thus can lead to these virtual-crystal-rooted models not accurately predicting the true phonon scattering rates in compositionally complex solids.

As an alternative framework to understanding vibrational heat transfer in compositionally complex materials, Hofmeister13 developed a formalism that considers the heat flux from the optical phonons, the scattering rates of which can be directly measured with optical spectroscopy (e.g., Fourier Transform Infrared spectroscopy and infrared variable angle spectroscopic ellipsometry (IR-VASE)). Due to the large number of dispersive, optical phonon branches in multi-atom ceramics, the role of optical phonons in thermal conductivity can be pronounced, if not dominant as compared to the low-energy acoustic phonon branches. The low number of acoustic modes in comparison to the high number of optical modes for compositionally complex materials moderates the acoustic phonons’ roles in heat propagation. Additionally, complex systems with acoustic-optical mode interference can increase phonon scattering further reducing the thermal current of acoustic phonons. For atoms with many optical phonon branches, acoustic-optical scattering can be the primary thermal resistance process to thermal conductivity and emphasize the significance of optical phonon modes relative to the acoustic phonon heat current. Mass density, unit cell volume, and modulus are factors that impact the frequency band gap between both modes. Further, optical phonon group velocities have finite velocities for wavevectors, \(\vec{k}\), away from the zone center or Brillouin zone edge, which is only marginally smaller than acoustic velocities; that is, averaging over the optical branches away from zone centers or edges will yield comparable group velocities, which is especially true for complex crystal structures with Brillouin zone folding14. Even at the expected high operating temperatures of these materials, the pertinence of optical mode heat transport escalates due to the Bose-Einstein nature of phonon transport. Giesting and Hofmeister15,16 applied this approach considering optical phonon heat fluxes to predict the thermal conductivity of several different oxides with no fitting parameters because of the direct correlation between the phonon scattering rates and the vibrational thermal conductivity. Similarly, Wu et al. showed a direct correlation between optical mode Full Width at Half Max (FWHM) captured from Raman spectroscopy and the thermal conductivity of rare-earth silicate oxyapatites17. Raman linewidths have also been investigated on other classes of low thermal conductivity materials such as halide perovskites exemplifying the robustness of correlation between optical mode scattering rates and thermal conductivities18,19.

In this work, we report on the room temperature thermal conductivities of single- and multi-cation rare earth sesquioxides and zirconates. We observe a reduction in thermal conductivity from the single to the multicomponent oxides, consistent with prior reports9,20,21. Amongst the single-component oxides, a larger mass difference between rare earth and oxygen resulted in a lower thermal conductivity. Additionally, the multicomponent oxides two-phase microstructure possessed reduced thermal conductivity. From IR-VASE, we extract dielectric functions for single and multicomponent oxides to measure the lifetimes of the optical phonon modes. We find that multicomponent oxides exhibit smaller lifetimes corroborating the reduction in thermal conductivity. We show that the thermal conductivity of these sesquioxides and zirconates can be well described via the theoretical framework by Giesting and Hofmeister13, while applying the more traditionally used virtual-crystal approximation to predict the thermal conductivity cannot capture our measured values or trends.

Our work also experimentally demonstrates that optical phonon energies redshift from the inclusion of additional cations, which is driven by the local lattice distortion induced from the addition of multiple cations, and not due to average mass changes. We demonstrate that, in low thermal conductivity materials, such as the rare earth zirconates, this lattice distortion-driven optical phonon mode shift can lead to further reductions in thermal conductivity. Density functional theory (DFT) simulations of representative single and multicomponent sesquioxides reveal that the distortion index is greater in the multicomponent oxides, indicating a rationale for the reduction in thermal conductivity and oscillator strength for optical phonon modes. Additionally, frozen phonon calculations were performed to quantify the phonon band structure of representative single and multicomponent sesquioxides and identify characteristics influencing thermal transport. Through the combined experimental measurements and computational work presented in this study, we identify key factors impacting the nature and behavior of phonon thermal conductivity in multiple component oxides.

Results and discussion

Eight rare earth sesquioxide (RE2O3), including four single-RE and multi-RE compounds, were investigated as well as three RE zirconates. The RE elements include Y, Ho, Er, Yb, Nd, Dy, Sm, Nd, La, and Ce, and the fabricated compounds are listed in Table 1. To fabricate the sesquioxides, precursor powders were mixed and densified using Spark Plasma Sintering (SPS). Following densification, samples were annealed between 1200 and 1500 °C in air. X-ray diffraction (XRD) and scanning electron microscopy (SEM) coupled energy dispersive spectroscopy (EDS) were used to investigate microstructure, phase distribution, and sample homogeneity (SI, Sections 1 and 2). The single and multi-cation RE oxides were revealed to be cubic crystal structures, whereas oxides with La and Ce had a two-phase microstructure. The three RE zirconates were synthesized with a wet chemical method to produce powders and densified via a cold pressing step and annealing at 1500 °C in air.

Table 1 Thermal conductivities and optical lifetimes of single and multicomponent rare earth oxides as well as the wavenumber and wavenumber redshift of the strongest IR modes
Full size table

Time ___domain thermoreflectance (TDTR), a contactless pump-probe thermometry technique, was employed to measure the room temperature thermal conductivities of the oxides22,23. All studied samples exhibit thermal conductivities ranging between 1.3 and 10.0 W m−1 K−1. Higher thermal conductivities were measured for the single-component oxides with a subsequent decrease in the multicomponent counterparts and zirconates, as shown in Table 124. Discussion of the trends are detailed below.

We can qualitatively understand the trends in phonon thermal conductivity from the kinetic theory of gases. In this approach, the thermal conductivity depends on the volumetric heat capacity (C), the group velocity of phonons (v), and the phonon mean free path (l) as25

$$\kappa=\frac{1}{3}{Cvl}$$
(1)

where, at high temperatures, volumetric heat capacity, C, can be approximated as25 C = 3Nkb, where kb is the Boltzmann constant, which describes the energy over all possible phonon modes for N atoms in a volume. Heat capacities of the single-component oxides were found in literature and calculated via the Neumann-Kopp rule for the multicomponent sesquioxides and zirconates which serves as an approximation to the heat capacity of homogeneously mixed systems26,27. The heat capacities of the rare earth sesquioxides are relatively similar and thus not an explanation for the apparent decrease in thermal conductivity. The reasons for similarities in heat capacity are comparable rare earth mass and electron configuration (apart from yttrium) and crystal structure for these sesquioxides. The group velocity, v, is found through the phonon dispersion and describes the average speed of phonons. The phonon group velocity of a material depends on the elastic moduli calculated from bulk and shear modulus. For the lanthanide-containing sesquioxides, there is marginal variance in phonon group velocity implying a minimal effect on the reduction of thermal conductivity28. Y2O3 has a slightly greater velocity which is evident in the larger thermal conductivity. This leaves the phonon mean free path as a likely explanation for the difference in thermal conductivity from single to multicomponent oxides. The mean free path, l, is the average distance between particle collisions and is defined as25 l = vτ, where τ is the average time between collisions. Scattering from boundaries like interfaces and polycrystalline grains as well as atomistic scattering from point defects affect the mean free path of a material, and as we show below, is most critical to quantify to understand the reductions in thermal conductivity of multi-cation oxides.

The mean free path of phonons in a crystal is a spectral quantity, and thus dependent on vibrational energy. Thus, we turn thermal conductivity formalisms beyond the gray kinetic theory approximation described above to conceptually understand the implications of phonon scattering on thermal conductivity reductions. To this end, another description for thermal conductivity from Callaway and Baeyer29 incorporated a Debye spectrum of vibrational states whereby integrating over all vibrational energies captured thermal conductivity. In this consideration, thermal conductivity is written as:

$$\kappa=\frac{{k}_{b}}{2{\pi }^{2}v}{\left(\frac{{k}_{b}T}{{{\hslash }}}\right)}^{3}{\int }_{0}^{\theta /T}{\tau }^{-1}(x)\frac{{x}^{4}{e}^{x}}{{\left({e}^{x}-1\right)}^{2}}{dx}$$
(2)

where \(\theta\) is the Debye temperature, T is the absolute temperature and \(\tau\) is the vibrational relaxation lifetime (inverse of scattering rate and analogous to the average time between particle collisions), and \(x\) is \(\hslash \omega {\left({k}_{b}T\right)}^{-1}\). This expression regards thermal conductivity in terms of the frequency-dependent scattering rate of all phonon-scattering processes including phonon-phonon, boundary, and defect scattering. The dependency of thermal conductivity on phonon scattering rate warrants their direct comparison as detailed in a later section, and especially emphasizes the importance of understanding high-frequency optical phonon scattering rates, as these scattering rates are much stronger than lower-frequency acoustic phonon scattering8.

The rate of optical phonon scattering in multi-cation oxides can be elucidated by measuring the lifetime of optical modes. The optical phonon lifetimes in the studied oxides were found from fitted oscillator models on complex frequency-dependent ellipsometric data measured via IR-VASE. The measured ellipsometric values (Ψ and Δ) represent the amplitude ratio and phase difference of the complex reflection coefficients (r) of the sample for p- and s-polarized light as30:

$$\rho=\frac{{r}_{p}}{{r}_{s}}=tan \left(\psi \right){e}^{i\Delta }$$
(3)

An isotropic optical model was built on measured ellipsometric data to extract the complex frequency-dependent dielectric function of each sample. Due to the dielectric nature of these samples, the real and imaginary portion of the complex dielectric function is described by the summation of multiple Lorentzian oscillators as31:

$$\varepsilon (\omega )={\varepsilon }_{1}(\omega )+i{\varepsilon }_{2}(\omega )={\varepsilon }_{\infty }+{\varSigma }_{i}\frac{{f}_{i}}{{\omega }_{i}^{2}-{\omega }^{2}-i{\varGamma }_{i}\omega }$$
(4)

where \({f}_{i}\), \({\omega }_{i}\), and \({\varGamma }_{i}\) are the oscillator strength, centroid frequency, and broadening of the ith oscillator, respectively. The parameters of each oscillator model were optimized to fit the model to the collected ellipsometric data by minimizing the mean square error. The extracted dielectric functions resulting from fitted oscillator parameters are shown in Fig. 1.

Fig. 1: Dielectric functions of sesquioxides and zirconates.
figure 1

The real (ε1) and imaginary (ε2) parts of the dielectric function of a single-cation oxides, b multi-cation oxides, and c single and multi-cation zirconates. Strong peaks in the imaginary parts correspond to transverse optical phonon modes. The optical modes of multi-cation oxides are broader, indicating greater anharmonicity from defect scattering.

Full size image

The optical phonon lifetime of each oscillator was calculated from the broadening parameter, which is directly related to the FWHM of the imaginary part of the dielectric function at that frequency, as:

$${\tau }_{i}=\frac{1}{{2{{\pi }}c\varGamma }_{i}}$$
(5)

where c is the speed of light. Finally, the weighted average of the oscillators was calculated to determine the optical phonon lifetimes for each material.

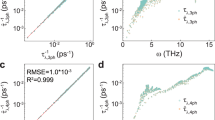
The calculated phonon-phonon lifetimes for the multi-cation oxides studied are listed in Table 1. The single-component oxides possess longer optical phonon lifetimes, which is evident from the imaginary part of their dielectric function exhibiting sharper and stronger peaks (corresponding to transverse optical modes) while the multicomponent sesquioxides and zirconates exhibit broader peaks (Fig. 1). The correlations between measured thermal conductivity and extracted phonon lifetimes are plotted in Fig. 2 for the studied materials. As shown in this figure, the thermal conductivities follow the same trend as the phonon lifetimes, indicating that the reduction in thermal conductivity for multicomponent oxides is due to an increase in phonon scattering rates (i.e., a decrease in phonon-phonon lifetimes). The zirconates, however, all exhibit low lifetimes that are within uncertainty with a marginal decrease in thermal conductivity from the Er2Zr2O7 to (Yb0.2Er0.2Dy0.2Sm0.2Nd0.2)2Zr2O7. One of the reasons for such low thermal conductivity in rare earth zirconates has been argued to be the presence of low-lying optical phonon modes that are attributed to the rare earth cation that interfere with heat-carrying acoustic modes and increase phonon scattering32. Consequently, characterizing optical phonon lifetimes from the weak oscillatory strength of lower energy modes introduces uncertainty into expected values. Lifetimes were heavily weighed by the weaker modes at higher energy that were challenging to quantitatively model but resultant lifetimes are within uncertainty. Uncertainty in the lifetimes is calculated from modal oscillator strength, wavelength, and damping coefficient.

Fig. 2: Thermal conductivity versus optical phonon lifetime.
figure 2

Thermal conductivity versus average optical phonon lifetime for the single and multicomponent oxides displaying the direct correlation.

Full size image

The samples in this study are all bulk ceramics thus boundary scattering will not influence the phonon scattering rates. The samples were synthesized and annealed through SPS and box furnace treatment, and thus polycrystalline. SEM images revealed the grain size to be almost invariant among the samples (see SI, Figs. 6–13). For solutions with cations of different masses and of greater weight disparity, adding more elements to the matrix reduced the mean free path as evidenced by the multi-cation oxides. The (Y0.33Yb0.33Er0.33)2O3 + 16 at.% La2O3 and (Y0.33Yb0.33Er0.33)2O3 + 16 at.% CeO2 are special cases where La and Ce were intentionally included to form a two-phase microstructure that provides an additional low thermal conductivity phase, which decreased the effective thermal conductivity. EDS analysis revealed regions containing an abundance of precipitated oxide (see SI, Figs. 14–17). It should be noted that both phases contained all 4 constituent cations and both compounds yielded the lowest thermal of the multicomponent oxides.

The three strongest optical modes are associated with oxygen displacements within the crystal. These modes have marginal cation contribution to the dipole depending on the specific cation. For Y2O3, the cation contribution is expected to be greater due to the relatively smaller difference in mass and greater bond strength between yttrium and oxygen which increases the strength of oscillation33. As the atomic mass difference increases for heavier sesquioxides, the cation contribution to mode strength decreases resulting in weaker oscillation strength. These cation-specific modes subsequently redshift to lower energies. Additionally, the frequency of the oxygen-localized modes shifts to lower energies with decreasing cationic radius caused by the softer bonding33. The zirconates exhibited one broad, weak peak that was fit using a convolution of multiple Gaussian oscillators as well as several smaller higher energy modes. We use Gaussians to fit the zirconate spectra to predict phonon linewidths following prior works determining linewidths in low thermal conductivity materials34. Also, the broad linewidths we observe that represent a convolution of multiple phonon IR resonances are in agreement with the broad Raman linewidths previously reported for similar low thermal conductivity zirconates21.

The strongest TO modes in the sesquioxides and zirconates have been tabulated in Table 1. For the peak modal energies of the multi-cation oxides (besides (Y0.33Yb0.33Er0.33)2O3), we observe modal red shifting for the oxygen-localized modes of the multi-cation oxides. As we have not measured the dielectric function of all the constituent oxides, the tabulated modal red shifting is with respect to a host lattice of Y2O3 and Er2Zr2O7. The (Y0.2Yb0.2Er0.2Ho0.2Nd0.2)2O3 maintained modal energies similar to that of Ho2O3 but maintained no characteristic modal energy of Y2O3 with little to no oscillatory broadening overlap. The red shifting of (Y0.33Yb0.33Er0.33)2O3 + 16 at.% La2O3, and (Y0.33Yb0.33Er0.33)2O3 + 16 at.% CeO2 was most apparent with no peak modal similarity of constituent sesquioxides and CeO2.

Regarding the zirconates, the TO spectral peaks of Er2Zr2O7 and Yb2Zr2O7 were 329 cm−1 (30.4 μm) and 319 cm−1 (31.3 μm) respectively whereas the spectral peak for (Yb0.2Er0.2Dy0.2Sm0.2Nd0.2)2Zr2O7 was 307 cm−1 (32.6 μm). One would expect in a solid solution, atoms vibrate at their innate frequencies and any overlapping modes would generate a convolved mode with a weighted average spectral peak35,36,37. While not all our constituent oxides were measured to obtain a spectrally averaged mode to compare to the multi-cation oxides, the oxides left unmeasured are all of lighter mass and would be expected to spectrally blueshift. On the contrary, modal red shifting is still observed. This suggests that large bonding distortion in compositionally complex materials affects the unique vibrations of their nearest neighboring atoms and changes the nature of the oscillatory frequency. Careful consideration of the chemistry in complex oxides would then allow for the tailoring of dielectric properties on the basis of local bonding distortion.

The scattering rates vary directly with thermal conductivity for the sesquioxides as shown in Fig. 2. We find the lowest thermal conductivity for (Y0.33Yb0.33Er0.33)2O3 + 16 at.% La2O3, and (Y0.33Yb0.33Er0.33)2O3 + 16 at.% CeO2. From DFT, this reduction in optical mode lifetimes is attributed to phonon softening where low-lying optical modes manifest as a result of greater mass and cation size discrepancies in rare earth cations (discussed later). While the change in scattering rate for the sesquioxides varies directly with the decrease in thermal conductivity, the scattering rates remain invariant for the zirconates, but a small reduction in thermal conductivity is observed for (Yb0.2Er0.2Dy0.2Sm0.2Nd0.2)2Zr2O7. Additionally, the peak mode frequency redshifts and the broadening terms differ for the 5-cation zirconate, which is indicative of a change in the phonon density of states that leads to the observed reduction in thermal conductivity. Cahill38 and Clarke39 both predicted the minimum limit to thermal conductivity relied on the smallest phonon mean free path, smaller modulus from weaker bonding, and a larger unit cell. At sufficiently high temperatures, a material’s heat capacity reaches the Dulong-Petit limit and the phonon mean free path approaches the interatomic spacing. The minimum thermal conductivity also makes assumptions regarding the vibrational states that won’t be realized until high temperature (i.e., the phonon spectrum can be described by a Debye spectrum where optical modes play a greater role in phonon propagation). The reduction in thermal conductivity we observe occurs due to additional scattering mechanisms from incorporated cations but does not approach the high temperature/scattering limit. Deciding what cations and how many are included provides a unique design knob controlling the phonon band structure, namely, by reducing the phonon energies via optical mode red shifting. This was observed for some of the multi-cation oxides with large differences in cation size and mass.

The experimental lifetimes found from IR-VASE were used in conjunction with literature heat capacities and average sound velocities to serve as a predictive model of thermal conductivity from Giesting and Hofmeister13. The calculated thermal conductivities were then compared to experimentally obtained thermal conductivities. For many of the sesquioxides, average velocities were calculated using the modulus of the material28,40,41,42,43,44,45,46,47. For the multi-cation oxides and zirconates, the Neumann-Kopp rule was utilized to quantify heat capacities and velocities. The subsequent results are plotted in Fig. 3. The calculated values only marginally underestimate values obtained experimentally, however, the general agreement of this model for all our samples is acceptable given the lack of fitting parameters. This slight underestimate is most likely due to uncertainty associated with sesquioxide sound velocity. The shear and bulk moduli used in calculations were often extrapolated to zero porosity using the Fryxell and Chandler48, Spriggs49, or Hasselman50 relation from experimental data or found through computational solutions51,52. Heat capacity values were consistent between experiment and calculated and the lifetimes displayed better correlation to experimental thermal conductivities. Thus, for all intents and purposes, using optical phonon lifetimes to calculate the thermal conductivity of these rare earth sesquioxides and zirconates provides an acceptable prediction.

Fig. 3: Experimental versus calculated thermal conductivity.
figure 3

Experimental thermal conductivity was evaluated with TDTR versus calculated thermal conductivity using literature heat capacities, group velocities, and experimental lifetimes evaluated with infrared spectroscopic ellipsometry.

Full size image

Compared to this thermal conductivity predictive model from Giesting and Hofmeister13, the alternative, more traditionally assumed approach is the VCA, which we also explored to assess its utility in predicting the thermal conductivity of multi-cation oxides7. This analytical expression is often used for alloying systems to predict thermal properties influenced by impurity disorder as well as strain and has served as an effective approximation for many alloys53,54,55. In this approach, the scattering cross section of acoustic phonons is calculated via8:

$${\varGamma }_{{{{\rm{md}}}}}={x}_{{{{\rm{i}}}}}\left[{\left(\frac{\Delta Mi}{M}\right)}^{2}+2{\left(\left(\frac{\Delta Gi}{G}\right)-2\gamma \left(\frac{\Delta \delta i}{\delta }\right)\right)}^{2}\right]$$
(6)

where xi is the fractional concentration of the ith constituent and M, G, γ, and δ are the atomic weight, elastic stiffness (modulus), anharmonicity constant, and ionic radius of the host lattice, respectively. \({\Delta M}_{i}\), \(\Delta {G}_{i}\), and \(\Delta {\delta }_{i}\) are the average differences between impurity atoms and host lattice. This term is used in the calculation of the mass disorder scattering rate8:

$$\frac{1}{\tau }=\frac{\varOmega }{4\varPi {\underline{c}}^{3}}{\varGamma }_{md}{\omega }^{4}$$
(7)

where Ω is the unit cell volume, \(\underline{c}\) is the average phonon velocity, and ⍵ is the modal frequency. Details and values used in VCA are provided in the Supplementary Materials (see SI, Section 5). As a prediction of the scattering rates, the model fails to accurately describe experimental trends. From the scattering cross section, the atomic weight difference is the most significant term and dominates the expression. In the case of multicomponent oxides, cations of similar mass understate the scattering cross section and diminish the VCA scattering rate. To compare VCA to experimental scattering rates, the difference between the solute cation and the Y2O3 (host lattice) was assessed to validate scattering caused by impurity disorder as shown in Fig. 4. The three-cation oxide (Y0.33Yb0.33Er0.33)2O3 fit the trend the best due to the larger variance in mass from alloying species unlike the other oxides with more lanthanides. Similar trends were observed in Braun et al.9 where VCA failed to predict thermal conductivity for five and six-cation oxides as well as a two-cation oxide with comparable atomic mass but succeeded for a two-cation oxide with differing atomic mass. The (Y0.33Yb0.33Er0.33)2O3 + 16 at.% CeO2 is expected to contain oxygen vacancies based on the previous literature56. These vacancies act as short wavelength phonon scattering sites that increase the rate of scattering. We quantified their contribution by calculating the point defect scattering cross section described by Qu et al.57 and found a marginal increase in VCA scattering rate and were still unable to capture the experimental results. Additionally, residual strain effects in the dual-phase compounds with cerium and lanthanum as well as the polycrystalline nature of these oxides may further increase the rate of scattering which is not captured in the VCA model. However, grain boundary scattering becomes a factor if the grains are on the length scale of the dominant scattering mechanism. This has been shown previously for some thermoelectric materials where nanocrystalline grains had a huge impact on VCA and experimental agreement58. Another work on polycrystalline yttria-stabilized zirconia indicated grain boundaries affected thermal conductivity below about 0.1 micron59. In our case, SEM revealed sample grains are 10 s of microns which are three orders of magnitude larger than the dominant scattering mechanism, i.e., the mass impurities. Rayleigh scattering from mass disorder dominates phonon transport on length scales much smaller than the grain boundaries in our materials rendering the contribution due to boundary scattering negligible. If grain boundaries were nanoscale and relevant, then a simple diffusive scattering expression to VCA could be applied. With this consideration, we expect negligible effects on thermal conductivity from boundary scattering.

Fig. 4: VCA versus impurity scattering rate.
figure 4

VCA scattering rate vs impurity scattering rate. The impurity scattering rate was taken as the difference between the multi-cation oxides (dopant) and Y2O3 (host lattice). VCA failed to predict impurity scattering rates for oxides with constituents of similar mass.

Full size image

To force the VCA to fit experimental data, we took a closer look at the parameters governing the lattice distortion imposed by mass impurity. Local lattice distortions described by interatomic force constants (IFCs) are encapsulated by \({\Gamma }_{{md}}\), and G, γ, and δ capture the IFCs in the model. Both G and δ can be readily acquired for the constituent oxides and taken as the average for multi-cation oxides, but γ is difficult to quantify for complex oxides. Previous work has assigned a value based on constituent oxides or fit for the term9. We calculated γ for the complex oxides, but the scattering rate data did not fit satisfactorily while remaining physical60,61,62. Discussion of γ calculations is expounded upon in the SI. This points to the importance of proper quantification of scattering rates when applying thermal conductivity models to multi-cation, compositionally complex materials, and the caution that one must be aware of when applying analytical forms of phonon-impurity scattering in VCA approaches when trying to predict the thermal conductivity of these materials, such as the multicomponent oxides.

To understand the factors influencing the increase in scattering rates for multicomponent oxides, DFT was employed to gain insight into local bonding order. The relaxed crystal structures of Y2O3, Yb2O3, and all four multicomponent compounds were calculated with DFT (see SI). From the crystal structure, each rare earth element is coordinated with six oxygen atoms. The bonding within each REO6 polyhedron can be analyzed to gain an understanding of how configurational entropy impacts the local bond distortions. The results of the REO6 polyhedron analysis are shown in Fig. 5.

Fig. 5: Polyhedral descriptors.
figure 5

Detailed analysis of the REO6 polyhedron in terms of six polyhedral descriptors from DFT calculations: Average RE–O bond length, average polyhedral volume, average distortion index, average quadratic elongation, average bond length variance, and average effective coordination number. Pure Y2O3 and Yb2O3 are included for comparison. The error bars in each are the standard deviation obtained from analyzing 32 independent REO6 polyhedra within each simulation cell.

Full size image

The two most discerning polyhedral descriptors that capture the impact of configurational entropy are the average distortion index and effective coordination number. The distortion index can be calculated as

$$D=\frac{1}{n}{\sum}_{i=1}^{n}\frac{|{l}_{i}-\underline{l}|}{\underline{l}}$$
(8)

where \(n\) is the number of bonds within a polyhedron, \({l}_{i}\) and \(\underline{l}\) are the distances from the central rare earth atom and the ith coordinating oxygen atom, and the average bond length in the REO6 polyhedron, respectively. We calculated the average distortion index for a unit cell with 32 rare earth atoms as \(\frac{1}{32}{\sum }_{j=1}^{32}{D}_{j}\) for all local REO6 polyhedra. A large average distortion index in (Y0.25Yb0.25Er0.25La0.25)2O3 and (Y0.25Yb0.25Er0.25Ce0.25)2O3 is indicative of the large RE–O bond length variation, which can serve as scattering centers for short wavelength phonons. In addition, the average effective coordination numbers of (Y0.25Yb0.25Er0.25La0.25)2O3 and (Y0.25Yb0.25Er0.25Ce0.25)2O3 are also relatively smaller when compared to that of (Y0.25Yb0.25Er0.25Nd0.25)2O3 and (Y0.25Yb0.25Er0.25Lu0.25)2O3. This is further evidence for relatively prominent local distortions in (Y0.25Yb0.25Er0.25La0.25)2O3 and (Y0.25Yb0.25Er0.25Ce0.25)2O3 when compared to (Y0.25Yb0.25Er0.25Nd0.25)2O3 and (Y0.25Yb0.255Er0.2Lu0.25)2O3 compounds. The local distortions are affirmation of the increased scattering rates of the multicomponent oxides resulting in a reduction in thermal conductivity. It is important to note that the DFT calculations do not capture the effect of inhomogeneities present through residual strains, short-range order, and vacancies that are likely present in the real material and may contribute further to the reduction in thermal conductivity. A future study with these in mind could fully elucidate the mechanisms behind the reduction.

The phonon dispersion curves of Yb2O3, (Y0.25Yb0.255Er0.2Lu0.25)2O3, and (Y0.25Yb0.25Er0.25La0.25)2O3 were calculated along high symmetry directions at 0 K using DFT. From Fig. 6., we observe a large optical phonon band gap around 217–267 cm−1 for Yb2O3. For (Y0.25Yb0.255Er0.2Lu0.25)2O3, the optical phonon band gap decreases and some low-lying optical modes around 80 cm−1 appear for certain symmetry directions. In (Y0.25Yb0.25Er0.25La0.25)2O3, the optical phonon band gap disappears, and more low-lying optical modes intersect with the acoustic modes in the 75–100 cm−1 frequency range.

Fig. 6: Phonon band structures.
figure 6

Phonon band structure results of Yb2O3, (Y0.25Yb0.255Er0.2Lu0.25)2O3, and (Y0.25Yb0.25Er0.25La0.25)2O3 at 0 K.

Full size image

Experimentally observed redshifts for modes around 280–360 cm−1 directly correspond to the increased bunching of optical modes around the optical mode band gap calculated from DFT. The DFT-calculated IR activity data for (Y0.25Yb0.255Er0.2La0.25)2O3, shown in Fig. 7, also captures the redshift and broadening of the optical modes around 200-400 cm−1, when compared to that of the (Y0.25Yb0.255Er0.2Lu0.25)2O3 compound. The phonon eigenvectors, along with their frequencies in cm−1, corresponding to the top three intense peaks for each compound are shown in Fig. 8. These eigenvectors represent distinct vibrational modes of oxygen atoms within the lattice structure. The point groups of all rare-earth atoms in both (Y0.25Yb0.255Er0.2Lu0.25)2O3 and (Y0.25Yb0.255Er0.2La0.25)2O3 compounds are \({C}_{1}\). The only irreducible representation in \({C}_{1}\) is \(A\), and all vibrational modes are IR active in \({C}_{1}\). The disparity caused by one cation significantly affects the phonon band structure, highlighting the importance of the local bonding environment on thermal conductivity. The vibrational frequencies generally inversely correspond to the atomic mass of the species present and directly correspond to the interatomic bond strength. This indicates that the lutetium-containing compound exhibits stronger bonding than the lanthanum-containing compound despite lutetium being heavier than lanthanum.

Fig. 7: Simulated IR spectra.
figure 7

DFT-calculated IR spectra for Yb2O3 (in blue), (Y0.25Yb0.255Er0.2Lu0.25)2O3 (in black), and (Y0.25Yb0.25Er0.25La0.25)2O3 (in red). The IR activity of (Y0.25Yb0.25Er0.25La0.25)2O3 shows a redshift and broadening compared to (Y0.25Yb0.255Er0.2Lu0.25)2O3.

Full size image
Fig. 8: Phonon eigenvectors of the Γ-point modes.
figure 8

Phonon eigenvectors of the Γ-point modes with frequencies in cm−1, which have the highest IR peak intensities in (a–c) (Y0.25Yb0.255Er0.2Lu0.25)2O3 compound and (d–f) (Y0.25Yb0.25Er0.25La0.25)2O3 compound. All phonon modes represent the vibrations of oxygen (O) atoms within the lattice, and the arrows indicate the directions of these vibrating atoms. Animations for each phonon mode (https://henriquemiranda.github.io/phononwebsite/index.html) can be found in the Supplementary Information.

Full size image

Additionally, the cut-off frequency (ωm) of acoustic modes is defined as the highest frequency along a high symmetry direction (e.g., Γ-H). Higher ωm indicates greater group velocity and stronger bonding63. In the three cases of Yb2O3, (Y0.25Yb0.255Er0.2Lu0.25)2O3, and (Y0.25Yb0.25Er0.25La0.25)2O3, ωm is about 83 cm−1, 70 cm−1, and 50 cm−1, respectively. This suggests the latter compound contains the lowest group velocity and weakest bonding of the three. This is also observed in the distortion index and effective coordination number where (Y0.25Yb0.25Er0.25La0.25)2O3 displayed a more distorted bonding environment because of softer local bonding. Moreover, the low-lying optical modes around 60 cm−1 in (Y0.25Yb0.25Er0.25La0.25)2O3 crossover with acoustic modes further from the Γ point. This crossing of acoustic and optical modes is significant because the shared interference yields strong phonon scattering. These low-lying optical phonons provide scattering channels for acoustic phonons emphasizing their contribution to thermal transport64. The primary difference between (Y0.25Yb0.255Er0.2Lu0.25)2O3 and (Y0.25Yb0.25Er0.25La0.25)2O3 is the atomic radii and mass of the fourth rare earth cation with lanthanum having a larger radius and lighter mass than lutetium. Despite its lighter mass, (Y0.25Yb0.25Er0.25La0.25)2O3 contains lower-frequency optical phonons and softer interatomic bonding. The reason is the greater deviation from average cation size and mass compared to (Y0.25Yb0.255Er0.2Lu0.25)2O3. The departure from similar bonding arrangements from similarities in constituent cations leads to softer bonding and increased mass scattering affecting both phonon scattering rates and thermal conductivities.

The dielectric tensor and the born effective charge tensor data for (Y0.25Yb0.255Er0.2Lu0.25)2O3 and (Y0.25Yb0.25Er0.25La0.25)2O3 were calculated using the density functional perturbation theory method65. The infrared (IR) activities were simulated using the method described by Skelton et al., with a linewidth of 16.5 cm−166. All phonon modes were visualized using a web app (https://henriquemiranda.github.io/phononwebsite/index.html).

All phonon modes represent the vibrations of oxygen atoms within the lattice and the arrows in Fig. 8. indicate the directions of these vibrating atoms. The point groups of all rare-earth atoms in both (Y0.25Yb0.255Er0.2Lu0.25)2O3 and (Y0.25Yb0.25Er0.25La0.25)2O3 compounds are C1. The only irreducible representation in C1 is A, and all vibrational modes are IR active in C1. The visualized phonon eigenvectors can be found in the Supplementary Information (see Supplementary data file, Phonon Eigenvectors).

To conclude, thermal conductivity measurements were conducted at room temperature using TDTR on various single and multi-cation rare earth sesquioxides and two-phase rare earth oxides as well as single and multi-cation rare earth zirconates. A reduction in thermal conductivity was observed from the single to multi-cation oxides. These measurements were corroborated with IR-VASE optical mode lifetimes. A clear trend is visible between thermal conductivity and lifetimes of the sesquioxides indicating scattering rate as the dominant factor leading to the decrease in thermal conductivity. However, the scattering rates and group velocities of the zirconates were invariant indicating that a change in the optical phonon energies led to the reduction in thermal conductivity, which we observe in our IR-VASE spectral via modal red shifting of the optical modes due to the local bonding distortion present. DFT was used to evaluate how local bonding distortions influence the phononic scattering rate observed through modal broadening and reduced thermal conductivity. Compared to single-cation oxides, the multi-cation oxides exhibited lower effective bonding coordination and greater bonding distortion. Additionally, larger differences in cation size and mass (e.g., the inclusion of La3+ and Ce4+) instigated greater phonon softening as seen from the multi-cation phonon dispersions. With this, we were able to tune the phonon band structure of multicomponent RE2O3 compounds so that it can mimic that of RE2Zr2O7, which are known for their low thermal conductivity. With control over which cations are incorporated into future HEOs and alloys, a unique opportunity to tune thermal transport is realized. The universality of this idea in complex oxides is still an open question, but our work lays a foundation for exploring an interesting design knob for thermal conductivity design that was previously not obvious to the community. The understanding of these underlying mechanisms impacting thermal transport is of key consideration for high-temperature applications of ceramics.

Methods

Fabrication

RE2O3 powders were calcined at 500 °C–600 °C in a box furnace (CM furnaces—Bloomfield, NJ) for 40 min. Individual RE oxide powders were measured out to equimolar quantities. The multicomponent compositions (Y0.33Yb0.33Er0.33)2O3 + 16 at.% La2O3 and (Y0.33Yb0.33Er0.33)2O3 + 16 at.% CeO2 were not measured to equimolar quantities because of the reduced solubility limit of La2O3 and CeO2 in Y2O367. Multi-cation oxide powder mixtures were ball-milled inside an HDPE bottle with six pieces of ZrO2 ball mill media for at least 12 h each.

Mixed rare earth powders were measured and poured into graphite foil-lined graphite dies (25.4 mm in diameter), then densified inside an SPS chamber (Thermal Technologies SPS Model 25-10—Santa Rosa, CA). Multiple programs were utilized for SPS synthesis, depending on the composition. SPS pucks, after processing, were heat treated in a box furnace at temperatures between 1200 °C and 1500 °C in air. Rare earth oxide mixtures were sintered at a relatively high temperature and extended dwell time to ensure the mixing of the powders into a homogenous mixture enabled by thermal diffusion68. After heat treatment, the samples were measured by the Archimedes method69 to determine their relative densities.

The RE zirconates were synthesized using a wet chemical method where metal nitrate salts were dissolved in deionized water and then mixed in the desired stoichiometric ratios. A chelating agent was added that polymerized to trap the homogeneously distributed cations. After the water is evaporated and the organic matter burned away, the metal oxide powder remains. The complete synthesis method can be found in ref. 70. After synthesis, the powders were pressed at 200 MPa and the green pellets were sintered at 1500 °C for 4 h in air.

Structural characterization

XRD analysis was conducted with an Empyrean Multipurpose X-ray Diffractometer (Malvern PANalytical, Westborough, MA) with a Cu-Kα (λ = 0.1541 nm) radiation source. Scans were taken from 10° to 80° 2θ with a step size of 0.014° 2θ and a collection time of 67.6 s step−1. A reflection-transmission (RT) spinner stage was used during XRD data collection, which rotated the samples at 15 rpm. HighScore Plus software71, equipped with the International Centre for Diffraction Data Powder diffraction files (PDF 4+)72, was used for phase identification of collected XRD spectra.

SEM (Quanta 650, FEI- Hillsboro, OR) and EDS (Oxford Instruments—AZtec software) analysis were utilized on rare earth oxide sintered compositions to analyze the homogeneity and phase distribution of samples after SPS synthesis and heat treatment.

Single-cation sesquioxides were characterized as being cubic phase. The (Y0.33Yb0.33Er0.33)2O3 and (Y0.2Yb0.2Er0.2Ho0.2Nd0.2)2O3 were characterized as cubic phase while the (Y0.33Yb0.33Er0.33)2O3 + 16 at.% CeO2 and (Y0.33Yb0.33Er0.33)2O3 + 16 at.% La2O3 were characterized to be cubic + fluorite and cubic + orthorhombic respectively. The phases of multi-cation oxides were assumed to be disordered cubic from XRD.

Thermal conductivity

TDTR was used to extract thermal conductivity values of oxide compositions. In this technique, the output of a pulsed, sub-picosecond Ti:Sapphire laser is split into two paths. The pump is used to heat the sample and induces a small temperature change in the material. The probe is delayed in time, relative to the pump, by a mechanical delay stage and monitors the change in reflectance due to the induced temperature change of the sample. By offsetting the probe in space, the thermal decay in the material can be directly monitored. Fitting this decay with the cylindrical heat equation yields thermal properties like thermal conductivity, heat capacity, and thermal boundary conductance. The thermal conductivities were corrected for porosity using the Maxwell relation: kdense = kmeasured [1/(1−1.5φ)] where φ is the volume fraction of pores using the theoretical density obtained from the XRD measurements. Higher-order corrections are possible but only have a limited impact on the computed conductivities.

The laser flash method73 was also used to measure the thermal diffusivity of the RE zirconates with a Netzsch LFA 457 MicroFlash instrument. The thermal diffusivity measurements were converted to thermal conductivity by the equation: k = αρcp where α is the thermal diffusivity, ρ is the measured density by the Archimedes method, and cp is the specific heat calculated by the Kopp–Neumann Law. These measurements were also porosity corrected. Rare earth zirconates were measured by Champagne et al.70.

Spectroscopic ellipsometry

Spectroscopic Ellipsometry using a JA Woollam IR-VASE Mk 2. was employed to analyze the dielectric function of rare earth oxides in the mid-infrared. The measurements were performed at multiple incident angles ranging between 60° and 75°, with a resolution of 8 cm−1 (~1 meV). Ellipsometric measurements are sensitive to surface roughness if the surface roughness is on the length scale of the incident probing light wavelength. Typically, this effect becomes significant at low wavelengths where collecting any spectrally-defined reflected light becomes challenging because of the length scale of surface features. Our samples were polished to ≤50 nm RMS roughness which is sufficient for probing long wavelengths that circumvent surface scattering. Models used Lorentzian oscillators for rare earth oxides and Gaussian oscillators for rare earth zirconates. Porosity can scatter the reflected light. For our ellipsometric models, we attempted to implement roughness layers and effective mean approximation void layers, but our model’s mean squared error decreased without the need for these layers. Included in the SI are the model fitting parameters with uncertainty which exonerates accurate fits. One issue that could affect measurement accuracy is if the backside of the sample is not sufficiently roughened. Backside reflections are incoherent with the desired reflections and lead to modeling inaccuracies such as incorrect material thickness, refractive index, and extinction coefficient. Our samples were opaque through their thickness so consideration of errant reflections was not necessitated.

DFT simulations

DFT is a quantum mechanical method that solves Schrödinger’s wave equation by formulating the quantum mechanical system as an energy-density-dependent problem. DFT calculations were performed using the open-source plane-wave pseudopotential code as implemented in the Quantum ESPRESSO package74,75. The conventional unit cell of cubic RE2O3 compounds consists of 80 atoms (32 rare earth and 48 oxygen). Four multicomponent compounds were selected: (Y0.25Yb0.25Er0.25La0.25)2O3, (Y0.25Yb0.25Er0.25Ce0.25)2O3, (Y0.25Yb0.25Er0.25Nd0.25)2O3, and (Y0.25Yb0.25Er0.25Lu0.25)2O3. We validated the reliability of the DFT calculations by first comparing the DFT-calculated lattice constants with that of the experimental data for Y2O3 and Yb2O3. The experimental lattice constants for Y2O3 and Yb2O3 are 10.604 Å and 10.43 Å, respectively. Our DFT-calculated lattice constants for Y2O3 and Yb2O3 are 10.5405 Å and 10.2094 Å, respectively. The trends agreed, which gave confidence in the calculated data. We could not perform a similar comparison for the multicomponent sesquioxide compounds because experimental lattice constant data do not exist for these compounds. We only model single-phase compounds and do not consider microstructure or size effects, e.g., two-phase mixtures, or grain boundaries. In the DFT calculations performed in this work, we did not include any finite temperature effects; therefore, these are 0 K calculations. The family of materials that we have explored in this work have melting temperatures (Tm) > 2000 K. The thermal conductivity measurements that we report correspond to data taken at T = 300 K. Since T/Tm is <0.15, we do not anticipate significant anharmonic effects to influence the DFT bond distortion data. Since the unit cell can accommodate 32 rare earth atoms, we divided the 32 atoms in equal proportions among the four rare earth elements. The well-known special quasi-random structures (SQS)76,77 method was used to mimic the high configurational entropy of the multicomponent compounds. Both the atom positions and unit cell dimensions of the SQS-generated structures were relaxed78. We used the Perdew–Burke–Ernzerhof optimized for solids generalized gradient approximation exchange-correlation functionals79 and ultrasoft pseudopotentials80. In our calculations, the 4f electrons of the rare earth elements are considered as core electrons to reduce the computational cost. Both the atom positions and cell parameters of the SQS-generated structures were relaxed until the total force and energy between the atoms was less than 10−4 Ry/Bohr and 7 × 10−10 Ry, respectively. At each stage of the relaxation, a self-consistent field calculation was performed with an energy cutoff of 7 × 10−8 Ry. We used a plane-wave kinetic energy cutoff of 60 Ry for the wavefunctions and 720 Ry for the charge density and potential as well as Γ-centered Monkhorst-Pack81 k-mesh of 2 × 2 × 2 geometry for the DFT calculation. Previously, Ping et al.82 used SQS and DFT to study the properties of five-component cubic bixbyite oxides (similar to our current work). The authors provide the crystal structure in the Supporting Information and the symmetry is broken (findsym)83 reports a space group of P1 for these structures. In another work, Meng et al.84 perform full relaxation of high-entropy rare-earth silicates. Therefore, our DFT relaxation strategy is not uncommon. To calculate the phonon dispersion curves, we performed frozen phonon calculations using the PHONOPY85,86 code, which uses the DFT forces from Quantum ESPRESSO as input for calculating the dynamical matrices and IFCs. We employed the relaxed crystal structures with 80 atoms for the frozen phonon calculations.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.