TRAPT: a multi-stage fused deep learning framework for predicting transcriptional regulators based on large-scale epigenomic data

Zhang, Guorui; Song, Chao; Yin, Mingxue; Liu, Liyuan; Zhang, Yuexin; Li, Ye; Zhang, Jianing; Guo, Maozu; Li, Chunquan

doi:10.1038/s41467-025-58921-0

Download PDF

Article
Open access
Published: 16 April 2025

TRAPT: a multi-stage fused deep learning framework for predicting transcriptional regulators based on large-scale epigenomic data

Guorui Zhang ORCID: orcid.org/0000-0002-7124-1309^1,2,3^na1,
Chao Song ORCID: orcid.org/0000-0001-5841-0334^1,2,4,5^na1,
Mingxue Yin^1,2,3^na1,
Liyuan Liu^1,2,3,
Yuexin Zhang^1,2,
Ye Li^1,2,3,
Jianing Zhang^1,2,
Maozu Guo ORCID: orcid.org/0000-0001-6228-6276⁶^na2 &
…
Chunquan Li^1,2,3,4,5^na2

Nature Communications volume 16, Article number: 3611 (2025) Cite this article

8727 Accesses
1 Citations
1 Altmetric
Metrics details

Subjects

Abstract

It is challenging to identify regulatory transcriptional regulators (TRs), which control gene expression via regulatory elements and epigenomic signals, in context-specific studies on the onset and progression of diseases. The use of large-scale multi-omics epigenomic data enables the representation of the complex epigenomic patterns of control of the regulatory elements and the regulators. Herein, we propose Transcription Regulator Activity Prediction Tool (TRAPT), a multi-modality deep learning framework, which infers regulator activity by learning and integrating the regulatory potentials of target gene cis-regulatory elements and genome-wide binding sites. The results of experiments on 570 TR-related datasets show that TRAPT outperformed state-of-the-art methods in predicting the TRs, especially in terms of forecasting transcription co-factors and chromatin regulators. Moreover, we successfully identify key TRs associated with diseases, genetic variations, cell-fate decisions, and tissues. Our method provides an innovative perspective on identifying TRs by using epigenomic data.

Programmable mRNA therapeutics for controlled epigenomic modulation of single and multiplexed gene expression in diverse diseases

Article Open access 13 March 2025

Integrative analysis of the 3D genome and epigenome in mouse embryonic tissues

Article Open access 16 December 2024

Characterizing cis-regulatory elements using single-cell epigenomics

Article 15 July 2022

Introduction

The intricate patterns of gene regulation are programmed by multiple upstream transcriptional regulators (TRs), such as transcription factors (TFs), transcription co-factors (TcoFs), and chromatin regulators (CRs), that can mediate the regulatory signals between promoters and distal enhancers¹. The onset of diseases is often associated with aberrant patterns of gene expression, underscoring the importance of identifying the TRs that control key programs of gene expression. Advancements in ChIP-seq and ATAC-seq techniques have enabled the clear illustration of cis- and trans-regulatory landscapes. The binding affinities of genomic TRs in conjunction with epigenetic information, such as histone modifications and chromatin openness, determine the cell-specific regulatory activities of TRs². Moreover, numerous studies have shown that TFs bind to specific cis-regulatory sequences within the genome, including enhancers and promoters, to modulate the expression of their target genes^3,4. Given the complexity of gene regulation, using a large amount of epigenomic data to identify the upstream synergistic regulatory features of genes is imperative for predicting TRs. A vast amount of epigenomic data, including ATAC-seq, DNase-seq, and ChIP-seq, have been accumulated due to rapid advances in high-throughput sequencing technologies. A major challenge in this context is to comprehensively collect and process these datasets from various sources. Furthermore, datasets from different origins encounter significant issues, including interference by noise, batch effects, and data redundancy. Consequently, it remains challenging to integrate these datasets, capture useful representations, and filter out noise.

A number of methods have been proposed to infer upstream TRs by using functional gene sets, including Enrichr⁵, TFEA.ChIP⁶, ChEA3⁷, MAGIC⁸, i-cisTarget⁹, BART¹⁰, and Lisa¹¹. Enrichr, TFEA.ChIP, ChEA3, and MAGIC use gene sets as inputs to predict TRs through enrichment analysis. These approaches involve statistical testing based on overlaps between the target genes of TRs and the input genes. Although they are capable of quick analyzes, they do not incorporate detailed information on cis-regulatory elements (CREs). As transcription factors function by binding to regulatory elements, information on the cis-regulatory profile is crucial for accurately inferring the regulators. i-cisTarget matches the CREs on the genome to predict TF activity through enrichment analysis. Unlike methods relying solely on gene sets, i-cisTarget uses CREs to more accurately simulate TF binding. However, this algorithm uses only CREs associated with the input gene set, which is inadequate for simulating the cis-regulatory profile of the entire genome. BART solves the problem of incomplete coverage of the cis-regulatory profile by inferring it from a large amount of H3K27ac ChIP-seq data through the regression-based MARGE¹² algorithm. Lisa, known as “MARGE second generation,” enhances prediction accuracy by incorporating DNase-seq data alongside H3K27ac ChIP-seq data to infer gene-related cis-regulatory profiles. Although BART and Lisa solve the problem of incomplete coverage of the cis-regulatory profile (ICCP), there is an inherent bias in TR binding that we refer to as transcriptional regulator binding preference (TRBP). Essentially, TRs are predisposed to associate with regions of active chromatin. More importantly, all currently available methods are limited to inferring upstream regulatory elements by using gene sets, but no technique is available for deducing the genome-wide binding sites of the TRs. There is an urgent need to develop approaches that consider the bidirectional regulatory relationships of cis-regulatory elements.

The use of epigenomic multi-omics data is fraught with complexity, including the presence of cross-model talk and noise. Prevalent algorithms use only traditional regression-based methods, such as Lisa, and ignore the effects of cross-model talk and noise when integrating multi-omics data. Moreover, the relationships between multi-omics data are not linear, but form a complex network. Deep learning algorithms have achieved considerable success in solving these specific biological problems^13,14. The initial step in applying data-driven deep learning approaches involves the extensive collection and processing of epigenetic data. In past work, we have developed several epigenetic regulatory databases, including TcoFBase¹⁵, CRdb¹⁶, TFTG¹⁷, SEdb¹⁸, and ATACdb¹⁹, that can extend the scope of epigenomic data. The transcription regulation databases TcoFBase, CRdb, and TFTG contain a large amount of data on transcription regulators, while SEdb and ATACdb, as epigenomic databases, contain the most comprehensive data on enhancers and chromatin accessibility. By integrating a large amount of epigenomic resources, we have constructed the most comprehensive epigenomic feature library available. Integrating such rich epigenomic data with cutting-edge deep learning techniques provided an unprecedented opportunity to unravel the complex landscapes of the epigenome.

In this study, we propose a data-inspired deep learning framework, called the TRAPT, that can leverage large-scale epigenomic datasets to assimilate advanced models of knowledge distillation and graph convolutional neural networks. We designed a multi-stage fusion-based deep learning approach to simultaneously integrate signals from the target gene cis-regulatory elements within the gene sets and the genome-wide binding sites of TRs, with the aim of obtaining the optimal representation of TR activity and predicting the key TRs for gene sets with context-specific regulation. To assess the effectiveness of our method, we predicted transcription factors, co-factors, and chromatin regulators on up to 570 TR knockdown/knockout datasets from the KnockTF²⁰ database. Benchmark tests were conducted against established tools, such as Lisa, BART, i-cisTarget, and ChEA3, and their results showed that TRAPT outperformed them in terms of predicting TR activity. We also leveraged TRAPT in a study on Alzheimer’s disease to successfully identify the key relevant TRs, such as REST. We ultimately applied TRAPT to datasets on human cell development and normal human tissues. It successfully predicted the critical regulatory factors controlling cell-fate decisions as well as tissue-specific regulators. It is easy to use, and can be accessed either through an online interface (https://bio.liclab.net/TRAPT) or via local installation (https://github.com/TOSTRING-Z/TRAPT).

Results

Overview of TRAPT

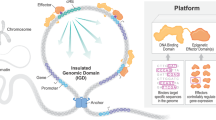
TRAPT is a multi-omics framework of integration that is designed for inferring TR activity from a set of queried genes. In simple terms, the model takes interest genes as input and outputs the activity score for each TR (Fig. 1a and Supplementary Fig. 1a). TRAPT applies a multi-stage fusion-based strategy to address the issues of TRBP and ICCP, which correspond to the prediction of downstream regulatory potential (D-RP) for transcription regulators (TRs) based on their genome-wide binding sites and upstream regulatory potential (U-RP) for target genes derived from their cis-regulatory elements (definitions of upstream and downstream are provided in Supplementary Note A.9). Therefore, we divide the model into the following key steps: (1) calculating the epigenomic regulatory potential (Epi-RP) and transcriptional regulator regulatory potential (TR-RP) (Figs. 1b), (2) predicting the D-RP of each TR with respect to the genes (Figs. 1c), (3) predicting the context-specific U-RP of the queried gene set (Figs. 1d), and (4) using the predicted regulatory potential from steps 2 and 3 to estimate the activity of TRs (Fig. 1e, f). To predicting the D-RP is a time-consuming task that does not involve calculations related to the user’s input gene set. Thus, with a modular approach, TRAPT does not repeat steps 1 and 2; instead, the pre-constructed Epi-RP, TR-RP, and D-RP serve as inputs for the subsequent modules (Supplementary Fig. 1a). We now elaborate on the details of each of the above steps.

In the first step, to calculate the regulatory potential of the epigenomes and TRs, we first collected over 20,000 datasets of epigenomic samples, including 1329 ATAC-seq, 1465 H3K27ac ChIP-seq, and 17,227 TR ChIP-seq datasets, and then subjected them to rigorous preprocessing. We then computed regulatory potential (RP) for each gene using large-scale epigenome data and a background knowledge library of TRs. A uniform weight decay strategy was applied to the epigenomic data, while a context-specific weight decay approach was implemented for individual TRs to capture their distinct regulatory patterns and scopes (see the Methods section) (Fig. 1a). We compared our findings with those of Chen et al., who classified TRs into long- and short-range categories (Supplementary Data 7), and found a significant overlap between the types of TRs identified in our analysis and those discovered by them²¹ (Supplementary Figs. 1f, g). All the RPs were integrated into two distinct components, Epi-RP and TR-RP, which served as the input in step 2.

The second step focuses on integrating Epi-RP and TR-RP to predict the TR-context-specific D-RP of each TR. The main challenge lies in integrating the differential omics predictions of TR with the relationships to epigenomic samples, as well as aggregating the regulatory potential signals corresponding to the epigenomic samples. Given the excellent performance of graph convolutional neural networks in network optimization and node information aggregation. Therefore, we reformulated the regulatory potential prediction problem into a network optimization task. With the input of the Epi-RP and TR-RP matrices generated in step 1, the k-nearest neighbors (kNN)²² algorithm was applied to construct a heterogeneous network between the TRs and epigenomic samples (e.g., CD4 + , CD8+ H3K27ac/ATAC-seq samples), which served as the initial epigenomic regulatory network (ERN). The edges in this network represented the potential tissue/cell type-specific associated regulation. This network is then optimized through a multi-modal knowledge distillation model, referred to as the D-RP model. Based on the network, we developed a multi-modal epigenome guided knowledge distillation model, named the D-RP model, to optimize the initial ERN and aggregate the epigenetic regulatory potential score. Specifically, the constructed regulatory potential matrix was input into the teacher model, a conditional variational autoencoder (CVAE), to learn distributionally smoothed joint embeddings of TR and epigenome samples by integrating multi-modal features. Concurrently, the constructed ERN was used as input for the student model. The model employed a variational graph autoencoder (VGAE) to learn low-noise, cross-modal, and distributionally unified representations. During training, the student model’s parameters were constrained by the teacher model’s omics discrimination knowledge, enabling the student model to further smooth its shallow embedding representations (Supplementary Fig. 3d). This constrained learning approach enhances the model’s robustness against overfitting and strengthens its generalization ability. The output of this step is the D-RP matrix, which represents the aggregated activity of regulatory elements near gene regions.

Inspired by an effective strategy that select important epigenomic samples from data containing noise and integrating them^11,12, in the third step, we developed the U-RP model, a knowledge distillation model constrained by low-dimensional epigenomic embeddings, to infer the regulatory potential of target gene cis-regulatory elements. The U-RP model takes the Epi-RP matrix and a queried gene set as inputs. The teacher model generates robust low-order representations of epigenomic data, while the student model learns these representations with constrained weights, enabling the selection of key epigenomic samples²³. During training, the teacher model extracts regulatory potential features associated with the queried genes, providing soft labels for the student model. Subsequently, the student model performs key epigenomic samples selection by learning these soft labels using a network architecture equipped with sparse group lasso (SGL)²⁴. By grouping the matrix of regulatory potentials based on the SGL according to its relevance to the queried genes, the student model imposed sparsity-related constraints both within and between groups. Samples within a group represented profiles of highly similar regulatory elements that may contain highly redundant samples. Unlike most linear methods of epigenomic sample selection, the U-RP model employed a nonlinear deep learning strategy, incorporating sample similarity constraints to reduce redundancy. This enabled precise selection of non-redundant, non-linearly combined epigenomic samples. The selected samples’ RP was used to construct a multi-layer neural network, with the fitted potential serving as the U-RP model’s output. The output of this step is the U-RP vector, which contains context-dependent information about chromatin accessibility (ATAC) and activity states (H3K27ac) associated with the queried genes.

The final step integrates the outputs of the D-RP and U-RP models to estimate TR activity. The input for this step includes the TR-RP matrix, D-RP matrix and U-RP vector. We then obtained the integrated regulatory potential (I-RP) of both modalities through the element-wise addition of the normalized TR-RP matrix to the D-RP matrix, followed by its element-wise multiplication with the U-RP vector. We subsequently quantified the association between each TR within both modalities and the set of queried genes by using the area under the ROC curve (AUC)¹⁰. Finally, The RP scores of the corresponding TRs from both modalities were merged to obtain the final, combined RP score. In summary, TRAPT integrated the regulatory potential of genome-wide binding sites of TRs and the regulatory potential of target gene cis-regulatory elements to infer the key TRs that regulate the queried gene set.

TRAPT demonstrates state-of-the-art performance on benchmark datasets

The performance of TRAPT was assessed using the “Target TR rank” metric, which evaluates the algorithm’s ability to predict the ranking of transcriptional regulators based on their regulated gene sets. For instance, when analyzing differentially expressed genes in a GATA6 knockout experiment, a higher ranking for GATA6 indicates better algorithm performance. To conduct a comprehensive evaluation, we integrated 570 TR knockdown/knockout datasets from the KnockTF database (Supplementary Note A.1 and Supplementary Data 5). After performing quality control, processing, and differential expression analysis, the top-ranking upregulated and downregulated genes were selected from each RNA-seq dataset as inputs to TRAPT. The performance was then evaluated by analyzing the ranking of the target transcriptional regulators.

We compared TRAPT with several methods that use gene sets as inputs, including Lisa, BART, and i-cisTarget, which uses TR-ChIP-seq data as the background. Moreover, we evaluated the conventional method of enrichment analysis, ChEA3, which primarily uses TR-related gene sets as its background (Supplementary Data 6). We comprehensively assessed the performance of the models by using various criteria, including the numbers of the top-10 and top-N TFs recovered, and their overall performance in terms of TF recovery. TRAPT delivered results that were 13% better than those of the second-best method (i.e., Lisa) in terms of the number of top-10 TFs recovered (Fig. 2a). Compared with the classic i-cisTarget method, its performance in predicting the top-10 TFs improved by over 200%. Moreover, TRAPT was significantly superior to conventional approaches to enrichment, such as ChEA3, which underscores the advantages of models predicated on the binding of transcription regulators. We subsequently calculated the number of correctly predicted TFs from cutoff ranks 1 to 10 at various thresholds, and assessed the performance of the models by using the AUC (Fig. 2a). TRAPT clearly delivered the best predictive performance (AUC, 0.643). Additionally, the mean reciprocal rank (MRR)²⁵ results (Fig. 2a) showed that the overall performance of TRAPT (MRR, 0.067) was superior to that of Lisa by 18% (MRR, 0.057), and to that of BART by 76% (MRR, 0.038). These results demonstrated TRAPT’s superior ability to predict TFs.

**Fig. 2: Evaluation of TRAPT and competing methods on TR knockdown/knockout and TF binding datasets.**

While previous methods have primarily focused on predicting the activity of TFs, the targeted collection of high-quality ChIP-seq data for transcription TcoFs and CRs in our approach (see the Methods section) enabled TRAPT to provide a more comprehensive prediction of various types of TRs. To conduct a deeper comparison, we evaluated the performance of the methods across TF, TcoF, and CR subsets. We found that TRAPT significantly outperformed currently available methods in predicting the TcoFs and CRs (Fig. 2b, c). We observed a significant decline in Lisa’s performance in predicting TcoFs compared with its performance in TF prediction (where it was second best; Figs. 2b and Supplementary Data 8). This occurred possibly because Lisa contains extensive data on TFs and CRs, but is lacking in TcoF data. Moreover, TRAPT’s performance in predicting chromatin regulators far surpassed that of Lisa (Fig. 2c). Its significant advantages in predicting TFs, CRs, and TcoFs was attributed to its use of a multi-stage strategy of fusion as well as its extensive library of TRs and epigenomic backgrounds.

TRAPT’s superior performance was not solely due to its use of additional background data on TRs. To illustrate this, we provided TRAPT as well as competing methods (Lisa and BART) with the same background data on TRs from the Cistrome database, and used KnockTF data as the benchmark. TRAPT outperformed Lisa by 30% and BART by 85.7% in terms of overall performance, even when using the same background data (Fig. 2e). Additional experimental analyzes were conducted on the TRAPT–Cistrome strategy to reinforce our conclusions. Specifically, we assessed the performance of TRAPT across three categories: TF, CR, and TcoF. TRAPT outperformed Lisa by 30.8% and BART by 115.7% in the top-10 ranking of TFs based on AUC scores (Supplementary Fig. 2b). We evaluated the overall performance of TRAPT for CR and TcoF, on which it surpassed Lisa by 198.4% and BART by 50.7%, respectively (Supplementary Fig. 2b). We also validated the methods using Lisa’s benchmark dataset and the same background data as the competing methods. The results also showed that TRAPT delivered the best performance (Fig. 2f).

We subsequently used target genes derived from differential expression and the binding of TFs, respectively, to explore the performance of different methods across various protein families. When using data on the target genes from TR knockout/knockdown and TR ChIP-seq, the results showed significant discrepancies for certain protein families (Fig. 2d and Supplementary Fig. 2a). For example, the performance on the TR knockdown/knockout datasets was notably superior for CP2- and RXR-like families compared with that on the datasets of TF binding, while the opposite outcomes were observed for families such as zf-C2H2, IRF, THR-like, and CSD. This difference was likely due to secondary transcriptional effects that occurred as a result of perturbations to the TRs, which were not directly linked to the original TFs²⁶. The results also indicated the potential for substantial impacts from secondary effects. Finally, a potential issue that may arise due to the vast amount of TR and epigenomic data was the slow speed of the algorithm. We benchmarked the runtimes of the TRAP, Lisa, and BART tools to account for this (Supplementary Fig. 1d). TRAPT surpassed the Lisa and BART algorithms in terms of speed, particularly in predicting the activity of individual TRs (Supplementary Fig. 1e).

Multi-stage fusion strategy boosts prediction of transcriptional regulators

We conducted extensive ablation tests to investigate the potential benefits of a multi-stage fusion-based strategy for predicting TRs. The U-RP model simulated the regulatory potential of target gene cis-regulatory elements to capture their context-specific epigenetic state. When the U-RP model was removed from our method, there was a significant decline in the overall performance of the method (Figs. 3a, b and Supplementary Fig. 3f). This showed that the U-RP model reasonably represented the epigenetic state of the set of input genes. The D-RP model predicted the epigenomic profile corresponding to the TR, and considers the TR’s preference for the genome under specific conditions. Our approach was unique in that it considered the activity of TR-related genome-wide binding sites. By combining the regulatory potential of TRs with that of the elements to which they bind, our method provided a comprehensive context-specific insight into TR function. To test its usefulness, we removed the D-RP model, and subsequently observed a significant decline in the overall performance of the method (Fig. 3a). This further demonstrated that accounting for the activity of regulatory elements in TR binding was highly effective in improving predictive performance. Furthermore, we were able to discern the regulatory preferences of each TR by calculating the ratio of its binding to distal enhancers. We thus developed specific regulatory potential models for each TR to describe their regulatory patterns (Supplementary Note A.6). Upon removing the TR-specific model of the regulatory potential, the overall performance of the basic model of regulatory potential declined in comparison with that of the specific model of regulatory potential (Figs. 3d and Supplementary Fig. 2d).

**Fig. 3: Evaluation of the performance of TRAPT in TR knockdown/knockout experiments on differential gene sets from the KnockTF database.**

TRAPT integrates multiple epigenomic features to predict the final TR activity. To gain a deeper understanding of the capabilities of each epigenomic module within TRAPT, we evaluated its predictive performance on target TRs. The results showed that the TRAPT-H3K27ac and TRAPT-ATAC epigenetic models exhibited superior predictive power for the upregulated and downregulated sets, respectively (Fig. 3g). Moreover, a significant drop in overall performance was observed when all epigenetic modules were removed, such that only the peak-in-promoter model remained (Fig. 3g, h). Moreover, the overall performance of the model declined as each epigenetic module was gradually removed (Fig. 3h). These findings suggested that TRAPT effectively integrated features from different epigenomic modules to deliver unbiased predictive performance. In further ablation experiments, we found that compared to the results obtained without knowledge distillation (NKD), the model using knowledge distillation (KD) demonstrated an improvement of 5.4% on the KnockTF benchmark dataset (Fig. 3c) and an improvement of 7.9% on the Lisa benchmark dataset (Fig. 3e). For the local performance metrics in predicting the top ten TRs, the KD group significantly outperformed the NKD group, with an AUC score exceeding that of the NKD group by 8 percentage points (Fig. 3e). By dividing the data into training and validation sets for the D-RP and U-RP models, a rapid decrease in the losses on both sets was observed (Supplementary Fig. 2c and Supplementary Fig. 3a), with and without knowledge distillation. Meanwhile, the D-RP student model converged more quickly with knowledge distillation and achieved higher final accuracy (Supplementary Fig. 3b). These results demonstrated that the use of knowledge distillation did not lead to model overfitting.

We inputted the TR-RP and Epi-RP matrices to generate a ground network of TRs and epigenomes by using the kNN algorithm. The D-RP model was designed to optimize the links between the TRs and epigenomes based on the observed links, while also restoring missing links. We thus evaluated the D-RP model based on its capacity for link prediction. The observed links were divided into training, validation, and test sets to simulate the missing links. By training the model on the training set and then checking the recovery of missing links on the test set, the ability of the D-RP model to infer the relationship between the TRs and epigenomes were evaluated. We observed that the losses incurred by both the teacher and student networks on the validation set decreased rapidly during training (Supplementary Fig. 3a), and their values of the area under the receiver operating characteristic (auROC) curve and the area under the precision-recall curve (auPRC) finally reached 0.81 and 0.84 on the test set, respectively (Supplementary Fig. 3c). Given the potential for a significant number of false-negative connections in empirical scenarios, we masked varying proportions of links to evaluate the stability of the model under different conditions of missing data. The results demonstrated that as the number of masked edges increased (up to a maximum of 15%), the recovery-related performance of the model remained robust, with the auPRC exceeding 0.82 and the average precision (AP) exceeding 0.8 (Supplementary Fig. 3e). The recovery-related effect of the model was thus satisfactory, and reflected the stability of the D-RP model in case of missing disturbances. We subsequently tested the performance of the U-RP model. It is designed to predict cis-regulatory profiles based on the queried gene sets and the Epi-RP matrix. We observed a rapid decline in the loss of the U-RP model on both the training and validation sets, regardless of whether knowledge distillation was used (Supplementary Fig. 2c and Supplementary Fig. 3a). A key challenge for the U-RP model is to select important epigenomic samples from redundant data, as they are expected to best represent the epigenetic state of the current context-dependent gene set. To address this challenge, we computed the performance of the model under different scenarios of sample selection. We observed that the rate of improvement in its performance significantly decreased when 10 features were chosen. This finding aligns with the conclusions of past research¹² (Supplementary Fig. 3g).

Finally, we compared the performance of TRAPT on upregulated and downregulated gene sets, and found that its predictions were better for downregulated than upregulated sets (Fig. 3f). This result indirectly proved that transcriptional activators were more common than transcriptional repressors⁷ (Supplementary Fig. 3g). We also found that most TRs either acted as either transcriptional activators or repressors, with a few, such as CTCF, NANOG, FOXA1, and ESR1, having dual functions (Fig. 3i). In conclusion, TRAPT accurately predicted transcriptional activators, repressors, and dual functions.

TRAPT predicts key transcriptional regulators in the ESR1 knockdown study

ESR1 is a key transcriptional factor associated with the ER-positive subtype of breast cancer, and significantly influences its development and progression by mediating the aberrant expression of numerous downstream risk-related genes. To validate TRAPT’s ability to identify key TRs in disease, we applied it to a gene set derived from human MCF7 ER+ breast cancer cells subjected to siRNA-mediated ESR1 knockdown. When given the differential gene set before and after ESR1 knockdown (Supplementary Fig. 4a, Supplementary Note A.2 and Supplementary Data 9), TRAPT accurately predicted the transcription factor ESR1 as occupying rank 1 in the downregulated gene set and rank 17 in the upregulated gene set (Fig. 4a). This result highlights ESR1’s dual role in both activating and repressing genes in breast cancer²⁷. Moreover, TRAPT identified the other top-ranking ESR1 associated with cancer-related transcription factors, transcription co-factors, and chromatin regulators such as FOXA1, EP300, and MED1 (Figs. 4d and Supplementary Fig. 4b). For example, GATA3 is a determinant transcription factor in mammary luminal cell fate²⁸. The pioneer factor FOXA1 influences the onset and progression of breast cancer by modulating genomic accessibility²⁹. The histone acetyltransferase EP300 acetylates ESR1, enhancing the expression of ESR1 target genes in breast cancer cells³⁰. Furthermore, the top-ranking TRs from the STRING³¹ database were involved in high-frequency interactions with one another (Fig. 4b). The co-expression analysis of the TCGA³² breast cancer dataset also revealed a strong relationship among the TRs (Figs. 4c, Supplementary Note A.3 and Supplementary Data 10), particularly GATA3, FOXA1, and ESR1. We also detected the same phenomenon in an analysis of GTEx breast tissue samples (Supplementary Fig. 4c and Supplementary Note A.3). Overall, TRAPT successfully identified ESR1 and associated transcription cofactors and chromatin regulators, as well as the potential interactions between these proteins and their genomic binding patterns, to validate the efficacy of TRAPT.

**Fig. 4: Illustration of the TRAPT framework by using downregulated genes from ESR1 knockout experiments in cases of gastric cancer and MCF7 breast cancer.**

The D-RP score reflects the epigenetic status of the TR. We combined it with the regulatory potential of the TR to better represent its activity. In theory, representations of TRs that incorporate epigenetic information should be able to clearly distinguish between the genes that they regulate. To validate this, we categorized the D-RP scores of the identified TRs into the queried genes and a background gene set. The top-ranking TRs, including the transcription factor ESR1 as well as its associated co-factors and chromatin regulators, scored significantly higher on the queried gene set than on the background gene set. ESR1 was the most significant among the TRs in both the ATAC and H3K27ac contexts (ATAC: p = 3.3e^-38, H3K27ac: p = 8.6e^-34), indicating that TRAPT effectively captured the epigenetic information of ESR1 in cancer. Moreover, the importance of other top-ranking TRs decreased with descending rank, including for NCOA3, NIPBL, and FOXA1 (Figs. 4e and Supplementary Fig. 4d). Notably, HDGF was at the bottom of the predictive rankings, with significantly lower importance compared to other TRs (ATAC: p-value = 0.449, H3K27ac: p-value = 0.046). These findings showed that the D-RP scores of TRs could be used to accurately discriminate between the genes that they regulate. To further validate the predictive capability of the interpolated I-RP scores, we constructed activity profiles of both interpolated and non-interpolated TRs. We observed that the top-ranking TRs with high I-RP scores yielded stronger signals for the corresponding queried gene sets (Fig. 4g).

ESR1 is capable of binding to enhancer elements that regulate distal target genes, such as ERα-occupied super-enhancers (ERSEs)³³, and TRAPT leverages distal information through specialized models of regulatory potential. To further investigate and predict the characteristics of genomic binding of the TRs, we categorized the enhancers near the queried genes into distal and proximal enhancers, and plotted the profile of the enhancer of each predicted TR. The predicted TRs upstream bound significantly more often in enhancer regions near the queried genes than in the background enhancer regions (Fig. 4f). Conversely, the predicted downstream HDGF bound less often in enhancer regions near the queried genes than in the background enhancer regions. Our analysis demonstrated a strong preference for GATA3 (proximal p-value = 9.7e^-120 <distal p-value = 1.4e^-62) and FOXA1 (proximal p-value = 2.0e^-51 <distal p-value = 5.4e^-22) to bind proximally to the genes, while ESR1 and EP300 did not exhibit a comparable preference. Finally, we visualized the tracks near several significantly downregulated, differentially expressed genes for ESR1, GATA3, FOXA1, EP300, and HDGF (Fig. 4h). All the predicted upstream TRs exhibited conspicuous patterns of binding near the genes, and tracks of the top 10 predicted epigenomic samples highlighted a significant enrichment in regulatory elements near the ESR1 binding sites. Moreover, similar patterns of genomic binding in the top predicted TRs, while no such pattern was evident in HDGF, which was predicted to be at the bottom (Fig. 4f). These findings further substantiated the reliability of TRAPT in predicting TFs as well as the associated transcriptional co-factors and chromatin regulators.

TRAPT predicts functional transcriptional regulators in post-GWAS analysis of Alzheimer’s disease

Genetic variations at specific DNA positions within the binding sites of TFs can alter their binding affinity, influencing gene expression and cellular processes. In light of this, we applied TRAPT to cases of Alzheimer’s disease (AD) with the aim of identifying the key TRs impacted by the causal variants. To this end, we used gene sets associated with AD as predicted by MAGMA³⁴, a tool designed to infer disease gene sets from GWAS-based summary statistics as inputs to our algorithm (Supplementary Data 11). We then conducted a binding analysis of the disease-associated TRs predicted by TRAPT, with the significant causal variants detected through fine mapping based on the GWAS (Fig. 5a). Integrating GWAS data with TRAPT’s predictions enabled us to demonstrate its ability to identify key TRs impacted by causal variants.

**Fig. 5: Prediction of functional transcriptional regulators for Alzheimer’s disease by using post-GWAS analysis.**

Specifically, we retrieved a GWAS dataset from causaldb³⁵, consisting of a sample of a European population (n = 408,942)³⁶, as the input for the fine mapping. We subsequently performed co-localization analysis on the disease-associated TRs and the predicted causal variants (Figs. 5a, Supplementary Note A.4 and Supplementary Data 3). Of the 305 SNPs bound by the top 25 predicted TRs of TRAPT, 68.2% belonged to AD-related causal variants (hypergeometric test p-value = 2.5e^-12). Conversely, of the 106 SNPs bound by the bottom 25 TRs, fewer than half were causal variants (hypergeometric test p-value = 0.971) (Fig. 5b). This indicated that TRAPT’s higher-ranked TRs were more closely associated with AD. To further investigate the relationship between individual TRs and AD, we conducted a more detailed co-localization analysis of the binding of each AD-related TR to the causal variants (Fig. 5c). The results revealed that the top-ranking TRs, such as SPI1, RELA, and REST, generally had a higher binding affinity for causal variants than for background variants. For example, SPI1, ranked first according to the predictions made by TRAPT, intersected with 71 causal variants and only 24 background variants (hypergeometric test p-value = 3.6e^-4). RELA, ranked second by TRAPT, intersected with 75 causal variants and only 33 background variants (hypergeometric test p-value = 2.7e^-3; Supplementary Data 2). We observed that the top-ranking TRs generally exhibited stronger associations with AD-related causal variants. To assess this observation, we developed a statistical test based on the GSEA³⁷ algorithm to verify the reliability of the predicted top-ranking TRs from a statistical perspective (see the Methods section). We found that the top-ranking TRs were significantly enriched (Fig. 5d; p-value = 2e-3), demonstrating that TRs that were ranked higher were more likely to bind to causal variants than those that were ranked lower.

To identify the disease-associated causal variants bound by TRs predicted by TRAPT and explore their potential associations, we then analyzed the co-localization between the causal variants and the predicted binding sites of the TRs. We retained the overlapping causal variants and ranked them based on FINEMAP³⁸ scores. Of the 1,000 causal variants selected, 208 were associated with TR binding, with rs10119 ranking as the top variant (Fig. 5c). Functional annotation analysis using VARAdb³⁹ revealed that rs10119 was regulated by multiple super-enhancers covering several important genes nearby, including APOE, TOMM40, and APOC1, and was a risk-related SNP for AD. We subsequently analyzed the co-localization between rs10119 and the predicted TRs. Notably, we observed binding in nine of the top-ranking 25 TRs in the 1 kB region upstream and downstream of rs10119, whereas the lower-ranked TRs did not exhibit any binding in these regions (Fig. 5e). A previous study has thoroughly validated the effect of REST, a transcription factor, as a universal feature of normal aging in human cortical and hippocampal neurons. It can also protect neurons from oxidative stress and amyloid β-protein toxicity. We observed that REST ranked high in TRAPT’s predictions, and previous studies have demonstrated its crucial role in AD development. It inhibits genes that promote cell death and AD pathology, while inducing the expression of genes associated with stress response⁴⁰. TRAPT identified top-ranking TRs like SPI1, STAT1, RELA, HDAC2, JUND, and HNF4A, which are causally associated with AD^41,42,43,44. We found that rs10119 was located exactly at a critical position in the chromatin loop structure, with many important TRs predicted by TRAPT binding in the upstream and downstream. Notably, we observed a substantial number of binding sites of our predicted TRs at TOMM40, APOC1, APOE, and CEACAM16 (Fig. 5fand Supplementary Fig. 5b). These genes are known to significantly influence the onset of AD^45,46,47,48. Meanwhile, we analyzed AD-related H3K27ac ChIP-seq datasets⁴⁹ to show that the binding peaks of the TRs near the rs10119 locus significantly overlapped with the H3K27ac profiles selected by the model, and notably overlapped with the H3K27ac profiles associated with AD. The model-selected samples were not from AD, indicating that in the absence of epigenomic data from the same disease context, it chooses samples with similar epigenetic signals as substitutes. This demonstrated the potential of TRAPT for application to diseases that it has not previously encountered. Moreover, several predicted TRs were closely associated with epigenetics, including HDAC2 and ZBTB33 (also known as Kaiso). Finally, we additionally analyzed another high-scoring causal variant, rs75627662, and observed extensive binding of top-ranked predicted TRs (Supplementary Fig. 5a).

TRAPT identifies transcriptional regulators associated with cell fate and tissue identity

TRs are crucial for coordinating gene expression programs, driving cell-fate decisions, and orchestrating intricate biological processes during cell differentiation and development. The binding affinity of TRs to proximal or distal cis-regulatory elements of downstream marker genes plays a crucial role in maintaining cell identity. To highlight TRAPT’s applicability to cell development, we determined its ability to capture key regulators for marker gene sets of a single cell dataset. Briefly, we reprocessed scRNA-seq data on human hematopoietic stem cells⁵⁰ (Supplementary Note A.5), visualized the first two principal components (Fig. 6a), and identified marker TRs between lineages of differentiation by using the classic model of landscapes of hematopoietic differentiation (Figs. 6b and Supplementary Fig. 6a). We then used TRAPT to identify the top five driving regulatory factors for different cell-fate directions of commitment (Fig. 6c). A total of 42 TRs were identified as potential key regulators of blood cell differentiation. To validate the advanced predictive ability of our tools, a systematic analysis of these 42 TRs was conducted. Notably, 29 are known to play regulatory roles in hematopoietic lineage development (Supplementary Table 1), with 10 TRs (log2FC > 0.5 and FDR < 0.05) exhibiting patterns of differential expression across differentiated lineages in the scRNA-seq dataset (Fig. 6c). The remaining significant portion of the TRs, while not classified as differentially expressed TRs, still played a critical role in the process of differentiation. Furthermore, we observed multiple TRs appearing across various lineages of differentiation, including EP300, SMAD1, LYL1, SPI1, LMO2, and TAL1 (Supplementary Fig. 6b). In addition, some TRs were found exclusively in single lineage branches. For example, STAT4 was identified in the LMPs−NK cell lineage branch as a known gene-regulating intracellular signal. Deleting STAT4 in NCR1-expressing cells results in impaired terminal differentiation of NK cells⁵¹. TCF4 is a key transcription factor in the LMPs-pDC lineage branch, crucial for pDC development⁵². We also applied TRAPT to human embryonic stem cells⁵³. Following dimension reduction and clustering, the cells were categorized into six main subgroups (Supplementary Fig. 6c). We identified marker genes for each differentiated cluster and the undifferentiated H1 and H9 clusters. Using TRAPT, we analyzed these genes and identified the key TRs for cell-fate decisions in each differentiated cluster. (Supplementary Fig. 6d). In the differentiation of H1 into trophoblast-like cells (TB cells), such TRs as GATA3, TFAP2A, and GATA2 exhibited higher activity. Notably, GATA2 and GATA3 have been shown to be selectively expressed in trophoblast progenitor cells during early mouse development, and directly regulate key genes⁵⁴. TRs like GATA6, SMAD2, and EOMES showed elevated activity in the differentiation of H1 into definitive endoderm cells (DE cells). Previous studies have revealed that GATA6 works with EOMES and SMAD2 to regulate the gene regulatory network associated with human definitive endoderm⁵⁵. TRAPT accurately identified driver regulators of cell-fate decisions, with a majority of these being cell-lineage-specific TRs that have been validated in the literature.

**Fig. 6: Identification by TRAPT of transcriptional regulators associated with cell fate and tissue identity.**

Subsequently, we analyzed RNA-seq data from 30 distinct normal human tissues retrieved from GTEx⁵⁶, and used limma⁵⁷ to identify the top 500 differentially expressed genes for each tissue (Supplementary Note A.5), and used them to predict the key TRs. Most regulators of tissue-specific markers were predicted as expected. For instance, MED1, TBX5, and GATA4 were enriched in the heart tissue. MED1 plays an important role in super-enhancer formation and maintenance, while GATA4 broadly occupies cardiac super-enhancers along with TBX5 to determine cardiomyocyte contractility, calcium handling, and metabolic activity⁵⁸. AR, FOXA1, and HOXB13 were identified as the top three TRs in the prostate, which is consistent with the role of FOXA1 and HOXB13 in regulating normal AR transcription during prostate epithelial development, as well as their involvement in oncogenic AR transcription during prostate carcinogenesis⁵⁹. Furthermore, certain tissues shared TRs, such as PPARG and CEBPA in the breast and adipose tissues^60,61, and TP63 and GRHL2 in the skin, esophagus, and vagina tissues^62,63,64, suggesting similarities in predominant cell types across these tissues. We then integrated the predicted scores of the top 10 TRs from each tissue for hierarchical clustering. Intriguingly, TRAPT identified similarities between tissues (Fig. 6c). For instance, the breast and adipose tissues formed a cluster owing to their predominant composition of adipocytes. The tissues from the uterus, ovary, and cervix formed a cluster because their surface and interior were covered by epithelial cells. We also generated a list of the 10 most important predicted TRs for each tissue type (Supplementary Data 4).

In conclusion, TRAPT efficiently predicted key TRs in the context of cell fate and across 30 human normal tissues, verifying its ability to process gene sets obtained from multiple phenotypes or conditional data, such as cohort-related data. A substantial number of these predicted TRs have been experimentally shown to have specific roles in these tissues, further verifying TRAPT’s reliability. TRAPT was a useful instrument for exploring and understanding the functions of key TRs in human physiological processes.

Discussion

Transcriptional regulators are essential for modulating gene expression patterns, coordinating the activation and repression of genes to maintain cellular homeostasis and guide developmental processes. Importantly, TR-mediated gene programs have a distinct epigenetic landscape and act as switches in changes of cell states and disease phenotypes^1,65. However, accurately predicting upstream TRs for any given gene set with biological meaning (i.e., differentially expressed genes or marker genes in single cell studies) remains challenging due to a lack of epigenomic data on TRs in many cell types. To address this issue, we proposed a deep learning framework, called TRAPT, that leverages two-stage knowledge distillation to extract the activity embedding of regulatory elements. TRAPT can predict the key TRs for context-dependent gene sets by integrating data from over 20,000 large-scale epigenomes and a comprehensive background knowledge library of TRs. TRAPT significantly improves the accuracy of TR predictions on large-scale benchmark datasets and outperforms prevalent methods such as Lisa, BART, i-cisTarget, and ChEA3 in predicting the overall ranking of TRs. We also used it to successfully identify key TRs associated with diseases, genetic variations, cell-fate decisions, and different types of tissues.

Current methods of TR prediction can be classified into two main categories. The first category consists of gene set-based methods, such as Enrichr, TFEA.ChIP, ChEA3, and MAGIC, which use TR-related gene sets as background data and apply statistical tests like the hypergeometric distribution to calculate TR importance. However, these methods cannot accurately simulate the binding of TRs and CREs. The second category, including i-cisTarget, BART, and Lisa, addresses this issue by simulating TR binding with CREs near genes to predict their activity. Nonetheless, these methods still have limitations, primarily their neglect of the binding preferences of TRs. TRAPT represents a third category of techniques that integrate the cis-regulatory elements of gene set with the genome-wide binding sites of TRs. Based on 570 TR-related datasets from knockout/silencing experiments and multiple criteria of evaluation, we found that TRAPT, as a method in the third category, significantly outperformed all other methods in predicting the overall ranking of the TRs. TRAPT’s significant advantage in predicting transcription factors, chromatin regulators, and transcription co-factors is attributed to its multi-stage fusion strategy and a comprehensive background library of TRs. Our method had the following advantages: (1) TRAPT used multi-stage fusion to simultaneously address the issue of incomplete coverage of the cis-regulatory profile and TRBP-related problems. (2) To mitigate the effects of noisy data, TRAPT applied a feature-based offline framework of knowledge distillation⁶⁶ in two stages. During the prediction of D-RP, we introduced VGAE, employing a reparameterization trick to project node representations into a uniform latent distribution form. By further incorporating CVAE as a teacher network, we leveraged its advantage in smoothing the latent space distribution to constrain the initial embeddings of VGAE, effectively reducing the disparities in the distribution of aggregated node features. In the prediction step of the U-RP, the teacher network extracted low-dimensional embedded representations of complex epigenomic information related to the queried gene set and guided the student network in selecting the optimal epigenetic sample set. The KD model was robust to noisy data, and significantly enhanced the capability to predict TR activity. It simultaneously maintained the speed of the algorithm even when the amount of TR data was more than twice that covered by the state-of-the-art algorithm with the highest coverage (Supplementary Figs. 1b, c). (3) We proposed leveraging graph theory to address the challenge of predicting the regulatory potential of the TRs at their genome-wide binding sites, which was particularly well suited for small epigenomic datasets. To explore the potential advantages of a multi-stage fusion strategy and knowledge distillation for the prediction of TRs, we conducted extensive ablation tests. We observed a significant decline in overall model performance when the U-RP and D-RP models were removed. Similarly, the overall performance of the model notably declined when knowledge distillation was eliminated. We evaluated the D-RP model from the perspective of link prediction. It demonstrated its capability to reconstruct previously unseen links on the test datasets. Moreover, the D-RP model maintained stable performance even when various proportions of links were masked. These results indicated that it optimized the epigenetic regulatory network.

Using 570 TR-related datasets, TRAPT outperformed state-of-the-art methods in inferring transcription regulators, especially in predicting transcription co-factors and chromatin regulators. We also verified that TRAPT maintained its superior performance even when ignoring the influence of background data. Our results revealed that the chromatin regulators, transcription co-factors, and transcription factors exhibited significant differences in genomic binding preferences (Supplementary Fig. 7d), highlighting the need to consider different types of TRs in research. TRAPT successfully identified ESR1 as top-ranking, along with associated transcription co-factors and chromatin regulators like EP300, in the ESR1 knockout experiment. We found that the top-ranking TRs exhibited significantly higher scores on the queried gene set. Notably, ESR1, through its binding to both distal and proximal enhancers, emerged as the most prominent TR in both the ATAC and H3K27ac contexts. This finding highlights the D-RP model’s representation module in TRAPT effectively captured the epigenetic information related to ESR1 in the context of cancer. TRAPT also identified TRs causally related to AD near rs10119, with higher-ranked TRs more likely located near causal SNPs. We ultimately applied TRAPT to datasets of human hematopoietic stem cells, human embryonic stem cells, and normal human tissues. It was able to successfully predict the critical regulatory factors controlling cell fate, including STAT4, TCF4, and GATA, as well as tissue-specific regulators such as MED1, TBX5, and GATA4.

TRAPT provided an informative perspective on integrating the epigenetic landscape of TRs. However, its performance was still constrained by the number of epigenomic samples. To date, TRAPT encompasses 17,227 TRs (Supplementary Data 1), 1,329 ATAC-seq samples, and 1,465 H3K27ac samples. Although it uses a comprehensive epigenomic dataset as the background, this does not ensure each TR can be paired with corresponding epigenomic samples. Transcription factors recruit co-factors to perform their functions, where the affinity of the co-factors can either enhance or reduce that of the transcription factors, depending on whether the former is acting as an activator or an inhibitor. Chromatin regulators also influence transcription factor activity by modifying chromatin structure. Despite extensive data on co-factors and chromatin regulators, the complex effects of interactions between TRs are not fully understood. In future work, we may consider incorporating gene regulatory networks to simulate the complex interactions within these organisms. We believe this will further extend the applicability of our model.

In conclusion, TRAPT applied a bidirectional strategy to integrate the epigenetic landscape to predict key TRs, and is expected to provide instrumental guidance for future research on and related computational analysis of transcriptional regulation.

Methods

Preprocessing of datasets of epigenomes and transcriptional regulators

Gene transcription programs are primarily regulated by the biological activities of transcription regulators, coordinated upstream epigenetic marks, such as histone modifications, and open chromatin states, which can establish and maintain the transcriptional landscape of a cell in response to various internal and external signals. Moreover, studies have demonstrated that epigenetic marks can partially simulate the regulatory shapes of the transcription regulators to fulfill the gaps in their coverage. Hence, integrating large-scale epigenomic data helps understand the cell-specific transcription mechanism of genes. In this study, we manually curated and processed ~20,000 raw epigenomic data sets from multiple sources, covering over 1000 tissue and cell types. All these datasets of epigenomes and transcriptional regulators provided comprehensive regulatory cues to infer the patterns of gene expression. We now detail the various methods used to process the data.

H3K27ac ChIP-seq data

The H3K27ac ChIP-seq datasets were obtained from SEdb2.0 in previous work by our research group. Briefly, we manually collected 1,739 samples, including experimental and control groups, from NCBI GEO/SRA^67,68, ENCODE⁶⁹, Roadmap⁷⁰, Genomics of Gene Regulation Project (GGR)⁶⁹, and National Genomics Data Center Genome Sequence Archive (NGDC GSA)^68,69. We obtained data on the peak signals of H3K27ac by using the Bowtie⁷¹ and BEDTools⁷² multicov tools to process the raw data.

Data on chromatin accessibility

The datasets of chromatin accessibility were obtained from ATACdb in previous work by our research group. Briefly, we manually collected 2,723 samples to cover several types of tissues or cells from NCBI GEO/SRA, and used the Bowtie and BEDTools multicov tools to identify signals representing the peaks of chromatin accessibility.

Data on transcription factors

The ChIP-seq datasets of the transcription factors were obtained from TFTG in previous work by our research group. Briefly, we manually collected 11,056 samples, cataloging a total of 1,218 human TFs. To provide more quality control information regarding ChIP-seq, such as the distribution of promoters, exons, and the proportion of UDHS, we then used the ChIPseeker⁷³ R package and BEDTools to compute the distributions of various genomic compositions and the UDHS coverage of each TF.

Data on transcription co-factors

The ChIP-seq datasets of the transcription co-factors were obtained from the TcoFBase in previous work by our research group. Briefly, we manually collected a list of TcoFs in mammals from TcoF-DB v2⁷⁴ and AnimalTFDB 3.0⁷⁵. We also collected 4246 TcoF-related ChIP-seq datasets of different types of human cells and tissues from ReMap, ENCODE, Cistrome⁷⁶, and ChIP-Atlas⁷⁷. We used the liftOver⁷⁸ tool from UCSC to convert all ChIP-seq peak data into the hg38 genome assembly. The ChIPseeker R package and BEDTools were used to compute the distributions of various genomic compositions and the UDHS coverage of each TcoF.

Data on chromatin regulators

The ChIP-seq datasets of the chromatin regulators were obtained from CRdb in previous work by our research group (reference). Briefly, we processed 2,591 CR-associated ChIP-seq datasets from GEO and ENCODE. We identified the binding regions of the CRs by using Bowtie, SAMtools⁷⁹, and MACS2⁸⁰, and calculated the distributions of various genomic compositions, and determined the coverage of union DNaseI hypersensitive sites (UDHS) of each TcoF by using ChIPseeker R package and BEDTools.

The large volume of collected data likely contained redundancies originating from the same sources. We calculated the peak correlations of all TRs, and retained only one of the samples in cases of a correlation value of one. Through this process of filtering, 17,227 unique peak files of TRs were retained (Supplementary Data 1).

In summary, TRAPT outperforms previously developed tools by leveraging a more comprehensive and higher-quality dataset. Specifically, TRAPT comprises 17,227 transcription factor (TR) data items, which is 2.49 times larger than Lisa’s dataset and 2.16 times larger than BART’s. Additionally, TRAPT’s chromatin accessibility data, surpasses the largest available datasets by 1.47 times (TRAPT: 1,329; Lisa: 904). Similarly, the H3K27ac dataset in TRAPT is 1.44 times larger than that of Lisa, further underscoring its superior data coverage and quality (Supplementary Figs. 1b, c).

TR and model of epigenomic regulatory potential

The regulatory potential of a gene can be determined by calculating the activity of cis-regulatory elements (CREs) close to it¹². To compute the TR-RP matrix, we collected peak data on 17,227 TRs from CRdb, TcoFBase, and TFTG. TRs influence gene expression by binding to CREs located upstream or downstream of the gene. Therefore, we focused only on CREs overlapping with TR binding sites to calculate gene regulatory potential (Supplementary Note A.7). We applied BEDTools to identify regions of overlap of the CREs for each TR. To standardize the terminology, we termed these regulatory elements as potential regulatory elements (PREs). The signal value of each PRE in a TR sample was defined as a binary value:

$${{PRE}}_{i}=\left\{\begin{array}{c}\begin{array}{cc}1 & {{\mbox{TR}}}\,{{\mbox{bound\,CRE}}}_{i}\\ 0 & {\mbox{other}}\end{array}\end{array}\right.$$

(1)

By aggregating the values of signals of the PREs within a range of 100 kB upstream and downstream of the target genes, the regulatory potential of each gene in each sample was computed to generate the TR-RP matrix. Each row of this matrix represents a TR, and each column represents a gene. The regulatory potential of the i-th gene in the j-th sample was defined as follows:

$${R}_{{ij}}=\frac{1}{K} {\sum}_{k\in {S}_{i}}{\omega }_{{ik}}{s}_{{ik}}$$

(2)

where ${\omega }_{{ik}}$ is the regulatory influence of the k-th PRE, located within a range of 100 kB of the TSS of gene j, and ${s}_{{ik}}$ is the value of the signal of the given PRE. The weight of each PRE is defined as:

$${\omega }_{{ik}}=\left\{\begin{array}{c}\begin{array}{cc}1 & x\in \left(0{kb},10{kb}\right)\\ \frac{3}{1+2{e}^{\alpha \left({x}_{k}-d\right)}} & x\in \left(10{kb},100{kb}\right)\end{array}\end{array}\right.$$

(3)

where ${x}_{k}$ is the distance between the current PRE and the TSS of the gene, with the hyperparameter d set to 10 kB. The parameter $\alpha$ controls the decay rate of regulatory influence:

$$\alpha=\frac{{\mathrm{ln}}\left(\frac{2}{m}-1\right)}{r-d}$$

(4)

where r was set to 100 kB, and m represents the weight of the TR. In this study, we used the “percentage of intergenic distance” calculated by ChIPseeker as the proportion of distal enhancers, and incorporated it as a weight parameter m in the specificity regulatory potential model for each TR.

To compute the Epi-RP matrix (with rows representing epigenomic samples and columns representing genes), we utilized BAM files from H3K27ac ChIP-seq and ATAC-seq data obtained from SEdb and ATACdb, respectively. We then applied the BEDTools multicov tool to count the number of reads on the PREs, and this yielded read signals for all PREs.

The computations were performed by using the same method as above, but we set the value of m of each epigenomic sample to 0.01. Furthermore, we used read signals instead of peak signals to compute the gene regulatory potential.

Ultimately, we simultaneously applied logarithmic standardization to the regulatory potential corresponding to each gene for both TR and the epigenome:

$${R}^{\prime} _{{ij}}=\log \left({R}_{{ij}}+1\right)$$

(5)

Predicting the regulatory potential via upstream transcriptional regulators

We leveraged a knowledge distillation (KD)-based model in our module to guide the student model to learn multi-modal epigenomic features and optimize the network of epigenomic relationships. KD is designed to compress and accelerate a given model by transferring knowledge from a complex model to a simplified one. Overfitting frequently occurs when making inferences regarding networks of epigenomic relationships. However, recent studies have shown that using knowledge-based distillation significantly enhances the performance of the student model and mitigates issues of model hallucination⁸¹. We proposed using KD to infer the genome-wide binding sites of each TR. Due to distribution differences between TRs and epigenomes (Supplementary Figs. 9b–e), a simple merger was not feasible. To more appropriately extract joint representations of the embeddings of the TRs and epigenomes, we used conditional variational autoencoders⁶⁰ (CVAEs) as the teacher network. CVAEs can not only master complex data representations, but also perform well in terms of integrating multi-modal data¹³. By incorporating the error in reconstruction and terms of regularization of the latent variables during training, CVAEs could learn to distinguish between feature representations. The model was actualized by minimizing the following loss function:

$$L={MSE}\left(X,f\left(Z,Y\right)\right)+{KL}\left[q\left({Z}^{\left(t\right)} | X,Y\right){||p}\left({Z}^{\left(t\right)} | X\right)\right]$$

(6)

where $X\in {R}^{m\times n}$ (m is the number of TR and epigenome samples, and n is the number of genes) represents the feature matrix assembled by integrating the TR-RP and Epi-RP matrices. Specifically, we concatenate the two types of Epi-RP matrices (H3K27ac and ATAC) with the TR-RP matrix by samples as the input for the model. $Y\in {R}^{m\times 2}$ is a one-hot matrix that represents the labels of the two types of omics data. Specifically, each type of epigenomic data corresponds to different conditions. In this context, TRAPT integrates two types of omics data, assigning a label of 0 to TR samples and a label of 1 to epigenome samples. Ultimately, we obtain a one-hot matrix with a feature dimension of 2. ${KL}\left[q\left(\cdot \right){||p}\left(\cdot \right)\right]$ denotes the Kullback-Leibler divergence between the reconstructed network and the (conditional) prior network. When the feature matrix and conditional matrix were inputted to the framework, it generated a low-dimensional joint representation of the embedding ${H}^{\left(t\right)}\in {R}^{m\times h}$ (where h is the dimensionality of the hidden layer) of the TRs and epigenomic samples:

$${H}^{\left(t\right)}={Relu}\left(f\left(X,Y\right){W}^{\left(1\right)}+{b}^{\left(1\right)}\right)$$

(7)

where ${W}^{\left(1\right)}\in {R}^{n\times h}$ and ${b}^{\left(1\right)}\in {R}^{1\times h}$ represent the weights and biases of the initial layer of the encoder, respectively. The complex network was represented by the relationship between the TR and the epigenome. To model this network, we applied VGAE⁸² as the student network and selected the 10 epigenomic samples closest to each TR to construct the adjacency matrix. We used kNN, with cosine similarity serving as the distance metric:

$${D}_{{ij}}=\frac{{\sum }_{k=1}^{N}{X}_{{ik}}{X}_{{jk}}}{\sqrt{{\sum }_{k=1}^{N}{X}_{{ik}}^{2}}\sqrt{{\sum }_{k=1}^{N}{X}_{{jk}}^{2}}}$$

(8)

where ${D}_{{ij}}\in {R}^{m\times m}$ represents the cosine similarity between the i-th TR and the j-th epigenomic sample. Specifically, the score of each edge in the network indicates the weight of the currently identified set of potential regulatory elements that are specific to tissue/cell types for the TR (with each epigenomic sample corresponding to a set of regulatory elements). N is the number of genes. We fed X and A into the model. They passed through the first layer of the GCN encoder to learn low-dimensional nodal representations ${H}^{\left(s\right)}\in {R}^{m\times h}$. These representations capture both single-modality information and the relationship between TRs and epigenomic samples. Given that the input was a heterogeneous network, it did not contain any information on the relationship of a single modality with itself. Subsequently, we used the second layer of graph convolution to generate the mean and variance, and, ultimately, used a reparameterization trick to derive the new nodal feature representation ${Z}^{\left(s\right)}\in {R}^{m\times z}$ (where z is the dimensionality of the hidden layer in the GCN module). The GCN is expressed as follows:

$${H}^{\left(s\right)}={Relu}\left({GCN}\left(A,X\right)\right)$$

(9)

$${Z}_{\mu }={GCN}\left(A,{H}^{\left(s\right)}\right)$$

(10)

$${Z}_{{\sigma }^{2}}={GCN}\left(A,{H}^{\left(s\right)}\right)$$

(11)

$${Z}^{\left(s\right)}={Reparametrize}\left({Z}_{\mu },{Z}_{{\sigma }^{2}}\right)$$

(12)

Finally, the VGAE used an inner product decoder to produce a reconstructed adjacency matrix:

$${A}^{\prime}={Sigmoid}\left({Z}^{\left(s\right)}\cdot {{Z}^{\left(s\right)}}^{T}\right)$$

(13)

The cross-entropy loss function ${L}_{C}$ is defined as the expectation of minimizing the discrepancy between the input and output networks:

$${L}_{D}=-E\left[\sum {A}_{i}\log \left({A}^{\prime} _{i}\right)\right]$$

(14)

The loss function of distillation ${L}_{D}$ is defined as:

$${L}_{D}=\frac{1}{2n}{||}{H}^{\left(s\right)}-{H}^{\left(t\right)}{||}$$

(15)

where ${||}\cdot {||}$ is the Euclidean norm. The final loss function L of the student network is defined as:

$$L={L}_{D}+{L}_{C}+{KL}\left[q\left({Z}^{\left(s\right)} | X,A\right){||p}\left({Z}^{\left(s\right)}\right)\right]$$

(16)

where ${KL}\left[q\left(\cdot \right){||p}\left(\cdot \right)\right]$ is the Kullback–Leibler divergence between the reconstructed distribution and the prior Gaussian distribution. We predict the D-RP corresponding to each TR as follows:

$${{\mbox{D-RP}}}_{i}=\frac{{\sum }_{j}^{M}{\omega }_{{ij}}{X}_{{ij}}}{\sqrt{{\sum }_{j}^{M}{X}_{{ij}}^{2}}}$$

(17)

where $X$ is derived from Epi-RP matrix, with ${X}_{{ij}}$ represents the regulatory potential vector of the i-th TR corresponding to the j-th neighboring epigenomic sample, and ${\omega }_{{ij}}$ signifies the normalized weight of the edge of the network for the j-th epigenomic sample of the i-th TR. M is the number of epigenomic samples. The D-RP matrix represents the aggregated activity of the genome-wide binding sites of the TRs near the genes, with higher values signifying a more intense level of transcriptional activity in the vicinity of the genes.

Predicting the regulatory potential via downstream gene sets

Two primary methods were used to predict target gene cis-regulatory elements. The first method infers regulatory elements near genes based on distance, such as the i-cisTarget approach. The second method used regression to select the epigenomic samples and predict the landscape of regulatory elements across the entire genome, such as the MARGE method. However, these methods fail to address epigenomic data redundancy and complex nonlinear relationships between samples. Inspired by this and several recent studies^23,83, we proposed a KD-based strategy to select the most probable epigenomic samples associated with the queried gene set. Initially, we calculated the correlation between the Epi-RP matrix and the queried gene set. Subsequently, we ranked the epigenomic samples in descending order based on the magnitudes of their correlations. Due to the large number of epigenomic samples, many originated from the same tissue, leading to redundancy. To address this, we empirically partitioned the matrix into groups of 10 samples. This grouping aimed to cluster similar epigenomic samples and enforce sparsity within and between groups to prevent redundancy and overfitting. The grouped Epi-RP matrix was fed to the teacher network. The latter was a neural network comprising three fully connected layers. We predicted the queried vector of binary genes $Z\in {R}^{n\times 1}$ by using the transposed matrix $X\in {R}^{n\times d}$ (where n signifies the number of genes and d denotes the number of TR samples) of the Epi-RP matrix. Specifically, each row of the Epi-RP matrix corresponds to a gene, and each column corresponds to an epigenomic sample, with the values in the matrix representing the regulatory potential scores (see Eq. 2 for calculation details). By transposing the matrix, we ensure that the input and output dimensions of the model are aligned. In this process, the queried gene set was used as the positive set, and we randomly selected 6,000 background genes as the negative set. To retain more information, we implemented temperature-scaled sigmoid (TSS) as the activation function in the output layer:

$${TSS}\left(x\right)=\frac{1}{1+{e}^{\frac{-x}{t}}}$$

(18)

where x denotes the input and t represents the temperature. This function maps the input values to an output value ranging from zero to one. As the value of the temperature gravitated toward infinity, the output of the function approximated the output of a standard sigmoid function. Conversely, at low temperatures, the output changes more gradually near zero and one. The final teacher model was represented as follows:

$${Y}^{\left(t\right)}={Relu}\left(X{W}^{\left(1\right)}+{b}^{\left(1\right)}\right)$$

(19)

$${Z}^{\left(t\right)}={TSS}\left({Y}^{\left(t\right)}{W}^{\left(2\right)}+{b}^{\left(2\right)}\right)$$

(20)

where ${Y}^{\left(t\right)}\in {R}^{n\times h}$ (h denotes the dimensionality of the hidden layer) signifies the extracted feature representation of the latent cis-regulatory profiles associated with the queried gene set. The corresponding weight matrices and biases between each pair of layers are ${W}^{\left(1\right)}\in {R}^{d\times h}$ and ${W}^{\left(2\right)}\in {R}^{h\times d}$, and ${b}^{\left(1\right)}\in {R}^{1\times h}$ and ${b}^{\left(2\right)}\in {R}^{1\times d}$, respectively. The teacher model was trained by minimizing the following loss function:

$$L={BCE}\left(Z,{Z}^{\left(t\right)}\right)$$

(21)

where BCE stands for binary cross-entropy, where the teacher model focuses on constructing the feature space and uses the fitted scores ${Z}^{\left(t\right)}$ as soft labels for the student model, thereby enabling the student model to concentrate more on the feature selection task. We trained the student network to predict the low-dimensional feature representation extracted from the intermediate layer of the teacher network by feeding the same data to it:

$${H}^{\left(s\right)}={Relu}\left(X{W}^{\left(3\right)}+{b}^{\left(3\right)}\right)$$

(22)

$${Y}^{\left(s\right)}={Relu}\left({H}^{\left(s\right)}{W}^{\left(4\right)}+{b}^{\left(4\right)}\right)$$

(23)

The SGL constraint is used in the first layer of the student network to select important features of the cis-regulatory profile by “sparsifying” the weight matrix through L2 regularization within groups and L1 regularization between groups:

$${SGL}={\lambda }_{1}{{||}{W}^{\left(3\right)}{||}}_{1}+{\lambda }_{2} {\sum}_{g}^{g\in G}\sqrt{{P}_{g}}{{||}{W}_{g}^{\left(3\right)}{||}}_{1}$$

(24)

The distillation loss function ${L}_{D}$ is defined as follows:

$${L}_{D}=\frac{1}{2n}{||}{Y}^{\left(s\right)}-{Y}^{\left(t\right)}{||}$$

(25)

The final loss function L of the student network is defined as follows:

$$L={\lambda }_{1}{{||}{W}^{\left(3\right)}{||}}_{1}+{\lambda }_{2} {\sum}_{g}^{g\in G}\sqrt{{P}_{g}}{{||}{W}_{g}^{\left(3\right)}{||}}_{1}+\frac{1}{2n}{||}{Y}^{\left(s\right)}-{Y}^{\left(t\right)}{||}$$

(26)

where ${\lambda }_{1}$ and ${\lambda }_{2}$ represent regularization parameters, ${W}_{g}^{\left(3\right)}$ is the first layer weight of variables in group g, ${P}_{g}$ is the number of variables in group g, and ${Y}^{\left(s\right)}$ is the output of the student model. We squared and summed the weights of the first layer ${W}^{\left(3\right)}\in {R}^{d\times h}$ of the student network as follows:

$$C={Diag}\left({W}^{\left(3\right)}{\left({W}^{\left(3\right)}\right)}^{T}\right)$$

(27)

where C represents the weights of all epigenomic samples. The choice of sample size may affect prediction results. We selected a varying number of epigenomic samples based on the weights of the student network model. The aim was to select the most appropriate sample size. We conducted multiple training sessions for the model by selecting different numbers of epigenomic samples and calculated the auROC to assess the performance of each candidate model. We determined that 10 epigenomic samples provided a reasonable choice (Supplementary Fig. 2e). We then trained a neural network model (NN model) by using the selected epigenomic samples, where the input was represented by $X{\prime} \in {R}^{n\times d{\prime} }$. $d{\prime}$ denotes the number of selected epigenomic samples. The output was the gene vector ${Z}^{\left(p\right)}\in {R}^{n\times 1}$:

$${Z}^{\left(p\right)}={Sigmoid}\left({Relu}\left(X{W}^{\left(1\right)}+{b}^{\left(1\right)}\right){W}^{\left(2\right)}+{b}^{\left(2\right)}\right)$$

(28)

We define the loss function as:

$$L=\frac{1}{2n}{||}{Z}^{\left(p\right)}-{Z||}$$

(29)

Ultimately, we inputted X to the previously trained model to derive the predicted gene U-RP. The U-RP vectors contain context-dependent information derived from a specific gene set. The variation in the values of these vectors represented the specificity of chromatin accessibility (ATAC) and states of activity (H3K27ac) with the locations of the genes.

Integrating regulatory potential and predicting transcriptional regulator activity

Having obtained the bidirectional regulatory potentials, we concurrently acquired information on the regulatory profile corresponding to the genome-wide binding sites of the TRs and the regulatory profile corresponding to the cis-regulatory elements of the queried gene set. Our objective was to derive the integrated regulatory activity of TRs that best represents the current state of gene transcription regulation (Supplementary Note A.8). Accordingly, we computed the I-RP for each TR:

$${{\mbox{I-RP}}}_{i}=\left(\frac{{ {R}^{\prime} }_{i}}{{|| {R}}^{\prime} {||}}+{{\mbox{D-RP}}}_{i}\right)\times {\mbox{U-RP}}$$

(30)

The AUC score can accurately represent the measurement of transcription factor enrichment^9,10. By transforming the queried gene set into binary form and computing the AUC for each TR based on its I-RP score, we combined the activity of TRs from the H3K27ac and ATAC epigenomes. The resulting activity score was then computed as follows:

$${{AS}}_{i}={\sum}_{j=1}^{M}\frac{{{AUC}}_{{ij}}}{{||}{{AUC}}_{j}{||}}$$

(31)

where ${{AS}}_{i}$ signifies the final activity of the i-th TR sample, ${{AUC}}_{{ij}}$ denotes the j-th epigenomic AUC score of the i-th TR sample, and M represents the total number of epigenomic modalities.

Calculation of enrichment scores and significance in post-GWAS analysis

Significance of transcriptional regulator

(1) Randomly select 1000 causal and 1000 non-causal variants to serve as the background variants. Concurrently select the top and bottom 25 TRs predicted by TRAPT. (2) Use the intersect tool in BEDTools to compute the number of overlaps between the selected variants and the binding sites of each TR. (3) Calculate the p-value of significance of each TR by using the hypergeometric test:

$$P=1- {\sum}_{i=0}^{x-1}\frac{\left(\begin{array}{c}k\\ i\end{array}\right)\left(\begin{array}{c}n-k\\ s-i\end{array}\right)}{\left(\begin{array}{c}n\\ s\end{array}\right)}$$

(32)

where x is the number of causal variants bound by the TR, k is the number of variants bound by the TR, n is the number of background variants, and s is the number of causal variants in the background.

Enrichment score (ES)

(1) Rank the TRs in descending order of activity. (2) Calculate their ES scores as follows:

$${ES}=\max \left({score}\right),{{score}}_{k}={scale}\left(\frac{k}{K}\min \left({logp}\right)- {\sum}_{i=1}^{k}\log {p}_{i}\right)$$

(33)

where k is the k-th transcriptional regulator and K is the number of selected TRs. This score is the standard Kolmogorov-Smirnov statistic.

Estimating significance

(1) Randomly shuffle the TRs and recalculate the enrichment score as ${{ES}}_{{NULL}}$. (2) Repeat the shuffle 1000 times and create a corresponding histogram of distribution of the enrichment scores ${{ES}}_{{NULL}}$. (3) Estimate the p-value by calculating the distribution that is greater than the observed ES.

Comparison between TRAPT and similar TR-ranking tools

We collected an extensive array of TR knockdown/knockout datasets from KnockTF, and chose the top 500 upregulated and downregulated differentially expressed genes for analysis. We also curated datasets of TF binding from GTRD, and retained all target genes and 66 benchmark TF datasets from Lisa, including both upregulated and downregulated gene sets (Supplementary Note A.10 and Supplementary Table 2). When comparing the datasets of TF binding, we removed data originating from the GTRD in the background TR ChIP-seq libraries of TRAPT. We used the offline toolkit available on the website of the official repository of the BART algorithm (https://github.com/zanglab/bart2). Similarly, we applied the offline toolkit accessible on the website of the official repository of the Lisa algorithm (https://github.com/qinqian/lisa). We used the tool for online analysis provided on the website of i-cisTarget (https://gbiomed.kuleuven.be/apps/lcb/i-cisTarget/), and procured the results of analysis of ChEA3 via the API online interface available on its official website (https://amp.pharm.mssm.edu/ChEA3).

Hyperparameters and training of the model

While training the teacher model of the D-RP model, we set the batch size to 32 and the learning rate to 0.01, and trained it for 100 epochs. For the student model, we set the learning rate to 0.01 and trained for 1000 epochs. A unified standard was used when training the teacher model, student model, and NN model of the U-RP model, with the batch size set to 32 and the learning rate to 0.001. The samples were randomly shuffled and trained for a total of 16 epochs.

Ablation study

Without interfering with the overall execution of the model, we separately removed the “U-RP model,” “D-RP model,” and “TR-RP model.” The same strategy was applied to the “TRAPT-H3K27ac epigenetic model,” “TRAPT-ATAC epigenetic model,” and “peak-promoter-model.” We also conducted ablation experiments on knowledge distillation. Finally, we calculated the MRR scores of the model after each modification to observe the decline in its performance, if any. The objective was to verify the efficacy of each of its components. The MRR was calculated as follows:

$${MRR}=\frac{1}{N} {\sum}_{i=1}^{N}\frac{1}{{r}_{i}}$$

(34)

where N refers to the number of predicted TRs and ${r}_{i}$ denotes the rank of the current predicted TR.

Model stability examination

We used the network constructed by using the kNN algorithm to generate perturbed datasets by masking 2%, 5%, 8%, 10%, 12%, and 15% of the links within the network. These masked links were randomly distributed to simulate real-world scenarios where interactions are unknown. When training the model, we treated these masked positive data as negatives. Once the training of the model had been completed, we calculated its average precision (AP) to evaluate its predictive performance on the test set. This process helped simulate unknown information in the data, and provided a comprehensive evaluation of model performance. The AP was calculated as follows:

$${AP}={\sum}_{i=1}^{n}\left({R}_{n}-{R}_{n-1}\right){P}_{n}$$

(35)

where ${P}_{n}$ and ${R}_{n}$ represent the precision and recall, respectively, as sorted by the threshold n.

Software and web tool

TRAPT software was developed in Python 3.11, and has been uploaded to GitHub (https://github.com/TOSTRING-Z/TRAPT) for user download and use. The current iteration of TRAPT operates on a Linux-based Apache web server (http://www.apache.org). We used Django v4.1.3 (https://www.djangoproject.com/) for server-side scripting. The interactive interface was designed and constructed by using Bootstrap v4.3.1 (https://getbootstrap.com/) and jQuery v3.2.1 (http://jquery.com). ECharts v5.4 (https://echarts.apache.org/) and DataTables v1.13.2 (https://datatables.net/) were implemented as the frameworks for graphical visualization, and the sqlite3 lightweight database was deployed to store the data tables.

Furthermore, we developed a corresponding web service (https://bio.liclab.net/TRAPT). The website was designed to accept gene sets input by users for analysis and allow for the easy retrieval of the analytical results. We have also included an email notification feature. The website displays all scores of TR activity on the results page, as well as the ranking and individual scores of each TR. It also provides details of annotations and the relevant information on quality control for each TR. The analysis interface provided the results of each benchmark dataset, including the analysis of differential expression and predictions of TRAPT. Moreover, we have also provided volcano plots-based visualization through a Shiny application (https://shiny.posit.co/). Compared with offline tools, online tools of analysis offer additional features for browsing the results. They enabled the visualization of the predicted 3D protein structure of each TR by leveraging predictions made by AlphaFold⁸⁴. Moreover, the online tools incorporated a genome browser⁸⁵ to facilitate user interaction with the genomic tracks associated with each TR.

Evaluation metrics

In the comparative analysis of our algorithm against other methods, we employed three key metrics to benchmark performance: the Area Under the Curve (AUC) and the Mean Reciprocal Rank (MRR). Briefly, we firstly calculated and plotted the number of correctly predicted TRs across cutoff ranks ranging from 1 to 10 at various thresholds. The performance was then quantified using the AUC. MRR is a metric parameter used to measure the overall performance of ranking algorithms²⁵.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

All datasets analyzed in this study are publicly available. The TR knockdown/knockout datasets were obtained from KnockTF and TF binding datasets from GTRD. The Lisa benchmark dataset can be accessed at http://lisa.cistrome.org/new_gallery/new_gallery.html. Moreover, the protein–protein interaction (PPI) networks were retrieved from the STRING database (https://string-db.org/). The breast cancer RNA-seq expression profiles are available from the TCGA (https://portal.gdc.cancer.gov/), while the breast RNA-seq expression profiles are available from the GTEx (https://www.gtexportal.org/home/). The ESR1 knockdown RNA-seq datasets are available at the Gene Expression Omnibus (GEO) repository under accession number GSE37820. The GWAS dataset was retrieved from causaldb (http://www.mulinlab.org/causaldb), and the Alzheimer’s disease-related H3K27ac data are accessible under GSE65159. The human hematopoietic stem cell dataset is available on GitHub (https://gitlab.com/cvejic-group/integrative-scrna-scatac-human-fetal#data), the human embryonic stem cells dataset is accessible under GSE75748, and the normal human tissue expression profiles were obtained from GTEx (https://www.gtexportal.org/home/). Source data are provided with this paper.

Code availability

The TRAPT algorithm was implemented in Python. The source code for it is available at https://github.com/TOSTRING-Z/TRAPT.

References

Lee, T. I. & Young, R. A. Transcriptional regulation and its misregulation in disease. Cell 152, 1237–1251 (2013).
Article CAS PubMed PubMed Central Google Scholar
Heintzman, N. D. et al. Distinct and predictive chromatin signatures of transcriptional promoters and enhancers in the human genome. Nat. Genet 39, 311–318 (2007).
Article CAS PubMed Google Scholar
Lambert, S. A. et al. The human transcription factors. Cell 172, 650–665 (2018).
Article CAS PubMed Google Scholar
Vaquerizas, J. M., Kummerfeld, S. K., Teichmann, S. A. & Luscombe, N. M. A census of human transcription factors: function, expression and evolution. Nat. Rev. Genet 10, 252–263 (2009).
Article CAS PubMed Google Scholar
Chen, E. Y. et al. Enrichr: interactive and collaborative HTML5 gene list enrichment analysis tool. BMC Bioinforma. 14, 128 (2013).
Article Google Scholar
Puente-Santamaria, L., Wasserman, W. W. & Del Peso, L. TFEA.ChIP: a tool kit for transcription factor binding site enrichment analysis capitalizing on ChIP-seq datasets. Bioinformatics 35, 5339–5340 (2019).
Article CAS PubMed Google Scholar
Keenan, A. B. et al. ChEA3: transcription factor enrichment analysis by orthogonal omics integration. Nucleic Acids Res 47, W212–W224 (2019).
Article CAS PubMed PubMed Central Google Scholar
Roopra, A. MAGIC: A tool for predicting transcription factors and cofactors driving gene sets using ENCODE data. PLoS Comput Biol. 16, e1007800 (2020).
Article ADS CAS PubMed PubMed Central Google Scholar
Herrmann, C., Van de Sande, B., Potier, D. & Aerts, S. i-cisTarget: an integrative genomics method for the prediction of regulatory features and cis-regulatory modules. Nucleic Acids Res 40, e114 (2012).
Article CAS PubMed PubMed Central Google Scholar
Wang, Z. et al. BART: a transcription factor prediction tool with query gene sets or epigenomic profiles. Bioinformatics 34, 2867–2869 (2018).
Article CAS PubMed PubMed Central Google Scholar
Qin, Q. et al. Lisa: inferring transcriptional regulators through integrative modeling of public chromatin accessibility and ChIP-seq data. Genome Biol. 21, 32 (2020).
Article PubMed PubMed Central Google Scholar
Wang, S. et al. Modeling cis -regulation with a compendium of genome-wide histone H3K27ac profiles. Genome Res 26, 1417–1429 (2016).
Article CAS PubMed PubMed Central Google Scholar
Lotfollahi, M. et al. Mapping single-cell data to reference atlases by transfer learning. Nat. Biotechnol. 40, 121–130 (2022).
Article CAS PubMed Google Scholar
Li, H. et al. Inferring transcription factor regulatory networks from single-cell ATAC-seq data based on graph neural networks. Nat. Mach. Intell. 4, 389–400 (2022).
Article Google Scholar
Zhang, Y. et al. TcoFBase: a comprehensive database for decoding the regulatory transcription co-factors in human and mouse. Nucleic Acids Res 50, D391–D401 (2022).
Article CAS PubMed Google Scholar
Zhang, Y. et al. CRdb: a comprehensive resource for deciphering chromatin regulators in human. Nucleic Acids Res 51, D88–D100 (2023).
Article CAS PubMed Google Scholar
Zhou, X. et al. TFTG: A comprehensive database for human transcription factors and their targets. Comput Struct. Biotechnol. J. 23, 1877–1885 (2024).
Article CAS PubMed PubMed Central Google Scholar
Wang, Y. et al. SEdb 2.0: a comprehensive super-enhancer database of human and mouse. Nucleic Acids Res 51, D280–D290 (2023).
Article ADS CAS PubMed Google Scholar
Wang, F. et al. ATACdb: a comprehensive human chromatin accessibility database. Nucleic Acids Res 49, D55–D64 (2021).
Article CAS PubMed Google Scholar
Feng, C. et al. KnockTF: a comprehensive human gene expression profile database with knockdown/knockout of transcription factors. Nucleic Acids Res 48, D93–D100 (2020).
Article CAS PubMed Google Scholar
Chen, C.-H. et al. Determinants of transcription factor regulatory range. Nat. Commun. 11, 2472 (2020).
Article ADS CAS PubMed PubMed Central Google Scholar
Yu, F. et al. Variant to function mapping at single-cell resolution through network propagation. Nat. Biotechnol. 40, 1644–1653 (2022).
Article CAS PubMed PubMed Central Google Scholar
Mirzaei, A., Pourahmadi, V., Soltani, M. & Sheikhzadeh, H. Deep feature selection using a teacher-student network. Neurocomputing 383, 396–408 (2020).
Simon, N., Friedman, J., Hastie, T. & Tibshirani, R. A sparse-group lasso. J. Computational Graph. Stat. 22, 231–245 (2013).
Article MathSciNet Google Scholar
Voorhees, E. M. The TREC-8 Question Answering Track Report. (1999).
Muhar, M. et al. SLAM-seq defines direct gene-regulatory functions of the BRD4-MYC axis. Science 360, 800–805 (2018).
Article CAS PubMed PubMed Central Google Scholar
Nilsson, S. et al. Mechanisms of Estrogen Action. Physiological Rev. 81, 1535–1565 (2001).
Article CAS Google Scholar
Pei, X.-H. et al. CDK inhibitor p18INK4c is a downstream target of GATA3 and restrains mammary luminal progenitor cell proliferation and tumorigenesis. Cancer Cell 15, 389–401 (2009).
Article CAS PubMed PubMed Central Google Scholar
Carroll, J. S. et al. Chromosome-wide mapping of estrogen receptor binding reveals long-range regulation requiring the forkhead protein FoxA1. Cell 122, 33–43 (2005).
Article CAS PubMed Google Scholar
Xu, B. et al. The LIM protein Ajuba recruits DBC1 and CBP/p300 to acetylate ERα and enhances ERα target gene expression in breast cancer cells. Nucleic Acids Res 47, 2322–2335 (2019).
Article CAS PubMed Google Scholar
von Mering, C. et al. STRING: a database of predicted functional associations between proteins. Nucleic Acids Res 31, 258–261 (2003).
Article Google Scholar
Cancer Genome Atlas Research Network. et al. The cancer genome atlas pan-cancer analysis project. Nat. Genet 45, 1113–1120 (2013).
Article PubMed Central Google Scholar
Zheng, Z.-Z. et al. Super-enhancer-controlled positive feedback loop BRD4/ERα-RET-ERα promotes ERα-positive breast cancer. Nucleic Acids Res 50, 10230–10248 (2022).
Article CAS PubMed PubMed Central Google Scholar
de Leeuw, C. A., Mooij, J. M., Heskes, T. & Posthuma, D. MAGMA: generalized gene-set analysis of GWAS data. PLoS Comput Biol. 11, e1004219 (2015).
Article PubMed PubMed Central Google Scholar
Wang, J. et al. CAUSALdb: a database for disease/trait causal variants identified using summary statistics of genome-wide association studies. Nucleic Acids Res. 48, D807–D816 (2020).
CAS PubMed Google Scholar
Schwartzentruber, J. et al. Genome-wide meta-analysis, fine-mapping and integrative prioritization implicate new Alzheimer’s disease risk genes. Nat. Genet 53, 392–402 (2021).
Article CAS PubMed PubMed Central Google Scholar
Subramanian, A. et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl Acad. Sci. USA 102, 15545–15550 (2005).
Article ADS CAS PubMed PubMed Central Google Scholar
Benner, C. et al. FINEMAP: efficient variable selection using summary data from genome-wide association studies. Bioinformatics 32, 1493–1501 (2016).
Article CAS PubMed PubMed Central Google Scholar
Pan, Q. et al. VARAdb: a comprehensive variation annotation database for human. Nucleic Acids Res. 49, D1431–D1444 (2021).
Article CAS PubMed Google Scholar
Lu, T. et al. REST and stress resistance in ageing and Alzheimer’s disease. Nature 507, 448–454 (2014).
Article ADS CAS PubMed PubMed Central Google Scholar
Kosoy, R. et al. Genetics of the human microglia regulome refines Alzheimer’s disease risk loci. Nat. Genet 54, 1145–1154 (2022).
Article CAS PubMed PubMed Central Google Scholar
Rangaraju, S. et al. Identification and therapeutic modulation of a pro-inflammatory subset of disease-associated-microglia in Alzheimer’s disease. Mol. Neurodegener. 13, 24 (2018).
Article PubMed PubMed Central Google Scholar
Liu, D. et al. Targeting the HDAC2/HNF-4A/miR-101b/AMPK pathway rescues tauopathy and dendritic abnormalities in alzheimer’s disease. Mol. Ther. 25, 752–764 (2017).
Article ADS CAS PubMed PubMed Central Google Scholar
Kumar, A. et al. Chemically targeting the redox switch in AP1 transcription factor ΔFOSB. Nucleic Acids Res. 50, 9548–9567 (2022).
Article ADS CAS PubMed PubMed Central Google Scholar
Roses, A. et al. Understanding the genetics of APOE and TOMM40 and role of mitochondrial structure and function in clinical pharmacology of Alzheimer’s disease. Alzheimers Dement 12, 687–694 (2016).
Article PubMed Google Scholar
Cooper, Y. A. et al. Functional regulatory variants implicate distinct transcriptional networks in dementia. Science 377, eabi8654 (2022).
Article CAS PubMed Google Scholar
Porcellini, E., Carbone, I., Ianni, M. & Licastro, F. Alzheimer’s disease gene signature says: beware of brain viral infections. Immun. Ageing 7, 16 (2010).
Article CAS PubMed PubMed Central Google Scholar
Haney, M. S. et al. APOE4/4 is linked to damaging lipid droplets in Alzheimer’s disease microglia. Nature https://doi.org/10.1038/s41586-024-07185-7 (2024).
Nativio, R. et al. An integrated multi-omics approach identifies epigenetic alterations associated with Alzheimer’s disease. Nat. Genet 52, 1024–1035 (2020).
Article CAS PubMed PubMed Central Google Scholar
Ranzoni, A. M. et al. Integrative single-cell RNA-Seq and ATAC-Seq analysis of human developmental hematopoiesis. Cell Stem Cell 28, 472–487.e7 (2021).
Article CAS PubMed PubMed Central Google Scholar
Scarno, G. et al. Divergent roles for STAT4 in shaping differentiation of cytotoxic ILC1 and NK cells during gut inflammation. Proc. Natl Acad. Sci. USA 120, e2306761120 (2023).
Article CAS PubMed PubMed Central Google Scholar
Reizis, B. Plasmacytoid dendritic cells: development, regulation, and function. Immunity 50, 37–50 (2019).
Article CAS PubMed PubMed Central Google Scholar
Chu, L.-F. et al. Single-cell RNA-seq reveals novel regulators of human embryonic stem cell differentiation to definitive endoderm. Genome Biol. 17, 173 (2016).
Article PubMed PubMed Central Google Scholar
Paul, S., Home, P., Bhattacharya, B. & Ray, S. GATA factors: master regulators of gene expression in trophoblast progenitors. Placenta 60, S61–S66 (2017).
Article CAS PubMed PubMed Central Google Scholar
Chia, C. Y. et al. GATA6 cooperates with EOMES/SMAD2/3 to deploy the gene regulatory network governing human definitive endoderm and pancreas formation. Stem Cell Rep. 12, 57–70 (2019).
Article CAS Google Scholar
GTEx Consortium. The genotype-tissue expression (GTEx) project. Nat. Genet 45, 580–585 (2013).
Article Google Scholar
Ritchie, M. E. et al. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res. 43, e47 (2015).
Article PubMed PubMed Central Google Scholar
Ang, Y.-S. et al. Disease Model of GATA4 mutation reveals transcription factor cooperativity in human cardiogenesis. Cell 167, 1734–1749.e22 (2016).
Article CAS PubMed PubMed Central Google Scholar
Singh, R. et al. TRAF4-mediated nonproteolytic ubiquitination of androgen receptor promotes castration-resistant prostate cancer. Proc. Natl Acad. Sci. USA 120, e2218229120 (2023).
Article CAS PubMed PubMed Central Google Scholar
Rosen, E. D. et al. C/EBPalpha induces adipogenesis through PPARgamma: a unified pathway. Genes Dev. 16, 22–26 (2002).
Article CAS PubMed PubMed Central Google Scholar
Tontonoz, P., Hu, E. & Spiegelman, B. M. Stimulation of adipogenesis in fibroblasts by PPAR gamma 2, a lipid-activated transcription factor. Cell 79, 1147–1156 (1994).
Article CAS PubMed Google Scholar
Koster, M. I., Kim, S., Mills, A. A., DeMayo, F. J. & Roop, D. R. p63 is the molecular switch for initiation of an epithelial stratification program. Genes Dev. 18, 126–131 (2004).
Article CAS PubMed PubMed Central Google Scholar
Qu, J. et al. Mutant p63 affects epidermal cell identity through rewiring the enhancer landscape. Cell Rep. 25, 3490–3503.e4 (2018).
Article CAS PubMed Google Scholar
Werth, M. et al. The transcription factor grainyhead-like 2 regulates the molecular composition of the epithelial apical junctional complex. Development 137, 3835–3845 (2010).
Article CAS PubMed Google Scholar
Bonasio, R., Tu, S. & Reinberg, D. Molecular signals of epigenetic states. Science 330, 612–616 (2010).
Article ADS CAS PubMed PubMed Central Google Scholar
Gou, J., Yu, B., Maybank, S. J. & Tao, D. Knowledge distillation: a survey. Int J. Comput Vis. 129, 1789–1819 (2021).
Article Google Scholar
Barrett, T. et al. NCBI GEO: archive for functional genomics data sets-10 years on. Nucleic Acids Res 39, D1005–D1010 (2011).
Article CAS PubMed Google Scholar
Kodama, Y., Shumway, M. & Leinonen, R. International nucleotide sequence database collaboration. the sequence read archive: explosive growth of sequencing data. Nucleic Acids Res 40, D54–D56 (2012).
Article CAS PubMed Google Scholar
ENCODE Project Consortium. The ENCODE (ENCyclopedia Of DNA Elements) project. Science 306, 636–640 (2004).
Article ADS Google Scholar
Bernstein, B. E. et al. The NIH roadmap epigenomics mapping consortium. Nat. Biotechnol. 28, 1045–1048 (2010).
Article CAS PubMed PubMed Central Google Scholar
Langmead, B. & Salzberg, S. L. Fast gapped-read alignment with Bowtie 2. Nat. Methods 9, 357–359 (2012).
Article CAS PubMed PubMed Central Google Scholar
Quinlan, A. R. & Hall, I. M. BEDTools: a flexible suite of utilities for comparing genomic features. Bioinformatics 26, 841–842 (2010).
Article CAS PubMed PubMed Central Google Scholar
Yu, G., Wang, L.-G. & He, Q.-Y. ChIPseeker: an R/Bioconductor package for ChIP peak annotation, comparison and visualization. Bioinformatics 31, 2382–2383 (2015).
Article CAS PubMed Google Scholar
Schmeier, S., Alam, T., Essack, M. & Bajic, V. B. TcoF-DB v2: update of the database of human and mouse transcription co-factors and transcription factor interactions. Nucleic Acids Res 45, D145–D150 (2017).
Article CAS PubMed Google Scholar
Hu, H. et al. AnimalTFDB 3.0: a comprehensive resource for annotation and prediction of animal transcription factors. Nucleic Acids Res. 47, D33–D38 (2019).
Article CAS PubMed Google Scholar
Mei, S. et al. Cistrome data browser: a data portal for ChIP-Seq and chromatin accessibility data in human and mouse. Nucleic Acids Res 45, D658–D662 (2017).
Article CAS PubMed Google Scholar
Oki, S. et al. ChIP-Atlas: a data-mining suite powered by full integration of public ChIP-seq data. EMBO Rep. 19, e46255 (2018).
Article PubMed PubMed Central Google Scholar
Haeussler, M. et al. The UCSC genome browser database: 2019 update. Nucleic Acids Res. 47, D853–D858 (2019).
Article CAS PubMed Google Scholar
Danecek, P. et al. Twelve years of SAMtools and BCFtools. Gigascience 10, giab008 (2021).
Article PubMed PubMed Central Google Scholar
Zhang, Y. et al. Model-based analysis of ChIP-Seq (MACS). Genome Biol. 9, R137 (2008).
Article PubMed PubMed Central Google Scholar
Liu, Y., Shen, S. & Lapata, M. Noisy Self-Knowledge Distillation for Text Summarization. in Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. 692–703 (Association for Computational Linguistics, Online, 2021).
Kipf, T. N. & Welling, M. Variational Graph Auto-Encoders. stat 1050, 21 (2016).
Yuan, L., Tay, F. E., Li, G., Wang, T. & Feng, J. Revisiting knowledge distillation via label smoothing regularization. in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 3903–3911 (2020).
Varadi, M. et al. Alphafold protein structure database: massively expanding the structural coverage of protein-sequence space with high-accuracy models. Nucleic Acids Res. 50, D439–D444 (2022).
Article CAS PubMed Google Scholar
Robinson, J. T., Thorvaldsdottir, H., Turner, D. & Mesirov, J. P. igv.js: an embeddable JavaScript implementation of the Integrative Genomics Viewer (IGV). Bioinformatics 39, btac830 (2023).
Article CAS PubMed Google Scholar

Download references

Acknowledgements

This work was supported by the science and technology innovation Program of Hunan Province [2024RC1062, 2024RC3212]; National Natural Science Foundation of China [62171166, 62302206, 62031003]; Research Foundation of the First Affiliated Hospital of University of South China for Advanced Talents [20210002-1005 USCAT-2021-01]; Provincial Key Laboratory of Multi-omics and Artificial Intelligence of Cardiovascular Diseases [2023TP1047]; Natural Science Foundation of Hunan Province [2023JJ40594, 2023JJ30536]; Clinical Research 4310 Program of the University of South China [No. 20224310NHYCG05].

Author information

These authors contributed equally: Guorui Zhang, Chao Song, Mingxue Yin.
These authors jointly supervised this work: Maozu Guo, Chunquan Li.

Authors and Affiliations

The First Affiliated Hospital & National Health Commission Key Laboratory of Birth Defect Research and Prevention, Hengyang Medical School, University of South China, Hengyang, Hunan, 421001, China
Guorui Zhang, Chao Song, Mingxue Yin, Liyuan Liu, Yuexin Zhang, Ye Li, Jianing Zhang & Chunquan Li
Hunan Provincial Key Laboratory of Multi-omics And Artificial Intelligence of Cardiovascular Diseases, University of South China, Hengyang, Hunan, 421001, China
Guorui Zhang, Chao Song, Mingxue Yin, Liyuan Liu, Yuexin Zhang, Ye Li, Jianing Zhang & Chunquan Li
Department of Biochemistry and Molecular Biology, School of Basic Medical Sciences, Hengyang Medical School, University of South China, Hengyang, Hunan, 421001, China
Guorui Zhang, Mingxue Yin, Liyuan Liu, Ye Li & Chunquan Li
School of Computer, University of South China, Hengyang, Hunan, 421001, China
Chao Song & Chunquan Li
Key Laboratory of Rare Pediatric Diseases, Ministry of Education, University of South China, Hengyang, Hunan, 421001, China
Chao Song & Chunquan Li
School of Intelligence Science and Technology, Beijing University of Civil Engineering and Architecture, Beijing, 100044, China
Maozu Guo

Authors

Guorui Zhang
View author publications
Search author on:PubMed Google Scholar
Chao Song
View author publications
Search author on:PubMed Google Scholar
Mingxue Yin
View author publications
Search author on:PubMed Google Scholar
Liyuan Liu
View author publications
Search author on:PubMed Google Scholar
Yuexin Zhang
View author publications
Search author on:PubMed Google Scholar
Ye Li
View author publications
Search author on:PubMed Google Scholar
Jianing Zhang
View author publications
Search author on:PubMed Google Scholar
Maozu Guo
View author publications
Search author on:PubMed Google Scholar
Chunquan Li
View author publications
Search author on:PubMed Google Scholar

Contributions

C.L. and M.G. conceived and designed the study. G.Z. and C.S. developed the algorithm of TRAPT. G.Z. C.S. and M.Y. interpreted the results and wrote the manuscript. L.L, Y.Z., Y.L. and J.Z. provided critical feedback during the study and helped revise the manuscript.

Corresponding authors

Correspondence to Maozu Guo or Chunquan Li.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Xin Gao and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Peer Review file

Description of Additional Supplementary Files

Supplementary Data 1

Supplementary Data 2

Supplementary Data 3

Supplementary Data 4

Supplementary Data 5

Supplementary Data 6

Supplementary Data 7

Supplementary Data 8

Supplementary Data 9

Supplementary Data 10

Supplementary Data 11

Reporting Summary

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Zhang, G., Song, C., Yin, M. et al. TRAPT: a multi-stage fused deep learning framework for predicting transcriptional regulators based on large-scale epigenomic data. Nat Commun 16, 3611 (2025). https://doi.org/10.1038/s41467-025-58921-0

Download citation

Received: 17 June 2024
Accepted: 01 April 2025
Published: 16 April 2025
DOI: https://doi.org/10.1038/s41467-025-58921-0