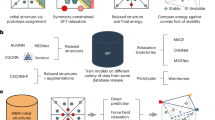
Abstract
Discovering new functional crystalline materials through computational methods remains a challenge in materials science. We introduce VQCrystal, a deep learning framework leveraging discrete latent representations to overcome key limitations to crystal generation and inverse design. VQCrystal employs a hierarchical VQ-VAE architecture to encode global and atom-level crystal features, coupled with an inter-atomic potential model and a genetic algorithm to realize property-targeted inverse design. Benchmark evaluations on diverse datasets demonstrate VQCrystal’s capabilities in representation learning and crystal discovery. We further apply VQCrystal for both 3D and 2D material design. For 3D materials, the density-functional theory validation confirmed that 62.22% of bandgaps and 99% of formation energies of the 56 filtered materials matched the target range. 437 generated materials were validated as existing entries in the full MP-20 database outside the training set. For 2D materials, 73.91% of 23 filtered structures exhibited high stability with formation energies below -1 eV/atom.
Similar content being viewed by others
Introduction
The discovery of new functional materials through computational methods represents a frontier in materials science. Despite centuries of exploration, humankind has only scratched the surface of the vast material search space, with an estimated 105–106 1,2,3 order out of 1010 4 theoretically possible solid inorganic materials having been identified to date. Expanding our catalog of known materials is crucial for scientific advancement, particularly as data-driven research methodologies become increasingly integral to modern materials science. Advancements in first-principles calculations have accelerated crystal discovery, a prevalent framework combines high-throughput virtual screening (HTVS)5 combined with density-functional theory (DFT)6. This approach, followed by DFT relaxation to assess structural stability, leads to databases like the Materials Project (MP)7 and OQMD8. While accurate, DFT’s computational demands limit large-scale applications, highlighting the need for more efficient methods.
Deep learning models offer a computationally efficient alternative to traditional first-principles calculations by generating new crystals through sampling from learned distributions. Methods9,10,11,12 based on generative adversarial network (GAN)13 drives a similar sampling distribution to the database distribution with a generator and a discriminator. But the inherent training instability and low sampling diversity restrict their application to specific subsets of crystalline materials like those with space group #22510,11, binary Bi-Se systems9, or alloys12. More general methods of discovering crystals are based on variational autoencoder (VAE)14,15 and diffusion model16. These models map the complex information of diverse unit cells onto a unified latent space, which enables the encoding and sampling of a wide variety of materials using a single model. Two notable examples of them are the Fourier-transformed crystal properties framework (FTCP)17 and the crystal diffusion variational autoencoder (CDVAE)18. FTCP uses a variational autoencoder model with invertible representation for crystal generation, incorporating composition and structure. The inverse design process utilizes a property-prediction head, with subsequent structure relaxation to enhance validity. But FCTP struggles with reconstruction and sampling validity. As an improvement, CDVAE uses a hybrid structure of VAE and diffusion models, using VAE for representation and a score-based diffusion model to iteratively refine structures, mimicking DFT relaxation. However, it still faces challenges in reconstruction and sampling validity, and lacks inverse design capability.
The development of deep learning pipelines for crystalline materials discovery and inverse design faces three primary challenges: Effective representation learning that facilitates bidirectional mapping between the crystal search space and a unified latent space. The ability to perform approximate structure relaxation through neural networks, thereby enhancing sampling reliability. And integration of a property prediction module and appropriate optimization algorithms for inverse design tasks across diverse dimensionalities. Current models have yet to successfully address these major challenges simultaneously.
In this study, the VQCrystal, an innovative framework for the design of crystalline materials, was developed to address all three primary challenges mentioned above. To the best of our knowledge, VQCrystal is the first deep generative model that employs a hierarchical vector-quantized variational autoencoder (VQ-VAE) architecture to encode the global and atom-level crystal features, which is an established technique for enhanced representation learning in image synthesis19,20, speech analysis21, and molecular modeling22,23. This intuition also aligns with the discrete nature of crystal structures, including finite symmetry operations, 230 distinct space groups24, and defined Wyckoff positions25. Additionally, VQCrystal leverages OpenLAM26, an established machine learning toolkit, for structural relaxation decoupled from the tasks of representation learning. For inverse design, VQCrystal is trained concurrently with an auxiliary task of predicting properties using the discretized global latent variable. During the sampling procedure, a Genetic Algorithm (GA) operating on codebook indices is employed to search for crystals with desired properties.
To benchmark the capabilities of VQCrystal, three open benchmark datasets, MP-2027, Perov-528, and Carbon-2429,30 were tested. Compared its performance against state-of-the-art deep learning models for crystal generation, VQCrystal achieved the highest validity and match rate, with 77.70% match rate, 100% structure validity, 84.58% composition validity, and 91.93% force validity on MP-20, with the best diversity with the Fréchet distance (FD)31 score of 0.152. Subsequent analyses show that the global and local latent space of VQCrystal are highly interpretable. To demonstrate VQCrystal’s applicability to real-world material design across diverse dimensionalities, two specific cases across dimensionalities were explored: 3D crystalline materials and 2D crystalline materials. Fifty-six out of the 20,789 3D crystals generated by VQCrystal trained on the MP-20 database27 were selected after removing duplicates, lanthanides, and a neural-network-based32,33 filtering under the criteria of bandgap (Eg) between 0.5 and 2.5 eV for conventional semiconductors, and formation energy (Ef) below −0.5 eV/atom for chemically stable compounds. DFT validation showed that 62.22% of the bandgaps and 99% of the formation energies matched the target range. Among the 20789 crystals, 437 materials, distinct from the training set, were validated by the dataset as duplicates of entries in the full database, with an average root mean square (RMS) distance of only 0.0509. For 2D materials, VQCrystal was applied to the C2DB database34, generating 12,000 structures. After the similar filtering processes above, 73.91% of the 23 filtered relaxed materials had formation energies below −1 eV/atom, indicating high chemical stability.
Results
VQCrystal model
The VQCrystal shown in Fig. 1 employs a hierarchical vector quantization architecture, which consists of three main components: the encoder, the vector quantization module, and the decoder, followed by auxiliary parts such as the property prediction head. The encoder in Fig. 1a is composed of a hierarchical network that extracts both local and global information from the crystal. The crystal is represented by a tuple consisting of the atomic number of the L atoms, their respective fractional coordinates, and the unit cell basis vectors. The local feature \({\hat{z}}_{l}\) is captured using a Transformer-based structure35, while the global feature \({\hat{z}}_{g}\) is obtained by summing two components: One part is extracted by applying a SE(3)-equivariant periodic graph neural network (GNN)36, CSPNet shown in Fig. 1d, to the input crystal to extract unified features, and the other part is derived by applying a Graph Convolutional Networks (GCN)4 to the local features to extract further information. The CSPNet shown in Fig. 1d updates node features ai, aj and their corresponding edge features rij, eij represents the adjacency matrix. These two components are summed together, followed by a pooling operation to get the final output \({\hat{z}}_{g}\). The use of SE(3)-equivariant graph networks for information extraction allows the model to effectively capture rotational and translational symmetries, making it ideal for handling crystalline structures (Fig. 2).
a Overview of the VQCrystal model. The model is divided into four main parts: local, global, quantization, and output. The local part consists of a simple transformer encoder that extracts local features. The global part captures global features using CSPNet (detailed in (d)) and a GCN block applied to the local features. After pooling, these blocks generate the global feature. The quantization part is elaborated in (b). The output part includes two decoders: the output decoder (detailed in (c)) and the property decoder on the left, which predicts the corresponding property from the extracted features. The red line means the procedure is used in sampling. b Quantization process for global and local features. Both the global and local features are passed through their respective codebooks, where they are quantized by a lookup-based replacement approach. The codebooks map the input features to their closest codebook entries. c The details of the decoder component. The decoder consists of a classic Transformer block, which includes LayerNorm (LN), multi-head attention with query-key-value (QKV) attention mechanism, and a lattice net to predict a lattice of crystals. d The details of the CSPNet component, which includes LayerNorm (LN) and intersection blocks to enhance feature interaction and improve representation learning.
The hierarchical vector quantization (VQ) module introduces discrete latent spaces and leverages a two-tiered approach, incorporating residual quantization (RQ)37 techniques to efficiently compress the latent representations while preserving critical information. The VQ module handles both local and global features, quantizing them into discrete representation space as zl and zg. Stochastic sampling of codes, shared codebooks, and k-means clustering initialization enhance the performance and stability of the VQ module. Figure 1b shows the quantization process for global and local features, with zl;1, zl;2 representing different codebook positions of codebook local. The decoder demonstrated in Fig. 1c reconstructs the original input from the quantized latent representations zl and zg, using a transformer-based structure. Q, K, V, and LN means QKV-attention and layernorm mechanisms originate from the Transformer structure. The lattice parameters are predicted using a multilayer perceptron (MLP) after reconstructing the atoms and fractional coordinates. Additionally, the concatenation of zl and zq is passed through an MLP-based property network to predict materials properties, such as formation energy, bandgap, and so on, to ensure that the latent contains several property information. The detail of the VQCrystal model is shown in the Method section.
The loss function of the VQCrystal model consists of several components, primarily focusing on the reconstruction loss and property regression loss. The reconstruction loss is used to penalize the difference between the reconstructed crystal structures and the original inputs. Both the atom features and fractional coordinates are reconstructed with respect to their respective input features. The final loss is a weighted sum of the property regression loss and reconstruction loss, which is detailed in the Method section.
Despite incorporating Transformer layers, the overall complexity of VQCrystal is dominated by the graph neural networks (GCN and CSPNet) with a time complexity of O(L ⋅ (∣E∣ ⋅ d2 + n ⋅ d2)), where L is the number of layers, ∣E∣ is the number of edges, n is the number of atoms, and d is the dimensionality of the features. For datasets like MP-2027, where n is much smaller than d, the effective complexity is dominated by terms involving d2 rather than the self-attention terms involving n2, allowing VQCrystal to efficiently handle sampling tasks. Full analysis of time complexity is shown in Supplementary Note 1B.
Sampling strategy
The VQCrystal framework employs a sampling pipeline comprising two critical stages: (1) codebook indices search and (2) post-optimization. Within this framework, each crystal structure is uniquely represented by a pair of codebook indices, (Iglobal, Ilocal), corresponding to global and local structural features, respectively. The global index, Iglobal, is defined as an array in \({{\mathbb{R}}}^{{D}_{{\rm{global}}}}\), while the local index, Ilocal, is characterized as an array in \({{\mathbb{R}}}^{N\times {D}_{{\rm{local}}}}\). In this notation, Dglobal and Dlocal represent the number of global and local quantizers, respectively, and N denotes the maximum number of atoms in the crystal structure. The sampling process commences with the random selection of a crystal from the database, whereupon its Ilocal is fixed, leaving Iglobal as the sole variable for optimization. This strategic approach significantly constrains the search space, enhancing computational efficiency. Subsequently, a genetic algorithm (GA) is applied to optimize Iglobal, employing a suite of evolutionary operators including mutation, crossover, and selection. The objective of this optimization is to identify Iglobal values that, when decoded, yield crystal structures with minimal total energy, as estimated by the OpenLAM framework. Subsequently, a post-optimization phase is initiated. This stage utilizes OpenLAM to perform structural relaxation on the selected crystal candidates. The process culminates in the retention of only those structures that satisfy two stringent criteria: an estimated formation energy Eform < 0 and a maximum atomic force fmax < 0.05 eV/Å. The details and ablation of the sampling strategy are described in the Method section and Supplementary Note 2, respectively.
Model performance on quantitative metrics
We evaluate the efficacy of our model on a diverse range of tasks to demonstrate its capability in generating high-quality structures of different crystals. Specifically, we focus on the training reconstruction indicators to evaluate the representation learning task and focus on the validity and diversity of the crystal generation task.
We conduct experiments on three datasets: MP-20, Perov-5, and Carbon-24 following previous works36. The MP-20 dataset selects 45,231 stable inorganic materials from Material Projects27, including experimentally-generated materials with at most 20 atoms in a unit cell. The Perov-5 dataset28 contains 18,928 perovskite materials with similar structures, each having five atoms in a unit cell. The Carbon-24 dataset29,30 includes 10,153 carbon materials, with unit cells containing between 6 and 24 atoms. For all datasets, we follow a 60-20-20 train-validation-test split following previous works36.
We compare our model with two types of baselines. The first type includes deep learning-based crystal generation models: FTCP17, Cond-DFC-VAE38, CDVAE, and our proposed VQCrystal. These models generate new structures based on learned distributions. We also consider the second type, including deep learning-based crystal structure prediction (CSP) models: P-cG-SchNet39 and DiffCSP36. Because CSP models can be adapted to do the crystal generation task by randomly sampling the given crystal composition. This comprehensive comparison highlights the effectiveness of our VQCrystal model in generating high-quality crystal structures.
Following common practice, we evaluate by matching the predicted candidates with the ground-truth structure. The match rate is the proportion of matched structures over the test set. The matching process uses the StructureMatcher class in pymatgen40 with thresholds stol = 0.5 angle_tol = 10, and ltol = 0.3. The RMS is calculated between the ground truth and the best matching candidate, normalized by \(\sqrt[3]{V/N}\), where V is the volume of the lattice, and averaged over the matched structures.
The results in Table 1 underscore the superior performance of our proposed VQCrystal model compared to other deep generative models. For the Perov-5 dataset, VQCrystal achieves a match rate of 95.60%, slightly lower than the best-performing baseline model, FTCP41, at 99.34%, but still a very high value, indicating an almost complete match. The RMS of VQCrystal is 0.0438, which is well below 0.1 Å, indicating that the differences are minimal and can be considered nearly identical in terms of actual crystal structures, despite the slight increase in RMS when compared to FTCP (0.0259). For the Carbon-24 dataset, VQCrystal attains a match rate of 70.03%, surpassing both FTCP’s 62.28% and CDVAE’s 55.22%, with an RMS of 0.2573, indicating comparable performance in terms of structure accuracy. For the MP-20 dataset, VQCrystal achieves a match rate of 77.70%, outperforming both FTCP’s 69.89% and CDVAE’s 45.43%, while the RMS of 0.088, though not as low as CDVAE’s or DiffCSP’s, is still below 0.1 Å–a very low value where the differences can be considered as minor internal variations within the crystal structure. These improvements highlight VQCrystal’s ability to capture the periodicity and discrete characteristics of crystal structures more effectively than other models. This can be explained by its use of discrete VQ to encode crystal structures, which aligns well with the inherent discrete nature of crystal lattices, providing a more accurate and effective representation.
To further evaluate the performance of our VQCrystal model, we conducted experiments on the crystal generation task. This task aims to generate new crystal structures that are valid, diverse, and have high coverage of the target space. We compare our model against several baseline methods using metrics of validity and diversity.
For validity, we consider structural validity, compositional validity, and force validity. The structural validity rate is calculated as the percentage of generated structures with all pairwise distances larger than 0.5 Å. The generated composition is considered valid if the total charge is neutral, as determined by SMACT42. For structure and composition validity, we follow the evaluation criteria established in previous generation works, particularly those outlined in the CDVAE paper18. The specific definitions and internal parameters are referenced from these prior works to ensure consistency. Force validity is evaluated using the OpenLAM model with DeePMD-kit v343 as the DFT estimator. A structure is force valid if the maximum force \({f}_{\max }\) is less than 0.05 eV/Å.
The diversity metric evaluates how well the generated structures explore the space of possible crystal structures beyond those found in the original dataset. We use two metrics for this: average minimum distance (AMD) and Fréchet distance (FD)31. The AMD measures the average minimum distance between any generated structure and the ground-truth structures using CrystalNN structural fingerprints44 as input, defined as,
The FD evaluates the distance between the distributions of generated and ground-truth structures, defined as,
where μg and μt are the means, and Σg and Σt are the covariances of the generated and ground-truth CrystalNN structural fingerprints44, respectively.
The results in Table 2 show that VQCrystal consistently achieves high validity rates across all datasets, with structural, compositional, and force validity metrics being significantly better than most baselines. Specifically, in the Perov-5 dataset, VQCrystal reaches 100.0% in structural validity, 97.48% in compositional validity, and an impressive 99.17% in force validity, outperforming other models by a considerable margin. Because non-diffusion-based models like FTCP have very low structural and compositional validity, they do not calculate force validity. Although diffusion models are theoretically proven as mathematical frameworks for deep potential simulation, they still do not perform as well as our explicit optimization approach, with DiffCSP only achieving 12.26% force validity.
For the other datasets, similar trends are observed. On the MP-20 and Carbon-24 datasets, VQCrystal demonstrates high force validity and other validity metrics, achieving a force validity of 91.93% on the MP-20 dataset and 74.22% on the Carbon-24 dataset, both significantly higher compared to other models.
The diversity metrics, e.g., AMD and FD, further validate the effectiveness of VQCrystal, indicating that it can generate a more diverse set of crystal structures. Since diffusion models are known for their diversity, it is pertinent to compare VQCrystal with diffusion-based methods like CDVAE. For the AMD metric, which measures average maximum deviation and indicates the spread of generated structures, VQCrystal achieves 0.247 on Perov-5, 0.248 on Carbon-24, and 0.160 on MP-20. These values are higher than those achieved by CDVAE, which has an AMD of 0.038 on Perov-5, 0.125 on Carbon-24, and 0.165 on MP-20. Similarly, for the FD metric, which measures feature distance and indicates the distinctiveness of generated structures, VQCrystal attains 0.312 on Perov-5, 0.515 on Carbon-24, and 0.152 on MP-20, compared to CDVAE’s 0.025 on Perov-5, 0.103 on Carbon-24, and 0.132 on MP-20. These results highlight VQCrystal’s superior ability to produce a diverse and distinctive set of crystal structures. Overall, these findings underscore the capability of VQCrystal in generating valid, diverse, and well-covered crystal structures, making it a robust tool for crystal structure prediction and generation tasks.
Interpretability
The sampling methodology of VQCrystal is valid only if certain prerequisites are met. First, the global latent variable must contain rich information about the crystal to ensure meaningful variations. The local latent variables must retain enough information to keep the sampling process controllable and consistent with the original structure. Lastly, the global latent space must be well-structured to help the genetic algorithm identify superior candidates. This section delves into the latent space and sampling process of VQCrystal to validate these prerequisites.
To substantiate the assertion that the global latents encapsulate comprehensive and abstract information, a crystal is randomly selected from the Perov-5 dataset, and its local latents are fixed. Subsequently, 1000 different compositions of global indices are sampled and decoded into 1000 crystal samples in conjunction with the fixed local latents. OpenLAM is utilized to estimate the total energy of these sampled crystals. The 1000 decoded global latents, each of 128 dimensions, are projected onto two dimensions using principal component analysis (PCA)45. The results are depicted in Fig. 3d, where each point corresponds to a global latent, color-coded based on the estimated energy of its respective sample. It is evident that the global latent space is well-organized by total energy, with high-energy regions smoothly transitioning to low-energy regions.
Further analysis aims to demonstrate that the global latent contains space group information. The MP-20 dataset is selected due to its rich diversity in space groups. About 10,000 crystals are chosen, and their global latents are projected onto two dimensions using PCA. The data is then visualized based on their space group information in Fig. 3a. The three most frequently occurring space groups are selected for detailed analysis (space group: P62, Fmmm, \(Pm\overline{3}m\)). A numerical analysis yields a Silhouette score46 of 0.478, with values above 0 generally suggesting that the data points are reasonably well-clustered. In this case, the high Silhouette Score indicates well-defined clusters, supporting that the global latent space captures space group information. This distinction is one aspect of the complex data in the global latent space, with more abstract details yet to be discovered.
To demonstrate that the local latent variables contain sufficient atomic information, the Perov-5 dataset, consisting of perovskite materials with elements at A/B/X positions, was used. To check for element type information, the position needs to be fixed and the B position together with four most common elements found at this position (Ba, Ru, Rb, Y) were selected. PCA was applied to reduce the dimensionality of the local latent to two components. The results were then plotted and shown in Fig. 3b. Additionally, to demonstrate that local latent variables capture positional information, the most frequent elements found at both A and B positions were selected. Due to the constraints of the ABX3 structure, where X is typically a non-metal and A and B are metals, only elements at the A and B positions were visualized. Fixing the element types (Sb as it’s one of the most frequent atoms appearing in AB position) and clustering based on positions. The results in both Fig. 3b, c showed clear clustering of positions and types for these elements, reinforcing that the local latent variables effectively capture both atomic and positional information. The Silhouette Score was calculated to further quantify the clustering quality. The Silhouette Score of 0.2688 and 0.2518 indicates a moderate level of separation between clusters, with values above 0 generally suggesting that the data points are reasonably well-clustered.
The previous parts demonstrated that the global latent space is well-organized by the crystal’s total energy (Fig. 3d), thereby facilitating genetic algorithm searches. This part further validates the functionality of the genetic algorithm by examining each species during the evolutionary iterations. Figure 3f depicts the statistics of the total energy of the crystals across different iterations. These values were collected from a random genetic search process starting with a random initial crystal. Each point in Fig. 3f represents a global latent in this evolutionary race, where the y-axis corresponds to the fitness function value during evolution, which is also the total energy of the decoded crystal as estimated by OpenLAM. A box plot for each race is provided to clearly illustrate the statistical distribution. It is evident that the overall total energy decreases as evolution progresses, with the 75th percentile dropping from approximately −21 to about −36. As the population iterates, the composition and lattice of the crystals gradually improve. Ultimately, the face-centered, body-centered, and specific point positions of the best sample in the final race are well-recognized by the VESTA software47.
Additionally, we projected the global latents onto two dimensions using PCA to visualize the evolutionary trends of the population. For clarity, Fig. 3e only visualizes the initial and final generations. The black border represents the convex hull for the points of each generation, calculated using the scikit-learn package. It is clearly seen that the samples in a race gather and converge as evolution progresses. Combined with the aforementioned conclusions, this indicates that the genetic algorithm effectively captures the organized properties of the global latent space and gradually optimizes the species by simulating the evolutionary process.
Reliable crystal generation cases of 3D materials
For the purpose of demonstrating the model’s capacity to generalize and reliably explore the search space of crystal structures, VQCrystal generates a large number of crystal structures, totaling 20,789 crystals trained on the MP-20 dataset. These crystals were first checked for duplicates within the training set. The “StructureMatcher” class from the pymatgen library40 was used to compare crystal structures and remove duplicates. After this process, 20,183 unique materials remained. These 20,183 materials were then compared against the complete MP database as of June 1, 2018, with 132082 materials to check for duplicates with known structures in the dataset, excluding the training set. Among 2.16% were found to be duplicates of structures in the MP database, corresponding to 437 materials. Supplementary information records the chemical formulas of these crystals and visualizes some representatives. Further analysis was performed by calculating RMS distances between the generated duplicates and their corresponding structures in the database. The average RMS distance for these duplicates was found to be 0.0509, with the smallest RMS distance reaching as low as 0.0001.
These results indicate that the duplicated structures are nearly identical to those in the database, validating the stability of the generated crystals. The close structural similarity to stable crystals in the MP database demonstrates that the generated materials are highly reliable and consistent with known stable structures.
To further demonstrate the reliability and practical applicability of the model, VQCrystal is applied to specific design cases. Figure 4a illustrates the workflow for inversely designing of materials based on target properties. We selected materials with a bandgap (Eg) between 0.5 and 2.5 eV, which is a desirable range for photovoltaic applications, and a formation energy (Ef) less than −0.5 eV/atom to ensure chemical stability. We used models trained on the MP database to generate these materials. Firstly, the 20,789 crystals generated by VQCrystal trained on the MP-20 data are screened to remove duplicates based on the complete Materials Project database as of June 23, 202327, leaving 19,776 unique structures. Following this, the structures are validated for compositional correctness using the SMACT library42, which checks for valid elemental combinations and charge neutrality. The validation process includes ensuring the elements’ oxidation states and electronegativity are appropriate for forming stable compounds. This screening results in a 67.21% pass rate, reducing the number of valid crystal structures to 13,292. Following this, the structures’ forces and energies are calculated using OpenLAM. Structures with an energy less than 0 and a maximum force (\({f}_{\max }\)) less than 0.05 eV/Å are considered stable. This step has a pass rate of 92.4%, resulting in 12,282 stable structures. Subsequently, structures with an excessive number of atoms, too many different types of elements, or containing lanthanide series elements are removed, leaving 2771 materials.
Then, we employed the MEGNet model32 and the ALIGNN model33, both of which are graph neural networks, to screen the target properties. The MEGNet model was trained on the MP database as of June 1, 2018, achieving a mean absolute error (MAE) of 0.028 eV/atom for formation energy and a test MAE of 0.33 eV for PBE bandgap. The ALIGNN model was trained on the JARVIS DFT dataset, with an MAE of 0.14 eV for the OPT bandgap and 0.033 eV/atom for formation energy. For the 2,771 materials, we predicted the bandgap and formation energy using both the MEGNet and ALIGNN regression models. Additionally, we used the MEGNet bandgap classifier to predict whether the bandgap is greater than 0 eV. We filtered the materials where the classifier predicted a bandgap greater than 0 eV and where all predicted properties fell within the specified ranges (bandgap between 0.5 and 2.5 eV, formation energy less than −0.5 eV/atom). This screening resulted in 92 materials. Figure 4b, c show the distributions of predicted formation energy and bandgap for the 12,282 materials before the removal of excessive elements, predicted using the MEGNet model. 90 out of 92 materials successfully passed the DFT relaxation process using the Vienna ab initio simulation package (VASP)48.
Next, we calculated the bandgap and formation energy of these 90 materials using first-principles calculations to validate the predictions Supplementary Note 5.
The calculated bandgaps and formation energies were then compared with the target of bandgap (Eg) between 0.5 and 2.5 eV, and formation energy (Ef) less than −0.5 eV/atom. The results showed strong agreement in terms of formation energy, with 89 out of 90 materials having a formation energy lower than −0.5 eV/atom, indicating an almost 100% hit rate for stability prediction, which strongly suggests the stability of the predicted crystals. Regarding the bandgap, 56 out of the 90 materials had a bandgap within the target range of 0.5 to 2.5 eV. Figure 4d, e shows the distribution of the designed 90 materials, while the red points indicate materials which hit the target of both Ef and Eg. The band structures are shown in supplementary materials. These results further confirmed the reliability of the VQCrystal model in predicting material properties, particularly for formation energy, and demonstrated the effectiveness of using machine learning models like MEGNet and ALIGNN for large-scale material discovery. Details of the generated materials are shown in Supplementary Note 6.
Generation cases of 2D materials
Two-dimensional (2D) materials have gained significant attention due to their unique physical and chemical properties, which offer promising applications in areas such as energy, electronics, and catalysis. Compared to 3D materials, 2D materials feature an ultra-thin structure and high surface area, allowing for exceptional electrical, optical, and mechanical behaviors49. Building upon the significance of 2D materials, we applied VQCrystal to generate new structures from a comprehensive 2D materials database called C2DB34,50. Specifically, we trained a VQCrystal model using the C2DB database, which contains a total of 3521 2D materials. The VQCrystal model was trained with a 60-20-20 train-validation-test split. On the validation set, the model achieved a match rate of 88.56%.
Afterward, we generated nearly 12,000 candidate materials, which were then filtered using the atomic simulation recipes (ASE)51 to determine whether they were truly two-dimensional. This process left us with 3521 materials. Subsequently, we removed duplicates by comparing the generated materials with the C2DB database, utilizing the “StructureMatcher” class from the pymatgen library with the parameters ltol = 0.3, stol = 0.5, and angletol = 10. After this deduplication step, 2638 candidate materials remained. Following the deduplication, we applied similar filtering steps as previously described, ensuring that the materials met criteria for elemental composition, structural validity, and reasonable force values. In addition, lanthanides, actinides, and structures containing an excessive number of different elements were removed. After this filtering process, 846 candidate materials remained. To assess the stability of these materials, MEGNet and ALIGNN models were used to predict the formation energy of the 846 materials, following the same procedure as in the inverse design of the MP-20 datasets. Materials with a predicted formation energy less than −0.5 eV/atom in both models were selected, resulting in 184 materials. A random selection of 26 materials from the filtered set underwent DFT relaxation, with 23 successfully passing the process. Further calculation of their formation energy. Out of the 23 materials, 19 exhibited a formation energy lower than -0.5 eV/atom, with 17 of them, representing 73.91%, having a formation energy lower than −1 eV/atom. This indicates a good level of stability for the generated two-dimensional materials. Figure 5 presents a selection of the generated two-dimensional materials, illustrating both their formation energy and total energy. These visual representations emphasize the effectiveness of the VQCrystal model in generating stable 2D materials, further supported by the energy analysis. Further information about the generated materials is shown in Supplementary Note 7.
Discussions
In this study, we introduce VQCrystal, an innovative pipeline for crystalline materials discovery that integrates a hierarchical VQ-VAE representation learning module, the open-source machine learning-based structural relaxation method OpenLAM, and a genetic algorithm. The effectiveness of incorporating discreteness in representation learning is demonstrated through benchmark performance on diverse datasets. Furthermore, metric analysis of the sampled novel crystals reveals that the VQCrystal pipeline successfully discovers both valid and diverse novel crystalline materials. Interpretation of the results indicates that VQCrystal has developed a highly interpretable latent space at both global and atomic levels. For inverse design tasks, we employed a genetic algorithm to search for stable candidates, followed by a series of filtering processes. In the case of 3D crystals, DFT validation confirmed that 62.22% of bandgaps and 99% of formation energies of the 56 filtered materials matched the target ranges of bandgap between 0.5 and 2.5 eV and formation energy below −0.5 eV/atom. For 2D crystals, DFT validation revealed that 73.91% of 23 filtered structures exhibited high stability, with formation energies below −1 eV/atom. Future work should focus on extending the VQCrystal pipeline to address crystal structure prediction (CSP) tasks, enabling the prediction of lattice parameters and atomic positions for specific chemical compositions. This extension would broaden the potential applications of VQCrystal, transforming it into a more fine-grained conditional crystal generation pipeline.
Methods
VQCrystal encoder
The hierarchical encoder of the VQCrystal model consists of two parts: the local feature encoder and the global feature encoder. The local features are extracted using a series of transformer layers, while the global features are obtained through a combination of graph convolution-based GCN layers and CSPNet convolution layers. The input to the encoder is a tensor F of shape (B, L, C) containing atom features and fractional coordinates, where C represents Catom + Ccoords, and a tensor lattice of shape (B, D) containing lattice parameters, where D = 6. The lattice tensor is expanded on the first dimension as B, L, D to fit the dimension with tensor F. These inputs are concatenated along the last dimension to form the input feature tensor Finput, whose shape is (B, L, C + D).
This concatenation results in a tensor of shape (B, L, Cinput), where Cinput = C + D. The combined features are then passed through multiple layers of transformer encoders35. Each transformer layer consists of a self-attention mechanism, expressed as,
where Q, K, V are the query, key, and value matrices, respectively, derived from the input feature tensor. After passing through multiple transformer layers, the outputs are summed to produce the local feature \({\hat{z}}_{l}\) having a shape of (B, Clatent).
To obtain the global feature \({\hat{z}}_{g}\), two graph models, GCN and CSPNet are applied on different inputs denoted as Finput and \({\hat{z}}_{l}\),
The local feature \({\hat{z}}_{l}\) is first passed through a GCN originated from CGCNN4. The updating of nodes and pooling in the GCN can be summarized as follows,
where li represents the output features of the i-th layer, li−1 represents the input features from the (i−1)th layer (with \({l}_{1}={\hat{z}}_{l}\)), \({l}_{i-1}^{{\prime} }\) represents the features from the graph transformer, j denotes the neighboring nodes, and fnbr represents the features of the neighboring nodes. k represents the number of atom nodes to pooling, W and \(W{\prime}\) are the weight matrices of the fully connected layers. σ and ReLU are the sigmoid and ReLU activation functions, respectively.
Note that the proposed graph transformer model is not the transformer block used to extract local features. It’s a part inside the GCN model to assist node updates. The proposed graph transformer model integrates the strengths of graph neural networks (GNNs) and transformer architectures to process graph-structured data effectively. The model comprises of graph attention mechanisms and transformer layers. The graph attention mechanism computes attention scores for each node pair using the formula \({\bf{S}}=\frac{{\bf{Q}}{{\bf{K}}}^{\top }}{\sqrt{{d}_{{\rm{model}}}}}\), where Q and K are the query and key matrices. These scores are then masked by the adjacency matrix A, S = S ⊙ A, and normalized using the softmax function \({{\bf{A}}}_{{\rm{attn}}}={\rm{softmax}}({\bf{S}})\). The output is computed as O = AattnV, where V is the value matrix. Each Graph Transformer Layer applies this attention mechanism, followed by a feedforward network with residual connections and layer normalization. The transformer layers consist of multi-head self-attention and feedforward networks to capture global dependencies. This layered architecture allows the model to learn both local graph structures and global sequence patterns.
To further enrich the feature representation, we apply CSPNet originated from DiffCSP36, directly to the input Finput. CSPNet inherently encodes periodicity, facilitating the modeling of the crystal structure. The key innovation is the incorporation of periodic E(3) invariance, which combines E(3) invariance (including translation, rotation, and reflection symmetries) with the periodicity inherent in crystal structures. This ensures that any transformation of the crystal coordinates does not alter the physical laws, thereby maintaining the crystal symmetrical restrictions.
Finally, the combination of GCN and CSPNet results in a comprehensive final global feature,
Hierarchical vector quantization
The hierarchical vector quantization (VQ) module of the VQCrystal model leverages a two-tiered approach, incorporating residual quantization (RQ) techniques to efficiently compress the latent representations while preserving critical information. This section details the VQ mechanism based on previous works2,37.
The VQ module is designed to handle two types of features, i.e., the local feature \({\hat{z}}_{l}\) of shape (B, L, Clatent) and the global feature \({\hat{z}}_{g}\) of shape (B, Clatent). The local feature \({\hat{z}}_{l}\) is a high-dimensional representation capturing fine-grained details, while the global feature \({\hat{z}}_{g}\) encapsulates broader contextual information.
Then, the local feature and global feature is quantized using the residual VQ scheme,
where RQ(z; C, D) represents the RQ of vector z using codebook size C and depth D37. Here, kd is the code index at depth d, Q(rd−1; C) is the quantization function that maps the residual rd−1 to the nearest code in the codebook C, rd is the residual vector at depth d, and e(kd) is the code embedding corresponding to the code index kd.
In addition, we define \({z}^{(d)}=\mathop{\sum }\nolimits_{i = 1}^{d}e({k}_{i})\) as the partial sum of up to d code embeddings, and zq = z(D) is the quantized vector of z. \({z}_{l}=\mathop{\sum }\nolimits_{i = 1}^{d}e({k}_{i}^{l})\) and \({z}_{g}=\mathop{\sum }\nolimits_{i = 1}^{d}e({k}_{i}^{g})\) is the final output of local and global features. The recursive quantization of RQ approximates the vector z in a coarse-to-fine manner. Note that z(1) is the closest code embedding e(k1) in the codebook to z. Then, the remaining codes are subsequently chosen to reduce the quantization error at each depth. Hence, the partial sum up to z(d) provides a finer approximation as d increases.
To enhance the performance and stability of the VQ module, several techniques are employed. Stochastic sampling of codes is used during quantization, where codes are stochastically sampled using a temperature parameter. A single shared codebook is utilized for all quantizers, simplifying the model and making the codebook size determination easier. The codebooks are initialized using k-means clustering to ensure that the initial code embeddings are well-distributed across the latent space.
Decoder and property prediction head
The decoder module of the VQCrystal model is designed to reconstruct the original input features from the quantized latent representations. The decoder architecture consists of several parts, each tailored to decode different aspects of the latent features, ensuring that both local and global information is accurately recovered.
The primary decoder is responsible for reconstructing the node features and positional information from the combined quantized local and global latent vectors. The input to the decoder is a combination of the quantized local feature zl and the upsampled global feature zg. This combined latent representation is then passed through multiple layers of linear transformations and transformer encoder layers to produce the final reconstructed output. The reconstruction process begins with upsampling the global feature zg to match the spatial dimensions of the local feature zl,
The combined latent representation zcombined of shape (B, L, Clatent) is processed through a series of Transformer Encoder layers. Each Transformer layer consists of multi-head self-attention and a feedforward neural network. The output of the transformer encoder, denoted as xrecon, has the shape (B, L, Catom + Ccoords), where Catom represents the reconstructed atomic features and Ccoords represents the reconstructed fractional coordinates.
Additionally, specialized decoders are used for reconstructing the lattice parameters and properties such as formation energy. The lattice decoder operates on intermediate reconstructions xrecon of atom features and fractional coordinates from earlier steps, using dedicated linear and Transformer layers to accurately match the target lattice parameters. The lattice decoder’s operation can be expressed as,
where \(\hat{L}\) of shape (B, Clattice) represents the reconstructed lattice parameters.
In contrast, the property decoder predicts properties directly based on the combined quantized local and global latent vectors zl and zg, without relying on intermediate reconstructions. The property prediction head is designed to predict specific properties, such as formation energy, using these quantized representations. The input to the property prediction head is the concatenated quantized local feature zl and global feature zg denoted as zcombined.
This combined latent representation is passed through a series of linear transformations and activation functions, together with a transformer, to extract the necessary information to predict the desired properties,
where \(\hat{P}\) represents the predicted properties, and fproperty denotes the function comprising the prediction head’s transformations and activations.
This approach leverages the flexibility of the VQCrystal model’s hierarchical decoding strategy to effectively process and predict various aspects of the input data. The design for the property prediction head effectively integrates and processes both local and global information, enhancing the model’s ability to forecast properties like formation energy, making VQCrystal a powerful tool for various applications in materials science and beyond.
Loss function
The loss function of the VQCrystal model consists of two main components: the reconstruction loss and the property regression loss. The total loss is a weighted combination of these components. The reconstruction loss measures the difference between the input and the decoded output for atom features, fractional coordinates, and lattice parameters. It is computed as the sum of three individual losses: atom features \({{\mathcal{L}}}_{{\rm{atom}}}\) (The loss is computed using a cross-entropy classification loss), fractional coordinates \({{\mathcal{L}}}_{{\rm{coords}}}\) (The loss is computed using mean squared error (MSE) loss on the positions), and lattice parameters \({{\mathcal{L}}}_{{\rm{lattice}}}\) (The loss is computed using MSE loss on the lattice parameters). Formally, the reconstruction loss can be written as:
where:
Here, xatom, xcoords, xlattice are the input atom features, fractional coordinates, and lattice parameters, respectively, while \({\hat{x}}_{{\rm{atom}}},{\hat{x}}_{{\rm{coords}}},{\hat{x}}_{{\rm{lattice}}}\) are their corresponding reconstructed outputs. The property regression loss is used to measure the difference between the predicted properties and the ground-truth properties, such as formation energy. This is computed using MSE loss:
where \(\hat{P}\) is the predicted property (e.g., formation energy) and Ptarget is the corresponding target property. The total loss is a weighted combination of the reconstruction loss and the property regression loss:
where λproperty is a hyperparameter that controls the relative weight of the property regression loss in the total loss. The codebook in the VQ module is updated using exponential moving average (EMA) rather than traditional methods. This allows for smoother updates and avoids the commitment loss that is common in traditional vector quantization methods. Therefore, the commitment loss term is not included in the total loss, making it:
Thus, the total loss function is optimized by minimizing the reconstruction loss and property regression loss, while the codebook update is performed via EMA without any commitment loss.
Overview of sampling pipeline
VQCrystal is a vector-quantized autoencoder designed to map the distribution of natural crystals to a fixed-size discrete latent space. Consequently, sampling with VQCrystal involves selecting a typical combination of codebook indices that can be decoded into stable crystals. These indices can be represented as a pair (Iglobal, Ilocal), corresponding to the codebook indices of global and local features, respectively. Iglobal is an array in \({{\mathbb{R}}}^{{D}_{{\rm{global}}}}\), with all elements selected from {1, 2, …, Vglobal}. Conversely, Ilocal is an array in \({{\mathbb{R}}}^{N\times {D}_{{\rm{local}}}}\), with all elements selected from {1, 2, …, Vlocal}. Here, Dglobal, Dlocal, Vglobal, Vlocal, and N denote the number of global or local quantizers, the size of the global or local codebook, and the maximum number of atoms in the crystal, respectively.
The challenge in sampling arises because not all regions of the latent space map to reliable samples. Therefore, developing strategies to search for reliable regions of the latent space and optimizing the sampled crystals is crucial. In our work, a genetic algorithm is adapted to selectively sample from the latent space, and we utilize OpenLAM to further optimize the generated crystals.
Additionally, VQCrystal employs a data-based sampling strategy where Ilocal is fixed to the Ilocal of a selected base crystal from the database, with Iglobal being the only variable sampled. This approach effectively reduces the potential search space from \({V}_{{\rm{local}}}^{N\times {D}_{{\rm{local}}}}\times {V}_{{\rm{global}}}^{{D}_{{\rm{global}}}}\) to \({V}_{{\rm{global}}}^{{D}_{{\rm{global}}}}\), thereby shortening the expected sampling time and increasing the success rate. Sampling only Iglobal is sufficient to generate diverse variants of the base crystal because the auxiliary tasks designed for the global latent space during training, such as crystal reconstruction and property prediction, ensure that the global latent space encodes rich and comprehensive features.
Searching strategy
Genetic algorithms (GAs) are a class of adaptive, heuristic search and optimization techniques inspired by the principles of natural selection and genetic evolution. In the context of problem-solving, a GA operates on a population of potential solutions, each represented as a string of symbols or a genome. These solutions are evaluated using a fitness function. The algorithm iteratively applies a set of genetic operators, i.e., selection, crossover, and mutation, to evolve the population toward better solutions over successive generations.
In our study, we utilize OpenLAM to estimate a solution’s formation energy, which serves as the fitness metric. The goal of the GA is to identify solutions with low formation energy. Initially, 64 solutions are randomly sampled to form the initial population, and the number of iterations is set to 10. During each iteration, all 64 solutions in the population are evaluated using the fitness function. The top 12 solutions, based on fitness, are selected as parents to generate 63 new solutions. This generation process employs a uniform crossover strategy at each dimension with a probability of 0.5, and a random mutation with a probability of 0.4. Meanwhile, the best solution from the original population is preserved for the next generation. Unlike standard GAs, which aim to find the single best solution, our approach retains all generated crystals with negative formation energy as successful samples.
Post-optimizing strategy
Although genetic algorithms (GAs) can already sample potentially stable crystals, a post-optimization procedure is introduced for the following reasons:
-
Additional constraints: Beyond having a negative formation energy, a stable crystal must also satisfy other constraints, such as exhibiting low forces.
-
Estimation errors: The formation energy estimated by neural networks contains inherent errors, as these neural networks approximate density-functional theory (DFT) results. Consequently, the outcomes of GAs need further optimization to ensure accuracy.
-
Structural refinement: Most crystals sampled by GAs can achieve greater stability with minor modifications to their unit cell structures.
We employed OpenLAM as our post-optimization method. In our experimental setup, each generated crystal undergoes optimization by OpenLAM for a maximum of 100 steps, with a force convergence criterion set at 0.04 eV/Å. Crystals that converge in both energy and force are deemed successfully optimized samples.
Data availability
The Perov-5, Carbon-24, and MP-20 datasets are queried from cdvae at https://github.com/txie-93/cdvae. The Materials Project dataset is queried from its website in June, 2023. (Note a query with the same criteria now would yield a different number of crystals from the recorded number in the study due to the updates and the addition of crystals of the Materials Project.). The C2DB50 database is required from the database of jarvis-tools52.
Code availability
The source code of VQCrystal is now avaliable at https://github.com/Fatemoisted/VQCrystal, including training/inference code, pre-trained models, reproducibility checkpoints, and the license file.
References
Pearson, K. Liii. on lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 2, 559–572 (1901).
Kajita, S., Ohba, N., Jinnouchi, R. & Asahi, R. A universal 3d voxel descriptor for solid-state material informatics with deep convolutional neural networks. Sci. Rep. 7, 16991 (2017).
Korolev, V., Mitrofanov, A., Eliseev, A. & Tkachenko, V. Machine-learning-assisted search for functional materials over extended chemical space. Mater. Horiz. 7, 2710–2718 (2020).
Xie, T. & Grossman, J. C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120, 145301 (2018).
Pyzer-Knapp, E. O., Suh, C., Gómez-Bombarelli, R., Aguilera-Iparraguirre, J. & Aspuru-Guzik, Alán What is high-throughput virtual screening? a perspective from organic materials discovery. Annu. Rev. Mater. Res. 45, 195–216 (2015).
Kohn, W. & Sham, Lu. Jeu Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133 (1965).
Jain, A. et al. Commentary: the materials project: a materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
Kirklin, S. The open quantum materials database (oqmd):assessing the accuracy of dft formation energies. npj Comput. Mater. 1, 15010 (2015).
Long, T. et al. Constrained crystals deep convolutional generative adversarial network for the inverse design of crystal structures. npj Comput. Mater. 7, 66 (2021).
Zhao, Y. et al. High-throughput discovery of novel cubic crystal materials using deep generative neural networks. Adv. Sci. 8, 2100566 (2021).
Zhao, Y. et al. Physics guided deep learning for generative design of crystal materials with symmetry constraints. npj Comput. Mater. 9, 38 (2023).
Li, Z. & Birbilis, N. Nsgan: a non-dominant sorting optimisation-based generative adversarial design framework for alloy discovery. npj Comput. Mater. 10, 112 (2024).
Goodfellow, I. et al. Generative adversarial networks. Commun. ACM 63, 139–144 (2020).
Kingma, D. P. & Welling, M. Auto-encoding variational bayes. Ppreprint at arXiv:1312.6114 (2013).
Ye, Cai-Yuan, Weng, Hong-Ming & Wu, Quan-Sheng Con-cdvae: a method for the conditional generation of crystal structures. Comput. Mater. Today 1, 100003 (2024).
Ho, J., Jain, A. & Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 33, 6840–6851 (2020).
Z, Ren. et al. An invertible crystallographic representation for general inverse design of inorganic crystals with targeted properties. Matter 5, 314–335 (2022).
Xie, T., Fu, X., Ganea, O.-E. & Barzilay, R & Jaakkola, T. Crystal diffusion variational autoencoder for periodic material generation. In International Conference on Learning Representations (ICLR) (2022).
van den, Oord, A., Vinyals, O. & Kavukcuoglu, K. Neural discrete representation learning. In Proc. 31st International Conference on Neural Information Processing Systems 6309–6318 (Curran Associates Inc., 2017).
Razavi, A., van den Oord, A. & Vinyals, O. Generating diverse high-fidelity images with VQ-VAE-2. In Proc. 33rd International Conference on Neural Information Processing Systems (Curran Associates Inc., 2019).
Cristina, G. et al. Low bit-rate speech coding with VQ-VAE and a WaveNet decoder. In ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) pages 735–739 (IEEE, 2019).
Wu, F. & Li, S. Z. Surface-VQMAE: vector-quantized masked auto-encoders on molecular surfaces. In Proc. 41st International Conference on Machine Learning 53619–53634 (JMLR.org, 2024).
Tomas H. et al. Simulating 500 million years of evolution with a language model. Science 387, 850–858 (2025).
Wondratschek, H. & Muller, U. International tables for crystallography, symmetry relations between space groups. Int. Tables Crystallogr. 5, 732–740 (2004).
Hahn, T. International Tables for Crystallography, Volume A: Space Group Symmetry (International Union of Crystallo, 1987).
deepmodeling. Openlam. https://github.com/deepmodeling/openlam (2024).
Jain, A. et al. The materials project: a materials genome approach to accelerating materials innovation. APL Mater 1, 011002 (2013).
Castelli, I. E. et al. New cubic perovskites for one-and two-photon water splitting using the computational materials repository. Energy Environ. Sci. 5, 9034–9043 (2012).
Pickard, C. J. & Needs, R. J. Ab initio random structure searching. J. Phys. Condens. Matter 23, 053201 (2011).
Pickard, C. J. & Needs, R. J. High-pressure phases of silane. Phys. Rev. Lett. 97, 045504 (2006).
Eiter, T. & Mannila, H. Computing discrete Fréchet distance (1994).
Chen, C., Ye, W., Zuo, Y., Zheng, C. & Ong, ShyuePing Graph networks as a universal machine learning framework for molecules and crystals. Chem. Mater. 31, 3564–3572 (2019).
Choudhary, K. & DeCost, B. Atomistic line graph neural network for improved materials property predictions. npj Comput. Mater. 7, 185 (2021).
Haastrup, S. et al. The computational 2d materials database: high-throughput modeling and discovery of atomically thin crystals. 2D Mater. 5, 042002 (2018).
Vaswani, A. et al. Attention is all you need. In Proc. 31st International Conference on Neural Information Processing Systems 6000–6010 (Curran Associates Inc., 2017).
Jiao, R. et al. Crystal structure prediction by joint equivariant diffusion. Adv. Neural Inform. Process. Syst. 36, (2024).
Lee, D., Kim, C., Kim, S., Cho, M. & Han, W.-S. Autoregressive image generation using residual quantization. In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition 11523–11532 (IEEE, 2022).
Court, C. J., Yildirim, B., Jain, A. & Cole, J. M. 3-d inorganic crystal structure generation and property prediction via representation learning. J. Chem. Inf. Model. 60, 4518–4535 (2020).
Gebauer, NiklasW. A., Gastegger, M., Hessmann, StefaanS. P., Müller, Klaus-Robert & Schütt, K. T. Inverse design of 3d molecular structures with conditional generative neural networks. Nat. Commun. 13, 973 (2022).
Ong, ShyuePing. et al. Python materials genomics (pymatgen): a robust, open-source python library for materials analysis. Comput. Mater. Sci. 68, 314–319 (2013).
Ren, Z. et al. An invertible crystallographic representation for general inverse design of inorganic crystals with targeted properties. Matter 5, 314–335 (2022).
Davies, D. W. et al. Smact: semiconducting materials by analogy and chemical theory. J. Open Source Softw. 4, 1361 (2019).
Zeng, J. et al. Deepmd-kit v2: a software package for deep potential models. J. Chem. Phys. 159, 054801 (2023).
Zimmermann, NilsE. R. & Jain, A. Local structure order parameters and site fingerprints for quantification of coordination environment and crystal structure similarity. RSC Adv. 10, 6063–6081 (2020).
Abdi, Hervé & Williams, L. J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2, 433–459 (2010).
Shahapure, K. R. & Nicholas, C. Cluster quality analysis using silhouette score. In 2020 IEEE 7th International Conference on Data Science and Advanced Analytics (DSAA) 747–748 (IEEE, 2020).
Momma, K. & Izumi, F. Vesta: a three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 41, 653–658 (2008).
A, G. K. & b, J. Furthmüller Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set - sciencedirect. Comput. Mater. Sci. 6, 15–50 (1996).
Zhang, H. Introduction: 2D materials chemistry. Chem. Rev. 118, 6089–6090 (2018).
Gjerding, MortenNiklas. et al. Recent progress of the computational 2d materials database (c2db). 2D Mater. 8, 044002 (2021).
Gjerding, M. et al. Atomic simulation recipes: a python framework and library for automated workflows. Comput. Mater. Sci. 199, 110731 (2021).
Choudhary, K. et al. The joint automated repository for various integrated simulations (jarvis) for data-driven materials design. npj comput. Mater. 6, 173 (2020).
Acknowledgements
This work is supported by the National Key R&D Program of China (2023YFA1608501), Shanghai Municipal Natural Science Foundation under Grant No. 24ZR1406600.
Author information
Authors and Affiliations
Contributions
H.Z. conceived the project and contributed to securing funding. H.Z. and Y.C. supervised the research. Z.Q. and L.J. developed and trained the neural networks and analyzed the results. H.C. calculated the theoretical properties of the generated materials. Z.Q. and L.J. wrote the original manuscript. D.M. and Z.D. contribute to the figures. S.S. and Y.M. contributed to the discussion of results and manuscript preparation.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Qiu, Z., Jin, L., Du, Z. et al. Massive discovery of crystal structures across dimensionalities by leveraging vector quantization. npj Comput Mater 11, 184 (2025). https://doi.org/10.1038/s41524-025-01613-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-025-01613-6