Introduction

A fundamental question that puzzles us today is the nature of the hypothetical dark matter (DM) that makes up a large portion of the entire Universe’s energy density, as inferred from multiple astrophysical and cosmological observations and simulations1,2,3. Due to its weak interaction with ordinary matter, DM is extremely challenging to search for. Moreover, as the frequency of DM is unknown, a search requires a scan over a huge frequency range from terahertz to hertz, involving different systems ranging from opto-mechanical4,5,6,7,8,9,10,11,12 and microwave13,14,15,16,17, which can easily take hundred of years with the state-of-the-art technology17,18. As much attention has been on utilizing quantum metrology, empowered by quantum resources such as squeezing14,15,17 and entanglement19, to boost the DM search, it is crucial to understand the ultimate precision limits of DM search allowed by quantum physics.

Axion dark matter search relies on microwave haloscopes—microwave cavities in presence of magnetic field13,14,15,16,17 that allows axion particles to convert to microwave photons. Such a search process can be modeled as a quantum sensing problem over a covariant bosonic quantum channel20,21, whose additive noise level reveals the existence of DM. The ultimate precision limit of DM search can therefore be understood from the ultimate precision limit of additive noise sensing. However, while the ultimate limits of phase sensing22, displacement sensing23,24, loss sensing25,26 and amplifier gain sensing27 have been explored, little is known about the limit of noise sensing28 in bosonic quantum channels when there is energy constraint.

In this paper, we derive the ultimate precision limit of energy-constrained26,27 noise sensing in covariant bosonic quantum channels, and therefore reveal the DM search performance limit allowed by quantum physics. Via quantum Fisher information (QFI) calculations, we show that entangled source in the form of two-mode squeezed vacuum (TMSV) is optimal for noise sensing in the parameter region of interest. On the other hand, (single-mode) squeezed vacuum source is only optimal in the lossless case, and even underperforms the vacuum limit when loss is large.

Next, we consider measurement protocols. Although it has been shown14,15,17 that squeezed vacuum input improves the performance of homodyne measurement, our analyses show that protocols with homodyne detection are sub-optimal in general. Instead, a “nulling” measurement strategy based on squeezing and photon counting is optimal and beats the homodyne detection by orders of magnitude. For vacuum input, the nulling strategy simplifies to direct photon counting. In particular, when implemented ideally in the lossless case, it takes 15dB of squeezing for a homodyne-based strategy to overcome the (photon counting) vacuum limit.

Finally, we interpret our results in DM search in the setting of microwave haloscopes. We show that the total Fisher information is proportional to the previously well-accepted figure of merit—the scan rate (information acquisition rate across all frequencies15,17,19) in homodyne detection. Then, we recover squeezing’s advantage over vacuum homodyne. However, we show that these strategies are below the vacuum-limit scan-rate (vacuum + photon counting), in the practical range of squeezing (<20 dB). In contrast, an entanglement-assisted strategy based on TMSV enables optimal advantage over the vacuum limit at an arbitrary squeezing level, achievable with our nulling receiver based on photon counting. This provides a guideline for the next-generation haloscopes—developing good microwave photon counting measurement is of high priority; while more exotic quantum sources such as Gottesman–Kitaev–Preskill state29 are not necessary since a simple TMSV state is optimal. Our results can also apply to a sensor-network19,30, all quantum advantages hold with an additional scaling advantage due to coherent signal processing.

Results

DM search as additive noise sensing

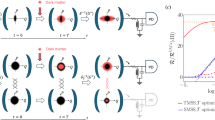
We consider dark matter search for the axion DM model (see Fig. 1), while we note that our results may also apply to other DM hypotheses. In a search for axion dark matter, an important experimental set-up involves a cavity in presence of electric and magnetic field (microwave haloscopes), where axion DM can couple to cavity modes. Due to the large number density, axion DM is assumed to behave as classical waves19—the mean field at position \(\overrightarrow{x}\) has the form:

$$\langle a\rangle ({m}_{{{{\rm{a}}}}},\overrightarrow{{k}_{0}},t)\propto \cos \left({\omega }_{0}t+\overrightarrow{{k}_{0}}\cdot \overrightarrow{x}+{\phi }_{{{{\rm{a}}}}}\right)\,,$$
(1)

where the center frequency ω0 is determined by the axion DM mass ma, \(\overrightarrow{{k}_{0}}\) is the wave factor and ϕa is a phase factor. As the potential DM induced cavity signal is weak, to determine the presence or absence of DM, one considers a long observation time, during which ϕa is completely random in [0, 2π). Due to the randomness of the axion field, the input-output relation of the cavity at each frequency ω can be effectively modeled as:

$${\hat{a}}_{{{{\rm{out}}}}}={\chi }_{mm}{\hat{a}}_{{{{\rm{in}}}}}+{\chi }_{ma}{\mu }_{{{{\rm{a}}}}}+\sqrt{1-{\chi }_{mm}^{2}}{\hat{a}}_{{{{\rm{B}}}}},$$
(2)

where

$${\chi }_{mm}^{2}(\omega )\simeq \frac{{({\gamma }_{m}-{\gamma }_{\ell })}^{2}/4+{\omega }^{2}}{{({\gamma }_{m}+{\gamma }_{\ell })}^{2}/4+{\omega }^{2}},$$
(3)
$${\chi }_{ma}^{2}(\omega )\simeq \frac{{\gamma }_{m}{\gamma }_{a}}{{({\gamma }_{m}+{\gamma }_{\ell })}^{2}/4+{\omega }^{2}},$$
(4)

are the susceptibilities determined by the cavity coupling rates (γm, γℓ and γa for measurement port, loss and axion), \({\hat{a}}_{{{{\rm{B}}}}}\) describes the thermal background with mean photon number determined by the cavity temperature. In general, γa ≪ γm, γℓ. For simplicity, we have omitted the noise independent phase factors, as it does not affect our analyses. Most importantly, the DM induced signal contributes to the additive noise—μa is a complex Gaussian random number with variance equaling na, the number of axion particles in the cavity. The search for DM is therefore a parameter estimation task of the additional additive noise \({\chi }_{ma}^{2}{n}_{{{{\rm{a}}}}}\) from axion DM.

Fig. 1: Conceptual plot of the entanglement-enhanced microwave haloscopes for axion dark matter search.
figure 1

A pair of entangled probes, including the signal (red beam) and the ancilla (blue beam), are generated at the bottom-left box. Note that the blue beam becomes inaccessible when entanglement assistance is forbidden. The signal probe is then shined on the input port of a microwave cavity, which is coupled with the axion (top-left beam) via a strong magnetic field. At this moment, the unknown parameter of axion is encoded on the signal probe, while the ancilla is shared with the receiver intact. The receiver applies a nonlinear processing to the returned probes jointly, e.g., a two-mode squeezer for the entanglement-enhanced case. Finally, the receiver collects the photon counts and estimate the unknown parameter of axion based on the readout. Background image credit: ©James Webb Space Telescope.

Full size image

The input-output relation in Eq. (2) is a special case of a phase-covariant bosonic Gaussian channel (BGC)20,21\({{{{\mathcal{N}}}}}_{\kappa ,{n}_{{{{\rm{B}}}}}}\) with transmissivity κ and dark count noise of mean photon number nB, which maps a vacuum input state to a thermal state with mean photon number nB and an input mean field α to output mean field \(\sqrt{\kappa }\alpha\). The transmissivity κ ranges from 0 to ∞: for 0 ≤κ < 1, \({{{{\mathcal{N}}}}}_{\kappa ,{n}_{{{{\rm{B}}}}}}\) is a thermal-loss channel, which corresponds to the ones in dark matter search Eq. (2); for κ = 1, \({{{{\mathcal{N}}}}}_{\kappa ,{n}_{{{{\rm{B}}}}}}\) is an additive white Gaussian noise (AWGN) channel; for κ > 1, \({{{{\mathcal{N}}}}}_{\kappa ,{n}_{{{{\rm{B}}}}}}\) is a thermal amplifier channel. For the channel to be physical, the dark photon count must be larger than the intrinsic amplification noise: \({n}_{{{{\rm{B}}}}}\ge \max \{\kappa -1,0\}\). Note that our definition of noise nB is different from some other conventions for the purpose of simplifying our notations, see “Methods”.

For the case of Eq. (2), the quantum channel is the thermal loss case, with transmissivity \(\kappa (\omega )={\chi }_{mm}^{2}(\omega )\) and the noise coming from the thermal background and DM axion:

$${n}_{{{{\rm{B}}}}}(\omega )=\left[1-{\chi }_{mm}^{2}\left(\omega \right)\right]{n}_{T}+{\chi }_{ma}^{2}\left(\omega \right){n}_{{{{\rm{a}}}}},$$
(5)

where the thermal photon number of the background environment mode, \({n}_{T}\equiv 1/[\exp \left(\hslash {{\Omega }}/{k}_{{{{\rm{B}}}}}T\right)-1],\) is approximately taken at the center frequency Ω.

Before we proceed with our analyses, we provide some realistic parameter settings. At practical operating condition17,19 of temperature T = 35 mK and frequency f ≃ 7 GHz, the environment thermal photon number nT ~ 10−4 from the Bose-Einstein distribution. According to theoretical predictions, axion density \({n}_{a}/V \sim 1{0}^{15}\frac{\lambda }{{{{\rm{km}}}}}{{{{\rm{cm}}}}}^{-3}\)19 is noticeably large in the microwave region, where λ is the De Broglie wavelength of DM. At the same time, the coupling between axion and cavity \({\chi }_{ma}^{2}\left(\omega \right)\) is extremely weak, such that the added noise \({\chi }_{ma}^{2}\left(\omega \right){n}_{a}\ll 1\) is infinitesimal and therefore hard to verify or nullify.

In the above we have modeled a single sensor case. However, as we will discuss at the end of the paper, identical sensor arrays can be reduced to the above single sensor case19, and therefore our results below can be adopted to sensor-networks.

General noise sensing strategies

We consider the estimation of additive noise nB in BGCs, assuming that the transmissivity is known from prior calibration. To measure the additive noise nB, one can in general input a probe system S in state \(\hat{\rho }\) and measure the output system R of the channel \({{{{\mathcal{N}}}}}_{\kappa ,{n}_{{{{\rm{B}}}}}}^{\otimes M}(\hat{\rho })\). Here, to achieve a good performance, we have considered probing the channel M times with input state \(\hat{\rho }\) potentially entangled across M probings and a joint measurement on the entire output. To model a physically meaningful setting operating with finite energy, the total mean photon number of the input state is constrained to be MNS over M modes.

A general strategy can also rely on entanglement to boost the sensing performance31,32,33. As shown in Fig. 2, this is implemented by allowing an ancilla A entangled with the probe, such that the joint state of system AS is pure. In general, one can write out the joint input-ancilla pure state as:

$${\left\vert {\psi }_{0}\right\rangle }_{AS}=\mathop{\sum}\limits_{{{{\boldsymbol{n}}}}\ge {{{\boldsymbol{0}}}}}\sqrt{{p}_{{{{\boldsymbol{n}}}}}}{\left\vert {\chi }_{{{{\boldsymbol{n}}}}}\right\rangle }_{{{{\rm{A}}}}}{\left\vert {{{\boldsymbol{n}}}}\right\rangle }_{S},$$
(6)

where \(\left\vert {{{\boldsymbol{n}}}}\right\rangle ={\otimes }_{\ell = 1}^{M}\left\vert {n}_{\ell }\right\rangle\) is the number state basis of the M-mode signal S, pn’s are probabilities and normalized to unity and ancilla states \(\{\left\vert {\chi }_{{{{\boldsymbol{n}}}}}\right\rangle \}\) are normalized but not necessarily orthogonal26,27. We adopt the vector notation n = {n1, ⋯ , nM}. For such a state, the energy constraint is specified as \(\mathop{\sum }\nolimits_{j = 1}^{M}\langle {\hat{a}}_{S,j}^{{\dagger} }{\hat{a}}_{S,j}\rangle ={\sum }_{{{{\boldsymbol{n}}}}}({p}_{{{{\boldsymbol{n}}}}}{\sum }_{j}{n}_{j})\le M{N}_{{{{\rm{S}}}}}\), where \({\hat{a}}_{S,j}\) is the jth signal mode. In an entangled strategy, one can perform measurement on the output R and the ancilla system in the quantum state:

$$\hat{\rho }({n}_{{{{\rm{B}}}}})={{{{\mathcal{N}}}}}_{\kappa ,{n}_{{{{\rm{B}}}}}}^{\otimes M}\otimes {{{\mathcal{I}}}}(\left\vert {\psi }_{0}\right\rangle \left\langle {\psi }_{0}\right\vert ),$$
(7)

where identity channel \({{{\mathcal{I}}}}\) models perfect ancilla storage.

Fig. 2: Schematic of the entanglement-assisted strategy.
figure 2

A probe system S is allowed to be entangled with an ancilla A. The probe S is input to the channel. The output system R is jointly measured with the ancilla A.

Full size image

In both strategies, we quantify the performance via the root-mean-square (rms) error δnB. In the following, we provide the ultimate limits on δnB, when one is allowed to optimize any entangled input-ancilla state \({\left\vert {\psi }_{0}\right\rangle }_{AS}\) (subject to the energy constraint) and any measurement strategy. Then we consider practical protocols consisting of a source and a measurement to achieve the limit in the parameter region of interest.

Ultimate limit on noise sensing

Given a fixed state \(\hat{\rho }({n}_{{{{\rm{B}}}}})\) dependent on parameter nB, the rms error in estimating nB when allowing an arbitrary measurement is lower bounded by the asymptotically tight quantum Cramér-Rao bound34,35,36:

$$\delta {{n}_{{{{\rm{B}}}}}}^{2}\ge \frac{1}{{{{\mathcal{J}}}}\left[\hat{\rho }\left({n}_{{{{\rm{B}}}}}\right)\right]}.$$
(8)

The quantity \({{{\mathcal{J}}}}\left[\hat{\rho }\left({n}_{{{{\rm{B}}}}}\right)\right]\) is the QFI37 defined via:

$${{{\mathcal{J}}}}\left[\hat{\rho }\left({n}_{{{{\rm{B}}}}}\right)\right]=\mathop{\lim }\limits_{\epsilon \to 0}\frac{8}{{\epsilon }^{2}}\left\{1-F\left[\hat{\rho }({n}_{{{{\rm{B}}}}}),\hat{\rho }({n}_{{{{\rm{B}}}}}+\epsilon )\right]\right\}$$
(9)
$$=-4{\partial }_{{{n}_{{{{\rm{B}}}}}}^{{\prime} }}^{2}F\left[\hat{\rho }({n}_{{{{\rm{B}}}}}),\hat{\rho }({{n}_{{{{\rm{B}}}}}}^{{\prime} })\right]{\left\vert \right.}_{{{n}_{{{{\rm{B}}}}}}^{{\prime} } = {n}_{{{{\rm{B}}}}}},$$
(10)

where the fidelity between two quantum states \({\hat{\rho }}_{0},{\hat{\rho }}_{1}\) is defined as \(F({\hat{\rho }}_{0},{\hat{\rho }}_{1})\equiv {{{\rm{Tr}}}}\sqrt{\sqrt{{\hat{\rho }}_{0}}{\hat{\rho }}_{1}\sqrt{{\hat{\rho }}_{0}}}\).

As QFI \({{{\mathcal{J}}}}\left[\hat{\rho }\left({n}_{{{{\rm{B}}}}}\right)\right]\) depends on the input-ancilla state via Eq. (7), in order to understand the ultimate limit of noise sensing precision, we need to maximize \({{{\mathcal{J}}}}\left[\hat{\rho }\left({n}_{{{{\rm{B}}}}}\right)\right]\) over all 2M-mode general quantum states \({\left\vert {\psi }_{0}\right\rangle }_{AS}\), subject to the total photon number constraint of MNS on the input system A. This is in general a challenging task, as the states can be arbitrary and entangled across 2M modes; however, we are able to obtain the following upper bound on \({{{\mathcal{J}}}}\left[\hat{\rho }\left({n}_{{{{\rm{B}}}}}\right)\right]\), via making use of the fidelity interpretation of QFI in Eq. (10). We detail the full proof based on unitary extension (UE) of channels in Supplementary Note 1.

Theorem 1 The quantum Fisher information per mode for energy constrained additive noise sensing of a phase-covariant Bosonic Gaussian channel \({{{{\mathcal{N}}}}}_{\kappa ,{n}_{{{{\rm{B}}}}}}\) has the following upper bound:

$${{{{\mathcal{J}}}}}_{{{{\rm{UB,UE}}}}}=\frac{1}{{n}_{{{{\rm{B}}}}}({n}_{{{{\rm{B}}}}}+1)}+\frac{\kappa {N}_{{{{\rm{S}}}}}\left(2{n}_{{{{\rm{B}}}}}-\kappa +1\right)}{{n}_{{{{\rm{B}}}}}{\left({n}_{{{{\rm{B}}}}}+1\right)}^{2}\left({n}_{{{{\rm{B}}}}}-\kappa +1\right)}\,,$$
(11)

where NS is the input mean photon number per mode. Furthermore, the upper bound is additive: \({{{\mathcal{J}}}}\left[\hat{\rho }\left({n}_{{{{\rm{B}}}}}\right)\right]\le M{{{{\mathcal{J}}}}}_{{{{\rm{UB,UE}}}}}\) for any 2M-mode input-ancilla state subject to mean photon number constraint MNS.

The additivity of the above upper bound can also be proven in a more general setting, where multiple channels are dependent on a global noise parameter θ. Consider a compound channel \({\otimes }_{\ell = 1}^{K}{{{{\mathcal{N}}}}}_{{\kappa }_{\ell },{n}_{{{{\rm{B}}}},\ell }(\theta )}\), the noise of each sub-channel nB,ℓ(θ) is a general smooth function of θ. Suppose one utilizes NS,ℓ mean photon number on each sub-channel, the total Fisher information about θ is upper bounded by:

$${{{{\mathcal{J}}}}}_{\theta }^{{{{\rm{UB,UE}}}}}=\mathop{\sum }\limits_{\ell =1}^{K}{\left[{\partial }_{\theta }{n}_{{{{\rm{B}}}},\ell }\right]}^{2}{{{{\mathcal{J}}}}}_{{{{\rm{UB,UE}}}}}({N}_{{{{\rm{S}}}},\ell },{\kappa }_{\ell },{n}_{{{{\rm{B}}}},\ell }),$$
(12)

where \({{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}({N}_{{{{\rm{S}}}}},\kappa ,{n}_{{{{\rm{B}}}}})\) makes the functional dependence explicit in Eq. (11). The detailed proof is presented in Supplementary Note 1. This additivity property is non-trivial as in general the inputs to different channels can be entangled.

Before proceeding to applying the upper bound, we would like to compare with some known results. In ref. 28, there is an upper bound from teleportation (TP)-stretching that holds for the energy unconstrained problem of noise estimation. In our notations, it provides an upper bound:

$${{{{\mathcal{J}}}}}_{{{{\rm{UB,TP}}}}}=\frac{1}{{n}_{{{{\rm{B}}}}}({n}_{{{{\rm{B}}}}}+1-\kappa )},$$
(13)

which holds true for arbitrary values of NS. In our analyses, we will obtain the best upper bound:

$${{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}=\min [{{{{\mathcal{J}}}}}_{{{{\rm{UB,UE}}}}},{{{{\mathcal{J}}}}}_{{{{\rm{UB,TP}}}}}],$$
(14)

combining both Eqs. (11) and (13). As shown in Fig. 3, in the practical region of squeezing (region below the cyan dashed line), \({{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}={{{{\mathcal{J}}}}}_{{{{\rm{UB,UE}}}}}\) is adopted; while in the large squeezing region (above the cyan dashed line), \({{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}={{{{\mathcal{J}}}}}_{{{{\rm{UB,TP}}}}}\) is adopted. It is noteworthy that the teleportation-based bound \({{{{\mathcal{J}}}}}_{{{{\rm{UB,TP}}}}}\) does not depend on the photon-number constraint NS. This is due to its derivation allows infinite energy—it is the QFI achieved by the Choi state of the channel, which is the channel output when the TMSV input becomes infinitely squeezed28. Naturally, it is a loose bound for finite NS. In contrast, our unitary extension bound \({{{{\mathcal{J}}}}}_{{{{\rm{UB,UE}}}}}\) is much tighter for small NS, but the assumption of receiver being able to access the environment of the unitary extension makes \({{{{\mathcal{J}}}}}_{{{{\rm{UB,UE}}}}}\) loose at the limit of large NS: When NS increases, eventually the environment contains too much information about the noise level; therefore, such assumed access to the environment increases the QFI drastically and makes the resulting QFI upper bound loose.

Fig. 3: Quantum Fisher information normalized by the ultimate limit \({{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}\).
figure 3

a Squeezed vacuum, \({{{{\mathcal{J}}}}}_{{{{\rm{SV}}}}}/{{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}\); b TMSV sources, \({{{{\mathcal{J}}}}}_{{{{\rm{TMSV}}}}}/{{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}\). Cyan dashed: \({{{{\mathcal{J}}}}}_{{{{\rm{UB,UE}}}}}={{{{\mathcal{J}}}}}_{{{{\rm{UB,TP}}}}}\); \({{{{\mathcal{J}}}}}_{{{{\rm{UB,UE}}}}} > {{{{\mathcal{J}}}}}_{{{{\rm{UB,TP}}}}}\) for larger G, namely one adopts \({{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}={{{{\mathcal{J}}}}}_{{{{\rm{UB,TP}}}}}\) above the cyan line, \({{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}={{{{\mathcal{J}}}}}_{{{{\rm{UB,UE}}}}}\) otherwise. The values of maximum and minimum in each subplot are highlighted in red. The range between the adjacent two contours is 0.1. nB = 10−3. As a reminder, \(G={e}^{2r}=\exp \{2{\sinh }^{-1}\sqrt{{N}_{{{\rm{S}}}}}\}\).

Full size image

Performance of Gaussian sources

With the ultimate limit in hand, we now consider QFI enabled by different type of input-ancilla states \(\left\vert {\psi }_{0}\right\rangle\). We consider M identical probes, each with mean photon number NS, i.e., \(\langle {\hat{a}}_{{{{\rm{S}}}}}^{{\dagger} }{\hat{a}}_{{{{\rm{S}}}}}\rangle \le {N}_{{{{\rm{S}}}}}\). Due to the additive nature of QFI for multi-copies, we will just consider the Fisher information for a single probe. All sources considered here are Gaussian21 and the QFI can be evaluated analytically, as we detail in Supplementary Note 2.

We begin with the NS = 0 case of vacuum input. The vacuum-limit (VL) QFI can be evaluated as:

$${{{{\mathcal{J}}}}}_{{{{\rm{VL}}}}}=\frac{1}{{n}_{{{{\rm{B}}}}}({n}_{{{{\rm{B}}}}}+1)}={{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}{| }_{{N}_{{{{\rm{S}}}}} = 0},$$
(15)

which also coincides with \({{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}\) at zero input photon. In this case the performance is limited by vacuum noise fluctuations, thus, we name the corresponding QFI as the vacuum limit. As we will address later, this vacuum limit is much better than the performance of vacuum input with homodyne detection, the latter often considered as benchmark in previous works15,17.

Now we consider exotic quantum resources to overcome the vacuum limit. We begin with the squeezed vacuum state, in absence of any entangled ancilla. Squeezed vacuum states have been considered in DM search15, however, the QFI enabled by it remains unclear. A squeezed vacuum state is prepared by applying single-mode squeezing \(\hat{S}(r)=\exp [-r({\hat{a}}_{{{{\rm{S}}}}}^{2}-{\hat{a}}_{{{{\rm{S}}}}}^{{\dagger} 2})/2]\) to a vacuum mode, where \({\hat{a}}_{{{{\rm{S}}}}}\) is the annihilation operator of the initial mode and r is the squeezing parameter. The resulting mode has mean photon number \({N}_{{{{\rm{S}}}}}={\sinh }^{2}r\) and quadrature variances \(G\equiv \exp (2r)\) and \(1/G\equiv \exp (-2r)\) for position and momentum, where we have chosen vacuum variance as unity. Here G is often referred to in decibels (dB) as the squeezing strength. A single-mode squeezed vacuum (SV) yields the following QFI:

$${{{{\mathcal{J}}}}}_{{{{\rm{SV}}}}}=\frac{{({n}_{{{{\rm{B}}}}}+1)}^{2}+{({n}_{{{{\rm{B}}}}}+2\kappa {N}_{{{{\rm{S}}}}})}^{2}+2\kappa {N}_{{{{\rm{S}}}}}\left(\kappa +1\right)}{\left[\kappa {N}_{{{{\rm{S}}}}}\left(2{n}_{{{{\rm{B}}}}}-\kappa +1\right)+{n}_{{{{\rm{B}}}}}\left({n}_{{{{\rm{B}}}}}+1\right)\right]\left[2{n}_{{{{\rm{B}}}}}\left({n}_{{{{\rm{B}}}}}+2\kappa {N}_{{{{\rm{S}}}}}+1\right)-2(\kappa -1)\kappa {N}_{{{{\rm{S}}}}}+1\right]}.$$
(16)

First, as a sanity check, with zero mean photon number NS = 0, the QFI result \({{{{\mathcal{J}}}}}_{{{{\rm{SV}}}}}=1/{n}_{{{{\rm{B}}}}}({n}_{{{{\rm{B}}}}}+1)={{{{\mathcal{J}}}}}_{{{{\rm{VL}}}}}\) agrees with the vacuum limit.

While when the input mean photon number NS ≫ 1 is large, \({{{{\mathcal{J}}}}}_{{{{\rm{SV}}}}}\simeq 2/{(1-\kappa +2{n}_{{{{\rm{B}}}}})}^{2}\) converges to a finite value; from the above, we see that single-mode squeezing can even worsen the performance when nB ≪ 1 in the lossy case of κ < 1. While at the lossless case of κ = 1, the squeezed state QFI \({{{{\mathcal{J}}}}}_{{{{\rm{SV}}}}}={{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}\) achieves the upper bound when \({n}_{{{{\rm{B}}}}}\ll \min [1,1/{N}_{{{{\rm{S}}}}}]\). The above performance from asymptotic analyses can be verified in an example in Figs. 3a and 4a, where we plot the relative ratio to the upper bound and the vacuum limit. Overall, we see close-to-optimal performance of single-mode squeezed vacuum only when κ ~ 1 is close to the lossless limit. Note that the optimality at κ ~ 0 is trivial and input-independent.

Fig. 4: Quantum Fisher information normalized by the standard quantum limit \({{{{\mathcal{J}}}}}_{{{{\rm{VL}}}}}\).
figure 4

a Squeezed vacuum, \({{{{\mathcal{J}}}}}_{{{{\rm{SV}}}}}/{{{{\mathcal{J}}}}}_{{{{\rm{VL}}}}}\); b TMSV sources, \({{{{\mathcal{J}}}}}_{{{{\rm{TMSV}}}}}/{{{{\mathcal{J}}}}}_{{{{\rm{VL}}}}}\). The values of maximum and minimum in each subplot are highlighted in red. The range between the adjacent two contours is 2 decibel. nB = 10−3. Note that in larger nB region neither source has much of advantage compared to vacuum. \(G={e}^{2r}=\exp \{2{\sinh }^{-1}\sqrt{{N}_{{{\rm{S}}}}}\}\).

Full size image

To further improve the performance, we consider entanglement-assisted strategies, where one stores an ancilla A entangled with the input signal S and jointly measure the signal and the ancilla for noise estimation. In this work, we consider entanglement in the form of TMSV, which are readily available in both optical ___domain and microwave ___domain. A TMSV state can be prepared by applying the two mode squeezing \({\hat{S}}_{2}(r)=\exp [-r({\hat{a}}_{{{{\rm{S}}}}}{\hat{a}}_{{{{\rm{A}}}}}-{\hat{a}}_{{{{\rm{S}}}}}^{{\dagger} }{\hat{a}}_{{{{\rm{A}}}}}^{{\dagger} })]\) to two vacuum modes. After the two-mode squeezing, the signal mode has mean photon number \({N}_{{{{\rm{S}}}}}\equiv \langle {\hat{a}}_{{{{\rm{S}}}}}^{{\dagger} }{\hat{a}}_{{{{\rm{S}}}}}\rangle ={\sinh }^{2}r\). Similar to the single-mode squeezing case, we define the squeezing strength \(G=\exp (2r)\), as such a TMSV state becomes two independent squeezed states of strength G via passing through a balanced beamsplitter. The QFI for noise estimation enabled by TMSV can be evaluated as:

$${{{{\mathcal{J}}}}}_{{{{\rm{TMSV}}}}}=\frac{(2{n}_{{{{\rm{B}}}}}-\kappa +1){N}_{{{{\rm{S}}}}}+{n}_{{{{\rm{B}}}}}-\kappa +1}{{n}_{{{{\rm{B}}}}}\left({n}_{{{{\rm{B}}}}}-\kappa +1\right)\left[(2{n}_{{{{\rm{B}}}}}-\kappa +1){N}_{{{{\rm{S}}}}}+{n}_{{{{\rm{B}}}}}+1\right]}.$$
(17)

Different from single-mode squeezing, we find that TMSV always overcomes the vacuum limit:

$$\frac{{{{{\mathcal{J}}}}}_{{{{\rm{TMSV}}}}}}{{{{{\mathcal{J}}}}}_{{{{\rm{VL}}}}}}=1+\frac{\kappa {N}_{{{{\rm{S}}}}}\left(2{n}_{{{{\rm{B}}}}}+1-\kappa \right)}{\left({n}_{{{{\rm{B}}}}}+1-\kappa \right)\left[(2{n}_{{{{\rm{B}}}}}+1-\kappa ){N}_{{{{\rm{S}}}}}+{n}_{{{{\rm{B}}}}}+1\right]}.$$
(18)

In particular, for the ideal lossless scenario of κ = 1, the TMSV source can be proven to be optimal in the weak noise limit, namely \({{{{\mathcal{J}}}}}_{{{{\rm{TMSV}}}}}/{{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}\simeq 1\) when \({n}_{{{{\rm{B}}}}}\ll \min [1,1/{N}_{{{{\rm{S}}}}}]\). Furthermore, the TMSV source achieves the teleportation bound exactly at the limit of large squeezing, NS → ∞. We verify the above conclusions numerically. In Fig. 3b, we indeed see the ratio \({{{{\mathcal{J}}}}}_{{{{\rm{TMSV}}}}}/{{{{\mathcal{J}}}}}_{{{{\rm{UB}}}}}\) is close to unity in most of the parameter space, not limiting to κ = 1. In Fig. 4b, we see that the TMSV source yields an appreciable advantage over the vacuum limit, which survives in the entire parameter region and is largest in the high squeezing and high transmissivity region, as expected from Eq. (18).

Measurement protocols on Gaussian sources

Now we consider the measurement to achieve the QFI for the various types of input quantum states.

When the input is vacuum, the output state is a thermal state with mean photon number nB, which is a photon-number diagonal state. Consequently, the vacuum limit can be achieved by a photon-counting measurement. Note that in this case homodyne detection on vacuum input is strictly sub-optimal, with the Fisher information:

$${{{{\mathcal{I}}}}}_{{{{\rm{Vac-hom}}}}}=\frac{2}{{(1+2{n}_{{{{\rm{B}}}}})}^{2}} < {{{{\mathcal{J}}}}}_{{{{\rm{VL}}}}}.$$
(19)

And the performance degradation from the vacuum limit is large when nB is small, as \({{{{\mathcal{I}}}}}_{{{{\rm{Vac-hom}}}}}/{{{{\mathcal{J}}}}}_{{{{\rm{VL}}}}} \sim 2{n}_{{{{\rm{B}}}}}\) in such a weak noise limit. This vacuum-homodyne performance is often regarded as the “standard quantum limit” in the literature15,16,17. The quantum optimum vacuum limit \({{{{\mathcal{J}}}}}_{{{{\rm{VL}}}}}\) has an infinite-fold advantage over the vacuum homodyne \({{{{\mathcal{I}}}}}_{{{{\rm{Vac-hom}}}}}\) as nB → 0. Via this Fisher information analyses, we make the advantage of photon counting proposed in ref. 16 rigorous.

Now we proceed to consider measurement for single-mode squeezed vacuum input. We propose two strategies shown in Fig. 5. First, let us begin with the homodyne measurement shown in Fig. 5a. As we detail in Supplementary Note 3, a simple homodyne detection on the squeezed quadrature (here the momentum quadrature \(\hat{p}\)) of a single-mode squeezed vacuum state provides the Fisher information:

$${{{{\mathcal{I}}}}}_{{{{\rm{SV-hom}}}}}=\frac{2}{{\left(2{n}_{{{{\rm{B}}}}}+2\kappa \left({N}_{{{{\rm{S}}}}}-\sqrt{{N}_{{{{\rm{S}}}}}\left({N}_{{{{\rm{S}}}}}+1\right)}\right)+1\right)}^{2}}\,.$$
(20)

Note that the protocol of squeezing followed up with anti-squeezing in the HAYSTAC experiment17 in theory yields the same Fisher information as direct homodyne (see Supplementary Note 3). In the HAYSTAC experiment, anti-squeezing is applied to make the signal robust against additional detection noises.

Fig. 5: Single-mode squeezing-assisted measurement strategies.
figure 5

a Homodyne measurement; b nulling receiver based on single-mode squeezing \(\hat{S}({r}^{\star })\) and photon detection (PD).

Full size image

Indeed, assuming homodyne detection, squeezed vacuum input provides a better performance, \({{{{\mathcal{I}}}}}_{{{{\rm{SV-hom}}}}}\ge {{{{\mathcal{I}}}}}_{{{{\rm{Vac-hom}}}}}\), with equality achieved at NS = 0 as expected. When the squeezing strength G is limited, the bottleneck is the homodyne measurement that fails to achieve the full potential of the squeezed vacuum source. With unlimited energy budget such that G → ∞, we have \({{{{\mathcal{I}}}}}_{{{{\rm{SV -hom}}}}}=2/{(2{n}_{{{{\rm{B}}}}}+1-\kappa )}^{2}\) which converges to the squeezed-vacuum quantum limit \({{{{\mathcal{J}}}}}_{{{{\rm{SV}}}}}\). However, compared with the vacuum limit \({{{{\mathcal{J}}}}}_{{{{\rm{VL}}}}}\) in Eq. (15), \({{{{\mathcal{I}}}}}_{{{{\rm{SV-hom}}}}}\) for squeezing-homodyne is only advantageous when κ is very close to unity. Figure 7 confirms the gap between the \({{{{\mathcal{I}}}}}_{{{{\rm{SV -hom}}}}}\) (purple) and the QFI of squeezed vacuum source \({{{{\mathcal{J}}}}}_{{{{\rm{SV}}}}}\) (blue dashed), also the promised advantage of \({{{{\mathcal{J}}}}}_{{{{\rm{SV}}}}}\) over the vacuum case \({{{{\mathcal{I}}}}}_{{{{\rm{Vac-hom}}}}}\).

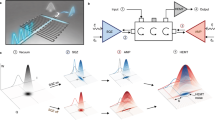
To exploit more advantage from single-mode squeezing, as shown in Fig. 5b we design a nulling receiver which is proven to be optimum at the nB → 0 limit. Specifically, the receiver first aims to null the return mode for squeezed-state sources by performing an anti-squeezing \(\hat{S}({r}^{\star })\) with \({r}^{\star }=-{\sinh }^{-1}(\sqrt{{N}_{{{{\rm{S}}}}}})\). In experiments, such an anti-squeezing can be realized via optical parametric amplification. Indeed, it successfully nulls the return mode to vacuum for an identity channel, while it leaves residue noise for a general BGC. At this moment, the photon count is subject to the probability distribution in the Legendre function, which yields Fisher information in Eq. (23) of Supplementary Information. At the identity-channel limit nB → 0, κ → 1, we find that the nulling receiver achieves the SV limit (see Supplementary Note 3):

$${{{{\mathcal{I}}}}}_{{{{\rm{SV -null}}}}}\simeq \frac{{(1+2{N}_{{{{\rm{S}}}}})}^{2}}{(1-\kappa ){N}_{{{{\rm{S}}}}}}\simeq {{{{\mathcal{J}}}}}_{{{{\rm{SV}}}}}.$$
(21)

As shown in Fig. 7, our numerical results of the nulling receiver (blue) achieves the optimal performance allowed by the squeezed vacuum source \({{{{\mathcal{J}}}}}_{{{{\rm{SV}}}}}\) (blue dashed) in both κ = 1 (subplot a) and κ = 0.6 < 1 (subplot b) cases. The nulling receiver secures the optimal advantage over the vacuum limit (gray dashed) when κ = 1, whereas the squeezed state source per se fails to beat the vacuum limit when κ = 0.6.

In the entanglement-assisted case, the receiver has access to both the ancilla A and the return R. We propose two measurement schemes shown in Fig. 6, one is based on Bell measurement [subplot (a)], the other is an extension of the nulling receiver proposed above [subplot (b)]. To begin with, we introduce the Bell measurement, where one performs homodyne detection after passing the return mode \({\hat{a}}_{{{{\rm{R}}}}}\) and the ancilla mode \({\hat{a}}_{{{{\rm{A}}}}}\) through a balanced beamsplitter. The Bell measurement on the TMSV input yields the classical Fisher information:

$${{{{\mathcal{I}}}}}_{{{{\rm{Bell}}}}}=\frac{1}{{\left({n}_{{{{\rm{B}}}}}+\kappa {N}_{{{{\rm{S}}}}}-2\sqrt{\kappa {N}_{{{{\rm{S}}}}}\left({N}_{{{{\rm{S}}}}}+1\right)}+{N}_{{{{\rm{S}}}}}+1\right)}^{2}},$$
(22)

which is sub-optimal in general. In particular, at the limit nB → 0, one can analytically show that \({{{{\mathcal{I}}}}}_{{{{\rm{Bell}}}}}\) is worse than \({{{{\mathcal{I}}}}}_{{{{\rm{SV -hom}}}}}\), the resolution of single-mode squeezing and homodyne. This is confirmed in Fig. 7. In the κ = 1 case of subplot (a), \({{{{\mathcal{I}}}}}_{{{{\rm{Bell}}}}}\) (orange) is constantly 3dB worse than \({{{{\mathcal{I}}}}}_{{{{\rm{SV-hom}}}}}\) (purple); in the κ < 1 case of subplot (b), \({{{{\mathcal{I}}}}}_{{{{\rm{Bell}}}}}\) drops after the squeezing strength G surpassed a threshold, as expected from Eq. (22).

Fig. 6: Entanglement-assisted measurement strategies.
figure 6

a Bell measurement; b nulling receiver based on two-mode squeezing \({\hat{S}}_{2}({r}_{2}^{\star })\) and photon detection (PD).

Full size image
Fig. 7: Comparison of the Fisher information of practical measurements (solid) with the quantum limits (dashed).
figure 7

The Fisher information is normalized by the standard Fisher information of homodyne on vacuum input. a κ = 1. b κ = 0.6. Both axes are plotted in the decibel (dB) unit. nB = 10−3. As a reminder, \(G={e}^{2r}=\exp \{2{\sinh }^{-1}\sqrt{{N}_{{{\rm{S}}}}}\}\).

Full size image

By contrast, the nulling receiver, now based on two-mode-anti-squeezing, is again near optimum at the nB → 0 limit for TMSV input. Specifically, the receiver aims to null the returned signal mode to vacuum for TMSV sources by \({\hat{S}}_{2}({r}_{2}^{\star })\) with \({r}_{2}^{\star }=-{\sinh }^{-1}(\sqrt{\kappa {N}_{{{{\rm{S}}}}}/[(1-\kappa ){N}_{{{{\rm{S}}}}}+1]})\). The return mode is nulled to vacuum over a pure loss channel at the limit nB → 0 (which does not work for amplifier channels or nB > 0). At this moment, the joint photon count statistics at the signal and ancilla modes can be analytically solved, which yields Fisher information Eq. (40) of Supplementary Information. At the low-noise limit nB → 0, we find that the nulling receiver achieves the TMSV limit (see Supplementary Note 3):

$${{{{\mathcal{I}}}}}_{{{{\rm{TMSV -null}}}}}\simeq \frac{1+{N}_{{{{\rm{S}}}}}}{[1+{N}_{{{{\rm{S}}}}}(1-\kappa )]{n}_{{{{\rm{B}}}}}}\simeq {{{{\mathcal{J}}}}}_{{{{\rm{TMSV}}}}}.$$
(23)

We numerically evaluate it in Fig. 7. In a wide range of G, the nulling receiver (red solid) is shown to achieve the QFI of the TMSV state source (red dashed). Remarkably, when κ < 1, the EA nulling receiver yields an appreciable advantage over the quantum limit of the single-mode squeezed-state source (blue dashed).

In the above, we have considered photon counting on both the signal and ancilla. It is noteworthy that the optimality still holds if the receiver only measures the signal, \({{{{\mathcal{I}}}}}_{{{{\rm{TMSV-null,signal}}}}}\simeq {{{{\mathcal{J}}}}}_{{{{\rm{TMSV}}}}};\) while if one only measures the ancilla, the performance is much worse, \({{{{\mathcal{I}}}}}_{{{{\rm{TMSV -null,ancilla}}}}}\simeq {\kappa }^{2}{N}_{{{{\rm{S}}}}}/[(1-\kappa ){\left(1+(1-\kappa ){N}_{{{{\rm{S}}}}}\right)}^{3}]\). On the other hand, the actual implemented nulling parameter r2 in experiments can deviate from our proposed value \({r}_{2}^{\star }\). In Supplementary Information III, we numerically compare the measure-both strategy and the measure-signal strategy—the measure-both strategy is much more robust than the latter against the deviation.

Overall, in the noise sensing scenario, nulling receivers based on (single-mode or two-mode) squeezing and photon counting performs much better than the quadrature measurements (homodyne for single-mode squeezing and Bell measurement for two-mode squeezing). Remarkably, even the classical vacuum source yields an achievable advantage up to ~30 dB with the assistance of photon number resolvable measurement (see gray dashed lines in Fig. 7). This is in contrast to the phase sensing scenario, as in noise sensing the photon number carries the information, while in phase sensing the quadratures carry the information.

Implications on axion dark matter search

Now we focus on the axion DM search with microwave cavity haloscopes and analyze the performance boost in more details. To maximize the initial search efficiently, the typical cavity linewidth is much larger than the predicted bandwidth of axion DM, thus an axion signal can be considered monochromatic18. The formal input-output relation can be found in Eq. (2). In this paper, we will frequently use the normalized coupling rates \({\tilde{\gamma }}_{m}\equiv {\gamma }_{m}/{\gamma }_{\ell }\) and \({\tilde{\gamma }}_{s}\equiv {\gamma }_{a}/{\gamma }_{\ell }\). In the formalism of bosonic Gaussian channel, here the input probe at detuning ω is subject to transmissivity \(\kappa (\omega )={\chi }_{mm}^{2}(\omega )\). From Eq. (2), the noise nB has contribution from both the environment thermal bath and the DM perturbation. As the contribution from DM is \({\chi }_{ma}^{2}{n}_{{{{\rm{a}}}}}\), we can relate the Fisher information \({{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}\) about DM density na and the Fisher information \({{{{\mathcal{J}}}}}_{{n}_{{{{\rm{B}}}}}}\) about bosonic channel additive noise nB via the parameter change rule, \({{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}={\chi }_{ma}^{4}{{{{\mathcal{J}}}}}_{{n}_{{{{\rm{B}}}}}}\). The classical Fisher information achieved by measurement, denoted as \({{{\mathcal{I}}}}\), can also be related similarly.

Now we consider the dark matter search process in more detail. As the center frequency of axion is unknown, one has to search through the whole frequency ___domain with a uniform prior. Consider a search protocol consisting of 2n + 1 measurements with large n, where the cavity resonance frequency is tuned such that the detuning ω to a fixed frequency covers the range of [−nΔω, nΔω] with a small discrete step Δω. Note that Fisher information is additive for independent measurements (c.f. joint quantum measurement), the total Fisher information about axion DM occupation number at the fixed frequency is the summation of the Fisher information at each measurement, \(\mathop{\sum }\nolimits_{k = -n}^{n}{{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}(k{{\Delta }}\omega )\,.\) Take the continuous limit of Δω → 0, n → ∞, the total Fisher information \(\mathop{\lim }\nolimits_{{{\Delta }}\omega \to 0}\frac{1}{{{\Delta }}\omega }\mathop{\sum }\nolimits_{k = -\infty }^{\infty }{J}_{{n}_{{{{\rm{a}}}}}}(k{{\Delta }}\omega ){{\Delta }}\omega\) is proportional to the continuous-spectrum total Fisher information38:

$${\mathbb{J}}\equiv \int\nolimits_{-\infty }^{\infty }{{{\rm{d}}}}\omega \,{{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}(\omega ),$$
(24)

up to a constant prefactor of 1/Δω. This prefactor shall not lead to divergence in practice because the scanning step is finite. Our approximation of the sum to the integral is valid as long as the susceptibility functions χma(ω), χmm(ω) are smooth enough relative to the discrete step Δω, which is indeed the case in DM scan19. The same procedure applies to define the continuous-spectrum total classical Fisher information for a particular measurement protocol as:

$${\mathbb{I}}=\int\nolimits_{-\infty }^{\infty }{{{\rm{d}}}}\omega \,{{{{\mathcal{I}}}}}_{{n}_{{{{\rm{a}}}}}}(\omega ).$$
(25)

As we will show later, considering homodyne measurement, the Fisher information \({{{{\mathcal{I}}}}}_{{n}_{{{{\rm{a}}}}}}\) (see Eq. (43) for noisy vacuum input and Eq. (53) of Supplementary Information for noisy squeezed vacuum) is equivalent to the squared signal visibility α2(ω)15,19, up to a constant factor. This Fisher information interpretation of the scan rate allows us to obtain insights to the DM scan rate from the total Fisher information \({\mathbb{I}}\). At the same time, \({\mathbb{J}}\) therefore characterizes the quantum limit of the scan rate given a specific input source and its upper bound will bring the ultimate limit of the DM scan rate.

Upper bound on DM scan rate

To obtain an upper bound on the performance of DM search, we assume that the input port can be arbitrarily engineered, without being affected by any additional thermal noise that often appears in experiments.

In general, we will utilize Eq. (14) to obtain the upper bound. However, as most of our evaluations are with limited NS of 10 or 20 dB of squeezing, we will focus on Eq. (11) to obtain analytical solution, while our numerical evaluation utilizes Eq. (14). For convenience, we will denote all results as “UB” without specifying “TP” or “UE”. From Eq. (11) and the parameter change rule, the Fisher information upper bound about na can be derived as:

$$\begin{array}{l}{{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{UB}}}}}= {\chi }_{ma}^{4}\left[\frac{1}{{n}_{{{{\rm{B}}}}}({n}_{{{{\rm{B}}}}}+1)}+\frac{{\chi }_{mm}^{2}{N}_{{{{\rm{S}}}}}\left(2{n}_{{{{\rm{B}}}}}-{\chi }_{mm}^{2}+1\right)}{{n}_{{{{\rm{B}}}}}{\left({n}_{{{{\rm{B}}}}}+1\right)}^{2}\left({n}_{{{{\rm{B}}}}}-{\chi }_{mm}^{2}+1\right)}\right],\end{array}$$
(26)

where we have not made the frequency dependence on ω explicit and nB can be taken as \((1-{\chi }_{mm}^{2}){n}_{T}\) due to the axion signal being weak.

Thanks to the additivity property of Eq. (12), the total Fisher information upper bound can be directly obtained through integration, \({{\mathbb{J}}}_{{{{\rm{UB}}}}}=\int{{{\rm{d}}}}\omega {{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{UB}}}}}(\omega )\). Note that this upper bound is general—it allows arbitrary entanglement across all frequencies. While the closed form solution is lengthy (see Supplementary Note 4), at the low temperature limit of nT ≪ 1, the scan rate upper bound has a simple form:

$${{\mathbb{J}}}_{{{{\rm{UB}}}}}\simeq 2\pi {\gamma }_{l}\frac{{\tilde{\gamma }}_{m}{\tilde{{\gamma }_{a}}}^{2}}{{n}_{T}}\left[\frac{1}{1+{\tilde{\gamma }}_{m}}+\frac{{N}_{{{{\rm{S}}}}}\left(1+{\tilde{\gamma }}_{m}^{2}\right)}{{\left(1+{\tilde{\gamma }}_{m}\right)}^{3}}\right].$$
(27)

The maximum of \({{\mathbb{J}}}_{{{{\rm{UB}}}}}\) can be obtained as:

$${{\mathbb{J}}}_{{{{\rm{UB}}}}}^{\star }=2\pi {\gamma }_{l}{\tilde{{\gamma }_{a}}}^{2}\frac{1+{n}_{T}+{N}_{{{{\rm{S}}}}}(1+2{n}_{T})}{{n}_{T}(1+{n}_{T})},$$
(28)

at the over coupling limit of \({\tilde{\gamma }}_{m}\to \infty\). It reveals an increasing quantum advantage proportional to NS over the vacuum limit (NS = 0).

With the upper bound in hand, in the following we consider the performance with different sources and measurements. As homodyne measurement using vacuum probes is prevalent in the experiment proposals at the current stage15,17,19, we take it as a benchmark for classical schemes, which is to be surpassed by the nonclassical probes and receivers. We will focus on parameters on par with the experiment reported in ref. 17, where the cavity is cooled to 61mK and the cavity resonant frequency is at around 10GHz.

Ideal input engineering

Here we focus on the ideal input engineering case where the input port is not affected by thermal noise before the probing. For these cases, all of our previous results can be directly translated to DM search with the parameter change rule of Fisher information—the Fisher information about na at detuning ω is:

$${F}_{{n}_{{{{\rm{a}}}}}}(\omega )={\chi }_{ma}^{4}(\omega ){F}_{{n}_{{{{\rm{B}}}}}}\left[{\chi }_{mm}^{2}(\omega ),(1-{\chi }_{mm}^{2}){n}_{T},{N}_{{{{\rm{S}}}}}\right],$$
(29)

where \({F}_{{n}_{{{{\rm{B}}}}}}[\kappa ,{n}_{{{{\rm{B}}}}},{N}_{{{{\rm{S}}}}}]\) is the corresponding Fisher information about additive noise nB for the channel \({{{{\mathcal{N}}}}}_{\kappa ,{n}_{{{{\rm{B}}}}}}\) when the signal mean photon number is NS.

Applying the above relation to Eq. (15) produces the vacuum limit of DM search \({{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{VL}}}}}\) and Eq. (19) produces the vacuum homodyne performance \({{{{\mathcal{I}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{V\; ac-hom}}}}}(\omega )\), which is the classical benchmark commonly referred to. With single-mode squeezing, applying the relation to Eq. (16) produces the single-mode squeezed vacuum performance limit \({{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{SV}}}}}\) and Eq. (20) produces the squeezing-homodyne performance \({{{{\mathcal{I}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{SV\; -hom}}}}}\). For entanglement-assisted strategies, applying the relation to Eq. (17) produces the TMSV performance limit \({{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{TMSV}}}}}\). Similar results also apply to the performance of the nulling receivers for both the single-mode squeezing input and TMSV input.

We evaluate the spectrum of the Fisher information for various probes and receivers in Fig. 8. Here the Fisher information quantities are normalized by \({{{{{\mathcal{I}}}}}^{\star }}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{Vac-hom}}}}}\equiv {{{{\mathcal{I}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{V ac-hom}}}}}(\omega =0){| }_{{\gamma }_{m} = {\gamma }_{m}^{\star }}\), the peak Fisher information of the classical benchmark at the critical coupling ratio \({\gamma }_{m}^{\star }={\gamma }_{\ell }\). In general, we see Lorentzian-type of envelops due to the \({\chi }_{ma}^{4}(\omega )\) term in Eq. (29). In subplot (a) of the critical coupling case (γm/γℓ = 1), the transmissivity κ(ω) = 0 at resonance ω = 0, and any input trivially converges to vacuum. When ω deviates from resonance, generally the Fisher information deviates from the peak value (peak sensitivity). Interestingly, the single-mode squeezed vacuum performance limit \({{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{SV}}}}}\) (blue dashed) is worse than the vacuum limit (gray dashed) for the range of detuning ω of interest, due to the loss in the probing. This can be intuitively understood by considering the anti-squeezed quadrature contributing greatly to noise while the squeezed quadrature is still almost vacuum at the large loss limit. This is also seen in Fig. 4a, where the ratio to vacuum limit also sharply decay when κ increases near κ = 0. By contrast, the TMSV state (red dashed) demonstrates a huge advantage over the whole frequency ___domain. Remarkably, in the presented scenarios \({{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{TMSV}}}}}\) achieves the upper bound (black dot-dash) almost everywhere, which indicates that the TMSV is the optimal input state here. Squeezed-vacuum homodyne performance (purple solid) is better than vacuum homodyne (gray solid) but worse than the vacuum limit (gray dashed) enabled by photon counting. In subplot (b), we consider the over-coupling case and the Fisher information spectrum broadens, while the peak sensitivity at ω = 0 decreases as expected. In both subplots, we find the nulling receiver (blue solid and red solid) to be optimal as expected.

Fig. 8: Frequency spectrum of the Fisher information with respect to the axion occupation number na.
figure 8

The values are normalized by the optimized peak value of vacuum-homodyne Fisher \({{{{{\mathcal{I}}}}}^{\star }}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{V ac-hom}}}}}\) and plotted in decibel unit. a γm/γℓ = 1; b γm/γℓ = 2G. Temperature T = 61 mK, cavity resonant frequency ωc = 2π ⋅ 10 GHz, squeezing strength G = 10 dB, γa/γℓ = 10−12.

Full size image

Now we proceed to analyze the scan rate from the total Fisher information. We begin with the performance enabled by homodyne detection, where closed-form solutions can be obtained. We put the lengthy expressions in Supplementary Note 4 and present our results for special cases or asymptotic analyses here. For vacuum input of NS = 0, we have:

$${{\mathbb{I}}}_{{{{\rm{V ac-hom}}}}}=2\pi {\gamma }_{\ell }{\tilde{\gamma }}_{a}^{2}\frac{4{\tilde{\gamma }}_{m}^{2}}{{\left(8{\tilde{\gamma }}_{m}{n}_{T}+{\left(1+{\tilde{\gamma }}_{m}\right)}^{2}\right)}^{3/2}}.$$
(30)

When nT ≪ 1, the optimum is achieved at \({\tilde{\gamma }}_{m}=2\) and \({{\mathbb{I}}}_{{{{\rm{V ac-hom}}}}}^{\star }=2\pi {\gamma }_{l}{\tilde{\gamma }}_{a}^{2}\times 16/27.\) As shown in Fig. 9a by the gray solid line, the optimal coupling ratio \({\tilde{\gamma }}_{m}\equiv {\gamma }_{m}/{\gamma }_{l}\) can be verified numerically, with peak value being zero dB due to normalization. For highly squeezed quantum source (NS ≫ 1) at low temperature (nT ≪ 1):

$${{\mathbb{I}}}_{{{{\rm{SV -hom}}}}}\simeq 2\pi {\gamma }_{\ell }{\tilde{\gamma }}_{a}^{2}\frac{64{\tilde{\gamma }}_{m}^{2}{N}_{{{{\rm{S}}}}}^{2}}{{\tilde{\gamma} }_{m}^{3/2}{\left[16{N}_{{{{\rm{S}}}}}+{\tilde{\gamma }}_{m}\right]}^{3/2}}.$$
(31)

The optimum \({{\mathbb{I}}}_{{{{\rm{SV -hom}}}}}^{\star }\simeq 2\pi {\gamma }_{\ell }{\tilde{\gamma }}_{a}^{2}\times 8{N}_{{{{\rm{S}}}}}/{3}^{3/2}\) is achieved at \({\tilde{\gamma }}_{m}\simeq 8{N}_{{{{\rm{S}}}}}\simeq 2G\). Indeed in Fig. 9a, we see the peak of the squeezing homodyne (purple solid) is when the coupling ratio is about 2G = 13 dB for the 10 dB squeezing. We see that squeezing homodyne provides an advantage of ~2.60NS over vacuum homodyne, as we confirm in Fig. 9b. Our analyses of homodyne-based strategy indeed recovers previous known results in refs. 15,19, even more precisely when we consider the extra thermal noise in the practical input source engineering case (see Supplementary Note 5). We also note that the optimal scan rate increases with squeezing gain G (equivalently NS) linearly. This is due to the larger effective bandwidth growing with G, while the peak sensitivity will saturate to a G independent constant.

Fig. 9: Total Fisher information.
figure 9

a Total Fisher information under various measurement coupling ratio over intrinsic loss γm/γℓ, squeezing strength G = 10 dB; b the optimized total Fisher information optimized with optimal γm/γℓ under various squeezing strength G. Y axis normalized by the optimized vacuum-homodyne total Fisher \({{\mathbb{I}}}_{{{{\rm{Vac-hom}}}}}^{\star }\), both axes plotted in decibel unit. \({{\mathbb{J}}}_{{{{\rm{TMSV}}}}}\), \({{\mathbb{J}}}_{{{{\rm{SV}}}}}\) are achieved by nulling receivers as shown in Fig. 8. The indicated gap in (b) is \(10{\log }_{10}(3\sqrt{3}/2) \sim 4.1\)dB. Temperature T = 61 mK, cavity resonant frequency ωc = 2π ⋅ 10GHz, γa/γℓ = 10−12.

Full size image

Now we evaluate the performance limits. For the vacuum limit, the total Fisher information has a closed form solution:

$${{\mathbb{J}}}_{{{{\rm{V L}}}}}=\int\nolimits_{-\infty }^{\infty }{{{\rm{d}}}}\omega {{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{VL}}}}}$$
(32)
$$=2\pi {\gamma }_{l}\frac{{\tilde{\gamma }}_{m}{\tilde{\gamma }}_{a}^{2}}{{n}_{T}}\frac{1}{\sqrt{{(1+{\tilde{\gamma }}_{m})}^{2}+4{n}_{T}{\tilde{\gamma }}_{m} }}$$
(33)
$$\simeq 2\pi {\gamma }_{l}{\tilde{\gamma }}_{a}^{2}\frac{1}{{n}_{T}}\frac{{\tilde{\gamma }}_{m}}{1+{\tilde{\gamma }}_{m}},$$
(34)

where in the last step we considered the nT ≪ 1 limit.

For the single-mode squeezing performance limit, instead of presenting the lengthy closed-form result (see Supplementary Note 4), we plot the results in Fig. 9. In subplot (a), a peak emerges for \({{\mathbb{J}}}_{{{{\rm{SV}}}}}\) (blue dashed) at γm/γℓ = 1 (0 dB), due to the peak in Fig. 8 that emerges only at critical coupling. For strong squeezing NS ≫ 1, the maximum total Fisher information:

$${{\mathbb{J}}}_{{{{\rm{SV}}}}}^{\star }=2\pi {\gamma }_{l}{\tilde{\gamma }}_{a}^{2}\frac{{(1+2{N}_{{{{\rm{S}}}}})}^{2}}{{N}_{{{{\rm{S}}}}}+{n}_{T}+2{N}_{{{{\rm{S}}}}}{n}_{T}},$$
(35)

is achieved at the over coupling limit of \({\tilde{\gamma }}_{m}\to \infty\). When nT ≪ 1, we can compare the performance of homodyne versus the limit enabled by squeezing, \({{\mathbb{I}}}_{{{{\rm{SV -hom}}}}}^{\star }/{{\mathbb{J}}}_{{{{\rm{SV}}}}}^{\star }=2/3\sqrt{3}\simeq 0.385\simeq -4.1\) dB. This constant factor difference can be verified numerically in Fig. 9b. At the same time, we note that it takes almost 40 dB of squeezing for the performance enabled by squeezed vacuum (purple solid and blue dashed) to reach the vacuum limit (gray dashed). This indicates the importance of a good photon counting detection in dark matter search.

In Fig. 9b, we also observe a minimum point of the total Fisher information with respect to the squeezing gain \(G\equiv 1+2{N}_{{{{\rm{S}}}}}+2\sqrt{(1+{N}_{{{{\rm{S}}}}}){N}_{{{{\rm{S}}}}}}\) for the squeezed vacuum source (blue dashed), in contrast to the monotonicity of all other sources. Indeed, the peak at \({\tilde{\gamma }}_{m}=1\) competes with the overcoupling limit at \({\tilde{\gamma }}_{m}=\infty\) as shown Supplementary Note 4. After G increases beyond a specific threshold, the overcoupling limit always dominates, which increases linearly with G. The linear growth at large G verifies Eq. (35), as G ~ 4NS when NS is large.

Finally, we address the total Fisher information enabled by the TMSV source:

$${{\mathbb{J}}}_{{{{\rm{TMSV}}}}}=\int\nolimits_{-\infty }^{\infty }d\omega {{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{TMSV}}}}}(\omega )$$
(36)
$$=2\pi {\gamma }_{l}\frac{{\tilde{\gamma }}_{m}{\tilde{\gamma }}_{a}^{2}}{{n}_{T}}\frac{1+{N}_{{{{\rm{S}}}}}+{n}_{T}+2{N}_{{{{\rm{S}}}}}\,{n}_{T}}{(1+{n}_{T})\sqrt{1+{\tilde{\gamma }}_{m}^{2}+2{\tilde{\gamma }}_{m}(1+2{N}_{{{{\rm{S}}}}})(1+2{n}_{T})}}$$
(37)
$$\simeq 2\pi {\gamma }_{l}{\tilde{\gamma }}_{a}^{2}\frac{1}{{n}_{T}}\frac{\left(1+{N}_{{{{\rm{S}}}}}\right){\tilde{\gamma }}_{m}}{\sqrt{1+{\tilde{\gamma }}_{m}^{2}+2{\tilde{\gamma }}_{m}(1+2{N}_{{{{\rm{S}}}}})}},$$
(38)

where in the last step we take the low temperature limit of nT ≪ 1. In the over coupling limit of \({\tilde{\gamma }}_{m}\to \infty\), the maximum achieves the upper bound:

$${{\mathbb{J}}}_{{{{\rm{TMSV}}}}}^{\star }\simeq {{\mathbb{J}}}_{{{{\rm{UB}}}}}^{\star },$$
(39)

as we can verify in Fig. 9 by comparing \({{\mathbb{J}}}_{{{{\rm{TMSV}}}}}^{\star }\) (red dashed) with the upper bound \({{\mathbb{J}}}_{{{{\rm{UB}}}}}^{\star }\) (black dot-dash). We also note that in general TMSV performance overwhelms the single-mode squeezing by a large factor 1/nT. As expected, the TMSV source yields an increasing advantage proportional to G over the vacuum limit.

In the above, we have assumed the squeezed vacuum and two-mode squeezed vacuums can be prepared perfectly. In practice, their preparations also have noise and we analyze this practical state engineering in Supplementary Note V. In this regime, the TMSV QFI still achieves the large advantage over the vacuum limit, while it now falls below the upper bound with a constant gap of around 6.9 dB.

Discussions

In this work, we have shown that an entanglement-assisted strategy with two-mode squeezed vacuum as source and nulling receiver (anti-two-mode-squeezing + photon counting) as detector is optimal for noise sensing. In terms of dark matter search, such a strategy provides the optimal scan-rate and outperforms the single-mode squeezed vacuum and homodyne strategy by orders of magnitude. In this regard, developing a quantum-limited photon counting detector, such as that in ref. 16 is crucial for the next-generation microwave haloscopes.

At the same time, our results reaffirm that other types of more exotic resources such as the Gottesman–Kitaev–Preskill (GKP) state29 are not necessary for microwave haloscopes19. For an energy constrained case, GKP states also obey the QFI upper bound, which is already achieved with squeezed vacuum states. Even when the energy constraint is relaxed, practical considerations also forbid GKP states to be worthwhile engineering in microwave haloscopes19.

In our dark matter search model, we have not considered the case of a local array of microwave cavities19,39,40,41, where the dark matter induced noise at different sensors are correlated. However, as ref. 19 showed, due to the correlation, the signals can be coherently combined and the problem can be reduced to a single sensor, especially for identical sensors (see Supplementary Note 6). The coherent combining between M identical sensors will provide a M2 boost to the scan rate, in addition to the quantum advantages considered here. One can adopt the protocols addressed in this work to sensor-networks via performing a passive linear network on the signal and send to all sensors, and then recombine with another passive linear network. Such sensor-network approach provides another approach of scan-rate boost without the need of a quantum-limited photon counting detector.

Methods

Bosonic Gaussian channel

A phase-covariant bosonic Gaussian channel \({{{{\mathcal{N}}}}}_{\kappa ,{n}_{{{{\rm{B}}}}}}\) is characterized by transmissivity/gain κ and additive Gaussian noise nB. Specifically, given a signal mode described by the annihilation operator \({\hat{a}}_{{{{\rm{S}}}}}\), which satisfies canonical commutation relation \([{\hat{a}}_{{{{\rm{S}}}}}^{{\dagger} },{\hat{a}}_{{{{\rm{S}}}}}]=1\), the annihilation operator of the return mode is given by the linear input-output relation:

$${\hat{a}}_{{{{\rm{R}}}}}=\sqrt{\kappa }{\hat{a}}_{{{{\rm{S}}}}}+\sqrt{1-\kappa }{\hat{a}}_{{{{\rm{E}}}}},$$
(40)

for 0 ≤ κ < 1, and:

$${\hat{a}}_{{{{\rm{R}}}}}=\sqrt{\kappa }{\hat{a}}_{{{{\rm{S}}}}}+\sqrt{\kappa -1}{\hat{a}}_{{{{\rm{E}}}}}^{{\dagger} }$$
(41)

for κ > 1.

For 0 ≤ κ < 1, the channel mimics a beamsplitter, attenuates the mean of input signal mode \({\hat{a}}_{{{{\rm{S}}}}}\) by \(\sqrt{\kappa }\) and mixes in the environment mode \({\hat{a}}_{{{{\rm{E}}}}}\) attenuated by \(\sqrt{1-\kappa }\). The environment mode \({\hat{a}}_{{{{\rm{E}}}}}\) is of mean thermal photon number nE. Overall, the additive noise mixed into the return is nB = (1 − κ)nE. Concretely, given a coherent-state input of mean α, the output is in the displaced thermal state of mean \(\sqrt{\kappa }\alpha\) and mean thermal photon number nB.

Practical source engineering

In an experimentally feasible scenario, the input is inevitably affected by thermal noise. To begin with, vacuum input is never perfect in an experiment. Practical vacuum input still has some weak thermal noise nT. In this case, the output of Eq. (2) is a thermal state with mean photon number \({\chi }_{mm}^{2}{n}_{T}+(1-{\chi }_{mm}^{2}){n}_{T}+{\chi }_{ma}^{2}{n}_{{{{\rm{a}}}}}={n}_{T}+{\chi }_{ma}^{2}{n}_{{{{\rm{a}}}}}\). From Eq. (15), the vacuum limit for axion sensing is therefore:

$${{{{\mathcal{J}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{V L}}}}}={\chi }_{ma}^{4}(\omega )\frac{1}{{n}_{T}({n}_{T}+1)}.$$
(42)

From Eq. (19), we have the performance of vacuum homodyne:

$${{{{\mathcal{I}}}}}_{{n}_{{{{\rm{a}}}}}}^{{{{\rm{V ac-hom}}}}}(\omega )={\chi }_{ma}^{4}(\omega )\frac{2}{{(1+2{n}_{T})}^{2}}.$$
(43)

Similarly, the nonclassical sources is also affected by thermal noise. Instead of single or two-mode squeezing on vacuum, the squeezing operations are performed on thermal states with mean photon number nT. To characterize nonclassical sources, we use the squeezing strength G, for both the single-mode and two-mode squeezers. The input photon number NS is contaminated by nT as \({N}_{{{{\rm{S}}}}}=[2({G}^{2}+1){n}_{T}+{(G-1)}^{2}]/4G\). The upper bound Eq. (14) with NS as the mean photon number of the processed input still applies, however is much loser due to the inevitable initial noise.

With the above input state adopting the thermal noise, the procedures for further analyses are the same as in the maintext: the squeezed sources are shined on the measurement port of the cavity, which is modeled by a phase-covariant BGC \({{{{\mathcal{N}}}}}_{{\chi }_{mm}^{2}(\omega ),{n}_{{{{\rm{B}}}}}(\omega )}\); finally the receiver measures the returned quantum states.

Note added to proof

Upon the completion of our manuscript, a related work42 appeared. There, a different model of displacement statistics is taken and the anti-squeezing and photon counting strategy for single-mode squeezed vacuum source is proposed, while no entanglement assistance is considered. Ref. 42 considers no additional loss or noise and therefore does not directly apply to dark matter haloscopes, where the predominant scenario is lossy for any off-resonance detuning or any detuning under unbalanced coupling, as we will explain in the next section.