Introduction

Quantum steering, a newly defined form of nonclassical correlation1, has attracted considerable attention in recent years2,3. By nonclassical, one refers to the fact that the correlation function can not be fully reproduced by models involving local hidden variables (LHVs)—even at an astronomical separation4,5,6,7. The most famous form of nonclassical correlation is Bell nonlocality8, in which no assumption is made on the outputs of the tested objects, namely, the outputs are directly determined by LHVs—this signifies the ultimate form of locality, and the disapproval of which thus indicates the strongest nonlocality. When one assumes that the tested objects are quantum states with the outputs complying with the laws of quantum mechanics (QM), the LHVs can determine only which of the states are tested, and hence the exclusion of LHVs proves only the objects as a whole is nonseparable (or quantum entanglement9 in a more popular way). When considering the case where just part of the objects are confined by QM, we have the definition of quantum steering, in which the beyond-QM part is often called the “steering party” and the QM part the “steered party”10.

With rigorous formulation and proof, quantum steering fits firmly between Bell nonlocality and quantum entanglement11. It has gone beyond just a theoretical concept12,13,14,15,16 and has been demonstrated in continuous-variable systems17,18,19,20,21, discrete systems of two dimensions22,23,24 or higher25,26,27, and of various degrees of freedom (DOFs)28,29,30,31,32. Similarly to Bell nonlocality and quantum entanglement, quantum steering is not only of fundamental interest but also has practical importance. For example, it has found various applications, such as one-sided device-independent quantum secure communication (1sDI-QKD)33, secure quantum teleportation34, secret sharing35, randomness certification36,37, and subchannel discrimination38.

Certifying steering nonlocality with physical apparatuses could be spoiled by security loopholes, such as locality39, freedom-of-choice40, and most notoriously detection41 loopholes closing which often demands the system with low noise and high collection efficiency. The event-ready implementation of steering could bypass the efficiency barrier yet requires the quantum repeater30. To overcome the efficiency barrier, most existing approaches change the measurement settings manually in order to avoid losses arising from active switching, which not only will open the locality loophole but more importantly hinders quantum steering from practical applications28,42,43. To date, the only loophole-free experiment40 achieves a switching rate up to 0.787 MHz using polarization DOF, which employs the three-setting Platonic-solid measurement scheme11. Such a measurement scheme has the measurement bases at the steering party uniformly distributed on the Bloch sphere. Though the scheme has achieved the optimal performance in detecting quantum steering, it requires amplitude modulation between the orthogonal bases if requiring more measurement settings (larger than three). Note that amplitude modulation could introduce cross-talk and extra loss in practical implementation. Moreover, all existing experiments rely on the free-space configuration (at least at the entanglement-generation phase) to preserve the necessary detection efficiency, but at the cost of system robustness and practicality. So far, a conclusive demonstration of steering nonlocality without applicability compromises is still lacking.

In this work, we provide an alternate measurement scheme which employs no amplitude but purely phase modulation to accommodate steering test to time-bin DOF and particularly telecommunication hardware thus achieving a GHz-level switching rate. We further quantitatively compare the performance of Platonic-solid and our phase-encoding measurement schemes, and find that they are almost the same when the noise is sufficiently low. Experimentally, we validate our scheme and certify steering nonlocality in a fully chip-fiber-based manner with the detection loophole closed. To overcome the high loss of phase modulation devices, we made a low-loss silicon chip and came up with a method of translating the phase modulation from measurement to before entanglement generation to mimic the active measurement implementation at the steering party. Our work for the first time brings detection-loophole-free steering nonlocality certification to a fully chip-fiber-based setup, notably with a 1.25 GHz measurement switching rate at the steered side. The system we built is versatile and field-use-friendly for it is easy to integrate, adapting to high-speed telecommunication modules, and robust to noise, thereby representing a solid step of steering nonlocality research from laboratory to application.

Results

Steering test

Here we consider the bipartite qubit scenario, in a steering test, the examiner (Bob) first receives a set of quantum states (called assemblage), and then selects a list of questions from a questionary to send them to the examinee (Alice). Each question has binary answers. Bob obtains his answer bit from the measurement outcome of the local quantum states prepared by Alice. We denote Bob’s measurement by y and the outcome by b. In the meantime, Bob makes no assumption on the method that Alice would take to get her answer bit, which we denote by A. After sufficient runs of questioning, Bob combines both of their answers to check the scores (correlation). Note that since the local quantum states are prepared by Alice, she can predict with certainty the outcome Bob would get if a specific question (measurement) is raised. However, this preset strategy has a limit in terms of correlation in the locality frame, similar to the classical bound for Bell inequality44. Formally, one terms the preset quantum states local hidden state model (LHSM) and defines it as

$${\sigma }_{b| y}^{{\rm{LHS}}}=\int{\sigma }_{\lambda }q(\lambda )p(b| y,\lambda )d\lambda ,\forall b,y,$$
(1)

where {σλ} is a set of positive matrices with some probability distribution q(λ)p(b∣y, λ), and λ is the local hidden variable held by Alice. Accordingly, one can define the steering parameter45

$${S}_{n}\equiv \frac{1}{n}\mathop{\sum }\limits_{k=0}^{n-1}\left\langle {A}_{k}{\hat{\sigma }}_{k}^{B}\right\rangle ,$$
(2)

which quantifies the correlation between the two parties, where n is the number of measurements, Ak ∈ { − 1, 1}, k ∈ {0, …, n − 1}, and \({\hat{\sigma }}_{k}^{B}\) is the measurement chosen by Bob with \(\left\langle {\hat{\sigma }}_{k}^{B}\right\rangle \in \{-1,1\}\). It is worth mentioning that the roles of the two parties can be swapped, and a similar steering parameter applies.

Without considering loopholes, it is safe to say that locality is breached by Alice if the answers she provides are strongly correlated thus surpassing the limit46. However, if there exists a hidden signaling between the parties, or Alice somehow can influence the measurement choice of Bob, she can easily fake a perfect correlation, which in fact opens the locality and free-of-choice loophole, respectively. In a trickier scenario, Alice may ignore the question Bob raised if the question is not the specific one she prepared. By reporting a null answer, Alice can significantly improve the correlation result, and there is in principle no way to verify whether the questions are fairly sampled. This leads to the fair-sampling assumption, which is known also as the detection loophole from experimental perspectives.

The locality and free-of-choice loophole are usually dealt with by enforcing a space-like separation between participants and using trusted random number generators. To address the detection loophole, one needs to consider a loss-tolerant LHSM to fairly evaluate the answers Alice reports. For the construction of such LHSMs, it is crucial to carefully choose Bob’s measurement settings. In this regard, the optimal set of measurements for detecting steering nonlocality using two-qubit Werner states has been investigated46, in the sense that it requires the minimal entanglement resource to demonstrate steering nonlocality given certain detection efficiency. However, this set of measurements is not compatible with the telecommunication system for it involves amplitude modulation of bases.

A recent study shows that it is possible to upper-bound the maximal correlation an LHSM could reach given any set of input settings47. In specific, this method reformulates the LHSM in the form of semidefinite programming (SDP)48,49, and considers the discarded outcomes arising from a mixed state that encompasses all the possible local states Bob might hold. As the mixed state contributes zero nonlocal correlation to the result, the effective correlation of the LHSM from all conclusive detection events can be extracted50.

Phase-encoding method

Time basis is commonly employed to encode information in telecommunication systems for its resistance to decoherence. Coherently splitting a single photon equally into two time-bins, so that it can either be detected at an early moment t0, or at a late moment t1. If we denote the state at t0 as \(\left\vert \,\text{E}\,\right\rangle\), and the state at t1 as \(\left\vert \,\text{L}\,\right\rangle\), a qubit can be defined in the time DOF: \(\left\vert \psi \right\rangle =(\left\vert \,\text{E}\right\rangle +{e}^{\text{i}{\phi }_{0}}\left\vert \,\text{L}\,\right\rangle )/\sqrt{2}\). Note that the superposition of the two states is limited by the coherence time of the photon.

By recording the arrival time, one essentially performs \({\hat{\sigma }}_{{\mathsf{Z}}}\) measurement on the photon, producing one of the two temporal outcomes. Further, by exploiting an asymmetric Mach-Zehnder interferometer (AMZI) which delays the early state to temporally overlapping with the late state, one obtains a different set of two incompatible outcomes from the two outputs of the interferometer and thus allows inference of retrieving the phase information. This corresponds to a \({\hat{\sigma }}_{\theta }\) measurement

$${\hat{\sigma }}_{\theta }=\cos (\theta ){\hat{\sigma }}_{{\mathsf{X}}}+\sin (\theta ){\hat{\sigma }}_{{\mathsf{Y}}},$$

where θ is the differential phase delay of the AMZI and \({\hat{\sigma }}_{{\mathsf{X}},{\mathsf{Y}},{\mathsf{Z}}}\) refers to the Pauli operators.

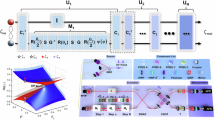
The phase modulation of θ can be accurately and swiftly implemented by using an electro-optical modulator. Thus it is convenient for Bob to construct an n-number measurement set \({\{{M}_{i}\}}_{n}\), with \({M}_{0}={\hat{\sigma }}_{{\mathsf{Z}}}\) and \({M}_{j}={\hat{\sigma }}_{\frac{j-1}{n-1}\pi },j\in \{1,\ldots ,n-1\}\). Fig. 1 gives the example of the measurement set when n = 9 in the Bloch sphere representation, in which the measurement set forms a regular right symmetric m-gonal bipyramid with m = 2(n − 1).

Fig. 1: The diagram of Bob’s measurements.
figure 1

In the Bloch sphere representation, M0 corresponds to \({\hat{\sigma }}_{{\mathsf{Z}}}\), and the rest of the measurements are uniformly distributed on the equator.

Full size image

Using the numerical methods47, we evaluate the performance of the phase-encoding measurement scheme introduced above, and find it is suboptimal when compared with the conventional Platonic-solid measurement scheme46 in terms of quantifying the steering nonlocality for a given state. However, with only phase-related measurement settings plus one computational basis setting, our scheme is compatible with the high-speed telecommunication system. We also find that when the noise is low, the two schemes have fairly close performance. An elaborate comparison between the phase-encoding measurements and the Platonic-solid measurements is provided in Supplementary Note 1.

Experimental setup

In a typical steering test, the steering party (Alice) who is untrusted gets access to the measurement setting only after the steered party (Bob) performs his measurement or receives the quantum state to be measured. Practically, this causal requirement leads to the symmetrical configuration in which both Alice and Bob place modulation devices at their measurements. However, the modulation introduces extra losses at the steering side. In specific, a phase modulator typically introduces about 3 dB insertion loss. To bypass the loss, we develop an ad hoc configuration to translate the modulation of Alice from measurement to entanglement generation. We note that this asymmetric configuration is for proof-of-principle demonstration with the locality loophole implied (see Supplementary Note 2 for discussion), and the symmetric configuration is needed when it comes to application scenarios.

Our asymmetric configuration proceeds as follows. Firstly, instead of a fixed entanglement state, we consider a set of two-qubit isotropic states entangled in time-bin DOF

$${\rho }_{AB}=\left\{v\left\vert \Psi (\alpha )\right\rangle \left\langle \Psi (\alpha )\right\vert +(1-v){\mathbb{I}}/4,0\le \alpha \le \pi \right\},$$
(3)

where \(\left\vert \Psi (\alpha )\right\rangle =\left({\left\vert \text{E}\right\rangle }_{A}{\left\vert \text{E}\right\rangle }_{B}+{e}^{{\rm{i}}\alpha }{\left\vert \text{L}\right\rangle }_{A}{\left\vert \text{L}\right\rangle }_{B}\right)/\sqrt{2}\), and v denotes the visibility of the maximally entangled state. We assume that the experimental noises and imperfections are reflected by the isotropic noise \({\mathbb{I}}/4\) that hampers the visibility, with a coefficient 1 − v, which is reasonable because the erroneous correlation data is unbiased to measurement settings (see Supplementary Note 6 for discussion).

Secondly, we apply the phase modulation (the α in \(\left\vert \Psi (\alpha )\right\rangle\)) based on injection-locking technique51 prior to the entanglement generation process, and regard this modulation as the mimicry of measurement implementation of Alice. The actual measurement at Alice’s side is fixed, and is regarded as the consequence of Bob’s choice. A detailed explanation on the equivalence of our asymmetric configuration and the convectional symmetric configuration in terms of revealing the nonlocal correlation of the quantum system is provided in Supplementary Note 2. It is important not to confuse the aforementioned asymmetric configuration with the intrinsic asymmetry of steering nonlocality47. The former describes the experimental setup which aims to close the detection loophole at the steering side, while the latter describes the (potential) asymmetry of the entanglement state. In particular, the state we adopt in Eq. (3) is symmetric, and we demonstrate steering from Alice to Bob in accordance with our asymmetric configuration.

Our experimental setup is sketched in Fig. 2. We take advantage of the spontaneous four-wave mixing (SFWM) effect in a silicon-on-insulator (SOI) spiral waveguide chip to generate the required quantum states, and the on-chip photon-pair generation rate (PGR) achieves 1.3 × 106 pairs s−1 mW−2. The design and fabrication details about the SOI chip and the experimental data of PGR are provided in Supplementary Note 3. The pump light is generated through a pair of distributed feedback (DFB) lasers concatenated via a circulator. The slave laser is gain-switched by square waves to produce 2.5 GHz light pulses, and the relative phases of these pulses are modulated by rapidly adjusting the output power of the master laser52. By impacting the modulated pump light into the SOI chip, we produce the set of states in Eq. (3). Passing through the SOI chip, two pump photons probabilistically annihilate for the creation of two entangled daughter photons. This third-order nonlinear process conserves energy and momentum, resulting in a broadband signal-idler spectrum. A dense wavelength division multiplexer (DWDM) module is then used to divide the spectrum into multiple wavelength channels. Here, we choose to use channels C29 and C38 (ITU grid specification; Full width at half maximum (FWHM): 100 GHz) for our demonstration. We also insert a filtering module with FWHM of 10 GHz after Bob’s AMZI (not shown in the figure) to overcome the filtering inefficiency53.

Fig. 2: Experimental setup.
figure 2

The setting signals on both sides and the 2.5 GHz pulse signal on the slave DFB are generated by an arbitrary wave generator (AWG) (not shown in the figure). PM: phase modulator; DFB: distributed feedback laser; DWDM: dense wavelength division multiplexer; AMZI: asymmetric Mach-Zehnder interferometer; TCSPC: time-correlated single photon counting; SNSPD: superconducting nanowire single-photon detector.

Full size image

The idler photon is directed into a homemade AMZI before local detection at Alice’s site. On the other hand, the signal photon is sent over a single-mode fiber to the receiver Bob. After the modulation by the phase modulator (PM), which corresponds to Bob implementing measurements, the signal photon then feeds through Bob’s AMZI and is sent to the detector. Alice and Bob’s AMZI’s have a nominally identical differential delay of 400 ps. They are independently phase-locked through temperature feedback on the interference of a continuous-wave reference laser that has the same central wavelength as Alice’s master DFB laser. For a detailed description on phase locking, see Supplementary Note 4.

To demonstrate steering nonlocality with the above setup, we consider the phase-encoding measurement set on Bob’s side, i.e., \({\{{M}_{i}\}}_{n}\), with \({M}_{0}={\hat{\sigma }}_{{\mathsf{Z}}}\) and \({M}_{j}={\hat{\sigma }}_{\frac{j-1}{n-1}\pi }\). We perform the complementary measurement \({\{\overline{{M}_{i}}\}}_{n}\), with \(\overline{{M}_{0}}=-{\hat{\sigma }}_{{\mathsf{Z}}}\) and \(\overline{{M}_{j}}={\hat{\sigma }}_{\left(1-\frac{j-1}{n-1}\right)\pi }\) on Alice’s side, though we do not assume the measurement is faithfully executed. The illustration of how the phase-related operators of \({\{{M}_{i}\}}_{n}\) and \({\{\overline{{M}_{i}}\}}_{n}\) correspond to the signal voltage respectively on the PM and the master laser is depicted in Fig. 3, where the signal voltage of the slave laser works as a temporal reference (See Supplementary Note 5 for technical details).

Fig. 3: Schematic of signal voltages.
figure 3

Taking n = 9 as an example, from top to bottom: (a) driving signal in the master DFB based on injection-locking technique; (b) driving signal in the phase modulator; (c) 2.5 GHz square wave signal in the slave DFB. The master laser and PM introduce complementary phases, which is equivalent to Alice and Bob performing complementary measurements.

Full size image

Test results

Should Alice indeed send half of the entangled pair to Bob, we can verify that Sn = − v, noting that \(\left\vert \Psi (\alpha )\right\rangle\) is perfectly anti-correlated with \({\{{M}_{i}\}}_{n}\) and \({\{\overline{{M}_{i}}\}}_{n}\) being measured, and \({\mathbb{I}}/4\) has no contribution to Sn. On the other hand, if Alice exploits the detection loophole and constructs an LHSM, she can reproduce the correlation results of the entanglement state. To demonstrate that the detection loophole is closed, a large steering parameter surpassing the criterion is required meaning that even with the help of detection loophole, the LHSMs fail to fully reproduce the observed correlation, which in turn verifies the detection-loophole-free nonlocality.

We denote by v* the critical visibility that a detection-loophole-assisted strategy could ever achieve, given certain detection efficiency ϵ. As we mentioned before, the relation between v* and ϵ can be formulated in a semidefinite programming problem, and can be numerically computed47. In Fig. 4a, we plot with solid lines the relation of v* – ϵ for n = 6, 7, 8, 9 respectively. It shows that the benefit of increasing measurement settings is to tolerate a lower critical detection efficiency that permits closure of the detection loophole given certain v, when v is approaching unity.

Fig. 4: The results of steering test.
figure 4

a The colored circles denote the measured steering parameters − Sn which quantify the degree of correlation. The bound of critical v* shown by solid lines is computed based on the loss-tolerant LHSM for n = 6, 7, 8, 9 respectively. b Pairwise time-bin histograms of AMZIs. The notations “A ± " and “B ± " denote the output ports of Alice’s and Bob’s AMZIs respectively. Correlation results in time basis are painted with blue (exemplified by A − & B −), and the ones in phase basis are in red. The erroneous results in time basis are estimated by the accidental coincidence counts in the adjacent time-bins (see the inset).

Full size image

To conclusively certify steering nonlocality, it thus requires − Sn > v*. It is worth noting that a full state tomography to estimate v is unnecessary, because (i) certifying steering nonlocality does not rely on the assumption that the state is entangled, (ii) drawing conclusions based on high fidelity can be inaccurate22,23,54. The remaining question lies in how to estimate Sn from the time-recording data. Specifically, for each pair of outputs of the AMZIs, there are three possible photon arrival times, which results in three equidistant coincidence peaks in the arrival-time histogram. The coincident events in the side peaks yield detections in the time basis (\({\hat{\sigma }}_{{\mathsf{Z}}}\)), according to which we compute the term of k = 0 in Sn. The coincidence which corresponds to the uncorrelated results in time basis is estimated by adopting the counts in the adjacent time-bins. Although the time basis is passively selected depending on the path that the photon takes at the first beam-splitter of the AMZI with a probability of 50%, this probabilistic process does not introduce postselection loophole55 as the data collected in time-basis contributes equally to the nonlocality analysis. On the other hand, the coincident events in the central peak yield detections in the phase basis (\({\hat{\sigma }}_{\theta }\)), according to which we compute the rest of the terms in Sn. An example of our time-recording data depicting by pairwise time-bin histograms is presented in Fig. 4b. The detailed method to obtain Sn are elaborated in Supplementary Note 6.

The measured losses on Alice’s side include on-chip transmission (− 2 dB), chip-fiber coupling (− 1.5 dB), DWDM (− 1 dB), fiber coupling (− 0.1 dB), AMZI (− 1 dB), filtering inefficiency (−0.5 dB), and SNSPD (− 0.5 dB), and the overall loss corresponds to the collection efficiency (− 6.6 dB). In the detection loophole context, we attribute all losses to the detector as one in principle cannot identify where exactly the specific photon is lost. Here, we adopt the Klyshko efficiency56 (also known as heralding efficiency, defined as the coincidence counts divided by the single counts of the opposite arm) to estimate the detection efficiency.

The results of Sn and ϵn are presented in Fig. 4a. In specific, S6 = − 0.9795 ± 0.0031, S7 = − 0.982 ± 0.0033, S8 = −0.9835 ± 0.0031, S9 = − 0.9805 ± 0.0032, and ϵ6 = 0.211 ± 0.0052, ϵ7 = 0.2172 ± 0.0055, ϵ8 = 0.213 ± 0.0051, ϵ9 = 0.2125 ± 0.005. It is clear that given certain detection efficiency, the obtained − Sn for n = 6, 7, 8, 9 lie above the critical v*, which indicates that the steering test is passed, and notably, without detection loophole.

Discussion and outlook

Although the theory allows the critical detection efficiency down to 11.1% with n = 9, the experimental noises and imperfections hamper the system from achieving the ideal performance. We attribute the non-unit degree of correlation in the phase basis mainly to the imperfect interference of the AMZIs, whose interference visibility is about 99.2% each. Regarding the erroneous correlation results in the time basis, we attribute it to the dark counts of the SNSPD which is about 100 Hz and the multi-photon components of the pump light which becomes significant when the pump power increases. When it comes to field tests, another issue that may significantly impact the correlation results is chromatic dispersion, as the transmitter and the receiver could be well separated, and in this case the dispersion compensation modules are required.

One promising application of our platform is the well-known 1sDI-QKD protocol33. For two measurement settings, the critical ϵ for 1sDI-QKD is about 65.9%33, which is beyond the performance of our present setup. However, as proved in ref. 33, securing 1sDI-QKD protocol amounts to demonstrating quantum steering, and thus we note that the critical ϵ for a multi-setting 1sDI-QKD protocol can be significantly reduced through increasing the number of measurement settings. As in our case the loophole at the transmitter side is closed, we propose that a transmitter-device-independent QKD (TDI-QKD) can be realized based on our work.