Kinetic ferromagnetism and topological magnons of the hole-doped Kitaev spin liquid

Kinetic ferromagnetism, resulting from the subtle interplay between the motion of electrons and their interactions, provides a counter-intuitive example of a strong interaction effect in condensed matter physics^1,2. Nagaoka³ famously showed how the interference of paths from a single hole doped into a half-filled Hubbard model with infinite repulsion U can lead to a ferromagnetic (FM) state in a system that typically supports antiferromagnetic (AFM) order. Given that the required large interaction limit is an experimental challenge, signatures of Nagaosa’s ferromagnetism have only recently been observed experimentally in quantum dots⁴ and semiconductor heterostructures⁵. In this context, intriguing questions are whether similar kinetic magnetism can appear in other correlated models that are experimentally accessible; and whether the kinetic FM state itself can be non-trivial, e.g., host chiral excitations.

Seemingly unrelated exotic phases of matter are quantum spin liquids (QSLs) characterized by long-range quantum entanglement and fractionalized spin excitations^{6,7,8,9,10,11,12,13}. The Kitaev honeycomb model is a celebrated example of a two-dimensional Z₂ QSL¹⁴. The famous exact solution shows that the Kitaev spin liquid (KSL)¹⁴ has a gapless ground state with Dirac-type Majorana excitations, while its static Z₂ flux excitations remain gapped. In recent years, the Kitaev honeycomb model has gained experimental relevance with several spin-orbit-coupled 4d and 5d transition metal candidate materials, such as Na₂IrO₃^15,16,17,18 and α-RuCl₃^{19,20,21,22,23,24,25}, having been proposed as promising realizations of Kitaev’s bond-anisotropic Ising interaction (K)^{26,27,28,29,30,31,32,33,34,35}. However, the KSL is fragile and residual zigzag magnetic order appears in all materials at low temperatures^36,37, because of the inevitable presence of additional interactions such as the off-diagonal symmetric (Γ) and Heisenberg (J) exchanges^19,29. Hence, understanding the robustness of the KSL in the extended K-Γ-J Kitaev model has become a subject of intense research^{29,38,39,40,41,42,43,44,45}, e.g. the K-Γ (with J = 0) is believed to remain disordered^29,46,47,48. Here, we explore a different route by studying the hole doping resilience of the KSL and uncover a surprising connection between the KSL and kinetic ferro-magnetism.

In this work, we account for the effects of hole doping by considering an extension of the Kitaev honeycomb model, referred to as the t-K model, where t denotes the hopping strength of doped holes. In the slow hole limit (t ≪ K), the KSL phase is robust and holes only introduce quasi-static vacancies^49,50, see Fig. 1a. However, in realistic systems, t is typically much larger than the Kitaev exchange K, and previous works based on parton mean-field theories suggested superconducting ground states in the hole-doped regime^51,52,53,54. Yet, our numerics does not support superconductivity at the considered low doping values; see Supplementary Note 2. Recently, a density matrix renormalization group (DMRG) study suggested a charge density wave ground state emerging on top of a hole-doped AFM KSL, in which the superconducting correlations fall off almost exponentially at long distances⁵⁵.

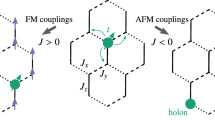
a Illustration of the t-K model with three types of bonds, γ = x, y, z. Sites j = 1, …, 6 label the convention for plaquette operators W_p. The system sustains the site-diluted KSL ground state with fractionalized spins (W_p ≈ 1) only for a slow hole (red ball). b For t ≿ K doping depletes plaquette operators W_p while simultaneously polarizing the spins, which leads to FM order along the [001] direction. c, d The ground-state phase diagram for the one-hole doped t-K model (K = 1) on a YC4 cylinder with length L_x = 12 (corresponding to a doping level of δ ≈ 0.01). The evolutions of (c) the magnetic moment M^z and (d) the average flux W_p indicate a phase transition from a site-diluted KSL (blue regime in insets) to a FM state (red regime) around t^* ≈ 0.28.

Full size image

We investigate the ground state of the t-K model by DMRG^56,57 and show that the FM KSL is remarkably fragile already for small and slow hole doping. For hopping strengths t of the order of the KSL’s flux gap, ΔE_v ~ 0.1K, the system is already partially FM polarized by the itinerant holes, spontaneously breaking the time-reversal symmetry, as illustrated in Fig. 1b. To account for our numerical results, we develop a parton theory incorporating fermionic holes and bosonic spinons/magnons. It unveils that the hole kinetic term effectively serves as a FM Heisenberg coupling destabilizing the KSL. In addition, our parton theory shows that the resulting FM order along the [001] direction originates from an order-by-disorder mechanism^58,59. We further uncover that the presence of a finite FM off-diagonal exchange, Γ > 0, shifts the magnetization direction from [001] to [111]. Remarkably, due to the change of spin polarization direction, the kinetic FM state becomes non-trivial. It spontaneously forms topological FM order with chiral magnon edge modes, akin to the FM state of the Kitaev model induced by a strong external magnetic field^60,61. Furthermore, we show that hole doping can significantly lower the critical field above which the field-polarized FM state appears in Kitaev candidate materials, such as α-RuCl₃.

Model Hamiltonian

The celebrated Kitaev honeycomb model is defined by the following Hamiltonian¹⁴

where \({S}_{j}^{\gamma }\) (γ = x, y, z) are the S = 1/2 spin operators and \({S}_{j}^{\gamma }{S}_{k}^{\gamma }\) are Ising couplings according to the γ-type of nearest-neighbor (NN) 〈jk〉 bonds (see details about the model in Supplementary Note 1). Microscopic derivations^{32,33,62,63,64} have shown that the Kitaev interaction of several material candidates is likely FM. Therefore, we focus on positive K and set K = 1 as the unit of energy. There exist conserved plaquette operators W_p on each hexagon p as

where the lattice sites j = 1, …, 6 correspond to the elementary hexagon plaquette p shown in Fig. 1a. The pristine KSL ground state has W_p = 1 for all plaquettes.

To describe the physics of hole doping, we introduce the t-K model^51,65,66

where \({c}_{s}^{\dagger }\) is the creation operator of an electron with spin index s = ↑, ↓ and the projector \({\mathcal{P}}\) removes doubly occupied states. Spin operators, \({S}_{j}^{\gamma }={{\bf{c}}}_{j}^{\dagger }{\sigma }^{\gamma }{{\bf{c}}}_{j}/2\), are given by the fermionic vectors \({{\bf{c}}}_{j}^{\dagger }=({c}_{j,\uparrow }^{\dagger },{c}_{j,\downarrow }^{\dagger })\) and the standard σ^γ Pauli matrices. The hole doping is parameterized by δ such that \({\sum }_{s}\langle {c}_{j,s}^{\dagger }{c}_{j,s}\rangle =1-\delta\). Note that the NN hopping is spin-independent and the effects of spin-orbital coupling are nevertheless retained in \({{\mathcal{H}}}_{{\rm{S}}}\)⁶⁵, resulting in a space symmetry group of D_3d. Besides, the t-K model is also symmetric under time reversal transformation and preserves the charge-U(1) conservation. The ground states for Eq. (2) are studied by the DMRG method in the form of matrix product states (MPS); see details in the “Methods” section.

Phase diagram

First, we focus on the one-hole doped system. The ground-state phase diagram on YC4 cylinders is analyzed by studying the average magnetic moments M = 〈S_i〉 and the average Z₂ flux W_p, as shown in Fig. 1c, d. For t < t^*, the ground state corresponds to a site-diluted KSL, where the kinetic energy of the holes is insufficient to overcome the Z₂ flux excitation gap ΔE_v ~ 0.1K. Instead, the presence of the slow-moving holes can be thought of as quasi-static vacancies within the KSL state^49,50. Although W_p slightly decreases as t increases in this phase, the system does not acquire any magnetization (see Supplementary Note 5).

We observe that a phase transition occurs at t = t^* ≈ 0.28K, as visible by kinks in the curves of both the magnetization and Z₂ flux, see inset plots of Fig. 1(c) and (d). As one of our main findings, already for t > t^* a FM phase appears with a finite magnetization along the [001] direction. We note that the first-order derivative of the ground-state energy also exhibits a kink around t^* ≈ 0.28K which suggests that the phase transition is of second order, see Supplementary Note 2.

This FM phase is an example of kinetic magnetism, which spontaneously breaks the time-reversal symmetry and arises solely from the holes’ kinetic energy. Remarkably, the KSL correlations are only partially depleted, as signaled by the gradual decrease of the Z₂ flux W_p in Fig. 1d. This coexistence of magnetization and finite plaquette flux is a general feature of the [001] FM phase until the system is fully polarized by a sufficiently large hopping strength. According to Nagaoka’s theorem, for a single-hole doped system³ in the thermodynamic limit, the saturated FM state is only reached for vanishing spin exchange (or in other words, the on-site Hubbard U → ∞). Therefore, the intriguing coexistence of FM order and KSL correlations could generally persist in systems described by the t-K model.

We further investigate whether FM order persists for multiple holes and study the magnetization as a function of hole density δ in Fig. 2. Unlike Nagaoka’s ferromagnetism, which may disappear for a thermodynamic density of holes⁶⁷, we find that the FM order observed in our work is robust and can be further enhanced with multi-hole doping. First, a larger δ can lower the critical value of t^*. For instance, at t = 0.2K, the system remains in the site-diluted KSL phase without any magnetization for δ ≲ 0.02, while a small but finite magnetic order emerges for δ > 0.02. For the hopping strength t which is already capable of polarizing spins at δ ≈ 0.01, a slight increase in δ can significantly enhance the magnetization until it reaches a saturation value at δ ≈ 0.05. Due to a rapid increase in entanglement entropy, our DMRG simulations face convergence problems for systems with even higher doping levels. Nevertheless, our results suggest that the ferromagnetic order is a generic feature of the t-K model, at least in the low doping limit δ ≤ 0.06.

The magnetization as a function of doping level δ for variable values of hopping strength on YC4 cylinders with length L_x = 12 and K = 1.

Full size image

Off-diagonal exchanges

Next, we study the hole-doped extended Kitaev honeycomb model, dubbed the t-K-Γ model, as a more realistic system that incorporates additional off-diagonal symmetric spin exchange parameterized by Γ. The spin part of the model now becomes

with α ≠ β ≠ γ for the Γ terms on γ-type bonds. Although the Γ term is typically believed to be AFM^46,68, here we focus on the effect of a FM Γ > 0 as this has the most interesting consequences.

In the absence of Γ, the spin polarization is always along the [001] direction (or by symmetry equivalently, the [010] and [100] directions), which can be attributed to an order-by-disorder mechanism as we will explain below. In Fig. 3a, we show that the presence of Γ > 0 can shift the spin polarization direction from [001] to [111]. Indeed, already a tiny value of Γ^* is sufficient to induce a significant change in the polar angle of magnetization, denoted as \(\phi \equiv {\cos }^{-1}({M}^{z}/| M| )\). For Γ = 0.02, the polar angle is already very close to the value of \({\phi }_{[111]}={\cos }^{-1}(1/\sqrt{3})\), which corresponds to a FM order along the [111] direction, see Fig. 3b. At Γ^* ≈ 0.01K, a noticeable kink in the first-order derivative of the ground-state energy in Fig. 3c indicates that this change in spin polarization direction is accompanied by a phase transition. We will discuss below that this transition leads to topologically non-trivial magnon excitations. The magnetization displays a dip around Γ^*, corroborating the findings from the analysis of the ground-state energy. Note that a moderately large Γ can also enhance the magnitude of the magnetization.

a The polar angle \(\phi \equiv {\cos }^{-1}\left({M}^{z}/| M| \right)\) representing the magnetization direction as a function of Γ, where ϕ = 0 indicates the [001] direction and the black dashed line the [111] direction. Inset: a finite FM Γ > 0 can induce a rotation of the spin polarization direction from [001] (transparent purple arrows) to [111] (solid red arrows) by an angle ϕ. b The amplitude of magnetization as a function of Γ for the one-hole doped model with t = 20K on a YC4 cylinder with length L_x = 12, corresponding to doping level δ ≈ 0.01. Inset: The first-order derivatives of ground-state energy versus Γ.

Full size image

Compared to the FM Γ, the perturbation of an AFM Γ has a much smaller impact on the [001] ordered ground state. For instance, a small AFM Γ ≈ −0.02 only induces a canting field in the [001] order. However, a FM Γ with a similar magnitude is sufficient to shift the polarization direction from [001] to [111].

Parton mean-field theory

In order to understand the selection of the FM moment direction and the impact of Γ, we develop a parton mean-field theory. To effectively describe the low-energy degrees of freedom in the kinetic FM phase, we consider the following parton representation for electron operators⁶⁹ with \({c}_{j,s}^{\dagger }\equiv {h}_{j}{b}_{j,s}^{\dagger }\). Here, \({b}_{j,s}^{\dagger }\)’s are Schwinger boson operators representing spinons, and h_j’s are fermionic holon operators representing empty sites. The local constraint, \({h}_{j}^{\dagger }{h}_{j}+{\sum }_{s}{b}_{j,s}^{\dagger }{b}_{j,s}=1\), ensures the original three-dimensional physical local Hilbert space. The parton theory is constructed such that it allows for spontaneous symmetry breaking toward ordered states.

The t-K-Γ model takes the form

with \({\hat{F}}_{jk}\equiv {\sum }_{s}{b}_{j,s}^{\dagger }{b}_{k,s}\) representing short-range FM spin correlations⁷⁰. One can observe that the hopping term in Eq. (4) connects the hole’s kinetic energy \({\hat{P}}_{jk}\equiv {h}_{j}^{\dagger }{h}_{k}\) with FM correlations \({\hat{F}}_{jk}\), suggesting that finite doping with dominant t dramatically renormalizes the spin-spin interactions and fosters FM order.

The second term in Eq. (4), \({\hat{H}}_{jk}^{\gamma }\), represents spin interactions as defined in Eq. (3), but expressed in terms of bosonic spinons instead of electron operators. We develop a large-N mean field theory within a Schwinger-boson approach^70,71,72 in which the spinon occupancy is given by \({n}_{b}={\sum }_{s}{b}_{j,s}^{\dagger }{b}_{j,s}=1-\delta\) (see Supplementary Note 3).

Guided by our DMRG results, our interest lies in the FM phase with t ≫ K. We also explored the possibility of a gapped QSL phase but found no evidence thereof in the limit of n_b → 1. Hence, the most natural ansatz is a FM state along the general direction of \((\sin \phi \cos \theta ,\sin \phi \sin \theta ,\cos \phi )\). For conveniently describing magnon excitations, we can replace the Schwinger bosons with Holstein–Primakoff (HP) bosons as^1,73

where \({a}_{j}^{\dagger }\) and a_j are the creation and annihilation operators for the HP bosons (magnons), respectively. Then we perform a standard Hartree-Fock decoupling of Eq. (4) to obtain a mean-field theory with separate hole and spin parts, dubbed \({{\mathcal{H}}}_{{\rm{h}}}\) and \({{\mathcal{H}}}_{{\rm{s}}}\), respectively. Here, \({{\mathcal{H}}}_{h}\) refers to a spinless free-fermion band with renormalized bandwidth by the factor \(| \langle {\hat{F}}_{jk}\rangle |\) and filling of δ. The spin part \({{\mathcal{H}}}_{{\rm{s}}}\) is treated in spin-wave theory (SWT) incorporating up to fourth-order Holstein–Primakoff expansions, and the spin amplitude is renormalized to S = n_b/2. The expectation values of FM spin correlations \({\hat{F}}_{jk}\) and hole’s kinetic energy \({\hat{P}}_{jk}\) are determined self-consistently. Remarkably, we can now see that for δ ≪ 1 the kinetic energy effectively acts as a FM Heisenberg interaction with a coupling constant J ≡ − 〈P_jk〉t/n_b ~ ∣t∣δ.

The semi-classical ground-state energy of the FM Kitaev honeycomb model (t = Γ = 0) turns out to be independent of ϕ and θ, yielding an emergent O(3) manifold of degenerate ground states. This classical O(3) degeneracy can be lifted by quantum fluctuations in a quantum order-by-disorder mechanism^58,59. Within SWT the quantum correction to the ground-state energy is E_s = − κ(κ + 2)N_cK/4 + 3κ(2κ + 1)N_c J + ∑_k,nω_k,n, where N_c is the number of the unit cells and ω_k,n are the two magnon bands of the honeycomb lattice. Note that ω_k,n depend on ϕ and θ implicitly, and thereby so does E_s. Our calculations reveal that a magnetization along the [001] direction (or equivalently, the [100] and [010] directions) is energetically preferred in accordance with our DMRG results (see Supplementary Note 3).

A complication arises from the fact that the semi-classical ground state of the pure Kitaev honeycomb model is a classical spin liquid⁷⁴ which is manifest in the linear SWT for arbitrary spin polarization directions as a nearly flat magnon band with almost zero energy (see Supplementary Note 3). Thus, an HP expansion that only includes the quadratic terms is insufficient to correctly capture the quantum fluctuations. We employ a nonlinear SWT by including the quartic terms in the HP expansion and treat these within the Hartree-Fock decomposition⁷⁵. We indeed find significant renormalizations of the flat magnon bands, for instance, a closing of the gap between formerly flat magnon bands in the nonlinear SWT for Γ = 0. More technical details can be found in Supplementary Note 3.

Including a FM Γ > 0 breaks the semi-classical O(3) degeneracy of the ground state. Our SWT shows that the semi-classical ground state has [111] magnetic order rather than [001], which is again consistent with our DMRG calculations, see Fig. 3b. From the magnetic field polarized regime of the Kitaev model, it is known that different polarization directions can have qualitatively different types of boundary magnon excitations as first pointed out in ref. ^60,61. For spins polarized along the [001] direction with Γ = 0, the two magnon bands touch linearly and are almost non-dispersive along one of two primitive vectors. The system thereby cannot support nontrivial boundary excitations. On the other hand, the introduction of a finite Γ > 0 modifies the magnon bands from the change of the spin polarization to the [111] direction. Consequently, the two magnon bands are separated by a gap and acquire non-zero Chern numbers (−1, 1) for the lower and upper magnon bands, respectively^60,76,77. Hence, as our second main result, we find that the kinetic FM state of the doped Kitaev model (with small Γ > 0) spontaneously breaks TRS forming a topological magnon insulator. This explains the phase transition found when turning on the off-diagonal Γ interactions, see Fig. 3.

To see how the change in spin polarization can give rise to chiral boundary states, we calculate the magnon bands within SWT on narrow cylinders. With PBCs along y-direction, k_y is still a good quantum number and the 2D systems can be treated as L_y independent 1D chains. The magnon spectra for the [001] and [111] ordered states are shown in Fig. 4a, d. Indeed, only the [111] ordered state has chiral boundary modes (green) as predicted.

a Magnon bands on a cylinder for a [001] ordered state within nonlinear SWT. The real-time dynamics of (b) spin current j_s(t, x) and (c) charge current j_c(x, t) for a [001] ordered state. These results are obtained by DMRG using one-hole doped YC3 cylinders (δ ≈ 0.013). For a–c, we set the off-diagonal exchange Γ = 0 and hopping strength t = 10K. The self-consistent solution with doping level δ = 0.01 gives kinetic hole energy \(\langle {\hat{P}}_{jk}\rangle \approx -0.93\times 1{0}^{-2}\) and FM spin correlation \(\langle {\hat{F}}_{jk}\rangle \approx 0.79\) on the x − (y-) type bonds as well as \(\langle {\hat{F}}_{jk}\rangle \approx 0.82\) on the z-type bonds. d Magnon bands within nonlinear SWT on a cylinder for the [111] ordered state. The chiral edge states are marked in green. The real-time dynamics of (e) spin current j_s(t, x) and (f) charge current j_c(x, t) for a [111] ordered states within DMRG. For d–f, we set Γ = 0.05K and t = 10K. The self-consistent solution with δ = 0.01 gives kinetic hole energy \(\langle {\hat{P}}_{jk}\rangle \approx -0.93\times 1{0}^{-2}\) and FM spin correlation \(\langle {\hat{F}}_{jk}\rangle \approx 0.85\) on all three type bonds.

Full size image

Real-time dynamics

So far our observation that a topological FM state is realized for the [111] direction solely relies on the parton+SWT description. A numerical confirmation by DMRG is complicated by the fact that the ground state is topologically trivial but only the magnon excitation spectrum carries signatures of the magnon Chern bands. Therefore, we study the distinct real-time dynamics of excitations in the [001] and [111] ordered FM states. To obtain an initial state with a magnon-like excitation at the boundary, we apply a local time-reversal operator at lattice site j, which couples to spin excitations for arbitrary spin polarizations, to a one-hole doped ground state \(\left\vert \Psi \right\rangle\) as

where \({\mathcal{K}}\) denotes the complex conjugate operator. Note that \({\sigma }_{j}^{y}\) also annihilates the components of \(\left\vert \Psi \right\rangle\) which contain a local hole at site j. As a result, in addition to flipping the spins at site j, it also weakly excites charge excitations and slightly modifies the global magnetization pattern. Starting with the prepared initial state \(\left\vert \Psi (j)\right\rangle\), the system is evolved by performing a standard real-time evolution, \(\left\vert \Psi (j,t)\right\rangle ={e}^{-i{\mathcal{H}}t}\left\vert \Psi (j)\right\rangle\); see “Methods” section for details.

We create a one magnon defect at site j in the leftmost column of the YC cylinders and follow the spin current for each column x defined as

with 〈. .〉 the expectation value with respect to \(\left\vert \Psi (j,t)\right\rangle\) and (x, y) denoting the lattice coordinates. Note that j_s(x, t) is obtained by summing over all the sites belonging to the x-th column, namely, summing over allowed k_y. Additionally, we also keep track of the charge current

where \({n}_{j}^{h}=1-{\mathcal{P}}{\sum }_{s}{c}_{j,s}^{\dagger }{c}_{j,s}{\mathcal{P}}\) is the occupancy of holes.

The simulations for the dynamics are performed on YC3 cylinders, and the results are shown in Fig. 4. We observe a distinct difference in the spin currents between the [001] and [111] ordered states, as evidenced by the leftmost boundary columns in Fig. 4b and e, respectively. The spin current in the [001] ordered state shows very little dynamics, as indicated by its small magnitude of j_s ~ 10⁻⁴ in Fig. 4(b). It can be attributed to the absence of distinct boundary modes and the almost vanishing velocity of magnon modes. In stark contrast, for the [111] direction j_s(x, t) exhibits a strong and long-live signal in the leftmost boundary as expected for a localized surface excitation. Note that Eq. (5) unavoidably involves excitations related to bulk magnon bands, which explains why the boundary spin current can leak into the bulk. We have checked that the magnetic field-induced topological FM in the [111] direction^60,61 shows a very similar response confirming the presence of chiral magnons.

The charge current for the [001] and [111] ordered states are very similar, see Fig. 4c and f, respectively. This is consistent with our parton mean-field theory. Both the [001] and [111] ordered states give rise to similar short-range FM spin correlations (see Supplementary Note 3), which suggests that the holon Hamiltonians are similar.

Implications for the field-polarized state of α-RuCl₃

Unlike the simplified models introduced in Eqs. (1) and (3), more realistic models for experimentally relevant materials are much more complicated. Here, we focus on α-RuCl₃ and related materials^31,33,78 which are often described by a number of parameters, including \(\{K,J,\varGamma ,\varGamma ^{\prime} ,{J}_{3}\}\). The corresponding Hamiltonian is expressed as

where α ≠ β ≠ γ and 〈ij〉₃ denotes the third NN bonds. Here, we have introduced minus signs for each parameter, which is opposite to what is often used in the literature. For simplicity, we focus on a specific point in the parameter space, given by

which is close to a set of parameters identified in ref. ⁷⁸ for α-RuCl₃, resulting in a zigzag-ordered ground state obtained by DMRG simulations. Moreover, an in-plane magnetic field suppresses the long-ranged zigzag order and ultimately polarizes the state for sufficiently strong fields. Furthermore, it has been proposed that an intermediate KSL state may separate these phases. To account for this effect, we introduce an additional Zeeman term in Eq. (8). The total spin Hamiltonian is then given by

where h_in represents the in-plane magnetic field along the \([1\bar{1}0]\) direction.

We then investigate how hole doping modifies the phase boundary of the zigzag phase. We add the same kinetic energy term for the holes as in Eq. (2), to the experimentally relevant Hamiltonian Eq. (10) and compute the ground-state phase diagram with DMRG; see Fig. 5. Remarkably, we find that the phase boundary between the zigzag and polarized phases is highly sensitive to hole doping. For a vanishing hopping strength, t → 0, the critical magnetic field required to polarize the spins is approximately \({h}_{in}^{* }\approx 0.085\). However, already for a small hopping t = 0.8K and low hole doping of δ = 0.0625, the critical magnetic field is reduced to \({h}_{in}^{* }\approx 0.04\). A larger value of t ≈ 1.8K can drive the zigzag order to a FM order (not shown). This can be understood by noting that ∣t∣δ effectively acts as a FM Heisenberg exchange constant J. The polarized phase is distinct from the kinetic FM phase, as the latter develops magnetic order spontaneously. The significant effect induced by the kinetic energy of holes, therefore, is a complicating factor in identifying to correct Hamiltonian parameters in comparison to experimental measurements.

The left inset shows a typical zigzag order at (t, h_in) = (0.3, 0.03) and the right one shows a polarized state at (t, h_in) = (0.5, 0.06). Positive and negative local magnetizations, \(\langle {S}_{j}^{x}\rangle\), are represented by red and blue dots, respectively, with their radii scaled according to the magnitude of \(\langle {S}_{j}^{x}\rangle\), with \(\langle {S}_{j}^{x}\rangle \approx 0.21\). The doping level is δ = 0.0625.

Full size image

In summary, we have studied the hole-doped Kitaev-Γ model using DMRG and effective parton descriptions. It is by now well known that the FM KSL is much more fragile with respect to the application of an external magnetic field compared to the AFM KSL⁷⁹. Similarly, our DMRG simulations suggest that the AFM KSL is also much more robust to hole doping. Meanwhile, distinct hole spectral functions have been numerically observed in FM and AFM KSLs, in which a dynamical Nagaoka ferromagnetism emerges in the FM KSL only⁸⁰. Concentrating on FM Kitaev exchange, we have shown here that small hole doping is sufficient to destabilize the KSL leading to a kinetic FM state generally coexisting with finite plaquette fluxes. We emphasize that, unlike the field-polarized phase in a magnetic field⁸¹, the doping-induced FM order breaks the time-reversal symmetry spontaneously. Due to the particle-hole symmetry of our model, our conclusions also hold for charge doping.

We developed a parton mean-field theory, incorporating fermionic holons and bosonic magnons, which indeed shows that hole condensation gives rise to effective FM Heisenberg exchanges. We found that in the absence of off-diagonal exchange Γ, the spin polarization is along the [001] direction due to an order-by-disorder mechanism, which is also supported by DMRG simulations. A FM Γ term switches the polarization direction to [111], which leads to a distinct topological FM phase with chiral boundary magnon excitations.

Our work raises a whole range of questions for future research. First, one could investigate flux threading and topological entanglement of the FM phase coexisting with finite plaquette fluxes to probe the presence of topological order. Second, it would be interesting to search for other kinetic FM phases of Hubbard models hosting chiral magnon excitations. Third, to further investigate the transition between the KSL and kinetic FM phases, it would be desirable to develop a parton theory incorporating bosonic holons and fermionic spinons. In this context, such a theory could be the starting point for a self-consistent random phase approximation⁸² or Gutzwiller-boosted DMRG^83,84,85,86 in order to study the ordering instabilities and spin excitation spectra. Forth, in our real-time evolution results we could observe that the excitations of spin induce a (weak) response of charge, and vice versa. This could possibly be captured by a time-dependent parton mean-field theory in future studies to explore the interplay of charge and spin transport⁸⁷. Fifth, a study of doping effects for realistic model Hamiltonians could unveil a new mechanism (see Supplementary Note 4) for stabilizing the zigzag magnetic orders observed experimentally. This could also be important for refining the microscopic models of RuCl₃ and its peculiar magnetic field response, both of which remain poorly understood⁷⁸. Sixth, the origin of the observed thermal Hall effect of RuCl₃⁸⁸ is hotly debated⁸⁹ and it would be very interesting to explore how the topological magnons of the weakly doped Kitaev model studied here may contribute.

In conclusion, the Kitaev honeycomb model continues to be a fertile soil for novel physics. We expect the interplay of Kitaev spin exchange with kinetic electron motion to hold further surprises in the future.

Details on the numerical methods

All simulations such as DMRG and real-time evolutions based on the MPS method were performed with the Python library TeNPy⁹⁰.

In order to implement DMRG calculations, the system is placed on a two-dimensional cylindrical geometry, dubbed YCL_y, with periodic boundary conditions (PBCs) along the short direction (with L_y unit cells), while the longer one (L_x) is open. We have used U(1) symmetry for particle number conservation. For Γ = 0, the additional Z₂ spin parity symmetry has been implemented. The typical bond dimensions are kept as large as χ = 4000 to reach the converged results.

The real-time dynamics is performed by the standard MPO-evolution algorithm. In practice, we approximately represent the short-time unitary operator,

as a compact matrix product operator (MPO)⁹¹, where a small time step dt = 0.01[K]⁻¹ has been used. Then the time evolution can be efficiently simulated by applying such an MPO to the initial state \(\left\vert \Psi (j,t=0)\right\rangle\) successively. At each intermediate step of the real-time evolution, one needs to truncate the MPO-evolved MPS. For bond dimension χ = 1000, we find that the truncation errors are close to zero when t < 3[K]⁻¹ and are always less than 10⁻⁵ during the whole evolution period of 5[K]⁻¹.