Introduction

Petri nets (PN) are specially designed bipartite graphs, introduced by Carl Adam Petri in 19621. Basic Petri nets consist of two types of nodes: places and transitions, with arcs linking the places and transitions, and tokens representing the states of the systems. In the context of intra-cellular molecular interactions, “places” correspond to entities such as proteins, RNAs, DNA regions, and chemicals, while “transitions” represent different types of biochemical reactions, such as catalysis, transcription, translation, and protein binding. Building on these fundamental concepts, Petri net formalism has been extended for modeling biological systems. Related Petri net formalism variants include colored Petri Net (CPN)2,3, fuzzy continuous Petri Net (FCPN)4, stochastic Petri Nets (SPN)5 and signaling Petri Nets (also called SPN)6.

With the development of Petri net formalism, these models have been successfully applied to biological systems, particularly in the study of intra-cellular molecular interactions. For example, Yu et al. combined CPN and machine learning techniques to model depression, estimating the influence of various hormones on the condition7. Gutowska et al. integrated Petri nets with ordinary differential equations (ODEs) to model the ATM/p53/NF-kappaB pathway8, leveraging the strength of both approaches. Pennisi et al. constructed a CPN model for immune system response9, while Liu et al. implemented an FCPN algorithm to simulate the heat shock response system10. Petri net modeling provides a structured and systematic framework for representing complex biological interactions, facilitating the analysis of dynamic behaviors and the identification of key regulatory components.

Although a database of pre-compiled Petri net model of biological systems11 have been established, and tools to map from systems biology markup language (SBML)12 to Petri net markup language (PNML) are available13, there remains a need for de novo construction of Petri net models for specific biological processes or diseases. Detailed protocols for building Petri nets for biological pathways and performing simulations with established tools have been described14,15,16,17, but manually constructing a Petri net model, even with the guidance of professional knowledge, can be a time-consuming process, taking hours or months depending on the network’s complexity. Many efforts have focused on automating the construction of reaction network models, as summarized in Table 1. These methods typically fall into two categories. The first computes the likelihood of reactions based on “first principles”, i.e., fundamental physical, chemical, or mathematical laws governing chemical reactions. Examples include STEERING WHEEL18, RTMR19, Chemoton20, pReSt21, YARP22, AutoMeKin23, and RMG24. While such methods are valuable for predicting new potential reactions without relying on empirical data, they tend to perform better for industrial chemical reactions than for biochemical reactions in living cells, where the in vivo environment is far more complex than in vitro chemical conditions.

Table 1 Recent advances in automatic construction of network models
Full size table

The second type of method focuses on automatically constructing Petri net models for biological systems. One example is the work of Chase Cockrell, Scott Christley, and Gary An in 2022, where they introduced a machine learning-based framework called MAGCC25. This framework extracts reaction rules from the literature, selects the appropriate model type (including Petri net), and generates executable code for the chosen model. Its key feature is the use of AI to automate knowledge base creation and simulation model construction. However, the accuracy of current AI models in natural language processing (NLP) and logical reasoning, particularly in scientific model construction, remains concerning. Another software, VANESA15,26, was originally published by Brinkrolf et al. in 2014, as an update to the semi-automatic approach MoVisPP11. VANESA automates network construction by querying knowledge bases and converting the resulting networks into Petri nets for simulation. While it can build customized networks for specific proteins or metabolites, VANESA relies on different databases for different types of biological networks: metabolic pathways are constructed from KEGG27,28, while protein interaction networks are drawn from Mint29, IntAct30, and HPRD31, leading to separation between networks of different omics.

To enable the rapid and automated construction of Petri net models for molecular interaction networks, we utilized the topological information from GIN version 2 (GINv2)32 to build initial networks and then convert the networks into Petri net models. GINv2 is a multi-omics network that we previously built for humans by integrating data from 10 knowledge bases, including KEGG, Reactome, PID etc.27,28,33,34,35,36,37,38,39,40,41,42. The databases that constitute GINv2 cover phosphorylation reactions, signaling, metabolic pathways, and integrate proteomic and metabolomic interactions, providing a comprehensive view of multi-omics intracellular molecular interaction networks. The structure of GIN, which we refer to as the “meta-pathway”, closely resembles that of a Petri net, making the conversion of meta-pathways to Petri nets feasible.

To automate the construction of Petri net models from GINv2, we developed an R package called GINtoSPN. This tool generates a topological network based on user-defined genes and chemicals and converts it into a marked Petri net model. We tested the tool by constructing a Petri net model using a refined list of NF1-related genes and an RNA expression dataset generated from 143 human normal skin fibroblast cells43. Simulations of the Petri net model under both normal and NF1-mutated conditions showed persistent accumulation of Ras proteins bond to GTP, while other molecules exhibited varying behaviors, suggesting that NF1 loss of function has individual-specific effects.

Results

Conversion of meta-pathways to Petri nets

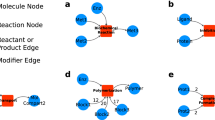
We previously introduced the concept of the meta-pathway structure by the construction of GIN, first from KEGG data for over 7000 species (the GIN version 1) and later by integrating 10 human knowledge bases (the GIN version 2)32,44. The key feature of the meta-pathway structure is the “intermediate” nodes we introduced in the graph to link the substrates, enzymes, and the products of biochemical reactions. Since the substrates and the enzymes must come into spatial proximity for a reaction to occur, there is a temporary state where all molecules involved form a transient “complex”. This led to the creation of “intermediate” nodes, which standardize the representation of both signaling and metabolic reactions (Fig. 1A, left). There are notable similarities between the meta-pathway structure and Petri nets. In a simple Petri net, “places” represent real entities or objects, which are equivalent to the nodes of molecules in GIN; “transitions” represent actions, corresponding to GIN’s intermediate nodes. However, because GIN was not originally designed for biological system simulations, it lacks an equivalent to Petri net “tokens”, which indicate the quantity of materials or signals held by places (Fig. 1A, right). Nevertheless, GIN contains extensive information on intracellular molecular interactions, especially for the human species. Bridging GIN and Petri nets will streamline the construction of Petri net models and extend GIN’s utility for biological network simulations.

Fig. 1: The strategies to construct Petri net models from GIN.
figure 1

A The structural similarities between meta-pathways and Petri nets. B The major steps in Petri net construction. GINtoSPN requires an input list of genes/chemicals to query the pre-built GINv2 and extract a topological sub-graph. The tool then converts the sub-graph into a Petri net in the mEPN style.

Full size image

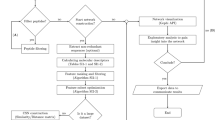
To enable automatic assembly of Petri net models from a given list of genes and/or chemicals, we developed an R package named GINtoSPN. The tool utilizes the topology information from a pre-built igraph object of GINv2, extracts the paths between the input genes/chemicals, predicts extra nodes that participate in the interactions, and converts the resulting sub-graph into a Petri net in the modified Edinburgh Pathway Notation (mEPN) style45,46,47 (Fig. 1B). Depending on the complexity of the graph derived from the input gene/chemical list, the entire process takes just seconds to minutes. The mEPN-styled Petri net model can be exported in GraphML format and directly loaded into Biolayout express3D48 for SPN simulations.

Construction of a Petri net model for neurofibroma

To demonstrate the application of our tool, GINtoSPN, for the automatic construction of Petri net models, we built mEPN-styled Petri net models for neurofibroma and neurofibromatosis type I (NF-1). NF-1 is caused by the mutation of the Neurofibromin 1 (NF1) gene, which accelerates the conversion of the active form of Ras protein, Ras-GTP, to its inactive form, Ras-GDP49,50. Mutations in the NF1 gene lead to abnormally high levels of active Ras, which in turn activates downstream AKT/mTOR, Raf/MEK/ERK, and Rac1/Cdc42 signaling pathways, promoting cell survival, growth, and proliferation51. NF-1 is associated with various manifestations such as multiple café-au-lait macules (CALMs), skin-fold freckling, iris Lisch nodules, and nervous system tumors. However, none of these features alone is sufficient for the diagnosis of NF152, and the phenotypes of the NF1 gene’s mutation can vary even among relatives53. This suggests that the effects of NF1 mutation on the intracellular molecular interaction networks may differ significantly between individuals. To our knowledge, no Petri net model has yet been built for NF-1, which could aid in analyzing the diverse responses to NF1 mutations across individuals.

We began by constructing a Petri net model for neurofibroma using the list of 19 genes related to the term “neurofibroma” in the Human Phenotype Ontology (HPO:HP:0001067). This term is associated with 24 diseases, including NF1. We extracted topological information from GINv2 and incorporated transcription factor (TF) to target relations from GTRD54,55. The resulting topological graph contains 91 nodes in total, with 25 proteins, 5 chemicals, 8 complexes, 16 promoters (labeled as “.state” in the graph), 16 RNAs, and 21 intermediate nodes (Fig. 2A). Notably, 19 new nodes, including proteins, chemicals and complexes, were introduced into the graph (Supplementary Table S1). Among these, several are well-known players in Ras signaling, such as TP53, RAC1, and ARRB1, while others, like KITLG and PDGFRB, act as ligands or receptors for the proteins in the input gene list. These results demonstrate that GINtoSPN can predict relevant associated nodes, supplementing potentially missing information from the given gene/chemical list.

Fig. 2: The topological graph and the Petri net constructed for neurofibroma.
figure 2

A The topological graph extracted from GIN. B The mEPN-styled Petri net model converted by GINtoSPN.

Full size image

Next, we converted the topological sub-graph into an mEPN-styled Petri net (Fig. 2B). To align with the definitions of a Petri net, new transition nodes were introduced during the conversion process to connect TFs to DNA, DNA to RNA, and RNA to protein, all following the mEPN style. Since the term “neurofibroma” in HPO is a general term associated with 24 different diseases and is not specific to NF-1, we chose not to add tokens to this Petri net model and proceeded to build an NF-1-specific model.

Construction of a Petri net model for neurofibromatosis type I

It is known that mutations of NF1 gene activate downstream signaling pathways and increase the risk of NF-1. To construct a Petri net model for NF-1, we first added the core genes of the downstream signaling pathways to the input gene list, including key genes from the PI3K/Akt and Ras/RAF/ERK pathways (Supplementary Table S2). Additionally, we selected phenotypes classified “very frequent” in NF-1 (ORPHA:636) according to HPO. Since each phenotype was linked to a list of genes, we performed an intersection analysis to identify shared gene modules associated with NF1 mutations (Fig. 3A). We identified two gene modules shared across six phenotypes (Supplementary Tables S3 and S4), one of which, multiple cafe-au-lait spots (HP:0007565), is a diagnostic criterion for NF-1 (Fig. 3A). The genes shared by these phenotypes were also added to the input gene list. The final list consisted of 43 genes and 1 chemical, CHEBI:37045 (purine-GTP) (Supplementary Table S5). Processing this input gene list by GINtoSPN using both GINv2 and GTRD resulted in a Petri net with 1157 places, 5356 transitions, and 12,336 arcs (Fig. 3B). Notably, the places in this Petri net model represent multiple types of molecules, including DNA (promoter regions), RNA, proteins/complexes, and chemicals (Fig. 3C), making the model compatible with multi-omics data.

Fig. 3: Construction of Petri net model for neurofibromatosis type I.
figure 3

A The Upset plot of the intersections between NF-1-related phenotypes. The blue shade marks the six phenotypes and their intersections. The red rectangles mark the intersections and the shared genes. B The Petri net model constructed for NF-1, without input tokens. Showing only a small part of the total net. Displaying the activity of NF1 to catalyze the conversion of HRas-GTP to HRas-GDP. C Pie chart of the composition of different types of nodes in the NF-1’s Petri net model.

Full size image

Simulation of normal and NF1-mutated model using real RNAseq dataset

To simulate the behavior of the NF-1 network before and after NF1 gene mutation, we constructed an NF1-mutated model by deleting the transitions catalyzed by NF1, specifically the conversion of Ras-GTP to Ras-GDP49,50 (Fig. 4A). Previous studies have shown that the elevated levels of the active form of Ras protein, Ras-GTP, are directly linked to the development of NF-150. To validate the NF-1 model, we used RNAseq data generated from 143 normal skin fibroblast cells from GSE11395743, treating the gene expressions as input tokens. To adhere to the mEPN style, 606 extra transition nodes and arcs were generated. We performed SPN simulations using Biolayout express3D for all 143 individuals’ gene expression profiles under both normal and NF1-mutated conditions. As expected, the tokens held by the nodes representing Ras-GTPs were elevated in the NF1-mutated condition compared to the normal state (Fig. 4B and C), while the tokens of Ras-GDPs showed no significant change in the NF1-mutated condition (Fig. 4B).

Fig. 4: Simulation of the normal and NF1-mutated SPN model.
figure 4

A Diagram of the NF1 gene’s function. NF1 catalyzes the hydrolysis of the active form of Ras proteins (Ras-GTP), which generates their inactive forms, Ras-GDP. Mutation of the NF1 gene will cause the abnormal accumulation of active Ras proteins and activate the downstream signaling pathways promoting survival, cell growth, and proliferation. B Simulation results of the tokens of KRAS with CHEBI:37038 (purine ribonucleoside 5’-diphosphate) or CHEBI:37045 (purine ribonucleoside 5’-triphosphate) under normal or NF1 mutated conditions. This plot shows only one individual from the 143 human samples of skin fibroblast cells. C Dot-plot of the fold changes and the significance (calculated by −log(p-value)) of the significantly changed molecules in the model under normal or NF1-mutated conditions. Each row is a node in the model. Each column is an individual. The names with “.state” refer to the gene’s promoter.

Full size image

Besides Ras proteins, we explored other molecules that exhibited substantial changes (Fig. 4C, Supplementary Data 1 and 2). Nodes were selected based on a fold change (>1.2 or <0.8) in the average token levels across 90-time blocks (excluding the first 10 time blocks, as the system may not have reached a steady state) in the NF1-mutated condition compared to the normal condition in at least one individual. P-values were calculated using Student’s t-tests (n = 90 for each of the mutated or normal conditions). Unlike the persistently up-regulated Ras-GTP-related molecules, we observed varied responses among different individuals to NF1 gene mutations, highlighting the complexity of the NF-1 disease. Among these molecules, PTEN, TP53, ESR1, RAC1, and CDC42 frequently appear as components of the complexes. PTEN has been implicated in neurofibroma development and malignant transformation56. Loss of function in PTEN and TP53 can lead to the transformation of benign neurofibromas, such as plexiform NFs, into malignant forms like malignant peripheral nerve sheath tumors (MPNST)57,58.

ESR1, which is an estrogen receptor, has been shown to be repressed by neurofibromin59, playing an important role in ER+ metastatic breast cancer60. Additionally, the Rac1 and Cdc42 signaling pathway is negatively regulated by NF161. Notably, we also observed significant changes in promoter regions, RNA and protein levels of PF4 and GUCA1C. In normal conditions, PF4 expression is very low among the 143 individuals (mean = 0.02, median = 0), and GUCA1C was not expressed at all. The changes in PF4 and GUCA1C were primarily driven by alterations in the transcription factors regulating these two genes. PF4, a platelet-derived chemokine (also known as CXCL4), has an unclear connection to NF-1, but a recent study suggests that PF4 can attenuate age-related hippocampal neuroinflammation and improve cognition in aged mice61. Considering NF-1 is frequently accompanied by nervous system abnormalities, such as specific learning disability (HP:0001328) and intellectual disability (HP:0001256), PF4-based treatments may provide the potential for alleviating cognition-related symptoms in NF-1 patients.

For GUCA1C's (guanylate cyclase activator 1C), its paralog, GUCA1A, is involved in cone–rod dystrophy, a genetic eye disease characterized by retinal pigment deposits, central scotomas, and chorioretinal atrophy. The fluctuations in GUCA1C may be related to co-occurring symptoms such as glaucoma (HP:0000501) and abnormality of retinal pigmentation (HP:0007703).

Discussion

In this paper, we developed a fast and efficient tool, GINtoSPN, for automatically inferring a directed topological graph of molecular interactions from a given gene/chemical list, and converting it into GraphML format in mEPN style, which can be easily loaded into Biolayout express3D for SPN simulations. To demonstrate the application of GINtoSPN, we constructed a list of genes related to NF-1, converted it into a topological graph, and generated a Petri net model in mEPN style. To validate the NF-1 model, we created an NF1-mutated model, then performed SPN simulations on both the normal and mutated models using RNA expression profiles generated from 143 normal human skin fibroblast cells. The simulations successfully captured the consistent upregulation of Ras-GTPs, along with substantial fluctuations in other molecules across different individuals. These results validate the biological relevance of the NF-1 model and highlight the individual variability in the response to NF1 gene mutations, suggesting that personalized precision treatments may be necessary for NF-1 patients.

The tool we developed in this work offers several key advantages: 1. It minimizes the requirement of specialized knowledge when assembling a new network. The molecular interactions were automatically extracted from GINv2, which is a multi-omics network integrating proteins and metabolites interactions. The TF-target relations can be retrieved from GTRD. New nodes are introduced by traversing the paths in GINv2 between the nodes in the input list. Therefore, users are not required to provide a comprehensive list of genes or chemicals, as the tool fills in missing nodes automatically. 2. It reduces the significant amount of time for Petri net construction. The task of inferring a topological network is paralleled, which is typically the most time-consuming step. This process takes only seconds to minutes, while the subsequent conversion step is completed within seconds. Compared to manually constructing a new Petri net model, which can take hours to months, this tool saves considerable time and labor, allowing for efficient construction and adjustment of complex Petri net models. 3. GINtoSPN supports various types of omics data for simulation, including transcriptomics, proteomics, and metabolomics. 4. This tool provides a seamless pipeline from the input gene/chemical list to SPN simulation. It incorporates omics-data as input tokens when available, and the output format, GraphML, is compatible with Biolayout express 3D for fast SPN simulation.

Our tool offers several distinct advantages compared to previous approaches. Unlike tools designed for the automatic construction of chemical reaction networks, which are typically used for industrial chemical processes, our method is specifically tailored to biochemical reactions within human cells. Additionally, our tool generates Petri net models in the mEPN style, making them compatible with SPN simulations, which are not supported by the chemical reaction network methods. Compared to MAGCC, which employs AI to construct knowledge bases and models for simulation, our tool leverages data from 10 well-established, experimentally validated knowledge bases, providing a higher level of confidence in model construction. Furthermore, unlike VANESA, which builds Petri net models from separate databases for metabolic and protein–protein interaction networks, our tool creates integrated multi-omics Petri net models. In summary, our approach uses a unique strategy that produces Petri net models with greater confidence and a more comprehensive, integrated view of molecular interactions.

After conversion by GINtoSPN, the package outputs the Petri net model in GraphML format, not in SBML, which is a widely used systems biology format supported by many software. The major reason for using GraphML format is that the software we use for the SPN simulations, Biolayer Express3D, accepts mEPN-styled GraphML files but does not support SBML format.

We prefer SPN simulation for several key reasons: Firstly, the global integrative network (GIN), from which we derive molecular interaction networks, does not include kinetic parameters for reactions. GIN consists of nodes representing molecules or intermediates, and directed edges that represent relationships between them. With given gene and chemical symbols or IDs, we can efficiently infer a sub-network by searching for paths between target nodes, though without reaction rates or other parameters. Additionally, GIN is compatible with various molecular interaction types beyond just signaling or biochemical networks. In our current study, we also integrate gene regulatory networks (e.g., transcription factor binding) and transcription/translation processes. Collecting kinetic parameters for each process across such diverse molecular interactions would be highly valuable for model construction but requires an enormous effort. Thus, for building Petri net models of multi-omics molecular interaction networks, we had to select a simulation method that does not depend on kinetic parameters or rate constants.

Secondly, SPN does not require prior knowledge of reaction rates for simulation, making it ideal for our approach to automatically construct Petri net models. While this may limit SPN’s ability to estimate absolute quantities of tokens, it can still effectively measure relative changes in tokens under different conditions (e.g., mutants vs. wild types). This is particularly useful in disease studies, where comparisons between healthy and diseased states are crucial.

Given that SPN simulation does not rely on kinetic parameters, and obtaining these parameters for all reactions in GINv2 is beyond current capabilities, we chose GraphML as the output format for our tool.

We acknowledge that GINtoSPN still has room for improvement. First, the tool does not compute an optimal layout for the nodes; currently, node coordinates are assigned randomly. While this does not affect the simulation, users who require a properly arranged network can easily load the output GraphML file into graph editors such as yED (yWorks, Tübingen, Germany; www.yworks.com), and use its layout computation functions to achieve a more visually organized display. Second, the tool currently relies on external data sources to include gene regulatory network interactions. This limitation stems from the scope of GINv2, which does not incorporate GRN data. As GIN continues to evolve and expand to include new data types like GRN and epigenetics markers, we expect to enhance GINtoSPN with additional functionalities that will accommodate these new data sources.

Methods

Basic concepts of Petri nets

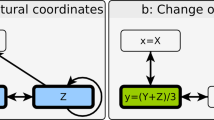
Petri nets are a mathematical tool used to model and simulate the behaviors of systems. Typical Petri nets consisted of places, transitions, and arcs. Places are often presented as circles (Fig. 5a), which usually refer to entities that participate in a process. Transitions are depicted as rectangles or bars (Fig. 5a), representing events or processes. Arcs are directed arrows that connect places and transitions (Fig. 5a). Places often hold tokens, which are illustrated as dots, representing the states of the system or the amount of the signals (Fig. 5a). Formally, a Petri net is defined as a four-tuple:

$${{\rm {PN}}}= \langle P,T,I,O \rangle$$
(1)

where

Fig. 5: Introductions to Petri nets, mEPN, and GINtoSPN conversion.
figure 5

A Basic components of a Petri net. B A simple demonstration of how firing a transition affects token distribution in a marked Petri net. C Components of mEPN notations and an example network. The example illustrates an integrated network of transcription factor bindings, RNA transcriptions, protein translations, protein complex formations, and metabolite reactions. D The conversion of GIN components to mEPN. Intermediate nodes of GIN may be converted to transition nodes of “Binding” or “Catalysis”, depending on the products of the reactions. Arrows with dashed lines indicate new transition nodes introduced into the network by the types of upstream and downstream nodes. For instance, a “Transcription” node is generated if the edge connects a “DNA region” and an “RNA” node. E The example network corresponding to B in GIN style. The network shows the translation of transcription factor G1’s RNA into protein, which binds to the DNA regions of G2 and G3, promoting the transcription of their RNAs. The proteins translated from these RNAs form a G2_G3 complex that catalyzes the conversion of Metabolite 1 into Metabolite 2.

Full size image

P = {p1, p2, … pm} is a finite set of places.

T = {t1, t2, … tn} is a finite set of transitions.

I = {i1, i2, … ik} is a finite set of input arcs, whose starting and ending nodes u and v follow: u\(\,\in\) P and v \(\in\) T.

O = {o1, o2, …, ol} is a finite set of output arcs, where u \(\in\) T and v \(\in\) P.

Petri nets are bipartite graphs, meaning places must connect to transitions, and transitions must connect to places (Fig. 5B). The distribution of tokens across places is referred to as the “marking”. Tokens can move between places according to the rules of “firing” (Fig. 5B). The firing of a transition represents the occurrence of an event, while the movement of tokens represents state changes. For instance, in Fig. 5B, before firing, place P1 holds two tokens while P2 has none. After firing, one token is removed from P1 and transferred to P2 via transition T1. Using this simple logic, we can model complex biological systems with Petri nets and simulate the flow of tokens, representing quantities like molecule counts or signal intensities.

The mEPN style and signaling Petri net simulation

To perform an SPN simulation, we first need to construct a Petri net model in Edinburgh Pathway Notation (mEPN) style. mEPN is a framework that represents various molecular components (places) and their interactions (transitions). Commonly used notations for places include DNA, RNA, proteins, protein complexes, and metabolites, while transitions include token input, binding, catalysis, transcription, and translation (Fig. 5C). For example, Fig. 5C illustrates an mEPN-styled Petri net involving three genes and two metabolites. “G1” represents gene 1, a transcription factor that binds to the promoter regions of G2 and G3, promoting the transcription of their mRNAs. After translation into proteins, the proteins from G2 and G3 form a complex that catalyzes the conversion of Metabolite 1 into Metabolite 2. It is important to note that token input is classified as a transition, with the number of input tokens indicated as the weight of the arc connecting the token input transition to the G1.RNA node.

After constructing a Petri net model in mEPN style, we can export the model in GraphML format and perform SPN simulation in Biolayout Express3D. A key feature of SPN is that it does not require the construction of equations or the specification of rate constants for model parameterization; instead, it relies primarily on the structure of the network. Parameterization is achieved through the distribution of tokens across the entity nodes. A single run of an SPN model consists of a series of time blocks, during which each transition is fired exactly once in a random order. In this work, we executed the simulation for 500 runs, averaging the results of a single entity node across these runs for each time block. A formal description of SPN simulation can be found in Ruths et al. 6.

Construction of a Petri net model in mEPN style using user-defined gene/chemical list

There are two major steps in constructing an mEPN-style Petri net model using GINtoSPN. The first step involves extracting molecular interactions from GINv2 and building a directed topological sub-graph. Because most genes and chemicals are separated by “intermediate” nodes in GIN, the input genes and chemicals are used as “seeds” for expanding the node collection to create a proper topological structure. The strategies for collecting nodes are different between signaling pathways and metabolic pathways. For signaling pathways, kinases are both enzymes and substrates/products of reactions, so genes are separated solely by intermediate nodes. A valid path is then constructed from the following nodes:

$${n}_{0},{n}_{0}\in \left\{{{\rm {input}}}\right\}$$
(2)
$$\left\{{n}_{1}\right\}={N}_{{{\rm {out}}}}\left({n}_{0}\right)\,{{\rm {and}}}\,{n}_{1}\in \left\{{n}_{;}\right\}$$
(3)
$${\left\{{n}_{2}\right\}=N}_{{{\rm {out}}}}\left({n}_{1}\right)\,{{\rm {and}}}\,{n}_{2}\in \left\{{{\rm {input}}}\right\}$$
(4)

where n0 is a starting node present in the input list, Nout is the function that retrieves all downstream nodes, n; denotes an intermediate node (indicated by the presence of ‘;’ in their names), and {input} is the set of input node names.

In contrast, in metabolic reactions, proteins typically serve as enzymes that catalyze the reactions. Consequently, genes are separated by both intermediate nodes and metabolite nodes. Therefore, metabolic paths are constructed from the following nodes:

$${n}_{0},{n}_{0}\in \left\{{{\rm {input}}}\right\}$$
(5)
$$\left\{{n}_{1}\right\}={N}_{{{\rm {out}}}}\left({n}_{0}\right),\,{{\rm {and}}}\,{n}_{1}\in \left\{{n}_{;}\right\}$$
(6)
$${\left\{{n}_{2}\right\}=N}_{{{\rm {out}}}}\left({n}_{1}\right),\,{{\rm {and}}}\,{n}_{2}\in \overline{\left\{{{\rm {protein}}}\right\}}$$
(7)
$${\left\{{n}_{3}\right\}=N}_{{{\rm {out}}}}\left({n}_{2}\right),\,{{\rm {and}}}\,{n}_{3}\in \left\{{n}_{;}\right\}\,{{\rm {and}}}\,{n}_{3}\in \left\{{n}_{1}\right\}$$
(8)
$${\left\{{n}_{{\rm {s}}}\right\}=N}_{{{\rm {in}}}}\left({n}_{1}\right),\,{{\rm {and}}}\,{n}_{{\rm {s}}}\in \overline{\left\{{{\rm {protein}}}\right\}}$$
(9)

where \(\overline{\left\{{\rm {{protein}}}\right\}}\) is the set of nodes that are not proteins nor intermediates (hence metabolites), Nin is the function that retrieves all incoming nodes, and ns represents a node that serves as the substrate of the reaction. The method for extracting molecular interactions from GINv2 has been compiled in the function “generate_node_collection” within our tool GINtoSPN. Specifically, the edgelist of GIN was loaded into R and was used to generate an igraph object. After extracting the nodes, a sub-graph was created using the igraph function ‘induced_subgraph’, which was then converted back into an edgelist.

To integrate the interactions from the gene regulatory network, we downloaded the TF-target relations from GTRD54,55, and searched for interactions between any TFs and target genes present in the node collections. The results were formatted into an edgelist and imported into R to be combined with the edgelist generated from the sub-graph induced from GIN. Subsequently, a new sub-graph was generated using the igraph function ‘graph_from_edgelist’. The sub-graph was adjusted for the nodes’ color and size using the function ‘adjustNode_color_size’ built-in GINtoSPN for representation (i.e. Fig. 2A).

The second step involves converting the igraph object of the sub-graph into mEPN style. The main conversion processes are encapsulated in a single function, “convert_graph_to_graphml”. This function requires three inputs: an igraph object extracted from GIN, a coding gene list, and a matching table of initial tokens and places.

The conversion begins by initializing a list with a standard GraphML header. The function then generates a vector of nodes and an edge list based on the igraph object. The nodes in the vector are converted to GraphML format according to the following rules:

Nodes included in the coding gene list are converted to places labeled “Protein” in mEPN style.

Nodes containing “;” in their names, indicating that they are intermediate nodes, are converted to transitions labeled “Catalysis” (for biochemical reactions) or “Binding” (for the formation of protein complexes) in mEPN style.

Nodes that are neither proteins nor intermediate nodes are converted to places labeled “Metabolite” in mEPN style (see Fig. 5D).

If DNA regions and RNAs are involved, they are converted to the corresponding components in mEPN style. Additionally, specific types of transition nodes, such as “Transcription” and “Translation,” are introduced if the tool detects edges between DNA, RNA, and protein nodes (see Fig. 5D). An example of a network in GIN style corresponding to the network in mEPN style shown in Fig. 5C is presented in Fig. 5E. Overall, this conversion step transforms networks like Fig. 5E into the format illustrated in Fig. 5C.

Additionally, if a list of input tokens is provided to the function, the nodes that intersect with both the input token list and the node list of the subgraph will be assigned two extra nodes: a ‘Token Input’ transition node and a ‘Degenerate’ node. The ‘Degenerate’ nodes are introduced to prevent the excessive accumulation of tokens of the molecules, as tokens are continuously generated from the ‘Token Input’ nodes. To avoid additional computation, the coordinates of the nodes are assigned random values, since the layout does not influence the results of the SPN simulation.

Following these rules, the conversion of the subgraph into mEPN style involves the following steps:

Generate a header for the new GraphML file.

Create an edge list of the biochemical reaction network, then loop through each edge with the following actions:

Check the types of the starting and ending nodes of the edge. If a node’s name is included in a precompiled protein list, it is classified as a protein node; if the name contains “;”, it is considered an intermediate node; if it includes “.DNA” or “.RNA”, it is categorized as a DNA region or RNA node, respectively. If the node does not fit any of these criteria, it is classified as a metabolite.

Convert nodes to places or transitions. Based on the types of the two nodes, create new node entities in GraphML format following mEPN notations (see Fig. 5D). The mEPN paradigm specifies settings for different types of places and transitions, including shape, width, height, color, and display text, all of which are recognized by Biolayout Express3D for SPN simulation.

Convert edges to arcs. During the conversion process, arcs can be of two types: ordinary arcs and inhibitory arcs. Similar to the node conversion, create new arc entities in GraphML format according to the specific design for both types of arcs in the mEPN paradigm.

Check for a list of input tokens. If provided, generate a token input transition node for each entity node (place) in the list, along with a degenerate node. Then, generate arcs to connect the token input node to the entity node with weights representing the number of input tokens. Also, it generates arcs connecting the entity node to the degenerate node. This is the only required parameterization step for SPN simulation.

Finalize the GraphML file by generating an ending.

Load the GraphML file into yEd and compute the layout using the “Layout” → “Hierarchical” option with default parameters.

Construction of a Petri net model for neurofibroma

The construction of an mEPN-style Petri net model for neurofibroma involves the following steps (in R environment):

Collect the genes associated with neurofibroma. The gene list was extracted from the R object of MSigDB62,63 C5 collection of HPO terms using the “read.GMT” function from the R package ‘ActivePathways’64.

Generate a collection of nodes based on GINv2 topology and the neurofibroma gene list. We utilized the generate_node_collection function from our tool GINtoSPN, specifying the neurofibroma gene list, the igraph object of GINv2, and a list of all coding genes in GINv2 to create a collection of nodes. This collection was then refined using the rm_unrelatedNodes and add_parentNodes functions to remove unrelated nodes and incorporate the parent nodes of intermediate nodes.

Construct an igraph object of the sub-graph. We employed the induced_subgraph and igraph::simplify functions from the igraph package to construct the igraph object for the neurofibroma network. For Fig. 2A, we adjusted the layout using the adjustNode_color_size function from GINtoSPN and the layout_with_fr function from the igraph package.

Convert the igraph object of the neurofibroma molecular interaction network into a Petri net in mEPN style. Using the igraph object of the neurofibroma network and the coding gene list, we converted the igraph object into a list containing the header, nodes, edges, and ending of a GraphML file. This list was then transformed into plain text and output to a file.

Compute the layout. We loaded the GraphML file into yEd, and computed the layout by using the “Layout” → “Hierarchical” option with default parameters.

This Petri net model was not marked and, therefore, was not used for SPN simulation.

Construction of Petri net models for neurofibromatosis type I

To build Petri net models for the SPN simulation of neurofibromatosis type I (NF-1), we specifically collected and refined a gene list associated with NF-1. This gene list was utilized to construct an igraph object in R, representing the molecular interaction networks of NF-1. We then converted the igraph object into marked Petri nets based on an RNA-seq dataset. The process details are as follows:

Build a gene list for NF-1. Core genes from downstream signaling pathways, specifically the PI3K/Akt and RAS/RAF/ERK pathways (see Supplementary Table S2), were added to the neurofibroma gene list to create a new NF-1 gene list. Phenotypes that “very frequently” co-occur with NF-1 (ORPHA636, https://hpo.jax.org/browse/disease/ORPHA:636) according to HPO, were selected, and gene lists associated with these phenotypes were used for intersection analysis. This analysis was performed using the R package “UpsetR”. Eight shared genes from the two modules were further incorporated into the NF-1 gene list, along with one chemical, CHEBI37045, which is purine-GTP.

Generate a collection of nodes based on GINv2 and the NF-1 gene list. First, we used the function “generate_node_collection” from GINtoSPN to generate a collection of nodes. Then we refine the node collection by the function “rm_unrelatedNodes” and “add_parentNodes” to remove unrelated nodes and add the parent nodes of the intermediate nodes.

Construct an igraph object of the sub-graph. We used the functions “induced_subgraph” and “igraph::simplify” from package “igraph” to construct an igraph object for the network of NF-1. We then added the formation paths for protein complex and new gene regulatory paths by the function “add_prcFormation_and_GRN” from GINtoSPN.

Convert the igraph object of NF-1’s molecular interaction network into marked Petri nets in mEPN style. The RNA-seq results generated by GSE113957 were used as the token input when building the marked Petri nets. The RNA-seq results were parsed into a matrix, where rows are genes and columns are human individuals. We first built the Petri net model for normal human cells by generating a list object containing the header, nodes, edges, and ending of a GraphML file. This mEPN-styled Petri net was further parameterized by incorporating the gene expression profiles. For each column of the gene expression matrix, each of the RNA nodes whose names are included in the RNA expression profiles are connected to a token input transition node and a degenerate transition node. 143 marked Petri nets in mEPN style were generated in the form of list objects by the function “convert_graph_to_graphml” from GINtoSPN. To simulate the loss of function effects of the NF1 gene, we deleted the transition nodes that were catalyzed by NF1 and all the related arcs. Similar to the normal human skin fibroblast cells, we generated 143 list objects of marked Petri nets in mEPN style for NF1 mutated conditions. All these lists were further converted to pure texts and output to a total of 286 GraphML files.

Signaling Petri net simulation by Biolayout express3D

The GraphML files were loaded into Biolayout express3D version 3.4 for SPN simulation. Upon loading, the software automatically recognized the mEPN-styled Petri net model and prompted for SPN simulation. The simulation parameters were as follows: Number of time blocks: 100; Number of runs: 500; SPN stochastic distribution: standard normal distribution; SPN transition type: consumptive transitions. The simulation results were then imported into R for further analysis. Nodes selected for Fig. 4C were based on a fold change (>1.2 or <0.8) of the average tokens across the 90 time blocks in the NF1-mutated condition compared to the normal condition, in at least one individual.