Revisiting hydrophobicity and its effectiveness in oil retention using microfluidic experiments

Multiphase flow is ubiquitous in subsurface processes such as enhanced oil recovery (EOR)^1,2, carbon sequestration^3,4, and subsurface remediation⁵. These technologies focus on making the target fluids such as hydrocarbons, carbon dioxide (CO₂), and non-aqueous phase liquids (NAPL) more manipulable to escape from a reservoir or keep them in an underground matrix. For instance, EOR aims to effectively extract oil stored in subsurface pores. However, for carbon sequestration, CO₂ needs to be securely contained underground. Simultaneously, in a permeable reactive barrier (PRB), one of the most popular in-situ groundwater remediation techniques, pollutants must be captured in the reactive materials (e.g., granular activated carbon, GAC). The successful implementation of these methods relies on a comprehensive understanding of the physical properties of porous media, such as porosity, permeability, and relative permeability⁶. The relative permeability is affected by the complex interplay between pore-level characteristics, including surface wettability, residual fluid morphology, and pore geometry⁷.

Wettability, which refers to a fluid’s tendency to spread over a solid surface owing to intermolecular tensions, is an important property to consider for multiphase flow through porous media⁸, because it can significantly influence capillary pressures, fingering mechanisms, phase saturation, and the relative permeability of each phase⁹. Wettability is classified into two types in this study, hydrophilic (water-wet) and hydrophobic (oil-wet), and is quantified by the contact angle at the fluid-fluid-solid interface: contact angle refers to the angle measured through the water on a flat solid surface where 0° < θ < 90° corresponds to hydrophilic systems and 90° < θ < 180° represents hydrophobic systems. Contact angle in porous systems is governed by the surface energy of the solid particles and the pore geometry, which includes factors such as pore size and heterogeneity^7,10,11. Therefore, pore geometry influences fluid distribution in multiphase flow in porous media not only by controlling flow paths but also by altering the contact angle.

To provide an example of altering the wettability of a medium in the oil or environmental industries, the injection of displacement liquids that alter the surface wettability to a more hydrophilic state, including low-salinity water flooding, surfactant flooding, and nanoparticle fluid flooding, has been found to be highly effective in EOR⁸. When dealing with porous media contaminated by NAPL, shifting the wettability from hydrophobic (NAPL-wet) to hydrophilic (water-wet) to enhance NAPL recovery is beneficial¹². In contrast, it is known that hydrophobic modification helps treat organic contaminants. For example, Yang et al.¹³ employed dimethyl dichlorosilane modification of GAC, enhancing the surface hydrophobicity and thereby augmenting the effectiveness of PRB by 20% in retaining NAPL contaminants under the flow rate of 2 mL/min.

Recent developments in pore-scale visualization using microfluidic devices have provided physical insights into multiphase flows. Microfluidics is a technology that allows for precise manipulation of small quantities of fluids, generally <1 μL, within a 2-D (or 2.5-D) microchannel device¹⁴. Using microfluidic platforms to explore fluid flows in porous media offers three key benefits: (1) enables real-time insights through direct microscopic observation; (2) captures pore-scale phenomena that can be used for upscaling, modeling, and comparison with macroscale results; and (3) requires minimal fluid or sample volumes, facilitating rapid screening and parallel experiments¹⁵. Microfluidic devices have advanced with high-precision pressure and flow control, allowing experimental setups to study miscible and immiscible displacements under various flow conditions.

Several microfluidic experiments have been conducted to evaluate the impact of media wettability on oil-water displacement^{12,16,17,18,19}. Yang et al.²⁰ observed consistently higher values of average finger width in hydrophilic experiments (979.5 μm) compared to hydrophobic experiments (687.3 μm), which indicates more stable oil displacement and higher efficiency of residual oil reduction in hydrophilic conditions. Omran et al.²¹ conducted microfluidic flooding experiments using polymer-coated silica nanoparticles in three wettability states: water-wet, intermediate-wet, and oil-wet. They found that the water-wet state showed higher residual oil reduction owing to a more stable front and slower displacement velocity than the intermediate and oil-wet states. The abovementioned studies evaluated the effect of wettability under constant flow rate conditions. However, Avendaño et al.²² produced opposite results regarding the impact of wettability on oil retention under the same capillary number conditions. Oil retention was lower in hydrophobic microfluidic chips owing to a stronger lateral flow of water, which led to a more uniform displacement front, a smaller volume of entrapped oil, and fewer large oil ganglia compared to hydrophilic conditions. Despite conflicting findings, it can be inferred that hydrophobic pore matrices would exhibit higher oil retention than hydrophilic ones because of the ability of hydrophobic surfaces to adsorb oil.

This study examines the water-oil displacement behavior within a natural aquifer composed of hydrophilic particles and a PRB designed to remove organic contaminants via hydrophobic sorption. PRBs are an innovative in situ solution for groundwater remediation²³, utilizing the natural hydraulic gradient to passively migrate contaminant plumes through reactive media^24,25,26. Within the PRBs, contaminants are either transformed into less harmful compounds or immobilized by binding to the reactive materials. The performance of PRBs is assessed using key metrics such as hydraulic conductivity, contaminant removal efficiency, and longevity²⁷, with longevity representing the PRB’s ability to maintain effective contaminant treatment over extended periods after field-scale installation²⁸. The performance of a PRB is closely linked to the choice of reactive materials. Among these, absorbents such as GAC are particularly beneficial for removing organic contaminants due to their hydrophobic sorption capacity. They effectively decontaminate groundwater without producing harmful by-products, thereby minimizing pore clogging and the need for filler replacement²⁹.

To the authors’ knowledge, no study has investigated the performance of hydrophobic adsorbents used in PRB at the pore level. It has also been overlooked that pressure gradients mainly cause fluid flow under natural underground conditions, whereas EOR or carbon sequestration deliberately pushes fluid into the subsurface medium at a controlled flow rate. Considering this, we conducted a thorough analysis of the oil retention efficiency by applying a consistent pressure difference between the inlet and outlet of the microfluidic chips and closely examined how the oil retention efficiency varied depending on the wettability. The primary purpose of this study was to investigate oil (i.e., diesel) retention and subsequent changes in relative permeability in porous media with different wettabilities, postulating the oil-water displacement process occurring in a NAPL-contaminated aquifer and PRBs adjacent to it. Owing to the benefits of utilizing the microfluidic model, real-time images of pore-scale information (e.g., local oil retention) can be effectively extended to continuum-scale information from multiscale perspectives. We also considered how the effect of wettability may change when the pore geometry is highly disordered, such as in realistic aquifers.

The experiments aimed to investigate (1) the displacement pattern of oil injection into water-saturated porous media; (2) the change in flow rate, oil ganglia distribution, and dynamic contact angle during water reinjection; and (3) the effect of the irregularity of the pore geometry on oil retention. The wetting principles are complicated when an irregular porous geometry is involved. Therefore, this discussion focuses on uniform-type chips with a flat solid surface and constant throat radius to facilitate contact angle measurement, permeability, and capillary pressure calculations under different wettability conditions.

Stable displacement during diesel injection into water-saturated chip

When diesel was injected into water-saturated uniform-type chips, it displaced nearly all the water, advancing as a uniform front and leaving only negligible water trapped in the pores, regardless of wettability or pressure difference conditions (Fig. S2). This behavior corresponds to a stable displacement regime, where fluid movement is dominated by viscous forces over capillary forces (i.e., viscosity-dominated flow), and the viscosity of the advancing fluid is higher relative to the defending fluid (see the following section referring to Lenormand’s diagram). Viscosity-dominated flow is featured by a high capillary number (\({Ca}\), see Eq. (5)), which occurs when the advancing fluid has a high viscosity or moves at a high velocity. While we were unable to directly measure the flow velocity (or flow rate) and the resulting capillary number of the advancing diesel due to limitations of the flow rate sensor, which could not accommodate organic solvents, the observed rapid movement and uniform displacement pattern of diesel consistent with the characteristics of a stable displacement regime as defined in the Lenormand diagram. This suggests that when contaminants with higher viscosity than water (e.g., diesel) enter an aquifer, they swiftly and evenly fill the surrounding medium under constant hydraulic gradients.

Effect of wettability on the water flow rate and diesel-ganglia distribution during water reinjection

We compared diesel retention in the pore network of chips with different surface wettabilities after reinjecting water into diesel-containing chips under constant pressure difference conditions. Interestingly, contrary to the findings of previous studies conducted under constant flow rate conditions^20,21,30, we observed significantly higher retention of diesel in the U-phil chip than in the U-phob chip under both pressure conditions (i.e., 50 and 100 mbar) (Fig. 1a and Fig. 2a–d). This may be attributed to the consistently higher flow rate within U-phob than in U-phil during water injection, particularly because of the constant pressure difference established at both ends of the chip (Fig. 1b). As described earlier, the total pressure drop along the throat comprises the viscous and capillary pressure drops in the immiscible fluid flow within the capillaries (see Eq.(5)). When the water contact angle with the grain surface exceeds 90° (i.e., a hydrophobic surface), the capillary pressure is negative (–) (see Eq.(6)). With the total pressure drop \(\Delta {P}_{t}\) held constant, any reduction in capillary pressure necessitates a compensatory increase in viscous pressure drops (\(\Delta {P}_{a}\) and \(\Delta {P}_{d}\)). This increase in the viscous pressure drops results in altered flow conditions, such as an increase in the flow rate (see Eq. (7)). Consequently, the flow rates of both fluids (i.e., water and diesel) should increase within the capillaries, which might exert greater shear forces and thus facilitate the displacement of a larger volume of entrapped diesel across the entire chip globally. However, under constant flow rate conditions, the positive capillary pressure in hydrophilic systems facilitates oil displacement by contributing to an increased total pressure drop. Conversely, negative capillary pressure diminishes the total pressure drop in hydrophobic systems, hindering oil displacement efficiency.

a The degree of diesel saturation in the microscopic images at ×10 magnification, and (b) the flow rate changes over time during water reinjection into the microfluidic chips with different surface wettability and pore geometry under different pressures.

Full size image

a U-phil at 50 mbar, b U-phob at 50 mbar, c U-phil at 100 mbar, d U-phob at 100 mbar, e R-phil at 100 mbar, and (f) R-phob at 100 mbar (the images at the left bottom of each image are at 10× magnification).

Full size image

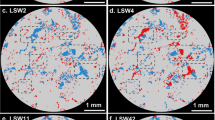
Microscopic images of the diesel distribution in the pore networks of the chips are shown in Fig. 2a–d, which provide insights into phenomena that are unobservable from the macroscopic scale indices (e.g., global oil saturation) and optimization of oil retention efficiency in PRBs. In the U-phil chips (Fig. 2a, c), the diesel ganglia formed convex-edged clusters or circular droplets. In contrast, concave shapes of the diesel meniscus were observed in the U-phob chips (Fig. 2b, d), and a significant amount of diesel was retained as a pendular ring between the grains under 100 mbar conditions. In addition, owing to surface hydrophobicity, diesel adhered to the grain surfaces as a thin film, which was difficult to count in image processing owing to the limited pixel resolution.

Our experimental results can be elaborated using the framework of the phase diagram proposed by Lenormand, et al.³¹ for immiscible two-phase flows (Fig. 3). In immiscible fluid displacement (imbibition and drainage), the flow patterns are determined by the capillary number (\({Ca}\))^32,33 and viscosity ratio (\(M\)):

where \(u\) denotes the flow velocity of the advancing fluid. The capillary number quantifies the relative effects of the viscous (numerator) and capillary forces (denominator) in the system. The capillary fingering pattern emerges at low capillary numbers, where viscous forces become negligible, and capillary forces dominate the displacement. In this regime, capillary fingers form loops and spread in multiple directions. When the advancing fluid is less viscous than the defending fluid and the capillary number is high, viscous fingering occurs, driven by prevailing viscous forces over capillary forces. Unlike capillary fingering, these fingers extend along the flow direction. Stable displacement is observed at high capillary numbers and viscosity ratios, where viscous forces in the injected fluid dictate. Capillary effects and pressure drop in the displaced fluid are negligible in both the viscous fingering and stable displacement regimes. The transition between these regimes is determined by the geometry of solid surfaces and the wettability of the fluids³⁴.

The gray regions represent the areas identified in the simulations by Lenormand et al.³¹, whereas the boundaries marked by red dashed lines correspond to experimental findings reported by Zhang et al.⁵⁴.

Full size image

The case of U-phil under 50 mbar fell in the capillary-fingering regime of Lenormand’s diagram (Fig. 3). In contrast, U-phil under 100 mbar and U-phob under 50 and 100 mbar conditions were in the transient zone, especially U-phob 100 mbar was closer to the stable displacement regime. The water flow velocity used to calculate the capillary number was determined as the flow velocity at the point when water first breaks through at the chip’s outlet. In the U-phil chips, the water flow patterns exhibited thin, finger-like structures alongside large oil clusters (Fig. 2a, c). At 50 mbar, water flow paths were found to exist only in the upper part of the inlet and spread toward the outlet (Fig. S3a and S3(b)). Conversely, the water path exhibited a greater thickness in the U-phob chips (Fig. S3c and S3(d)), similar to a stable (uniform) displacement regime rather than capillary fingering, which was particularly evident under the 100 mbar condition.

Just before terminating the water reinjection, the relative permeability of water (\({k}_{{rw}}\)) under identical pressure conditions of the U-phob chip was higher than that of the U-phil chip (Table 1). \({k}_{{rw}}\) is defined as the ratio of the effective water permeability, \({k}_{w}\) (the permeability of water when water-oil flows as a two-phase flow through a porous medium), to the absolute water permeability, \(k\) (the permeability of water when water flows as a single phase through a porous medium).

where \({Q}_{w}\) is the flow rate of water, \(L\) is the length of the pore network (2 cm), \(A\) is the cross-sectional area of the pore network (2 × 10^–3cm²), and \(\Delta P\) is the pressure difference. This was because the amount of diesel retained in the U-phob chip was smaller than that in the U-phil chip; therefore, water flow was facilitated in the U-phob chip with more water pathways. Our experimental results confirmed that microscale wetting properties might alter macroscale properties such as \({k}_{{rw}}\).

Changes in contact angle and flow rate over the transient state

In microfluidics, a transient state represents a dynamic condition where the system’s properties vary over time, whereas a steady state denotes a stable condition in which the system’s properties remain constant over time³⁵. In the transient states of our experiments, the contact angle of water increased, irrespective of the surface wettability or pressure difference (Fig. 4a). This increase leads to a reduction in the capillary pressure (see Eq.(6)), as shown in Fig. 4b. Revisiting the “bundle of capillaries” model, this phenomenon finds an explanation through the hysteresis loop observed in the drainage-imbibition cycle (Fig. 5a): As water saturation increased, capillary pressure decreases both in the drainage through the U-phob chip and the imbibition through the U-phil chip. Under constant-pressure conditions, the decline in capillary pressure triggers an increase in viscous pressure, consequently increasing the overall flow rate (see Eq.(7)). As illustrated in Fig. 5b, except for the U-phil 50 mbar condition where no clear and consistent tendency was observed, the flow rate increases with increasing water saturation during the transient state of water reinjection under all experimental conditions.

a The initial contact angle at which water is reinjected into the microfluidic chips and the contact angle after the end of the experiments, and (b) capillary pressures.

Full size image

a The hysteresis loop defined by drainage–imbibition cycle (modified from Armstrong et al.⁷) and (b) the relationship between flow rate and water saturation until there is no change in the amount of oil retained inside the microfluidic chips on the microscope image.

Full size image

Oil retention in irregular pore geometry

The pore geometry has a direct effect on the fluid flow velocity through changes in the length or tortuosity of the flow pathways and affects the apparent wettability, which differs from surface wettability, an intrinsic property determined by the material’s surface chemistry³⁶. Furthermore, pore geometry exerts a significant influence on fluid entrapment mechanisms in conjunction with the capillary number and mobility ratio^37,38. We continued the experiment using rock-type microfluidic chips to investigate the influence of pore geometry on the dynamics of fluid-fluid displacement in porous media and retained oil distribution. However, because the chip has an irregular grain size and pore diameter, thus accurate quantification of the impact of pore geometry on immiscible fluid flow dynamics is unavailable. As an approximate guide, half the median pore diameter was used as the throat radius (\(R\)) to calculate the capillary pressure drop (Eq. 6) of rock-type chips.

When comparing the oil ganglia areas of the uniform-type and rock-type chips under 100 mbar conditions (Figs. 1a, 5a), less oil was retained in the rock type under hydrophilic conditions. In comparison, more oil is retained in the rock type under hydrophobic conditions. During water reinjection, the contact angle decreased for the R-phil chip and increased for the R-phob chip, which was not consistent with the uniform-type chips (Fig. 4a). This can be attributed to the wider average pore/throat diameter of the rock type (Fig. 9), which is approximately three times larger than that of the uniform type. As the throat radius increased, the capillary pressure decreased under hydrophilic conditions, leading to an increase in the flow rate owing to the higher viscous pressure. In contrast, the capillary pressure increases under hydrophobic conditions, resulting in a decrease in the flow rate. Consequently, under hydrophilic conditions, more oil was displaced from the rock-type than from the uniform-type, and under hydrophobic conditions, more oil was displaced from the uniform-type than from the rock-type.

The impact of irregular pore geometry is evident in the distribution and dynamics of the oil ganglia. By categorizing the oil ganglia into three groups based on their size (cluster, ambiguous, and blob), significant differences were observed between the uniform- and rock-type chips. Under hydrophilic conditions, the proportion of cluster-sized oil ganglia decreased in the rock-type, accompanied by an increase in the ganglia of other sizes. Conversely, under hydrophobic conditions, the proportions of cluster- and ambiguous-sized oil ganglia increased (Fig. 6b). The predominance of larger oil ganglia in the R-phil condition compared to the R-phob condition is attributed to phase distribution during oil entrapment via the by-passing mechanism. In hydrophilic systems, oil, as the non-wetting phase, is retained in larger pores, whereas in hydrophobic systems, oil, as the wetting phase, is retained in smaller pores.

a Area and (b) areal fraction of oil ganglia by size in microfluidic chips with different surface wettability and pore-network geometry.

Full size image

Microscopic observations revealed contrasting patterns in rock-type pore networks from uniform-types (Fig. 2d, f); large concave-edged oil clusters were observed between grains in the R-phob chip, which was a phenomenon unseen in the U-phob chip. This shift is attributed to the increase in the average pore diameter and decrease in the flow rate in the uniform type compared to the rock-type under hydrophobic conditions, facilitating the entrapment of more oil between grains. Nevertheless, a higher quantity of oil was retained in the hydrophilic chip than in the hydrophobic chip for the rock-type chip, similar to the uniform-type chip.

The oil clusters in the R-phil chip were pushed by the water flow through the narrow throat and broken into small blobs over time. These smaller blobs exhibit faster movement than the clusters, resulting in a decline in the total volume of oil retained on a global scale. This phenomenon is known as ganglion dynamics³⁹; the movement of disconnected bodies of oil is induced by a snap-off that occurs when the swelling of the wetting films in the throat corners generates discrete non-wetting phase droplets. (Fig. 7). Unlike the U-phil chip, in which the oil saturation level stabilized relatively quickly, the R-phil chip experienced a continuous reduction in the oil mass by snap-off, leading to a gradual increase in the flow rate to a quasi-steady state.

A scene where a blob (marked with a blue border) disconnected from a cluster (marked with a red border) through snap-off observed under R-phil 100 mbar conditions. Subsequently, the blob moved rapidly along the water flow and vanished from the microscope image.

Full size image

An additional experiment was conducted for a longer period (3 h) in R-phil at 100 mbar to determine the time required to stabilize oil retention and flow rate. Oil saturation and flow rate were measured at 30-sec intervals for 1 h and then at 5-min intervals. Consequently, after 3600 sec, the oil saturation decreased (Fig. S4(a)) and an increase in flow rate (Fig. S4(b)) continued, but gradually converged to a constant value. According to Rücker et al.⁴⁰, the onset of ganglion dynamics in the imbibition process occurs at approximately 75% oil saturation, with the oil ganglia becoming immobile at approximately 30% saturation. Therefore, although not confirmed in this additional experiment, the contribution of the ganglion dynamics may disappear after a sufficient amount of time.

A slow reduction in diesel retention and an increase in water flow rate were also observed in the R-phob chips over time as in the R-phil chips, despite their different oil dynamics. During drainage, the non-wetting phase (i.e., water in the hydrophobic chips) strives to maintain continuity within the pore network, particularly consisting of larger pore throats. Consequently, when water encounters a narrow throat at the displacing front, it bypasses the throat because of the negative capillary pressure in the hydrophobic surfaces, does not overcome the high entry pressure, and fails to displace the oil ahead of it. This causes diesel to become trapped between the water flow paths. In some cases, when the pore throat is wide in the direction of water entry, the oil ganglia move slowly in the direction of the water flow. A slower decline in oil retention and a gentler increase in the water flow rate resulted from the hydrophobicity of R-phob, as opposed to the condition of R-phil chips, where ganglion dynamics occur.

Microfluidic chips were used to investigate the effect of surface wettability on oil retention and water permeability in porous media under static-pressure-difference conditions. The experiment revealed that negative capillary pressure drops on hydrophobic surfaces led to higher velocities of the water phase and stronger shear forces in the pore throats compared with hydrophilic surfaces during water reinjection into oil-filled porous media at a constant pressure gradient. Unlike previous studies under constant flow rate conditions, this led to lower oil retention on hydrophobic surfaces than on hydrophilic surfaces on a global scale. Under hydrophobic conditions, the displacing front of the water showed a relatively constant stable displacement flow regime, whereas under hydrophilic conditions, the oil became largely trapped between the water flow paths owing to the capillary fingering regime. This paradoxically results in lower oil retention under hydrophobic conditions, which are generally recognized to retain oil better because of their hydrophobicity. Accurately quantifying the impact of pore geometry on fluid flow dynamics is challenging because of the differences in porosity and average pore size compared to uniform-type chips. Despite this, we found that irregularities in pore geometry affected the dynamics and distribution of oil ganglia, showing distinct patterns in rock-type chips. In the R-phil chip, the snap-off phenomenon led to a gradual decrease in oil retention, and the flow rate increased over time, whereas the R-phob chips exhibited a slower oil retention reduction than the R-phil chips. This study explained that pore-filling sequences are a consequence of fluid flow in a pore throat and ultimately determine bulk properties such as the degree of oil retention and relative permeability.

Our findings indicate that it is probable that NAPL-contaminated aquifers could serve as a persistent source of oil blobs capable of traveling significant distances, given the heterogeneous pore structure of actual aquifers resembling rock-type microfluidic chips and their hydrophilic nature. Furthermore, when employing hydrophobic materials in adsorption-based subsurface remediation, it is essential to recognize that they may provide good permeability but have limited longevity in constant hydraulic gradient conditions. These findings, derived from pore-level analysis, underscore the potential of microfluidic devices as powerful tools for advancing groundwater remediation through PRB technology.

Microfluidic system setup

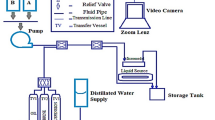
The microfluidic system used in the current study comprised a flow pressure controller, flow rate sensor, microfluidic chip, and a microscope equipped with camera devices, as shown in Figs. 1b, 8a. A pressure-driven flow controller (OB1 MK3 + , Elveflow, Paris, France) was used to induce a fluid flow through the chip under constant pressure. A flow rate sensor (MFS, Elveflow) was used to measure the real-time flow rate of deionized (DI) water into the diesel-filled chip between the reservoir and the chip (Fig. 8b). A microfluidic chip was placed on the holder, and the system was connected to fluorinated ethylene propylene tubing with an inner diameter of 1/16” (IDEX Health & Science, WA, USA). A microscope equipped with a digital camera (DEM-7045T, Dongwon CNS Edu., Seoul, South Korea) recorded the real-time flows within the chip, which were processed using image analysis software (ImageView 4.11 v., ToupTek Photonics Co., Ltd., Hangzhou, China).

a The diesel injection into the water-saturated chip and (b) the water injection into the diesel-filled chip.

Full size image

Four types of microfluidic chips (Micronit Microtechnologies, Enschede, The Netherlands) were used, including those with (1) uniform-type pore network geometry with hydrophilic surface properties (hereafter denoted as U-phil), (2) uniform-type with a hydrophobic surface (U-phob), (3) rock-type pore network with hydrophilic (R-phil), and (4) rock-type with a hydrophobic surface (R-phob). Detailed information on the microfluidic chips is shown in Fig. 9. The uniform-type chips comprised homogeneous diamond-shaped pillars (Fig. 9a). In contrast, the rock-type chips have heterogeneous pore geometries similar to those of the field aquifer media (Fig. 9b). The mean permeability of the chips provided by the manufacturer was 2.47 μm² (2.5 Darcy) for uniform- and rock-type chips⁴¹, which was similar to the values estimated in our preliminary study (2.37–2.57 μm² for uniform-type and 2.07–2.78 μm² for rock-type) for the entire part of the chip, including the inlet and outlet sections.

a Uniform-type and (b) rock-type microfluidic chips manufactured by Micronit. Uniform- and rock-type chip porosity values were referenced from Pradhan et al.⁵⁵ and Omran et al.²¹, respectively. Our preliminary experiments determined the permeability of the chips.

Full size image

Operation of the microfluidic system

For uniform-type chips, diesel was injected into the water-saturated chips at two different pressures, 50 mbar (for 10 min) and 100 mbar (for 5 min), using a flow pressure controller simulating a NAPL pool. Subsequently, DI water was reinjected twice as long as that for oil injection at the same pressure (i.e., for 20 min at 50 mbar and 10 min at 100 mbar). Diesel and water injections were conducted only at 100 mbar for the rock-type chips because a pressure difference of 50 mbar was insufficient to overcome the entry pressure of the narrow pores of the rock-type chips. Table 2 summarizes the pressure differences (between the inlet and outlet of the chip) and the injection time used for each experiment. By alternating the liquid that should advancing (displacing) and defending (displaced) the pores in the chips, the behavior of the fluids within the chip was observed over the experimental timeframe using a camera-equipped microscope. All experiments were conducted at room temperature, 20 °C.

Prior to injecting the fluids into the chips, the fluids were dyed to enhance the visibility of their flows within the chips; the DI water was dyed blue with Brilliant Blue FCF (20% w/w, ROHA Dyechem Pvt. Ltd., Maharashtra, India), and the diesel was dyed red with Oil Red O (5 mg/mL, Sigma-Aldrich, MO, USA). The diesel used in the experiment has a dynamic viscosity of 2.44 mPa·s and an interfacial tension (IFT) of 22.06 mN/m with DI water. Dynamic viscosity was estimated using a Physica Couette-type rheometer (Physica MCR301, Anton Paar, Graz, Austria). The IFT was measured using the pendant drop method with a contact angle meter (DSA 25, KRUSS, Hamburg, Germany).

As the first step of the experiment, the chips were saturated with DI water. For the uniform-type, the chips were completely saturated with water at a flow rate of 500 μL/min using a syringe pump (Legato 210, KD Scientific, MA, USA) and 25 mL gastight glass syringe (Hamilton 1000 Series, Hamilton, NV, USA). The chips were then left to stand at atmospheric pressure for approximately 2 h to stabilize the pressure inside the chip. Owing to the irregular pore structure, an additional process was implemented for the water saturation of the rock-type chips: the rock-type chips were purged with CO₂ gas for 40 min. Then, isopropyl alcohol (IPA) was injected from the outlet at a flow rate of 500 μL/min using the syringe pump. Simultaneously, the inlet side was connected to a 20 mL plastic syringe to manually apply negative pressure. Subsequently, the chips were left for approximately 2 h, and DI water was injected at 120 mbar to displace the IPA entirely using a flow pressure controller.

Quantification of the fluid behaviors in microfluidic chips (image processing)

The videos were split into snapshots per second, and each snapshot was processed in a constant manner using the open-source software Fiji (ImageJ)⁴². Before calculating the oil ganglia size and contact angle, the images were corrected to create a uniform background by reducing the difference between the dark and bright fields. The images were converted to binary images using the ‘threshold’ function. The pore size distribution of the pristine rock-type chips was calculated through image processing; the empty rock-type chip image was taken from Omran et al.²¹, and a histogram representing the pore size distribution was obtained using the ‘local thickness’ function (Fig. 9b). The median pore diameter of the rock-type was 260 μm.

After water reinjection, the proportion of the diesel remaining in the pore network was calculated from the image using the ‘area fraction’ function and divided by the porosity value. Furthermore, the size of each oil ganglion was quantified using the ‘MorphoLibJ’ plugin in Fiji⁴³. This method was employed to compare the size distributions of the remaining oil ganglia at 100 mbar under different pore geometries and surface wettability conditions (U-phil, U-phob, R-phil, and R-phob chips). First, the oil ganglia were individually labeled (Fig. S1), and the area of each ganglion was estimated. The oil ganglia were classified into blobs, ambiguities, and clusters according to their size. Due to the different sizes of pore and throat diameters of the uniform and rock-type chips, the maximum area for blobs was determined as approximately 15,000 μm² (comparable to a circular oil ganglia diameter of 70 μm, which is the midpoint between throat and pore widths) for the uniform-type and 80,000 μm² (comparable to a circular oil ganglia diameter of 320 μm, which is the 75th percentile of the pore size distribution) for the rock-type. In contrast, oil ganglia with an area exceeding five times the maximum blob area (over 75,000 μm² for the uniform type and 400,000 μm² for the rock type) were classified into clusters, whereas those falling between the size of the blob and cluster were labeled as ambiguous.

We also measured the contact angles between water and the solid (grain) surface within the chips to calculate the capillary pressure (\({P}_{c}\)) and capillary number (\({Ca}\)). These measurements were obtained from images captured immediately after water reinjection into the oil-filled chips and after the experiment. Ten points were randomly selected from each image to measure the contact angles by drawing tangents to the water-oil and water-solid interfaces and measuring the angle between these tangents. Their average and deviation values were used to compare the capillary pressure and number under different experimental conditions.

The composition of total pressure drop in a capillary during immiscible displacement

To comprehend the displacement between the immiscible fluids (i.e., water and diesel) in a porous matrix, we adopted the “bundles of capillaries” model, which has often been used as a conceptual model for describing capillarity in porous media. This model simplifies porous materials into several aligned and separate capillary tubes⁴⁴. Upon this assumption, the total pressure drops, \(\Delta {P}_{t}\) between both ends of a capillary (i.e., throat) can be decomposed into the capillary pressure drop (\(\Delta {P}_{c}\)) and the viscous pressure drops of advancing (displacing) and defending (displaced) fluids (\(\Delta {P}_{a}\) and \(\Delta {P}_{d}\), respectively) (Fig. 10):

The curvature of the interface between immiscible fluids results in capillary pressure. It is defined as the pressure difference at the interface of the two fluids and is represented by the Young–Laplace equation:

where \(\gamma\) is the IFT between defending and advancing fluids, \(\theta\) is the contact angle, and \(R\) is the radius of curvature at the fluid-fluid interface; in our case, \(R\) is the radius of the throat. The viscous pressure drop in each fluid can be approximated using Poiseuille’s equation⁴⁵:

where \({\mu }_{i}\) and \({L}_{i}\) (i = a or d) are the dynamic viscosity and the capillary length occupied by fluid, and \(Q\) is the volumetric flow rate of fluids. Although the capillaries in the microfluidic chips were not cylindrical, Poiseuille’s equation was still valid, indicating that the viscous pressure drop was proportional to the fluid flow rate.

The total pressure drops (\(\Delta {{\rm{P}}}_{{\rm{t}}}\)) at the specific capillary length (\({\rm{L}}\)) comprises the capillary pressure drop (\(\Delta {{\rm{P}}}_{{\rm{c}}}\)) and two viscous pressure drops of advancing (\(\Delta {{\rm{P}}}_{{\rm{a}}}\)) and defending (\(\Delta {{\rm{P}}}_{{\rm{d}}}\)) fluids.

Full size image

Trapping mechanisms

During immiscible displacement, the trapping of the defending fluid can occur within pore throats, forming disconnected fluid units referred to as ganglia. These residual trapped fluids impact relative permeability by obstructing or altering the flow pathways of the advancing fluid.

The two primary trapping mechanisms are by-passing and snap-off^46,47. By-passing occurs due to the selective occupation of the advancing fluid according to capillary pressure during piston-like displacement. This mechanism, observed during both drainage and imbibition, can be described using the pore doublet model⁴⁸. As illustrated in Fig. 11, by-passing leads to the non-wetting phase being isolated in larger pore throats with lower capillary pressure and the wetting phase becoming trapped in smaller pore throats. Snap-off occurs when a wetting film forms on the solid surface at throat corners, swells, and eventually bridges across the throat, destabilizing the interface and isolating the non-wetting phase. Especially under strong imbibition conditions (contact angle <45°), a phenomenon called corner flow precedes the snap-off, in which the wetting phase flows along the solid surface without entering the pore center^18,49. Both by-passing and snap-off are strongly influenced by the size and connectivity of pores, wettability, and the pore-throat aspect ratio^50,51,52,53.

a Trapping of the non-wetting phase during the imbibition process and (b) trapping of the wetting phase during the drainage process.

Full size image