Main

Driven by wind and ocean currents, sea ice exhibits a dynamic nature1. This constant movement fosters convergence and shear among the ice masses, leading to the formation of pressure ridges—distinct and elevated features with sails and keels, disrupting the otherwise level sea ice surface2. Pressure ridges have a pivotal role in the Arctic environment, influencing the energy3 and mass balance of sea ice4, as well as the biogeochemical cycle and the ecosystem5. The portion above the water line, the sails, facilitates momentum transfer from the atmosphere into the ocean6,7 and affects snow accumulation in winter8 and the formation of melt ponds in summer9, which in turn accelerate sea ice retreat. The ridge keels are shelter for ice-associated organisms across trophic levels5,10, and promote turbulent mixing, thereby greatly enhancing nutrient availability and supporting a larger biomass than the surrounding-level ice.

Over the past three decades, the extent of Arctic sea ice has shrunk11, and the ice has become thinner12, younger13 and more dynamic (that is, faster14). Although these trends are well documented, it is unclear whether there have been corresponding changes in surface roughness and morphological features, such as pressure ridges. This is mainly because year-round satellite observations that could resolve small-scale features like pressure ridges have only become available in recent years15,16. Given the critical role of pressure ridges in the Arctic environment, two important hypotheses emerge: (1) a thinner and younger ice cover has less time to accumulate deformation, resulting in an Arctic-wide reduction in pressure ridge density (for example, ref. 17); (2) conversely, a thinner and more dynamic ice cover is more susceptible to deformation (for example, ref. 18), leading to an increase in surface roughness and pressure ridges.

In this study, we present a 30-year time series of changes in pressure ridge density, spacing and height from extensive airborne laser altimetry surveys conducted across the Arctic since the 1990s, with a focus on two long-term monitoring regions (Fig. 1a,b): the outflow of the Transpolar Drift (TPD) (red polygon) and the Lincoln Sea (blue polygon). The TPD, which transports sea ice from the Russian shelf to Fram Strait19, encompasses much of the Arctic Ocean and has an important role in the redistribution of biota and biogeochemical material across the Arctic5,10,19. In contrast, the Lincoln Sea, with its thick, resilient multi-year ice, is considered part of the Last Ice Area, critical for the survival of ice-dependent species and a potential refuge for ice-associated ecosystems in a warming climate20. We examine the interannual variability and trends of these contrasting regions, investigate the role of the ice age as a key factor in the observed differences and finally assess Arctic-wide changes in ridge morphology, specifically addressing the effects of thinner, younger ice on ridge formation.

Fig. 1: Overview of surveying activities and platforms.
figure 1

a, Airborne sea ice surveys carried out in the Arctic between 1993 and 2023: the black lines show the flights during which sea ice surface profiles were obtained using SBLAs. The origins (red and blue dots with white filling) of the surveyed sea ice were determined with satellite data by tracing the ice back in time from the Lincoln Sea (blue trajectories) and the ‘outflow’ of the TPD (red trajectories). b, Close-up of the two long-term monitoring sites: the Lincoln Sea (blue) and the TPD (red). c, Overview of the platforms and sensors used for surface profiling during the specified periods. The background photo (E. Horvath, AWI) highlights the typical patterns of pressure ridges. Credit: c(photograph), E. Horvath, AWI; c(schematic), Theresa Schreglmann, AWI.

Full size image

Changing Arctic pressure ridge morphology

Measurements of Arctic sea ice surface elevation were conducted with single-beam laser altimeters (SBLAs), which are routinely operated by the Alfred Wegener Institute (AWI) on survey flights over the Arctic sea ice. With a high spatial resolution of approximately 0.5 m and a small footprint of just a few centimetres, the SBLAs effectively detect morphological features such as pressure ridges, rubble fields and hummocks21. Over the past 30 years (1993–2023), ~76.000 km of previously unpublished surface profile data were collected during 52 campaigns in several regions of the Arctic (Fig. 1a) using different aircraft (Fig. 1c). An overview of the individual campaigns, the sensor instrumentation and data DOIs can be found in Extended Data Figs. 1 and 2, and Supplementary Tables 1 and 2. To obtain the sea ice surface profiles, the laser data are processed using the procedures described in Methods (‘SBLA data processing and ridge detection’). Hereafter, a ridge detection algorithm identifies individual pressure ridges along flight transects (schematic drawing in Fig. 1c), their height (HS (m)), density (DR (n km−1)) and the spacing between them (SR (m)), using a minimum ridge height detection threshold (H0) set to 0.6 m. This threshold ensures that only features taller than 0.6 m are identified as ridges (for example, refs. 4,6). Through cross-comparisons with other sensor data, it has demonstrated high accuracy and consistency (Methods ‘Uncertainties of SBLA’). Since HS, and hence the derivatives DR and SR, show negligible seasonal dependence (Extended Data Fig. 4b and Methods ‘Compilation of time series’), data collected during different seasons (for example, spring and summer) can be displayed and analysed together in Fig. 2. Around one-third of the airborne data shown in Fig. 1a were gathered in the TPD and in the Lincoln Sea, whereas the TPD time series extends back to 1993 and the Lincoln Sea series only begins in 2004. By backtracking the surveyed sea ice using satellite data (IceTrack, as detailed in Methods ‘Sea ice age and trajectories’), we can determine the typical drift paths and origins of sea ice in the two regions (blue trajectories for Lincoln Sea and red trajectories for TPD sea ice). The respective age of the surveyed ice is presented in Fig. 3a,b.

Fig. 2: Changing pressure ridge morphology.
figure 2

a,b, Time series (mean ± s.d.) of pressure ridge densities (DR (n km−1)) for sails higher than 0.6 m in the two regions (TPD (a), Lincoln Sea (b)) across different campaigns. The size of the symbols indicates the survey distance covered per campaign. Trends (black lines) with 95% CIs (grey shading) are illustrated in the background. c,d, Development (mean ± s.d.) of ridge spacing (SR (m)) for TPD (c) and Lincoln Sea (d). e,f, Height (HS (m)) of sails larger than 0.6 m for TPD (e) and Lincoln Sea (f). g,h, Calculated 10 m neutral atmospheric drag coefficient (Cdn10) for H0 = 0.4 m for TPD (g) and Lincoln Sea (h). Statistical metrics (see Methods for details) are provided in Supplementary Table 3.

Full size image
Fig. 3: Sea ice morphology versus age.
figure 3

a,b, Mean age (years) of surveyed sea ice (+ s.d., trend lines and credibility) at the TPD (red) (a) and in the Lincoln Sea (blue) (b). The statistical metrics are listed in Supplementary Table 3. c–f, Histograms showing pressure ridge density (c), spacing (d), atmospheric drag coefficient (e) and sail height (f) separately for five different ice age classes. The vertical lines represent the mean values for each age class. The mean, mode and median ridge morphology metrics are provided in Extended Data Table 1.

Full size image

The comprehensive aggregation of data from extensive airborne surveys over Arctic sea ice reveals a previously undocumented and statistically significant decline in pressure ridge density (DR, Fig. 2a,b), height (HS, Fig. 2e,f) and a corresponding increase in spacing (SR, Fig. 2c,d) across the two monitoring regions. The observed trends are driven by a stepwise pattern, transitioning from higher values before ~2007 to reduced values thereafter. The Lincoln Sea, with its historically thicker and older ice, shows more pronounced shift compared to the TPD. The decrease in DR is nearly double that observed in the TPD, with reductions of −2.33 n km decade−1 (14.9%) and −1.32 n km decade−1 (12.2%), respectively. Similarly, HS decreases by 0.14 m per decade (10.4%) in the Lincoln Sea compared to 0.04 m per decade (5%) in the TPD. A reduction in DR and HS is accompanied by an increase in SR (20.4 m per decade in the TPD; 16.7 m per decade in the Lincoln Sea), although differences between regions are less strong. Details on how trends are computed are provided in Methods (‘Compilation of time series’). Assessing long-term trends in ridge width (WS) is not possible because seasonal effects of, for example, snow accumulation, prevent us from merging spring and summer data (Extended Data Fig. 4b). Nonetheless, given that WS is inherently linked to HS, a reduction in width over the observation period is likely (Extended Data Fig. 3). Fewer and smaller pressure ridges mean in turn that the ice surface has become smoother, with a greater proportion of homogeneous and undeformed level ice. This directly impacts the momentum transfer from the atmosphere to the ice, as evidenced by a notably reduced atmospheric surface drag coefficient (Cdn10, Fig. 2g,h). Note that DR and HS are major contributors to this coefficient (form drag). For a description of how Cdn10 is calculated, see Methods ‘Atmospheric neutral drag coefficient’. The reduction in Cdn10 is substantially more pronounced in the Lincoln Sea (−0.61 × 10−3) compared to the TPD (−0.16 × 10−3). Possible implications of the observed changes are discussed in the final section (‘Arctic-wide changes and implications’). Negative trends are consistent across a range of minimum ridge height detection thresholds (for example, H0 = 0.4, 0.8 and 1.2 m; Extended Data Fig. 5), which confirms the robustness of our observations.

Linking sea ice age and ridge morphology

DR and HS (SR) showed higher (lower) values in the TPD before 2007 and reduced (increased) values after that period (Fig. 2). This pattern aligns with observations of sea ice roughness9 (Table 5 in ref. 22) and thickness in the same area23 and further south in Fram Strait12. The stepwise transition from a thicker and deformed, to a thinner and more uniform ice cover has been associated with a loss of old ice and a reduced residence time of sea ice and growth12. As in the TPD, the time series for the Lincoln Sea indicates a change in ridge morphology with higher DR and HS before 2009 and 2010 and reduced values thereafter. This transition period coincides with a large shift in the multi-year ice (MYI) budget around 2008, followed by anomalously low MYI melt and anomalously high replenishment years24.

First evidence that sea ice age is an important driver of regional variability in ridge morphology was provided by Duncan & Farell17. While their study provides initial insights from a 3-year period after the launch of the ICESat-2 satellite in 2018, our airborne data extend these findings with a broader temporal coverage. A comparison of ridge densities from all available survey flights (1993–2023, entire Arctic; Fig. 1) with the ice age determined through back trajectories substantiates the statistical relationship between ridge morphology and age, with a correlation coefficient (R) of 0.49 (P < 0.01; Extended Data Fig. 6). By assigning mean morphological characteristics to their corresponding age classes (Fig. 3c–f), we further elucidate this relationship (Methods ‘Ridge morphology and ice age’): the mean, median and mode of DR and Cdn10 (Fig. 3c,e and Extended Data Table 1), as well as the mean and median of HS (Fig. 3f) progressively increase with ageing sea ice, while spacing (Fig. 3d) decreases. Because ridges continue to form and accumulate over time, the relationship between age and morphology is cumulative in nature. This cumulative relationship is confirmed by ICESat-2 observations: in Supplementary Fig. 1, we segmented satellite-based HS and SR observations according to ice age and found that the relative morphological differences between ice age classes align with those presented in Fig. 3d,f, although the absolute values differ because of the larger sensor footprint of the ICESat-2 satellite16 (Supplementary Information: HS and SR derived from the ICESat-2 measurements).

From the differences in DR between ice age classes, we can derive the number of ridges formed per year, hereafter referred to as ridging events (ER, n km year−1). It is noteworthy that most pressure ridges develop during the first year (ER = 7.4 n km year−1, indicated by the red vertical line in Fig. 3c and Extended Data Table 1), with a marked decline to ~1.8 ridging events (average) in subsequent years. The decreasing ER with increasing ice age can be explained primarily by a thickening of the ice cover.

Following the hypothesis formulated by Rampal et al.18, which posits that a thinner and more dynamic ice cover is more susceptible to deformation, we anticipated an increase in ridging among the thinner and younger first-year ice (FYI) and second-year ice (SYI) classes over time. However, contrary to expectations, Fig. 4a–c does not show any significant changes in DR, SH and SR for FYI or SYI from 1993 to 2023 (Methods ‘Ridge morphology and ice age’). Instead, all three parameters have shown remarkable stability over the last three decades, suggesting that the likelihood of a ridge event has not increased, regardless of ice type.

Fig. 4: Morphology of FYI and SYI.
figure 4

a–c, Anomalies (campaign average minus long-term mean from all campaigns) for the three parameters DR (a), SR (b) and HS (c) are shown separately for FYI (red) and SYI (orange). The size of the symbols indicates the number of survey km collected during each campaign over the respective ice age class. The vertical lines provide the s.d. Trend lines (dashed for FYI, solid for SYI) are plotted on top.

Full size image

The stability of the relationship between ice age and ridge morphology is a prerequisite for the estimates of Arctic-wide change discussed in the next section. Several factors may contribute to this observed stability, which we outline below. The most plausible explanation is that the thicknesses of the FYI and SYI have not changed much since the 1990s. It is also possible that although the ice cover is becoming more mobile14, the resulting increase in deformation18 is not yet high enough to alter the ridge morphology of FYI and SYI. Furthermore, any increase in deformation rates could be offset by other processes, such as dynamic ice growth through mechanisms like ice rafting, the formation of small-scale ridges undetectable within current measurement uncertainties or changes in sea ice properties (for example, strength). The limited sampling of FYI and SYI in the 1990s and potential biases in age estimates from back trajectories are also noted.

Arctic-wide changes and implications

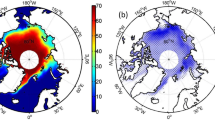
The Arctic-wide estimates of changes in ridge morphology presented in Fig. 5 have been obtained by assigning the mean DR, Cdn10 and ER values to the corresponding ice age classes extracted from the pan-Arctic ice age product (National Snow and Ice Data Center (NSIDC)) (Methods ‘Arctic-wide application’). The figure illustrates an Arctic-wide decrease in both pressure ridge density and drag coefficient by 4% and 5% per decade, respectively (black lines in Fig. 5d,f). These changes are particularly pronounced in regions experiencing strong MYI loss (Fig. 5a,c). Notably, the Beaufort Sea and the Last Ice Area exhibit the most significant reductions in DR (13% and 10% per decade) and a decline in Cdn10 values (13% and 11% per decade). In contrast, DR and Cdn10 are unchanged in areas that were and still are predominantly characterized by FYI, particularly the Russian shelf seas. Despite pressure ridges becoming less frequent, the annual number of ridging events is on the rise (9% per decade; Fig. 5e, black line), especially after 2007. This apparent contradiction is the consequence of an increasing FYI fraction, which is more prone to deformation and ridging (Fig. 3c). The most pronounced increase in ER can be observed in areas where a transition from perennial to seasonal ice cover occurs, for example, areas that adjoin the Russian shelf seas in the north and in the entire Beaufort Sea (Fig. 5b).

Fig. 5: Arctic-wide estimates.
figure 5

a–c, Spatial trends in winter (April) pressure ridge density (DR, a), number of ridging events per year (ER, b) and atmospheric drag coefficient (Cdn10, c) over Arctic sea ice from 1992 to 2022. d–f, Corresponding time series of DR (d), ER (e) and Cdn10 (f) for the whole Arctic (black), the Beaufort Sea (red) and the Last Ice Area (blue). The boundaries of the Beaufort Sea and the Last Ice Area are marked using black polygons in b. Trends are indicated by the dashed lines. In addition, the 95% confidence interval (CI) (Methods) is provided (slope, lower range, upper range, P value).

Full size image

These Arctic-wide estimates are based on several assumptions: (1) airborne observations provide a representative picture and accurately reflect changes across the entire Arctic; (2) the morphology of ice ridges can be adequately described by their age; and (3) this relationship is consistent over time. The agreement between observed trends in the Lincoln Sea and reconstructed time series, as shown in Extended Data Fig. 7, lends credibility to these estimates. Both observed and reconstructed trends in DR and HS are closely matched, although the reconstructed values are consistently lower. This discrepancy suggests that while our approach effectively captures relative regional changes and differences, estimating absolute changes requires more complex modelling assumptions. Furthermore, changes in the marginal ice zone may not be accurately reflected by our current methodology, given the impact of the shortening of the winter season on the morphological properties of FYI.

Comparative analysis between the observed and reconstructed Lincoln Sea time series in Extended Data Fig. 7 bolster our confidence, showing close agreement in trends of ridge density (DR) and height (HS), although reconstructed values are systematically lower. These findings underscore that while the Arctic-wide application adeptly captures relative changes and regional variations, estimating absolute changes necessitates greater caution and more sophisticated modelling approaches. Additionally, the observed shortening of the winter season probably affects the morphological properties of FYI, particularly in the marginal ice zone, a dynamic not fully captured by our current methodology.

The observed decrease in both density and height of pressure ridges, as documented in this study, provides observational long-term evidence supporting the hypothesis of Duncan and Farell17 of an Arctic-wide change in ridge morphology due to the loss of older ice. Furthermore, there is indication that a higher FYI fraction increases the overall deformation in the Arctic and acts as a negative feedback mechanism on pan-Arctic ridge morphology: the greater the proportion of younger ice classes, the faster the pan-Arctic mean ridge rate, dampening an overall decline in ridges with age. Thus, the hypotheses put forward at the beginning of our study are not mutually exclusive; rather, they have a moderating effect on each other.

Advanced models capable of resolving both thermodynamic and dynamic processes in sea ice of different ages are essential to fully quantify the effects of decreasing pressure ridges on the sea ice mass balance, snow redistribution and melt pond formation, and the wider implications for biogeochemical cycles and ecosystems. The latter depends on a deeper understanding of the ecological significance of pressure ridge age. This is particularly important as the proportion of ridges that do not survive their first summer is increasing. How a reduced surface drag coefficient, and hence diminished momentum transfer from the atmosphere to the sea ice, affects the drift velocity of sea ice is another question that arises from this study. Assuming constant mean wind speed and atmospheric stability, one might expect a slowdown in drift velocity (for example, refs. 7,25). However, previous studies showed an increase in drift speed, which cannot be explained by stronger atmospheric forcing alone14. It is probable that additional processes, which have changed over the past decades, compensate for the reduced surface drag coefficient. These include an intensification of near-surface ocean currents26,27, a smoothing of the ice bottom topography reducing the keel drag28, and an enhanced responsiveness of sea ice to wind because of changes in mechanical strength, thickness or concentration29. Hence, accurately projecting the future dynamics of a seasonally ice-covered ocean and its implications for global warming scenarios necessitates the integration of variable surface and basal drag coefficients7,25, and a more complex rheology (for example, refs. 30,31) into climate models.

Methods

Airborne laser altimeter surveys

This study capitalizes on data from airborne laser altimeter surveys over the Arctic sea ice. Airborne laser altimeters emit laser pulses to accurately measure surface elevation profiles with a high spatial resolution and a centimetre-scale footprint size. The data used in this study to investigate interannual variability and trends in ridge morphology were collected exclusively using SBLAs flown over sea ice from several platforms by the AWI between 1993 and 2023. The first AWI survey flights over sea ice with an SBLA sampling a frequency high enough to identify individual pressure ridges, were conducted in 1993. From then on, survey flights were repeated on a regular basis in Fram Strait and the central Arctic Ocean. Flights that took place in the 1990s used an IBEO PS100 altimeter mounted on the research aircraft Polar-2 (Dornier DO-228), and helicopters operated from the research icebreaker RV Polarstern. The technical specification and resolution of the applied laser altimeters are listed in Supplementary Table 1. Since 2001, surveys have been primarily carried out with the Electromagnetic (EM)-Bird32, a towed sensor system equipped with an SBLA (RIEGL-LD90 or ASTECH-LDM). The EM-Bird is operated at 15 m above the ice surface. It measures sea ice thickness by calculating the difference between the EM-derived distance to the ice-water interface and an SBLA-derived distance to the snow and ice surface. Initially, the use of the EM-Bird was limited to helicopters, with surveys mainly conducted from icebreakers or coastal stations in Canada, the United States and Russia. However, the integration of the EM-system onto the research aircraft Polar-5 and 6 (Basler BT-67) in 2009 enabled more flexible and extensive application32. This led to the establishment of a long-term airborne sea ice monitoring programme called IceBird, conducted twice a year during spring and summer when ice extent is at its maximum or minimum. Key regions for survey activities are Fram Strait, the central Arctic Ocean and the Last Ice Area north of Canada. On surveys carried out with Polar-5 and 6, a laser scanner (VQ580, RIEGL) mounted at the bottom of the aircraft is operated together with the EM-Bird system. In this study, we used data from the scanner only to compensate for occasional failures of the EM-system (<1%) to maintain the consistency of the primary observation data. Moreover, scanner data were used to assess the quality of the surface scans derived from the SBLA through cross-comparison33. Extended Data Figs. 1 and 2 and Supplementary Table 2 provide an overview of the individual campaigns, the locations and months when the surveys were carried out, and the type of aircraft and sensor used.

SBLA data processing and ridge detection

In this study, we applied a method developed by Hibler34 to extract the sea ice surface height profile and pressure ridge morphology from laser altimetry surveys over sea ice. This robust technique has been used in several studies between the 1970s and 1990s (for example, refs. 21,35) and more recently4,6,36 to detect pressure ridge sails and determine their height and spacing37,38, applied to analyse and characterize ice regimes of different ages and deformation stages, and to investigate6,39 the influence of sea ice topography on atmospheric drag. We describe the processing scheme below. For a more detailed discussion of the methodology and the implications of choosing different filters and parameterizations, see ref. 6.

Following Hibler34, we first isolated the surface profile from low-frequency variations associated with the aircraft motion. This involved three steps: (1) a high-pass filter was applied to the data, allowing only wavelengths smaller or frequencies higher than a predefined cut-off value to pass through. The resulting output retains the profile roughness, albeit with a minor residual influence from the aircraft; (2) from the filtered profile, minimum points were identified. These points, which represent the maximum distance between the aircraft and the surface, were then connected using straight-line segments on the original profile; (3) finally, straight-line segments were low-pass-filtered to generate a reconstruction of the aircraft’s altitude variation. The surface height profile was then derived by subtracting the flight curve from the laser altimeter profile.

Before deriving the ridge statistics, it is necessary to identify and eliminate open water in the surface height profiles using auxiliary data: alongside laser profiling with the SBLA during the early 1990s, surface temperatures were concurrently recorded using a radiation sensor (KT19, Heitronics40). As these flights were conducted early in the season (March and April), open water is characterized by notably higher temperatures than the surrounding ice. Consequently, identifying and isolating open water is straightforward. In contrast to this approach, surface profiles obtained from the laser altimeter mounted on the EM-Bird were corrected for open water by using the measured ice thickness. For our categorization, ice thicknesses below 20 cm were considered indicative of open water23. For the two campaigns where information about surface temperatures or ice thickness was unavailable (ARK-XI/1 and ARK-XII; Supplementary Table 2), we used satellite-derived estimates of ice concentration as corrective measures. The satellite product used aligns with the ones used for the backtracking of sea ice (Methods ‘Sea ice age and trajectories’).

The surface height profiles obtained from Hibler’s method do not represent the actual freeboard of the ice. Rather, they show the elevation of the ice surface relative to the surrounding-level ice (HL). To detect pressure ridges, we applied filter techniques used by, for example, refs. 6,41,42. An algorithm detects the local maxima based on a predefined minimum height threshold (H0). A local maximum is classified as a pressure ridge sail if it meets the Rayleigh criterion, which requires that the troughs descend to a height at least half that of the local maximum21,43. The highest point of a ridge is defined as the ridge sail height (HS). WS denotes the ridge width. The ridge sail spacing (SR) provides the peak-to-peak distance between consecutive HS maxima. Ridge density (DR) is defined as the number of ridges (n) per km. In the literature, DR is often used to detect trends in the frequency of pressure ridges over time or across regions, while SR reveals differences in their distribution patterns.

For further data analysis (for example, backtracking of sea ice) and construction of the time series, we divided the profiles into sections of 10 km each and computed the means, medians and modes for HS, SR, WS and DR. The chosen segment length of 10 km aligns with the resolution of commonly used satellite-based sea ice products and was proposed by Lüpkes et al.44 as a reasonable minimum length scale for surface drag parameterization. An average distance over 10 km may mask out variability that can be found in profiles of such length. However, the validity of the typical exponential fit for individual height distributions and of the lognormal fit for individual spacing distributions is independent from the mean (for details, see ref. 43, and Tables 2 and 3 in ref. 38).

In this study we used a H0 value of 0.6 m to detect pressure ridges and determine the DR, SR and HS (Fig. 2a–f). Following Newmann et al.45, the threshold is well above the height of snow features and the measurement uncertainty (compare with ‘Uncertainties of SBLA’). In addition, the choice is consistent with the ICESat-2 studies in refs. 16,17,46 on the variability of Arctic pressure ridges, which allows comparison. For the calculation of the neutral atmospheric drag coefficients (Cdn10 as in Fig. 2g,h), we used an H0 value of 0.4 m as in ref. 6.

Atmospheric neutral drag coefficient

The atmospheric neutral drag coefficient (Cdn10) was calculated in accordance with ref. 6, where the measured sea ice surface profile is related to a 10 m neutral drag coefficient. The idea behind the parameterization used goes back to refs. 47,48, whose authors distinguished the influence of small-scale roughness (skin drag) and larger distinct obstacles (form drag). Thus, the neutral drag coefficients are given by the sum of the skin and form drag coefficients. In this article, we applied the concept as in refs. 6,7,46, whose authors formulated the basic equations according to the partitioning concept in the form proposed by Garbrecht et al.41, including, for example, parameterization of the coefficient of resistance for individual ridges. For the neutral 10 m skin drag coefficient, a constant value (8.38 × 10−4) was chosen, which was determined from flights over level ice41. Form drag was parameterized as a function of HS and SR (equations 3 and 4 in ref. 6).

Uncertainties of SBLAs

The accuracy of the reconstructed surface profiles from laser altimeter data is influenced by many factors. The sensors themselves represent the smallest error source, demonstrating a high level of accuracy as illustrated in Supplementary Table 1. Also, the efficacy of the Hibler method for segregating the surface height profile from aircraft motion is high and no manual correction was required37. According to the author, who compared the outcome of a fully automated procedure with manually corrected altitude derivatives, a manual correction of processed data has minimal impact on the derived density (+0.97%), height (+0.79%) and spacing (0.43%) of pressure ridges. Another error source is introduced when an SBLA is mounted inside the towed EM-Bird, rather than directly on the aircraft. Turbulent flight conditions can cause pitch and roll movements of the EM-system, leading to an overestimation of surface height measurements by as much as 19.2 cm, as indicated by the available recordings. To investigate the impact of a swinging EM platform on pressure ridge detection37, comparison data were obtained by the SBLA mounted inside the towed EM-Bird and an altimeter operated simultaneously on the aircraft. The results indicate that the towed laser can underestimate ridge density by up to 0.45 n km−1and ridge height by approximately 5 cm, while overestimating spacing by 2.25 m (see also Table 5.1 in ref. 33). However, as most measurements in this study were conducted using the SBLA mounted inside the towed EM-Bird—with the early 1990s being the exception—we surmise that the systematic error potentially arising from using different sensors on varying platforms is small.

Sea ice age and trajectories

In this research, we used satellite-based estimates of sea ice age and drift trajectories to spatially filter airborne observations before constructing the time series (Fig. 2a–h). This process is facilitated by a Lagrangian drift model called IceTrack, which was also used later to investigate the relationship between sea ice age and ridge morphology (Figs. 3 and 4). For an Arctic-wide application of the observed relationships, we applied a gridded sea ice age dataset provided by the NSIDC (Fig. 5). Below we describe two sea ice age datasets used in our study and highlight their differences.

IceTrack is a Lagrangian drift analysis system used to trace the midpoints of the 10-km-long surface profile segments back in time. This system, extensively used in several studies (for example, refs. 49,50) and detailed in ref. 19, computes trajectories using three different ice drift products: the OSI-405-c motion product (Ocean and Sea Ice (OSI) Satellite Application Facility (SAF))51; the Center for Satellite Exploitation and Research (CERSAT) MERGED-motion product52; and the Polar Pathfinder daily motion vectors (v.4.1)53 (NSIDC). The latter was only applied in the summer months (June–August) before 2012. The tracking approach works as follows: sea ice is tracked backward from starting points on a daily basis, halting when the ice hits the coastline or fast ice edge or when the satellite-based ice concentration (provided by OSI-430-a and OSI-450-a, OSI SAF) at a particular ___location falls below 15%. The ice’s age inferred from the temporal length of the trajectories54 is used to quantify the uncertainties in sea ice trajectories on a broader temporal and spatial scale by comparing them with drifting buoys. We found that the deviation between actual and virtual tracks was rather small (60 ± 24 km after 320 days). IceTrack’s efficacy in differentiating zones of varying ice ages and their origins, even in complex coastal settings, is demonstrated in Supplementary Fig. 2.

The NSIDC ice age product consists of tracking sea ice in a similar Lagrangian manner using weekly gridded ice motion vectors (v.4.1)53. The weekly product is provided on a 12.5 × 12.5 km grid. The physical approach is slightly different from IceTrack and follows the ‘oldest ice age assignment’: if two parcels of different ages are advected into the same grid cell, the oldest age is taken for that grid cell, under the assumption that younger ice is easier to deform than older ice13. The accuracy of the NSIDC ice age estimates is lower than that of IceTrack. This is because the underlying sea ice motion data product underestimates drift velocities, especially in coastal areas55. Furthermore, selecting the oldest ice in the case formulated above may overestimate the age of the ice by prioritizing small concentrations of old ice56. Nevertheless, the NSIDC sea ice age product is a widely used reference for the changing Arctic sea ice cover because of its high consistency and temporal and spatial coverage (for example, ref. 57).

Compilation of time series

The spatial boundaries of the two long-term monitoring sites (TPD and Lincoln Sea) were defined around the recurrent flight patterns of recent years. Survey data within 50 km of the coast were excluded from the time series in Fig. 2 because of potential statistical bias from increased ridge formation parallel to the coast, as observed in ref. 58. Furthermore, surveys conducted within 100 km of the ice edge and over ice with less than 80% concentration were not considered. Moreover, the Lincoln Sea time series was cleaned of FYI because it is locally formed in a polynya and may bias interannual variability and trends. Note that FYI was identified using IceTrack (Methods ‘Sea ice age and trajectories’). The TPD time series, on the other hand, was cleaned of ice originating from the Beaufort Sea. For this purpose, the ice that was formed west of 150° E was filtered out. The longitudinal cut-off was chosen based on Fig. 2d in ref. 19, which shows the typical course of the TPD between 1991 and 2018.

The time series shown in Fig. 2 includes data collected during different seasons, assuming that the seasonal dependence of the morphological parameters presented is negligible. This assumption is supported by a comprehensive year-round study of the morphological evolution of an FYI ridge carried out by Salganik et al.8 during the MOSAiC expedition. The authors found that while the width of ridges changed throughout the season because of snow accumulation and melting, the height of the sails did not decrease during the transition from winter to summer. Instead, HS increased by 3 cm relative to the surrounding-level sea ice, with consolidation being the main factor contributing to the uplift of the HS. Our airborne observations confirm the findings in ref. 8. In Extended Data Fig. 4, we compare the HS and WS of survey flights conducted over the same ice during the IceBird campaigns and MOSAiC4 in spring and the following summer. For the IceBird flights, such ‘revisits’ were identified using IceTrack. For MOSAiC, GPS tracks from deployed buoys were used. The absence of snow caused WS to be 2.36 m (IceBird) and 3.17 m (MOSAiC) narrower in summer than in spring. However, like the observations in ref. 8, the difference between the observed HS in spring and summer was negligible (0.03 m for IceBird and 0.02 m for MOSAiC). Given the minor seasonal variations observed, we propose that HS and its derivative parameters DR, SR and Cdn10 can be collectively analysed and displayed across seasons (Fig. 2), suggesting negligible seasonal influence.

Trends in the time series for the different variables were analysed separately using generalized linear mixed effect models with campaign as the random intercept. Temporal autocorrelation was accounted for by including a continuous autoregressive process for a continuous time covariate (years). SR, HS, Cdn10 and age were log-transformed to ensure normal distribution of all response variables. In Supplementary Table 3, we present the sample size, t-values, significance level (P) and median slope with 95% CI. All statistical tests were done in R v.4.3.1. The trends presented in Fig. 2 remain robust to adjustments in the spatial boundaries of the key regions.

Ridge morphology and ice age

In the histograms of Fig. 3c–f, we explore differences in ridge morphology between individual ice age classes. Note that, unlike Fig. 2, the morphological data shown in Figs. 3 and 4 are based on all survey flights carried out in the Arctic between 1992 and 2023. Ice age was sourced from IceTrack. We chose IceTrack because its underlying motion products have lower uncertainties compared to those derived from NSIDC-based ice drift data55. Ice ages were categorized into five distinct classes: 1 year (FYI); 2 years (SYI); 3 years; 4–7 years; and 8–16 years. Profiles taken in areas with less than 80% ice concentration or near the coast and ice edge were excluded. The 4–7 and 8–16 year age classes have a wider range to account for the reduced accuracy of age determination for very old ice (4+ years) and its less frequent occurrence. For the pressure ridge characteristics that depend on length scales (DR and Cdn10), histograms were created using the 10 km averages. For HS and SR, full resolution was used. Before plotting, the frequencies for each ice class were normalized to ensure uniform scaling and comparability, which is particularly beneficial for sparsely represented older age classes. The mean, mode and median ridge morphology metrics for each age class are presented in Extended Data Table 1, with the means also visually indicated by vertical lines in the histograms of Fig. 3c–f.

The variability of HS, SR and DR within individual age classes is examined in Fig. 4a–c, using surface profile segments that were classified as FYI and SYI using IceTrack, discarding those near coasts (>50 km), ice edges (>100 km) or with a loose ice cover (>80% ice concentration). Campaign averages for FYI and SYI are depicted as anomalies from the long-term mean.

Arctic-wide application

Arctic-wide estimates of changes in ridge morphology were made by assigning the mean DR and Cdn10 values from Extended Data Table 1 to the corresponding ice age classes obtained from the NSIDC ice age product. We used the gridded NSIDC product instead of IceTrack age information because it is available for the entire Arctic and over the full observation period. Beforehand, the NSIDC ice ages were categorized into the same five age classes as shown in Fig. 3. We limited Arctic-wide estimates to April because in this month the ice cover is still dense and uncertainties of satellite-based age products are low (compared to summer months with surface melt55). Our analysis was confined to the period from 1993 to 2022, for which observational data are available. From the gridded fields, we extracted trends for each grid cell (shown in Fig. 5a–c) and compiled time series for three specific regions (Fig. 5d–f): the entire Arctic Ocean (black lines), the Beaufort Sea (red lines) and the Last Ice Area (blue lines). The delineation of the Beaufort Sea follows the definition in ref. 13. Because there are no fixed boundaries for the Last Ice Area, their selection is somewhat arbitrary. The trend lines (slopes), CIs (95% boundaries of the range of slopes) and significance levels shown in Fig. 5e,f were calculated by assigning the number of grid cells available for each NSIDC ice class to randomly drawn DR (Cdn10) values from the normal (gamma) distribution of the respective ice age class. We verified the quality of the Arctic-wide application through a reconstruction of observations in the Lincoln Sea (DR and HS) using the age of the surveyed sea ice (NSIDC) and the metrics provided in Extended Data Table 1. The results are shown in Extended Data Fig. 7. For this reconstruction, the survey flights conducted in the Lincoln Sea were excluded from the underlying metric.