Topological acoustofluidics

Originating in condensed matter physics, topological wave materials have been actively investigated to create analogues of electron properties such as pseudospin textures^1,2,3,4,5,6. The non-trivial nature of the pseudospin lattice and its intrinsic topological invariants support robust wave propagation along the edge, which protects it from defects, disorder and backscattering^7,8,9. These topological properties have been demonstrated primarily in the context of robustness, but their fundamental pseudospin textures and resulting practical applications have yet to be fully explored^{10,11,12,13,14,15}. Recently, electron vortices in graphene were observed in a pattern analogous to theoretical hydrodynamic flow¹⁶, while the valley vortices and topological current of electrons remain visually unknown^17,18. Leveraging this analogy between hydrodynamics and electrons, the complex interaction between topological wave materials and real-world hydrodynamics could provide promising possibilities for imaging the topological physics of materials^{19,20,21,22,23}. By adding tracer particles to hydrodynamic fluids, the fundamental physics of valley pseudospin and transport of electrons in graphene could be visually analogized within topological wave materials. In natural materials, the complex interaction among various degrees of freedom has allowed the direct visualization of quantized vortices^24,25 and driven the modern development of exotic topological phenomena, such as topological non-trivial polar vortices^26,27, anisotropic topological superconductivity²⁸ and crystalline-symmetry-allowed orientations of edge states²⁹. So far, signatures of topological wave materials have been predominantly studied with a single phase of matter (solid or air) and a single degree of freedom (valley or spin)^19,30,31. Little is understood about their complex interactions with hydrodynamics, and most importantly, the application of topological wave materials in life sciences still needs to be explored.

The complex interaction between topology and nonlinear fluid dynamics could offer promising opportunities beyond topological robustness for both fundamental pseudospin and practical applications. This potential could be realized through topological wave materials coupled with microfluidics^{15,32,33,34,35}. A visual connection could be established between atomic-scale electron vortices and microscopic particle imaging by harnessing the tractable nature of tracer particles in microfluidics^16,25. For example, valley states of electrons in graphene could be mapped into valley streaming vortices in fluids, while topological currents of electrons could be analogous to backward-immune particle transport^17,20,36. This direct connection could further deepen the understanding of topological state transition by three-dimensional confocal microscopic imaging.

For practical applications in the life sciences, aqueous liquids with topological states could lead to exotic families of biomedical devices for unconventional bioparticle manipulation. The valley states, represented by the chirality of the vortex, could be selectively excited to exhibit either a clockwise or anticlockwise feature^20,37. This single-mode vortex in fluids could allow the synchronous rotation of bioparticles and, more importantly, create a biological cosmos using DNA and their interaction with other biological molecules. In microfluidics, the conventional acoustic modes extend into the lossy bulk and are prone to attenuation in fluids, limiting their nanomaterial manipulation capabilities. The edge states, with a field pattern confined to the ___domain interface, have been shown to enhance the power emission in a topological photonic laser⁸. These confined topological states would be of interest in phononics to increase acoustic energy density for manipulating biological nanoparticles and molecules in life sciences. Nevertheless, the direct realization of topological phenomena within a microfluidic chip is exceptionally challenging. The main problems are the unexplored intensity of valley spin, the complexities of the interaction between acoustic field and nonlinear fluid dynamics, and the involvement of the substrate’s crystallographic structure.

In this work, we present the inaugural demonstration of on-chip topological acoustofluidics driven by the complex interaction among phonon valleys, nonlinear fluid dynamics and substrates’ crystallographic structure within microfluidics. The valley states are realized by exciting surface acoustic waves (SAWs) on a 128° Y-cut lithium niobate (LiNbO₃) chip and then transitioned into a fluid layer via the solid–fluid interface. By harnessing the tractable nature of tracer particles in fluids, we visualized the valley state as valley streaming vortices while also demonstrating chiral streaming vortices for backward-immune particle transport. Using tracer particles, we created arrays of clockwise and anticlockwise valley vortices due to an enhancement in elastic spin density. Moreover, we discovered topological pressure nanowells induced by the elastic valley spin and nonlinear fluid dynamics interaction, where the confined edge modes lead to a notable increase in acoustic energy and reduce the size of particle manipulation down to DNA molecules. Furthermore, we observed the orientation dependence of topological acoustofluidic edge states, which is reminiscent of polarized valleys induced by the substrate’s crystallographic structure. We simulated the polarized valley arrays in the momentum space and theoretically derived the edge state dispersion from an effective Hamiltonian. We also simulated a 93.2% modulation in edge bandwidth at different crystallographic orientations. These interactions offer promising opportunities for both fundamental physics and real-world applications, such as the discovery of exotic topological wave phenomena, the visualization of elastic valley spin and the implementation of topological materials in life sciences.

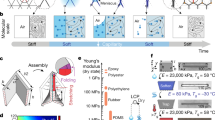
We designed topological acoustofluidic chips consisting of microscale solid–fluid dual-phase domains within a microfluidic chamber (Fig. 1a and Supplementary Note 1). The graphene-like hexagonal lattice structure is designed to create elastic valley spin analogous to the valley pseudospin of electrons in graphene^10,17. Here, elastic spin is an actual physical quantity with units of angular momentum, while pseudospin is resembled by a SU(2) mathematical framework without units of angular momentum³⁸. In the solid ___domain, we electroplated a hexagonal valley phononic crystal (VPC) of copper pillars on 128° Y-cut LiNbO₃ (Fig. 1a,b). The elastic valley spin from VPCs can periodically modulate SAWs to guide them along the ___domain interface. In the fluid ___domain, a liquid layer was added into a polydimethylsiloxane (PDMS) chamber, contributing to nonlinear fluid dynamics (Supplementary Fig. 1). We first studied the complex interaction between elastic valley spin and nonlinear fluid dynamics (Fig. 1c), whereas the substrate’s crystallographic structure is discussed in the last section. This interaction is realized along the solid–fluid interface: the vortex features transition into streaming vortices, and the vertical displacements of pillars leak energy into surrounding fluids.

a, Schematic of the designed topological acoustofluidic device on a 128° Y-cut LiNbO₃ substrate, where electroplated copper pillars are in contact with the fluid loaded in a PDMS microchamber. b, False-coloured scanning electron microscopy image of the electroplated copper pillars, indicating the topologically different VPC domains (blue) and the straight ___domain interface (red). Scale bar, 72 μm. c, Unit cell schematic showing valley eigenmode transport from solid copper pillars to the fluid layer. The red arrows reveal the valley vortex streaming in fluids by transitioning valley spin from a large pillar to the overlying fluids. d, The band structure for SAWs in the solid–fluid coupled hexagonal lattice. The red and blue lines represent dispersion curves without and with inversion symmetry, and the grey lines are for Rayleigh mode SAWs. e, Images showing the acoustic pressure amplitude |p| (colour) and the Poynting vector for acoustic intensity at the q⁺ and p⁻ points of the K valley on the first and second bands. f, The time evolution of simulated displacement field (colour) and energy flow’s Poynting vector at the q⁺ and p⁻ valley states when the fluid height is close to the copper pillar height.

Full size image

Figure 1d shows the simulated band structure of the modulated SAWs in fluids. When the copper pillars share the same diameter, the band diagram features Dirac points at the Brillouin zone corners (K and K′). A bandgap opens at K (K′) valley from 21.5 MHz to 24.3 MHz by breaking the inversion symmetry with unequal pillar diameter d_L = 0.53a and d_S = 0.27a and lattice constant a = 72 µm (Fig. 1d). Here L and S refer to large and small pillars, respectively. Figure 1e shows simulated eigenmode profiles in the first (q) and second (p) band of the K valley at different fluid heights. The fluid height h_W relative to the copper pillar height h_C is essential to successfully transferring spin textures from the solid ___domain to the fluid ___domain. When h_W > h_C, the time-averaged Poynting vector of vortex intensity rotates clockwise and anticlockwise around the centre region of a hexagonal unit at q⁺ and p⁻, respectively. When h_W ≈ h_C, the vortex feature appears at q⁺ but disappears at p⁻, and a low-pressure region appears around displaced pillars (Supplementary Fig. 2). By contrast, in the solid ___domain of Fig. 1f, the time evolution of Poynting vectors for energy flow at p⁻ and q⁺ maintains the chiral vortex feature when h_W ≈ h_C, despite its inability to transition to the fluid ___domain smoothly. Details about the transition of elastic valley spin from the solid ___domain to the fluid ___domain are shown in Supplementary Fig. 2.

It should be noted that the structure parameters should be carefully designed (Supplementary Note 2). For example, a large bandgap is required to achieve narrow edge-state confinement by increasing the sublattice asymmetry, which is advantageous for observing single-mode edge states (Supplementary Figs. 3–5). Meanwhile, the sublattice asymmetry should be within a range to ensure a well-defined non-trivial Berry curvature (Supplementary Fig. 4). Finally, the fluid height h_W needs to be larger than the pillar height to ensure the successful transfer of valley vortex energy from the solid ___domain to the fluid ___domain (Supplementary Fig. 2).

Spin or pseudospin is the fundamental physics in topological materials^10,37. Such spin textures, analysed by the measurement of substrate displacement³⁸, have yet to be visualized. Here, we created valley vortices and valley edge transport in fluids, and more crucially, we achieved highly tunable elastic valley spin intensity for nano-to-microsized particle manipulation. We first investigated the transition of valley vortex states on topological acoustofluidic chips. In a hexagonal unit (Fig. 2a), by inversing the pillar diameter, two topologically different valley-Hall phases can be obtained: VPC1 (middle of Fig. 2a) and VPC2 (bottom of Fig. 2a). These two valley-Hall phases showing opposite chirality have been numerically studied³⁹. We experimentally observed the chiral vortices in VPC1 (Supplementary Video 1) and in VPC2 (Supplementary Video 2) along a straight interface. This visualization is achieved by harnessing the tractable nature of 200 nm fluorescent suspended particles.

a, Schematic of two VPCs. Top: the valley states are labelled in a hexagonal unit. Middle: VPC1 with Δd = d_L − d_S to enable a clockwise valley vortex. Bottom: VPC2 with Δd = d_S − d_L to enable an anticlockwise valley vortex. The red colour on small pillars indicates vertical displacements. b, Scanning electron microscopy image of a straight interface between VPC1 and VPC2. The red and blue arrowed circles represent chiral vortices. Scale bar, 72 µm. c, The simulation result at 23.6 MHz showing the acoustic pressure (colour) and the chiral vortex features for acoustic intensity. d, Experimental visualization at 23.6 MHz showing topological pumping of 200 nm particles in a backward-immune way with chiral streaming vortices along the interface. Scale bar, 72 µm. e, A phase diagram of Dirac frequency versus lattice constant and Young’s modulus in solid field. f, Schematic analogy of valley states between phonons and electrons, where the clockwise and counterclockwise fields are defined as spin-down and spin-up, respectively. g, Valley acoustofluidic centrifuge of 1 µm particles, where particles were concentrated at the centre of hexagonal units with false-coloured pillars. Scale bar, 36 µm. h, Valley acoustofluidic synchronous rotator of 1 µm particles, where arrays of valley streaming vortices around small pillars (spin-down) were observed. Scale bar, 100 µm. The images show the acoustic pressure (colour) and the Poynting vector for acoustic intensity (g and h). The experimental data represent the mean ± standard error of the mean from the results of n = 3 devices (g and h).

Source data

Full size image

One of the most critical features of topological edge states is the backscattering immune wave transport⁷. To confirm this character, we investigated the particle movement at topological edge modes (Fig. 2b). Figure 2c shows the simulated chiral vortex feature of the acoustic intensity fields at edge modes. In Fig. 2d, we experimentally observed the topological transport of 200 nm polystyrene in a backward-immune way enabled by chiral streaming vortices (Supplementary Videos 3 and 4). Note that, unlike the valley propagating edge modes that can directionally couple into ambient space (Supplementary Fig. 5)^40,41, the local streaming vortices cannot outcouple from the interface into surrounding fluids because the lattice structure is necessary to maintain the valley spin.

Although the visualization of elastic valley spin is realized, highly tunable spin density would be expected for bioparticle manipulation across a wide size range and convenient observation of topological spin textures. To reveal the valley physics controlled by different materials, we first studied the dependence of Dirac frequencies on Young’s modulus and lattice constants (Supplementary Note 3)^{42,43,44,45,46}. In Fig. 2e, the Dirac frequency increases with decreasing lattice constant and increasing Young’s modulus. At the microscale lattice constant, we calculate the valley spin against different materials with varying Young’s modulus (Supplementary Fig. 6). The valley spin density along the z axis is determined by³⁸

where ρ is the material density, ω is the angular frequency and u is the displacement. It shows a highly tunable valley spin density. This remarkable range is attributed to the variation in substrate displacement, which tends to be larger at a smaller value of Young’s modulus.

We then experimentally verify the tunability of elastic valley spin using 1 μm polystyrene tracer particles. In Fig. 2f, the elastic valley spin has implications for two-dimensional crystals in valleytronics because it could resemble pseudospin textures described by electron valley states^10,17,36. For instance, while the valley pseudospin up and down of electrons and holes can be excited with circularly polarized photons^47,48,49, we anticipate similar clockwise (spin-down) and anticlockwise (spin-up) valley spins from elastic valley phonons^14,37,38. In addition, their valleys in momentum space exhibit a similar honeycomb lattice structure. Importantly, unlike valley pseudospin, which is currently unmeasurable, elastic valley spin could be measured locally in real space³⁸. In Fig. 2g, we simulated the valley vortex field for q mode. At a small valley spin density (Fig. 2g), the particles were concentrated at multiple hexagonal unit centres instead of embodying streaming vortices, referred to as valley acoustofluidic centrifuge. By contrast, the clockwise valley streaming vortices (spin-down) for 1 μm particles were observed around small pillars at q mode on a different topological acoustofluidic platform with the increase of valley spin density (Fig. 2h and Supplementary Video 5), referred to as valley acoustofluidic synchronous rotator. Note that the valley streaming velocity at p mode is slower than that at q mode owing to the smaller calculated valley spin density (Supplementary Fig. 7 and Supplementary Video 5). These results indicate that a large valley spin is needed for the rotation of large micrometre-sized particles. Overall, these results could allow valley spin visualization as streaming vortices and enable unconventional manipulation of nano-to-micrometre-sized particles.

Strikingly different from that in solid or air systems, we discovered exotic topological pressure wells in the fluid phase (Fig. 3a). Here, we combined this concept with confined edge modes to develop topological microfluidic devices for molecule manipulation (Supplementary Note 4). The topological pressure wells are nonlinear acoustic streaming pressure and can dominate over valley streaming vortices by tuning the height of water fluids close to that of copper pillars (Fig. 3a and Supplementary Fig. 2). In Fig. 3b, we simulated the pressure gradient around a small pillar and the pressure fields gradually decrease when approaching the small pillar, revealing the emergence of topological pressure well. This result is consistent with the experimentally observed trajectories of 1 µm polystyrene particles, where particles are pushed by acoustic forces and migrate to pressure minima wells around the small pillar. With time-series analysis from 0 to 13.6 s, an evenly distributed circle consisting of 1 µm particles was formed around the small pillars (Supplementary Video 6), verifying the existence of topological pressure wells. Furthermore, we can easily tailor topological pressure well intensities by tuning the input voltages. In Fig. 3c, the higher input voltages lead to stronger topological pressure well intensities and, therefore, larger particle movement velocities (Supplementary Videos 6 and 7).

a, Schematic of topological pressure wells along the edge for particle concentration. The red on the small pillars represents the energy field, and the blue colour gradient around the small pillars indicates topological pressure wells. b, Simulated pressure well and measured time-series observation of 1 µm particle around a small pillar. The yellow arrows represent the 1 µm particle trajectories over time. Scale bar, 10 µm. c, Measured particle velocities of 1 µm polystyrene along a straight interface as a function of excitation frequencies and input voltages. d, Simulated energy fields and measured fluorescence intensity distributions for VPCs without interface and with a Z-shaped interface around the frequency of 23.8 MHz, respectively. Scale bar, 200 µm. e, Measured fluorescence intensity at positions far from (point A), near (points B, C, and D) and without (point E) interface in d. The light-blue region represents the frequency range of the edge state. The data represent the mean ± standard deviation. f, Simulated topological pressure wells (left) and measured fluorescence intensity distribution of 200 nm polystyrene (right) along a straight interface. Scale bar, 20 µm. g, A comparison of simulated energy intensity between topological SAWs and conventional SAWs in solid field. h, Simulated energy fields and measured manipulation of 60 nm polystyrene and DNA molecules at edge-state frequency (33.83 MHz) in a topological device with lattice constant a = 50 µm. Scale bar, 50 µm. The data represent the mean ± standard deviation. i, A comparison of measured fluorescence intensities for concentrated 1 µm polystyrene particles, 60 nm polystyrene particles and DNA molecules using different methods. The experimental data represent the mean ± standard error of the mean from the results of n = 3 DNA samples and polystyrene particles.

Source data

Full size image

Next, we demonstrated the robustness of topological pressure wells along a Z-shaped interface (Fig. 3d and Supplementary Fig. 8). In striking contrast to the rapid disappearance away from the interface, the measured fluorescent particle intensity is well distributed along the interface, in good agreement with the simulated energy field. Within the edge-state frequency range, the measured intensities at points B to D are much higher than those at points A and E (Fig. 3e). Beyond this range, the fluorescence intensity distributions at different points become complex and indicate a random behaviour due to the existence of propagation mode within VPCs and scatterings at the ___domain interface. In Fig. 3f, we further verify the dominance of topological pressure wells over valley streaming vortices by the concentration of 200 nm polystyrene particles around the small pillars, which is different from the chiral streaming vortices of 200 nm in Fig. 2d.

We then exploited the feature of confined edge modes to develop a topological phononic tweezer for molecule manipulation (Supplementary Note 4)⁸. The simulation results indicate that the energy intensities at topological edge states can outperform those at conventional SAWs up to two orders of magnitude (Fig. 3g,h). We excited topological devices at edge mode and trivial bulk mode together with conventional SAW devices. Then, we measured the fluorescent distribution for 1 µm polystyrene, 60 nm polystyrene and DNA molecules. From the observed images (Fig. 3h and Supplementary Fig. 9), the topological acoustofluidic devices are strong enough to manipulate DNA molecules. In Fig. 3i, the fluorescence intensity columns clearly show that the topological acoustofluidic devices evidently surpass the capabilities of their trivial bulk counterparts and conventional acoustofluidic devices, which often have difficulties in manipulating nanomaterials^{50,51,52,53,54}. The attributes at topological edge modes can explain this remarkable performance enhancement. In contrast to bulk modes, which transfer energy into the entire bulk lattice, the topological edge modes strongly confine the acoustic energy to the edge (Fig. 3g,h). Moreover, topological pressure wells are at deep-subwavelength dimensions down to 1/150 of the acoustic wavelength, which corresponds to a dimension scale of approximately 780 nm. This result unveils an exotic topological wave phenomenon in fluids that could lead to the development of topological molecule tweezers.

In natural topological materials, crystalline symmetry has driven the emergence of exotic physical and topological phenomena^26,28,29 (Supplementary Note 5). Here, we extended this concept to topological wave materials and investigated the dependence of edge mode on the crystallographic structure of the substrate (Fig. 4a,b). By varying the crystal orientations in low-symmetry 128° Y-cut LiNbO₃, our numerical study uncovered a twofold rotational symmetry for the edge states (Fig. 4c). As the angle θ increases from 0° to 180°, the edge-state bandwidth (Δf) gradually reaches the maximum at 90° while being minimum at around 0° and 180°. We found that Δf exhibits a 93.2% modulation in different angles and a 53.7% improvement at 90° relative to its counterparts with isotropic crystalline lattice (Methods and Supplementary Fig. 10). This orientation dependence and extended bandwidth are essential for designing monolithically integrated edge modes such as beam splitters and waveguide-ring resonators. In Fig. 4d, we defined the centre of the edge-state frequency as 0 and experimentally measured the edge-state localization length at different orientations, confirming the orientation dependence.

a, Schematic for in-plane rotation angle θ between the copper lattice ___domain interface and the x axis of LiNbO₃ substrate. Here, θ = 0 corresponds to the edge interface alignment along the x axis of LiNbO₃. b, Schematic for the LiNbO₃ crystalline lattice structures. c, Simulated edge-state bandwidth as a function of θ at different pillar diameter ratios (d_L/d_S). The bandwidth Δf refers to the frequency range between the offset and the onset of the edge state. d, The measured propagation length at different edge-state frequencies for 0°, 45° and 90°. The data represent the mean ± standard deviation from the results of n = 3 devices. e, The deviation of the edge-state eigenfrequency to the Dirac frequency as a function of \(\delta {k}_{x}a\) for 0°, 45° and 90°. f, The equifrequency contour of the first Brillouin zone at 0°, 45° and 90°. g–i, Plots of simulated energy intensity and measured fluorescence intensity spectra at 0° (g), 45° (h) and 90° (i). j–l, The edge mode mapped with the fluorescence intensity distribution across various frequencies at 0° (j), 45° (k) and 90° (l). Scale bar, 100 µm.

Source data

Full size image

To theoretically understand the valley–crystalline structure interaction, we derive the edge states at different crystalline orientations with an effective Hamiltonian⁵⁵

Here, ν_D is the group velocity, δk = k − k_K is the relative wave vector to the K valley, σ_i are the Pauli matrices and Δ_P is proportional to the bandwidth of the bandgap \(2({\nu }_{D}|{\Delta }_{{\mathrm{P}}}|)\). We suppose that \(A=\varPhi {{\mathrm{e}}}^{i\delta {\mathbf{k}}_{x}+\kappa y}\) is an edge state with Φ being the spinor of valley spin. Then, the edge state travelling along the x direction has the dispersion relation

where δω is the deviation of edge-state eigenfrequency to Dirac frequency at \(\updelta {{k}}_{x}=0\). When \(\updelta {{k}}_{x}=0\), \(\updelta \omega =0\) and ω is the Dirac frequency at the gapless valley (Supplementary Note 5). We theoretically calculate the \(\updelta \omega\) from equation (3), based on the values of group velocity and relative wave vector along the ΓK direction at different crystal orientations, as shown in Fig. 4e. It is observed that the edge bandwidth at 90° is much larger than those at 0° and 45°. This difference can be explained by the equifrequency contours and band structures (Fig. 4f and Supplementary Fig. 10). The valley–crystalline structure interaction creates polarized and canted valleys, resulting in a calculation angle at 45° and a small group velocity at 0°.

To further confirm the valley–crystalline structure interaction, we examined the mapping of the acoustofluidic edge states for SAWs at 0°, 45° and 90°. In Fig. 4g–i, the simulated energy fields and measured fluorescent particle intensities confirm the orientation dependence of edge states (Supplementary Fig. 11). Figure 4j–l show the edge modes mapped at four selective frequencies. These results show that the edge-state localization length and bandwidth at 0° is much smaller than that at 90°, indicating a strong directionality. We then evaluate the influence of this interaction in a waveguide-ring resonator at 0° and 90°. In Supplementary Fig. 12, the measured fluorescence intensities along the hexagonal circulation loop at 90° strongly outperform those at 0°. These results unravel the orientation dependence of edge states driven by the valley–crystalline structure interaction and highlight the importance of crystalline structure in developing on-chip topological wave materials.

In summary, we have observed valley and chiral vortices driven by the complex interaction between elastic valleys and nonlinear fluid dynamics. Such features allow particles to be synchronously rotated and transported in a backward-immune way. Moreover, we discovered the emerging topological pressure wells in fluids. By harnessing the feature of confined edge modes, the topological pressure nanowells lead to the experimental concentration of DNA molecules. This could enable imaging of the behaviour of biological molecules in fluid and solid structures. Furthermore, we uncovered the orientation dependence of topological acoustofluidic edge states on the crystallographic structure of substrates. Together, our results highlight pathways for visualizing fundamental physics in topological materials and bridging topological materials to life sciences.

These findings beget meaningful opportunities and avenues for future exploration. They allow a deep understanding of topological spin textures and their state transitions. Our observations establish an unprecedented connection between atomic-scale electrons and microscopic particle imaging at the unit cell and lattice levels. A wide range of scenarios in electronic and atomic systems involving spin textures could be visualized in the microscale fluid phase. Moreover, our findings transcend the boundary of topological physics in electronic, atomic, photonic and acoustic systems and create opportunities for unconventional manipulation of particles, cells and molecules for mechanobiological studies.

Device fabrication and characterization

We used a 128° Y-cut LiNbO₃ piezoelectric substrate (Precision Micro-Optics). Small pillars are designed along the edge to test the edge modes because the excitation of large pillars along the edge requires an antisymmetric phononic source. The design parameters shown in Figs. 1–3 were d_L = 0.53a and d_S = 0.27a, while those in Fig. 4 were d_L = 0.48a and d_S = 0.32a, to study the edge-state bandwidth at different angles. The critical dimension tolerance of the mask for pillar fabrication is 0.5 μm. Chirped interdigital transducers (IDTs) were exploited in all devices except for nanomaterial concentration of 60 nm polystyrene and DNA molecules, where a straight IDT was utilized.

A photo of the topological acoustofluidic device is shown in Supplementary Fig. 1. To fabricate the device, the IDT pattern was transferred onto LiNbO₃ by photolithography, followed by metal (Cr/Au 5/100 nm) deposition by electron-beam evaporation. After a lift-off process in acetone, a metal (Ti/Cu 10/250 nm) seed layer was deposited on LiNbO₃ using electron-beam evaporation. On this LiNbO₃ wafer, the phononic structure patterns were formed by photolithography and the development of an AZ9260 photoresist in an AZ400K 1:4 developer. With 30-µm-thick AZ9260 as a mask, the phononic structures of copper pillars were electroplated on a LiNbO₃ wafer. Then, acetone, APS-100 copper etchant and buffered oxide etchant solution were sequentially utilized to remove AZ9260 and the seed layer. The obtained device was later immersed in a (3-aminopropyl)triethoxysilane solution (Sigma-Aldrich) to enhance its bonding with PDMS. Finally, after oxygen plasma treatment, a PDMS microchamber with punched holes for fluid injection was bonded to the wafer. For comparison, the different topological acoustofluidic devices designed to enhance valley spin density were fabricated with SU8 pillars on polymethyl methacrylate substrates through photolithography, owing to the low Young’s modulus.

Numerical simulations

All numerical simulations were carried out through a commercial finite-element solver (COMSOL Multiphysics). To simulate the interaction between acoustic and fluid fields, a solid mechanics module, electrostatics module and pressure acoustic module were implemented for eigenfrequency and eigenmode study. A creeping flow module was added for acoustic streaming and pressure well study. In the band structure study, all the boundaries were set with Floquet periodic boundaries. In the edge-state study, the boundaries along the edge were set as Floquet periodic boundaries; in the direction perpendicular to the edge, they were selected as plane-wave radiation for water fluids and low-reflection boundary for LiNbO₃, respectively. In the eigenmode study, the boundaries of LiNbO₃ were set as low-reflection boundaries, the bottom of LiNbO₃ was established as a fixed boundary and the boundaries of water fluids were set as plane-wave radiation. The properties of all electroplated copper pillars are density 8,960 kg m⁻³, Poisson ratio 0.34, Young’s modulus 108 ± 4.5 GPa determined by nanoindentation (Bruker Hysitron TI980 Triboindenter) and height about 28.5 ± 2.0 µm measured by three-dimensional optical profiler (Zygo NewView 5000).

Experimental measurements

The fluorescent polystyrene particles (1 μm, 200 nm and 60 nm) were purchased from Bangs Laboratories and dispersed in 0.5% sodium dodecyl sulfate water solutions. λDNA molecules were purchased from Takara and stained with DAPI (Thermofisher) at a concentration of 100 μg ml⁻¹. Before sample loading, PDMS microchambers were flushed and coated with a 5% Pluronic F-127 (Sigma-Aldrich) solution. Once mounted on a microscope stage, the devices were driven by a continuous sinusoidal signal generated by a functional generator (E4422B, Agilent) and magnified by an amplifier (25A250A, Amplifier Research). Different fluorescence microscopes were used for precise experimental observation. The chiral streaming vortices and time evolution of particle movement were monitored with an inverted fluorescence microscope (Eclipse Ti, Nikon), and the particle concentration was recorded with an upright fluorescence microscope (BX51W1, Olympus). Data were further processed through a particle image velocity program in MATLAB. For transmission measurements, a Gaussian pulse was generated by a function generator (AFG3011, Tektronix) and magnified by the amplifier before being sent to the input IDTs. At the same time, the transmitted signal was received by output IDTs and measured by an oscilloscope (Tektronix, DPO3034). The normalized transmission is obtained by comparing topological devices with and without a straight interface to evaluate the influence of edge states.

Derivation of edge states from an effective Hamiltonian

For simplicity, we suppose that a ___domain interface is oriented along the x direction and constructed by two VPCs with \({\Delta }_{{\mathrm{P}}} > 0\) for\(y < 0\) and \(-{\Delta }_{{\mathrm{P}}} < 0\) for \(y > 0\).

The effective Hamiltonian is then \({H}_{K}(\updelta \mathbf{k})={\nu }_{{\mathrm{D}}}\updelta {{k}}_{x}{\sigma }_{x}+{\nu }_{{\mathrm{D}}}\updelta {{k}}_{y}{\sigma }_{y}\) \(-{\nu }_{{\mathrm{D}}}{\Delta }_{{\mathrm{P}}}{\sigma }_{z}\) for \(y > 0\) and \({H}_{K}(\updelta \mathbf{k})={\nu }_{{\mathrm{D}}}\updelta {{k}}_{x}{\sigma }_{x}+{\nu }_{{\mathrm{D}}}\updelta {{k}}_{y}{\sigma }_{y}+{\nu }_{{\mathrm{D}}}{\Delta }_{{\mathrm{P}}}{\sigma }_{z}\) for \(y < 0\). We consider a vector A with eigenfrequency \(\updelta \omega\) as an eigenstate. A governing equation \(({\nu }_{{\mathrm{D}}}\updelta {{k}}_{x}{\sigma }_{x}-{\nu }_{{\mathrm{D}}}i{\vartheta }_{y}{\sigma }_{y}+{\nu }_{{\mathrm{D}}}{\Delta }_{{\mathrm{P}}}{\sigma }_{z})\mathbf{A}=\updelta \omega \mathbf{A}\) is derived for \(y < 0\) by substituting \(\updelta {{k}}_{y}\) with the operator \(i{\vartheta }_{y}\). Then, we consider the edge state has the format \(\mathbf{A}=\varPhi {{\mathrm{e}}}^{i\updelta {{k}}_{x}x+\kappa y}\), where Φ is a spinor of valley spin with \(\varPhi ={\sigma }_{x}\varPhi\) due to band inversion. Substituting A and Φ into the governing equation, we have \({\nu }_{{\mathrm{D}}}\updelta {{k}}_{x}\varPhi +{\nu }_{{\mathrm{D}}}({\Delta }_{{\mathrm{P}}}-\kappa ){\sigma }_{z}\varPhi =\updelta \omega \varPhi\). To balance the equation, the dispersion relation \(\updelta \omega ={\nu }_{{\mathrm{D}}}\updelta {{k}}_{x}\) is derived for \(y < 0\) and a similar argument gives the same dispersion for \(y > 0\).

Comparison of band structure and edge states with isotropic and anisotropic lattice structures

On an LiNbO₃ with isotropic lattice structure, numerical results for projected edge states occupy a similar frequency range regardless of the orientation angle θ. For example, the topological chips with d_L = 0.48a and d_S = 0.32a with a pillar height of 29 µm and a lattice constant of 72 µm open a similar bandgap from 22.4 to 24.1 MHz and construct a similar edge state from 22.87 to 23.8 MHz at different θ. In our experiment, the LiNbO₃ exhibits anisotropic lattice structure, and the bandwidth for projected edge states depends strongly on θ (Fig. 4c and Supplementary Fig. 10). At θ = 90°, the edge-state bandwidth is 1.43 MHz from 22.13 to 23.56 MHz, while at θ = 0° this bandwidth becomes narrower from 22.67 to 23.41 MHz. This comparison indicates a 93.2% modulation in the bandwidth of edge states.