Main

The generation and characterization of attosecond pulses of extreme ultraviolet (XUV) light has provided access to the motion of electrons on their natural timescale, in atoms1,2,3, molecules4,5 and solids6,7,8,9,10,11, and given rise to new fields of research (for example, attochemistry12,13 and lightwave electronics14,15,16). Traditionally, attosecond pulses have been generated via high harmonic generation and characterized temporally via attosecond streaking17,18. At longer wavelengths, in the near infrared (NIR), sub-femtosecond pulses with much higher peak powers have been generated via pulse synthesis19,20. However, the generation of intense, ultrashort pulses in the ultraviolet (UV), the spectral region between the XUV and visible (VIS)–NIR (this is highly interesting as here most elements exhibit valence electron resonances as opposed to XUV, which predominantly excites core-level electrons3,21), has been challenging. Attosecond metrology itself has expanded in a new direction in recent years, where the electric field of light is used as the carrier of the details of light–matter interaction22, while the petahertz bandwidth of the field-resolved measurement techniques23,24,25 results in attosecond time resolution. Simultaneously, the confluence of nonlinear fibre optics and high-field laser science has enabled the extension of soliton dynamics to radically new regimes providing a robust alternative to light field synthesis26,27 and a unique way of realizing sources of few-cycle UV pulses with high peak and average power26,28. While pulses as short as 1.9 fs at around 260 nm and with hundreds of nanojoules of energy have been generated via frequency upconversion (harmonics)29,30, such an approach provides poor spectral tunability, and extension to shorter wavelengths is limited by the current chirped-mirror technology. Meanwhile, exploiting resonant dispersive wave (RDW) emission in gas-filled hollow-core fibres (HCFs) has allowed the generation of pulses with comparable durations31,32, tunable wavelength from the VIS to the vacuum UV, and over ten times higher energies, even with compact HCF systems33.

In this work, we combine the recent advances in attosecond metrology and soliton dynamics in HCFs and demonstrate the extension of the bandwidth of nonlinear photoconductive sampling (NPS). This field-sampling technique, similar in function to the Auston switch34 for recording picosecond field transients, utilizes strong-field photo-injection of charge carriers into the detection medium (in the present case, argon gas), and it was proven to work in the NIR and VIS regions by benchmarking against attosecond streaking35. Now, we push the bandwidth even further into the deep UV (DUV) and show that it can be used to detect pulses at wavelengths as short as 150 nm (~8 eV). To demonstrate this, we record the electric field of self-compressed attosecond solitons and the emitted RDW in the DUV. We show that this enables fine tuning of the waveforms emerging from the soliton dynamics and, thus, measurement of subcycle light transients at optical wavelengths with durations of ~350 as full width at half maximum (FWHM) of E2(t). Moreover, by isolating the RDW, we demonstrate DUV pulses as short as 0.9 fs. Finally, as a proof of concept, we use these attosecond pulses as a gate for measuring NIR pulses, thus demonstrating access to extreme nonlinear optics in a previously inaccessible spectral range on these timescales.

Results

NPS of attosecond pulses

Figure 1 shows the basic concepts for the generation (Fig. 1a) and characterization (Fig. 1b) of attosecond waveforms in the NIR and UV spectral regions. First, we launch pulses with peak power P0 and duration τ0 of a single optical cycle into a hollow-core waveguide filled with helium and tune the pressure such that the dispersion β2 < 0 and the soliton order

$$N=\sqrt{\frac{{{\gamma }}{P}_{0}{{{\tau }}}_{0}^{2}}{\left|{{{\beta }}}_{2}\right|}} > 1,$$
(1)

with γ being the nonlinear parameter of the fibre \(\gamma \approx \frac{4\uppi }{\lambda }\frac{{\rho n}_{2}}{3{a}^{2}}\) (ref. 27). There, ρ is the ratio of gas density to that of standard conditions, n2 is the Kerr nonlinear refractive index under those conditions, and a is the hollow-core radius of the fibre. The interplay of self-phase modulation-induced spectral broadening and anomalous dispersion (due to the negative β2) leads to soliton self-compression, followed by pulse break-up and the emission of RDWs once the pulses reach their minimum supported duration26. The emission wavelength depends on the zero-dispersion wavelength, and by adjusting the helium pressure, we continuously tune the phase-matching to RDWs in the spectral region between 200 nm and 270 nm (refs. 27,36,37,38).

Fig. 1: Generation and detection of a self-compressed attosecond soliton and dispersive wave.
figure 1

a, The simulated evolution of the electric field transient as it propagates along the hollow-core waveguide filled with helium gas. The colour scale shows the instantaneous frequency of the field, with the emergence of the RDW shown in purple. The dynamics of soliton self-compression and RDW emission are different in their modification of adjacent half-cycles of the field, enhancing and shortening the primary half-cycle of the waveform. b, The measurement scheme for NPS of the generated DUV RDW emission and solitons. The injection and drive pulses are colinearly focused into a gas jet. The injection pulse ionizes the gas via nonlinear photon absorption, while the DUV drive pulse accelerates the free charges. The electrodes detect the generated current.

Full size image

These waveforms are directly delivered into a vacuum chamber with decreasing pressure along the fibre and without any transmissive optical elements, to avoid introducing dispersion and thus preserve their duration31. To illustrate the process, in Fig. 1a, we show the simulated evolution of the electric field along the fibre. As the single-cycle pulse propagates, the typical action of self-phase modulation results in a redshift of the rising edge and blueshift of the falling edge. Simultaneously, the resulting positive chirp is compensated by the negative group delay dispersion of the waveguide mode, while the field dependence of the group delay causes a steepening of the carrier trailing edge. Thereby, the soliton dynamics reshape the field, cycle by cycle, resulting in the formation of an attosecond transient followed by the emission of an RDW after ~8 cm. The self-steepening of the carrier wave is not as extreme as in the mid-infrared39,40; the effect, however, is crucial to achieving fields of few-hundred attosecond duration and to enhancing the conversion efficiency of the RDW.

In the time ___domain, the resulting electric field is the superposition of the soliton and the RDW it emitted: the two combine to produce a short electric field transient. Without additional filtering, this transient is the result of the soliton dynamics.

We measure the electric-field transient using NPS. In this method, the drive field accelerates charges that have been rapidly injected by an ultrashort gate pulse, producing an optically driven current approximately proportional to the drive field’s vector potential at the moment of injection. Measurements with this technique have been conducted in various materials, including dielectrics41, nano-antennas25 and gases42. Here, we use strong ultrashort VIS–NIR laser pulses (injection) to free electrons in argon via high-order nonlinear absorption, which are accelerated by the field under study (the drive field), resulting in an asymmetry of the charge distribution to be detected by the electrodes, as shown in Fig. 1b.

After the waveguide, the orthogonally polarized injection and drive pulses (the fibre output) are combined using a perforated mirror and focused collinearly onto an argon jet, as shown schematically in Fig. 2. Two electrodes measure the induced current as a function of the delay between the two waveforms. The strong nonlinearity of the absorption of the injection pulse confines the injection of charge carriers to a duration of hundreds of attoseconds, and the resulting temporal gate allows waveform sampling of the drive with a comparable resolution. It has been shown that the measured electric current Idrift(τ) maps the vector potential of the drive pulse convolved with a gating function G(t). In the frequency ___domain, we can approximate the signal at low pressures as43

Fig. 2
figure 2

Measurement set-up for the soliton and RDW generation and characterization via NPS.

Full size image
$${I}_{{\rm{drift}}}\left({\rm{\omega }}\right)=\frac{{e}^{2}{N}_{{{\mathrm{at}}}}}{{m}_{{\mathrm{e}}}}{A}_{x}\left({\rm{\omega }}\right){G}^{*}({\rm{\omega }}),$$
(2)

where Nat is the concentration of atoms, e > 0 is the elementary charge and me is the mass of the electron. The vector potential of the probe field is Ax(t), and, in the frequency ___domain, its electric field is \({\widetilde{E}}_{x}\left(\omega \right)=i\omega { \tilde{\rm{A}} }_{x}\left(\omega \right)\). The spectral response function \({G}^{*}({\rm{\omega}})\) is the complex conjugate of G(ω), the Fourier transform of G(t). In Fig. 3, we show the HCF output electric fields obtained by deconvolving the recorded delay-dependent signal with the response function G(t), calculated by solving the time-dependent Schrödinger equation numerically with the tRecX code44 in the single-active-electron approximation. In the simplest, classical rate-equation-based interpretation of the formation of the current, the response function would be the ionization rate of the gas, but the more general response function used here is modified by electronic coherence and the influence of the ionic Coulomb potential43.

Fig. 3: Measured electric field of self-compressed soliton and RDW.
figure 3

a, The measured and simulated electric field of the soliton plus RDW for optimal CEP. b, The intensity representation of the fields shown in a highlights the short pulse duration of the generated ~350 as light transient (E2). The intensity envelope is 0.83 fs. c, The electric field of the Si-wafer filtered pulse, with E2 FWHM of 0.9 fs and intensity envelope of 1.39 fs. d, The Fourier transform (squared amplitude and spectral phase) of the Si-wafer filtered pulse versus the wavelength, together with the spectrum measured with a calibrated UV spectrometer, clearly showing the RDW around 235 nm. The spectral range reaches from 150 nm (2 PHz) to approximately 1,100 nm (0.27 PHz).

Full size image

We filled the input end of the fibre with 10 bar of helium to obtain soliton order N ≈ 1.9 and set the RDW phase-matching at wavelengths around 240 nm (Methods). As the fibre output lies in vacuum, the transients propagate without any major dispersion-induced temporal stretching until reaching the argon target. The extremely broad bandwidth of our argon-based NPS allows the transient to be recorded in a single measurement, although the frequencies of the underlying soliton and RDW are separated by almost 1 PHz. In this fashion and by optimizing the carrier-envelope offset phase (CEP), we can tune the input pulse to get the shortest transients.

In Fig. 3a, the measured electric field is compared with the simulated field. Experimentally, we achieve a pulse duration as short as 352 as at FWHM for the squared electric field (and 0.83 fs when considering the intensity envelope as defined in the Methods) in the optical ___domain (Fig. 3b). In the simulations, the duration of the squared field is 411 as. The measured electric field features low frequencies on the leading edge and higher frequencies on the trailing edge corresponding to the RDW. In the frequency ___domain, the overall bandwidth exceeds 1 PHz, with the RDW manifesting as an isolated peak centred around 230 nm.

It is also useful to isolate the UV pulse without substantially altering its spectral phase. Using a silicon wafer placed at Brewster’s angle for 800 nm (~74°), we can suppress the long wavelengths, isolating the RDW and thus measuring the UV waveform with reduced intensity. The resulting field of the filtered light corrected by its gating function is shown in Fig. 3c. The FWHM duration of the resulting real squared field is ~0.90 fs and ~1.39 fs when considering the FWHM intensity envelope. The corresponding spectrum is in agreement with the one independently measured by an amplitude-calibrated spectrometer, as shown in Fig. 3d. In both measurements, the soliton tail (the wavelengths longer than ~350 nm) is not fully suppressed, and in the NPS measurement, these spectral components exhibit a larger amplitude. We attribute this to unaccounted spatial averaging at the focal spot.

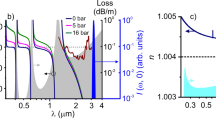
By changing the pressure of helium at the fibre input, we can continuously shift the RDW phase-matching wavelength and generate few-cycle UV pulses at shorter wavelengths. In Fig. 4, we show the spectra and the waveforms measured after the fibre when varying the pressure from 10 bar to 6 bar (Fig. 4a), together with the corresponding numerical simulations (Fig. 4b). As we decrease the pressure, the RDW shifts to shorter wavelengths, and with 6 bar, we generate radiation at around 200 nm. However, as we do not change the input energy, also the soliton order decreases, resulting in a lower conversion efficiency to the higher-frequency UV. In Fig. 4c, we show the waveforms measured with NPS for each He-filling pressure, showing the different electric fields after interacting in the fibre with the different amounts of gas. Because the CEP was not optimized for these measurements, the field is not necessarily the shortest transient. However, the overview clearly shows the dynamics, letting the RDW evolve. The change in spectrum, acquired via Fourier transformation of the NPS field, is shown in Fig. 4d.

Fig. 4: Pressure tuning of the emitted transient.
figure 4

a,b, The pressure at the entrance of the HCF was varied from 6 to 10 bar experimentally measured with an UV spectrometer (a) and in the simulations (b). Typically, the peak of the RDWs experiences a shift in wavelength. It moves towards lower wavelengths with lower pressures. Keeping the input intensity constant, the RDW gets weaker with lower pressures. c,d, The NPS measurements show the electric field for the different pressures (c) and the corresponding spectra, derived via Fourier transformation (d).

Full size image

Nonlinear processes induced by attosecond DUV pulses

In the measurements above, the attosecond field transient’s contribution to the measured signal was linear, as only its temporal structure was examined. However, its energy content is sufficient to also perform the role of an attosecond pump pulse, allowing strong-field NIR-DUV experiments with high temporal resolution. As a proof of principle, we changed the configuration shown in Fig. 1 to use the pulses for their opposite tasks.

When the pulse intensities are reversed, such that the DUV beam is now much stronger compared with the NIR beam, and the electrodes are rotated by 90°, the two pulses exchange roles (Figs. 2 and 5d). Now, the DUV pulse acts as an ultrashort injection, delivering the gate for the field sampling. The electrodes are now aligned with the polarization of the NIR beam, hence acting as a drive field. In argon, single-photon ionization requires wavelengths shorter than 79 nm. Hence, the photoionization of argon by the RDW is at least a two-photon or three-photon process. As we can detect a current, we show that the DUV–NIR pulse is nonlinearly absorbed by the argon, leading to free electrons. The derived electric field and the corresponding spectrum are shown in Fig. 5e,f. To compare this measurement with the standard configuration, the fibre was removed, and the fibre input (VIS–NIR) was measured (Fig. 5a–c). As the two interferometer arms are separated by a perforated mirror, the spectrum shown in Fig. 5c, measured in the standard configuration, differs from the reversed configuration owing to spatial differences, which was confirmed by a spectrometer measurement. In time, the pulses are comparable, proving that the attosecond transient can be utilized as a nonlinear pump pulse.

Fig. 5: Ionization gate triggered by attosecond soliton.
figure 5

a, A typical NPS measurement configuration without soliton generation when the fibre is removed. b, The measured electric field of the VIS–NIR pulse that is usually used as fibre input with an intensity envelope FWHM of 2.9 fs. c, The Fourier transform of the field shown in b together with the spectrum measured with a spectrometer. d, The reversed measurement configuration with fibre and rotated NPS sample to use the attosecond DUV–NIR beam as the injection pulse and the NIR beam as the drive. The DUV–NIR beam is strong enough to ionize argon via a two-photon or three-photon transition assuming the DUV drive contains the same measured photon energies as presented above. The FWHM pulse duration of the intensity envelope is 2.1 fs. e,f, The electric field measured in the reversed configuration (e) and its spectrum (f).

Full size image

Discussion, conclusions and outlook

Soliton compression dynamics in HCFs are a viable route to field-resolved experiments with intense attosecond pulses. An appropriately chosen combination of fibre diameter, length25,45 and gas allow the direct emission of single-cycle transients spanning the NIR to DUV without the need for postcompression, yielding a compact and reproducible attosecond light source. Compared with other approaches such as field synthesis, this approach does not offer as much fine-grained control over the resulting waveform, but in cases where the required field is simply close to the transform-limited one, bypassing the need for chirped mirrors in the DUV greatly increases the upper limit on the frequency of the pulse. Furthermore, the single-beam path simplifies the experimental set-up considerably, and it is expected to provide improved stability.

Enabling attosecond pump–probe experiments to be performed in the DUV will provide access to a new class of attosecond experiments in solids and molecules46, where an intense, attosecond pump pulse can be made resonant with transitions between the valence and conduction bands or those between the highest-occupied and lowest-unoccupied molecular orbitals, and the consequences of the interaction may be directly observed through the reshaping of the field of the attosecond pulse. This work provides a cycle-by-cycle measurement of the energy transfer, providing even better time resolution than the attosecond-scale envelope of the pulse.

Moreover, these results give the opportunity to measure electronic coherences and their decay in molecules with a method similar to field-resolved infrared spectroscopy47. In this scheme, the molecular vibrations are impulsively excited, which can now be altered to an attosecond DUV excitation of an electronic wavepacket48, performing oscillatory migration within the molecule. The decay can be observed by sampling the radiation with the presented NPS set-up and provides direct information about the lifetime of electronic coherences in molecules. Furthermore, this technique might provide an electronic fingerprint, enriching the understanding of molecular behaviour, for example, in human blood plasma.

In addition, attosecond spectroscopy of coherent Bloch wavepacket dynamics could now be performed in wide-bandgap-materials, providing interesting insights into electronic processes with attosecond resolution. With this newly available energy range, detailed studies of wavepacket motion and interactions can be observed at previously inaccessible time ranges49, pushing studies of semiconductor physics and lightwave electronics to a new level.

Methods

Laser system

We used a commercial Ti:sapphire oscillator (Femtolasers Rainbow), providing NIR pulses centred at 780 nm with a repetition rate of 78 MHz. The CEP is measured and stabilized with an f–0f interferometer, using the difference frequency generation (DFG) signal generated in periodically poled lithium niobate. Via a loop to an acousto-optic modulator, adjusting the power of the pump laser, the CEP is stabilized. The pulses with energies of 2.4 nJ are amplified in a chirped pulse amplifier, consisting of a stretcher, a nine-pass cryo-cooled Ti:sapphire amplifier (Femtolasers Femtopower HP) and a transmission grating compressor. After the first four passes in the amplifier, the repetition rate is reduced to 4 kHz with a pulse picker, and the dispersion and spectral shape of the pulses is optimized by an acousto-optic dispersive programmable filter (Fastlite DAZZLER). After the amplifier, the pulses have 1 mJ energy and a pulse length of approximately 25 fs. These pulses are spectrally broadened via self-phase modulation in a 1.5-m-long gas-filled HCF. With 1.6 bar of neon in the fibre, the output spectrum reaches from 350 nm to 1,100 nm. The reflection of the output window of the broadening fibre tube is sent to a second CEP stabilization loop that compensates for long-term drifts, consisting of a f–2f interferometer. After passing four sets of chirped mirrors, the spectrum reaches from 400 nm to 1,050 nm and the pulses are compressed to about 3 fs (FWHM of the intensity envelope, evaluated from NPS). The compressed pulses are guided with a periscope into a vacuum chamber that contains the set-up shown in Fig. 2 for experiments.

The VIS–NIR field (red) is split into two arms with a perforated mirror. The reflected, stronger beam traverses a delay stage and is rotated in polarization by 90° with a wire-grid polarizer and Si wafer at the Brewster angle. The other beam is focused into a gas-filled HCF where DUV light is generated. The fibre is 12 cm long, has a core diameter of 100 µm and has a pressure gradient to deliver the DUV directly into vacuum. After collimation, the beam is either fully reflected via mirrors or filtered by a reflection of a Si wafer under the infrared Brewster angle (~74°). The two arms are recombined with another perforated mirror and focused onto the NPS sample, in which the gas is surrounded by two cupper wires in this work. The generated current signal is acquired via lock-in detection (see details in 'Data acquisition').

For diagnostic purposes, the collimated fibre output can be sent out of the vacuum chamber through a MgF2 window. This option is used to align the fibre around the beam on a proper mode and output power. Moreover, after the perforated mirror, a translation stage enables capturing and redirecting of the beam into the UV spectrometer (VS7550 VUV Mini Spectrometer from Resonance). In addition, after the NPS sample, the beam is refocused outside to another spectrometer and camera to find and optimize the temporal and spatial overlap of the two arms.

Data acquisition

The electric-field waveforms were recorded via NPS with a signal produced in argon. Two electrodes, which are simply two copper wires, are mounted around the gas nozzle. As the UV driving pulses have p-polarization, the electrodes are aligned accordingly, left and right of the gas jet. For the second experiment, the VIS–NIR field is used as the drive pulse, which is s-polarized. Consequently, the electrodes are rotated to sit above and below the gas jet. Each of the electrodes is connected to a transimpedance amplifier (FEMTO DLPCA-200) that amplifies the current between the electrode and the ground with a gain of 109 V A−1. Furthermore, this voltage signal is detected via a lock-in amplifier (Zurich Instruments MFLI). To use lock-in detection, the laser pulse needs to be modulated at a reference frequency50. Here, the CEP was flipped for every consecutive pulse between 0 and π. Therefore, the used reference frequency is 2 kHz.

Numerical simulations

To simulate the nonlinear propagation of optical pulses along the waveguide, we solve a unidirectional full-field equation51 including photoionization of the gas via the Perelomov–Popov–Terent’ev rate, modified with the Ammosov–Delone–Krainov coefficients52. For this, we use the numerical code described in ref. 53 using the Marcatili expressions for the dispersion and the optical loss54, with the χ(3) of He given in ref. 55 and its full dispersion curve obtained using Sellmeier coefficients given in ref. 56. The variation of pressure p(z) along the propagation direction z is included via the following expression30: \(p\left(z\right)={p}_{0}\sqrt{1-z/L}\), where p0 is the maximum pressure and L is the fibre length. As an input for the simulation, we use the electric field waveforms measured at the fibre input and select the energy to 15.5 µJ in order to match the experimentally measured and numerically simulated pulse energy at the fibre output.

To calculate the soliton orders as a function of the He pressure, we use the expression for N given in equation (1) and assuming 2.4-fs input pulses with a central wavelength of 700 nm (this is exactly the average wavelength calculated using the spectrum of the input electric field).

We estimate the RDW emission frequency by setting the gas pressure and the laser power at the fibre input such that the following dephasing rate is zero:

$$\theta \left(\omega \right)=\beta \left(\omega \right)-\left({\beta }_{0}+{\beta }_{1} \left(\omega -{\omega }_{{{\mathrm{sol}}}}\right)+\frac{\gamma {P}_{{\mathrm{p}}}\omega }{{\omega }_{{{\mathrm{sol}}}}}\right),$$

where β0 is the propagation constant, β1 is the inverse group velocity at the soliton central frequency (β0, β1 and γ are gas-dependent parameters) and Pp is the soliton peak power27.

Data analysis and NPS response

To derive the electric field from the measured photocurrent Idrift(t), we perform the following data analysis. First, the signal is multiplied with a Tukey filter in the time ___domain, and zero-padding is used to interpolate the spectrum. In the frequency ___domain, a super-Gaussian bandpass filter is applied. Because the measured current is approximately proportional to the vector potential, we multiply the signal by the factor iω in the frequency ___domain to obtain the electric field. Moreover, the data are corrected by the numerically calculated response function \({G}^{*}({\rm{\omega}})\):

$$E\left({{t}}\right)={\rm{iFFT}}\left(\frac{i\omega \times {\rm{FFT}}\left({I}_{{\rm{drift}}}\left(t\right)\times {\rm{tukey}}-{\rm{filter}}\right)\times {\rm{sgbpfilter}}}{{G}^{* }\left(\omega \right)}\right).$$

Definition of the intensity envelope

The rapidly varying electric field of light is directly recorded in these measurements, but defining a smoothly varying envelope function is sometimes desirable for comparison with other results in ultrafast optics. The intensity envelope associated with the electric field is obtained via the complex analytic signal associated with it.

$$\widetilde{E}\left(t\right)=E\left(t\right)+\frac{i}{\pi }{\rm{p}}.{\rm{v}}.{\int }_{-\infty }^{{\infty }}{\rm{d}}\tau \frac{E\left(t\right)}{t-\tau }.$$

that is, the real part of the analytic signal \(\widetilde{E}\left(t\right)\) is the electric field E(t), and its imaginary part is the Hilbert transform of the electric field. The form of the intensity envelope is given by the squared modulus of the analytic signal

$$I\left(t\right)\propto {\left|\widetilde{E}\left(t\right)\right|}^{2}.$$