Pressure-enhanced splitting of density wave transitions in La₃Ni₂O_7–δ

The discovery of superconductivity in La₃Ni₂O_7–δ under pressure (p) has attracted notable attention^1,2,3,4,5. This interest is accentuated by the material’s critical temperature T_c ≃ 80 K, which is above the boiling point of liquid nitrogen, positioning La₃Ni₂O_7–δ within the category of high-temperature superconducting materials. A recent study⁴ suggests that superconductivity in La₃Ni₂O_7–δ emerges on the suppression of a competing density wave (DW) order. In particular, it was found that the DW-like anomaly in resistivity, which sets in at ambient pressure at around T_DW ≃ 140 K, is progressively suppressed with increasing p, whereas the onset of a superconducting transition emerges at p ≃ 7 GPa (Fig. 1). Similar DW anomalies were detected at ambient pressure in specific heat and magnetization experiments^6,7, as well as by means of nuclear magnetic resonance^8,9. However, the origin of the competing DW order remains a matter of ongoing investigations. Charge ordering in NiO₂ planes induced by oxygen orderings^10,11, or charge DW instabilities induced by one-dimensional Fermi surface nesting^6,12, were suggested to account for these anomalies. However, there is no direct evidence for the charge ordering in La₃Ni₂O_7–δ reported up to now. A more recent work¹³ reported the observation of a spin DW (SDW) type of order in La₃Ni₂O_7–δ by means of the muon-spin rotation/relaxation (μSR) technique. The ambient-pressure zero-field μSR experiments reveal the presence of static long-range magnetic order with the transition temperature of T_N ≃ 148 K. The SDW ordering was further confirmed by the resonant inelastic X-ray scattering¹⁴ and nuclear magnetic resonance experiments¹⁵.

The solid symbols represent pressure dependence of the SDW ordering temperature (T_SDW) as obtained in ZF and WTF μSR experiments (closed red and black circles) and the DW ordering temperature (T_DW) obtained in resistivity studies (blue stars) in the present work. The half-down filled symbols are T_DW versus p data^4,6,16,17. The half-up filled symbols represent the pressure dependence of the onset of the superconducting transition temperature \({T}_{{\rm{c}}}^{\;{\rm{onset}}}\) (refs. ^{1,2,3,4,16,41,42}). The lines are guides for the eye.

Full size image

Consequently, a question arises: whether the competing DW order is magnetic in origin, as suggested by the similar ambient-pressure values of DW transition temperatures T_DW ≃ 140–150 K (refs. ^{4,6,7,8,9,16,17}) and T_SDW ≃ 150 K (refs. ^13,15), or is the unspecified DW different in origin and coexisting with the SDW? In particular, in the single-layer La₂NiO₄ and three-layer La₄Ni₃O₁₀ Ruddlesden–Popper lanthanum nickelates, the coexistent spin and charge orders were detected^18,19. In order to address this question, in this work, comprehensive μSR and resistivity experiments under hydrostatic pressure conditions were performed. The primary aim was to determine whether or not the SDW order follows the same pressure dependence as the DW order. At ambient pressure, our results corroborate the findings of other work^13,15, in which an SDW type of magnetism was detected with a transition temperature of T_N ≃ 151 K. The DW transition, corresponding to the local minimum on the resistivity curve, sets 20 K lower at T_DW ≃ 131 K. Under increasing pressure, the magnetic ordering temperature was observed to rise at a rate of dT_N/dp ≃ 2.8 K GPa^–1, which is not only opposite in sign but also substantially smaller in magnitude compared with dT_DW/dp ≃ –26 K GPa^–1 (Fig. 1). The comparison of our experimental data with magnetic-dipole-field calculations also corroborates the notion of coexisting magnetic SDW and non-magnetic DW orders. Both these observations suggest that the competing DW order, which is suggested to compete with superconductivity in La₃Ni₂O_7–δ, is probably non-magnetic in origin. These results contribute to a deeper understanding of the intricate relationship between magnetism and superconductivity in this complex oxide, offering new insights into the nature of the competing phases in high-temperature superconductors.

Ambient-pressure μSR

The zero-applied-field (ZF) μSR response of La₃Ni₂O_7–δ measured at ambient pressure at T = 10 K is presented in Fig. 2. Figure 2a,b shows the ZF asymmetry spectra, representing the time evolution of the muon-spin polarization and the Fourier transformation showing the distribution of the internal fields, respectively.

a, Zero-field μSR time spectra of the La₃Ni₂O_7–δ sample measured at T = 10 K. The red line is a fit of equation (2) to the data. b, Fourier transform of the data presented in a. The dashed lines represent individual fit components. c, T dependencies of the ZF μSR signal fractions. d, T dependencies of the internal field of the fast-precessing and slow-precessing components. The solid line is the fit of the power law (equation (1)) to the B_int,Fast(T) data. The displayed error bars for parameters obtained from the μSR data correspond to one standard deviation from the χ² fits.

Source data

Full size image

The data were analysed by using equations (2) and (3) described in the Methods. The fit results reveal that the transversal part of equation (3) consists of three terms: the fast-precessing, slow-precessing and non-precessing fast-relaxing ones (Fig. 2b show the notations). The corresponding internal fields (labelled B_int) at T = 10 K are 0.15 T, 0.01 T and 0 T. This is reminiscent of the low-T (T ≲ 40 K) ZF μSR results of LaFeAsO (that is, the parent compound of the 1111 family of Fe-based superconductors) consisting of three magnetic components with the corresponding internal-field values of 0.17 T, 0.02 T and 0 T (ref. ²⁰). Note that the fit with the simple cosine type of oscillating functions (equation (3)) suggests the consistency of our ZF μSR data with the commensurate magnetic order (Supplementary Note 4 and Supplementary Fig. 3).

The temperature evolution of the magnetic fractions is presented in Fig. 2c. The analysis reveals that for T ≲ 150 K, approximately 90% of the full asymmetry is assigned to the magnetic contribution. Considering that the remaining 10% might be partially explained by the contribution of muons stopped outside the sample (3–5%, in line with the sample dimensions and GPS (general purpose surface) muon spectrometer characteristics²¹) as well as by muons stopped within the lanthanum silica apatite impurity phase (of the order of 8%; Supplementary Note 1 and Supplementary Fig. 1), this suggests that magnetism in the La₃Ni₂O_7–δ sample studied here is representative for the bulk. The transition from the magnetic to the non-magnetic state (from f_m ≃ 0.9 to f_m = 0) is rather sharp, thereby suggesting that magnetism in La₃Ni₂O_7–δ sets in homogeneously.

Figure 2c shows that the volume fraction of the slow-oscillating component remains nearly temperature independent, whereas fractions of the fast-relaxing and fast-oscillating components show opposite trends. With increasing temperature, the fast-relaxing signal develops at the expense of the fast-oscillating component (Fig. 2c).

A possible explanation is that the fast-relaxing component originates from muons that stop in highly magnetically disordered regions, thereby experiencing a large distribution of fields and dephasing quickly. Conversely, the fast-precessing component is from muons that sit in the same crystallographic site, but in regions of well-ordered magnetism. The change in amplitude suggests that as the temperature increases, the volume fraction of the disordered-type sites goes up (and hence the relaxing fraction increases) at the expense of the well-ordered regions (and hence the oscillating fraction drops). This could happen if, for example, the correlation length decreases with increasing temperature, meaning the ordered regions shrink and the disordered ones grow.

The internal magnetic field (that is, the magnetic order parameter) decreases with increasing temperature and vanishes at T_N (Fig. 2d). The temperature behaviours of both fast-precessing (B_int,Fast) and slow-precessing (B_int,Slow) internal fields remain nearly the same (Fig. 2d), suggesting the presence of at least two non-equivalent muon stopping sites within the magnetic unit cell of La₃Ni₂O_7–δ. The solid line in Fig. 2b represents a fit of a phenomenological power-law function expressed as²²

to B_int(T) of the fast-oscillating component. The fit results in a magnetic transition temperature of T_N = 151.5(1.2) K and exponents α = 1.58(9) and β = 0.26(2). The obtained magnetic ordering temperature is in agreement with that of recent resistivity^4,7, nuclear magnetic resonance^9,15 and μSR experiments¹³. The exponent β ≃ 0.26 suggests a second-order-type phase transition and is rather close to a critical exponent of 1/3 expected for three-dimensional magnetic systems²³.

Candidate magnetic structure(s) of La₃Ni₂O_7–δ

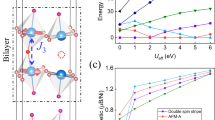
Different magnetic ground states were proposed for La₃Ni₂O₇ (refs. ^14,15,24); however, no technique has thus far provided an unambiguous determination. To explore the feasibility of candidate magnetic structures, the dipole fields at muon stopping sites were calculated. The proposed structures focus on Ni moment arrangement within the a–b plane, which leaves a large number of possible configurations both due to possible different c-axis stacking patterns (where weak intralayer coupling was suggested¹⁴) and by changing the moment direction. Varying either of these parameters does not qualitatively change the results; therefore, the best match to experiment for different a–b plane configurations is presented in Fig. 3. One important result is that some of the Ni sites lack a magnetic moment; otherwise, the slow-precessing component (corresponding to a low magnetic field at the muon site) is not observed. This suggests that La₃Ni₂O₇ must host charge DW and SDW, analogous to a stripe-type order in cuprate high-temperature superconductors.

a, Muon stopping sites as calculated with DFT + μ. Despite all the shown sites being crystallographically equivalent, for some magnetic structures, they are not magnetically equivalent. The Ni and La planes are highlighted in different colours. b, Magnetic-field distribution p(B) (from Fig. 2b), but with the zero-field peak removed, highlights two internal fields seen by muons. c–e, Simulations of p(B) values for different magnetic configurations. The magnetic unit cells are shown as the insets. O atoms are hidden for clarity. f, Spin susceptibility for the tight-binding parameterization²⁸. g, Fermi surface and dominant scattering vector Q_SDW ≈ X₁.

Source data

Full size image

There are two proposed arrangements of the missing moments, the first (Fig. 3c) with two adjacent lines of vacancies in the [110] direction, and the second (Fig. 3d) with only one line separated by the lines of moments. Experimentally, B_int,Fast/B_int,Slow ≃ 15 (Fig. 2c), which can be obtained for either vacancy structure by varying the c-axis stacking and moment direction. The moment carried by Ni (m_Ni) might be estimated from the magnitude of the field at the muon site (Supplementary Note 8 and Supplementary Table II). If the moment points in the a–b plane, then m_Ni = 0.48–0.67μ_B, in good agreement with the fluctuating moment of m_Ni = 0.55μ_B (ref. ²⁵). Conversely, a lower value is required if the moment points parallel to the c axis, namely, m_Ni = 0.28–0.31μ_B. In addition, our calculations exclude all the magnetic structure models without zero-moment lines, that is, models with magnetic moments on all the Ni sites, as these consistently would not exhibit low-field muon sites in contrast to our experimental observation (Fig. 3c,e).

A long-range commensurate magnetic order with the ordered moments ranging from 0.3μ_B to 0.7μ_B should be detected by neutron experiments. The fact that neutrons do not see the magnetic order²⁴ might be related to the difference in correlation length between μSR and neutron techniques. Muons are known to require a shorter coherence length in order to obtain an oscillatory signal^26,27. An indirect confirmation of a short magnetic coherence length in La₃Ni₂O₇ might be the presence of the non-oscillating fast-relaxing component, which increases as it approaches T_N (Fig. 2b,c). It seems that the short magnetic correlation length limits the amount of coherent magnetic fraction already at low temperatures, whereas the development of the fast-relaxing signal at the expense of the fast-oscillating component suggests further shortening of the coherence length as a function of temperature.

To proceed further with possible magnetic structures, the spin susceptibility at ambient pressure in the paramagnetic state was calculated within the framework of a tight-binding parameterization²⁸. Note that in bilayer systems, like La₃N₂O₇, the spin susceptibility can be decomposed into the even (\({\chi }_{{\rm{S}}}^{\;{\rm{even}}}\)) and odd (\({\chi }_{{\rm{S}}}^{\;{\rm{odd}}}\)) channels following the scheme outlined elsewhere²⁹. The resulting \({\chi }_{{\rm{S}}}^{\;{\rm{odd}}}\) and \({\chi }_{{\rm{S}}}^{\;{\rm{even}}}\) components of the spin susceptibility are presented in Fig. 3f. The details of the calculations are provided in Supplementary Note 9. The dominant peak in odd susceptibility is connected to scattering between the bonding (α) and antibonding (β) bands, and it peaks near the wavevector Q_SDW ≈ (π/2, π/2) = X₁, which is visualized within the pseudo-tetragonal description¹⁴ in Fig. 3g. Peaks around X₁ = (π/2, π/2) and X₂ = (π/2, –π/2) are slightly different in magnitudes due to the intrinsic orthorhombicity in the system, making instability along X₁ more preferable. The peak at Q_SDW implies instability towards the double stripe order within each layer and, as it occurs in the odd-spin channel (that is, for q_z = π/d, where d is the thickness of the bilayer sandwich), the antiferromagnetic coupling between the stripes along the c direction. Note that to project magnetization into real space and make comparisons with our experimental finding, the magnetization on the lattice can be written as \({\overrightarrow{M}}_{1}({{\bf{R}}}_{j})={\overrightarrow{\varDelta }}_{{\rm{SDW}}}\cos \left({{\bf{Q}}}_{{\rm{SDW}}} {{\bf{R}}}_{j}+\uppi /4\right)\) (Fig. 3e) and \({\overrightarrow{M}}_{2}({{\bf{R}}}_{j})={\overrightarrow{\varDelta }}_{{\rm{SDW}}}\cos \left({{\bf{Q}}}_{{\rm{SDW}}} {{\bf{R}}}_{j}+\uppi /2\right)\) (Fig. 3d), but requires the inclusion of higher harmonics (Fig. 3c) as \({\overrightarrow{M}}_{3}({{\bf{R}}}_{j})={\overrightarrow{\varDelta }}_{{\rm{SDW}}}\left[\sqrt{2}\cos \left({{\bf{Q}}}_{{\rm{SDW}}} {{\bf{R}}}_{j}+\uppi /4\right)+\cos \left(2{{\bf{Q}}}_{{\rm{SDW}}} {{\bf{R}}}_{j}\right)\right]\).

High-pressure μSR and resistivity experiments

The μSR experiments under quasi-hydrostatic pressure conditions were performed at pressures of p = 0 GPa, 1.28 GPa and 2.31 GPa. Two sets of experiments were conducted: the first with a weak (5 mT) magnetic field applied perpendicular to the initial muon-spin polarization (weak transverse field (WTF)) and the second performed under ZF. The details of the ZF μSR and WTF μSR data analysis procedures, as well the determination of the magnetic ordering temperature from WTF μSR data (T_N,WTF), are discussed in Supplementary Notes 4 and 5.

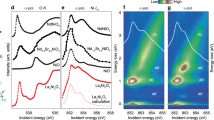
Temperature dependencies of the internal field of the fast-precessing component (B_int,Fast) measured at various pressures are presented in Fig. 4. The solid lines correspond to the fit of equation (1) to the B_int(T) data. To avoid the high sensitivity of the fit parameters (that is, B_int(0) and T_N) to the values of exponents α and β, they were fixed at α = 1.58 and β = 0.26 as obtained in the ambient-pressure studies (as discussed earlier and shown in Figs. 2d and 4a). The pressure dependencies of the fit parameters, namely, the magnetic ordering temperatures T_N,WTF, T_N,ZF and the zero-temperature value of the internal field B_int(0), are plotted in Fig. 4b,c. Both T_N values, as determined in the WTF μSR and ZF μSR experiments, increase with increasing pressure. The linear fits result in equal slopes with dT_N/dp = 2.8(3) K GPa^–1. The internal field, which is proportional to the value of the ordered magnetic moment on the Ni site (B_int(0) ∝ m_Ni), shows different tendencies. The ordered moment is nearly pressure independent, or may even slightly decrease with increasing pressure as dln[B_int(0)]/dp ≡ dln[m_Ni]/dp ≃ −0.3% GPa^–1 (Fig. 4c).

a, Temperature dependencies of the internal field of the fast-precessing component measured at pressures of p = 0 GPa (ZP), 1.28 GPa and 2.31 GPa. b, Pressure dependencies of the magnetic ordering temperatures as determined in WTF μSR and ZF μSR experiments. The solid lines are linear fits with T_N,WTF(p) = 148.3(1.5) + p × 2.8(4) and T_N,ZF = 150.7(5) + p × 2.8(3). c, Pressure dependence of the internal field of the fast-precessing component. The solid and dashed lines are linear fits with B_int(0, p) = 143.7(3) – p × 0.44(22) and B_int(0, p) = 143.2(4), respectively. The error bars for individual data points correspond to one standard deviation from the χ² fits.

Source data

Full size image

The resistivity (ρ) under pressure experiments were preformed at pressures of p = 0 GPa, 0.61 GPa, 0.98 GPa, 1.49 GPa and 1.97 GPa (Fig. 5). Following refs. ^{4,6,6,7,8,9,16,17}, the local minima in ρ(T) could be associated with the DW transition of unknown origin. The DW transition temperature T_DW was obtained from parabolic fits of ρ(T) in the vicinity of the local minima and it is plotted in Fig. 5b. T_DW decreases with increasing pressure as T_DW(p) = 132.3(1.6) – p × 25.7(1.2).

a, Temperature dependencies of the resistivity measured at pressures of p = 0 GPa, 0.61 GPa, 0.98 GPa, 1.49 GPa and 1.97 GPa. The arrows represent the DW transition temperature T_DW. b, Dependence of T_DW on pressure. The solid line is a linear fit: T_DW(p) = 132.3(1.6) – p × 25.7(1.2).

Source data

Full size image

Our pressure data suggest that the DW order of unknown origin detected in resistivity experiments differs from the SDW magnetic order probed by means of μSR. Indeed, (1) the ambient-pressure value of the DW transition temperature (T_DW(p = 0) ≃ 131 K) is approximately 20 K lower compared with the SDW one (T_SDW(p = 0) ≃ 151 K), and (2) the SDW and DW ordering temperatures have opposite pressure behaviours. T_SDW increases with increasing pressure by approaching T_N ≃ 155 K at 2.31 GPa, whereas T_DW decreases to T_DW ≃ 82 K at p = 1.97 GPa. Pressure, therefore, enhances the split between SDW and DW transitions from 20 K at p = 0 to 70 K at p ≃ 2.0 GPa.

The discovery of superconductivity in Nd_0.8Sr_0.2NiO₂ films³⁰ and in bulk La₃Ni₂O_7–δ under pressure¹ has sparked notable research interest in unravelling the pairing mechanism in nickel oxide systems. This discovery raises a crucial question: are the mechanisms governing superconductivity in nickelates analogous to those observed in copper oxide superconductors?

In copper oxide superconductors, the phase diagram includes spin and charge orders alongside superconductivity, and it is widely acknowledged that static and dynamic spin and charge orders play pivotal roles in the superconductivity mechanism^{31,32,33,34,35,36,37}. Elucidating competing orders in various nickel oxides is crucial for a comprehensive understanding of their electronic properties. In a similar vein, prior studies have revealed the presence of two distinct types of order in non-superconducting nickelate materials like La_2−xSr_xNiO₄ (ref. ³⁸), La₄Ni₃O₁₀ (ref. ¹⁹) and hole-doped La₄Ni₃O₈ (refs. ^39,40). Crucially, the ground state of La₃Ni₂O_7–δ also displays characteristics associated with a DW-like order^4,6,7,8,9,13. This intriguing scenario is particularly noteworthy because these conditions align with those conducive to the emergence of high-temperature superconductivity in this material. This is evidenced by the suppression of a DW-like anomaly in resistivity as the material approaches the superconducting dome under pressure⁴.

Our experiments unveil the presence of commensurate magnetic order, as well as the critical temperature associated with the DW anomaly. One of the pivotal findings in our paper is the observation that pressure induces an elevation in the magnetic ordering temperature, underscoring the resilience of magnetism under external pressure. Notably, this behaviour stands in stark contrast to the substantial suppression, specifically by nearly 50 K within the same pressure range, of the transport anomaly associated with the DW instability (Fig. 5). The distinctive pressure-induced response in La₃Ni₂O_7–δ, as well as the results of the dipole-field calculations, implies the simultaneous existence of two separate orders in its ground state: magnetic and most likely charge DW orders. Remarkably, our results point to a pressure-enhanced decoupling between these two distinct orders. In cuprates or hole-doped nickelates like La_2−xSr_xNiO₄, the relationship between spin and charge orders is particularly intricate, with both orders being strongly intertwined and exhibiting similar responses to external parameters. However, this intricate interplay differs in La₃Ni₂O_7–δ, where the behaviour of spin and charge orders deviates from this pattern. Here the response to external parameters reveals a distinct and less correlated behaviour between spin and charge orders compared with the observed intertwining in cuprates and hole-doped nickelates. This distinction underscores the unique electronic characteristics and order interplay in La₃Ni₂O_7–δ, adding to the complexity of the superconducting mechanism in this nickel oxide system.

Sample preparation

The La₃Ni₂O_7–δ sample was synthesized by means of the solid-state reaction described in Supplementary Note 1. The X-ray diffraction studies confirm the presence of the main fraction La₃Ni₂O_7–δ (δ ≃ 0) and a small amount (of the order of 8%) of the impurity phase of lanthanum silica apatite (Supplementary Note 1 and Supplementary Fig. 1).

μSR experiments

ZF and WTF μSR experiments were carried out at the Paul Scherrer Institute. Experiments under ambient pressure were performed at the πE3 beamline using the GPS spectrometer⁴³. Experiments under the quasi-hydrostatic pressure conditions were conducted at the μE1 beamline using the GPD (general purpose decay) spectrometer^44,45. A pressure of up to 2.3 GPa was generated in a double-walled clamp-type cell made of non-magnetic MP35N alloy⁴⁴. As a pressure-transmitting medium, Daphne 7373 oil was used.

Muon stopping sites and dipole-field calculations

The muon stopping sites in La₃Ni₂O₇ were calculated by means of a DFT + μ approach⁴⁶ using the MuFinder application⁴⁷. The dipole-field calculations utilized the MUESR code⁴⁸.

ZF μSR data analysis procedure

The fit to the experimental data was performed using the following functional form:

Here A_s/A_bg and P_s(t)/P_bg(t) are the initial asymmetry and time evolution of the muon-spin polarization of the sample (s)/background (bg) contribution. The sample part is further divided into magnetic (m) and non-magnetic (nm) contributions, with weights f_m and 1 – f_m, respectively, and

Here γ_μ = 851.616 MHz T^–1 is the muon gyromagnetic ratio, λ is the exponential relaxation rate and f_i is the volume fraction of the ith magnetic component. The indices 2/3 and 1/3 account for powder averaging, where 2/3 of the muon spins precess in internal fields perpendicular (transversal (T)) to the field directions and 1/3 remain parallel (longitudinal (L)) to B_int,i (refs. ^{26,49,50,51,52,53,54}).

Resistivity experiments

Experiments under ambient pressure were performed by using the resistivity option hardware and software of the Quantum Design Physical Property Measurement System. Experiments under pressure were performed with the same instrument by using Almax easylab Pcell15/30 module⁵⁵.

Inclusion and ethics

We have read the Nature Portfolio Authorship Policy and confirm that this manuscript complies with the policy information about authorship: inclusion and ethics in global research.