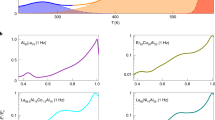
Abstract
Given the vast differences in interaction details, describing the dynamics of structurally disordered materials in a unified theoretical framework presents a fundamental challenge to condensed-matter physics and materials science. Here we numerically investigate a double-percolation scenario for the two most important relaxation processes of supercooled liquids and glasses, the so-called α and β relaxations. For several simple glass formers, we find that when monitoring the dynamic shear modulus as temperature is lowered from the liquid state, percolation of immobile particles takes place at the temperature locating the α process. Mirroring this, upon continued cooling into the glass state, the mobile-particle percolation transition pinpoints a β process whenever the latter is well separated from the main (α) process. For two-dimensional systems under the same conditions, percolation of mobile and immobile particles occurs nearly simultaneously, and no β relaxation can be identified. Our findings suggest that a general description of glassy dynamics should be based on a percolation perspective.
This is a preview of subscription content, access via your institution
Access options






Similar content being viewed by others
Data availability
All of the data used to generate Figs. 1–6 are available via Zenodo at https://doi.org/10.5281/zenodo.13925660 (ref. 96).
Code availability
The simulation package LAMMPS (https://www.lammps.org) was used for all molecular dynamics simulations. The code and scripts of the analysis are available via Zenodo at https://doi.org/10.5281/zenodo.13925660 (ref. 96).
Change history
07 March 2025
A Correction to this paper has been published: https://doi.org/10.1038/s41567-025-02860-6
References
Harrison, G. The Dynamic Properties of Supercooled Liquids (Academic, 1976).
Angell, C. A. Formation of glasses from liquids and biopolymers. Science 267, 1924–1935 (1995).
Ediger, M. D., Angell, C. A. & Nagel, S. R. Supercooled liquids and glasses. J. Phys. Chem 100, 13200–13212 (1996).
Debenedetti, P. G. & Stillinger, F. H. Supercooled liquids and the glass transition. Nature 410, 259–267 (2001).
Dyre, J. C. The glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 78, 953–972 (2006).
Berthier, L. & Biroli, G. Theoretical perspective on the glass transition and amorphous materials. Rev. Mod. Phys. 83, 587–645 (2011).
Hunter, G. L. & Weeks, E. R. The physics of the colloidal glass transition. Rep. Prog. Phys. 75, 066501 (2012).
Wang, W. H. The elastic properties, elastic models and elastic perspectives of metallic glasses. Prog. Mater. Sci. 57, 487–656 (2012).
McKenna, G. B. & Simon, S. L. 50th anniversary perspective: challenges in the dynamics and kinetics of glass-forming polymers. Macromolecules 50, 6333–6361 (2017).
Alba-Simionesco, C. & Tarjus, G. A perspective on the fragility of glass-forming liquids. J. Non-Cryst. Solids X 14, 100100 (2022).
Hecksher, T., Nielsen, A. I., Olsen, N. B. & Dyre, J. C. Little evidence for dynamic divergences in ultraviscous molecular liquids. Nat. Phys. 4, 737–741 (2008).
Lamb, J. Viscoelasticity and lubrication: a review of liquid properties. J. Rheol. 22, 317–347 (1978).
McCrum, N. G., Read, B. E. & Williams, G. Anelastic and Dielectric Effects in Polymeric Solids (Wiley, 1967 [Dover edition, 1991]).
Dyre, J. C. & Olsen, N. B. Minimal model for beta relaxation in viscous liquids. Phys. Rev. Lett. 91, 155703 (2003).
Kremer, F. & Schönhals, A. (eds) Broadband Dielectric Spectroscopy (Springer, 2003).
Yu, H. B., Wang, W. H., Bai, H. Y. & Samwer, K. The β-relaxation in metallic glasses. Natl. Sci. Rev. 1, 429–461 (2014).
Richert, R. Supercooled liquids and glasses by dielectric relaxation spectroscopy. Adv. Chem. Phys. 156, 101–195 (2015).
Luo, P., Wen, P., Bai, H. Y., Ruta, B. & Wang, W. H. Relaxation decoupling in metallic glasses at low temperatures. Phys. Rev. Lett. 118, 225901 (2017).
Johari, G. P. & Goldstein, M. Viscous liquids and the glass transition. II. Secondary relaxations in glasses of rigid molecules. J. Chem. Phys. 53, 2372–2388 (1970).
Goldstein, M. Viscous liquids and the glass transition: a potential energy barrier picture. J. Chem. Phys. 51, 3728–3739 (1969).
Ediger, M. D. Spatially heterogeneous dynamics in supercooled liquids. Annu. Rev. Phys. Chem. 51, 99–128 (2000).
Berthier, L., Biroli, G., Bouchaud, J.-P., Cipelletti, L. & van Saarloos, W. (eds) Dynamical Heterogeneities in Glasses, Colloids and Granular Media (Oxford Univ. Press, 2011).
Karmakar, S., Dasgupta, C. & Sastry, S. Growing length scales and their relation to timescales in glass-forming liquids. Annu. Rev. Cond. Mat. Phys. 5, 255–284 (2014).
Chang, C. et al. Liquid-like atoms in dense-packed solid glasses. Nat. Mater. 21, 1240–1245 (2022).
Yu, H.-B. & Wang, Q. Liquid-like clusters in glassy solids as a unique state of matter: dissipative but non-diffusive. Next Mater 3, 100168 (2024).
Yang, Q., Pei, C.-Q., Yu, H.-B. & Feng, T. Metallic nanoglasses with promoted β-relaxation and tensile plasticity. Nano Lett. 21, 6051–6056 (2021).
Zhou, Z.-Y., Yang, Q. & Yu, H.-B. Toward atomic-scale understanding of structure-dynamics-properties relations for metallic glasses. Prog. Mater. Sci. 145, 101311 (2024).
Qiao, J. C. et al. Structural heterogeneities and mechanical behavior of amorphous alloys. Prog. Mater. Sci. 104, 250–329 (2019).
Wang, W. H. Dynamic relaxations and relaxation-property relationships in metallic glasses. Prog. Mater. Sci. 106, 100561 (2019).
Peng, S.-X. et al. Uncovering β–relaxations in amorphous phase-change materials. Sci. Adv 6, eaay6726 (2020).
Ngai, K. L., Casalini, R., Capaccioli, S., Paluch, M. & Roland, C. M. Do theories of the glass transition, in which the structural relaxation time does not define the dispersion of the structural relaxation, need revision? J. Phys. Chem. B 109, 17356–17360 (2005).
Ngai, K. L., Habasaki, J., Prevosto, D., Capaccioli, S. & Paluch, M. Thermodynamic scaling of α-relaxation time and viscosity stems from the Johari-Goldstein β-relaxation or the primitive relaxation of the coupling model. J. Chem. Phys. 137, 034511 (2012).
Ngai, K. L. Universal properties of relaxation and diffusion in complex materials: originating from fundamental physics with rich applications. Prog. Mater. Sci. 139, 101130 (2023).
Kudlik, A., Benkhof, S., Blochowicz, T., Tschirwitz, C. & Rössler, E. The dielectric response of simple organic glass formers. J. Mol. Struct. 479, 201–218 (1999).
Götze, W. Complex Dynamics of Glass-Forming Liquids: A Mode-Coupling Theory (Oxford Univ. Press, 2009).
Kaufmann, S., Wefing, S., Schaefer, D. & Spiess, H. W. Two-dimensional exchange nuclear magnetic resonance of powder samples. III. Transition to motional averaging and application to the glass transition. J. Chem. Phys. 93, 197–214 (1990).
Arbe, A., Richter, D., Colmenero, J. & Farago, B. Merging of the α and β relaxations in polybutadiene: a neutron spin echo and dielectric study. Phys. Rev. E 54, 3853–3869 (1996).
Olsen, N. B. Scaling of β-relaxation in the equilibrium liquid state of sorbitol. J. Non-Cryst. Solids 235, 399–405 (1998).
Schneider, U., Brand, R., Lunkenheimer, P. & Loidl, A. Excess wing in the dielectric loss of glass formers: a Johari-Goldstein β relaxation? Phys. Rev. Lett. 84, 5560–5563 (2000).
Scalliet, C., Guiselin, B. & Berthier, L. Excess wings and asymmetric relaxation spectra in a facilitated trap model. J. Chem. Phys. 155, 064505 (2021).
Guiselin, B., Scalliet, C. & Berthier, L. Microscopic origin of excess wings in relaxation spectra of supercooled liquids. Nat. Phys. 18, 468–472 (2022).
Ciamarra, M. P., Ji, W. & Wyart, M. Local vs. cooperative: unraveling glass transition mechanisms with SEER. Proc. Natl Acad. Sci. USA 121, e2400611121 (2024).
Wolynes, P. G. Randomness and complexity in chemical physics. Acc. Chem. Res. 25, 513–519 (1992).
Broadbent, S. R. & Hammersley, J. M. Percolation processes. I. Crystals and mazes. Math. Proc. Camb. Philos. Soc. 53, 629–641 (1957).
Stauffer, D. & Aharony, A. Introduction to Percolation Theory 2nd edn (Taylor & Francis, 1992).
Grimmett, G. Percolation, 2nd edn (Springer, 1999).
Isichenko, M. B. Percolation, statistical topography, and transport in random media. Rev. Mod. Phys. 64, 961–1043 (1992).
Dyre, J. C. Solid-that-flows picture of glass-forming liquids. J. Phys. Chem. Lett. 15, 1603–1617 (2024).
Stillinger, F. H. Relaxation and flow mechanisms in “fragile” glass-forming liquids. J. Chem. Phys. 89, 6461–6469 (1988).
Glotzer, S. C. Spatially heterogeneous dynamics in liquids: insights from simulation. J. Non-Cryst. Solids 274, 342–355 (2000).
Pastore, R., Ciamarra, M. P., de Candia, A. & Coniglio, A. Dynamical correlation length and relaxation processes in a glass former. Phys. Rev. Lett. 107, 065703 (2011).
Ruta, B. et al. Atomic-scale relaxation dynamics and aging in a metallic glass probed by X-ray photon correlation spectroscopy. Phys. Rev. Lett. 109, 165701 (2012).
Douglass, I. M. & Dyre, J. C. Distance-as-time in physical aging. Phys. Rev. E 106, 054615 (2022).
Diezemann, G. A free-energy landscape model for primary relaxation in glass-forming liquids: rotations and dynamic heterogeneities. J. Chem. Phys. 107, 10112–10120 (1997).
Sillescu, H. Heterogeneity at the glass transition: a review. J. Non-Cryst. Solids 243, 81–108 (1999).
Fredrickson, G. H. & Andersen, H. C. Kinetic Ising model of the glass transition. Phys. Rev. Lett. 53, 1244–1247 (1984).
Garrahan, J. P. & Chandler, D. Geometrical explanation and scaling of dynamical heterogeneities in glass forming systems. Phys. Rev. Lett. 89, 035704 (2002).
Ritort, F. & Sollich, P. Glassy dynamics of kinetically constrained models. Adv. Phys. 52, 219–342 (2003).
Chacko, R. N. et al. Elastoplasticity mediates dynamical heterogeneity below the mode coupling temperature. Phys. Rev. Lett. 127, 048002 (2021).
Zhang, G. et al. Structuro-elasto-plasticity model for large deformation of disordered solids. Phys. Rev. Res. 4, 043026 (2022).
Ozawa, M. & Biroli, G. Elasticity, facilitation, and dynamic heterogeneity in glass-forming liquids. Phys. Rev. Lett. 130, 138201 (2023).
Costigliola, L., Hecksher, T. & Dyre, J. C. Glass-forming liquids need facilitation. Proc. Natl Acad. Sci. USA 121, e2408798121 (2024).
Stevenson, J. D. & Wolynes, P. G. A universal origin for secondary relaxations in supercooled liquids and structural glasses. Nat. Phys. 6, 62–68 (2010).
Gao, L., Sun, Y. & Yu, H.-B. Mobility percolation as a source of Johari-Goldstein relaxation in glasses. Phys. Rev. B 108, 014201 (2023).
Donati, C. et al. Stringlike cooperative motion in a supercooled liquid. Phys. Rev. Lett. 80, 2338–2341 (1998).
Russina, M., Mezei, F., Lechner, R., Longeville, S. & Urban, B. Experimental evidence for fast heterogeneous collective structural relaxation in a supercooled liquid near the glass transition. Phys. Rev. Lett. 84, 3630–3633 (2000).
Long, D. & Lequeux, F. Heterogeneous dynamics at the glass transition in van der Waals liquids, in the bulk and in thin films. Eur. Phys. J. E 4, 371–387 (2001).
Shi, Y. & Falk, M. L. Strain localization and percolation of stable structure in amorphous solids. Phys. Rev. Lett. 95, 095502 (2005).
Starr, F. W., Douglas, J. F. & Sastry, S. The relationship of dynamical heterogeneity to the Adam-Gibbs and random first-order transition theories of glass formation. J. Chem. Phys. 138, 12A541 (2013).
Cicerone, M. T., Zhong, Q. & Tyagi, M. Picosecond dynamic heterogeneity, hopping, and Johari-Goldstein relaxation in glass-forming liquids. Phys. Rev. Lett. 113, 117801 (2014).
Yu, H.-B., Richert, R. & Samwer, K. Structural rearrangements governing Johari-Goldstein relaxations in metallic glasses. Sci. Adv. 3, e1701577 (2017).
Betancourt, B. A. P., Starr, F. W. & Douglas, J. F. String-like collective motion in the α- and β-relaxation of a coarse-grained polymer melt. J. Chem. Phys. 148, 104508 (2018).
Caporaletti, F. et al. A microscopic look at the Johari-Goldstein relaxation in a hydrogen-bonded glass-former. Sci. Rep. 9, 14319 (2019).
Caporaletti, F. et al. Experimental evidence of mosaic structure in strongly supercooled molecular liquids. Nat. Commun. 12, 1867 (2021).
Spieckermann, F. et al. Structure-dynamics relationships in cryogenically deformed bulk metallic glass. Nat. Commun. 13, 127 (2022).
Novikov, V. N., Rössler, E., Malinovsky, V. K. & Surovtsev, N. V. Strong and fragile liquids in percolation approach to the glass transition. Europhys. Lett. 35, 289–294 (1996).
Shiraishi, K., Mizuno, H. & Ikeda, A. Johari–Goldstein β relaxation in glassy dynamics originates from two-scale energy landscape. Proc. Natl Acad. Sci. USA 120, e2215153120 (2023).
Fragiadakis, D. & Roland, C. M. Molecular dynamics simulation of the Johari-Goldstein relaxation in a molecular liquid. Phys. Rev. E 86, 020501 (2012).
Kob, W. & Andersen, H. C. Testing mode-coupling theory for a supercooled binary Lennard-Jones mixture I: The van Hove correlation function. Phys. Rev. E 51, 4626–4641 (1995).
Zaccone, A. Theory of Disordered Solids (Springer, 2023).
Phillips, J. C. & Thorpe, M. F. Constraint theory, vector percolation and glass formation. Solid State Commun. 53, 699–702 (1985).
Tatsumisago, M., Halfpap, B. L., Green, J. L., Lindsay, S. M. & Angell, C. A. Fragility of Ge-As-Se glass-forming liquids in relation to rigidity percolation, and the Kauzmann paradox. Phys. Rev. Lett. 64, 1549–1552 (1990).
Schrøder, T. B. & Dyre, J. C. ac hopping conduction at extreme disorder takes place on the percolating cluster. Phys. Rev. Lett. 101, 025901 (2008).
de Souza, V. K. & Harrowell, P. Rigidity percolation and the spatial heterogeneity of soft modes in disordered materials. Proc. Natl Acad. Sci. USA 106, 15136–15141 (2009).
Marruzzo, A., Köhler, S., Fratalocchi, A., Ruocco, G. & Schirmacher, W. Vibrational anomalies and marginal stability of glasses. Eur. Phys. J. Spec. Top. 216, 83–93 (2013).
Ghosh, A. et al. Direct observation of percolation in the yielding transition of colloidal glasses. Phys. Rev. Lett. 118, 148001 (2017).
Lemaitre, A. Structural relaxation is a scale-free process. Phys. Rev. Lett. 113, 245702 (2014).
Tahaei, A., Biroli, G., Ozawa, M., Popovic, M. & Wyart, M. Scaling description of dynamical heterogeneity and avalanches of relaxation in glass-forming liquids. Phys. Rev. X 13, 031034 (2023).
Hasyim, M. R. & Mandadapu, K. K. Emergent facilitation and glassy dynamics in supercooled liquids. Proc. Natl Acad. Sci. USA 121, e2322592121 (2024).
Ruta, B., Pineda, E. & Evenson, Z. Relaxation processes and physical aging in metallic glasses. J. Phys. Condens. Matter 29, 503002 (2017).
Heyes, D. M. & Melrose, J. R. Percolation cluster statistics of Lennard-Jones fluids. Mol. Phys. 66, 1057–1074 (1989).
Thompson, A. P. et al. LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171 (2022).
Schirmacher, W. et al. The nature of non-phononic excitations in disordered systems. Nat. Commun. 15, 3107 (2024).
Zhang, H.-R. et al. Fragility crossover mediated by covalent-like electronic interactions in metallic liquids. Mater. Futur. 3, 025002 (2024).
Brown, W. M. & Yamada, M. Implementing molecular dynamics on hybrid high performance computers—three-body potentials. Comput. Phys. Commun. 184, 2785–2793 (2013).
Gao, L., Yu, H.-B., Schrøder, T. B. & Dyre, J. C. Data and code of “Unified percolation scenario for the α and β processes in simple glass formers”. Zenodo https://doi.org/10.5281/zenodo.13925660 (2024).
Acknowledgements
The computational work was carried out on the public computing service platform provided by the Network and Computing Center of HUST. We thank the National Natural Science Foundation of China for support (grant no. 52071147 (H.-B.Y.)). This work was also supported by the VILLUM Foundation’s Matter grant no. VIL16515 (J.C.D.).
Author information
Authors and Affiliations
Contributions
H.-B.Y. and J.C.D. devised the project. L.G. and H.-B.Y. performed the simulations with input from T.B.S. and J.C.D. All authors wrote and revised the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Lothar Wondraczek, Reiner Zorn and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–25, discussion and Tables 1–5.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Gao, L., Yu, HB., Schrøder, T.B. et al. Unified percolation scenario for the α and β processes in simple glass formers. Nat. Phys. 21, 471–479 (2025). https://doi.org/10.1038/s41567-024-02762-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-024-02762-z
This article is cited by
-
Unveiling hidden particle-level defects in glasses
Nature Communications (2025)
-
Glass is a matter of time
Nature Physics (2025)
-
Pursuing a general description of glassy dynamics: A percolation perspective
Science China Physics, Mechanics & Astronomy (2025)