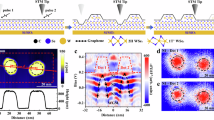
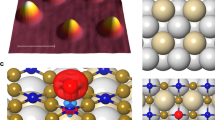
Abstract
Intra-atomic orbital hybridization and interatomic bond formation are the two fundamental processes when real atoms are condensed to form matter1,2. Artificial atoms mimic real atoms by demonstrating discrete energy levels attributable to quantum confinement3,4,5,6,7,8. As such, they offer a solid-state analogue for simulating intra-atomic orbital hybridization and interatomic bond formation. Signatures of interatomic bond formation have been extensively observed in various artificial atoms9,10,11,12,13,14,15,16,17. However, direct evidence of the intra-atomic orbital hybridization in the artificial atoms remains to be experimentally demonstrated. Here we realize the orbital hybridization in artificial atoms by altering the shape of the artificial atoms. The anisotropy of the confining potential gives rise to the hybridization between quasibound states with different orbital quantum numbers within the artificial atom. These hybridized orbits are directly visualized in real space in our experiment and are well reproduced by both numerical calculations and analytical derivations. Our study opens an avenue for designing artificial matter that cannot be accessed on real atoms through experiments. Moreover, the results obtained inspire the progressive control of quantum states in diverse systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
27,99 € / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
199,00 € per year
only 3,90 € per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
Source data are provided with this paper.
Code availability
Codes are provided in the Supplementary information.
References
Brown, T. L. et al. Chemistry: The Central Science (Pearson, 2015).
Oxtoby, D. W., Gillis, H. P. & Butler, L. J. Principles of Modern Chemistry (Cengage Learning, 2016).
Kouwenhoven, L. P., Austing, D. G. & Tarucha, S. Few-electron quantum dots. Rep. Prog. Phys. 64, 701–736 (2001).
Reimann, S. M. & Manninen, M. Electronic structure of quantum dots. Rev. Mod. Phys. 74, 1283–1342 (2002).
Buluta, I., Ashhab, S. & Nori, F. Natural and artificial atoms for quantum computation. Rep. Prog. Phys. 74, 104401 (2011).
Ashoori, R. C. Electrons in artificial atoms. Nature 379, 413–419 (1996).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998).
Karrai, K. et al. Hybridization of electronic states in quantum dots through photon emission. Nature 427, 135–138 (2004).
Schedelbeck, G., Wegscheider, W., Bichler, M. & Abstreiter, G. Coupled quantum dots fabricated by cleaved edge overgrowth: from artificial atoms to molecules. Science 278, 1792–1795 (1997).
Oosterkamp, T. H. et al. Microwave spectroscopy of a quantum-dot molecule. Nature 395, 873–876 (1998).
Bayer, M. et al. Coupling and entangling of quantum states in quantum dot molecules. Science 291, 451–453 (2001).
Krenner, H. J. et al. Direct observation of controlled coupling in an individual quantum dot molecule. Phys. Rev. Lett. 94, 057402 (2005).
Rodary, G. et al. Real space observation of electronic coupling between self-assembled quantum dots. Nano Lett. 19, 3699–3706 (2019).
Fu, Z.-Q. et al. Relativistic artificial molecules realized by two coupled graphene quantum dots. Nano Lett. 20, 6738–6743 (2020).
Dou, W. et al. High-yield production of quantum corrals in a surface reconstruction pattern. Nano Lett. 23, 148–154 (2023).
Ge, Z. et al. Giant orbital magnetic moments and paramagnetic shift in artificial relativistic atoms and molecules. Nat. Nanotechnol. 18, 250–256 (2023).
Zheng, Q. et al. Molecular collapse states in graphene/WSe2 heterostructure quantum dots. Phys. Rev. Lett. 130, 076202 (2023).
Silvestrov, P. G. & Efetov, K. B. Quantum dots in graphene. Phys. Rev. Lett. 98, 016802 (2007).
Pereira, V. M., Nilsson, J. & Castro Neto, A. H. Coulomb impurity problem in graphene. Phys. Rev. Lett. 99, 166802 (2007).
Matulis, A. & Peeters, F. M. Quasibound states of quantum dots in single and bilayer graphene. Phys. Rev. B 77, 115423 (2008).
Wang, Y. et al. Observing atomic collapse resonances in artificial nuclei on graphene. Science 340, 734–737 (2013).
Zhao, Y. et al. Creating and probing electron whispering-gallery modes in graphene. Science 348, 672–675 (2015).
Freitag, N. M. et al. Electrostatically confined monolayer graphene quantum dots with orbital and valley splittings. Nano Lett. 16, 5798–5805 (2016).
Gutiérrez, C., Brown, L., Kim, C.-J., Park, J. & Pasupathy, A. N. Klein tunnelling and electron trapping in nanometre-scale graphene quantum dots. Nat. Phys. 12, 1069–1075 (2016).
Lee, J. et al. Imaging electrostatically confined Dirac fermions in graphene quantum dots. Nat. Phys. 12, 1032–1036 (2016).
Ghahari, F. et al. An on/off Berry phase switch in circular graphene resonators. Science 356, 845–849 (2017).
Jiang, Y. et al. Tuning a circular p–n junction in graphene from quantum confinement to optical guiding. Nat. Nanotech. 12, 1045–1049 (2017).
Bai, K.-K. et al. Generating atomically sharp p–n junctions in graphene and testing quantum electron optics on the nanoscale. Phys. Rev. B 97, 045413 (2018).
Gutiérrez, C. et al. Interaction-driven quantum Hall wedding cake-like structures in graphene quantum dots. Science 361, 789–794 (2018).
Zheng, Q., Zhuang, Y.-C., Sun, Q.-F. & He, L. Coexistence of electron whispering-gallery modes and atomic collapse states in graphene/WSe2 heterostructure quantum dots. Nat. Commun. 13, 1597 (2022).
Ren, H.-Y., Ren, Y.-N., Zheng, Q., He, J.-Q. & He, L. Electron-electron interaction and correlation-induced two density waves with different Fermi velocities in graphene quantum dots. Phys. Rev. B 108, L081408 (2023).
Ren, H.-Y., Mao, Y., Ren, Y.-N., Sun, Q.-F. & He, L. Tunable quantum confinement in individual nanoscale quantum dots via interfacial engineering. ACS Nano 19, 1352–1360 (2025).
Zhang, J. et al. Double quantum dots in atomically-precise graphene nanoribbons. Mater. Quantum. Technol. 3, 036201 (2023).
Banszerus, L. et al. Single-electron double quantum dots in bilayer graphene. Nano Lett. 20, 2005–2011 (2020).
Garreis, R. et al. Long-lived valley states in bilayer graphene quantum dots. Nat. Phys. 20, 428–434 (2024).
Tong, C. et al. Pauli blockade of tunable two-electron spin and valley states in graphene quantum dots. Phys. Rev. Lett. 128, 067702 (2022).
Yang, H., Kim, S. W., Chhowalla, M. & Lee, Y. H. Structural and quantum-state phase transitions in van der Waals layered materials. Nat. Phys. 13, 931–937 (2017).
Wang, R. et al. Strategies on phase control in transition metal dichalcogenides. Adv. Funct. Mater. 28, 1802473 (2018).
Huang, H. H., Fan, X., Singh, D. J. & Zheng, W. T. Recent progress of TMD nanomaterials: phase transitions and applications. Nanoscale 12, 1247–1268 (2020).
Yin, X. et al. Recent developments in 2D transition metal dichalcogenides: phase transition and applications of the (quasi-)metallic phases. Chem. Soc. Rev. 50, 10087–10115 (2021).
Ren, Y.-N. et al. In situ creation and tailoring of interfacial quantum dots in graphene/transition metal dichalcogenide heterostructures. Phys. Rev. B 110, 125416 (2024).
Zhou, X.-F. et al. Relativistic artificial molecule of two coupled graphene quantum dots at tunable distances. Nat. Commun. 15, 8786 (2024).
Shytov, A. V., Katsnelson, M. I. & Levitov, L. S. Atomic collapse and quasi-Rydberg states in graphene. Phys. Rev. Lett. 99, 246802 (2007).
Moldovan, D., Masir, M. R. & Peeters, F. M. Magnetic field dependence of the atomic collapse state in graphene. 2D Mater. 5, 015017 (2017).
Morgenstern, M. et al. Origin of Landau oscillations observed in scanning tunneling spectroscopy on n-InAs(110). Phys. Rev. B 62, 7257–7263 (2000).
Acknowledgements
This work was financially supported by the National Key R and D Programme of China (grant nos. 2024YFA1409002, 2021YFA1400100 and 2021YFA1401900), the National Natural Science Foundation of China (grants nos. 12374034, 11921005, 12141401, 12425405 and 12404198), the Innovation Programme for Quantum Science and Technology (grant no. 2021ZD0302403), ‘the Fundamental Research Funds for the Central Universities’ (grant no. 310400209521), the China National Postdoctoral Program for Innovative Talents (grant no. BX20240040) and the China Postdoctoral Science Foundation (grant no. 2023M740296). The computational resources are supported by High-performance Computing Platform of Peking University. The devices were fabricated using the transfer platform from Shanghai Onway Technology Co., Ltd.
Author information
Authors and Affiliations
Contributions
L.H. and Q.-F.S. conceived the work and designed the research strategy. Y.M. carried out the analytical analysis and numerical calculations under the supervision of Q.-F.S. H.-Y.R., X.-F.Z. and Y.-N.R. fabricated the samples and performed the measurements. H.-Y.R., Y.-N.R., H.S., Y.-H.X. and L.H. analysed the experimental data. Y.M., Y.-C.Z. and Q.-F.S. analysed the numerical data. All authors wrote the paper together.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Florian Libisch and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Analytical and numerical LDOS of quasibound states (0, 1) and (1, 1).
a and b. The distribution of states (0, 1) and (1, 1), respectively. Left panel: The LDOS maps from the analytically solved wavefunctions. Middle panel: The numerically calculated LDOS maps for a circular QD. Right panel: The numerically calculated LDOS maps for an elliptical QD.
Extended Data Fig. 2 Almost unhybridized orbital states under an almost circular confinement with dr′ = 0.03.
a. Left panel: A STM image (Vb = 600 mV, I = 130 pA) of the almost circular QD with anisotropy degree \({{dr}}^{{\prime} }=\,0.03\) embedded in the graphene/WSe2 heterostructure. The radius \({r}_{0}\approx 9\,{\rm{nm}}\). The yellow dashed line shows outline of the circular QD. The height profile along the red dashed line is shown with solid red line. Top right panels: Atomic-resolved STM image on (1 T’ phase) and off (2H phase) the QD, respectively. Bottom right panels: The FFT image obtained from the STM image on and off the QD, respectively. The white and green circles show reciprocal lattices of graphene and WSe2, respectively. The unlabeled bright spots correspond to the reciprocal moiré superlattices and higher-order scattering. b. The dI/dV spectroscopic map versus the spatial position along axis of the almost circular QD. Orbital states can be clearly observed in the QD. The first four states are labelled by wavefunctions and black dashed lines. The two yellow dashed lines mark the size of the QD.
Extended Data Fig. 3 Hybridized orbital states under an elliptical confinement with dr′ = 0.07.
a. A STM image (Vb = 600 mV, I = 100 pA) of the elliptical QD with anisotropy degree \({{dr}}^{{\prime} }=\,0.07\) embedded in the graphene/WSe2 heterostructure. The minor radius r1 is approximately 12.5 nm, and the major radius r2 is approximately 14.5 nm. The height profile along the red dashed line is shown with solid red line. b. The dI/dV spectroscopic maps versus the spatial position along the major axis (left panel) and minor axis (right panel) of the elliptical QD, respectively. Orbital states can be clearly observed in the QD. The first four states are labelled by wavefunctions and black dashed lines in the right panel. The yellow dashed lines mark the size of the QD. c. dI/dV maps of different orbital states. For an elliptical confinement, the anisotropy of confining potential results in orbital hybridization between the s-orbital and d-orbital states, giving rise to new states sd+ \({\psi }_{(\mathrm{0,2})}+\alpha {\psi }_{(\mathrm{2,1})}\) and sd- \(-\alpha {\psi }_{(\mathrm{0,2})}+{\psi }_{(\mathrm{2,1})}\), which exhibit θ-shaped and rotated θ-shaped features marked by the green dotted lines, respectively. The yellow dashed lines show outlines of the elliptical QD.
Extended Data Fig. 4 Hybridized orbital states under an elliptical confinement with dr′ = 0.08.
a. A STM image (Vb = 450 mV, I = 300 pA) of the elliptical QD with anisotropy degree \({{dr}}^{{\prime} }=\,0.08\) embedded in the graphene/WSe2 heterostructure. The minor radius r1 is approximately 6 nm, and the major radius r2 is approximately 7 nm. The height profile along the red dashed line is shown with solid red line. b. The \(-{d}^{3}I/{{dV}}^{3}\) spectroscopic maps versus the spatial position along the major axis (left panel) and minor axis (right panel) of the elliptical QD, respectively. Orbital states can be clearly observed in the QD. The first four states are labelled by wavefunctions and black dashed lines in the right panel. The yellow dashed lines mark the size of the QD.
Extended Data Fig. 5 Hybridized orbital states under an elliptical confinement with dr′ = 0.16.
a. The dI/dV spectroscopic map versus the spatial position along the major axis of the elliptical QD in Fig. 2c. Orbital states can be clearly observed in the QD. The two yellow dashed lines mark the size of the QD.
Extended Data Fig. 6 Hybridized orbital states under an elliptical confinement with dr′ = 0.17.
a. Left panel: A STM image (Vb = 500 mV, I = 100 pA) of the elliptical QD with anisotropy degree \({{dr}}^{{\prime} }=\,0.17\) embedded in the graphene/WSe2 heterostructure. The minor radius r1 is approximately 7.6 nm, and the major radius r2 is approximately 10.7 nm. The height profile along the red dashed line is shown with solid red line. Top right panels: Atomic-resolved STM image on (1 T’ phase) and off (2H phase) the QD, respectively. Bottom right panels: The FFT image obtained from the STM image on and off the QD, respectively. The white and green circles show reciprocal lattices of graphene and WSe2, respectively. The unlabeled bright spots correspond to the reciprocal moiré superlattices and higher-order scattering. b. The dI/dV spectroscopic maps versus the spatial position along the major axis (left panel) and minor axis (right panel) of the elliptical QD, respectively. Orbital states can be clearly observed in the QD. The first four states are labelled by wavefunctions and black dashed lines in the right panel. The yellow dashed lines mark the size of the QD. c. dI/dV maps of different orbital states. For an elliptical confinement, the anisotropy of confining potential results in orbital hybridization between the s-orbital and d-orbital states, giving rise to new states sd+ \({\psi }_{(\mathrm{0,2})}+\alpha {\psi }_{(\mathrm{2,1})}\) and sd- \(-\alpha {\psi }_{(\mathrm{0,2})}+{\psi }_{(\mathrm{2,1})}\), which exhibit θ-shaped and rotated θ-shaped features marked by the green dotted lines, respectively. The yellow dashed lines show outlines of the elliptical QD.
Extended Data Fig. 7 Hybridized orbital states under an elliptical confinement with dr′ = 0.18.
a. Left panel: A STM image (Vb = 400 mV, I = 120 pA) of the elliptical QD with anisotropy degree \({{dr}}^{{\prime} }=\,0.18\) embedded in the graphene/MoSe2 heterostructure. The minor radius r1 is approximately 8.4 nm, and the major radius r2 is approximately 12.1 nm. The height profile along the red dashed line is shown with solid red line. Top right panels: Atomic-resolved STM image on (1 T’ phase) and off (2H phase) the QD, respectively. Bottom right panels: The FFT image obtained from the STM image on and off the QD, respectively. The white and green circles show reciprocal lattices of graphene and MoSe2, respectively. The unlabeled bright spots correspond to the reciprocal moiré superlattices and higher-order scattering. b. The dI/dV spectroscopic map versus the spatial position along the major axis of the elliptical QD. Orbital states can be clearly observed in the QD. The two yellow dashed lines mark the size of the QD. c. dI/dV maps of different orbital states. For an elliptical confinement, the anisotropy of confining potential results in orbital hybridization between the s-orbital and d-orbital states, giving rise to new states sd+ \({\psi }_{(\mathrm{0,2})}+\alpha {\psi }_{(\mathrm{2,1})}\) and sd- \(-\alpha {\psi }_{(\mathrm{0,2})}+{\psi }_{(\mathrm{2,1})}\), which exhibit θ-shaped and rotated θ-shaped features marked by the green dotted lines, respectively. The yellow dashed lines show outlines of the elliptical QD.
Extended Data Fig. 8 Hybridized orbital states under an elliptical confinement with dr′ = 0.19.
a. Left panel: A STM image (Vb = 500 mV, I = 100 pA) of the elliptical QD with anisotropy degree \({{dr}}^{{\prime} }=\,0.19\) embedded in the graphene/WSe2 heterostructure. The minor radius r1 is approximately 7.6 nm, and the major radius r2 is approximately 11.2 nm. The height profile along the red dashed line is shown with solid red line. Top right panels: Atomic-resolved STM image on (1 T’ phase) and off (2H phase) the QD, respectively. Bottom right panels: The FFT image obtained from the STM image on and off the QD, respectively. The white and green circles show reciprocal lattices of graphene and WSe2, respectively. The unlabeled bright spots correspond to the reciprocal moiré superlattices and higher-order scattering. b. The dI/dV spectroscopic map versus the spatial position along the major axis of the elliptical QD. Orbital states can be clearly observed in the QD. The two yellow dashed lines mark the size of the QD. c. dI/dV maps of different orbital states. For an elliptical confinement, the anisotropy of confining potential results in orbital hybridization between the s-orbital and d-orbital states, giving rise to new states sd+ \({\psi }_{(\mathrm{0,2})}+\alpha {\psi }_{(\mathrm{2,1})}\) and sd- \(-\alpha {\psi }_{(\mathrm{0,2})}+{\psi }_{(\mathrm{2,1})}\), which exhibit θ-shaped and rotated θ-shaped features marked by the green dotted lines, respectively. The yellow dashed lines show outlines of the elliptical QD.
Extended Data Fig. 9 Hybridized orbital states under an elliptical confinement with dr′ = 0.21.
a. A STM image (Vb = −140 mV, I = 150 pA) of the elliptical QD with anisotropy degree \({{dr}}^{{\prime} }=\,0.21\) embedded in the graphene/WSe2 heterostructure. The minor radius r1 is approximately 7.8 nm, and the major radius r2 is approximately 12 nm. b. The dI/dV spectroscopic map versus the spatial position along the minor axis of the elliptical QD. Orbital states can be clearly observed in the QD. The first four states are labelled by wavefunctions and black dashed lines. The two yellow dashed lines mark the size of the QD. c. dI/dV maps of different orbital states. For an elliptical confinement, the anisotropy of confining potential results in orbital hybridization between the s-orbital and d-orbital states, giving rise to new states sd+ \({\psi }_{(\mathrm{0,2})}+\alpha {\psi }_{(\mathrm{2,1})}\) and sd- \(-\alpha {\psi }_{(\mathrm{0,2})}+{\psi }_{(\mathrm{2,1})}\), which exhibit θ-shaped and rotated θ-shaped features marked by the green dotted lines, respectively. The yellow dashed lines show outlines of the elliptical QD.
Extended Data Fig. 10 LDOS evolution of hybridized states from s2 (0, 2) and d1 (2, 1).
From the leftmost panel to the rightmost panel: \({{dr}}^{{\prime} }=0,0.05,0.10,0.15,0.20\), the other parameters are the same and shown in Supplementary information. a1-a5. The space-energy LDOS for the five potentials, along the minor axis of ellipse. The red, yellow, green, and blue color bars respectively indicate the energy of quasibound states s1, p1, sd+ , sd-. b1-b5, c1-c5. The numerically calculated spatial distributions of hybridized states sd+ , sd- evolved as the QD is deformed from circle to ellipse. d1-d5, e1-e5. The spatial distributions of sd+ and sd- obtained from the combination of analytical wavefunctions \({\psi }_{{sd}+}={\psi }_{(\mathrm{0,2})}+\alpha {\psi }_{(\mathrm{2,1})}\) and \({\psi }_{{sd}-}=-\alpha {\psi }_{(\mathrm{0,2})}+{\psi }_{(\mathrm{2,1})}\). From left to right: α = 0.0, 0.3, 0.5, 0.7, 0.9.
Supplementary information
Supplementary Information
This file contains Supplementary Notes 1–7, figures, Table 1, codes and references.
Source data
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Mao, Y., Ren, HY., Zhou, XF. et al. Orbital hybridization in graphene-based artificial atoms. Nature 639, 73–78 (2025). https://doi.org/10.1038/s41586-025-08620-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-025-08620-z