Main

In recent years, the advent of new computing models has instigated notable advancements in computational technology. These technologies are primarily dedicated to accelerating linear computation. Specifically, matrix MAC operations play a pivotal role in deep learning and neural networks5,6,7. They form the core of numerous machine learning algorithms and account for most computational resources required for training and inference. However, MAC operations are power-intensive, exacerbating power consumption and operational requirements of transistors. This situation is worsened by the increasing complexity of computation models and the growing need for real-time processing. Driven by the conflict between the limitation of digital semiconductor techniques and the strong demand for higher performance, alternative computing platforms have been proposed, such as photonic computing, shifting from traditional electronic computing8,9,10,11,12,13,14. This transformation, although still in its nascent stages, presents a promising solution to challenges posed by the growing demand for high-speed, low-latency data processing15,16. The advantage of photonic computation derives from the unique properties of light, allowing simultaneous multiplication and accumulation processes as optical signals travel through guided-wave circuits. Such massive parallel operations substantially reduce data movement, thereby conserving energy. Furthermore, light-based devices can avoid the resistive losses and heating issues encountered by their electronic counterparts, potentially enhancing their energy efficiency13,14.

However, even though the concept of optical computing was introduced several decades ago17, a resurgence of interest has recently been spurred by rapid progress and recent innovations in silicon photonics, nanophotonics and materials science1,18,19,20,21,22. A variety of technical developments in integrated photonics has demonstrated their potential for accelerating computation11,12,23,24. These efforts, complemented by promising results on optical transformers and nonlinear activation functions, have confirmed the extensive potential of photonics as a platform for multitask, high-performance computing16,25,26. Recent studies have also shown that integrated silicon photonics can perform training tasks27,28. Moreover, photonic computing has demonstrated its potential to solve complex problems more efficiently29,30,31,32.

Although new optical materials, architectures and strategies have been introduced to photonic computing to improve either their performance or their throughput, these demonstrations have been limited to single components or small-scale circuits. The real potential of photonic computing lies in very-large-scale integration and volume manufacturing technologies that could overturn or add value to traditional computing architectures. Such advantages are yet to be demonstrated in hardware, with several critical challenges still to be addressed. First, with the absence of storage in the optical ___domain, photonic computing must rely on optical-electronic cointegration and conversion of signals from one ___domain to the other. Second, like other technologies such as computing in memory33, photonic computing operates in the analogue ___domain, which means that it faces challenges in computation accuracy, especially for large, complex circuits. Third, photonic computing requires the development of compatible models and algorithms to be implemented on this new form of hardware.

In this paper, we present experimental results showing a marked advancement in highly integrated photonic computing technology—the development of an optical 64 × 64 matrix-vector computing acceleration chip that integrates more than 16,000 photonic components with advanced packaging. Performance analyses of this system indicate its potential for high throughput and, especially, low latency, surpassing traditional electronic-based solutions in terms of latency by two orders of magnitude. Our system design directly addresses the three above-mentioned challenges and illustrates the possibilities of using light for computation on large scales, representing an important milestone in photonic computing commercialization.

Optical MAC for heuristic recurrent algorithm

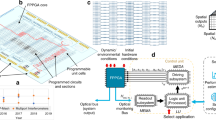
As an analogue computing approach, photonic computing has the potential advantage of achieving high bandwidth, high energy efficiency and low latency. High-bandwidth photonic computing relies on high-speed optical signal processing that can reach more than 100 Gbps (ref. 34). Energy efficiency can be further improved in architectures making use of wavelength multiplexing and/or new material platforms13,35. However, realizing latency speedups is technically very challenging, as they rely on large-scale optical vectors and matrices to avoid time penalty from matrix decomposition or multicycle analogue-to-digital conversions. In a digital MAC operation, such as systolic arrays in tensor processing units (TPUs)36, dot-product operations are decoupled and operate through the matrix elementwise (Fig. 1a, inset). Although the energy consumption can be greatly reduced by limiting short-reach data transfer between neighbouring units, the latency grows substantially as the matrix size expands, as shown by the red curve in Fig. 1a. By contrast, latency in photonic circuits is only limited by the optical path length, which scales linearly with matrix size. Latency can therefore be smaller than 10 ns or limited by a small amount of clock cycles, which remain negligible compared with latency in digital circuits, even for large matrix sizes (approximately 50). The growth factor of optical MAC (oMAC) latency is only several picoseconds, which is close to one-thousandth of TPUs (see Supplementary Note A and Extended Data Fig. 1). This contrast highlights the potential of scaled-up photonic accelerators for applications that require large throughput and ultralow latency.

Fig. 1: Latency comparison and principle of the heuristic recurrent algorithm.
figure 1

a, Comparison of latency between oMAC and TPU systolic array, a typical enhanced MAC operation. In the TPU, we assume that the clock frequency is 700 MHz (TPU v1)36 and the latency accumulates by orders of magnitude with the increase of clock cycles and matrix size linearly. By contrast, the latency only increases linearly with the expanding matrix size in oMAC owing to the change of path length, limited to nanoseconds. b, Principle of the heuristic recurrent algorithm for oMAC. St denotes the current data vector and W denotes the weight module representing the transition probability.

Full size image

Relying on large throughput and low latency, large-scale photonic computing systems are an ideal platform to implement heuristic algorithms for combinatorial optimization tailored for photonic platforms, such as photonic recurrent Ising samplers31,32. Here we focus on solving combinatorial problems that can be cast into an arbitrary quadratic Hamiltonian form:

$$H(K)=-\frac{1}{2}\sum _{1\le i,j\le N}{\sigma }_{i}{K}_{ij}{\sigma }_{j}$$
(1)

in which K denotes an N × N matrix and σ ∈ {−1, 1}N. This Hamiltonian is that of an Ising model32, which equivalently describes the interaction of many particles in terms of the coupling matrix K and spin states σ or normalized spin states S ∈ {0, 1}N, with σ = 2S − 1.

This algorithm can be implemented in a photonic computing system with a specifically designed architecture as shown in Fig. 1b. The photonic circuits can map the arbitrary Ising Hamiltonians described in equation (1). At time step t − 1, the spin state is encoded in the data module and fed into the matrix weight module for linear MAC operations. At the receivers, a nonlinear operation as well as various types of amplitude noise are imparted to the signals to implement an equivalent nonlinear threshold comparison31. The output from the comparator is recurrently sent back as the new input vector at step t to the linear MAC ___domain. This recurrent algorithm converges to the ground-state distribution of the corresponding Ising model, therefore finding the minima of equation (1) with high probability.

The recurrent matrix that is multiplying the current spin state is W and is mapped to the Ising model of interest K (see Methods and ref. 31). The algorithm shown in Fig. 1b relies on iterative matrix MAC computation, indicating that the computation speed of the full workload depends heavily on the speed and latency of each MAC cycle. Therefore, photonic computing can achieve marked performance improvement in these tasks by effectively using the advantages of high computing speed and low latency.

System and implementation

To implement the system that can achieve the target performance running the above-described heuristic recurrent algorithm, large-scale photonic circuits that can support considerably large matrix size are necessary, with the challenges of high integration form factor and consistent device performance. Figure 2 shows the highly integrated 64 × 64 Photonic Arithmetic Computing Engine (PACE) that we developed in this work. As shown in the architecture in Fig. 2a, this system is built to efficiently implement the heuristic recurrent algorithm described in the previous section. A hybrid architecture is chosen with a photonic integrated circuit (PIC) and an electronic integrated circuit (EIC) integrated in a system in package (SiP), in which 1 × 64 optical data and 64 × 64 weight modules execute the oMAC operation. Adjacent analogue and digital circuits in the EIC handle control and iterative logics. Signals are exchanged through a high-speed electrical-to-optical conversion by optical modulators and optical-to-electrical conversion by photodetectors. The digital circuits in the EIC handle the data feed-in, read-out and logic operations, as well as the clock and control. An embedded static random-access memory (SRAM) is designed to manage data storage. The initial vector S, referring to St in Fig. 1b, and weight data are injected into the corresponding vector drivers and weight drivers from the Serial Peripheral Interface (SPI) bus to drive the vector and weight modulators. The preset threshold values are sent to the comparators. The system then starts the iterative cycles. In a standalone iteration, processed vector results through the photonic channels are sent to the comparators to generate a new state vector S′, referring to St+1 in Fig. 1b. The new vector and the corresponding eigenvalue are stored in the SRAM as well as being sent back as the starting vector to re-drive the vector modulators in the next iteration. A total of 5,000 iterations is performed to guarantee the convergence of the solutions (see Methods and Extended Data Fig. 1).

Fig. 2: PACE system implementation.
figure 2

a, PACE system architecture. Blue blocks indicate analogue ___domain components and brown blocks indicate digital ___domain components. RX, receiver, including transimpedance amplifier (TIA) connecting to the photodetectors; TX, transmitter, including DAC and drivers for the vector modulators; WTX, weight DAC and driver for the weight modulators. b, Numbers of optical components and pins as the oMAC matrix scales up. c, Integrated PACE system board in PCIe-card-size form factor. SOM stands for system on module, connecting with PACE SiP through the SPI and bridging to the host computer through Ethernet IO. d, Diagram of the advanced packaged SiP with 2.5D flip-chip bonding. Inset, packaged SiP with fibre attach and wire bonds to the substrate. FA, fibre array. e, PIC chips with signal flow diagram. External laser sources are coupled through the fibre-attached ports and flow through the vector modulator array. The resulting signals are then modulated in the weight module and collected at the receiver arrays. The top trace shows the signal redistribution layer and power grid at the back-end-of-line metals. f–h, Critical functional components and their performance in the PACE PIC, including grating coupler (f), Mach–Zehnder modulator (g) and Ge photodetector (h). The data points represent the mean values of device specs in the system. Shaded areas denote the min–max ranges. Insets, microscope images of the corresponding devices. Scale bars, 10 μm (f,h), 50 μm (g). i, SNR versus matrix size for the PACE system versus regular design. Regular design is the same system built on the basis of photonic devices reported in ref. 41.

Full size image

To establish an oMAC system with matrix size larger than 64, more than 10,000 optical components and more than 10,000 pins to route signals are required, as shown in Fig. 2b. Thus, high integration with advanced packaging is required. A traditional form factor with individual optical components and electrical components connected through a separate board would fail owing to component sizes and the level of integration density, which is limited by the physical limit of packaging in integrated photonics37. The PACE system, targeting highly integrated form factor, is built on a PCIe-size card with integration of the PIC and the EIC to form the SiP. The full system is controlled through the SPI with a system on module (SOM) board and communicates with the host through Ethernet IO (Fig. 2c). To achieve the high-density signal connections, the PACE system uses a 2.5D advanced packaging solution with flip-chip bonding to assemble the PIC, EIC and the substrate as shown in Fig. 2d. The inset shows a top view of the SiP with the fibre attach to connect the PIC with external laser that drives the chip (also see Supplementary Note A for integration details).

The EIC is designed on the basis of a 28-nm commercial CMOS technology and the PIC is built on a commercial 65-nm silicon photonics technology with integration of more than 16,000 photonics components in a single chip, as illustrated in Fig. 2e. The photonic circuits are designed in an incoherent light architecture with series of data modules, weight modules and receiver arrays, which are implemented with optical modulators and photodetectors38,39. Four external continuous-wave lasers in an array are coupled into the circuits from the attached fibre array, through high-performance grating couplers. The operating power ranges from sub-mW to about 30 mW for each laser channel in the system (see Supplementary Note A). The average coupling efficiency reaches about −1 dB at a central wavelength near 1,310 nm, as shown in Fig. 2f. A 1 × 64 binary vector is fed into the vector modulator array in the PIC through the digital-to-analogue converters (DACs) and drivers in the EIC to achieve the bright and dark states in optical signals, corresponding to the 1 and 0 states in the vectors.

The modulated vector signals are then sent to a 64 × 64 matrix weight module for further modulation to fulfil the equivalent linear matrix-vector multiplication. The vector and weight data are modulated through two different sets of optical Mach–Zehnder modulators, with typical extracted modulator spectra as shown in Fig. 2g. The vector modulator array includes 64 identical units of Mach–Zehnder modulators operating at 1 GHz with non-return-to-zero modulation schemes40 (see Supplementary Note A and Extended Data Fig. 2 for all critical optical device information).

Because the matrix weights are fixed for a given Ising problem, the weight modulator module is designed differently from the vector modulator array. To implement the reconfigurable weight units, the weight modulators are optimized to operate at a lower frequency of 10 MHz, while being driven with much higher bit resolution by adjacent DACs and drivers. The correspondingly designed modulation accuracy is 8 bits. The output optical signals are converted and merged at the photodetector arrays and amplified through transimpedance amplifiers (TIAs). Thousands of the integrated germanium photodetector cells work as the receiver arrays to collect the modulated signal and fulfil the optical signal addition functionality. The responsivity of photodetectors is statistically tested to be highly consistent with each other around 1 A W−1, as shown in Fig. 2h. Finally, the amplified signals are compared with 8-bit comparators in the EIC ___domain and converted back into vectors for recurrent vector generation for the next iteration. In the operation, the system can achieve a throughput of approximately 8.19 TOPS. The energy efficiency is measured to be around 4.21 TOPS W−1 excluding lasers and 2.38 TOPS W−1 including lasers (see Supplementary Note A). To guarantee computation accuracy and to mitigate the challenge in the system calibration, all integrated components are designed with extremely tight specification variation. Without tightly controlled device variations, the signal-to-noise ratio (SNR) and hence the computation accuracy would seriously degrade. The impact is expected to be even greater when the system scales up to more components and a larger matrix size, as shown in Fig. 2i. On average, more than 12 dB of SNR improvement is achieved in the PACE system when compared with the commonly reported photonic design41 (see Supplementary Notes A and B and Extended Data Fig. 3).

To fully implement the heuristic architecture as explained in the algorithm, the PACE system needs to introduce controllable noises in the circuits to achieve efficient bit flips and hence to implement an effective search of the solution. Several sources of controllable noise are present in our system. The added noise primarily comes from the laser, analogue driver, TIA, as well as digital noise designed in the digital control circuits. The noise generated from the photonic circuits is considerably smaller. To increase the noise-driven bit flipping while maintaining the balance of the system that leads to convergence, the SNR is actively tuned by the input laser power, receiver TIA gain configuration and digital noise injection in the digital ___domain.

Optical matrix MAC accuracy study

We then calibrate the system and characterize the performance of the system on optical matrix multiplication, which is the core of our heuristic algorithm (see Supplementary Note B). To verify the MAC performance in the photonic ___domain, the system is characterized in terms of bit accuracy. Figure 3a shows a measured dot-product error distribution for 30,000 random vectors injected into the system in two different sets of weight matrix configurations that match our demonstrated workload, without any real-time active feedback tuning of the weights. An average error of 0.06 least significant bits (LSB) with standard deviation σ ≈ 1.18 LSB is achieved (for another result for randomized weight configurations, see expended characterization in Supplementary Note C and Extended Data Fig. 4). Correspondingly, the effective number of bits (ENOB) distribution reaches 8 bits for more than 65% probability and more than 7 bits for greater than 80%, as shown in Fig. 3b. The channel-to-channel bit accuracy presented in Fig. 3c also reveals that an average of close to 7.61-bit accuracy is achieved in the system under 25 MHz data rate, without any active feedback control. A specific preliminary calibration is applied to maintain the system accuracy. The system is also tolerant to a ±5 °C temperature fluctuation with downgrade of an effective bit (see Supplementary Note B). The ambient temperature dependence can be mitigated and the bit accuracy is expected to be further improved with active feedback control and monitoring of the system implemented.

Fig. 3: Optical matrix multiplication accuracy analysis.
figure 3

a, Distribution of single dot-product operation accuracy over 30,000 random vector dot-product operations in two different weight matrix configurations, showing an average error of 0.06 LSB and standard deviation of 1.18 LSB. b, Histogram of ENOB among all random dot-product events. c, The channel-by-channel ENOB statistics in the PACE photonic circuits. The dashed red line denotes an average of 7.61 ENOB among all channels. The error bars denote the standard deviation and the shaded area denotes the range of the maximum and minimum ENOB in the test.

Full size image

Ising demonstration

Ising problems, which represent typical NP-complete optimization problems, can be solved efficiently with the PACE system. To fully verify the advantages of photonic computing, as a proof of concept, we specifically demonstrate a graph max-cut or two-colouring problem in this prototype system. The Ising model/max-cut separates vertices into two partitions by minimizing the number of edges with each of the spin up/down partitions (shown as yellow/blue vertices, respectively, in Fig. 4a) and maximizing the number of edges with different spins (shown as grey vertices in Fig. 4a). The system runs for 5,000 iterations before converging to a solution. The system SNR is tuned through different configurations of laser power and TIA gain in the analogue ___domain, as well as digital noise in the digital ___domain, to efficiently converge to its solutions while making use of the intrinsic dynamic noise of our system. The typical initial, intermediate and final states corresponding to a minimum coloured edge of 9 are illustrated in Fig. 4b–d. The insets of the 2D-mapped figures can provide an intuitive visual depiction of the relative proportions of yellow, blue and grey vertices within each state. Also, a similar demonstration is designed for an equivalent image memorization problem42. In this case, a 64-size graph with 197 edges can be extracted from a flattened 8 × 8-pixel RGB image (Fig. 4e), corresponding to the graph’s negated symmetrized adjacency matrix. Evolving dynamically through a random initial state, the PACE system finally converges to the solution corresponding to the target image showing a cat, as shown in Fig. 4h (see Methods).

Fig. 4: Two Ising models configured in the system.
figure 4

a, A 63 × 63 max-cut problem-solving a 1 × 63 vector dataset with its random initial state (b), intermediate computation state (c) and final solution state (d). Insets, 2D-mapped edges that match with the states. e, A 64 × 64 squeezed imaging-searching problem, to search for the encoded image with the minimum energy states, with its random initial state (f), intermediate computation state (g) and final solution state with a ‘cat-like’ ground-state solution image (h).

Full size image

We then characterize the performance of our system in solving Ising problems (see Methods, Supplementary Note A and Extended Data Fig. 5). The system clock is set at 1 GHz (see Supplementary Note A) and the latency in each loop can be configured from 1 to 26 ns. The results from all iterations are recorded in the system memory. With ten batches of 2,000 Ising convergence tests, the average convergence rate to find the best solutions is more than 92.72% with a lowest latency of 5 ns, as shown in Fig. 5a. The average convergence ratio decreases to less than 25% at a latency of 2 ns, owing to the intrinsic delay limitations introduced by signal processing cycles as well as the clock speed. The limitation can be lifted or improved by using alternative device design with higher bandwidth and higher clock speed of operation with tighter circuits design in both the EIC and the PIC12,24,43. The convergence rate can reach nearly 100% with a larger latency setting in the two demonstrated models. It indicates that the computation latency of the PACE system can achieve a minimum of 5 ns. This is nearly 500 times faster than a single iteration when running the same workload on a commercial high-end NVIDIA A10 GPU, for which greater than 2,300 ns latency is measured.

Fig. 5: PACE Ising convergence and its comparison with a commercial A10 GPU.
figure 5

a, PACE Ising convergence rates versus latency. The error bars denote the standard deviation of ten random tests. Inset, non-convergence when the light is off in the circuit, indicating the effectiveness of oMAC and that pure hardware noise alone cannot induce convergence. b, Statistics of the number of iterations to solution at 5 ns latency, over 2,000 random input states. Inset, minima energy evolution in the iterative search. Dashed red line denotes the target minima energy. c, Statistics of the number of iterations that converge at 2 ns latency in the PACE system. Inset, energy evolution over 5,000 iterations for an unconverged case. Dash red line denotes the target minima energy. d, Comparison of the number of iterations to solution between the PACE system and the commercial GPU. The average counts are 537 for the PACE system and 347 for the NVIDIA A10 GPU, shown by dashed lines. Inset, comparison of single cycle latency and total time consumption between the PACE system and the NVIDIA A10 GPU. PACE data are multiplied by 100 for visual comparison.

Full size image

Figure 5b,c shows histograms of the total iteration counts required for Ising convergence in one batch at latencies of 5 and 2 ns, respectively. With further signal and calibration improvement, a latency of 3 ns could be realized in future devices. For comparison, we also extracted the histogram of the Ising calculation running on a A10 GPU using the same heuristic recurrent algorithm, in which noise is added in the digital ___domain. The performance results are then compared with the PACE system under 5 ns latency configuration, as shown in Fig. 5d. The histograms exhibit strong similarity, with average numbers of iterations required for convergence of 347 and 537 for the GPU and the PACE system, respectively. Correspondingly, a total computation time of 2.7 μs is realized with the PACE system, much shorter than the 798.1 μs computation time with the GPU, as shown in the inset of Fig. 5d. This reflects a two-orders-of-magnitude acceleration in the PACE system compared with the GPU (see Supplementary Note D and Extended Data Figs. 6 and 7 for more details). This result highlights the advantage of photonic computing on latency and computation speed realized by the PACE system.

Conclusion

In conclusion, we have successfully implemented a highly integrated 64 × 64 photonic accelerator system based on commercial silicon photonics technology. The photonics MAC circuits are realized with more than 16,000 components integrated on a single chip. An average bit accuracy of 7.61 bits is achieved in the system and applications for solving the max-cut problem with ultralow latency are demonstrated. The performance to solve the same computation workload is compared with that of a commercial high-performance A10 GPU. The experimental results reveal that more than two-orders-of-magnitude improvements in latency and computing time are achieved with oMAC in the PACE system compared with the commercial GPU. We believe that this demonstration could benefit the exploration of new computing models, system architectures and applications based on large-scale integrated photonics circuits.

Methods

Ising problem

The Hamiltonian of a general Ising problem is given by

$$H(K)=-\frac{1}{2}\sum _{1\le i,j\le N}{\sigma }_{i}{K}_{i,j}{\sigma }_{j}-\sum _{i}{b}_{i}{\sigma }_{i},$$
(2)

in which Ki,j represents the element of an N × N matrix that describes the coupling between σi and σj. The K matrix is assumed to be symmetric, Ki,j = Kj,i. bi represents the applied external magnetic field, which is often neglected to benchmark Ising solvers. The Ising problem is to find the spin vector to minimize the H(K).

In this work, we use a class of heuristic recurrent algorithms that has been proposed as an effective approach for solving Ising problems with integrated photonics31,44. In the photonic hardware implementation, it is necessary to convert the spin vector σ ∈ {−1, 1} into a binary vector S ∈ {0, 1}, in which each element Si is defined as (σi + 1)/2. This binary vector will be initiated randomly and then iterated. Each iteration of the loop involves the following operations:

In each iteration, a noisy matrix-vector multiplication is performed, denoted as

$${v}_{t}=W\times S+{\rm{Noise}},$$
(3)

in which W is derived from the matrix K (ref. 31).

vt is then compared with the threshold vector T to yield the input vector vt+1 of the next iteration.

$${v}_{t+1}^{i}=\left\{\begin{array}{c}0\,{\rm{when}}\,{v}_{t}^{i} < {T}^{i}\\ 1\,{\rm{when}}\,{v}_{t}^{i}\ge {T}^{i}\end{array}.\,\right.$$
(4)

The threshold vector T is pre-computed, for which each element can be described as

$${T}^{i}=\sum _{j}{W}_{ij}/2.$$
(5)

Ising workload implementation

In the image memorization example (pixellized image of a cat), we iterated over a 1 × 64 vector, whereas the image of the cat is an 8 × 8 image. The image needs to be flattened to a 1 × 64 vector to be iterated.

Explanation of convergence

In the Ising demonstration experiments, the number of iterations is configured to 5,000 and the results of each iteration are recorded. When the iterations complete, the energy corresponding to each result is calculated to determine whether any vector reached the minimum energy state. If any result reaches the minimum energy state, the calculation is considered converged. Extended Data Fig. 5 shows both the converged case (panel a) and the unconverged case (panel b). Both cases began with their own random inputs and their initial energies were approximately −40. Furthermore, the theoretical minimum energy value, indicated by the dashed line, is −84. It is evident that the system can rapidly iterate towards the optimal solution when the laser is on. Conversely, when the laser is off, the energy increases to approximately −20, which is even worse than a random input.

When the laser is turned off, no photocurrent is generated and the system output becomes close to the analogue-to-digital converter bias of 128, mainly influenced by the noise from the TIA. The standard deviation of TIA noise is about 2 LSB (least significant bits of the analogue-to-digital converter) for all channels. If the thresholds of the comparators are set far away, for example, 6 LSB apart, some channels may find it difficult to toggle their outputs. This will greatly increase the probability of these channels being embedded with fixed 0s and 1s during the iteration. Consequently, the entire system fails to achieve convergence.