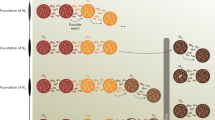
Abstract
The demographic history of a population underlies patterns of genetic variation and is encoded in the gene-genealogical trees of the sampled haplotypes. Here we propose a demographic inference framework called the genealogical likelihood (gLike). Our method uses a graph-based structure to summarize the relationships among all lineages in a gene-genealogical tree with all possible trajectories of population memberships through time and derives the full likelihood across trees under a parameterized demographic model. We show through simulations and empirical applications that for populations that have experienced multiple admixtures, gLike can accurately estimate dozens of demographic parameters, including ancestral population sizes, admixture timing and admixture proportions, and it outperforms conventional demographic inference methods using the site frequency spectrum. Taken together, our proposed gLike framework harnesses underused genealogical information to offer high sensitivity and accuracy in inferring complex demographies for humans and other species.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
27,99 € / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
209,00 € per year
only 17,42 € per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
The individual-level genetic data for Native Hawaiian and Latino datasets were derived from the Multiethnic Cohort and are available on dbGaP (accession numbers phs000220.v2.p2 and phs002183.v1.p1).
Code availability
The gLike package is available on its GitHub page (https://github.com/Ephraim-usc/glike). The version of gLike as well as codes used for simulation and plotting presented in this study can also be found on Zenodo (https://doi.org/10.5281/zenodo.14708630)52.
Change history
17 June 2025
A Correction to this paper has been published: https://doi.org/10.1038/s41588-025-02257-4
References
Schlebusch, C. M. & Jakobsson, M. Tales of human migration, admixture, and selection in Africa. Annu. Rev. Genom. Hum. Genet. 19, 405–428 (2018).
Chiang, C. W. K. et al. Genomic history of the Sardinian population. Nat. Genet. 50, 1426–1434 (2018).
Micheletti, S. J. et al. Genetic consequences of the transatlantic slave trade in the Americas. Am. J. Hum. Genet. 107, 265–277 (2020).
Patterson, N. et al. Ancient admixture in human history. Genetics 192, 1065–1093 (2012).
Peter, B. M. Admixture, population structure, and F-statistics. Genetics 202, 1485–1501 (2016).
Lipson, M. Applying f4‐statistics and admixture graphs: theory and examples. Mol. Ecol. Resour. 20, 1658–1667 (2020).
Lohmueller, K. E. The distribution of deleterious genetic variation in human populations. Curr. Opin. Genet. Dev. 29, 139–146 (2014).
Keinan, A. & Clark, A. G. Recent explosive human population growth has resulted in an excess of rare genetic variants. Science 336, 740–743 (2012).
Wang, S. R. et al. Simulation of Finnish population history, guided by empirical genetic data, to assess power of rare-variant tests in Finland. Am. J. Hum. Genet. 94, 710–720 (2014).
Medina-Muñoz, S. G. et al. Demographic modeling of admixed Latin American populations from whole genomes. Am. J. Hum. Genet. 110, 1804–1816 (2023).
Uricchio, L. H., Zaitlen, N. A., Ye, C. J., Witte, J. S. & Hernandez, R. D. Selection and explosive growth alter genetic architecture and hamper the detection of causal rare variants. Genome Res. 26, 863–873 (2016).
Li, H. & Durbin, R. Inference of human population history from individual whole-genome sequences. Nature 475, 493–496 (2011).
Sheehan, S., Harris, K. & Song, Y. S. Estimating variable effective population sizes from multiple genomes: a sequentially Markov conditional sampling distribution approach. Genetics 194, 647–662 (2013).
Schiffels, S. & Durbin, R. Inferring human population size and separation history from multiple genome sequences. Nat. Genet. 46, 919–925 (2014).
Terhorst, J., Kamm, J. A. & Song, Y. S. Robust and scalable inference of population history from hundreds of unphased whole genomes. Nat. Genet. 49, 303–309 (2017).
Palamara, P. F., Lencz, T., Darvasi, A. & Pe’er, I. Length distributions of identity by descent reveal fine-scale demographic history. Am. J. Hum. Genet. 91, 809–822 (2012).
Browning, S. R. et al. Ancestry-specific recent effective population size in the Americas. PLoS Genet. 14, e1007385 (2018).
Gutenkunst, R. N., Hernandez, R. D., Williamson, S. H. & Bustamante, C. D. Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet. 5, e1000695 (2009).
Bhaskar, A., Wang, Y. X. R. & Song, Y. S. Efficient inference of population size histories and locus-specific mutation rates from large-sample genomic variation data. Genome Res. 25, 268–279 (2015).
Kamm, J., Terhorst, J., Durbin, R. & Song, Y. S. Efficiently inferring the demographic history of many populations with allele count data. J. Am. Stat. Assoc. 115, 1472–1487 (2020).
Excoffier, L. et al. fastsimcoal2: demographic inference under complex evolutionary scenarios. Bioinformatics 37, 4882–4885 (2021).
Excoffier, L., Dupanloup, I., Huerta-Sánchez, E., Sousa, V. C. & Foll, M. Robust demographic Inference from genomic and SNP data. PLoS Genet. 9, e1003905 (2013).
Liu, X. & Fu, Y.-X. Stairway Plot 2: demographic history inference with folded SNP frequency spectra. Genome Biol 21, 280 (2020).
McVean, G. A genealogical interpretation of principal components analysis. PLoS Genet. 5, e1000686 (2009).
Opgen-Rhein, R., Fahrmeir, L. & Strimmer, K. Inference of demographic history from genealogical trees using reversible jump Markov chain Monte Carlo. BMC Evol. Biol. 5, 6 (2005).
Fan, C., Mancuso, N. & Chiang, C. W. K. A genealogical estimate of genetic relationships. Am. J. Hum. Genet. 109, 812–824 (2022).
Hudson, R. R. Gene genealogies and the coalescent process. In Oxford Surveys in Evolutionary Biology Vol. 7 (eds Futuyma, D. & Antonovics, J.) 1–44 (Oxford Univ. Press, 1990).
Griffiths, R. C. & Marjoram, P. Ancestral inference from samples of DNA sequences with recombination. J. Comput. Biol. 3, 479–502 (1996).
Lewanski, A. L., Grundler, M. C. & Bradburd, G. S. The era of the ARG: an introduction to ancestral recombination graphs and their significance in empirical evolutionary genomics. PLoS Genet. 20, e1011110 (2024).
Brandt, Y. C. et al. Evaluation of methods for estimating coalescence times using ancestral recombination graphs. Genetics 221, iyac044 (2022).
Peng, D., Mulder, O. J. & Edge, M. D. Evaluating ARG-estimation methods in the context of estimating population-mean polygenic score histories. Genetics https://doi.org/10.1093/genetics/iyaf033 (2025).
Brandt, D. Y. C., Huber, C. D., Chiang, C. W. K. & Ortega-Del Vecchyo, D. The promise of inferring the past using the ancestral recombination graph. Genome Biol. Evol. 16, evae005 (2024).
Pearson, A. & Durbin, R. Local ancestry inference for complex population histories. Preprint at bioRxiv https://doi.org/10.1101/2023.03.06.529121 (2023).
Wang, Z. et al. Automatic inference of demographic parameters using generative adversarial networks. Mol. Ecol. Resour. 21, 2689–2705 (2021).
Adrion, J. R. et al. A community-maintained standard library of population genetic models. eLife 9, e54967 (2020).
Sun, H. et al. The impact of global and local Polynesian genetic ancestry on complex traits in Native Hawaiians. PLoS Genet. 17, e1009273 (2021).
Jeon, S. et al. Genome-wide trans-ethnic meta-analysis identifies novel susceptibility loci for childhood acute lymphoblastic leukemia. Leukemia 36, 865–868 (2022).
Myers, S., Fefferman, C. & Patterson, N. Can one learn history from the allelic spectrum? Theor. Popul. Biol. 73, 342–348 (2008).
Kubatko, L. S., Carstens, B. C. & Knowles, L. L. STEM: species tree estimation using maximum likelihood for gene trees under coalescence. Bioinformatics 25, 971–973 (2009).
Pickrell, J. K. & Pritchard, J. K. Inference of population splits and mixtures from genome-wide allele frequency data. PLoS Genet. 8, e1002967 (2012).
Molloy, E. K., Durvasula, A. & Sankararaman, S. Advancing admixture graph estimation via maximum likelihood network orientation. Bioinformatics 37, i142–i150 (2021).
Nielsen, S. V. et al. Bayesian inference of admixture graphs on Native American and Arctic populations. PLoS Genet. 19, e1010410 (2023).
Deng, Y., Nielsen, R. & Song, Y. S. Robust and accurate Bayesian inference of genome-wide genealogies for large samples. Preprint at bioRxiv https://doi.org/10.1101/2024.03.16.585351 (2024).
Kelleher, J., Etheridge, A. M. & McVean, G. Efficient coalescent simulation and genealogical analysis for large sample sizes. PLoS Comput. Biol. 12, e1004842 (2016).
Kelleher, J. et al. Inferring whole-genome histories in large population datasets. Nat. Genet. 51, 1330–1338 (2019).
Wohns, A. W. et al. A unified genealogy of modern and ancient genomes. Science https://doi.org/10.1126/science.abi8264 (2022).
Speidel, L., Forest, M., Shi, S. & Myers, S. R. A method for genome-wide genealogy estimation for thousands of samples. Nat. Genet. 51, 1321–1329 (2019).
Sheng, X. et al. Inverted genomic regions between reference genome builds in humans impact imputation accuracy and decrease the power of association testing. HGG Adv. 4, 100159 (2023).
Loh, P.-R. et al. Reference-based phasing using the Haplotype Reference Consortium panel. Nat. Genet. 48, 1443–1448 (2016).
Woerner, A. E., Veeramah, K. R., Watkins, J. C. & Hammer, M. F. The role of phylogenetically conserved elements in shaping patterns of human genomic diversity. Mol. Biol. Evol. 35, 2284–2295 (2018).
Lin, M. et al. Population-specific reference panels are crucial for genetic analyses: an example of the CREBRF locus in Native Hawaiians. Hum. Mol. Genet. 29, 2275–2284 (2020).
Fan, C. Ephraim-usc/glike: v1.0. Zenodo https://doi.org/10.5281/zenodo.14708630 (2025).
Acknowledgements
We would like to thank I. Mathieson, S. Mathieson and L. Speidel for discussions and advice. Research reported in this publication was supported by National Institute of Health under award number R35GM142783 and R01HG12605 to C.W.K.C., R35GM137758 to M.D.E., R01HG012133 and P01CA196569 to N.M. and by Programa de Apoyo a Proyectos de Investigación e Innovación Tecnológica–Universidad Nacional Autónoma de México (PAPIIT–UNAM) under award number IN215524 to D.O.-D.V. The funders had no role in the study design, data collection and analysis, decision to publish or preparation of the manuscript. Computation for this work was supported by the University of Southern California’s Center for Advanced Research Computing (https://carc.usc.edu).
Author information
Authors and Affiliations
Contributions
C.W.K.C., D.O.-D.V. and C.D.H. conceived of the study. C.F. and C.W.K.C. designed the study. C.F., J.L.C. and B.L.D. performed the analysis. B.L.D. curated the data. C.F., M.D.E., N.A.M. and C.W.K.C. interpreted the data. C.F., J.L.C., M.D.E. and C.W.K.C. wrote the manuscript with input from all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Genetics thanks Laurent Excoffier, Harald Ringbauer and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 The expected coalescence distribution based on the inferred demography matches the simulated input.
(A) We simulated 100 equal-distant trees of 1000 haplotypes were simulated on a 30 Mb chromosome, under the same demography as in Fig. 2a. The demography is inferred by gLike on the true trees with default settings, and the expected coalescence distribution is computed by simulation of 10,000 trees under the inferred demography. The two distributions are highly consistent, except for small random fluctuations on the observed distribution. (B) The same experiment as in (A), but tsdate reconstruction is applied to the observed trees, the parameters are then inferred by gLike on the reconstructed trees, and tsdate reconstruction is again applied to the simulated trees under the inferred parameters. Vertical dash lines indicate t1, t2, and t3 in the simulated demography, corresponding to the time of the more recent admixture event, the more distant admixture event, and the split of three ancestral populations, respectively.
Extended Data Fig. 2 The inferred distribution of coalescence under the three-way admixture demography as function of input parameter Ne during ARG inference.
For ARG inference based on (A) tsdate, (B) Relate, and (C) Relate with branch sampling, the left panels show the times of coalescences (that is, inner nodes) in ascending order in a genealogical tree of 1000 haplotypes simulated under the three-way admixture demography as in Fig. 2a. Different color bands show 2 times standard deviation across 50 independent simulations. Right panels show TMRCA in the true tree versus the reconstructed tree, using Ne = 10,000, which we use as default for all ARG inference in this study. Results from 50 independent simulations are pooled for display.
Extended Data Fig. 3 Log likelihood distribution around Nooa values for different thresholds of maximum number of edges connecting all states between two time points.
For computational efficiency, if the total connections between two adjacent layers of the GOS exceeds a customizable hyperparameter, κ, gLike will approximate via sampleing (see Methods for details). Here we evaluate the impact of setting this threshold, κ, on the apparent biased estimate of Nooa parameter in Fig. 4. A total of 50 replicate experiments were conducted in each panel. Solid circles and error bars indicate mean and standard deviation, respectively, across the replicates. In each replicate experiment, 100 equally distant trees of 1000 haplotypes were simulated on a 30 Mb chromosome from population ADMIX under the same demography as in Fig. 4. The log-likelihood (logP) of observing these 100 trees were calculated by gLike assuming different Nooa values and all other demographic parameters fixed at true values. The logP calculated from the true Nooa = 1867 were subtracted from all logP values, for comparability between replicates. As we increased the default threshold for connections before gLike begin approximating the likelihood, the maximum likelihood estimate (dashed line) also tended towards the true value (solid line), suggesting that the exact computation of likelihood is unbiased, though approximation for computational reasons could lead to bias.
Extended Data Fig. 4 Average gLike runtime on a single genealogical tree with varying sample sizes.
50 replicate experiments were conducted for each sample size. Solid circles indicate the average runtime on each tree, and squares indicate the average time spent on scipy logsumexp function for each tree. Error bars indicate the standard deviation across 50 replicates. In each replicate experiment, 100 equally distant trees of 1000 haplotypes were simulated on a 30 Mb chromosome under the same three-way admixture demography as in Fig. 2.
Extended Data Fig. 5 Robustness of gLike against misspecified continuous migrations.
The same experiment in Fig. 4a except that the true demography contains AFR-EUR, AFR-ASIA, EUR-ASIA and AFR-OOA continuous migrations that are set to be 1x (A), 10x (B) and 100x (C) of their rates as in the stdpopsim 4B11 model. gLike was applied on the true trees in the same way as in Fig. 4a, assuming no continuous migrations. Note that the 1x continuous migrations have no visible impact on the results, while 100x continuous migrations lead to considerable underestimations of \({t}_{3}\), \({t}_{4}\) and \({N}_{{\rm{afr}}}\), due to the accumulation of coalescences earlier than expected in a migration-free demography. Boxplots display the first, second (the median), and third quartiles of the data, with whiskers extending from the box to the farthest data point lying within 1.5x of the inter-quartile range.
Extended Data Fig. 6 Unidentifiability between population sizes and growth rates.
The log-likelihood of the gLike model on the population sizes (at time of admixture) and growth rates of the Latinos and Native Hawaiians in a grid of possible parameters. All other parameters were fixed at their estimates shown in Fig. 6. This result indicates the potential bias when estimating entangled parameters, because the hill-climbing optimization could stop anywhere along the red curve, depending on the initial values.
Supplementary information
Supplementary Information
Supplementary Notes, Supplementary Figs. 1–11 and Supplementary Tables 1–6.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Fan, C., Cahoon, J.L., Dinh, B.L. et al. A likelihood-based framework for demographic inference from genealogical trees. Nat Genet 57, 865–874 (2025). https://doi.org/10.1038/s41588-025-02129-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41588-025-02129-x