A high spatial resolution dataset for methylmercury exposure in Guangdong-Hong Kong-Macao Greater Bay Area

Mercury (Hg) is a global persistent neurotoxic substance^1,2,3. Inorganic mercury can be methylated into methylmercury (MeHg) with more toxicity by biochemical reaction⁴, ultimately harming human health. Dietary intake is the primary way of human exposure to MeHg⁵. Excessive and long-term low-dose MeHg intake poses a significant threat to human health, such as kidney and cardiovascular diseases⁶, psychological and neurological deficits⁷, and fetus intelligence quotient decrements⁸. Many countries have signed the Minamata Convention to protect human health from anthropogenic emissions and releases of Hg and Hg compounds⁹. Constructing a high spatial resolution dataset for dietary MeHg exposure can reveal spatially explicit hotspots of dietary MeHg exposure. This further helps to evaluate and reduce MeHg-related health risks.

The Guangdong-Hong Kong-Macao Greater Bay Area (GBA) is a world-class urban agglomeration. It consists of nine cities in the Pearl River Delta Area (including Guangzhou, Shenzhen, Zhuhai, Foshan, Huizhou, Dongguan, Zhongshan, Jiangmen, and Zhaoqing), Hong Kong Special Administrative Region (referred to as Hong Kong), and Macao Special Administrative Region (referred to as Macao). GBA is one of the regions with the most vigorous economic vitality in China and even the world¹⁰. The GBA consumes large amounts of rice and fish which are two primary pathways of dietary MeHg exposure^11,12. Consequently, there is a potentially high risk of dietary MeHg exposure for the population of the GBA. Constructing a high spatial resolution dataset for dietary MeHg exposure in the GBA can lay the foundation for evaluating and reducing MeHg-related health risks of the GBA.

Existing studies on dietary MeHg exposure of the Chinese population mainly focus on the national and provincial scales. Little attention is paid to the high spatial resolution inventories of dietary MeHg exposure at the urban agglomeration (especially the GBA) scale. For example, Chen et al.¹³ compiled an inventory of dietary MeHg exposure for each province of China in 2010 and then revealed the related health risks. Li et al.¹² constructed an inventory of dietary MeHg exposure via seafood consumption by different age groups in coastal areas of Guangdong. Chen et al.¹⁴ adopted the total diet study method to estimate the dietary MeHg exposure of the adult population in Hong Kong. For the Hg-related high spatial resolution datasets, Chang et al.¹⁵ have constructed a high spatial resolution dataset for anthropogenic atmospheric mercury emissions in China during 1998–2014 at a 1 km resolution. Li et al.¹⁶ mapped China’s MeHg-related health risks in 2010 at the 1 km × 1 km grid scale. However, a time-series high spatial resolution dataset for dietary MeHg exposure in the GBA is still insufficient. Such a time-series dataset can reveal the spatially explicit hotspots, distribution patterns, and variation trend of dietary MeHg exposure in the GBA.

This study aims to construct a gridded dataset for dietary MeHg exposure of the GBA with the 1 km × 1 km spatial resolution during 2009–2019. According to previous studies^17,18, food types considered in this study include rice and fish (including freshwater and marine fish). This study first compiles a time-series inventory of dietary MeHg exposure for each county/district in the GBA during 2009–2019. Subsequently, it spatializes the dietary MeHg exposure in the GBA at the 1 km × 1 km scale, using gridded data on food consumption expenditure in the GBA as the proxy. This dataset can describe the spatially explicit hotspots, distribution patterns, and variation trend of dietary MeHg exposure in the GBA. It lays the foundation for evaluating and controlling MeHg-related health risks of the GBA.

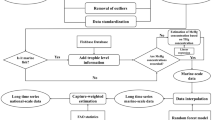
The construction of the time-series high spatial resolution dataset for dietary MeHg exposure in the GBA mainly consists of two steps (Fig. 1). We first construct the dietary MeHg exposure inventory for each county/district of the GBA, based on MeHg concentrations of foods (i.e., rice and fish in this study) and per capita rice and fish intake. Most counties/districts in this study are divided according to the current administrative divisions of the People’s Republic of China. It is worth noting that Guangming District, Longhua District, and Pingshan District of Shenzhen city were inaugurated late and there are few officially published data. According to the original affiliation of these three districts, Guangming District, Longhua District, and Baoan District are merged as Baoan District; Pingshan District and Longgang District are merged as Longgang District. Subsequently, we spatialize the dietary MeHg exposure inventory at 1 km × 1 km scale, using gridded data for food consumption expenditure of counties/districts as the proxy.

Procedures for constructing high spatial resolution dataset for dietary MeHg exposure in the GBA.

Full size image

Constructing dietary MeHg exposure inventory of counties/districts

Constructing dietary MeHg exposure inventory of counties/districts includes two steps: compiling MeHg concentrations of foods and evaluating estimated daily intake (EDI). According to previous studies^17,18, food types considered in this study include rice and fish (including freshwater and marine fish).

Compiling MeHg concentrations of foods

This study collects the MeHg concentrations of rice and fish from published literature^{19,20,21,22,23,24,25,26,27,28,29,30,31} (see Supplementary Table 1). The data on MeHg concentrations of rice and fish for the GBA are scarce during 2009–2019. As an alternative, we use the MeHg concentration data for Guangdong province. Approximately 70% of the sampling sites for the concentration data we collected are located in the GBA. Thus, the concentration data we collected could represent the MeHg concentrations of foods in the GBA to some extent.

We collect the MeHg concentration data of each food type across different time points to reflect the temporal variation trends during 2009–2019. It is worth noting that the MeHg concentration data for each food type during 2009–2019 are discontinuous. For missing data in intermediate years, this study estimates them by an interpolation method. Taking the intermediate years between 2010 and 2014 as an example, the interpolation processes for 2011, 2012, and 2013 are as follows.

For the other missing data, this study estimates them based on the assumption that the changing rates in adjacent years are the same. If there are two or more values for MeHg concentration of a food in the same year, this study takes the average as the MeHg concentration of this food in that year.

Evaluating estimated daily intake (EDI)

Calculating the EDI requires the data on per capita intakes of foods and MeHg concentrations of foods. The data on per capita intakes of foods at the county/district level are unavailable from existing statistics. We assume that the per capita intakes of foods by urban and rural residents in each county/district are, respectively, the same as those in the corresponding city. Consequently, we can calculate the EDI of MeHg by residents in each county/district based on the EDIs of MeHg by urban and rural residents at the city level and the urbanization rate of each county/district.

Firstly, we evaluate the EDIs for urban and rural residents at the city scale by multiplying the municipal per capita intakes of foods with MeHg concentrations of foods. The per capita intakes of foods in each city of the GBA can be derived from the data on per capita food consumption. Per capita food consumption is close to per capita food intake, but they are different. We use the ratio of national per capita food intake to national per capita food consumption to derive the per capita food intake in each city of the GBA, based on the per capita food consumption in each city of the GBA. The national per capita food intake of rural and urban residents can be obtained from the China Health and Nutrition Survey (CHNS)³². Most city level and national data on per capita food consumption (kg*year⁻¹*capita⁻¹) of rural and urban residents can be obtained from City Statistical Yearbooks^{33,34,35,36,37,38,39,40,41} and China Statistical Yearbook⁴², respectively. The data for per capita food consumption in Hong Kong can be obtained from the Hong Kong Population-based Food Consumption Survey^43,44. For the missing data of certain cities (e.g., Jiangmen and Zhongshan), we use the average level of cities with similar per capita GDP. In particular, among the GBA, the per capita GDP of Macao is close to that of Hong Kong. The dietary pattern of Macao’s residents is close to that of the Pearl River Delta⁴⁵ and Zhuhai is adjacent to Macao. Therefore, we use the per capita food consumption of Hong Kong and dietary structure of Zhuhai to calculate the per capita food consumption of Macao.

Meanwhile, for certain years, food categories of the physical per capita food consumption data are highly aggregated. We disaggregate the data by two methods. Preferentially, we divide the monetary per capita consumption expenditure of particular food products (Yuan year⁻¹ capita⁻¹) by corresponding consumer prices. Alternatively, we disaggregate the data according to the proportions of food production. The data for monetary per capita food consumption expenditure, consumer prices, and food production can be obtained from the yearbooks mentioned above.

The EDI at the city level is calculated with Eq. (1) and Eq. (2).

The notation I_i,j indicates per capita intake (g d⁻¹ capita⁻¹) of food i in city j and CON_i,j indicates per capita consumption (g d⁻¹ capita⁻¹) of food i in city j. The noataions NI_i and NCON_i represent national per capita intake and per capita consumption of food i in China, respectively. The notation EDI_j denotes the EDI of MeHg in city j; C_i represents the MeHg concentration of food i in Guangdong; and BW means the average weights of Chinese adult males (66.2 kg) and females (57.3 kg)⁴⁶.

Secondly, we downscale the EDI of MeHg by residents from the city scale to the county/district scale, based on the EDIs of MeHg by urban and rural residents at the city level and the urbanization rate of each county/district. The EDI at the county/district scale is calculated with Eq. (3).

The notation EDI_n denotes the EDI of MeHg for county/district n in city j; UEDI_j and REDI_j indicate the EDIs of MeHg by urban and rural residents in city j, respectively; and r refers to the urbanization rate of county/district n.

Spatializing county/district level inventory to grid scale

We use the gridded data on food consumption expenditure of counties/districts in the GBA as proxy data to spatialize the dietary MeHg exposure (i.e., EDI of MeHg) of counties/districts. In this way, we can construct a high spatial resolution dataset for dietary MeHg exposure in the GBA. Here we take 2010 as an example to explain the spatializing procedures.

1. (1)

   We obtain and calibrate the gridded population data in the GBA. The gridded population data are from the LandScan population dataset developed by Oak Ridge National Laboratory⁴⁷, covering the Pearl River Delta in Guangdong Province, Hong Kong, and Macao during 2009–2019. In this study, we assign zero to the gridded population where the value is null. It is worth noting that the total population of each county/district in the gridded population dataset is inconsistent with that of official statistics. We hence calibrate the gridded population dataset for each county/district according to the total population data in City Statistical Yearbooks, as shown in Eq. (4).

   $${p}_{n,i}^{2010}={g}_{n,i}^{2010}\times \frac{po{p}_{n}^{2010}}{{\sum }_{i}{g}_{n,i}^{2010}}$$

   (4)

   The notations p_n,i²⁰¹⁰ and pop_n²⁰¹⁰ denote the population of grid i in county/district n (after calibration) and the population of county/district n from official statistics in 2010, respectively. The notation g_n,i²⁰¹⁰ represents the population of grid i in county/district n in 2010 from gridded population dataset before calibration.

2. (2)

   We multiply the per capita food consumption expenditure of counties/districts by gridded population to obtain the gridded data for food consumption. The data for per capita food consumption expenditure of counties/districts are unavailable from official statistics. One way to estimate per capita food consumption expenditure of counties/districts is multiplying the total per capita consumption expenditure of each county/district with Engel’s coefficient. Another way is calculating the ratio of per capita food consumption expenditure to per capita disposable income in each city and then using this ratio to adjust per capita disposable income of each county/district. These data can be obtained from City Statistical Yearbooks and County/District Statistical Yearbooks.

   The gridded food consumption expenditure of the GBA in 2010 is calculated with Eq. (5).

   $$CO{N}_{n,i}^{2010}={p}_{n,i}^{2010}\times pCO{N}_{n,i}^{2010}$$

   (5)

   The notation CON_n,i²⁰¹⁰ represents the food consumption expenditure in grid i of county/district n in the GBA and pCON_n²⁰¹⁰ denotes the per capita food consumption expenditure of county/district n in 2010.

3. (3)

   Consequently, the dietary MeHg exposure in each grid of the GBA is calculated with Eq. (6).

The notation EDI_n,i²⁰¹⁰ denotes the EDI of MeHg in grid i of county/district n and EDI_n²⁰¹⁰ represents the total EDI of MeHg in county/district n in 2010.

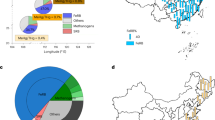
This dataset is publicly available under Zenodo⁴⁸. Its values are in μg kg⁻¹ d⁻¹. The GBA consists of the Pearl River Delta, Hong Kong, and Macao, and we hence classify the gridded data on dietary MeHg exposure into three parts (i.e., the Pearl River Delta, Hong Kong, and Macao). The data files are in tif format and named based on the years. Table 1 shows the naming protocol for this dataset.

This study uses the methods from peer reviewed literature to construct the gridded dataset for dietary MeHg exposure in the GBA. For example, the methods for calculating the per capita intake and EDI are from Chen et al.¹³ The method to spatialize the dietary MeHg exposure is from Li et al.¹⁶. However, there are still uncertainties in the dataset of this study, mostly from the assumptions of calculation methods.

1. (1)

   When data for counties/districts are unavailable, we calculate them by referring to parameters of corresponding cities or Guangdong Province. This assumption would lead to uncertainties of the results. For example, the data for per capita food consumption of counties/districts in the GBA are unavailable from official statistics, and hence the EDI of MeHg at the county/district level cannot be obtained directly. We referred to the EDIs of MeHg by urban and rural residents at the city level in the calculations. This assumption would result in uncertainties in the estimated EDI of MeHg at the county/district level.

2. (2)

   The processing of the gridded population data would also lead to uncertainties. For areas with extremely low population density (e.g., areas close to the coast and mountains or areas with large landscapes), their gridded population values are null. We assume that the population density of these areas is zero. Thus, ‘zeros processing’ is performed for the data with null values.

3. (3)

   For Hong Kong and Macao, their population data from official statistics are temporally discontinuous. This study uses the interpolation method to estimate the missing values for intermediate years.

We conducted 10,000 Monte Carlo simulations of the variables in the construction of the MeHg intake inventory, and the statistical distributions of the P10 and P90 values are set as the lower and upper limits of the uncertainty range. Detailed uncertainty results for the EDI of MeHg are shown in Supplementary Table 2. The uncertainties of this dataset can be reduced through three aspects. (1) Improving the statistical system of countries/districts in the GBA could reduce the data unavailability. This can avoid parts of the assumptions and related uncertainty during the calculation of the EDI of MeHg at the county/district level. (2) Improving the accuracy of the proxy gridded data (i.e., to be more consistent with official statistics) can also reduce the uncertainty of gridded dietary MeHg exposure in the GBA. (3) For the estimation of missing data in certain years, more advanced methods (e.g., machine learning and artificial intelligence) can be used to complement the interpolation method. The combination of these methods is a promising way to reduce the uncertainty of estimated data.

To evaluate the rationality of our dataset, we compare our results of dietary MeHg exposure with published data (Table 2). Liu et al.¹⁷ analyzed China’s average dietary MeHg exposure in 2011. Our result in the GBA is similar to that of Liu et al. However, the result of this study is much different from that of Shao et al.¹¹ in the Pearl River Delta. There are mainly two reasons. (1) The food scope is different. Existing studies regard rice and fish to be food sources of dietary MeHg exposure17,18. Thus, this study only considers rice and fish. Other food types in Liu et al.¹⁷ and Shao et al.¹¹ are not included. (2) The quality and sources of data are different. The data of our study and Liu et al.¹⁷ are from official statistics (CHNS with large samples) and peer reviewed literature. Shao et al.¹¹ conducted a questionnaire survey with relatively small samples. Moreover, about half of the survey areas in the study of Shao et al.¹¹ are located in fishing villages with relatively high fish consumption.