Background & Summary

Climate change and variability have a significant impact on natural and human systems1. The instrumental data are critically important for the study of the characteristics and mechanism of climate change and varilibility, and the detection and attribution of climate change signals often rely on long-term recorded instrumental data2. Moreover, the instrumental data are more representative and accurate than other meteorological data (such as reanalysis data and modeling data, etc.)3,4. However, there are many reasons causing the lack of instrumental data in early period5, such as war or fire accidents.

There are four most representative long-term observational surface air temperature datasets in global land: Global Historical Climatology Network (GHCN)-monthly (GHCNm) dataset6,7, Climatic Research Unit (CRU) dataset8,9, Goddard Institute for Space Studies (GISTEMP) dataset10,11 and Berkeley Earth Surface Temperature (BEST)12. However, all these are monthly data sets. In the analysis of climate change trends, daily surface air temperature (SAT) data are more useful than monthly air temperature data and can provide more detailed information of land SAT change including extreme temperature change13,14. The urgent need to investigate extreme weather and climate change facilitated the development of global land daily SAT datasets15,16,17,18. These datasets include the Met Office Hadley Centre climate extremes datasets HadEX19 and HadEX220, and the Global Historical Climatology Network–Daily datasets GHCND20,21 and GHCNDEX20, which were all applied widely in studies of global and regional extreme climate change. The results of the studies based on these datasets showed widespread and significant changes in the SAT extremes, with those indices derived from daily minimum temperature generally showing more significant trends over the past decades19,20.

The National Meteorological Information Center of China Meteorological Administration (CMA) assembled a set of new global land daily SAT data (GLSDT-V1.0)22,23. This dataset consists of three global daily SAT data sets, one regional daily SAT data set and five nationally exchanged daily SAT data sets22. Later, CMA and China University of Geosciences (CUG, Wuhan) improved the GLSDT dataset, by integrating other international and national datasets with a good observational coverage in a few large regions like East Asia, Europe, Australia and Canada24. The renewal dataset has been applied in analyses of global and regional land extreme SAT change24,25. In addition, CMA also developed a series of high-quality and homogenized daily SAT datasets of the time periods in China mainland since 1950s, which have been extensively used in studies of regional extreme climate change26,27,28.

However, all of the global daily SAT datasets mentioned above have relatively short time series of observation records, usually beginning from 1950s. Due to the lack of observation of early periods and century-long high-resolution daily SAT data, previous analysis has focused mainly on the past 50 or 60 years. The study of extreme temperature change in earlier period (before 1950s) is limited to a small area, including Italy, France, Norway, Britain, Australia and Japan etc29,30,31,32,33,34,35. There are also some studies on Centennial extreme temperature change in a few cities in China36,37,38,39. All of these works are of great value for the detection and attribution of extreme temperature changes over 50–60 years in the global land, and over the last more than 100 years in some areas, but the understanding of century-long extreme SAT change over the global land or a sub-continental region like China mainland is lacking.

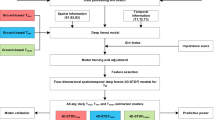
There is no complete centennial daily SAT dataset covering the whole China mainland so far, which is obviously not conducive to the detection, attribution and simulation of extreme climate change in the country in recent 100 years and plus. Therefore, this paper mainly used the early meteorological observation data of China (1840–1951) provided by the CMA and Atmospheric Circulation Reconstruction over the Earth (ACRE) regional foci (ACRE China)40,41 to develop a centennial daily SAT dataset of China. Long-term SAT series (from 1840 to 2020) of 60 major cities in China were collected, with the data recovered and digitized by ACRE China making up the data gaps in the corresponding cities and regions of China. A series of steps, such as quality control, interpolation of missing data, splicing with modern data, and homogenization, were applied to synthesize and homogenize the SAT data (Fig. 1). A century-long China homogenized daily SAT dataset (CUG-CMA CHDT)42 of 1840–2020 was finally formed.

Fig. 1
figure 1

Technical steps for the creation of the century-long China homogenized daily surface air temperature dataset (CUG-CMA CHDT).

Full size image

The homogenized CUG-CMA CHDT, which includes station and grid versions, is the first China daily SAT dataset with time period longer than 100 years. It will facilitate the monitoring and research of extreme temperature change and variability in the country, where the rapid regional climate warming and urbanization have brought about high risk to the societal and natural systems.

Methods

Data-source introduction

The early sub-daily metrological records from 1840 to 1950 and modern daily and hourly meteorological records China from 1961 to 2020 were provided by National Meteorological Information Center, CMA and ACRE China.

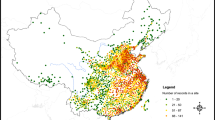
The early sub-daily temperature records came from 194 stations in 60 Chinese key cities. There are 1–9 stations in each city. The data at each station provide longitude and latitude information, data source (Table 1), temperature unit, observation time system (Table 2), regular temperature observation records, maximum temperature (Tmax) and minimum temperature (Tmin) observation records. The geographic distribution of the 194 sites is shown in Fig. 2. It can be seen that the eastern sites are relatively denser, while the western sites are sparser, which is mainly because the western region is characterized by high mountains and deserts, with sparsely settled population and underdeveloped economy and urbanization as compared to the eastern reason.

Table 1 Data code and source.
Full size table
Table 2 Observation time system.
Full size table
Fig. 2
figure 2

Geographic distribution of 60 city stations with total 194 observational sites in China mainland (Triangles of different colours represent the number of sub stations in the city).

Full size image

The early SAT data (1840–1950) are mainly from nine different sources (see Table 1). Because the observation sources are different, the corresponding observation time system and temperature unit are not the same. There are nine different observation time systems (see Table 2). In the case of codes 7, 8 and 9 in Table 2, these observation time systems need to be determined by the method introduced in section determination of observation time system, which sets the precondition for the interpolation of missing data.

The early SAT data of the stations recorded the fixed-time temperature, daily Tmax and daily Tmin. The observation period was from 1841 to 1950. The length of observation data varied from less than one year to 70 years, including 31 stations with observations less than one year, 76 stations with observations 1 to 5 years and 8 stations with observations 40 to 70 years (Table 3). The long sequence sites (40–70 years) are all distributed in central and eastern China. All observational sites have varied years of lacking data. Information of the missing data or the data integrity is shown in Table 4. There are 57 stations with no missing data (that is, Tmax and Tmin observation records exist for all the days), accounting for 29.38% of all stations, and 124 stations with data integrity reaching 80%, accounting for 63.91% of all stations. There are two sites whose data integrity is 0, that is, there are only regular time observation records, and Tmax and Tmin observation records are missing. In this case, the Tmax and Tmin observation records need to be interpolated from the fixed-time observation records by the method in Section temporal interpolation below.

Table 3 Observation time length of 194 stations (1840~1950).
Full size table
Table 4 Data integrity of Tmax and Tmin of 194 stations during observation period (1840~1950).
Full size table

Because the observation time system and temperature unit of the early data are not unified, the following assumptions were made during the data processing:

  1. (1)

    For the same city, the observation instruments and methods used for obtaining the data from the same source are consistent, that is, there is no systematic deviation in the data. For the same observation station, it is assumed that the change of longitude and latitude is caused by the relocation of the station, and the relocation station has a high stability, that is, there is no situation where the station will be moved back in a short period of time (one month).

  2. (2)

    Records with the same longitude and latitude are assumed to belong to the same observation site in the city.

The modern data of the 60 key cities provide accurate longitude and latitude information, hourly regular (fixed-time) temperature observation record, and Tmax and Tmin record. The unit of temperature data is centigrade (°C), and the observation time system is universal time (UTC – 0). Because these data are automatically observed by the instrument and are under the quality control of the CMA, the integrity and quality of the data during the observation period are guaranteed accordingly.

Data Processing Methods

Quality control

Quality control of the data was made by applying the quality-control module of RClimdex software43. The main steps of quality control are as follows:

  1. 1)

    Check whether the station longitude and latitude value exceeds the geographical range of the country. The longitude range of each station should be between 73° E and 136° E and the latitude range should be 3° N to 54° N respectively. If the station is out of range, then it is excluded. No station is out of the longitude and latitude range.

  2. 2)

    Date repeatability check. Check whether there is the same date in the same station. If so, delete the duplicate date data. A total of 208 consecutive days of data of different stations were deleted.

  3. 3)

    If the same temperature of Tmax or Tmin occurs continuously for 10 days or more, it is regarded as lack of measured value.

  4. 4)

    Internal consistency check. If the Tmin is higher than the Tmax, the Tmax and Tmin of the day are assigned as missing values. After this step of inspection, it was found that the phenomenon of Tmin higher than Tmax occurred in 634 days at 82 stations.

    Because the early data are rare, we conducted a manual inspection on the 634 days of abnormal data. We found that some of these errors are caused by the swapping of Tmax and Tmin positions, and some are caused by the fact that 3 is regarded as 8 or 8 is regarded as 3 or 2 is regarded as 3 when digitizing the early data. Then we checked the abnormal values of these abnormal days one by one, and compared them with the temperature records of the week before and after the abnormal days. Some abnormal values (606 days) were manually modified if the causes were clarified. For example, if the values of Tmax and Tmin were swapped wrongly, they were changed back to the original values; if the errors were produced in digitization of data, the temperatures was corrected according to the paper records.

  5. 5)

    Local climatological extremum check. Each weather station sets the upper and lower variation range of daily temperature in 366 days of a year according to the historical actual temperature of the station. If it exceeds this range, it will be treated as abnormal value, and will be assigned as missing values. This range is set as ±5 times of the standard deviation of the average value in the climate reference period (1961–1990). The reason for choosing 5 times standard deviation as the threshold is that 5 times standard deviation is relatively loose and will not kill real extreme values by mistake.

Determination of observation time system

The observation time system in the period before 1950 is very complex, as shown in Table 2. For the observation records with the observation time system of Code 7, 8 and 9, it is necessary to conduct a separate manual reconfirmation. In this paper, the minimum difference method is created to assist the judgment of observation time system. The essence of the minimum difference method is that, if two different observation sites in the same city are in the same time zone, the sum of squares of the difference (SSD) of the temperature values of the two stations at the same time is the smallest. This can be illustrated as follows: Assume that there are two different observation sites A1 and A2 in city A. By default, A1 shares the same observation time system with A2, so the SSD between the temperature values of A1 and A2 at regular time is smallest:

$${SSD}={\sum ({{{\bf{A}}}_{{\bf{1}}}}_{{\boldsymbol{i}}}-{{{\bf{A}}}_{{\bf{2}}}}_{{\boldsymbol{i}}})}^{{\bf{2}}}\,({\rm{i}}=1,2,3\ldots 24)$$
(1)

where \({{{\bf{A}}}_{{\bf{1}}}}_{{\boldsymbol{i}}}\) is the temperature data of i time of the station before 1950, and \({{{\bf{A}}}_{{\bf{2}}}}_{{\boldsymbol{i}}}\) is the temperature data of i time of the modern station.

For example, the observation time system of Beijing station in April 1951 is unknown. However, there are nine times of regular observations in this month, i.e., 5:00, 7:00, 9:00, 11:00, 13:00, 15:00, 17:00, 19:00 and 21:00. In order to determine the observation time system of this observation period in Beijing, we can use the existing 24-hour temperature observation records to calculate the 24-hour average temperature record in April in Beijing. Figure 3 shows the temperature comparison, with an assumption that the early SAT data of Beijing shares the same observation time system with the temperature data of modern Beijing (UTC-0). It can be seen that there is a phase difference between them. Figure 4 gives the variation of SSD with lag time. It can be seen that, when the lag time is 5 hours, the SSD is smallest. What’s more, when the early SAT data are delayed for 5 hours, the early SAT data and modern SAT data can be well overlapped (Fig. 5). Therefore, it can be determined that the time zone difference between the early station and the modern station is 5 zones. According to Fig. 4, it can be determined that the time zone of the early site is UTC-5. This method can be used to determine the time system for all stations with unknown time zone.

Fig. 3
figure 3

Comparison of temperature at Beijing station during the same period between early and modern observation sites.

Full size image
Fig. 4
figure 4

Variation of sum of squares of temperature difference between two observation sites at the same time period with lag time.

Full size image
Fig. 5
figure 5

Temperature contrast with 5 hours lag between early and modern observation sites at Beijing station.

Full size image

Determining main sequence

For the early-period SAT data (i.e., 1840–1950), the same city has multiple observation sites from different sources, so it is also necessary to determine a main sequence when merging these records. The principle of selecting the main sequence is that the sequence with the longest observation time and relatively complete records is determined as the main sequence. Then the subsequence from other observation sites is merged into the main sequence by interpolation method illustrated in Section temporal interpolation to form the final station sequence of the city.

Temporal Interpolation

Ridge regression

Ridge regression is a regularization method most often used in regression analysis dealing with ill-posed problem44. This method is applied to solve the problem of failure of least squares estimation under multicollinearity. Ridge regression is a supplement to the least square regression. It loses unbiasedness in exchange for high numerical stability, and thus obtain higher calculation accuracy45. Usually, the R-squared value of ridge regression equation is slightly lower than that of ordinary regression analysis, but the significance of regression coefficient is often significantly higher than that of ordinary regression, having greater practicability in dealing with collinearity problems and pathological data46.

Ordinary least squares commonly used in regression analysis is an unbiased estimation. For a well posed problem, X is usually full rank.

$$X\theta =y$$
(2)

Using the ordinary least square method, the loss function is defined as the square of residual error, and the minimize loss function is:

$${||{X}\theta -{y}||}^{2}$$
(3)

The above optimization problems can be solved by gradient descent method or directly by the following formula:

$$\theta ={\left({X}^{T}X\right)}^{-1}{X}^{T}y$$
(4)

When X is not the full rank of a column, the determinant of \({X}^{T}X\) is close to 0. Then the above problem becomes an ill posed problem, in which using the traditional least square method lacks stability and reliability.

In order to solve the problem, there is a need to transform the ill posed problem into a well posed problem. This can be done by adding a regularization term to the loss function and changing it into a well posed problem:

$${||{X}\theta -{y}||}^{2}+{||\tau \theta ||}^{2}$$
(5)

Among them, define \(\tau =\alpha I\), so that

$$\theta \left(\alpha \right)={({X}^{T}X+\alpha I)}^{-1}{X}^{T}y$$
(6)

In the above formula, I is the identity matrix.

Procedure of temporal interpolation

After quality control, unit conversion (Fahrenheit unified into degree Celsius), and observation time system conversion (unified as UTC-8), a new dataset was obtained. However, there are still many situations in this basic dataset, such as missing data of Tmax and Tmin. Totally, 137 stations have missing data, 57 stations do not have missing data, and the missing rate of stations reaches 70.62%. Because the early daily SAT data are very precious, it is necessary to make most use of all the data. In this case, we need to interpolate these missing data of Tmax and Tmin. The ridge regression model is mainly used here, and the idea of the method refers to Ren et al.38.

Considering the following example. When the fixed-time record of an early observation site A in a city is m, n, j, but the Tmax and Tmin data of the site are not measured, the nearest modern station B (within 3 km between A and B) can be determined. At this time, assuming that, station A and B belong to the same micro climate region, and they share the same temperature distribution characteristics. The relationship between temperature data in m, n, j time and Tmax, Tmin can be derived from the temperature data of B station from 1961 to 1978. The data from 1961 to 1978 were selected because China started reform and opening up policy in 1978, and in order to avoid the impact of regional to local socio-economic activities on climate, the data after 1978 were not selected. In particular, the usage of the data before 1978 can effectively avoid the impact of urbanization on SAT observations as much as possible, and keep good consistency with the early temperature data, which can further improve the fitting effect of the model. Thus, Tmax and Tmin data of station A can be interpolated.

The specific procedure is as follows: the temperature data of site B from 1961 to 1978 includes hourly temperature data (i.e., 24-hour temperature data) and Tmax and Tmin, as well as Tm, Tn, Tj corresponding to those recorded at site A. Because the temperature change has obvious seasonality, in order to make the regression model more reasonable, the data of site B was divided into 12 months, and the relationship between Tmax, Tmin and Tm, Tn, Tj of each month was trained by using ridge regression model. The steps were as follows: the 12-month temperature data (Tmax, Tmin, Tm, Tn, Tj) were divided into training set and verification set according to the ratio of 7:3. Python language and machine learning was used to get the relationship between Tmax (Tmin) and Tm, Tn, Tj in each month. The optimal learning model of each month in different cities was determined by setting different random seeds (0.001~1000). Then the obtained model expression was substituted into the early data of the missing extreme value data, and the interpolation of the early missing extreme value data can be completed.

$${T{\max }}_{{Bi}}={a}_{i}{{Tm}}_{{Bi}}+{b}_{i}{{Tn}}_{{Bi}}+{c}_{i}{{Tj}}_{{Bi}}+{D}_{i}\,({\rm{i}}=1,2,\ldots 12)$$
(7)
$${T{\min }}_{{Bi}}={{aa}}_{i}{{Tm}}_{{Bi}}+{{bb}}_{i}{{Tn}}_{{Bi}}+{{cc}}_{i}{{Tj}}_{{Bi}}+{{DD}}_{i}\,({\rm{i}}=1,2,\ldots 12)$$
(8)

where \({T{\max }}_{{Bi}}\) and \({T{\min }}_{{Bi}}\) are the maximum and minimum temperature of site B in the i month, respectively. \({{Tm}}_{{Bi}}\), \({{Tn}}_{{Bi}}\) and \({{Tj}}_{{Bi}}\) are the temperature value at m, n, j time of site B in the i month respectively. ai, bi, ci, Di, aai, bbi, cci and DDi are the regression coefficients.

Using the 12-month relationship obtained in site B, we can get the missing value of Tmax and Tmin of site A.

After time interpolation, 64477 days of data of 60 cities are interpolated. The specific interpolation days of each city are shown in Table 5. It can be seen from Table 5 that Xujiahui Station has the largest number of temporal interpolation days, 21594 days, followed by Beijing Station, 10091 days. Shijiazhuang Station has no data requiring temporal interpolation. There are 10 stations with more than 1000 days of temporal interpolation.

Table 5 Statistics of days of temporal interpolation and data merge of 60 cities.
Full size table

Splicing data sequences from different sites

After the temporal interpolation, Tmax and Tmin data were obtained. On this basis splicing of data can be performed, which was mainly to concatenate the data from different secondary sites onto the main sequence. This can also be called data merge. The merge was mainly divided into the following two steps.

Data merge (a)

There are 194 observation sites in the 60 cities, and each city has 1–9 sites or sub-stations. The data of the sub-stations need to be spliced onto the data series of main stations of the corresponding cities, so as to obtain the relatively long and complete temperature series of the city.

Beijing was taken as an example. There are six observation sites in Beijing: 2900101, 2900102, 2900103, 2900107, 2900108 and 2900109. The details of each site are shown in Table 6 and Fig. 6.

Table 6 The information of 6 observation sites of Beijing.
Full size table
Fig. 6
figure 6

Observation period of temperature data at various sub-stations in Beijing.

Full size image

Figure 6 shows that the observation period of temperature series at sub-station 2900102 is the longest and relatively continuous. Therefore, the sequence of 2900102 was set as the main sequence of the city, and the data from other five sub-stations were spliced onto the main sequence in turn. The interpolation can be classified into two categories: 1) data merge with intersecting observation period of main sequence (data merge (a)); 2) data merge without intersecting with the observation period of the main sequence (data merge (b)). The two methods are different.

Data merge (a) is mainly to pick out the overlapped part of the two observation periods separately, assuming that the overlapping part length is n days. The data of main sequence coincidence part is MS, and that of sub sequence coincidence part is SS. Then, n days were divided into training set and test set according to the ratio of 4:1 and the relationship between MS and SS was obtained by using following formula:

$${\rm{MS}}={\rm{aSS}}+{\rm{b}}$$
(9)

Using the relation obtained, the data of the observation period in which the sub sequence and the main sequence are not overlapped were interpolated into the main sequence.

For data merge (b), another method was used for interpolation. The idea is similar to temporal interpolation and needs to be conducted month by month.

Taking sub-station 2900101 as an example, the modern stations A and B are closest to site 2900101 and site 2900102 (main sequence station) in 2400 automatic station. In principle, the linear distance between site 2900101 (2000102) and station A (B) should not exceed 3 km, so as to ensure that A (B) station and site 2900101 (2900102) station are in the same climate zone and have the same temperature characteristics. This paper used the data of modern sites A and B from 1961 to 1978 to characterize the temporal patterns of the early observation site 2900101 (2900102). The years of 1961–1978 were chosen to avoid the possible urbanization effect on SAT variation after the reform and open up of the country.

For Tmax, for example, the daily data of stations A and B from 1961 to 1978 were divided into 12 months. For each month, the model was trained according to the ratio of training set: verification set = 4:1, and the relationship between A and B in each month was obtained by formula:

$${{\rm{T}}\max }_{{\rm{Bi}}}={{\rm{m}}}_{{\rm{i}}}{{\rm{T}}\max }_{{\rm{Ai}}}+{{\rm{n}}}_{{\rm{i}}}\,({\rm{i}}=1,2,3\ldots 12)$$
(10)

where TmaxBi and TmaxAi are the maximum temperature for the i month at site B and site A, respectively, and mi and ni are the regression coefficients of the i month.

The relationship between station A and B was directly applied to the early observation sites.

$${{\rm{T}}\max }_{2900102{\rm{i}}}={{\rm{m}}}_{{\rm{i}}}{{\rm{T}}\max }_{2900101{\rm{i}}}+{{\rm{n}}}_{{\rm{i}}}\,({\rm{i}}=1,2,3\ldots 12)$$
(11)

where Tmax2900102i and Tmax2900101i are the maximum temperature for the i month at site 2900102 and site 2900101, respectively, and mi and ni are the regression coefficients of the i month. After the process, Tmax of site 2900101 can be concatenated onto the main sequence (site 2900102).

The same method could be made for Tmin. The procedure used for other cities was the same as that of Beijing.

The statistics of the days of the two types of spatial interpolation (data merge (a) and data merge (b)) are shown in Table 5. There are 14 urban stations with data merge (a)and 39 urban stations with data merge (b). In data merge (a), 4 stations have less than 1000 interpolation days, and 11 stations have less than 1000 interpolation days in data merge (b).

Data merge (b)

After completing the interpolation in section temporal interpolation, the daily SAT dataset of 60 key cities is preliminarily obtained. However, the temperature series of some cities in 1840~1950 is not complete enough, and there is a few areas where the observation stations are relatively denser than in other areas. In order to obtain a more even spatial distribution and a better temporal continuity and completeness of the data series, it is necessary to further merge the stations in the 60 cities to obtain a set of new station temperature data with longer time series and higher integrity.

The method for merging the data between cities is the same as shown in section data merge (a). The two cities having cross-time segment would be picked out for building model, according to the ratio of 4:1 (training set: test set). The principle is that the difference between longitude and latitude of the two cities is less than 2.5 ° and they are in the same climate zone, which can ensure the model has higher reliability. After interpolation, the data of the original 60 cities were interpolated into the dataset of 45 cities. The station list of cities changed in the interpolation is shown in Table 7.

Table 7 Station list of cities involved in interpolation.
Full size table

The spatial distribution of urban sites after the data merging procedure is shown in the Fig. 7. It can be seen that most of the major urban sites in China are retained. The urban sites are representative and relatively evenly distributed across the country, except for the western and northeast regions, where there are large area and sparse population, and the distribution of urban stations is relatively sparse.

Fig. 7
figure 7

The ___location distribution of 45 key city stations and the length of their temperature series.

Full size image

The spliced days of the 11 retained cities are shown in Table 8. After this step of interpolation, the 11 cities have obtained the longest early series on the basis of the existing instrumental data.

Table 8 Statistics of spliced days of 11 cities.
Full size table

Merging the data

Since the early SAT data were recorded from 1840 to 1950, it is necessary to supplement the modern SAT data. The splicing principle is proximity: the nearest modern observation station was chosen according to the longitude and latitude of the early main sequence stations. Then the SAT data of modern station is directly added into the early SAT data. Figure 7 also shows the the length of their temperature series of the 45 key city stations after merging. There are 20 stations with observation record more than one hundred year, which includes Beijing (143 years, data integrity: 78%), Xujiahui (or Shanghai, 135 years, data integrity: 93%), Xiamen (133 years, data integrity: 97%) Beihai (132 years, data integrity: 93%), Wuhan (131 years, data integrity: 90%), Shapingba (or Chongqing, 130 years, data integrity: 99%), Wenzhou (130 years, data integrity: 93%), Jiujiang (129 years, data integrity: 94%), Yantai (127 years, data integrity: 93%), Yichang (125 years, data integrity: 90%), Nanjing (122 years, data integrity: 87%), Shantou (122 years, data integrity: 85%), Hangzhou (118 years, data integrity: 83%) and Hengyang (108 years, data integrity: 96%), Tanggu (or Tianjin, 105 years, data integrity: 93%), Haikou (103 years, data integrity: 94%), Dalian (102 years, data integrity: 89%), Shenyang (101 years, data integrity: 88%), Qinghuangdao (100 years, data integrity: 87%) and Qingdao (100 years, data integrity: 82%). The length of temperature observation sequence of 17 stations is between 80 and 100 years. The sequence length of the remaining seven sites is between 68 and 80 years. It can be seen that the centennial sequence stations are mainly distributed in East China, central China and North China. The main reason is that the economic development of these regions was relatively good and the population was relatively large, so the early-period observation was relatively perfect compared with other regions.

Homogenization of the data

The RHtestV4 software developed by Wang and Feng47 was used to test and correct the inhomogeneity of the daily SAT data at the 45 stations. The software can test and correct the discontinuous points of daily SAT series at the target stations with or without reference series. However, the lack of reference series will reduce the reliability of the detection results. Therefore, in the process of inhomogeneity detection and correction, high-quality reference series was constructed for each of the target station series. The data of the reference series are from Berkeley earth merged dataset – version 2 dataset12, which is a set of multi-source fusion data by integrating more than ten sets of temperature data such as Global Historical Climate Network (GHCN), US Historical Climate Network (USHCN), Hadley Centre / Climate Research Unit Data Collection (CRU), etc. The length of the temperature series is relatively long, and the earliest observation year of the East Asian series started from 1853, which can better meet the observation length requirements of the reference series.

The following methods and steps were used to test and determine the reference series: firstly, taking the target station as the center, select the reference stations within the radius of 500 km, and ensure that the altitude difference between the reference station and the target station is less than 200 m. Then, the correlation coefficient between the first-order target series and the first-order reference sequence was calculated, and the reference series with correlation coefficient >0.8 were selected. Because RHtest uses only one reference series to test the heterogeneity of the target sequence, obvious breakpoint in the reference series is likely to introduce additional inhomogeneity to the target series in the detection process. Therefore, the homogeneity of the selected reference series should be preliminarily tested. To avoid too complex process and the cost of overlong computation time, the reference series were tested without reference or metadata (documents that record historical information such as station movements, thermometer replacements, environmental changes, etc). In this way, reference series that contain significant breakpoints were discarded, and the average of multiple homogeneous reference series was used to test the homogeneity of target series.

Insufficient reference series may not help to achieve the purpose of eliminating the potential breakpoints, but too many reference series may lead to too smooth series and lose the original local climatic variability in turn. Through experiments and referring to previous studies48,49, we considered that the number of reference series between 3 and 5 was applicable for inhomogeneity testing. Also, the reference series must overlap the target series in length for at least 50% of the target ones. When qualified reference series are less than 3, the testing was carried out without reference series.

The square of correlation coefficients between reference and target series were taken as the weights to form averaged reference series by using the weighted average method. After which, the homogeneity of the averaged reference series will be tested again and the inhomogeneous ones were discarded, then the inhomogeneity test of the corresponding target series was carried out using no reference series. For all of the tests, the confidence level was set to 99.99% to ensure the recognized breakpoints were the most significant ones.

As shown in Table 9, Tmax and Tmin sequences of the 45 stations in China can be basically matched with homogeneous reference sequences.

Table 9 Construction of reference sequence and its heterogeneity test.
Full size table

The detection was first conducted to the monthly data which were converted from daily ones, then, the quintile matching (QM) method13 was used to adjust the daily temperature data according to the detection results. In order to reduce the uncertainty during the adjustment as much as possible, and avoid the adjustment of too many unnecessary breakpoints (which may result from the local climatic variabilities, rather than the non-climatic factors), the adjustment values of the breakpoints were limited: the averages of the daily highest Tmax and lowest Tmin in each year of the target station series were taken as the upper and lower bounds of the threshold; if the absolute values of the adjustments were less than 1/20 of the difference between the upper and lower thresholds, the breakpoints were not adjusted (only for those not supported by metadata), and the original characteristics of the series were retained to avoid falsely adjustments of possible weather and climatic variabilities.

Since the constructed reference sequence may not completely cover the observation period of the target series, parts of the series beyond the reference coverage have not been tested. Therefore, a second detection for the target series was carried out with no reference series involved, but only the breakpoints beyond the coverage will be adjusted.

Taking Fuzhou Station as an example to demonstrate the effect of homogenization correction. Figure 8 shows the time series of Fuzhou Station before and after correction, as well as the correction curve of each series. It is obvious that the abrupt change points of the Tmax and the Tmin at Fuzhou Station were in 1937, and the average correction values were about –2.4 °C and –1.8 °C, respectively. The correction made the early sequence segments of Fuzhou Station move down as a whole, correcting the abnormal high temperature phenomenon in the early period.

Fig. 8
figure 8

Comparison of daily air temperature series of Fuzhou Station before and after correction.

Full size image

Totally, there are 45 stations, 33 Tmax data series, 38 Tmin data series, 66 breakpoints of the Tmax data series and 86 breakpoints of the Tmin data series, undergoing adjustments in the process of homogenization (Fig. 9). The stations with large number of adjustments include Xujiahui, Beijing, Tangshan, and Nanjing, and stations with less adjustments include Yinchuan, Lanzhou, and Jiujiang, etc. Figure 10 shows the frequency distribution of the adjustment values for Tmax and Tmin at all the adjusted stations. More than 60% adjustment values for Tmax (Tmin) are concentrated between −1.5 °C (−1.8 °C) and + 0.7 °C ( + 0.9 °C). The negative adjustments are more frequent than the positive ones, which is consistent with the works conducted for homogenization of monthly mean SAT data in China50,51. This occurs because the relocations (changes) of stations in China, in both the modern time and the early period of instrumental observations, were usually characterized by the moves from urban areas to rural areas, leading to an abrupt rise in temperature after the changes52,53.

Fig. 9
figure 9

Numbers of the adjustments for stations, SAT series and all breakpoints in data homogenization.

Full size image
Fig. 10
figure 10

Frequency distribution of the adjustment values for daily Tmax and Tmin homogenization at all the 45 stations.

Full size image

Grading the data with ADW method

After the homogenization of the SAT data, the first daily SAT dataset of time period 1840–2020 at 45 stations of China had been established. The dataset was developed jointly by the researcher of CUG(Wuhan) and CMA, and it was named as CUG-CMA China Historical Daily surface air Temperature Dataset (CUG-CMA CHDT). The homogenized SAT data were interpolated to grids using the Angular Distance Weighting (ADW) method54. The grid data can be more conveniently applied in studies and regional climatology and climate change. ADW method is widely used because it is more flexible than other methods when dealing with irregular station data55, and compared with other methods, it has higher computational efficiency while the interpolation error are similar56.

A fixed correlation decay distance (CDD) of 1000 km of ADW method was adopted in this study. The specific steps are as follows:

  1. 1)

    Defining a correlation function57:

    $$r={e}^{\frac{-x}{{x}_{0}}}$$
    (12)

    where X is the distance from the station to the center of the corresponding grid point, and X0 is CDD, i.e., 1000 km.

  2. 2)

    Define distance weight:

    $${w}_{i}={r}^{m}$$
    (13)

    It is found that the RMSE of cross validation decreases with the increase of m; but when m is 4, it provides a reasonable trade-off between reducing error and reducing spatial smoothing, while allowing more distant stations to influence the grid value.

  3. 3)

    Defining the weight of combination angle distance55:

    $${W}_{i}={w}_{i}\left\{1,+,\frac{\sum _{k}{w}_{k\lceil 1-\cos ({\theta }_{k}-{\theta }_{i})\rceil }}{\sum _{k}{w}_{k}}\right\},\,{\rm{i}}\ne k$$
    (14)

We have made an detailed introduction to the relevant ADW program and have shared it on the webpage. (https://cran.r-project.org/web/packages/adw/vignettes/Introduction.html). The gridding accuracy was set as 2.5° × 2.5°. The reason for choosing this precision is that the number of sites in the dataset is relatively small, and choosing a finer precision may lead to poor gridding effect. In addition, the numerical simulation work for exploring the trend of extreme temperatures in China over the past century will use a model with the accuracy of 2.5° × 2.5°, and this is also an important reason for choosing this accuracy. In the process of gridding, only when there are stations within a distance of 2.5 grid point near the center of the grid point and the number of stations is greater than 3, will the station data be gridded into that grid point. Therefore, due to the sparsity of stations in the western region and the lack of data, the quality of the results in the western region of China are far behind those of the eastern region.

Data Records

The dataset is available at Figshare42. External users could apply to CMA to gain access to the aft-1950 data of the 45 stations used in this paper at website https://data.cma.cn/, and could contact the corresponding authors to obtain the before-1951 data of the 45 stations.

Technical Validation

Cross-validation of interpolation methods

In order to be rigorous and to verify the credibility of the regression model, several cases assessment were conducted. However, due to the length limitation of the article, only one individual example (Chengdu case) is shown here. Chengdu station was taken as an example (Fig. 11). Taking the cross period data of two early observation sites in Chengdu as the prototype, the cross period data was divided into 7:3. Because these extreme temperature data are all known, the 0.3 part could be regarded as unknown, and we then could compare the predicted value and actual value obtained by the regression model to check the prediction effect of the model. As can be seen from Fig. 13, the difference between the predicted value and the actual value is not large. The sample size tested is 335. The mean square error (MSE) of the Tmax value is 1.86, the root mean squared error (RMSE) is 1.36, the mean absolute error (MAE) is 0.94, and the correlation coefficient between the predicted and actual values is 0.989, which has passed the confidence level test at 99.99%; The MSE of the Tmin value was 1.20, RMSE was 1.10, MAE was 0.73, the correlation coefficient between the predicted and actual values was 0.988, which passed the confidence level test at 99.99%. Therefore, the reliability of the interpolation results is very high and convincing. It is worth noting that the temperature forecast on some days is different, mainly because it is a pure mathematical model that does not fully consider other weather factors affecting Tmax and Tmin.

Fig. 11
figure 11

Comparison between predicted and actual temperature values of Chengdu Station.

Full size image

In addition to the Chengdu station, we also verified 5 other stations (see Table 10). In order to avoid lengthy articles, the relevant figures were not included in the main text, but the error statistics results are shown in Table 10. From Table 10, it can be seen that the sample size of the six sample sites ranges from 335–1594 days, but the interpolation error statistics are relatively small and within a reasonable range. Therefore, it can be seen that the interpolation method of ridge regression is reliable.

Table 10 Error statistics and sample size for all six sites.
Full size table

Comparison to other data

There had been no high-resolution and century-long station SAT dataset of China, and it is impossible to make a comparison of the data with other station data. However, a comparison of the data with Climatic research unit (CRU) grid temperature dataset and Berkeley dataset was made, to check their consistency.

The CRU dataset and Berkeley dataset are two of the most widely used global land SAT datasets at present. They provide the global monthly data with 0.5 ° grid resolution covering the land surface from 1901 to 2020. Although they included errors in regions like western China caused by interpolation, they can still be used as an approximate reference with certain reliability. Because the CRU dataset and Berkeley dataset are a monthly grid dataset, it is necessary to change the daily value of the CUG-CMA CHDT data to the monthly value for comparison, and to transform the CRU data to station data. Because the Berkeley dataset downloaded did not provide Tmax and Tmin data, only provide Tave data, then a comparative analysis of the Tave sequences of the three datasets was conducted (Fig. 12). From Fig. 12(a), it can be seen that the overall trend of the Tave sequences for the three datasets is consistent, showing an upward trend. The CUG-CMA dataset had smaller values compared to the Berkeley and CRU datasets in the early stages (1900–1940), and there was little overall difference in values among the three datasets from 1940–2000. However, the CUG-CMA dataset had larger values compared to the Berkeley and CRU datasets from 2000–2020. From Fig. 12(b) and (c), it can be seen that the difference between the CUG-CMA dataset and the Berkeley dataset is 0.05 °C per decade, and the difference with the CRU dataset is 0.03 °C per decade. When compared with the Berkeley dataset, negative anomalies were predominant from 1900 to 1960, and positive anomalies were predominant from 1960 to 2020. The same phenomenon was observed when compared with the CRU dataset. Overall, the Tave sequence of the CUG-CMA dataset is still more extreme compared to the Berkeley and CRU datasets, as evidenced by lower temperature values in the early stages and higher temperature values in 2020. The larger trend of annual mean temperature in the CUG-CMA dataset may have been caused by the homogenization of the data series. According to previous studies, homogenization process would induce a recovered urbanization effect in the temperature data series in case of station relocation from urban to rural areas53,58.

Fig. 12
figure 12

A comparison of the CUG-CMA CHDT with the CRU and Berkeley temperature datasets. Shown are the difference series of annual mean temperature between the CUG-CMA CHDT and the CRU/Berkeley datasets.

Full size image

The above result is from a comparison based on the grid data (Tave). To further assess the difference of the datasets, extreme temperature data (Tmax and Tmin) from the CRU dataset were extracted and compared with the CUG-CMA dataset on a basis of station observations. Because the CUG-CMA dataset is a daily dataset, while the CRU dataset is a monthly dataset. Therefore, we need to convert the CUG-CMA dataset into monthly data for comparison. The specific method is to calculate the average temperature value for each month, but if there are 7 or more missing measurements recorded each month, they will be recorded as missing measurements for that month. Because the accuracy of the CRU dataset is 0.5° × 0.5°, which is fine enough, we only need to determine the corresponding grid point in the CRU dataset based on the longitude and latitude of the target site in the CUG-CMA dataset, and then extract the data of that grid point and compare it with the monthly data of the converted CUG-CMA dataset. Here shown are the correlation of SAT series between the two datasets at four city stations with the longest SAT time series: Beijing (CN00003, 143 years), Xiamen (CN00004, 133 years), Xujiahui (CN00028, 135 years) and Beihai (CN00039, 132 years) (Fig. 13). The correlations between the four longest SAT sequences in the CUG-CMA CHDT and the CRU data at the city stations are all very good for both Tmax and Tmin. What’s more, the RMSE and MAE values of the four city stations are relatively small, indicating that the difference between the two datasets is not significant.

Fig. 13
figure 13

Comparison of CUG-CMA CHDT dataset and CRU dataset at four city stations and their correlation coefficients (cor) 、 RMSE and MAE result. All of the correlations are statistically significant at the 99% confidence level.

Full size image

In summary, whether it is the comparison of grid data or site data, the CUG-CMA dataset is not significantly different from other datasets, proving the consistency of the CUG-CMA dataset with the currently used datasets in China.

Dataset evaluation

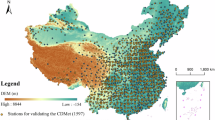
We evaluated the dataset using crossing validation to estimate the errors associated with ADW method. This involved removing each station from the dataset, and then using the ADW interpolation technique to estimate the temperature anomaly time series for that station using data from the surrounding stations. We compute RMS errors on the basis of the differences between the actual station time series and the interpolated station time series. The results (Fig. 14) show that, on average, the RMS errors are around 2.31 °C for Tmax and 1.86 °C for Tmin. Errors are typically larger for Tmax than for Tmin, which passed the 95% significance test. This may be because the variance of the Tmax is larger than that of the Tmin, so interpolation results in the RMSE of Tmax being higher than that of Tmin. Overall, the variance error between the Tmax and Tmin is the smallest in the east and the largest in the west. Overall, the variance error between the highest and lowest temperatures is the smallest in the east and the largest in the west. It is worth noting that interpolation was not successful in the two western sites (Urumqi and Lasa site) because there were not enough stations within a limited range nearby for interpolation.

Fig. 14
figure 14

Cross-validated annual average station interpolation RMSE for the 1900–2020 period for variance error of (a) Tmax and (b) Tmin.

Full size image

Overall, the grid data error obtained using the ADW interpolation method is within a controllable range, and the grid products are reliable.