Background & Summary

Large-scale, long-term datasets of precipitation and temperature are crucial for understanding the global environmental system1. Additionally, climate change dictates adaptation planning, requiring robust future-climate datasets. Especially for Canada, climate change poses great risks to the ecosystem, society, and economy2. Canada’s mean annual temperature has increased by around 1.7 °C over the past few decades, roughly double the average global rate3,4. This change has caused local and regional alterations in hydroclimatic variables. Hence, the country’s infrastructure sustainability, coastal communities, human health, and ecosystems are high-risk aspects for the future, especially in northern regions4. For example, current approaches for the design and rehabilitation of Canada’s infrastructure are based on historical hydroclimatic data, ignoring future changes5. Changes in the agricultural sector have been recorded, expecting amplification due to warming6. These fields and other aspects, including the assessment of future flooding impacts in Canada7, require high-resolution datasets of future projections. Therefore, it is crucial to acquire knowledge on future climatic conditions through reliable datasets to propose and plan adaptation/mitigation strategies or to change policies8.

Global Climate Models (GCMs) provide future climate simulations under different emission scenarios. The latest Coupled Model Intercomparison Project Phase 6, CMIP69, offers the largest number of simulations and the highest spatial resolution, using an advanced set of emission scenarios compared to its predecessors (e.g., CMIP5, CMIP3)8,10. However, GCM spatial resolutions are relatively coarse for local applications and still have biases at regional scales2. Therefore, downscaling and/or bias-correction techniques are required for developing, proposing, or planning any strategies at local scales. Additionally, a robust climate change assessment requires an ensemble with a high number of simulations per model11. Recent literature has emphasized these needs and has proposed datasets and approaches to fill this gap2,12,13,14.

Few studies, however, have produced global or pan-Canadian CMIP6 (or CMIP5) fine-scale spatial simulations, and most of them have a low temporal resolution (i.e., monthly). For example, Mahony et al.11 selected an eight-model ensemble from CMIP6 to downscale monthly climate normals in North America at the spatial resolution of ~1 km. At the same resolution, Navarro-Racines et al.12 developed a global dataset of monthly maximum and minimum temperatures and total precipitation for 35 CMIP5 models. At the daily scale, Noël et al.15 provided a global dataset of temperature and precipitation from five CMIP6 models at 0.1° × 0.1° spatial resolution. Other studies offered fine-resolution CMIP6 or CMIP5 projections for countries other than Canada (e.g., Europe16, Japan17, Norway18). The Government of Canada offers publicly available datasets of daily temperature and precipitation using CMIP5 and CMIP6 models at 10 km resolution19 (CanDCS-U6 and CanDCS-M6: Canadian Downscaled Climate Scenarios–Univariate or Multivariate, respectively, method from CMIP6). However, these do not include simulations from all available CMIP6 models (26 models used for downscaling), utilize one realization per model (two in one case), and are driven by only three different emission scenarios (i.e., SSP1-2.6, SSP2-4.5, and SSP5-8.5). Similarly, the recent “Ensemble de Simulations Post-traitées d’Ouranos” ESPO-G6-R2 v1.0 dataset20,21 comprises 14 models, with one realization-member for each, driven by only two emissions scenarios (SSP2-4.5 and SSP3-7.0). However, utilizing all members of a given model for bias-adjusted simulations improves the accuracy of projections by capturing internal variability, quantifying uncertainty, and providing a more realistic understanding of potential future climate scenarios, including extremes. CMIP6 simulations from all models, realizations, and SSPs are essential for more comprehensive and reliable climate projections, supporting informed decision-making on adaptation and mitigation strategies in regions like Canada.

To our knowledge, there is no published dataset of future climate projections for Canada that combines the majority of CMIP6 simulations with a fine spatial resolution of 0.1° × 0.1° (11.1 km) for daily precipitation and temperature. To address this, we produce pan-Canadian, fine-scale projections of temperature and precipitation, using several climate models and corresponding ensemble members of CMIP6. Specifically, according to the available CMIP6 simulations at the time of the study, we use 581 simulations from 27 GCMs for temperature and 693 simulations from 34 models for precipitation, under four Shared Socio-economic Pathways (SSPs, SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5). We excluded the models (HadGEM, KACE, and UKESM) that employ a calendar year of 360 days (assuming all months have 30 days) to avoid invalid or missing dates. We utilize the Ensemble Meteorological Dataset for North America (EMDNA) as the reference observational dataset with a fine spatial resolution of 0.1°22. We bias-correct the CMIP6 series with a semi-parametric approach to avoid (1) the assumption that observations and projections follow the same distribution (i.e., parametric approach), and (2) the high dependency on observational data (i.e., non-parametric approach). The novel Semi-Parametric Quantile Mapping (SPQM)23,24 preserves the wet/dry spells by maintaining the monthly probability of dry. We deem that SPQM-CMIP6-CAN25 will be a valuable dataset for hydrometeorological and interdisciplinary studies, allowing for the assessment of climate change impacts and the application of mitigation strategies at local, regional, and pan-Canadian scales.

Methods

Study area

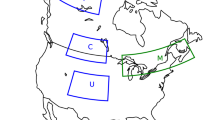
Canada, as a vast country, encompasses various climate types (Fig. 1), classified by the Government of Canada as follows: Arctic Mountains and Fiords, Arctic Tundra, Atlantic Canada, Great Lakes, Mackenzie District, North British Columbia Mountains, Northeastern Forest, Northwestern Forest, Pacific coast, Prairies, and South British Columbia Mountains26,27. As a result, Canada has a wide range of climate conditions, with the Prairies having extreme climate variability (cold winters and warm summers) and the Pacific and Atlantic coasts having milder climates compared to the rest. Regional climates are notably shaped by dominant westerly winds, humid air influx from the Gulf of Mexico, cold and dry air intrusion from the Arctic, and the intricate interplay between the Great Lakes and the lower atmosphere. The average total annual precipitation is 596 mm, and the average temperature is −5.82 °C. The region is divided into 9 zones to improve computational efficiency, as shown by the grey lines in Fig. 1. These zones are selected based on the number of grids within each zone, to ensure that the memory and time required for bias-correcting each simulation (one realization of one climate model in a specific zone) do not exceed 60 GB of memory and 3 hours of runtime on the supercomputer.

Fig. 1
figure 1

Climate zones across Canada and the regions used to organize the bias-corrected dataset.

Full size image

Dataset

We considered the Ensemble Meteorological Dataset for North America (EMDNA22,28) data (1979–2014) as a reference for quantile mapping (QM) of the climate model simulations. The EMDNA dataset extends until 2018. However, we selected the years up until 2014 to match the starting year (2015) of CMIP6 projections. The EMDNA data are at the daily scale and have a spatial resolution of 0.1° × 0.1°22. The dataset is composed of a blend of station observations and reanalysis model outputs. The station data are provided by a serially complete dataset for North America (SCDNA); they have been thoroughly quality-checked, and missing values were imputed by data providers using a robust series of methods, including QM, and machine learning. The three reanalysis products used, include the fifth generation of European Centre for Medium-Range Weather Forecasts (ECMWF) atmospheric reanalyses of the global climate (ERA529), the Modern-Era Retrospective analysis for Research and Applications, Version 2 (MERRA-230), and the Japanese 55-year reanalysis (JRA-5531). The reanalysis products were regridded, corrected, and merged using Bayesian model averaging. Station and reanalysis data were merged with Optimal Interpolation (OI). While this dataset is a composite of station and reanalysis datasets, we refer to it as “observations” throughout this paper. This terminology is adopted because the dataset’s development specifically represents observational data.

All climate models and corresponding ensemble members available during our analysis were considered for the Tier-1 Shared Socio-economic Pathways (SSPs), SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5 for the period of 2015–2100. The first number on the SSP label represents a specific SSP that describes developments of society and policies in the absence of climate change, and the second number describes effective radiative forcing in watts per square meter (W/m²) by 2100 globally32. We considered a total of 581 simulations corresponding to 27 models for temperature and 693 simulations corresponding to 34 models for precipitation. Details of climate models, their original resolutions, and the number of simulations considered per model are given in Table 1. All the simulations were regridded to 0.1° × 0.1° resolution prior to the bias correction, following the EMDNA grid, using the bilinear interpolation remapping technique.

Table 1 Number of simulations for precipitation (and temperature) for each climate model and scenario.
Full size table

Bias correction technique

We used the SPQM method to bias-correct the temperature and precipitation simulations23,24. In contrast to conventional methods that typically maintain the proportional shifts between projections and historical simulations while aligning projections with the observed marginal distribution33,34,35, SPQM method uses a parametric distribution fitted to the reference dataset to guide the mapping of the empirical quantiles of projections. At each grid point, the daily data are quantile mapped on a monthly basis to consider the seasonal variability. To preserve the climate change signal, we detrended the simulations before bias correction from the whole time series. Therefore, the detrended simulations and observations have the same marginal distribution (i.e., the QM process is not affected by trends in the simulations). After applying the SPQM technique, we added the trend back to the bias-corrected time series to preserve the signal of non-stationarity in CMIP6 projections. Removing the linear trends before quantile mapping and adding them back to the output showed a considerable improvement compared to the basic quantile mapping techniques33.

For a specific grid point, the steps to perform SPQM are:

  1. 1.

    Fit a parametric distribution to the observations: Gamma distribution for non-zero precipitation values (analytically using the method of moments) and Skew-normal distribution for temperature (numerically using the method of maximum likelihood).

  2. 2.

    Remove the linear trend in simulations. For precipitation, detrending is performed by standardizing the projections such that they are divided by the linear trendline magnitudes at each time step. For temperature, detrending is applied by subtracting the trendline mean at each time step.

  3. 3.

    Estimate empirical non-exceedance probabilities for detrended, standardized simulations using the Weibull position formula.

  4. 4.

    Apply the quantile mapping technique by inputting the empirical probabilities of simulations into the fitted quantile function of observations, aligning simulated data with observed data’s statistical characteristics.

  5. 5.

    Reinsert simulation trends into the bias-corrected time series to reflect non-stationarity in CMIP6 projections. For precipitation, the trend is given back to the simulations by multiplying with the trendline time series over the first value of the trendline. For temperature, the trend is reinserted by adding the removed trendline mean at each time step.

As an initial step for precipitation bias correction, we matched the threshold of non-zero precipitation to preserve the observed monthly probability of dry (P0) for each month (i.e., the monthly intermittency). A threshold is usually set either by the data providers or the modellers for the trace precipitation. This threshold plays a crucial role in defining a dry day and calculating the probability of dry. Several thresholds are used in literature. For example, Polade et al.36 and Mengel et al.37 considered 1 mm/day and 0.1 mm/day for both observations and simulations, respectively. Polade et al.36 showed that the multi-model-ensemble mean yearly frequency of dry days in the historical simulations matches GPCP observations when using a threshold of 1 mm/day. Vincent et al.37 considered 1 mm/day for Canadian catchments to obtain extreme precipitation indices. Therefore, we selected 0.1 mm as the threshold due to working with gridded datasets. As a result, any values below 0.1 mm in the reference dataset, EMDNA, were set to zero. For each month, the observed P0 was then estimated under this assumption. To ensure the simulations matched the observed P0, we calculated the quantile in the simulations corresponding to the observed P0, which provided the simulation threshold (thressim). Finally, we adjusted the nonzero values in the simulations by subtracting thressim and adding 0.1 mm.

The steps described above were applied separately to each month. This allowed for the generation of simulated precipitation/temperature values that are representative of each specific month, taking into account the characteristics of the observed data for that period and maintaining seasonality. Even though QM was applied separately for each specific month, the same distribution family was used for each variable with slight differences in the parameters. Accordingly, the continuity of the overall time series was maintained (Figure S1 shows an example of this continuity). This aspect is crucial in ensuring that the statistical properties related to the timing and sequencing of events, which are essential in hydrological and climatological studies, are not disrupted by the bias correction process. The SPQM method is considered to perform better than existing QM techniques23,24,38.

Data Records

NetCDF files containing the SPQM-CMIP6-CAN dataset25, encompassing bias-corrected daily precipitation and average temperature data for the period 2020–2100 are available for every zone (refer to Fig. 1 for zones). These files encompass a total of 693 simulations for precipitation and 581 simulations for average temperature, collectively amounting to approximately 28 TB of data. These datasets have been archived within the Federated Research Data Repository (FRDR; https://doi.org/10.20383/103.0829). Furthermore, accompanying the data is a map presenting the delineation of the nine distinct zones along with their respective coordinates (latitude and longitude), provided in the form of comma-separated (CSV) files.

Technical Validation

Previous works have validated both precipitation and temperature provided by the SPQM-CMIP6-CAN dataset at various spatiotemporal scales23,24,27,39. For precipitation, validations included evaluating the SPQM-CMIP6-CAN dataset in the Bow River basin in Canada on a daily scale24. The dataset effectively reproduced wet/dry spell lengths (a feature that is generally not simple to reproduce40), extreme precipitation at the 95 and 99th percentiles, and the frequency of precipitation exceeding 10 mm and 20 mm thresholds through distribution matching. Comparative analyses between the SPQM-CMIP6-CAN dataset and those derived from widely used bias correction methods, such as quantile delta mapping (QDM) and statistical transformations of cumulative distribution functions such as splines, demonstrated superior performance24. For temperature, the assessments extended to include an examination of extreme climate indices estimated from SPQM-CMIP6-CAN, revealing minor disparities across the methodologies in global and Canadian cities at monthly and annual scales23,27. Further, the SPQM method was also evaluated against QDM for extreme precipitation39.

Here, we present a thorough and consistent assessment of precipitation and temperature data offered by the SPQM-CMIP6-CAN dataset, covering Canada at a high resolution of 0.1° × 0.1°. Specifically, our evaluation encompasses two main aspects. First, a temporal validation is performed in which we demonstrate (1) how the SPQM-CMIP6-CAN dataset shows seamless continuity with observations for all SSPs and (2) how the dataset preserves the observed distribution while capturing key characteristics of future projections (probability of magnitudes and non-stationarity). Second, a spatial validation is performed in which we show (1) the impact of spatial aggregation on the dataset’s integrity and (2) the spatial distribution of precipitation and temperature using regional maps. Note that all demonstrations are performed on an annual scale because of the excessive computational demands for processing daily data at such fine spatial resolutions across Canada. However, we conducted additional validations on a daily scale using a single simulation from the CanESM5 climate model (refer to Section 4.3). The data is available on a daily scale, allowing end-users to conduct further validations tailored to specific regions or applications.

Before diving into the extensive validations of this dataset, an initial quality control validation was performed to ensure that the values remained within a realistic range. Considering all bias-corrected values across time and space, the daily precipitation absolutely ranges between 0 and 357.11 mm, while the daily average temperature across Canada during 2015–2100 estimated by each SSP ranges between −7.90 and 9.45 °C.

Temporal Validation

The bias-corrected time series of future simulations exhibit smooth continuity after the observed period while preserving the variability and non-stationarity of each scenario (Figs. 2, 3). Annual average temperature (Tavg) in Canada increases under the different SSPs of CMIP6 (Fig. 2, the first column). In the most optimistic scenario (SSP1-2.6), Tavg is projected to stabilize around −3.6 °C from 2070 onward, representing an increase of 2.05 °C compared to the observed average during 1979–2014. This scenario aims for rapid emission reductions, leading to limited warming in the latter half of the century, as reported by the IPCC AR6 (Lee et al., 2021). When examining the latitudinal variation of Tavg (Fig. 2, the second column), the projections show the same pattern and variability as the observed temperature per latitude, with an increasing magnitude over time. Overall, temperatures decrease with increasing latitude. The differences in temperature between the historical period, near future, and far future become more pronounced from SSP1-2.6 to SSP5-8.5 (Fig. 2), as expected. Notably, temperature variations per latitude are particularly substantial in Northern Canada for latitudes above 70°N, with slight variations also observed in some regions of Southern Canada around 50°N. This variability is evidenced by the oscillations in the second column of Fig. 2 and confirmed by previous studies41,42. Conversely, regions between 50°N and 70°N exhibit a smoother increasing pattern.

Fig. 2
figure 2

The annual mean temperature for Canada during historical and future periods for: (a) SSP1-2.6, (b) SSP2-4.5, (c) SSP3-7.0, and (d) SSP5-8.5. The first column is the time series of the annual average temperature. The shaded area shows the absolute range across 581 simulations, and the dark lines show the multi-model mean. The second column shows the latitudinal variations of the average annual temperature; the black line represents the historical average of the EMDNA dataset during 1979–2014, while the coloured lines show the average of all projections and longitudes at each specific latitude for two future durations of 2029–2064 and 2065–2100.

Full size image
Fig. 3
figure 3

The annual mean precipitation for Canada during historical and future periods for: (a) SSP1-2.6, (b) SSP2-4.5, (c) SSP3-7.0, and (d) SSP5-8.5. The first column is the time series of the annual average precipitation. The shaded area shows the absolute range across 693 simulations, and the dark lines show the multi-model mean. The second column shows the latitudinal variations of the average annual precipitation; the black line represents the historical average of the EMDNA dataset during 1979–2014, while the coloured lines show the average of all projections and longitudes at each specific latitude for two future durations of 2029–2064 and 2065–2100.

Full size image

Similar results were obtained from validating projected precipitation values against observations. As global warming intensifies, precipitation levels also experience an upward trend across the different SSPs, showing how the dataset preserves the non-stationarity of projections (Fig. 3). SSP1-2.6 exhibits a milder slope compared to the other scenarios, plateauing during the latter half of the century, similar to the temperature projections. However, SSP5-8.5 displays the steepest slope, indicating intensified precipitation across Canada. While the difference in precipitation intensification between the near and far future is not as pronounced as that of temperature, precipitation does show an increasing trend with higher latitudes (Fig. 3; the second column). Notably, there is significant variability in precipitation changes at low latitudes (around 50°N) and high latitudes (around 75°N) in the historical period. Similar variability is reproduced by the bias-corrected simulations in this latitude range. Southern Canada, encompassing multiple climate zones, is projected to experience a wide array of changes in future precipitation patterns. This diversity is highlighted by the pronounced oscillations observed between latitudes 40°N and 60°N, as depicted in the second column of Fig. 3. Additionally, Northern Canada primarily consists of Arctic regions where various oceanic perturbations can lead to different atmospheric responses to climate change43.

The SPQM-CMIP6-CAN data preserves the observed distributions, accompanied by either a shift in magnitude or densities across different climate zones for the different scenarios during 2064–2100 (Fig. 4; details of each subplot are shown in Figures S2–S12). In regions such as the Northeastern Forest, Atlantic Canada, and Great Lakes, the future distributions exhibit a positive shift in magnitude without changing densities. This behaviour indicates that the most probable values are expected to increase with the same frequency as the corresponding observed values. Conversely, the North British Columbia (BC) Mountain and Pacific Coast regions show an intensification of the most probable values, characterized by high magnitudes and frequencies. Other regions, including the Prairies, South BC Mountain, Arctic Tundra, and Arctic Canada, exhibit a decrease in the peak of the probability density function (PDF) with shifts towards higher temperatures. In these regions, the most probable magnitudes increase with less frequency. This pattern may be attributed to the dry nature of these regions, which limits the retention of atmospheric moisture, resulting in less warming (as seen in the Prairies). Additionally, the South BC Mountain and Pacific Coast regions experience high-frequency oceanic cycles that can modulate the impacts of global warming. Lastly, the projected most probable annual temperatures in the Arctic Tundra and Arctic Mountains increase with warming scenarios but with lower frequencies. However, the tails of the distributions become heavier under the global warming scenarios, indicating an increase in the occurrence of extreme temperatures. Noteworthy, SSP3-7.0 seems to be less smooth than other SSPs, which may indicate less agreement among CMIP6 projections for this scenario. Also, SSP3-7.0, along with SSP5-8.5, shows a slightly different distribution shape than the rest of the scenarios and observations. This slight difference mainly appears at the peaks of distributions, showing a flatter peak compared to the rest, especially in the Mackenzie district and Northeastern Forest. This behaviour may originate from steeper trends accompanied by the highest-emission scenarios.

Fig. 4
figure 4

The PDF plots of the annual average temperature for the 11 climate zones across Canada, show the reproduction of the observed distribution for all scenarios: SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5 during 2065–2100. Solid lines indicate the multi-model means for all grid points inside each climate zone, while the shaded regions indicate the empirical 95% confidence interval. The observed black line spans from 1979 to 2014 time series, while the SSPs span from 2065 to 2100.

Full size image

The PDFs of average annual precipitation reveal three distinct patterns in comparison to observations (Fig. 5; details of each subplot are shown in Figures S13–S23). First, certain regions exhibit a projected increase in the most probable precipitation magnitudes while maintaining the observed frequencies of historical values. These regions include South BC, the Pacific Coast, the Arctic Tundra, Atlantic Canada, and the Great Lakes. Second, other regions, such as the Prairies, North BC, Northwestern Forest, and Mackenzie District, display reductions in PDF peaks accompanied by higher magnitudes and heavier tails. This pattern suggests a lower frequency of increased most probable values but more frequent extreme precipitation events. The third pattern observed in the PDFs is characterized by higher peaks with heavier tails. In the Arctic Mountains and Fiords, the PDF peaks are intensified without a shift in the most probable values, indicating that historical values occur with a higher frequency. Similarly, in the Northeastern Forest, the projected peaks exceed the observed ones, accompanied by an increase in the most probable values. This behaviour implies an increase in both the magnitude and frequency of the most probable precipitation values. Heavy tails, indicating more frequent extreme events, are also observed in this region. Note that the differences between scenarios are relatively minor, suggesting that sensitivities among global warming scenarios are less pronounced in precipitation compared to temperature. For further validation insights, Figures S24, S25 illustrate how effectively the bias-corrected data preserves the observed distributions compared to the non-bias-corrected (raw) simulations.

Fig. 5
figure 5

The PDF plots of the annual average precipitation for the 11 climate zones across Canada show the reproduction of the observed distribution for all scenarios: SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5. Solid lines indicate the multi-model means for all grid points inside each climate zone, while the shaded regions indicate the empirical 95% confidence interval. The observed black line spans from 1979 to 2014 time series, while the SSPs span from 2065 to 2100.

Full size image

Spatial validation

The SPQM-CMIP6-CAN simulations reproduce the same pattern of spatial variability, indicating an effective correction process reproducing the spatial patterns observed in the raw simulations. Substantial regional variability in average annual temperature is evident throughout Canada during 2064–2100 (Fig. 6, the first column). Figure 6 highlights that warming is more pronounced in the high latitudes of Canada than in the lower latitudes, a phenomenon known as Arctic Amplification. This observed trend, documented in various studies44,45,46,47, is primarily due to the reduction of sea ice and snow, which decreases surface albedo. Normally, ice and snow reflect a significant amount of sunlight (high albedo), but as they melt, darker land or ocean surfaces absorb more solar energy (low albedo), leading to further warming48. This process, along with factors like changes in ocean heat transport and atmospheric greenhouse gas concentrations, accelerates warming in the Arctic more than in other regions. This rapid warming in the Arctic is evident in the bias-corrected projections as we move from the least emission scenario (SSP1-2.6; Fig. 6b) to the highest emission scenario (SSP5-8.5; Fig. 6e). The precipitation data exhibits a strong spatial variability consistent with observations, documented records, and literature (Fig. 6, the second column). While the differences among scenarios are not as pronounced as those observed in temperature, there is a slight increase from one scenario to the next. Across Canada, the majority of regions are projected to witness heightened precipitation levels39,49,50,51,52. The eastern and western coasts notably demonstrate more substantial increases in precipitation, while the Prairies region experiences a more moderate intensification.

Fig. 6
figure 6

Average annual temperature (the first column) and precipitation (the second column) in Canada for (a) the observations (1979–2014) and far future (2065-2100) in the four SSPs: (b) SSP1-2.6, (c) SSP2-4.5, (d) SSP3-7.0, and (e) SSP5-8.5.

Full size image

Finally, ensuring consistency in the behaviour of a dataset when aggregated or remapped to different spatial resolutions is paramount. This consideration arises from the presence of diverse observational datasets across regions, each with its own spatial resolutions, necessitating preprocessing steps such as mapping, interpolation, or aggregation. To assess the robustness of our dataset in this context, we examine the aggregated the Tavg at various spatial resolutions (0.2° 0.4°, 0.6°, 0.8°, and 1°) throughout Canada (Fig. 7a,b). The SPQM-CMIP6-CAN dataset exhibits a consistent pattern across the different spatial resolutions and SSPs, with the interquartile ranges closely aligning with the observed values. However, as global warming intensifies, the median of Tavg demonstrates a gradual increase from SSP1-2.6 to SSP5-8.5 for all resolutions in the near and far future, indicating a more accelerated warming trend in the latter half of the century. Notably, the projected Tavg displays a bimodal distribution, with one peak surpassing observations in SSP3-7.0 and SSP5-8.5 and another falling below observations in SSP1-2.6 and SSP2-4.5, a result of the greenhouse gas concentration trajectories associated with each SSP. Similarly, we assess the aggregated average annual precipitation across various spatial resolutions (Fig. 7c,d). The interquartile ranges align with observed values, with heavier tails that are consistent among the various spatial resolutions. The same results hold true for precipitation. Nevertheless, it’s noteworthy that the variability among SSPs for precipitation is less pronounced compared to temperature.

Fig. 7
figure 7

Average annual temperature and precipitation aggregated at various spatial resolutions: 0.2°, 0.4°, 0.6°, 0.8°, and 1°, across Canada. (a) is for the near future 2029–2064, and (b) is for the far future 2065-2100. (c) and (d) are the same as (a,b) but for precipitation. The violin plots only show the absolute range among all grid cells and CMIP6 simulations for the future scenarios.

Full size image

Extra validation insights

We provide additional insights into the temporal and spatial validation of SPQM-CMIP6-CAN on a daily scale for the CanESM5 model, covering both temperature and precipitation. Our analysis focuses on daily precipitation in a Prairie region (longitude −120 to −114 and latitude 49 to 55). The spatial pattern of the product on a given day appears as coherent as the observed pattern (Fig. 8a,c). The raw simulation (Fig. 8d) resembles an aggregated reference dataset (Fig. 8b); thus necessitating the remapping and bias-correction techniques for acquiring fine-resolution grid information. Following this remapping, the SPQM method’s bias-correction procedure is applied on a one-to-one grid basis. The same results hold for the temperature variable (Fig. 9). This demonstration of spatial coherence is also extended to another region west of Hudson Bay (longitude 254 to 260 and latitude 55 to 61; Figures S26, S27).

Fig. 8
figure 8

The spatial pattern of the daily precipitation for the (a) reference dataset at 0.1°, (b) aggregated reference dataset at 2°, (c) the bias-corrected dataset using the SPQM method for a CanESM5 simulation at 0.1°, and (d) the original raw simulation for a CanESM5 simulation at 2° on a single day that corresponds to panel (c). These figures are a demonstration of the employed datasets and the bias-corrected product in a Prairie region.

Full size image
Fig. 9
figure 9

The spatial pattern of the daily temperature for the (a) reference dataset at 0.1°, (b) aggregated reference dataset at 2°, (c) the bias-corrected dataset using the SPQM method for a CanESM5 simulation at 0.1°, and (d) the original raw simulation for a CanESM5 simulation at 2° on a single day that corresponds to panel (c). These figures are a demonstration of the employed datasets and the bias-corrected product in a Prairie region.

Full size image

For the whole Canada, we plotted the probability of zero precipitation, mean, and standard deviation monthly to display seasonal variations in these summary statistics. Although the procedure aims to preserve the monthly probability of zero to set the threshold in simulations for daily precipitation, these probabilities still increase with global warming due to the preservation of trends in projections (Figure S28). The spatial coherence of the summary statistics is maintained for future SSPs and is amplified with increasing radiative forcings from SSP1-2.6 to SSP5-8.5 for both precipitation and temperature (Figures S29–32). These findings highlight the robustness and precision of the SPQM-CMIP6-CAN method in accurately representing daily climatic variables while preserving critical seasonal and spatial patterns.

To provide a comprehensive analysis of the transition from observed to projected data, we focus on the period from 2014 to 2016, bridging the gap between the end of observations and the start of projections for both precipitation and temperature (Figs. 10, 11). This critical transition period allows us to evaluate the consistency and reliability of the projections in comparison to historical observations. In the Prairies region, the time series data for daily precipitation and temperature during this period exhibit a smooth transition, indicating a robust bias-correction technique. This smooth transition reinforces the temporal validation on an annual scale, as demonstrated in Section 4.1. Furthermore, the preservation of monthly patterns for both precipitation and temperature underscores the accuracy of the projections. Seasonal variations, which are crucial for understanding regional climate dynamics, remain consistent between the observed and projected data. This smooth transition and seasonality preservation are also apparent for the west of Hudson Bay region (Figures S33, S34). By maintaining these monthly variations, the bias-corrected dataset ensures that critical seasonal phenomena, such as rainfall distribution and temperature fluctuations, are accurately represented. This fidelity to observed patterns enhances the credibility of our projections and provides a solid foundation for further climate impact studies in the Prairies region and beyond. Overall, the smooth transition and preservation of seasonal patterns validate the effectiveness of our bias-correction and remapping techniques, ensuring that SPQM-CMIP6-CAN is reliable for future climate scenarios.

Fig. 10
figure 10

The average daily precipitation in a Prairies region focusing on the transition between the end of observations (the black lines) to the start of projections (the coloured lines). The subplots show the different scenarios for the projections: (a) SSP1-2.6, (b) SSP2-4.5, (c) SSP3-7.0, and (d) SSP5-8.5.

Full size image
Fig. 11
figure 11

The average daily temperature in a Prairies region focusing on the transition between the end of observations (the black lines) to the start of projections (the coloured lines). The subplots show the different scenarios for the projections: (a) SSP1-2.6, (b) SSP2-4.5, (c) SSP3-7.0, and (d) SSP5-8.5.

Full size image

Usage Notes

SPQM method is a robust bias correction technique, particularly in the context of climate projections, that can be implemented efficiently on fine spatiotemporal scales and voluminous climate model outputs23,27. This method offers a way to map projected quantiles onto observed parametric distributions while preserving the empirical probabilities, trends, and variabilities associated with future magnitudes. The preservation of linear trends is crucial since they are commonly observed in non-stationary features of temperature and precipitation projections. Additionally, it has been shown that detrended quantile mapping (QM) outperforms traditional QM methods33. The SPQM method also takes into account the seasonality of observed parametric distributions, acknowledging that these distributions can vary on a monthly basis. Recently, further advancements have been made to the SPQM method to incorporate wet and dry spells in daily precipitation data24. Importantly, the SPQM method relies on observations and projections and does not depend on historical simulations, thus eliminating an additional source of uncertainty. By combining the advantages of parametric and non-parametric techniques while preserving non-stationarity, the SPQM method mitigates the potential accumulation of errors and uncertainties associated with fully parametric techniques and avoids reliance solely on the quality of observations, as is the case with non-parametric techniques. We also note that the same bias-correction method can be applied to historical simulations. Given the less possibility of encountering significant trends, this approach would simplify the application of the proposed method to historical data.

However, it is important to acknowledge the limitations of bias correction techniques and the assumptions they entail, including the SPQM method. The main assumption of QM techniques is that projections follow the same distribution as observations, which is not always physically justifiable. Although the ensemble range aligns with similar studies51, it could increase if a fully non-parametric method is employed. Additionally, Maraun53 highlighted several shortcomings of QM techniques. Firstly, the overestimation of the area means, and extremes was the main issue facing QM techniques, which was caused by neglecting trends in projections. The presence of trends within the time series leads to the generation of high values, which are attributed to non-stationarity rather than being a consequence of the distribution’s inherent shape. This problem was solved when trends were preserved in the recent advancements to QM, including SPQM24,27,33,54. Secondly, having observations and projections at different spatial resolutions makes the QM technique bridge this difference in the spatial resolutions. SPQM performs the correction of the quantiles following the re-gridding process of both observations and projections to the same spatial resolution.

Thirdly, QM techniques do not account for spatiotemporal dependency structures or patterns. We emphasize that this bias-correction method is a univariate technique that does not consider spatial patterns as any QM-based bias-correction method. Although this dataset is offered at a high-resolution spatial scale of 0.1° (~10 km), Please note that this product is not dynamically downscaled. The employed method is based on a one-to-one grid bias-correction technique that preserves the different distributions, and probabilities of dryness (in the case of precipitation) for each cell are considered according to high-resolution observations or reference datasets. The spatial coherence results from the employed remapping technique which in the case of SPQM-CMIP6-CAN is the bilinear interpolation technique prior to the bias correction procedure. We note that this shortcoming comes with any QM-based bias-correction method, and it could only be mitigated by employing an advanced bias-correction process that considers the spatial dependency, such as image-processing-based downscaling methods55,56,57. However, these advances have not been completely evaluated and deployed. Consequently, SPQM-CMIP6-CAN still is very valuable for practical application concerning the overall insights of climate change impacts in that region.

We align with Maraun53 that stochastic and multivariate bias correction techniques can probably bridge the third issue, reproducing the spatial patterns. We also acknowledge that various forms of dependency can be considered in multivariate bias correction techniques, such as the interconnection between climate indices and precipitation and temperature changes. Zhao et al.58 also pointed out that QM is skillful in correcting biases in Australia, yet it does not reproduce the variability or the coherence. However, several studies employed and investigated the bias-corrected datasets in several case studies, and they proved to be in good alignment with observed data59,60,61,62.

In addition to the detailed validation conducted for SPQM-CMIP6-CAN, we rigorously evaluated the performance of precipitation and average temperature. This included analyzing daily time series, annual totals (or averages for temperature), annual maxima, and annual minima (temperature only). The results for one grid are presented in Figures S35–S41. While the average temperature is reasonably well-described by the three-parameter distribution used in this study (skew normal), the left tail, which represents extreme cold temperatures, was not captured perfectly (Figure S42). Addressing this limitation may require a more sophisticated distribution to accurately represent temperature extremes, posing a challenge to the operational feasibility of the methods employed. Yet the dataset is valuable for water resources management, enabling accurate estimation of water availability and demand and supporting reservoir operations, irrigation scheduling, and drought monitoring. In agriculture and crop modelling, bias-corrected datasets provide vital inputs for crop models, allowing for precise assessments of agricultural productivity, yield forecasts, and optimal planting and harvesting times. They also contribute to urban planning and infrastructure design by assessing the potential impacts of climate change on urban environments, evaluating the vulnerability of infrastructure to extreme weather events, and informing adaptation measures. Furthermore, downscaled and bias-corrected datasets are essential for studying the effects of climate change on ecosystems, biodiversity, and species distribution patterns, aiding in the design of conservation strategies and the identification of priority areas for habitat protection. They are also critical for public health applications, particularly in assessing health risks associated with heatwaves and developing effective heatwave warning systems. Overall, bias-corrected temperature and precipitation datasets enhance our understanding of climate change impacts and support decision-making across various sectors63,64,65,66,67,68.