Background & Summary

In March 2023, the United Nations (UN) convened the second global Water Conference, the first such gathering in nearly 50 years, with the aim of accelerating progress on water-related Sustainable Development Goals (SDGs)1. At this meeting, the UN Water Community emphasized the importance of prioritizing water in the context of climate change2,3, as water is the primary medium through which humans experience the effects of climate change. Surface water, a critical source for human societies4,5, constitutes a significant portion of the world’s fresh water resources6,7. In some countries, particularly China, surface water resources management policies are typically formulated based on prefecture-level administrative units, including prefectures, leagues, and regions8,9. However, significant gaps remain in the research on surface water resources in China, primarily due to the absence of a comprehensive dataset at the prefectural level. The lack of complete and usable surface water resources dataset has hindered the development of effective water resources management strategies in China.

Currently, several surface runoff datasets are available at global and national levels, including CNRD v1.0, GRUN, ISIMIP2a, and ISIMIP3a10,11,12,13. These datasets are primarily generated through simulations that incorporate key geographical elements, such as meteorology and vegetation, at the grid scale, rather than directly observed surface water data14,15,16,17. This approach introduces significant limitations, as the absence of observed surface water data as a benchmark makes it difficult to comprehensively assess the accuracy of these simulations. Additionally, substantial discrepancies in the simulated surface water quantities and spatial distributions among these datasets, further complicating their reliability18. Moreover, the relatively coarse spatial resolutions of these datasets (0.5° or 0.25°) restrict their ability to accurately calculate surface water resources at the prefectural level, these datasets are only lower than that of certain smaller prefectures, introducing significant uncertainty when comparing these datasets to measured data. As a result, these datasets may not fully capture surface water resources at the prefecture scale and require validation with observed data to be considered reliable for water resources management.

Although surface water resources data for most prefectures in China are available through national and provincial water resources bulletins, no comprehensive dataset encompassing all prefectures has been compiled. This gap largely stems from the substantial and intricate effort required to create a long-term, nationwide dataset. Additionally, administrative changes and redivisions in many prefectures since the early 2000s, combined with incomplete provincial water resources bulletins, have led to significant data gaps19. These challenges further complicate the development of a thorough surface water resources dataset. Consequently, there is an urgent need to develop a dataset based on measured data to comprehensively document China’s surface water resources.

To address the existing gap in surface water resources datasets, we compiled and integrated publicly available surface water data from national and provincial water resources bulletins at the prefecture level. Using 14 machine learning models, we predicted and filled in missing data (21.3%), resulting in the creation of a high-precision, long-term dataset spanning from 2000 to 2020, named the “China National Surface Water Resources Dataset (CNSW 1.0).” This dataset includes 16 separate datasets covering China’s surface water resources over 21 years, across 341 lower-level administrative units in mainland China, excluding Hong Kong and Macau. CNSW 1.0 serves as a benchmark for validating the accuracy of surface runoff products and enables exploration of the temporal and spatial dynamics of surface water resources in China. It supports the development and implementation of water resources management policies at the administrative level. Additionally, it aligns with the goals set by the World Water Congress and supports the achievement of SDGs by 2030, promoting a harmonious balance between human activities and nature and enhancing proactive risk management.

Method

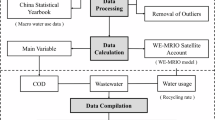
CNSW 1.0 reconstruction framework

The reconstruction of CNSW 1.0 involves two main steps, as illustrated in Fig. 1. First, we collected surface water resources data from provincial water resources bulletins in China spanning from 2000 to 2020. This initial dataset contained 21.3% missing values (Supplementary Table 1) and serves as the foundation for CNSW 1.0, acting as the dependent variable for predicting missing data using 14 machine learning models. Second, we selected 21 key variables (listed in Supplementary Table 2) related to meteorology, soil type, vegetation, and topography as predictors. Meteorological factors serve as the direct drivers of surface water resources, while soil (contents of Slit, Sand, and Clay), topographic (DEM and Slope), and vegetation (NDVI, LAI, and GPP) factors represent surface characteristics that directly influence the partitioning of precipitation20. Therefore, these factors are crucial for predicting the formation processes of surface water resources. Variable preprocessing methods for machine learning models are in Supplementary Note 2. The dataset was then divided into training and prediction subsets, with a 9:1 split for model training and testing. After training the models, we predicted the missing surface water data and combined these predictions with the measured dataset to form CNSW 1.0. The final dataset includes 16 components: 14 derived from machine learning predictions, one based on the median of predictions, and one based on the mean of predictions. To address the issue of administrative boundary adjustments, this study distinguished two scenarios and adopted different approaches accordingly. First, when entire prefectures were merged into new administrative units (e.g., Hancheng City in Shaanxi Province and Laiwu City in Shandong Province), data were aggregated directly by summation. Second, for cases involving the division of one prefectures into multiple cities (e.g., the 2003 administrative adjustment of Ningxia Autonomous Region and the division and merger of Chaohu City in Anhui Province), machine learning models were employed to reconstruct and predict data, ensuring data consistency and accuracy.

Fig. 1
figure 1

The CNSW 1.0 reconstruction framework.

Full size image

Machine learning models and performance evaluation

Machine learning regression models are widely used for predicting continuous variables21,22,23,24,25 and have been extensively applied in hydrology for tasks such as streamflow prediction26,27,28,29,30,31, precipitation forecasting32,33,34,35,36,37, water quality assessment38,39,40, groundwater level change prediction41,42,43,44,45, and evapotranspiration estimation23,46,47,48,49,50. Key models include linear regressions (e.g., generalized linear models, elastic net regression)30,34,42,45, decision tree regression27, support vector machine regression26,27,31,38,45,46,47,50, ensemble learning models (random forest, gradient boosting regression)27,32,34,38,45,47,50, neural network models29,43,45,50 and generalized additive models51,52,53). These algorithms used historical data to identify patterns, enabling both the reconstruction of missing historical data and predictions of future data54,55,56,57,58,59,60,61. In this study, 14 machine learning models (Table 1) were utilized to predict missing surface water resources data in China for the period of 2000–2020. Detailed explanations of the principles and parameter tuning methods for these machine learning models are provided in Supplementary Note 1. Model performance was evaluated using metrics such as root mean square error (RMSE), coefficient of determination (R2), percent bias (PBIAS), and normalized error (NE), with detailed calculation formulas provided in Eqs. 1–4.

$$RMSE=\sqrt{\frac{1}{{\rm{n}}}{\sum }_{i=1}^{n}{(\overline{{y}_{i}}-{y}_{i})}^{2}}$$
(1)
$${R}^{2}=\frac{{({\sum }_{i=1}^{n}({y}_{i}-\overline{{y}_{i}})({y}_{i}-\overline{y}))}^{2}}{{\sum }_{i=1}^{n}{({y}_{i}-\overline{{y}_{i}})}^{2}{({y}_{i}-\overline{y})}^{2}}$$
(2)
$$PBIAS=\frac{{\sum }_{i=1}^{n}|{y}_{i}-\overline{{y}_{i}}|}{{\sum }_{i=1}^{n}{y}_{i}}\times 100 \% $$
(3)
$$NE=\frac{|{y}_{i}-\overline{{y}_{i}}|}{\frac{1}{{\rm{n}}}{\sum }_{i=1}^{n}\overline{{y}_{i}}}$$
(4)

Where \(\overline{{y}_{i}}\) is the Predicted value, yi is the observed value, \(\overline{y}\) is the mean of the observed values, and n is the sample size.

Table 1 Machine learning models used in this study.
Full size table

Quality evaluation and comparison of reconstructed CNSW 1.0

In addition to evaluating the performance of the machine learning models, it is crucial to assess the simulation accuracy of CNSW 1.0 across China and within specific administrative regions. The validation and comparison framework for CNSW 1.0 is illustrated in Supplementary Figure 2. We collected annual total surface water volume data for China and its provincial units from 2000 to 2020, and computed the total surface water volume for seven administrative regions: North China (NC), East China (EC), Central China (CC), South China (SC), Northeast China (NE), Northwest China (NW), and Southwest China (SW) (Supplementary Figure 1). This dataset, covering the period from 2003 to 2020(several provinces did not publicly disclose their annual surface water resources data from 2000–2002), was used to create the Chinese Surface Water Resources Simulation Accuracy Validation Dataset. Validation of CNSW 1.0 was performed using this dataset as a benchmark, with the coefficient of determination (R2) and percentage bais (PBIAS) employed as the metric. The R2 values and percentage bais (PBIAS) for CNSW 1.0 were calculated for both national and regional scales, with the formula for R2 and PBIAS provided in Eqs. (2, 3).

Furthermore, the CNSW 1.0 constructed in this study was compared with other 4 runoff datasets in terms of simulation accuracy, time series, and spatial distribution. The runoff datasets used for comparison include CNRD v1.0, GRUN, ISIMIP2a, and ISIMIP3a. ISIMIP2a includes averages of 18 model simulations derived from 6 models with 3 types of driving data, while ISIMIP3a includes averages of 14 runoff datasets. As the time scale of ISIMIP2a only extends to 2010, the comparison of the multi-year average spatial distribution characteristics of surface water resources used data from 2000 to 2010, covering 11 years for each dataset.

Data Records

The CNSW 1.0 encompasses surface water resources data for 341 prefectural-level administrative units in mainland China over a period from 2000 to 2020, comprising a total of 16 surface water datasets. The data are stored in both CSV and shapefile (SHP) formats, unit is mm. The naming convention for annual spatial distribution shapefiles follows the structure “CNSW_1.0_YYY_ZZZZ.shp,” where “YYY” represents the model’s name, and “ZZZZ” denotes the year. The naming convention for multi-year average spatial distribution shapefiles is “CNSW_1.0_mean_YYY.shp,” and for the spatial evolution trend shapefiles, it is “CNSW_1.0_trend_YYY.shp.” A total of 368 shapefiles are provided, which approximately take up 7.2GB of disk space, and it can be accessed through figshare62. Additional information, such as region, province, and prefecture area, is also stored in the files.

Technical Validation

Validation of machine learning models

Among these models, the RF model demonstrates the lowest RMSE at 53.87 mm, outperforming the BR, GBM, and SVR models, which have RMSE values of 54.23 mm, 77.59 mm, and 91.88 mm, respectively (Table 2). RF also achieves the highest R2 of 0.98, followed closely by BR, GBM, and SVR with R2 values of 0.98, 0.97, and 0.95. BR shows the lowest PBIAS at 6.79%, indicating the best performance in terms of bias, while RF, SVR, and GBM follow with PBIAS values of 6.85%, 11.27%, and 11.45%, respectively. Conversely, the PR and BLR models exhibit poorer performance, with PBIAS values of 26.56% and 24.39%, respectively. The DTR model performs the worst, with an RMSE of 178.08 mm, R2 of 0.82, and PBIAS of 28.6% (Supplementary Figure 3). Overall, RF and BR models demonstrate the best performance in the training dataset, with GBM and SVR also performing well, while PR, BLR, and DTR show inferior results.

Table 2 Machine learning models used in this study.
Full size table

In evaluating the performance of the test datasets, SVR exhibits the best results, with an RMSE of 93.07 mm, an R2 of 0.95, and a PBIAS of 14.87%. The RF model also performs commendably, with an RMSE of 98.77 mm, an R2 of 0.94, and a PBIAS of 15.13%. The BR and GBM models also demonstrate strong performance, with BR achieving an RMSE of 102.82 mm, an R2 of 0.93, and a PBIAS of 15.72%, while GBM shows an RMSE of 99.27 mm, an R2 of 0.94, and a PBIAS of 15.74%. Density scatter plots (Supplementary Figure 4) illustrate that the predictions of SVR, RF, GBM, and BR closely align with the y = x line, indicating superior performance. Conversely, the DTR model continues to underperform, with an RMSE of 167.50 mm, an R2 of 0.82, and a PBIAS of 29.08%. PR and BLR also show suboptimal performance.

In the training dataset (Fig. 2), the RF and BR models significantly outperform the other models. In the test dataset, SVR, RF, BR, and GBM models all derive superior results compared to the other models, with SVR slightly surpassing RF, BR, and GBM. Overall, SVR achieves the best performance in the test dataset, while RF, BR, and GBM also perform well. A comprehensive analysis of both training and test datasets highlights that BR, GBM, RF, and SVR exhibit the strongest overall performance, whereas BLR, PR, and DTR show relatively poor performance.

Fig. 2
figure 2

Normalized error statistics for machine learning models train and test datasets.

Full size image

Time series

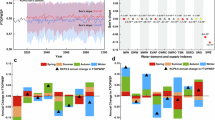
CNSW 1.0 derived 16 datasets at the prefecture-level. In addition to the 14 datasets derived from various machine learning models, this study also calculates the average and median of these model predictions, resulting in two additional datasets of prefecture-level surface water resources for China. We analyzed the temporal trends in surface water runoff depth (Fig. 3a), the multi-year average spatial distribution (Fig. 3b), and the spatial evolution trends (Fig. 3c) of surface water resources in China from 2000 to 2020 across all 16 datasets.

Fig. 3
figure 3

Spatiotemporal evolution characteristics of CNSW 1.0 from 2000–2020. (a) Temporal trends. (b) Spatial distribution characteristics of multi-year average surface water resources. (c) Spatial evolution patterns of surface water resources.

Full size image

Temporal analysis (Fig. 3a) reveals that, except for the dataset simulated by the MLP model, surface water resources in China exhibited an upward trend from 2000 to 2020, though this trend is not statistically significant. Notably, years such as 2002, 2006, 2010, 2012, 2015, 2016, 2019, and 2020 experienced relatively high surface water resources, while years like 2004, 2007, 2009, and 2011 were characterized by lower levels. According to the China Water resources Bulletin, the total surface water resources in China increased at an average annual rate of 1.77 mm from 2000 to 2020. Among the simulations, GAM, GPR, KNN, RF, and SVR closely matched the observed values, whereas the MLP model exhibited a trend contrary to the actual surface water resources trend, indicating suboptimal performance.

Spatial distribution

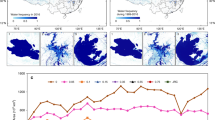
Figure 3b illustrates the multi-year average spatial distribution of surface water resources in China as simulated by each model. While all models consistently identify the abundant water regions in SE, their results diverge in Northwest, Northeast, and Southwest. The areas with the least surface water resources are found in NC and NW, particularly within endorheic basins and non-monsoon regions. In contrast, SE displays the highest surface water availability which were largely attributed to its elevated precipitation levels.

The analysis reveals that regions experiencing a decline in surface water resources are concentrated in four key areas: the NW inland river basins, NC and EC, the Southwestern river basins, and the Southeastern coastal region (Fig. 3c). Conversely, the most substantial increases in surface water resources are observed in the border areas of Jiangxi, Anhui, Zhejiang, and Jiangsu provinces. Additionally, Qinghai Province, Sichuan Province, Guizhou Province, and the three northeastern provinces exhibit notable increases in surface water resources. The Ili Kazakh Autonomous Prefecture in Xinjiang also shows significant growth in surface water availability.

Quality evaluation and comparison

This study assesses the deviation of each dataset in CNSW 1.0 from the total surface water resources reported by the China Water Resources Bulletin using the formula for annual totals. A PBIAS value closer to zero indicates a smaller discrepancy between the dataset and the Bulletin’s reported (Tables 3, 4). Among the datasets, simulations by BLR, BR, ENR, GLM, LR, and SVR closely matched the observed totals in the early years. However, in recent years, these simulations generally show lower values than those observed. Specifically, BLR’s simulated totals were accurate up to 2012 but fell below observed values post-2013. BR’s simulations were higher than observed totals before 2007 but were lower in most subsequent years, except for 2015. ENR showed similar discrepancies. GLM results were higher than observed values before 2006 (except 2003) and slightly lower thereafter (except 2008 and 2012). LR exhibited discrepancies comparable to GLM. SVR data were slightly higher than observed values until 2015 (except 2003) but fell below observed totals from 2016 onward.

Table 3 PBIAS of CNSW 1.0 (1).
Full size table
Table 4 PBIAS of CNSW 1.0 (2).
Full size table

Across all datasets, simulations of total surface water resources in China by DTR, PR, RF, GAM, GBM, GPR, KNN, Median, and Average generally yielded lower values than the observed totals. Specifically, DTR consistently underestimated the total surface water resources, with an average discrepancy of approximately 9%. Simulated totals from PR and RF were also slightly lower than observed values. GAM’s simulations were below observed totals in all years except 2000 and 2002. GBM simulations were lower in all years except 2000–2003. GPR’s simulations were lower than observed values in all years except 2000. The discrepancies for KNN and Median were similar to those of GPR. The Average dataset’s simulations closely aligned with observed values before 2006 but showed a slight decrease afterward. Notably, only the MLP consistently overestimated total surface water resources across almost all years, with a significant overestimation of 38% in 2000. Additionally, while observed surface water resources increased from 2014 to 2015, MLP simulations indicated a decrease, and in 2018, MLP showed an increasing trend contrary to the observed decline.

In addition to assessing discrepancies in simulated total surface water resources across China, we also evaluated the accuracy of CNSW 1.0 at the provincial and regional scales using metrics of R2 and PBIAS (Fig. 4 and Supplementary Figures 5, 6). Nationally, eight datasets—GAM, GBM, GPR, KNN, PR, RF, and the average and median values—demonstrated exceptional simulation accuracy (R2 > 0.95), with RF achieving the highest accuracy (R2 = 0.98). However, PBIAS analysis revealed varying stability. BR showed the lowest absolute national bias (−1.65%), indicating excellent stability, whereas RF, despite high accuracy, exhibited a negative bias (−8.14%). In contrast, MLP had both poor accuracy (R2 = 0.55) and severe overestimation (PBIAS = 11.55%), highlighting significant deficiencies. At the regional scale, substantial spatial variability was observed. CC showed near-perfect accuracy (R2 = 0.99) and negligible bias (PBIAS = 0.09%) due to complete data coverage. SC also displayed high accuracy (R2 > 0.95) and minimal bias (PBIAS < 0.55%). EC had generally excellent accuracy (R2 > 0.95), with RF (R2 > 0.95, PBIAS = 0.79%) and SVR (PBIAS = 0.21%) performing optimally. WS exhibited accuracy discrepancies, with GAM, PR, and RF showing good performance (R2 = 0.90–0.95), yet significant underestimations occurred (RF: PBIAS = −22.07%). WN faced greater challenges due to sparse data; RF achieved highest accuracy (R2 = 0.88) and relatively lower bias (PBIAS = 5.51%), whereas MLP and GAM showed extreme deviations (PBIAS: 64.56%, 50.79%). In NC, all models had moderate accuracy (R2 < 0.90), with severe MLP overestimation (PBIAS = 206.42%) contrasting with BLR’s best regional accuracy (R² = 0.880). NC showed RF as the top-performing model (R2 = 0.837, PBIAS = 3.73%), whereas ENR and MLP obviously underperformed (R2 < 0.40). Several provinces, including Beijing, Chongqing, and Shanghai, showed perfect accuracy (R2 = 1.00, PBIAS = 0%). RF consistently demonstrated robust accuracy and bias control across diverse provinces: Ningxia (R2 = 0.97, PBIAS = −0.64%), Anhui (R2 = 0.91, PBIAS = −0.43%), and Yunnan (R2 = 0.95). Conversely, severe datasets deficiencies were evident in Heilongjiang and Shanxi provinces, with MLP showing obvious overestimations (Heilongjiang: PBIAS = 367.27%, Shanxi: PBIAS = 145.80%) and negligible accuracy (R2 ≈ 0).

Fig. 4
figure 4

CNSW 1.0 simulation accuracy(R2) and bias(PBIAS) across the whole China and the seven major administrative regions. (a) R2. (b) PBIAS.

Full size image

Considering both R2 and PBIAS, the RF model emerged as the most optimal choice across national, regional, and provincial scales. While the BR model exhibited the lowest absolute bias at the national level, its performance declined significantly in regional applications, particularly in East and Southwest China. In contrast, RF effectively balanced high predictive accuracy with controlled bias, consistently maintaining R² values above 0.80 and achieving notably low biases even in regions with complex hydrological conditions. This comprehensive evaluation highlights RF’s robustness and adaptability, making it the preferred model for reliable surface water resource simulations across diverse hydrological contexts.

Intermodel comparison

This study compares the CNSW 1.0 dataset with four other datasets—CNRD v1.0, GRUN, ISIMIP2a, and ISIMIP3a—across four dimensions: simulation accuracy, total surface water resources discrepancies in China, prefecture-level discrepancies, and spatial distribution from 2000 to 2010. The end years for the datasets are 2018 for CNRD v1.0, 2014 for GRUN, 2020 for ISIMIP2a, and 2019 for ISIMIP3a. For consistency, spatial distribution analysis is restricted to the 2000–2010 period, while other comparisons utilize the full available time span. ISIMIP2a and ISIMIP3a averages are based on 18 and 14 qualifying models, respectively.

The comparative analysis of CNSW 1.0 datasets (RF, Average, Median) against alternative runoff datasets (CNRD v1.0, GRUN, ISIMIP2a, and ISIMIP3a) reveals significant differences in both R2 and PBIAS at national, regional, and provincial scales. At the national scale (Fig. 5a,b), ISIMIP2a shows the highest simulation accuracy (R2 = 0.98), equal to CNSW 1.0’s RF model (R2 = 0.98). However, ISIMIP2a demonstrates substantial bias (PBIAS = −10%) compared to CNSW 1.0 datasets, which maintain biases within 10%, highlighting their stability. Conversely, GRUN significantly underestimates water resources nationally (PBIAS = −31.7%), while CNRD v1.0 and ISIMIP3a display substantial overestimations exceeding 10%. Regionally, CNSW 1.0’s RF consistently exhibits superior overall performance. In CC, RF achieves near-perfect accuracy (R2 ≈ 1.0, PBIAS ≈ 0%), in stark contrast to the substantial biases observed in CNRD v1.0 (44.37%) and GRUN (−56.1%). Similarly, in EC, RF maintains high precision (R2 > 0.95, PBIAS < 1%), whereas CNRD v1.0 and GRUN exhibit considerable deviations. In NC, RF outperforms alternative datasets with superior accuracy (R2 = 0.84, PBIAS = 3.73%), significantly reducing the overestimation seen in CNRD v1.0, ISIMIP2a, and ISIMIP3a. For EN, RF achieves comparable accuracy (R2 ~0.88, PBIAS = 0.66%) to ISIMIP datasets (PBIAS = −0.24% and 13.64% for ISIMIP2a and ISIMIP3a), while GRUN markedly underestimates regional water resources (−57.52%). In Northwest China, comparative datasets systematically overestimate surface water resources (CNRD v1.0: 59.23%, GRUN: 47.44%, ISIMIP3a: 31.08%), whereas ISIMIP2a underestimates (−18.58%). In contrast, RF maintains robust performance with controlled bias (R2 = 0.88, PBIAS = 5.51%). In humid South China, RF demonstrates exceptional accuracy (R2 > 0.95, PBIAS ≈ −0.51%), distinctly outperforming comparative datasets such as GRUN and CNRD v1.0. The WS region presents challenges for all models, with RF exhibiting a systematic underestimation, yet remaining comparable to GRUN and performing better than ISIMIP2a. These findings underscore RF’s overall superiority in maintaining high accuracy and minimizing bias across diverse hydrological conditions.

Fig. 5
figure 5

Comparative analysis of CNSW 1.0 versus CNRD v1.0, GRUN, ISIMIP 2a, and ISIMIP 3a in simulating China’s surface water resources. Comparison of R2 (a) and PBIAS (b) at national and regional scales.

Full size image

At the provincial scale (Fig. 6a,b), CNSW 1.0 consistently outperforms comparative datasets, with RF and median estimates maintaining biases within 1% in Guangdong, Guangxi, Hainan, Guizhou, and Jiangxi. In contrast, alternative datasets exhibit extreme deviations: CNRD v1.0 overestimates water resources in Hebei (276.13%) and Ningxia (365.32%), while GRUN underestimates in Heilongjiang (−51.77%) and Jilin (−62.36%). ISIMIP2a shows severe overestimations in North China (Hebei: 248.90%, Shanxi: 182.93%) and underestimations in the Southwest (Sichuan: −28.61%, Xinjiang: −59.46%). ISIMIP3a amplifies these biases, particularly in Hebei (422.99%) and Shanxi (346.62%), though with improved performance in Guangdong (−7.82%). Despite localized challenges, such as RF biases in Tibet (−51.97%), CNSW 1.0 exhibits superior stability across diverse hydrological conditions.

Fig. 6
figure 6

Comparative analysis of CNSW 1.0 versus CNRD v1.0, GRUN, ISIMIP 2a, and ISIMIP 3a in R2 (a) and PBIAS (b) at provincial scale.

Full size image

Overall, CNSW 1.0’s datasets effectively integrate observed data with interpolative methods, achieving robust accuracy (R2 is generally above 0.90) and superior bias control at all scales. While comparative datasets occasionally match CNSW 1.0’s accuracy in specific regions, they often exhibit varied regional biases due to their reliance on purely predictive methods. This analysis underscores CNSW 1.0’s distinct advantage in accurately simulating China’s prefectural surface water resources across diverse hydrological conditions.

Figure 7 depicts the discrepancies in prefecture-level simulations between CNSW 1.0 and the four runoff datasets. CNSW 1.0 operates at a spatial resolution of 0.25°, whereas the other datasets use a coarser resolution of 0.5°. GRUN’s simulations consistently yield lower values than CNSW 1.0, exhibiting the lowest R2 value. In contrast, CNRD v1.0 forecasts higher runoff values compared to CNSW 1.0. ISIMIP2a tends to overestimate runoff in prefectures with less than 400 mm of surface water resources and underestimate in those with more than 400 mm. ISIMIP3a shows a similar pattern but with a threshold of 800 mm, overestimating in prefectures with less than 800 mm and underestimating in those with more. The density scatter plots illustrating discrepancies for all models in ISIMIP2a and ISIMIP3a are provided in Supplementary Figures 9, 10.

Fig. 7
figure 7

Comparative analysis of CNSW 1.0, CNRD v1.0, GRUN, ISIMIP 2a and ISIMIP 3a in simulating China’s surface water resources. Discrepancies in surface water resource simulations at prefecture-level cities.

Full size image

Figure 8 illustrates the time series trends of measured versus simulated total surface water resources in China. CNRD v1.0 consistently overestimates values, with significant discrepancies in 2007 and 2013. GRUN tends to underestimate, with notable inconsistencies in 2001, 2007, and 2014. ISIMIP3a also shows overestimation, though less pronounced than CNRD v1.0, with discrepancies in 2007 and 2014. ISIMIP2a aligns most closely with the measured data, except for 2002, although its time series extends only to 2010, shorter than CNSW 1.0 and the other datasets. Overall, CNSW 1.0 demonstrates superior performance in terms of simulation accuracy, time series alignment, and total volume compared to the four other runoff datasets.

Fig. 8
figure 8

Comparative analysis of CNSW 1.0, CNRD v1.0, GRUN, ISIMIP 2a and ISIMIP 3a in simulating China’s surface water resources. Time series of China’s surface water resources.

Full size image

Among these, CNRD v1.0 most closely aligns with CNSW 1.0, particularly in North China (Fig. 9). GRUN displays notably different spatial distribution patterns, with generally lower surface water levels across all regions. ISIMIP2a accurately reflects the surface water distribution in southern China but shows significant deviations from CNSW 1.0 in northern regions. ISIMIP3a fails to capture the spatial variability of surface water resources in southern China and exhibits poor performance in the north. The spatial distribution characteristics for all years in ISIMIP2a and ISIMIP3a are further detailed in Supplementary Figures 11, 12.

Fig. 9
figure 9

Comparative analysis of CNSW 1.0, CNRD v1.0, GRUN, ISIMIP 2a and ISIMIP 3a in simulating China’s surface water resources. Comparison of spatial distribution of multi-year average surface water resources (2000–2010).

Full size image

Usage Note

In this study, we developed a framework for reconstructing prefectural-scale surface water resources. By analyzing surface water data from 341 prefectures in China for the period 2000 to 2020 and integrating predictions from 14 machine learning regression models to address missing data, we created China’s first long-term, prefecture-level surface water resources dataset, named CNSW 1.0. This dataset, covering 2000 to 2020, was rigorously validated using multiple methods. Systematic precision validation and comparative evaluations demonstrate that CNSW 1.0 exceeds current mainstream natural runoff gridded datasets in simulation accuracy, temporal consistency, and spatial distribution, effectively filling the gap in China’s prefectural-level surface water data.

The reconstructed CNSW 1.0 dataset can facilitate further research in the following areas:

  1. 1)

    Water use planning and management: This dataset can assist in the rational planning of agricultural, industrial, and domestic water use, thereby enhancing water use efficiency.

  2. 2)

    Disaster prevention and mitigation: The dataset supports monitoring and analysis of surface water changes, enabling the prediction and management of natural disasters such as floods and droughts, thus aiding in the formulation of measures to minimize losses.

  3. 3)

    Policy formulation: The surface water data provides a scientific basis for government and relevant agencies to design and implement effective water resources policies and regulations.

  4. 4)

    Benchmark for hydrological models: CNSW 1.0 serves as benchmark data for hydrological model calibration, providing a valuable reference for improving model accuracy and reliability.

All data are stored in CSV and SHP formats, allowing users to read and process them using platforms such as R, Python, MATLAB, and ArcGIS. Users can select the most appropriate data for their research needs. Among all datasets, we highly recommend CNSW 1.0 (RF). For studies focusing on specific administrative regions, users can take the average of the top five models with the highest simulation accuracy for that region to obtain a more precise regional surface water resources dataset.