Introduction

In fluid dynamics, several areas inspire the researchers to further study and explore applicability and analysis. The flow of squeezing between two parallel circular walls is one of them because of its many valuable and varied applications in our current life reality. The primary vital application is the heart, where it pumps blood to the entire body through pressure. It also has industrial applications and engineering such that injection molding and polymer processing. Stefan1 publication of a classical study of squeezing flow through the use of lubrication to generate a homogeneous compression provides an aspect to study squeezing flow system. This study is inspired by a series of studies on squeezing flow system investigated by many researchers. Ahmed et al.2 studied the unsteady squeezing flow considering the viscosity mainly affected by the temperature by applying the killer box method. Çelik et al.3 investigated the influence of heat transfer and velocity on squeezing flow by the Gegenbauer Wavelet Collocation Method. Sobamowo et al.4 used both methods of differential transformation and variation of parameters to study the effect of a magnetic field on Casson nanofluid’s squeezing flow through a porous medium. Çelik5 studied the effect of viscosity on squeezing flow in a magnetic field for a specific type of fluid known as Copper-water and Copper-kerosene. Noor et al.6 discussed the impact of Cattaneo–Christov heat and mass fluxes on nanofluid’s squeezing flow. Usman et al.7 introduced new improvements to the wavelets method that helped to analyze the unsteady flow of nanofluid between two disks. Thumma et al.8 examined the influence of convection on the flow problem of electromagnetohydrodynamic radiative between two circular plates. Some other recent studies that have addressed squeezing flow can be seen in the literature9,10,11,12,13,14.

In the previous research, squeezing flow has been studied using different numerical methods, but stochastic numerical computing that is dealing with artificial intelligence is utilized to analyze the fluidic systems recently.

The accurate results provided by stochastic numerical computing have been employed to provide new research in various fields such as fluid mechanics15,16,17, biological research18,19, business and finance systems20,21, models of Panto-graph delay differential systems22,23,24, plasma science25, thermodynamics26, magneto-hydrodynamics27, solid conductive materials28, atomic physics29 and other researches of interest.It is worth noting that artificial intelligence is also able to keep pace with modern problems that are emerging in the world in various fields, such as Covid 1930,31.

In this study, the system of (USF-CPP) is performed by an intelligent computing paradigm of Levenberg-Marquard backpropagation neural networks (LMBNN). The research proceeds in several steps that can be summarized as follows

  • Levenberg-Marquard backpropagation neural networks (LMBNN) is developed to discuss the impact of different scenarios connected with the squeezing flow system (USF-CPP).

  • The governing flow system (USF-CPP) based on partial differential equations (PDEs) is transformed into differential equations (ODEs) for better applicability of networks (LMBNN).

  • Runge-Kutta method is used to generate a dataset for the USF-CPP problem, which is finally prepared for neural network infrastructure, i.e., LMBNN by variation of Reynolds number and volume flow rate.

  • LMBNN processes that are testing, training, and validation applied on system presenting the squeezing flow model USF-CPP for various scenarios and cases.

  • The mean square error discusses the results of LMBNN, dynamics of state transition, analysis of error histograms, and regression illustrations.

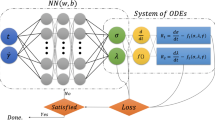
The workflow overview of solving USF-CPP with the proposed model LMBNN is presented in (See Fig. 1). The Mathematical formulation of the USF-CPP model exposure in “Solution methodology” section. The present model solution Procedure has been displayed in “Results and discussion” section. The accuracy of the output, the proposed LMBNN, is showing in “Conclusions” section. The conclusion of the research is given in the last section.

Figure 1
figure 1

The diagram of the proposed LMBNN for solving the USF-CPP model.

Full size image

Mathematical formulation

The geometry of the squeezing flow of an incompressible two-dimensional viscous fluid between two parallel plates shown in (See Fig. 2). The distance between the two circular plates at any time t is \(2\ell (t)\). The speed at which the upper and lower plates move each other is v(t). Select the r-axis as the model’s central axis, and the z-axis is normal to it. For axisymmetric flow, assumed that the plates approach symmetrically with respect to r-axis.

Figure 2
figure 2

System scheme of USF-CPP.

Full size image

The governing system32 become in form

$$\begin{aligned}&{\frac{1}{r} \partial _{r}(ru)+\partial _{z}w=0,} \end{aligned}$$
(1)
$$\begin{aligned}&{\rho (\partial _{t}u+u\partial _{r}u+w\partial _{z}u)=-\partial _{r} p+\mu \left( \nabla ^{2}u-\frac{u}{r^{2}}\right) ,} \end{aligned}$$
(2)
$$\begin{aligned}&{\rho (\partial _{t}w+u\partial _{r}w+w\partial _{z}w)=-\partial _{z} p+\mu \nabla ^{2}w,} \end{aligned}$$
(3)

where

$$\begin{aligned} \begin{aligned} \nabla ^{2}&=\partial ^{2}_{r^2}+\frac{1}{r}\partial _{r}+\partial ^{2}_{z^2},\\ \partial _{k}&=\frac{\partial }{\partial {k}}\ \ \ {\mathrm{and}} \ \ \partial ^{2}_{k^2}=\frac{\partial ^2}{\partial {k^2}}.\\ \end{aligned} \end{aligned}$$
(4)

Subject to the boundary conditions

$$\begin{aligned} \begin{aligned} u=0\ {\mathrm{and}} \ w=v_w(t),\ \ at \ \eta&=1\\ \partial _ {\eta }u=0\ {\mathrm{and}} \ w=0,\ \ at\ \eta&=0 \end{aligned} \end{aligned}$$
(5)

where \(\eta =\frac{z}{\ell (t)}\), u radial velocity and w axial velocity.

To simplify the complex system of differential equations above and make it easier to find and analyze the results, we use similarity transformations and the following equation yields.

$$\begin{aligned} {Re\Big [(\eta -f) d^3_{\eta ^3}f+2d^2_{\eta ^2}f\Big ]+d^4_{\eta ^4}f=Qd^2_{\eta ^2}f,} \end{aligned}$$
(6)

where both Re and Q are constant.

The circular plates diverge when \(Re\>0\), while converges towards each other when \(Re<0\) and the squeezing flow are symmetrical with the velocity profiles, provided \(\ell (t)\>0\). As well if \(Q=-Re\) then Eq.(6) is reduced to

$$\begin{aligned} {Re\Big [(\eta -f)d^3_{\eta ^3}f+3d^2_{\eta ^2}f\Big ]+d^2_{\eta ^2}f=0,} \end{aligned}$$
(7)

where

$$\begin{aligned} \begin{aligned} d_{\eta }=\frac{d}{d{\eta }}\ \ \ {\mathrm{and}} \ \ d^{2}_{\eta ^2}=\frac{d^2}{d{\eta ^2}}. \end{aligned} \end{aligned}$$
(8)

With the following boundary conditions

$$\begin{aligned}&f^{\prime}(1)=0\ {\mathrm{and}} \ f(1)=1,\ \ at \ \eta =1\\&f^{\prime\prime}(0)=0\ {\mathrm{and}} \ f(0)=0.\ \ at \ \eta =0 \end{aligned}$$
(9)

Solution methodology

The Levenberg Marquardt (LM) training technique is an efficient technique in the field of intelligent computing. It is designed to calculate the second-order training fast, and it requires that the output of the neural network operation is a single neuron (See Fig. 3).

Figure 3
figure 3

A single neural model structure.

Full size image

Implement the Levenberg Marquardt technique in MATLAB based on using the command of the neural network toolbox “nftool” to fit the problem. The total data for LMBNN is 1001 found between 0 and 1 by setting 0.001 as steps, using the Runge-Kutta technique through the “NDSolve” built-in function for numerical solution in Mathematica. The dataset values for \(f(\eta )\) were randomly used for each of the training, validation, and testing with \(70\%\), \(15\%\), \(15\%\), respectively. For accurate results, select 60 as the number of neurons. The LMBNN is a computational model with Double neural network coats (See Fig. 4).

Figure 4
figure 4

Installation of neural network.

Full size image

Results and discussion

The numerical application based on LMBNN is presented here for the squeezing flow model obtained in Eqs. (6-9). The proposed LMBNN is implemented for six scenarios by variation of Re, Q, with three different cases for each scenarios, as shown in Table 1. Notice that the equation associated with value variation is used in each scenario.

Table 1 Scenarios and cases distribution for USF-CPP model.
Full size table

Figures 5, 6, 7 shows that performance, states, and error histograms for all six scenarios in case 2 for USF-CPP, respectively. Studies of regression are given (See Fig. 8). The fitting of solution respective six scenarios of case 2 is presented (See Fig. 9). Also, LMBNN outcomes are comparing with the standard outcomes (See Figs. 10, 11).

The mean squared error (MSE) for all three operations is given (See Fig. 5) to validate all different scenarios. Epochs performance clearly Check in 408, 109, 4, 325, 214, 3 while MSE is around (\(10^{-12}\) to \(10^{-13}\), \(10^{-11}\) to \(10^{-12}\), \(10^{-06}\) to \(10^{-07}\), \(10^{-10}\) to \(10^{-11}\), \(10^{-12}\) to \(10^{-13}\), \(10^{-05}\) to \(10^{-06}\)) respectively (See Fig. 5).

The gradient of case 2 for all six scenarios respectively around (\(4.95\times 10^{-09}\), \(9.72\times 10^{-08}\), \(2.66\times 10^{-05}\), \(5.48\times 10^{-08}\), \(9.98\times 10^{-08}\), \(9.11\times 10^{-06}\)) and the backpropagation measures is around (\(10^{-13}, 10^{-14}, 10^{-10}, 10^{-11}, 10^{-14}, 10^{-07}\)) (See Fig. 6). Analyze of the varition error histograms for differents points is presented (See Fig. 7). The zero axes along with the error box of reference for all six scenarios in case 2 is around (\(5.33\times 10^{-09}\), \(1.49\times 10^{-07}\), \(1.79\times 10^{-05}\), \(-1.3\times 10^{-06}\), \(-9.1\times 10^{-08}\), \(-6.4\times 10^{-05}\)). (See Fig. 8) the value of R rotates statically about one , where it is the value concerned to judge the quality of the operations.

The performance result of the LMBNN is thouhtful with the standard numerical result presented from the Runge-Kutta technique along with the input error dynamics between 0 and 1 with step-size 0.001 has come (See Fig. 9). The maximum error achieved for a data operations are less than (\(1\times 10^{-06}\), \(1\times 10^{-05}\), \(2\times 10^{-03}\), \(4\times 10^{-05}\), \(5\times 10^{-06}\), \(4\times 10^{-02}\)) respectively.

Moreover, the LMBNN results are clarified for the (\(f(\eta )\), \(f'(\eta )\)) for different scenarios of squeezing flow model which is shown (See Figs. 10a, c, e, 11a, c, e) respectively. And it corresponds with the given results from the Runge-Kutta numerical solution in impact scenarios and cases. In (Figs. 10a, c, e, 11a) offer the effect of the positive and negative cases of the Reynolds number Re on the each of the profiles \(f(\eta )\), \(f'(\eta )\) , and since it is clear that an increase in the value of Re leads to an increase in the value of profiles. While, in (Fig. 11c, e), we note that an increase in the value of the volume flow rate Q leads to a decrease in the value of both profiles \(f(\eta )\), \(f'(\eta )\). But in the Fig. 10c the velocity profile is increasing function of Re for \(\eta \) less than 0.4 and reverse trend is observed when \(\eta \) is greater than 0.4. The absolute error for different scenarios is calculated from standard solutions (See Figs. 10b, d, f, 11b, d, f), respectively. indicate that AE is about (\(10^{-07}\) to \(10^{-06}\) ,\(10^{-07}\) to \(10^{-03}\), \(10^{-07}\) to \(10^{-03}\), \(10^{-07}\) to \(10^{-05}\), \(10^{-08}\) to \(10^{-04}\), \(10^{-07}\) to \(10^{-03}\)) for scenarios respectively.

Finally, the solution processes appeared while, running LMBNN, such as MSE, performance, gradient, Mu, epochs, and the time each of the three cases is listed in Table 2. The performance of LMBNN in Table 2 is around (\(10^{-14}\) to \(10^{-13}\), \(10^{-12}\) to \(10^{-06}\), \(10^{-12}\) to \(10^{-07}\), \(10^{-12}\) to \(10^{-07}\), \(10^{-13}\) to \(10^{-07}\), \(10^{-12}\) to \(10^{-06}\)) respectively. These graphical and tables results presented above discern the accuracy of using LMBNN computing to solve the variants of USF-CPP.

Figure 5
figure 5

LMBNN Performance based on MSE for USF-CPP (Case 2).

Full size image
Figure 6
figure 6

LMBNN Performance based on Gradient, Mu, and validation for USF-CPP (Case 2).

Full size image
Figure 7
figure 7

LMBNN studies based on error histogram for USF-CPP (Case 2).

Full size image
Figure 8
figure 8

LMBNN studies based on regression for USF-CPP (Case 2).

Full size image
Figure 9
figure 9

LMBNN analyses based on fitness function for USF-CPP (Case 2).

Full size image
Figure 10
figure 10

LMBNN Result and numerical reference results of USF-CPP for S1 to S3.

Full size image
Figure 11
figure 11

LMBNN Result and numerical reference results of USF-CPP for S4 to S6.

Full size image
Table 2 Numerical results of LMBNN for USF-CPP.
Full size table

Conclusions

In this paper, the intelligent computing paradigm of Levenberg-Marquard backpropagation neural networks (LMBNN) offered a numerical solution of USF-CPP by simplified the system into an equivalent nonlinear ordinary differential equation with suitable transformation. The Runge-Kutta method is implemented for the USF-CPP dataset by variation of Reynolds number and volume flow rate. The \(70\%\), \(15\%\), and \(15\%\) of points are determined for training, testing, and validation for various scenarios of LMBNN. The best agreement of both proposed and reference results along with the level is \(10^{-06}\) to \(10^{-14}\). Also, The velocity profile \(f'(\eta )\) is directly proportional to the increase of Reynolds number Re and inversely proportional to the volume flow rate Q. Moreover, verifying the scheme accuracy results is achieved through graphs and tables illustrations such as mean square error, state transition dynamics, analysis of error histograms, and regression.

In the future, it will introduce mechanics through new platforms based on artificial intelligence to provide more accurate and efficient results33,34,35,36.