Introduction

The spatial patterns of trees and their interactions provide critical information on community structure, species coexistence and significantly determine reproduction, growth, mortality, dispersal, resource use, gap creation, and understory development1,2. Especially for the natural forest, the complex spatial structure directly affects the seed spreading and the rejuvenation process of seedlings, resulting in the change of stand space. Therefore, it is imperative to evaluate the unpredictable potential processes through the current forest structure3, starting point for the change of natural forest succession. Disturbance is the driving force of forest succession, the degree of disturbance determines the direction of stand development and structure, including regeneration, species composition, community dynamics, and light mechanism of the forest4,5,6.

Coniferous and broad-leaved mixed forest is the main forest type in Changbai Mountain area, and this kind of forest usually shows high species richness and unique species composition7. It is important to understand the biological characteristics and potential ecological processes of forests in this area8. In recent decades, due to various disturbances (natural disasters and unreasonable logging), a large number of natural secondary forests appeared in this area, while coniferous and broad-leaved mixed forest resources with primitive characteristics were very scarce. This phenomenon had a significant negative impact on the productivity and function of the forest9,10. For the deepening of people's understanding of the protection of forest resources in this area, a large number of studies had been carried out, such as the status and change of ecosystem service11, modeling stand growth dynamics12, the mechanism of forest regeneration13, biodiversity14, the developing status or behavior of plant communities15, etc. However, there are relatively few studies on the changes in stand structure, especially under different succession stages and disturbance16,17.

The existing studies mainly focused on the distribution of tree size, the degree of size heterogeneity, the spatial correlation of trees in different forest layers, and various methods, including distance-related spatial structure function and distance-independent spatial structure–function. For example, Hao et al. investigated spatial patterns and associations of main tree species among different tree height layers using O-ring statistics, which was based on a 25-ha broad-leaved Korean pine (Pinus koraiensis) mixed forest plot of Changbai Mountain of northeastern China18. The results indicated that the spatial pattern and associations of main tree species were closely related to tree height class and environmental heterogeneity. Zhao et al. used variance to mean ratio, cluster index, and Cassie index to examine the horizontal distribution patterns of saplings in the spruce-fir coniferous and broad-leaved mixed forest of Changbai Mountain and their results showed that the saplings were mainly distributed in clusters, and the degree of clustering decreased with the increase of height19. Li et al. reported the priority of felling trees based on the distance-independent spatial indexes (uniform angle index; mingling index and dominance index) and believed that using these indicators can reduce the subjectivity of the selection process and improved the speed and accuracy of the choice of trees to be harvested in uneven-aged mixed forests20. The above-mentioned studies only considered the spatial distribution or interspecific correlation of tree species and did not give reasonable explanations for the results produced by different methods.

In this study, two standard plots of 1-ha were set, one of them was a sample plot with retrograde succession after disturbance, and the other was an undisturbed sample plot. Spatial pattern function, pair correlation function, Weigand classification scheme and marker variation were used to analyze the spatial pattern and interspecific correlation of main tree species in two plots. We assumed that: (i) the spatial patterns of species and their interspecific correlation are related to scale, and the proportion of species composition; and (ii) using different spatial indices and functions to analyze spatial patterns may produce different results. Based on the above-mentioned assumptions, we tried to solve the following research questions:

  1. (1)

    What is the species distribution pattern of dominant tree species in different disturbance plots?

  2. (2)

    Is the result of the spatial index consistent with the spatial function?

  3. (3)

    Is there any spatial correlation between tree diameters, and if so, is the performance of the diameter correlation consistent with the spatial scale correlation?

Results

Stand Structure

Table 1 shows the results of structural characteristics for species in the entire plots. Betula platyphylla (Bp) ranked as the most dominant in disturbed plot, with the highest values of a number of individuals (664) and basal area (11.321 m2/ ha), as shown in Table 1. However, only 214 trees existed in undisturbed plot, in which basal area was 3.385 m2/ha. Pinus koraiensis (Pk) had the largest DBH in both disturbed and undisturbed plots, which was 56.2 cm and 55.5 cm, respectively. Populus davidiana (Pd) and Betula costata (Bc) only existed in the disturbed plot, and their basal area were 2.136 and 0.706 m2/ha, which ranked third and fourth, respectively. Acer mono (Am) and Tilia amurensis (Ta) ranked third and fourth in undisturbed plot, with density 168 and 121, and basal area 1.592 and 1.784 m2/ha, respectively. The range of Gini index was from 0.36 to 0.47 and 0.61 to 0.75, respectively.

Table 1 Structural characteristics for species in the entire plots.
Full size table

The diameter distributions of different species are shown in Fig. 1. In disturbed plot, Pk and Bc had reverse J-shape curves. Pd had a unimodal diameter distribution, while Bp showed an almost bimodal distribution. In an undisturbed plot, the diameter distributions of four tree species showed bell-shaped curves, and number of trees first increased and then decreased with increasing size.

Figure 1
figure 1

Diameter distributions of four dominant species trees in both disturbed (left) and undisturbed (right) plots. Red color represents Pinus koraiensis Sieb. et Zucc. (Pk), green color represents Betula platyphylla Suk. (Bp), yellow color represents Populus davidiana Dode (Pd), bule color represents Betula costata Trautv. (Bc), cyan color represents Acer mono Maxim. (Am), and purple color represents Tilia amurensis Rupr. (Ta). The color in the following figure is the same meaning.

Full size image

Species uniform angle indices and spatial distribution patterns

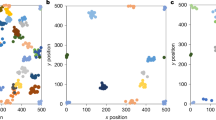
Frequency distributions of the spatial structural indices are shown in Fig. 2. The uniform angle indices of all species in both entire plots mainly distributed from 0.5166 to 0.5449 and 0.4773 to 0.6000, indicating that the distributions of tree species were mainly random. In the disturbed plot, weak uniform distribution occurred except Bc. However, only Pk showed similar weak homogeneity in the undisturbed plot. When the value of the uniform angle indices was equal to 0.75, there were significant differences in two plots. The frequency of four species exhibited essentially the same in the disturbed plot, while Pk, Bp and Ta exhibited higher inhomogeneity than Am. The univariate spatial distributions of all trees in both plots exhibited in Fig. 3. Trees of Bp showed clustered distribution between 0–9 and 14–23 m scales in the disturbed plot. Pk trees were observed aggregated at short (0–5 m) scales. Some species, such as Pd and Bc in the disturbed plot, showed clustered distributions in most of the scales. In the undisturbed plot, trees of Pk and Ta showed clustered distribution at 0–8 m and 0–5 m scales, while regular trends at 24–30 m and 13–23 m scales, respectively. Bp and Am trees exhibited aggregated distributions at scales between in 0–7 m, 13–20 m and 0–2 0 m. And then, these trends became random distributions at large interval scales, respectively.

Figure 2
figure 2

Frequency distribution of the structural indices for dominant species in the disturbed (above) and undisturbed (below) plots.

Full size image
Figure 3
figure 3

Spatial patterns of the four dominant tree species in both disturbed (above) and undisturbed (below) plots. The Y axes represents the g(r) values, which is an index of spatial pattern; the X axes represents the spatial distance scales. Black solid lines correspond to expected values for a random distribution. Different colored solid lines show actual g(r) values, gray shaded area represents 95% confidence intervals generated from 499 Monte Carlo simulations under the null hypothesis of complete spatial randomness.

Full size image

Species mingling and neighborhood comparison index

The average mingling indexes varied from 0.5124 to 0.7671 and 0.3425 to 0.8202, respectively. In the disturbed plot, weak, middle and strong mingling could be observed in species Bp. while the frequencies of the mingling index in species Pk, Pd and Bc showed an increasing trend in the disturbed plot. In the undisturbed plot, the species Bp, Am and Ta showed a high level of mixing, especially the mingling index of Ta was more distributed in 0.75 and 1.00 values. The species Pk was distributed in all values of the degree of mingling indexes, but the degree of weak and middle mingling was higher than the degree of strong and extremely strong. The frequency of neighborhood comparison index distributed ranges from 0.3475 to 0.6951 and 0.4374 to 0.6443 in both disturbed and undisturbed plots (Fig. 2).

In the disturbed plot, the neighborhood comparison index of Bp was mainly distributed in the values of 0.00, 0.25, and 0.5, and these values explained that the diameters with more than 80% target trees were larger than those of neighbor trees, which was in the absolute dominant position. Frequency distributions of Pk and Bc mainly focused on the values of 0.5, 0.75 and 1.00, which explained that these two species existed smaller than neighbors. The species Pd distributed evenly among all the values, and the average neighborhood comparison index was closed to 0.5 (0.4800). Pk was the chief species in the undisturbed plot, but the degree of dominance (frequency in the value 0.00) was inconspicuous. The average neighborhood comparison index of Bp trees was closed to 0.5 (0.5093), which was in the moderate position. The frequencies of an index in Am and Ta was mainly distributed in the values of 0.75 and 1.00, which explained that these two species existed smaller trees than neighbors. However, these trends changed slowly in this plot (Fig. 2).

Species associations and classification scheme

In the disturbed plot, Bp was positive correlated to Pk at scales ≤ 5 m and 19–21 m, tendencies towards segregation emerged at another scale. However, Bp and Pd trees showed significant aggregation at 8–30 m scales. On the contrary, Bc trees were negatively associated with Bp and Pk trees at larger scales. The trends of positive associations between Pk-Pd and Pd-Bc species pairs increased with scales, but species pairs of Pd-Bc showed negative association at scales ≤ 12 m. In the undisturbed plot, segregation trend of species pair of Pk and Bp was observed at ≤ 13 m scales, and when the scales increased, independent and positive associations emerged. In almost all scales, Pk and Am trees exhibited spatial independence. Trees of Ta were also negatively associated with Pk at scales 0–9 m. Species of Bp was conspicuous aggregated with Am and Ta at 0–16 m and 0–9 m scales, but this aggregate trend in species of Bp-Ta changed independent and segregation with the scales (17–30 m) accumulated. Am trees showed segregation versus Ta trees at short scales (0–3 m) and a tendency toward segregation at larger scales (27–30 m). More details can be seen in the supplementary Table S2.

The results of species association classification using the Wiegand scheme were basically consistent with the consequences of the bivariate pair correlation (Fig. 4). In addition, there were some partial overlaps among species pairs of Bp-Pk, Bp-Pd and Pk-Pd in the disturbed plot, which could be an indication of site homogeneity. However, in the undisturbed plot, partial overlaps were almost not existed among species pairs, which could be proof of the site heterogeneity.

Figure 4
figure 4

Species association classification using the Wiegand scheme in both disturbed (left) and undisturbed (right) plots.

Full size image

Species size diversity

Mark variogram showed positive correlations among all tree species at scales ≤ 12 m, 27–30 m and ≤ 6 m in two plots (Fig. 5). Consistent with the results of spatial distribution patterns (Fig. 2), and combined with the consequence of neighborhood comparison index (Fig. 1), mark variogram in Bp trees indicated that aggregation between large diameter Bp trees and other small-diameter trees occurred in the disturbed plot. Similarly, the mark variograms of Pk and Pd trees showed clumped distributions among the disturbed plot and the competition pressure between neighbors and references were also greater. The mark variogram of Bc trees showed no spatial correlation of tree diameter between co-dominant neighbors and references at any scale. Trends of mark variogram in trees of Pk and Bp were similar to the result of all trees. According to Fig. 1, mark variogram in Pk trees also indicated an aggregation between large diameter Pk trees and other small-diameter trees. In contrast to Pk trees, Am and Ta trees showed spatial no correlation at most scales. Only at scales of 14 m and 17 m, species of Ta showed a negative autocorrelation.

Figure 5
figure 5

Mark variograms for dominant species in the disturbed and undisturbed plot. The Y axes represents the γm(r) values, which is a measure of the similarity of the marks (here tree DBH) depending on the distance between points; the X axes represents the spatial distance scales. Black solid lines γm = 1 correspond to the values for the case with independent marks. Different colored solid lines show actual γm(r) values, where pink color represents all trees and gray shaded area indicates upper and lower of the limit 99% confidence envelopes.

Full size image

Discussion

After suffering from a serious disturbance, the natural forest can be divided into secondary, deforested and primary forest, according to the level of degradation21. The forest type of the undisturbed plot is broadleaved Korean pine forest. Korean pine forest, also called primary forest, which shows limited effects of human disturbance, has maintained its basic primitive forest form and relatively high stand stability22,23. The results of Table 1 and Fig. 1 are consistent with the spatial characteristics. These findings were attributed to the selective logging which took place 36 years ago, and most broad-leaved pioneer trees, such as Bp and Pd, regenerated under the canopy gaps24. As the dominant tree species, Pk kept the diameter distribution rule of the natural forest, but in the disturbed plots, the number of trees decreased. Univariate pair correlation function g(r) for most standing trees showed clustered patterns in almost all scales, except Pk trees. The species Pk in the disturbed plot was observed that aggregate pattern at fine scales, which could be attributable to the limited seed dispersal ability of the tree species, include the character of tree seeds (e.g., the larger-sized pine cones of coniferous tree species), or the spread ability of seeds was obstructed by the complex shape of breaches25,26,27. Environmental heterogeneity might have been contributed to the aggregated distributions at large scales28,29. The same result was observed in the undisturbed plot, in which the Pk trees showed a clumped distribution at scales 0–8 m. However, Trees of Bp and Am exhibited aggregation predominantly at two-thirds (< 20 m) scales. Besides environmental heterogeneity, this phenomenon might also be ascribed to logging, and several canopy gaps were created. Some intolerant tree species, such as birch and maple, got more light resources, grew good under the gaps, and showed agminated trends at coarse scales30,31. Forest spatial patterns are closely related to the distance scale32,33. However, there was some discrepancy between the uniform angle index and the pair correlation function. Shaaban et al. considered that the uniform angle index could not distinguish aggregation patterns in most cases27. Río et al. doubt about the measurement advantage of the angle measurement between neighborhoods in the distance-independent method34. The spatial distribution of trees may fit one pattern at one interval and another at a different interval35. This may suggest that the uniform angle index lacks the analysis and prediction of large-scale spatial patterns and can only analyze the spatial pattern between adjacent trees.

The value of the species mingling index not only reflects the average mixing state of a stand, but also expresses the diversity of tree species36. For the species mingling index, trees of Bp showed a low average value (0.5124) in the disturbed plot, while a high average value (0.7593) in the undisturbed plot. This result suggested that: (1) higher diversity in the undisturbed plot than the disturbed plot; (2) with the advance of progressive succession, the status of pioneer species was gradually reduced; (3) the proportion of Bp trees was decreased with an increasing degree of mixing. Trees of Pk, on the contrary, exhibited the opposite trend from Bp in the mingling index, which showed a high average value (0.6621) in the disturbed plot, and a low average value (0.3425) in the undisturbed plot. Graz discovered that the mingle degree of tree species in stand decreased with the increase of tree species composition proportion, and suggested that the mingling index was sensitive to the proportion of the species37. Our results are consistent with the findings of the Graz’s study. Similarly, trees of Pd and Bc in the disturbed plot, and trees of Am and Ta in the undisturbed plot, kept a high mingling index, because of their low species density proportion (Table.1).

Through bivariate pair correlation function and the Wiegand scheme with species association, we found that the species of Pd was positively associated with Bp and Pk at large scales (≥ 8 m and ≥ 14 m) in the disturbed plot. Since trees of Bp and Pk were ranked the first and second-largest individuals, and as the above mentioned Pk trees, meanwhile, were mainly small trees, these phenomena were not surprising. These findings are consistent with the previous work38. In the classification of species association using the Wiegand scheme, we found similar results, such as Bp trees was mixing with Pk, partial overlap with Pd, and segregation with Bc. The species pairs of Pk and Bp were also positively associated at specific scales, which suggested limited seed dispersal of the coniferous species, and Pk could thrive under Pd or Bp canopies39. Trees of Bc was negatively associated with the other three species at coarse scale intervals, which illustrated that canopies of some tree species provide unsuitable habitats for the recruitment of Bc, presumably through attenuation of incoming radiation31. We conclude that different species have different habitat requirements for persistence and recruitment40. In addition, the number of Bc trees was lower in the disturbed plot, indicating that the negative correlation was credible. In the undisturbed plot, trees of Pk were negatively associated with Bp and Ta at 0–13 m and 0–9 m scales, while no relevancies was observed between the species pairs of Am and Pk, and Am and Ta at the most scales. Pk was the dominant species in this plot, and the limited resources available could not meet the demand for all trees. Therefore, “self-thinning” likely triggered among the co-dominant or intermediate trees, so as to produce spatial segregate and independent41. The results of classification of species association showed the same. However, trees of Bp were positively associated with Am and Ta at some scales, which attributed to these tree species forming such situations in the early stage of succession8. According to the Wiegand scheme classification, trees of Bp was mixed with Ta and Am, but some segregation trends also exhibited between Bp and Am.

Shaaban analyzed the size differentiation between the reference and the neighbor trees using the differentiation index. However, this index is sometimes easy to confuse, that is, the partial information of the degree of differentiation cannot accurately determine whether the reference tree is surrounded by thicker adjacent trees27. Therefore, this study used the neighborhood comparison index which could more accurately quantify the degree of size differentiation among trees42. Combined with the mark variograms, the size relationship between the reference and the neighbor trees was further explained accurately. According to the neighborhood comparison index, Bp was the dominant species in the disturbed plot, and the nearly 80% proportion of more than two neighbor trees whose DBH was less than the reference tree. Meanwhile, combined with the results of the mark variograms, it was known that the diameters of Bp trees were larger than that of their adjacent trees with positive autocorrelation at fine scales. In this plot, the number of Pk trees was ranked only second to Bp trees. However, Pk was at a disadvantage in niche, which also proved that most of Pk trees grown under the canopy of Bp trees, which could provide good shade conditions for the growth of Pk trees, making Pk become the dominant tree species in the later stage of succession43. The neighborhood comparison index of Pd trees was close to 0.5, but the mark variograms showed obvious positive autocorrelation at a coarse scale, indicating that there were both big and small diameter sized positive autocorrelation neighbors with Pd trees. The small number of Bc trees showed the spatial no correlation of tree diameter.

Suzuki et al. specified that negative autocorrelation was uncommon in natural forests in which trees are distributed in a spatially random or clustered way, which is the instance in our research. In the undisturbed plots, the neighborhood comparison index of Pk and Bp showed that they were in the dominant and moderate positions, respectively44. According to the mark variograms, the young recruited trees of Pk were mainly aggregated with big diameter Pk trees on a particular scale (< 10 m), which also confirmed the seed dispersal mechanism of Pk18. Although Bp tended to be moderate, according to the results of the uniform angle index and bivariate pair correlation function g(r), the diversity of tree species gathered around the reference was higher than that of Pk trees, indicating that broad-leaved tree species had a strong tillering ability in the process of growth.

Conclusions

In this study, we used the spatial index and spatial pattern statistics to explore the spatial pattern and interspecific correlation of main tree species in the mixed forest under different degrees of disturbance and the spatial correlation of DBH of tree species based on Mark variograms. The findings of the current study may aid in efforts of forest management planning and ecosystem services. Tree species that showed positive correlations, such as species of Pk, can grow better under the crown of broad-leaved trees (Bp and Ta), which provided a reference basis for tree species after-culture of artificial aids to natural regeneration in disturbed plots. Meanwhile, different research methods of spatial distribution also help to improve the accuracy of spatial distribution and the interspecific association of tree species. However, due to the limited experimental conditions, we did not include saplings of DBH < 5 cm in our analysis. Therefore, there was a lack of results on spatial distribution between adult trees and saplings. Besides, the assembly of long-term monitoring data should be combined to analyze the influence of interference mechanism on the spatio-temporal dynamic change of tree species patterns in future research.

Materials and methods

Study area

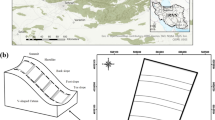
The study area is located in Wangqing County, Yanbian Autonomous Prefecture, located at Jilin province, in northeastern China (43° 06ʹ–44° 03ʹ N, 129° 51ʹ–130° 10ʹ E) (Fig. 6). This region belongs to the monsoon climate. The annual average temperature ranges from 3.7 to 4.2 °C, and the annual precipitation ranges from 580 to 700 mm. The frost-free period is 110 to 140 days. The number of days with annual snow cover ranges from 70 to 100 days, with a depth of 20–30 cm. The annual sunshine is 2700 h.

Figure 6
figure 6

Location map of disturbed and undisturbed plots in Wangqing County, Northeast China.

Full size image

Before the nineteenth century, there was little human disturbance in the Changbai Mountains' forests, but during the twentieth century, human disturbance became more frequent and severe, and the area of primary forest decreased by 70.4 percent from 1950 to 1986, unreasonable logging and overgrazing45,46. Because Korean pine is a dominant tree species of primary forest in northeastern China. These forests are the most productive, such as the wood quality of Korean pine is very good, and the seed can be bought at a higher price. Therefore, these forests are threatened by Human activities31,47. After suffering from a serious disturbance, the natural forest can be divided into secondary and primary forest, according to the level of degradation. In this study, we chose these two forest types as disturbed and undisturbed sample plots.

Data collection and analysis

We established the plot in an unevenly aged polar-birch secondary natural forest in 2012. The trees of this plot were formed by succession after logging (1986). The next year (2013), the other plot was established in the natural broad-leaved Korean pine forest that suffered from little disturbance because the plot was in the demonstration area in the local area. The acreage of both plots was 100 m × 100 m. Each plot was divided into regular grid 25 subplots of 20 × 20 m, and the grid intersections were marked with metal pipes. The coordinates, diameter at breast height (DBH), height of the standing free trees with > 5 cm DBH, which included juveniles and mature trees were measured in each subplot. The individuals were identified by their scientific species names.

The importance value (IV) is a comprehensive quantitative indicator used to characterize the status and role of each species in a community. In this research, IV was composed of relative density, relative frequency and relative dominance, which were equal to one-third of the sum of the above-mentioned three indexes. Detailed descriptions of the IVs can be found in Zhang et al.26. Finally, according to the ranking of important values, the top four tree species were selected as the main research tree species in both disturbed & undisturbed plots. The dominant tree species are Betula platyphylla Suk. (Betulaceae), Pinus koraiensis Sieb. et Zucc. (Pinaceae), Populus davidiana Dode (Salicaceae), Betula costata Trautv (Betulaceae), Acer mono Maxim (Aceraceae) and Tilia amurensis Rupr (Tiliaceae), more detailed description could be seen in the supplementary Table S1.

Both spatial indices in short distances (e.g., uniform angle index, mingling index, and neighborhood comparison index) and spatial functions (univariate and bivariate pair correlation function, mark variogram, and the Weigand scheme) were used to assess the spatial distribution of trees, respectively.

Spatial indices

Uniform angle index (Ui) describes the degree of regularity of the four trees' spatial distribution nearest to a target tree i. The concept is based on the classification of the angles αj (j from 1 to n) between the immediate neighbors of the n trees with reference to a target tree. Uniform angle index is defined as the ratio of all the reference angles αj smaller than the standard angle α0 to the total number of αj48. The Ui formula is as follows:

$$\begin{gathered} U_{i} = \frac{1}{4}\sum\limits_{j = 1}^{4} {z_{ij} } \hfill \\ z_{ij} = \left\{ \begin{gathered} 0, \, if\alpha_{j} < \alpha_{0} \hfill \\ 1,{\text{ otherwise }} \hfill \\ \end{gathered} \right.{\text{ and }}0 \le U_{i} \le 1 \hfill \\ \end{gathered}$$
(1)

The degree of isolation of tree species can be expressed as the mingling index (Mi). The mingling index describes the degree of spatial isolation of tree species in mixed forests and is defined as the proportion of the four nearest neighboring trees of another species48. It is expressed by the formula:

$$\begin{gathered} M_{i} = \frac{1}{4}\sum\limits_{j = 1}^{4} {z_{ij} } \hfill \\ z_{ij} = \left\{ \begin{gathered} 0,{\text{ neighbor }}j{\text{ belongs to the same species as the reference tree }}i \hfill \\ 1,{\text{ otherwise}} \hfill \\ \end{gathered} \right. \hfill \\ {\text{ and }}0 \le M_{i} \le 1. \hfill \\ \end{gathered}$$
(2)

The neighborhood comparison index (Ni) can be expressed as the competitive pressure of forest building group species and is defined as the size differentiation between neighboring trees and is calculated based on the ratio between thinner and thicker DBH of four nearest neighboring trees. The formula of Ni is as follows:

$$\begin{gathered} N_{i} = \frac{1}{4}\sum\limits_{j = 1}^{4} {k_{ij} } \hfill \\ k_{ij} = \left\{ \begin{gathered} 0,{\text{ if neighbor }}j{\text{ is smaller than the reference tree }}i \hfill \\ 1,{\text{ otherwise}} \hfill \\ \end{gathered} \right. \hfill \\ {\text{ and }}0 \le N_{i} \le 1 \hfill \\ \end{gathered}$$
(3)

Spatial patterns statistics

Comparing with the Ripley’s K function, the pair-correlation function g(r) is closely related to the second-order product density and can effectively prevent cumulative effects. The g-function was calculated as follows:

$$g(r) = \frac{dK(r)}{{dr}}/2\pi r,{\text{ for }}r > 0$$
(4)

The univariate pair correlation function is the expected density of points within a given distance r of an arbitrary point, divided by the intensity of the pattern. The bivariate pair correlation function is the ratio of the observed mean density of points of pattern 2 at distance r of an arbitrary point of pattern 1 to the expected mean density of pattern 2. When the spatial pattern of the trees is complete spatial randomness (CSR), the value of g(r) = 1 means that the trees are randomly distributed and independent association in a certain scale, the value of g(r) > 1 means aggregation and positive association, and g(r) < 1 means regularity and negative association over the entire plot49,50.

All associations of the tree species may show high variability; therefore, a two-dimensional classification space based on the two summary statistics K12(r) and D12(r) was used51. K12(r) was the bivariate Ripley K function and D12(r) was the nearest-neighbor distribution. The expectations of the two summary statistics under both the CSR and independence null models yield \({\mathrm{D}}_{12}\left(\mathrm{r}\right)=1-exp(-{\uplambda }^{2}\pi {\mathrm{r}}^{2})\) and \({\mathrm{K}}_{12}\left(\mathrm{r}\right)=\pi {\mathrm{r}}^{2}\). Both K12(r) and D12(r) were implemented to construct the scheme's two axes. The two axes P(r) and M(r) are defined as follows:

$$\begin{gathered} P(r) = \frac{{(D_{12} (r) - E[D_{12} (r)]}}{{SD[D_{12} (r)]}} \hfill \\ M(r) = \frac{{(K_{12} (r) - E[K_{12} (r)]}}{{SD[K_{12} (r)]}} \hfill \\ \end{gathered}$$
(5)

where \({D}_{12}\left(r\right)\) and \({K}_{12}\left(r\right)\) are estimated from observed data and the operators E[.] and SD[.] indicate the expectation and standard deviation of summary statistics at the neighborhood r under independence, respectively. The theoretical value of the two summary statistics K12(r) and D12(r) under the null model are subtracted from those observed to set the case of null association P(r) = M(r) = 052.

The statistics M(r) and P(r) evaluate two fundamental aspects of bivariate point patterns. If the proportion of the nearest neighbors within the range r is less than expected, P(r) value will be negative and vice versa. The distribution of P(r) and M(r) under the null model can be approximated by the standard normal distribution, thus the box delimited by values of [–2.33, 2.33] (which correspond to a p-value of 0.025 for two summary statistics individually) approximates the area where the null hypothesis cannot be rejected, and a given species departs more strongly from independence the farther away it is located from the box. Several fundamental types of spatial association patterns are possible for each neighborhood r53,54:

Type 0: no departures: neither K12(r) nor D12(r) show significant departure from the null model.

Type I: Segregation: Species pairs located in the lower-left quadrant show segregation because there are fewer individuals of species j within neighborhoods of radius r around individuals of species i than expected under the null model (M(r) < 0 and P(r) < 0).

Type II: Partial overlap: Species pairs located in the upper-left quadrants show partial overlap because individuals of species j occur more often within neighborhoods of radius r around individuals of species i, but a notable proportion of individuals of species i have fewer neighbors of species j than expected under the null model (M(r) > 0 and P(r) < 0).

Type III: Mixing: Species pairs located in the upper-right quadrant show a high degree of spatial association (mixing) because here individuals of species j occur more often within neighborhoods of radius r around individuals of species i, and individuals of species i have more neighbors of species j, than expected under the null model (M(r) > 0 and P(r) > 0).

Type IV: This association type is predicted to occur rarely when trees of species i are highly aggregated and few trees of species j overlap the cluster of species i (M(r) < 0 and P(r) > 0).

The spatial correlation of tree diameter was analyzed using a mark variogram. The mark variogram, γm(r) is a measure of the similarity of the marks (here tree DBH) depending on the distance between points and provides two critical characteristics: range from correlation and the strength of interaction. The definition of mark variogram can be described in following equation:

$$\gamma_{m} = 1/2E(m(x)) - (x + r)^{2} /\sigma_{m}^{2}$$
(6)

where, x and x + r denote the locations of two arbitrary points. When the distribution of trees is independent of the tree diameters, γm(r) takes the value of 1. In the presence of segregation, correlation is negative and γm(r) > 1. In contrast, a positive correlation indicates that the pairs of trees tend to have similar marks and results in γm(r) < 1.

General tests of hypotheses for spatial patterns statistics

The complete spatial randomness (CSR) null hypothesis was used in the spatial distribution of each tree species36. We postulated that taller tree height classes suppress the recruitment and growth of lower layers for the bivariate statistic, but lower layers do not affect higher trees55. Therefore, we fixed the upper layer tree height class locations and randomized the locations of the lower tree height class using a Poisson cluster null model. The null hypothesis for spatial correlation of tree diameters was complete spatial independence of the tree diameter distribution. This hypothesis was tested using the random labelling test56.

For all the analyses, we used 499 randomizations in the null model of Monte Carlo simulations to provide 99% confidence intervals57. To avoid edge effects, translation correction was used in the analyses. The spatial scale of distribution patterns (univariate) was selected in 0–25 m range, which is 1/4 of the minimum plot dimension58. The interspecific association was 0–30 m range, because of interaction between individuals can affect a limited scale and a larger scale has no biological significance1. To standardize, we chose 0–30 m range as the pattern scales. The Winkelmass 1.0 and Programita (2018) were used to compute the spatial indices and spatial patterns statistics51,59.