Introduction

It is essential to assess the risk of projects in high-risk areas with the economy growing, more and more projects are built and run in high-risk areas. The subsequent hostile threats resulted in significant losses and damages to project employees and assets. But only a limited fraction of security-related studies on projects in high-risk areas are currently available. Such studies, which are comparatively reliable but primarily rely on traditional risk assessment methods1 to determine risk levels and safety precaution recommendations, lack quantitative defensive Information about the defender.

The optimum defensive resource value and the optimum defensive strategy for the defender are obtained by the target loss probability model2,3 which is based on game theory and the Bayesian game model4 from the perspective of attack-defense confrontation, respectively. The target loss probability model, which is based on zero-sum game theory and has a developed application in the field of assessing the risk of terrorist attacks, but the criteria for quantifying and assigning factors in the model need to be improved5; the Bayesian game model, which is based on the static game theory of incomplete information, has been developed and widely used in network attack-defense scenarios, but it is rarely used in the field of realistic security risk assessment. In addition, the model’s primary problem is that it is not accurate enough to be used in realistic security risk assessment. The developed model’s relative simplicity, the quantification of attack-defense strategies should be improved, and the model’s priori probability value rely on historical experience, should have a higher objective6.

By combining the characteristics of projects in high-risk areas, redefining and quantifying the factors in the target loss probability model, and creating a set of attack-defense strategies under Bayesian game, this paper develops a security risk assessment model for projects in high-risk areas based on the two models and the existing relevant research7. In the Bayesian game model, the result of the target loss probability model is utilized as the priori probability value to assess the project's risk in the high-risk area and give objective, quantitative defensive information, including the optimum defensive resources and strategies8.

Methodology

Figure 1 depicts the overall framework of the risk assessment model based on the target loss probability model and the Bayesian game model. To construct and quantify the index system in the target loss probability model—target value V, attacker’s resources A, and defender’s resources D—to ascertain the project risk level and the optimum value for defensive resources, the method uses the cases related to project security in high-risk areas that have been gathered. It also combines traditional risk assessment theory with expert experience. In order to quantitatively determine the optimum defensive strategy for the project, a group of attack—defense strategies for security events in high-risk areas was first constructed and quantified, the research result of the target loss probability model was used as the prior probability value in the Bayesian game model, and then reasonably adjust the defensive resources for the project by the assessed risk level and optimum defensive resource value9.

Figure 1
figure 1

Framework for risk assessment of the projects in high-risk area.

Full size image

Construction of target loss probability model

The target loss probability model proposed by Major2 is based on the zero sum game—the attack and defense revenue matrix is zero. The problem it discusses and solves is: for a specific target, if terrorists launch an attack with certain resources, and the defender allocates resources to defend the target, how to determine the probability of target loss under the situation of the game between the attacker and the defender. On this basis, this paper applies the target loss probability model to the social security risk assessment of the projects in high-risk areas. The attack and defense parties are the enemies who attack the projects and the security management personnel of the projects. At the same time, combining the characteristics of the attack and defense parties in the social security incidents of the projects, we give new definitions to the factors in this model—target value V, attacker A, defender D, and take social security threat incidents as the target value, The two sides of the attack and defense are hostile elements and security management personnel from the projects. By studying the adversarial game process between the attack and defense sides, the risk level and optimal defense resource value are determined. The improved simplified model is as follows:

  • V: The target value, represented by the letter V, is the high-risk area project security event. The loss of consequences brought on by the security event defines the target value V, because it reflects the likelihood and desire of the attackers to launch an attack, and the attractiveness of the security event to the attackers.

  • A: The attacker is the enemy side in the security event involving the project in the high-risk area, and the attacker's total resources are AT. The attacker chooses the attack target and specific attack resources A to launch the attack, and the attack resources are primarily determined by the level of social security in the host country, the level of social security in the region, the capabilities of terrorist organizations in the region, the capabilities of public order and criminals in the region, ethnic and religious conflicts, and the attractiveness of the project.

  • D: The defender is the project's risk manager in the high-risk area, and its total resource allocation is DT, which allots defensive resources D to counteract various attacks. The defensive resources are determined based on the safety management organization structure of the project, security personnel strength of the project, security layout and physical protection of the project, technical protection of the project, emergency response, commuter security, sustainable compliance operation capability of the project.

  • The risk value is represented by the function \({\text{p(V,A, D)}}\).

  • The anticipated loss formula is as follows: The attacker constantly seeks to maximize attack likelihood and consequence loss, while the defender seeks to decrease it.

    $${\text{EL}}\;{ = }\;{\text{ V}} \cdot {\text{p(V, A, D)}}$$
    (1)

Based on this simplified model, it is known that when the defender defends against an assault using specific defensive resources and the attacker uses specific attack resources, the probability of loss for the attacked target is:

$${\text{p}}\left( {\text{V,A,D}} \right)\;{ = }\;\frac{{{\text{EL}}}}{{\text{V}}}\;{ = }\;{\text{exp}} - \left( {\frac{{{\text{A}} \cdot {\text{D}}}}{{\sqrt {{\text{V}}_{{}} } }}} \right){{ \times }}\left( {\frac{{{\text{A}}^{{2}} }}{{{\text{A}}^{{2}} {\text{ + V}}}}} \right)$$
(2)

\(- \frac{{{\text{A}} \cdot {\text{D}}}}{{\sqrt {\text{V}} }}\) denotes the probability of the attacker launching an attack and \(\frac{{{\text{A}}^{{2}} }}{{{\text{A}}^{{2}} {\text{ + V}}_{{}} }}\) denotes the probability of the attacker’s successful attack.

When under assault, the defender must continuously allocate defensive resources to the attack target with a high expected loss value (EL) until the attack target’s EL value approaches equilibrium. When the target EL values are equal, at which point \(\text{EL } = {\text{ EL}}^{0}\). Assuming that k is a normalization constant and that qi represents the probability that target i will be attacked:

$${\text{q}}\;{ = }\;\frac{{ - {\text{k}}}}{{{\text{V}}\frac{\partial }{{\partial {\text{D}}}}{\text{p}}\left( {{\text{V}}_{{}} {\text{,A,D}}} \right)}}\;{ = }\;\frac{{\text{k}}}{{{\text{VA}}^{{0}} {\text{EL}}^{{0}} {\text{V}}^{{ - \frac{{3}}{{2}}}} }}{ = }\frac{{{\text{k}}\sqrt {\text{V}} }}{{{\text{A}}^{{0}} {\text{EL}}^{{0}} }}$$
(3)

According to this equation, the attack resources allocated by the attacking side to the target are roughly equal to the open square of the target value. where A0 is the optimum attack resource, which can be solved by the following equation:

$${\text{A}}^{{0}} {\text{(V,D) = }}\frac{{{\text{V}}^{{\frac{{3}}{{2}}}} }}{{\text{D}}}{ + }\frac{{1}}{{9}}\sqrt {{\text{V}}^{{3}} {{ + 27 }} \times \frac{{\sqrt {3} \cdot {\text{V}}^{{3}} }}{{{\text{D}}^{{2}} }}} - \frac{{1}}{{3}}{{ \times }}\frac{{\text{V}}}{{\frac{{{\text{V}}^{{\frac{{3}}{{2}}}} }}{{\text{D}}}{ + }\frac{{1}}{{9}} \cdot \sqrt {{\text{V}}^{{3}} {{ + 27 }}\times\frac{{\sqrt {3} \cdot {\text{V}}^{{3}} }}{{{\text{D}}^{{2}} }}} }}$$
(4)

From Eqs. (2) and (4), the solution equation for the optimum defensive resource is as follows:

$${\text{D}}^{{0}} \;{ = }\;\frac{{\sqrt {\text{V}} }}{{{\text{A}}^{{0}} }}\;{{ \times }}\;{\text{ln}}\left[ {\frac{{\text{V}}}{{{\text{EL}}}}{{ \times }}\frac{{\left( {{\text{A}}^{{0}} } \right)^{{2}} }}{{\left( {{\text{A}}^{{0}} } \right)^{{2}} {\text{ + V}}}}} \right]$$
(5)

Construction of Bayesian game model10

Bayesian game model first evaluates the target value, summarizes the types of security events in high-risk areas and behaviors of attackers to construct a strategy set for both attackers and defenders. Then, the modle quantifies the cost- benefit by substituting the attack-defense benefit matrix into the Bayesian framework11, at the same time, using the result of the target loss probability model as the priori probability. The Bayesian attack defense game model is shown in Fig. 2.

Figure 2
figure 2

Bayesian game.

Full size image

Notations and definitions of Bayesian model model

The relevant symbols and definitions in the Bayesian attack defense game model are shown in Table 1.

Table 1 Definition of notation related to Bayesian model.
Full size table

Bayesian strategy set and cost–benefit

The set can be used to represent the attacker's strategy in a high-risk area project attack- defense scenario:

$${\text{A}}\;{ = }\;{\text{(a}}_{{1}} {\text{,a}}_{{2}} {,} \ldots {\text{,a}}_{{\text{n}}} {)}$$
(6)
$$\begin{array}{*{20}c} {s.t.} & {} \\ \end{array} 0 \le a_{1} ,a_{2} , \ldots ,a_{n} \le 1$$
(7)
$${\text{a}}_{{1}} {\text{ + a}}_{{2}} { + } \cdots + {\text{a}}_{{\text{n}}} = 1$$
(8)
$${\text{S}}_{{\text{A}}} \;{ = }\;\left. {\left\{ {{\text{A}} \in {\text{R}}^{{\text{n}}} {:}\;{0} \le {\text{a}}_{{\text{i}}} \le {1}\;{\text{ for}}\;{\text{ i}}\;{ = }\;{1,2,} \ldots {\text{,n,}}\mathop \sum \limits_{{\text{i = 1}}}^{{\text{n}}} {\text{a}}_{{\text{i}}} \;{ = }\;{1}} \right.} \right\}$$
(9)

This strategy can be described as a model of resource distribution for the defender:

$${\text{D}}\;{ = }\;{\text{(d}}_{{1}} {\text{,d}}_{{2}} {,} \ldots {\text{,d}}_{{\text{n}}} {)}$$
(10)
$$\begin{array}{*{20}c} {{\text{s}}{\text{.t}}{.}} & {{\text{d}}_{{1}} } \\ \end{array} {\text{ + d}}_{{2}} { + } \cdots {\text{ + d}}_{{\text{n}}} \;{ = }\;{\text{D}}_{{\text{T}}}$$
(11)

The defender’s strategy set is described as follows:

$${\text{S}}_{{\text{D}}} \;{ = }\;\left\{ {\left. {{\text{D}} \in {\text{R}}^{{\text{n}}} {:0} \le {\text{d}}_{{\text{i}}} \le {\text{D}}_{{\text{T}}} \;{\text{for}}\;{\text{ i}}\;{ = }\;{1,2,} \ldots {\text{,n,}}\mathop \sum \limits_{{\text{i = 1}}}^{{\text{n}}} {\text{d}}_{{\text{i}}} \;{ = }\;{\text{D}}_{{\text{T}}} } \right\}} \right.$$
(12)
$${{\upmu }}_{{\text{k}}} \left( {{\text{0}}\;{\text{ < }}\;{{\upmu }}_{{\text{k}}} \;{{ < }}\;{\text{1,}}\;\;\mathop \sum \limits_{{{\text{k = 1}}}}^{{\text{m}}} {{\upmu }}_{{\text{k}}} \;{{ = }}\;{{1}}} \right)$$
(13)
$${\text{U}}_{{\text{a}}}^{{\text{k}}} \;{ = }\;\mathop \sum \limits_{{\text{i = 1}}}^{{\text{n}}} {\text{p}}_{{\text{k}}} \times {\text{G}}_{{\text{k}}} \times {\text{P}}_{{\text{D}}} {,}\;{\text{k = 1,2,}} \ldots {\text{,m}}$$
(14)

The expected losses and gains of the defender can be expressed as:

$${\text{L}}\;{ = }\;\mathop \sum \limits_{{\text{i = 1}}}^{{\text{n}}} \left[ {\mathop \sum \limits_{{\text{k = 1}}}^{{\text{m}}} {\upmu }_{{\text{k}}} {\text{p}}_{{\text{k}}} {\text{LP}}_{{\text{D}}} } \right]$$
(15)
$${\text{U}}_{{\text{d}}} \,{ = }\; - {\text{L}}$$
(16)

By applying the most effective strategy, the attacker maximizes his expected benefit. Attacker A’s optimization problem is expressed as follows:

$${\text{maxU}}_{{\text{a}}}^{{\text{k}}} \;{ = }\;{\text{max}}\mathop \sum \limits_{{\text{i = 1}}}^{{\text{n}}} {\text{p}}_{{\text{k}}} \times {\text{ G}}_{{\text{k}}} \times {\text{ P}}_{{\text{D}}} {,}\;\;{\text{k}}\;{ = }\;{1,2,} \ldots {\text{,m}}$$
(17)

The defender’s objective is to minimize expected loss by allocating limited defense resources optimally to counter various sorts of attackers.

$${\text{maxU}}_{{\text{d}}} \;{ = }\;{\text{minL}}\;{ = }\;{\text{min}}\mathop \sum \limits_{{\text{i = 1}}}^{{\text{n}}} \left[ {\mathop \sum \limits_{{\text{k = 1}}}^{{\text{m}}} {\upmu }_{{\text{k}}} \times {\text{p}}_{{\text{k}}} \times {\text{ L }}\times {\rm P}_{{\text{D}}} } \right]$$
(18)

The Nash equilibrium is reached when the attack-defense sides are unable to increase or decrease their benefits by adjusting their strategies. For the complete information game, the Hessani transformation12 must be used to solve the static Bayesian Nash equilibrium. As a consequence, the Bayesian Nash equilibrium must satisfy the two following formulas:

$$\mathop \sum \limits_{{\text{i = 1}}}^{{\text{n}}} {\text{p}}_{{{\text{k}}^{*} }} {\text{LP}}_{{{\text{D}}^{*} }} \ge \mathop \sum \limits_{{\text{i = 1}}}^{{\text{n}}} {\text{p}}_{{\text{k}}} {\text{LP}}_{{{\text{D}}^{*} }} {\text{,p}}_{{\text{k}}} \in {\text{S}}_{{\text{a}}}^{{\text{k}}} {,}\;{\text{k}}\;{ = }\;{1,2,} \ldots {\text{,m}}$$
(19)
$$\mathop \sum \limits_{{\text{i = 1}}}^{{\text{n}}} \mathop \sum \limits_{{\text{k = 1}}}^{{\text{m}}} {\upmu }_{{\text{k}}} {\text{p}}_{{{\text{k}}^{*} }} {\text{LP}}_{{{\text{D}}^{*} }} \le \mathop \sum \limits_{{\text{i = 1}}}^{{\text{n}}} \mathop \sum \limits_{{\text{k = 1}}}^{{\text{m}}} {\upmu }_{{\text{k}}} {\text{p}}_{{{\text{k}}^{*} }} {\text{LP}}_{{\text{D}}} {,}\;{\text{d}} \in {\text{S}}_{{\text{d}}}$$
(20)

Combination weighting method based on game theory

The subjective and objective weighting method based on game theory13, which combines the respective advantages of the two methods to determine the weights, is founded on the fundamental idea of minimizing the difference between combination weights and individual weights, thereby minimizing the sum of deviations to maximize the interests of both attackers and defenders. The following are the method’s primary solution steps:

•For a basic set of weight vectors \(U = \left\{ {u_{1} ,u_{2} , \ldots ,u_{n} } \right\}\), these n vectors are arbitrarily linearly combined into a set of possible weights:

$${\text{U}}\;{ = }\;\mathop \sum \limits_{{\text{k = 1}}}^{{\text{n}}} {\upalpha }_{{\text{k}}} {\text{u}}_{{\text{k}}}^{{\text{T}}} \;\;\left( {{\upalpha }_{{\text{k}}} > 0} \right)$$
(21)

where u is one possible weight vector of the set of possible weight vectors and \(\alpha_{k}\) is a weight coefficient.

•According to game-theoretic principles, the linear combination weight coefficients are optimized by reducing the deviation of u from the individual uk in order to find consensus between the various weights \(\alpha_{k}\).

$${\text{min}}\left\| {\mathop \sum \limits_{{\text{j = 1}}}^{{\text{n}}} {\upalpha }_{{\text{j}}} \times {\text{ u}}_{{\text{j}}}^{{\text{T}}} - {\text{u}}_{{\text{i}}}^{{\text{T}}} } \right\|_{{2}} \;\;\left( {{\text{i}} = 1,2, \ldots ,{\text{n}}} \right)$$
(22)

The first order derivative needed for the optimization of the aforementioned equation can be determined using the matrix differentiation property as follows14:

$$\mathop \sum \limits_{{\text{j = 1}}}^{{\text{n}}} {\upalpha }_{{\text{j}}} \times {\text{ u}}_{{\text{i}}} \times {\text{ u}}_{{\text{j}}}^{{\text{T}}} \;{ = }\;{\text{u}}_{{\text{i}}} \; \times {\text{ u}}_{{\text{i}}}^{{\text{T}}} \;\;\left( {{\text{i}} = 1,2, \ldots ,{\text{n}}} \right)$$
(23)

which corresponds to the system of linear equations:

$$\left[ {\begin{array}{*{20}c} {{\text{u}}_{{1}} \cdot {\text{u}}_{{1}}^{{\text{T}}} } & {{\text{u}}_{{1}} \cdot {\text{u}}_{{2}}^{{\text{T}}} } & \cdots & {{\text{u}}_{{1}} \cdot {\text{u}}_{{\text{n}}}^{{\text{T}}} } \\ {{\text{u}}_{{2}} \cdot {\text{u}}_{{1}}^{{\text{T}}} } & {{\text{u}}_{{2}} \cdot {\text{u}}_{{2}}^{{\text{T}}} } & \cdots & {{\text{u}}_{{2}} \cdot {\text{u}}_{{\text{n}}}^{{\text{T}}} } \\ \vdots & \vdots & \vdots & \vdots \\ {{\text{u}}_{{\text{n}}} \cdot {\text{u}}_{{1}}^{{\text{T}}} } & {{\text{u}}_{{\text{n}}} \cdot {\text{u}}_{{2}}^{{\text{T}}} } & \cdots & {{\text{u}}_{{\text{n}}} \cdot {\text{u}}_{{\text{n}}}^{{\text{T}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\upalpha }_{{1}} } \\ {{\upalpha }_{{2}} } \\ \vdots \\ {{\upalpha }_{{\text{n}}} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {{\text{u}}_{{1}} \cdot {\text{u}}_{{1}}^{{\text{T}}} } \\ {{\text{u}}_{{2}} \cdot {\text{u}}_{{2}}^{{\text{T}}} } \\ \vdots \\ {{\text{u}}_{{\text{n}}} \cdot {\text{u}}_{{\text{n}}}^{{\text{T}}} } \\ \end{array} } \right]$$
(24)

• After deriving \(\left( {{\upalpha }_{{1}} {,}\;{\upalpha }_{{2}} {,}\; \ldots {,}\;{\upalpha }_{{\text{n}}} } \right)\) from this equation, it is normalized to:

$${\upalpha }_{{\text{k}}}^{*} { = }\frac{{{\upalpha }_{{\text{k}}} }}{{\mathop \sum \nolimits_{{\text{k = 1}}}^{{\text{n}}} {\upalpha }_{{\text{k}}} }}$$
(25)

The final weights are derived as follows:

$${\text{u}}^{*} { = }\mathop \sum \limits_{{\text{k = 1}}}^{{\text{n}}} {\upalpha }_{{\text{k}}}^{*} \cdot {\text{u}}_{{\text{k}}}^{{\text{T}}}$$
(26)

Construction of index system and attack-defense strategy set for projects in high-risk area

Construction of V, A, D index system

The methods used to construct the index system of each factor in the target loss probability model are literature collection and case study, and the construction principles should follow objectivity, typicality, operability and hierarchy. To this end, it should not only refer to the general attack-defense resource index system—the fundamental theory of risk assessment, but also combine the characteristics of projects in high-risk areas with real case studies. Therefore, when constructing the index system, it should also take into account the characteristics of projects in high-risk areas, realistic cases, pertinent literature, pertinent official websites, and the experience and knowledge of experts for revision in addition to referencing the general attack-defense resource index system-the basic theory of risk assessment. The target loss probability model is used to determine the risk level and the optimum defensive resource value on the basis of this index system, and the values of V, A, and D are determined by a combination weighting method based on game theory (fuzzy comprehensive evaluation method15 and entropy value method16). The indicators are constructed as depicted in Table 2.

Table 2 V, A, D indicators of projects in high-risk area.
Full size table

The following table provides instances of indicator quantification, with the quantification of indicators for both attackers and defenders set at three levels and the quantification of indicators for target values set at five levels. Table 3 describes the quantitative grading of social security indicators, while Table 4 describes the quantitative grading of indicators for the degree of functional operation damage of the target project17.

Table 3 Index level description of social security level.
Full size table
Table 4 Index level description of degree of damage to project operations.
Full size table

Construction of Bayesian game strategy set and quantification of the cost–benefit

The construction of the attack and defense strategy set in the Bayesian attack and defense game model and the quantification of cost–benefit grading are based on the DMAT classification method in the field of network attack and defense. The attack-defense resource index system is the major reference point for constructing the Bayesian attack-defense game strategy set for the project. In addition, it is also associated with realistic attack-defense cases. The attack-defense cost–benefit values have a range of 0–100, and the type of attackers is subdivided into public order/criminal criminals18 and local armed elements/terrorists19 based on the severity of the injury. The attack strategy is developed from the standpoint of typical strategies used in realistic cases, the cost of attack is taken into account from the enemy's weaponry, strategy, and type, and the benefit to both the attackers and defender is taken into account from the severity of the damage the enemy has caused. Split the cost–benefit of public order/criminal criminals into five categories, and local armed elements/terrorists into four categories. Table 5 provides the quantified cost benefit values for the attacking party.

Table 5 Quantification of the cost–benefit of the attacker’s strategy.
Full size table

Set the cost of each benchmark defensive strategy to range from 0 to 10, and the overall cost of defense to be 100. Based on the attack strategies, considering the difficulty and consequences of defending the attack behavior, and taking the project physical protection, technical protection, and security personnel protection strategies as the benchmark, an attack strategy oriented defense strategy is proposed to determine the cost–benefit of attack—defense. Table 6 describes the defense strategy set and costs.

Table 6 Defensive strategy set.
Full size table

The Bayesian attack-defense game can be solved using the attack-defense benefit matrix and the prior probability value after determining the cost–benefit ratios of attack and defense. The attack-defense benefit matrix and the prior probability value are input into the gambling game software20 to solve the Bayesian Nash equilibrium-optimum defensive strategy.

Results and discussion

Case validation

This study chooses a project in a high-risk ___location and conducts a case validation through field trips, conferences, and data collection, in order to confirm the validity of the model and the logic of the risk assessment procedure.

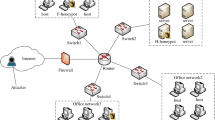
The project's basic setup is as follows: it encompasses an area of approximately 6000 acres, has a perimeter of approximately 10 km, 30 fence posts in total, three entrances and exits, and a regular, roomy surrounding road that is close to the local public safety department, fire department, and medical department. SPU (police) is responsible for guarding the project perimeter and protecting employees during their intermediary transportation, while security is responsible for the internal security work of the project, mainly maintaining order and dealing with emergencies. The project is placed in an extremely dangerous and complex social security environment, and its personnel precautions, physical precautions, technical precautions, and emergency response and disposal measures are either inadequate or generic. The project layout is shown in Fig. 3.

Figure 3
figure 3

Aerial view of project layout.

Full size image

The project’s risk assessment is validated based on the built security risk assessment model of the project in the high-risk area and the real scenario of the project, with the results as follows.

Results and discussion

Results of target loss probability model of the project

Combination weighting based on game theory of V, A, D

Table 7 shows the result values of the attacker’s resource value A.

Table 7 The value of attacker’s resource—A.
Full size table

Table 8 shows the result values of the defender’s resource value D.

Table 8 The value of defender’s resource—D.
Full size table

Table 9 shows the result values of the value of target’s resource V.

Table 9 The value of target’s resource—V.
Full size table
Results of target loss probability model

In order to do dynamic analysis, the target value—V, attacker’s resource—A, and defender’s resource—D are input into the target loss probability model. The results are shown in Table 10 and Fig. 4.

Table 10 Results of target loss probability model of the project.
Full size table
Figure 4
figure 4

Probability value P and loss expectation EL with different defensive resources.

Full size image

The adjustment of defense resource values will cause the probability of target loss to change, thereby affecting the risk level faced by the project. Therefore, the risk level can be divided based on the defense resource values. Figure 4’s target loss probability model results show that when defensive resources increase from 0.5 to 1.5, the target loss probability value is high and the project risk level is at its highest; by increasing defensive resources, the target loss probability value can be effectively reduced, lowering the risk level; when defensive resources from 1.5 to 2, the target loss probability value significantly decreases, and at this time, the project risk level is at its medium; when defensive resources are increased from 2 to 3, the target loss probability value and project risk level are the lowest,but there is no discernible change in the target loss probability value with the increase of defense resources, and the defense resources are now excessive. This is further supported by the expected loss EL result graph, which shows that the expected loss value reduces noticeably when defensive resource levels rise from 0.5 to 2, but does not alter much as defensive resource levels rise further. Combined with the target loss probability result value in Table 10, it can be seen that the risk level of the project is medium, and the optimum defensive resource should be increased by D0 over the basic defensive resource. Based on the results of the risk assessment, while considering the weaknesses in the actual safety prevention of the project, the optimum defense resource A0 is increased for the three aspects of the video surveillance system, the outlet control system and the quality of the security personnel, thereby reducing the target loss probability value. At this time, the target loss probability value is 0.024282469, with a low risk level, and there is no problem of excessive defense resources.

The existing literature on project risk assessment in high-risk areas is mostly based on traditional risk assessment theories to assess risk levels, such as Varbuchta et al.21, which expands the risk variables in large-scale transportation infrastructure projects on the basis of traditional risk assessment and applies them to the executed project assessment process; Li et al.22 combined risk management and public safety triangle theory to assess the risk level from vulnerability, threat, and key factors. In this paper, the target loss probability model is applied to the traditional risk assessment process, and indicators are constructed from the perspective of an attack-defense game in combination with realistic attack-defense scenarios. While obtaining the risk assessment level, the optimum defensive resource value facing the attacker is given.

Bayesian game model results of project

Quantitative values of the cost–benefit of attack and defense

Table 11 shows the quantification of attack and defense costs and benefits.

Table 11 Quantification of the cost–benefit of the attack-defense strategies.
Full size table
Mixed strategy Nash equilibrium solution—gambit software analysis

Figure 5 shows the attack and defense game tree constructed under different attacks. Figures 6 and 7 show the Nash equilibrium solutions for different types of attackers, respectively.

Figure 5
figure 5

Game tree of attack-defense under different types of attacks.

Full size image
Figure 6
figure 6

Nash equilibrium of the game under the type of law and order/criminal elements.

Full size image
Figure 7
figure 7

Nash equilibrium of the game under the type of local armed elements/terrorists.

Full size image

The Bayesian attack-defense game model’s findings show that Sa4 assassination/shooting, Sd2, is the most likely attack-defense strategy when confronting law and order/criminal elements, while Sa8 explosion/bombing, Sd6, is the most likely attack-defense strategy when confronting local armed elements/terrorists. At this point, the attack-defense games have each reached mixed strategy Nash equilibrium. The project security manager should increase D0 for the resources in strategies Sd2 and Sd6, respectively, in conjunction with the target loss probability model's optimum defensive resource value. This will not only significantly lower the project risk level, but will also maximize the sensible allocation of the optimum defensive strategy and resource value.

The prior probability value in existing Bayesian game models primarily relies on expert experience and historical data, and is mostly applied to network attack-defense game scenarios. For instance, Liu et al.23,24 proposed a generalized method of perfect Bayesian Nash equilibrium (BNE) for solving actual network attack-defense; Wang et al.25 combined Bayesian game theory and Markov decision methods to construct an incomplete information stochastic game model. However, the model in this study uses the target loss probability result as the attacker's prior probability value, combining the traits of high-risk projects to create Bayesian attack-defense games with various attacker types in realistic attack-defense scenarios, and more objectively determining the optimum defensive strategy against various attackers.

Conclusion

This paper constructs a security risk assessment model for projects in high-risk areas from the perspective of an attack-defense confrontation game to determine the risk level and optimum defensive information, and verifies the scientificity of the model using the example of a project in a high-risk area, which is based on the traditional risk assessment theory, the target loss probability model, and Bayesian game model. This model combines the characteristics of both attack and defense sides in project security in high-risk areas, innovatively taking security events and resources of both attack and defense sides as factors in the target loss probability model, and quantitatively assigning values based on these factors to obtain relevant risk values; at the same time, the types and strategies of attackers are classified to construct a Bayesian game model, and the target loss probability result is taken as its prior probability to obtain the optimum defensive strategy.

The model is modeled from the perspective of offensive defense confrontation game, solves the problem of focusing on the attacker’s analysis in the traditional risk assessment and defending’s insufficient analysis, quantitatively determines the defense’s optimum defense information, while solving the issue of unclear defense strategy classification in the previous Bayes offensive game model in the target loss probability model, the precursor probability value is not quantitative, the lack of consideration of the game dynamics process.

However, the target loss probability model and Bayesian game model used in project risk assessment models in high-risk areas are based on zero sum non cooperative game theory and incomplete information static game theory, respectively, which have certain limitations. Subsequent research can propose new risk assessment models based on different practical application scenarios and in combination with different game basic theories26. The key issue of this model is the identification of a project safety risk index and the screening and quantification of the index. Subsequent research can consider determining risk factors and indicators at various levels through the collection of big data and texts.