Introduction

Carbon fiber reinforced plastics (CFRP) has been widely applied in airplane and transportation, and the potential difference in CFRP and metal limits the fastener material. Usually, titanium alloy is adopted as the fastener material, such as high lock bolts, blind rivets, and rivets. Therefore, the demand for titanium alloy rivets will be increasing due to their excellent corrosion resistance, superior intensity, and low cost. Meanwhile, the difficult deformation and sensitivity to a strain rate of titanium alloy rivets are easy to result in driven head cracks1 and non-uniform interference-fit size2, which need to be solved. How to improve the interference-fit size uniformity of CFRP laminates riveted lap joints interference-fit size connection and the quantification of riveting interference-fit size have attracted much attention. A transversal ultrasonic vibration-assisted riveting process is developed to improve the plasticity of titanium alloy rivet and investigate the effect of amplitude, vibration time, and roughness on interference-fit size because the advantages of ultrasonic vibration-assisted forming technology can not only improve the metallic plasticity3, 4, but also mechanical properties5, 6. Hu et al.7 found that the ultrasonic dynamic impact effect can significantly improve the plasticity of metal and reduce the surface roughness of specimens. Zhou et al.8 investigated the effect of ultrasonic vibration on aluminum and titanium of lightweight metals, and the results showed that ultrasonic softening is affected by not only vibration amplitude but also frequency, and ultrasonic vibration also can refine the grains for lightweight metals. Djavanroodi et al.9 developed the superimposing ultrasonic vibration-assisted equal channel angular pressing, which can not only decline the punch load but also improve the mechanical properties. Zhuang et al.10 researched the mechanism of ultrasonic-assisted compression and found that both the flow stress and surface roughness declined.

Although ultrasonic vibration technology has been applied for decades, seldom scholars applied it in the riveting process. Interference-fit size is an important evaluation standard for the performance of riveted joints, hence it is necessary to investigate the effect of ultrasonic vibration parameters on interference-fit sizes. Lots of scholars have researched the relationship between interference-fit size and mechanical performance. Jiang et al.11 comprehensively studied the effect of different sidewall intersection angles of rivet dies on interference-fit size, and the fatigue tests showed that the pull-out fatigue property of the 80° driven head was the best due to its more uniform and moderate interference-fit size. Wei et al.12 carried out the fatigue tests for the CFRP joints with blind bolts of different interference-fit sizes, and found that the best interference-fit size of CFRP bolted lap joints under different cyclic stress were different, such as, the bearing stress was more than 660 MPa, the best corresponding interference-fit size was 1.8%. Li et al.13 studied the effect of interference-fit size and different percentages of ultimate bearing strength on the bearing fatigue response of CFRP/Ti alloy bolted joints and found that the fatigue life of interference-fit size under high tensile stress was 2.1%, the longest fatigue life of interference-fit size under low cycle stress was 1.2%. Hu et al.14 investigated the relationship between interference-fit size and stiffness of CFRP bolted lap joints, the results showed that the interference-fit size corresponding to the highest stiffness of CFRP bolted lap joints was 1.2%. To sum up, the effect of the interference-fit size of lap joints with the aluminum alloy rivet, high-locking bolt, and blind bolt et al. on mechanical properties are different, but the interference-fit sizes of CFRP riveted lap joints with better mechanical performances are lower than 2%.

An inhomogeneous expansion of the rivet shaft is the primary cause to restrict the improvement of riveting quality, which has attracted much attention. The non-uniform deformation of titanium alloy rivets is much worse than aluminum due to its poor plasticity. However, the unclear effects of ultrasonic vibration energy on interference-fit size distribution, hence it is necessary to explore the relationship between the ultrasonic vibration parameters and the interference-fit size and improve the uniformity of the interference-fit size. Scholars have explored ways to improve the uniform interference-fit size in both process and algorithm optimization. Skorupa et al.15 designed a novel rivet with a compensator, and a better uniform interference-fit size and fatigue performance were achieved. Cui et al.16 investigated the interference-fit size and forming mechanism of adiabatic shear bands with trapezoidal section rivet dies, and found that a reasonable riveting dies angle can effectively improve the uniformity of interference-fit size. Wang et al.17 proposed an integration method to optimize riveting parameters of pressure, riveting time, and dwelling time using the finite element method and Kriging metamodels with particle swarm optimization, and the optimized riveting parameters could improve the deformation homogeneity. Cao et al.18 developed a special gasket to restrain the expansion of the rivet shaft and inhibited the hole damage of CFRP caused by a large interference-fit size. In addition, scholars19, 20 also proposed the electromagnetic riveting process to achieve the uniform expansion of the aluminum alloy rivet shaft. Although the uniformity of interference-fit size in the riveted lap joints can be well improved, the quantitative and control method of interference-fit size is still lacking.

In this study, the unclear effects of ultrasonic parameters on the interference-fit size and mechanical performances of CFRP riveted lap joints were explored. First, the interference-fit sizes of CFRP riveted lap joints are measured, and introduced the coefficient of variance and the average value of interference-fit size. Second, the response surface algorithm, interpolation algorithm, and random forest are adopted to quantify and control the interference-fit size of CFRP riveted lap joints, and the optimized interference-fit sizes {IA, ICV-min, (C1, C2, C3)} are verified by experiments. Furthermore, the tensile tests were carried out, and the fracture mode and morphology were analyzed and observed.

Experimental procedures

Transversal ultrasonic vibration-assisted riveting system

In Fig. 1, the developed transversal ultrasonic vibration-assisted riveting (TUVAR) system mainly consists of a drive unit, an ultrasonic vibration assistance unit, and a data acquisition unit. The ultrasonic vibration assistance unit is in charge of providing acoustic energy. Specifically, when connecting with the power, the ultrasonic generator transfers the low-frequency electric energy to high-frequency electric energy. Then the ultrasonic transducer is used to transfer the electric energy to mechanical energy, furtherly the ultrasonic horn amplifies the vibration amplitude. Finally, the high-frequency mechanical vibration with an amplified amplitude is applied to rivets, until the compression is completed. In the TUVAR process, the vibration amplitude has a significant effect on the plasticity improvement of the Ti-alloy rivet based on the previous study4, which would further affect the rivet deformation and joint performance. The amplitudes with different power were measured by a dial indicator (Syntek-JR3), and the measured results are shown in Fig. 2.

Figure 1
figure 1

The schematic of the TUVAR system27.

Full size image
Figure 2
figure 2

The relationship between input power and amplitude27.

Full size image

Specimen preparation

The T700 CFRP laminates and Ti-45Nb rivets were selected for interference-fit sizes optimization and tensile specimens. T700 CFRP was using a unidirectional carbon fiber/epoxy with a thickness of 0.15 mm per ply (provided by GW COMPOS Company Ltd., China). The fabricated T700 CFRP laminate processes a thickness of 2.3 mm with 16 piles, the ply orientation of T700 CFRP is[0°/90°/45°/− 45°/− 45°/45°/90°0°]2 s, and the weight fraction of carbon fiber is about 60%. Material properties of the fabricated CFRP laminates are presented in Table 1. Moreover, the Fabricated Ti-45Nb rivets (provided by CAG Company Ltd., China) were annealed by heating in a vacuum (less than 0.1um mercury) to a temperature within the range of 1450–1600 °F, holding at heat for sufficient time to produce a recrystallized structure that will meet the requirements of 3.5. Material properties of the Ti-45Nb are presented in Table 1. In addition, the sizes of CFRP riveted specimens according to the ASTM D566121 are shown in Fig. 3, and W/D ≥ 6, E/D ≥ 3.

Table 1 Mechanical properties of the sample4.
Full size table
Figure 3
figure 3

Dimensions of the CFRP laminates riveted lap joint (dimension in mm).

Full size image

Experimental procedure

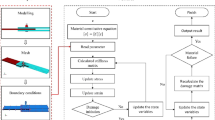
The experimental procedure is divided into three parts, as shown in Fig. 4. Part 1: the experiments of orthogonal and single factor were carried out, and the diameters of the deformed rivet bar were measured with three positions1, 18, as shown in Fig. 5. Furthermore, the relative interference-fit size {I1, I2, I3} of three positions were calculated by Eq. (1), and the average relative interference size (IA) and coefficient of variance of relative interference size (ICV) were introduced, the corresponding calculation equations are following in Eqs. (2, 3), respectively. Part 2: the {I1, I2, I3, IA, ICV} data set was analyzed by surface response algorithm (RSA), the relationship between ultrasonic process parameters vibration amplitude (C1), vibration time (C2), and roughness of rivet end surface (C3) with {I1, I2, I3, IA, ICV} are established, and the effective weight and P value were analyzed. Moreover, the random forest algorithm and extremely randomized trees are combined to evaluate the contribution value of process parameters, the corresponding calculation equations as follows from Eqs. (4, 5, 6, 7, 8). Furthermore, the minimum coefficient of variance of relative interference-fit size (ICV-min) and IA was as response targets, the user-defined subroutine using Python to optimize the (C1, C2, C3) by interpolation algorithm. The optimized {IA, ICV-min, (C1, C2, C3)} groups were verified by experiment, and the mean absolute percentage error (MAPE) of experimental and predicted {IA, ICV-min} was calculated. Part 3: the tensile tests specimens with {IA = 1.4%, 1.6%, 1.8%, 2.0%, and 2.2%} were carried out, the results of tensile ultimate strength were analyzed, and the fracture morphology was observed by HIROX-2000 ultra-depth three-dimensional microscope.

$$I = \frac{{D_{1} - D_{0} }}{{D_{0} }} \times 100\%$$
(1)

where D and D0 are the diameters of the deformed rivet shaft and initial riveting hole.

$$I_{A} = \frac{1}{N}\sum\limits_{i = 1}^{N} {I_{i} }$$
(2)

where IA presents the average relative interference size; N is the number of the measured positions of each deformed rivet; Ii is the relative interference size with different measured positions.

$$I_{CV} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {\Delta I_{i} - \frac{1}{N}\sum\limits_{i = 1}^{N} {\Delta I_{i} } } \right)^{2} } } /\left( {\frac{1}{N}\sum\limits_{i = 1}^{N} {\Delta I_{i} } } \right)$$
(3)

where ICV presents the coefficient of variance of relative interference size, i.e. the evaluation index of interference-fit size uniformity. To accurately evaluate the contribution value of the TUVAR process parameters, the random forest, and extremely randomized trees are adopted to quantize the weight magnitude of the process parameters22, 23. Considering the disadvantages of the algorithm analysis, the random forest and extremely randomized trees are used to authenticate and take the mean of multiple cycles superposition calculation.

Figure 4
figure 4

Experimental process of interference-fit size optimization.

Full size image
Figure 5
figure 5

Experimental process of interference-fit size optimization24.

Full size image

Experimental results and discussions

Interference-fit size analysis

Interference-fit size has a significant effect on the mechanical properties of CFRP riveted lap joints25. The relative interference-fit sizes {I1, I2, I3} correspond to the measured positions (P1, P2, P3) based on Fig. 5. Each position of the deformed rivet bar was repeated three times at intervals of 120° using a Vernier caliper with the precision of 0.01 mm. Furthermore, the {I1, I2, I3, IA, ICV} are calculated with Eqs. (1, 2, 3), respectively. The calculated results of {I1, I2, I3, IA, ICV} were listed in Table 2, where scheme 0 is the conventional riveting process without ultrasonic vibration, the scheme 1–28 are the transversal ultrasonic vibration-assisted riveting (TUVAR). But scheme 16 is disqualification, because of the severe damage around the CFRP riveted hole. It could be seen that the ICV of scheme 0 is 0.369, which is much larger than the ICV of TUVAR schemes. Therefore, the uniformity of the interference-fit size can be well improved by transversal ultrasonic vibration. It also could be seen that the IA of scheme 16 is 0.0504, which is much larger than the upper limit value of 0.02 of interference-fit size for CFRP laminates riveted lap joints. It is because the acoustic energy with the largest amplitude 31 μm and vibration time 2.0 s, which make the Ti-45Nb rivet soften and promote the severe deformation of the rivet, and leadqa to the IA of scheme 16 remarkable increase.

Table 2 The calculated results of the {I1, I2, I3, IA, ICV}.
Full size table

As shown in Fig. 6, the {I1, I2, I3, IA, ICV} of conventional riveting (scheme 0) and the typical TUVAR (scheme 9) at the same pressure and velocity are compared. It could be seen that the interference-fit size of P1 declined, and the interference-fit size of P2 improved under TUVAR. Hence, the TUVAR can well overcome an aperture constraint and promote the hole entrance material to flow into the P2 region, which improves the uniformity of interference-fit size a lot, and it has been identified from the microscale24. Besides, the IA of TUVAR increases by about 14.7%, because more material from the driven head flows into the riveted hole under TUVAR. The comparison of ICV of conventional riveting and TUVAR showed that the ICV decreases about 9 times. Hence, a much more uniform interference-fit size of CFRP riveted lap joint can be achieved with the assistance of transversal ultrasonic vibration, which contributes a possibility for the interference-fit size quantization of riveted lap joint.

Figure 6
figure 6

The comparison of {I1, I2, I3, IA, ICV}: conventional riveting (scheme 0), TUVAR (scheme 9).

Full size image

Interference-fit size optimization by response surface algorithm

The user-defined RSA is used for the process data set in Table 2, and the variance analysis result (Model, C1, C2, C3) of the {I1, I2, I3, IA, ICV} are displayed in Table 3. It is acknowledged that the P ≤ 0.05, the model, and factors are significant. The predicted models for {I1, I2, I3, IA, ICV} are shown in Eqs. (4, 5, 6, 7, 8). According to the evaluation index of P-value, the models of {I1, I2, I3, IA} are significant, except the ICV. It means that the model relationship between the ICV and (C1, C2, C3) is poorly reliable, hence the process parameter (C1, C2, C3) cannot be directly optimized by the ICV model. Therefore, the predicted function of Eq. (8) cannot be straightly applied to the reserve solving and optimizing the TUVAR process parameters, Eq. (3) is still adopted to calculate the ICV.

Table 3 Variance analysis of the {I1, I2, I3, IA, ICV}.
Full size table

According to the independent P-value of (C1, C2, C3) on {I1, I2, I3, IA}, it could be obtained that C1 and C2 have a significant effect on {I1, I2, I3, IA}, except C3. For ICV, the independent P-values of (C1, C2, C3) are larger than 0.05, which is insignificant. Besides, the significance ranking of (C1, C2, C3) on {I1, I2, IA} is C1 > C2 > C3, and the significance ranking of (C1, C2, C3) on I3 is C2 > C1 > C3. The reason for the significance ranking of I3 is considering that the ultrasonic vibration attenuation transfer mode leads to softening effect reduction in the P3 area. Meanwhile, the random forest algorithm and the extremely randomized trees were used to verify and quantify the contribution values of process parameters (C1, C2, C3) for the RSA results. After several times training by random forest algorithm, the results are shown in Fig. 7. It could be seen that the contributions of process parameters (C1, C2, C3) have a good consistency with the P values of (C1, C2, C3) by RSA, which further identify the analysis results RSA is reliability. In Fig. 7, the effect weight values of process parameters (C1, C2, C3) for {I1, I2, I3, IA, ICV} are {I1: (0.576,0.276,0.148), I2: (0.532,0.288,0.190), I3: (0.406,0.422,0.152), IA: (0.463,0.380,0.156), ICV: (0.511,0.295,0.149)}, respectively.

Figure 7
figure 7

Quantitative weight coefficient: the effect weight of (C1, C2, C3) on {I1, I2, I3, IA, ICV}.

Full size image

According to the RSM analyzed results, the relationship between parameters and {I1, I2, I3, IA, ICV} are built by the least square method (as shown in Eq. 4). To reveal the interaction of process parameters (C1, C2, C3) on the IA, the four-dimensional bubble charts and RSA charts are combined based on experimental results and Eqs. (5, 6, 7, 8), as displayed in Fig. 8. In Fig. 8a, it could be seen that the larger of amplitude and time is, the larger IA is achieved. In Fig. 8b–d, it can be seen that amplitude and time have a larger effect on IA, and the effect of roughness on IA is minimal. Due to the insignificant effect of parameters on ICV, the corresponding four-dimensional bubble charts, and RSA charts are not analyzed.

$$y^{\prime}\left( x \right) = \beta_{0} + \sum\limits_{i = 1}^{n} {\beta_{i} x_{i} } + \sum\limits_{i = 1}^{n} {\beta_{ii} x_{i}^{2} } + \sum\limits_{i = 1}^{n} {\beta_{ij} x_{i} } x_{j} + \varepsilon$$
(4)

where xi is the process parameter, ε is a residual error, and β0 βi βii βij are undetermined coefficients.

$$\begin{aligned} I_{1} = & 0.0781838 - 0.00406381C_{1} - 0.0171465C_{2} - 0.00953967C_{3} + 0.968158 \times 10^{ - 4} C_{1}^{2} + 0.00400439C_{2}^{2} \\ & \quad + 0.00505722C_{3}^{2} + 0.00118399C_{1} * C_{2} - 0.536399 \times 10^{ - 3} C_{1} * C_{3} - 0.00540458C_{2} * C_{3} \\ \end{aligned}$$
(5)
$$\begin{aligned} I_{2} = & 0.0693615 - 0.00366412C_{1} - 0.0186017C_{2} - 0.00846697C_{3} + 8.84606 \times 10^{ - 5} C_{1}^{2} + 0.00362884C_{2}^{2} \\ & \quad + 0.00447198C_{3}^{2} + 0.00115261C_{1} * C_{2} - 4.9163 \times 10^{ - 4} C_{1} * C_{3} - 0.00408892C_{2} * C_{3} \\ \end{aligned}$$
(6)
$$\begin{aligned} I_{3} = & 0.0293963 - 3.29405 \times 10^{{{ - }4}} C_{1} - 0.00442068C_{2} - 0.00809061C_{3} + 2.56606 \times 10^{ - 5} C_{1}^{2} + 0.0021805C_{2}^{2} \\ & \quad + 0.00270885C_{3}^{2} + 0.000159745C_{1} * C_{2} - 2.98161 \times 10^{ - 4} C_{1} * C_{3} - 3.41037 \times 10^{ - 4} C_{2} * C_{3} \\ \end{aligned}$$
(7)
$$\begin{aligned} I_{A} = & 0.0589805 - 0.00268578C_{1} - 0.0133896C_{2} - 0.00869902C_{3} + 7.0312 \times 10^{ - 5} C_{1}^{2} + 0.00327124C_{2}^{2} \\ & \quad + 0.00407935C_{3}^{2} + 0.000832113C_{1} * C_{2} - 4.42085 \times 10^{ - 4} C_{1} * C_{3} - 0.00327818C_{2} * C_{3} \\ \end{aligned}$$
(8)
$$\begin{aligned} I_{CV} = & 0.654294 - 0.0338104C_{1} - 0.244662C_{2} - 0.0434314C_{3} + 5.32342 \times 10^{ - 4} C_{1}^{2} + 0.032368C_{2}^{2} \\ & \quad + 0.0136514C_{3}^{2} + 0.0100315C_{1} * C_{2} - 0.0012415C_{1} * C_{3} - 0.0142186C_{2} * C_{3} \\ \end{aligned}$$
(9)
Figure 8
figure 8

Bubble chart and RSA of IA: (a) bubble chart, (b) amplitude-time, (c)amplitude-roughness, (d) time-roughness.

Full size image

Therefore, according to the RSA and interpolation method, a user subroutine is defined by Python. First, the IA is the quantized target of interference-fit size to obtain the data set {(C11, C22, C33) … (C1i, C2i, C3i)}. Then the data set {(C11, C22, C33) … (C1i, C2i, C3i)} are transferred to Eqs. (4, 5, 6) to achieve data set {(I11, I22, I33) … (I1i, I2i, I3i)}. Furthermore, the data set {(I11, I22, I33) … (I1i, I2i, I3i)} are inputted in Eq. (3) to calculate and output data set {ICV1 … ICVi}, then looping comparison the ICV1 to ICVi and confirming the ICV-min, as shown in Fig. 4. Finally, based on ICV-min to confirm the optimal process parameters (C1, C2, C3). The optimized and predicted {IA-p, ICV-min, (I1, I2, I3), (C1, C2, C3)} are listed in Table 4. It could be seen that the value of ICV-min is less than 0.1, except for predicted schemes 1 and 11. But the maximum deviation of (I1, I2, I3) for predicted schemes 1 and 11 are 0.0033 and 0.0048, respectively, compared with the maximum deviation of (I1, I2, I3) for conventional riveting is 0.0128, the uniformity of interference-fit size significantly improves.

Table 4 Predicted results of relative interference sizes by interpolation algorithm.
Full size table

Considering the unavoidable measurement error leading to IA out of tolerance, the predicted schemes {2, 4, 6, 8, 10} were verified by TUVAR experiments. And Eq. (9) is used to calculate the mean absolute percentage error (MAPE) of IA and ICV. The results of verification experiments and the MAPE analysis of IA and ICV are listed in Table 5. Furthermore, the bar charts of IA and ICV MAPE are displayed in Fig. 9, which could be a more intuitive comparison of MAPE values. Comparing with the predicted IA (IA-p) and experimental measurement IA (IA-m), it could be seen that the values of IA MAPE are lower than 10%. Therefore, the IA-p and IA-m have good consistency. In addition, the minimum IA MAPE of 1.099% is achieved, when the IA is 0.018. However, the values of ICV MAPE are larger than 10%, except the Scheme 6, the values of ICV MAPE for Scheme 2 and Scheme 4 are less than 20%, and the values of ICV MAPE for Scheme 8 and Scheme 10 are larger than 20%. Therefore, the consistency of ICV-m and ICV-p is poor, but the minimum ICV MAPE is 5.630% when the IA is 0.018. To sum up, when the IA is 0.018, both the MAPE(IA) and MAPE(ICV) are minimum.

$$MAPE = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {\frac{{\hat{y}_{i} - y_{i} }}{{y_{i} }}} \right| \times 100\% }$$
(10)

where \(\hat{y}_{i}\) represents the predicted value of IA by interpolation algorithm, yi is the measured value of IA by experiments.

Table 5 The results of verification experiments and the MAPE analysis of IA and ICV.
Full size table
Figure 9
figure 9

The bar chart of MAPE: (a) MAPE-IA, (b) MAPE-IA.

Full size image

Mechanical property analysis

Tensile tests of TUVAR riveted lap joint specimens were carried out with the relative interference size IA = {1.4%, 1.6%, 1.8%, 2.0%, and 2.2%}. The repeated results of tensile tests for different relative interference-fit sizes are listed in Table 6. The typical average load–displacement curves of five groups of specimens are displayed in Fig. 10a. The load–displacement curves are divided into three-stage, i.e. stage 1: hole elastic deformation, stage 2: hole plastic deformation, and stage 3: hole failure. In stage 1, the maximum tensile strength of the interference-fit sizes IA = {1.6%, 1.8%, 2.0%, 2.2%} have a good consistency, and the elastic maximum tensile load is about 3800N. However, the maximum bearing load of the interference-fit size IA = 1.4% in stage 1 is lower than the interference-fit sizes IA = {1.6%, 1.8%, 2.0%, 2.2%}, and the elastic maximum tensile load is about 3600 N. In stage 2, it could be obtained that the tensile load of I = 1.4% is still less than others. The ultimate strength of different interference-fit sizes is listed and marked with red rectangular regions.

Table 6 The repeated results of tensile tests for different interference sizes.
Full size table
Figure 10
figure 10

Analysis of tensile experiments: (a) typical average tensile curve with different IA, (b) maximum load analysis.

Full size image

To straightly analyze the variation tendency of tensile strength with the different interference-fit sizes, the relationship between the relative interference-fit sizes and maximum load is displayed in Fig. 10b. It could be seen that the tensile strength increases at first and then declines with the increase of interference-fit size. There is a maximum ultimate strength when the interference-fit size IA = 2.0%, and the difference in tensile strength is not significant with IA = 1.8%. An appropriate interference-fit size is beneficial to the stiffness improvement of the CFRP riveted lap joints. However, the maximum tensile strength of the specimen with the interference-fit size IA = 2.2% is lower than IA = {1.8%, 2.0%}. This phenomenon may be attributed to the severe damage to the hole wall surface by the rivet rod expansion after the TUVAR, especially the micro-scale carbon fiber damage in local regions. Moreover, earlier researches13, 26 showed that micro-scale damage near the hole surface area varies with interference-fit size. As a consequence, appropriate interference-fit size can well realize a close fit between the deformed rivet shaft and the hole wall. Meanwhile, uniform interference-fit size can increase the actual contact and provide a reaction force of the hole wall, and decline the stress value and uniform stress distribution. However, the large interference-fit size (e.g. IA = 2.2%) will induce delamination, fiber fracture et al., which resulted in the reduction of riveted lap joints. As a result, proper interference-fit size is beneficial to the improvement of the ultimate tensile strength of CFRP laminates riveted lap joints, whereas an excessive interference fit can reduce the maximum tensile strength.

Conclusion

In this paper, the TUVAR experiments were carried out to investigate the effect of process parameters on the interference-fit size of the CFRP riveted lap joints. Multiple arithmetics are combined to optimize the TUVAR process parameters and quantized the interference-fit size. Meanwhile, the tensile tests were carried out to identify the accuracy of the optimized results. the main conclusions were drawn as follows:

  1. (1)

    Compared with conventional riveting, the P2 position interference-fit size of TUVAR increases, significantly, and the P1 position interference-fit size declines a lot. the coefficient of variance of relative interference size decreases about 9 times, and the uniformity of interference-fit size under the TUVAR improves significantly

  2. (2)

    The results of the quantitative weight coefficient show that process parameters have a significant effect on {I1, I2, I3, IA}. In addition, the vibration amplitude is the maximum weight coefficient, then the time and roughness, and the average weight coefficients are 0.497, 0.336, and 0.167, respectively

  3. (3)

    The MAPE results of the IA and ICV by the inverse solving algorithm and the experiment showed that the MAPE of the IA is lower than 10%, which has a good prediction accuracy. But the MAPE of the ICV is larger than 20% when the interference-fit size is over 2.0%, which showed that uniform interference-fit sizes of TUVAR are difficult to achieve by combining with the MAPE of the IA.

  4. (4)

    The results of tensile tests showed that the best interference-fit size of the riveted specimen under the TUVAR is 1.8% or 2.0%, and the maximum tensile load arrives at 4562.564 N. Compared with the interference size of the riveted specimen under conventional riveting, the tensile load improves by 6.94%.