Abstract
In this study, we developed a new method of topology optimization for truss structures by quantum annealing. To perform quantum annealing analysis with real variables, representation of real numbers as a sum of random number combinations is employed. The nodal displacement is expressed with binary variables. The Hamiltonian H is formulated on the basis of the elastic strain energy and position energy of a truss structure. It is confirmed that truss deformation analysis is possible by quantum annealing. For the analysis of the optimization method for the truss structure, the cross-sectional area of the truss is expressed with binary variables. The iterative calculation for the changes in displacement and cross-sectional area leads to the optimal structure under the prescribed boundary conditions.
Similar content being viewed by others
Introduction
Topology optimization is the problem of finding a combination of components that provides high performance at a low cost, such as in designs of bridges, towers, and so on1,2,3. When trying to solve a combinatorial optimization problem such as topology optimization, it is possible to get stuck in a local solution during the computation. Therefore, repeated calculations are required with small steps to obtain a globally optimal solution4. Such small steps increase the computational cost, and thus computational methods that avoid getting stuck in local solutions are becoming increasingly important.
In recent years, quantum computers have been applied to solving some practical problems5,6,7,8,9,10. Quantum computers are attracting attention owing to their capability to perform calculations faster than classical computers for some problems.
Quantum computers use properties such as quantum superposition and quantum entanglement to achieve high-speed computation. A bit used in a classical computer represents a state of 0 or 1. In contrast, a qubit used in a quantum computer can handle a superposition of 0 and 1. This allows multiple states to be computed in parallel. Quantum entanglement also enables the handling of quantum interactions between distant qubits11,12. In a classical computer, the state of one bit does not affect the state of other bits, whereas in a quantum computer, a change in the state of one qubit can in conjunction change the state of other qubits. This interaction between different qubits is called quantum entanglement. This makes it possible to manipulate multiple interacting qubits simultaneously13,14.
Schematic of the system of quantum annealing14.
There are two types of quantum computer, i.e., the quantum gate model15,16,17 and quantum annealing18,19,20. The quantum gate model has been studied more extensively than quantum annealing, and it is observed to be more efficient than classical computers for some calculations, such as simulations of quantum mechanics21,22,23,24,25,26,27. However, the large-scale circuits with a large number of qubits, which are the basic elements are still unstable. Quantum annealing, on the other hand, also uses qubits as basic elements and specializes in solving discrete optimization problems.
The difference between gate-based quantum computers and quantum annealers lies in the difference in the method of quantum computation. Gate-based quantum computers performs quantum computations by applying a series of quantum gates to manipulate the quantum state of qubits. Quantum annealers, on the other hand, are a physical implementation of the adiabatic theorem. The adiabatic theorem states that when a quantum state is the ground state in an initial Hamiltonian if the Hamiltonian changes slowly enough, the quantum state maintains the ground state of the Hamiltonian after the change. In quantum computers, the quantum states are disturbed by unwanted state changes caused by noise to the quantum system28. This is because it is difficult to isolate the qubits sufficiently from the effects of external noise, in contrast to a classical computer, which has a robust on/off state of transistor switches distinguished by billions of electrons29. For this reason, gate-based quantum computers generally cannot perform calculations robust to noise unless the error rate of the gate is kept below a certain level30. However, there are theoretically noise-tolerant computational schemes in quantum computers, and adiabatic quantum computation (AQC) is one of them. The reason why AQC is robust to noise is claimed in the literature31 as follows: (1) The phase of the ground state does not affect the effectiveness of the algorithm. (2) Transitions between eigenstates are problematic for AQC, but AQC is efficient only when the minimum energy gap of the Hamiltonian is not too small, and should be robust against decoherence in such situations. (3) If the error in the Hamiltonian due to noise changes slowly and the initial and final errors are not too large. The nature of AQC allows for reasonably large deviations from the original Hamiltonian. Since the quantum annealing machine is one implementation of AQC, the quantum annealing machines are expected to be robust against noise. In 2023, a quantum computer capable of handling more than 5,000 qubits was developed by D-Wave21.
Quadratic Unconstrained Binary Optimization (QUBO) is a type of combinatorial optimization problem that can be solved by quantum annealing. The following equation describes the Hamiltonian of QUBO:
The Hamiltonian of QUBO is the sum of the product of two binary variables \(q_{i}\) and \(q_{j}\) multiplied by a constant \(-Q_{i j}\). Converting the combinatorial optimization problem into QUBO Hamiltonian, it can be computed using quantum annealing26,32,33,34,35.
Quantum annealing is based on the principle of the tunneling effect caused by quantum fluctuations, which induces state transition, achieving the ground state. The ground state is finally achieved by the operation of quantum fluctuations, i.e., by first giving large quantum fluctuations and then gradually minimizing them. Figure 1 shows a schematic of quantum annealing. Quantum annealing has already been applied to solving discrete optimization problems such as traffic volume control and nurse scheduling36,37,38. Some studies have shown a marked increase in computational speed by a factor of approximately 100 million.
Recently, a method of solving linear systems called FEqa has been proposed for problems discretized by the finite element method39. In this method, the finite element problem is calculated using a classical computer, and quantum annealing is used to minimize the residuals. Quantum annealing may have more advantages in structural optimization problems. This is because quantum annealing finds the global optimal solution efficiently, which leads to a higher computation speed than in the case of using a classical computer.
The objective of this study is to develop an optimization method for truss structures by quantum annealing. To represent real numbers using binary variables, among various methods for representing the real numbers40,41,42,43,44,45, we employ the method of “combinatorial random number sums”46. The deformation analysis of a truss structure with quantum annealing is performed by expressing the nodal displacement with binary variables. The Hamiltonian is formulated on the basis of the elastic strain energy for infinitesimal deformation and the position energy of the truss structure. The optimization analysis of the truss structure is performed by quantum annealing by also expressing the cross-sectional area of the truss structure as a binary variable.
There are several prior studies that have used quantum annealing to optimize truss structures. In a previous study, a topology optimization method for quadrilateral elements using quantum annealing has been proposed47,48. On the other hand, our research aims to optimize the cross-sectional area of a truss, which is a different target problem. There is also research that transforms the problem of optimizing the cross-sectional area of a truss structure into a form that can be solved by quantum annealing using the principle of minimum potential energy in the form of order reduction49. This work requires the introduction of ancilla qubits to simultaneously optimize the displacement and the cross-sectional area. While this method has a formulation similar to the classical method, it cannot handle large problems. However, our method can handle large problems because it can be analyzed by annealing without using ancilla qubits by introducing an approximation for small deformations. In addition, this study employs binary sums for the representation of real numbers, but for complex problems, the correct solution may not be obtained. On the other hand, our study uses a random combinatorial sum representation of real numbers, which may lead to more accurate solutions46.
The objective of the optimization problem in this study is to find the truss structure with the lowest displacement and highest stiffness under the same boundary conditions, with the design condition being the cross-sectional area. To achieve this, the deformation analysis and the calculation of the cross-sectional area changes are performed using quantum annealing. In the deformation analysis, the objective function is first minimized and consists of the sum of the elastic strain energy of the truss and the energy due to external forces. A small deformation approximation is used to formulate the objective function using nodal displacements as variables. Then, the objective function, defined as the elastic strain energy of the truss, is maximized in the section on changes in the cross-sectional area. Additionally, a constraint is imposed to keep the total sum of the truss sectional areas constant, using sectional areas as the variables.
The variables used in the calculations in this study are displacements and cross-sectional areas, which are continuous variables, while the variables that can be used in quantum annealing are binary variables. Therefore, it is necessary to represent real numbers using binary variables. In this study, real numbers are represented using the method called the combinatorial random number sums. Using this method, the objective function can be converted to a QUBO format, which allows for quantum annealing computation.
Methods
Combinatorial random number sums46
To perform an annealing analysis, the elastic strain energy and potential energy of a truss structure must be expressed in the format of QUBO. First, since displacements and cross-sectional areas, which are design variables of the analysis of actual trusses, are real numbers, they should be represented in the binary variables. For this purpose, real numbers are expressed as the combinatorial random number sums46. An image of this approach is shown in Fig. 2.
The real number r in the range of the constant \(-a - a\) is represented by a combination of N qubits \(q_{\alpha }\) that take zeros or ones, as in the following equation:
where \(\varepsilon _{\alpha }\) is a uniformly distributed random number between 0 and 1 generated by a classical computer. In this study, 16 binary variables, i.e., qubits are used for each of the x, y, and z components of one displacement or one cross-sectional area.
Conversion of elastic strain energy to QUBO
The total strain energy of a truss structure is equal to the sum of the elastic strain energies of the trusses of the structure. The sum of the elastic strain energies can be formulated in the format of QUBO to allow the quantum annealing analysis of the truss structure.
By considering the element (K) bounded by nodes i and j as shown in Fig. 3, we obtain the elastic strain energy \(E^{(K)}\) as
where \(k^{(K)}\) is the \(i-j\) spring constant of the element (K), \({\varvec{x}}_{i}\) is the coordinate vector of node i, and \(l_{i j}^{(K)}\) is the natural length of the element (K) with nodes i and j.
Next, an infinitesimal deformation approximation is applied to the elastic strain energy. If we let \({\varvec{x}}_{i}^{0}\) be the natural position of i and \({{\varvec{u}}_{i}}\) be the displacement of i, we have \({\varvec{x}}_{i}={\varvec{x}}_{i}^{0}+{{\varvec{u}}_{i}}\). An infinitesimal deformation approximation of Eq. (3) gives the following equation:
where \((x_{i}^{0 x}-x_{j}^{0 x})\), \((x_{i}^{0 y}-x_{j}^{0 y})\), \((x_{i}^{0 z}-x_{j}^{0 z})\), \(l_{ij}^{(K)}\), and \(k^{(K)}\) are constants, while \((u_{i}^{x}-u_{j}^{x})\), \((u_{i}^{y}-u_{j}^{y})\), \((u_{i}^{z}-u_{j}^{z})\) are variables. Note that in the deformation of the equation from the second to the third line, terms above the second order with respect to displacement were neglected because of the small deformation. The third to fourth lines of the equation transformation utilized the fact that for sufficiently small \(x=2((x_{i}^{0 x}-x_{j}^{0 x})(u_{i}^{x}-u_{j}^{x})+(x_{i}^{0 y}-x_{j}^{0 y})(u_{i}^{y}-u_{j}^{y})+(x_{i}^{0 z}-x_{j}^{0 z})(u_{i}^{z}-u_{j}^{z}))/l_{ij}\), the following equation holds.
By using combinatorial random number sums in Eq. (2) for \(\left( u_{i}^{x}-u_{j}^{x}\right)\), \(\left( u_{i}^{y}-u_{j}^{y}\right)\) and \(\left( u_{i}^{z}-u_{j}^{z}\right)\) , we can convert this approximate expression (4) to a QUBO expression.
Conversion of potential energy to QUBO
Here, we let W be the load applied to the ith node. The potential energy difference \(\Delta U\) after the y-directional deformation becomes
By using combinatorial random number sums in Eq. (2) for \(u_{i}^{y}\), we can convert this expression to a QUBO expression.
Optimization analysis of truss structure by quantum annealing
The optimization process is divided into two processes: the first is a deformation analysis and the second is a cross-sectional area optimization. These processes are iteratively repeated to obtain a truss structure that maximizes stiffness and minimizes displacement.
The spring constant \(k^{(K)}\) of the truss element (K) is expressed in terms of the cross-sectional area as
where \(C^{(K)}\) is Young’s modulus and \(A^{(K)}\) is the cross-sectional area of the truss element (K)
By rewriting Eq. (4) using Eq. (7), we obtain the following equation:
To make the cross-section \(\Delta A^{(K)}\) a variable, it is expressed as a binary variable as in the following equation:
where \(\Delta A^{(K)}\) takes the value \(-N \leqq \Delta A^{(K)} \leqq N\), and \(\Delta A^{(K)}\) is expressed as a combination of powers of 2, thereby allowing values of \(\Delta A^{(K)}\) to be changed gradually.
To find the truss structure that maximizes stiffness to minimize the deflection under the condition of constant weight, the Hamiltonian of Eq. (8) is inverted from a positive to negative value as
Since the Hamiltonian for the cross-sectional area calculation (Eq. (10)) and the Hamiltonian for the balance calculation (Eq. (8)) are inversely positive and negative respectively, they cannot be optimized simultaneously in a single calculation. Therefore, in this study, the displacement and cross-sectional area calculations are performed separately, and both calculations are repeated for structural optimization.
-
Step 1
First, initial conditions are set. The initial conditions for this study are shown in Tables 1 and 2.
-
Step 2
The balance of the truss structure is calculated. In this case, the displacements are taken as variables, and the cross-sectional areas as constants. Since the summation of the elastic strain energy and potential energy of the truss should be minimized, the Hamiltonian H used in this calculation can be obtained from Eqs. (8) and (6) as
$$\begin{aligned} H=H_{1}+H_{2}, \end{aligned}$$(11)where \(H_{1}\) and \(H_{2}\) are expressed as
$$\begin{aligned} \begin{aligned} H_{1}&=C^{(K)}A^{(K)}/l_{i j}^{(K)} \left( \left( x_{i}^{0 x}-x_{j}^{0 x}\right) \left( u_{i}^{x}-u_{j}^{x}\right) /l_{i j}^{(K)}+\left( x_{i}^{0 y}-x_{j}^{0 y}\right) \left( u_{i}^{y}-u_{j}^{y}\right) /l_{i j}^{(K)}\right. \\&\left. \quad +\left( x_{i}^{0 z}-x_{j}^{0 z}\right) \left( u_{i}^{z}-u_{j}^{z}\right) /l_{i j}^{(K)}\right) ^{2} \end{aligned} \end{aligned}$$(12)and
$$\begin{aligned} H_{2}=Wu_{i}^{y}, \end{aligned}$$(13)respectively. Here, if the displacements of node i i.e., \(u_{i}^{x}\), \(u_{i}^{y}\) and \(u_{i}^{z}\) are not fixed, \(A^{(K)}\) is set as the value of the initial cross-sectional area. Here, \(u_{i}^{x}\), \(u_{i}^{y}\) and \(u_{i}^{z}\) are represented by a combination of binary variables using combinatorial random number sums in Eq. (2). When the displacements of node i i.e., \(u_{i}^{x}\), \(u_{i}^{y}\), and \(u_{i}^{z}\) are fixed, they are set as \(u_{i}^{x}=0\), \(u_{i}^{y}=0\) and \(u_{i}^{z}=0\). The displacements are updated to the value obtained.
-
Step 3
The value of the cross-sectional area is searched to maximize the elastic strain energy of the truss structure under the condition that the summation of the cross-sectional areas of the trusses is constant. In this case, the cross-sectional areas are taken as variables and displacements as constants. The following penalty function is added to the Hamiltonian to set the sum of the cross-sectional areas of the truss structure, denoted as \(A_{sum}\):
$$\begin{aligned} H_{N1}=\left( \sum A^{(K)}-A_{sum}\right) ^{2}. \end{aligned}$$(14)If the value of the summation of the cross-sectional areas of all elements changes from the constant of \(A_{sum}\), \(H_{N1}\) increases and the solution is removed from the candidates.
Using Eq. (10), we express the Hamiltonian H used in this calculation as
$$\begin{aligned} H=H_{3}+H_{N1}, \end{aligned}$$(15)where
$$\begin{aligned} \begin{aligned} H_{3}&=-C^{(K)}(A^{(K)}+\Delta A^{(K)})/l_{i j}^{(K)}\left( \left( x_{i}^{0 x}-x_{j}^{0 x}\right) \left( u_{i}^{x}-u_{j}^{x}\right) /l_{i j}^{(K)}+\left( x_{i}^{0 y}-x_{j}^{0 y}\right) \left( u_{i}^{y}-u_{j}^{y}\right) /l_{i j}^{(K)}\right. \\&\quad \left. +\left( x_{i}^{0 z}-x_{j}^{0 z}\right) \left( u_{i}^{z}-u_{j}^{z}\right) /l_{i j}^{(K)}\right) ^{2} \end{aligned} \end{aligned}$$(16)Here, \(\Delta A^{(K)}\) is represented by a combination of binary variables using combinatorial random number sums in Eq. (2). The cross-sectional areas are updated to the value obtained.
Repeat steps 2 and 3. (Fig. 4) The Leap Hybrid Solver from D-Wave is used for these analyses50.
Results
Deformation analysis of truss structures by quantum annealing
Deformation analysis was performed by applying the forced displacement and compression to a truss consisting of 42 truss elements as shown in Fig. 5. The analysis conditions are shown in Table 1.
Calculation condition for structural optimization
Two-dimensional problem
Optimization calculations are performed for a wall-hung truss structure consisting of 29 truss elements. The node at the left end is fixed and a load is applied to the lower right, as shown in Fig. 6. The analysis conditions are shown in Table 2.
Now, we find the truss structure that maximizes stiffness to minimize deflection under the condition of constant weight.
Three-dimensional problem
Structural optimization was performed for a wall-hung truss consisting of 60 elements as shown in Fig. 7. The analysis conditions are shown in Table 3.
Result of deformation analysis of truss structure by quantum annealing
The result of the analysis of compression is shown in Fig. 8. The blue line represents the before deformation, and the red line represents the after deformation. It was found that the compression in the y-direction is accompanied by an elongation in the x-direction. This result confirms the usefulness of quantum annealing using the formulated Hamiltonian for the analysis of truss deformation.
Result of optimization analysis of truss structure by quantum annealing
Two-dimensional problem
The two-dimensional optimization analysis was performed in 30 steps. The initial condition is shown in Fig. 9a, the results at step 15 are shown in Fig. 9b, and the results at step 30 as shown in Fig. 9c. The strain of each truss element is shown in color contours. The blue dots are the nodes before deformation and the red dots are the nodes after deformation. Similar to the results of the analysis of beam bending, the truss elements on the upper side of the structure are in tension and the truss elements on the lower side of the structure are in compression. The structure shows a tapered shape that is similar to the conventional optimal shape when loads are applied to the end side, as seen in conventional optimization methods. By setting a limit on the value of the cross-sectional area that can increase or decrease significantly at one time, we can repeatedly conduct the calculations while maintaining the relationship between the displacement and the cross-sectional area.
Three-dimensional problem
The three-dimensional analysis was performed in 30 steps. The initial condition is shown in Fig. 10a, the result at step 15 is shown in Fig. 10b, and the result at step 30 is shown in Fig. 10c. The strain in each truss element is shown in color contours. The three-dimensional truss also shows a structure that tapers on the loaded-end side.
Discussion
In this study, we proposed a method to perform deformation analysis and topology optimization analysis for truss structures by quantum annealing. We proposed a Hamiltonian with elastic strain energy for deformation analysis. For optimization analysis, we proposed a Hamiltonian and a method to solve the optimization of the structure. By expressing nodal displacements as binary variables and using the elastic strain energy and position energy of the truss as objective functions, we confirmed that the proposed method enables us to analyze the truss deformation with quantum annealing. Figure 11 shows a graph plotting how the mean square error from the exact solution MSE changes as the number of qubits used for the single real number is changed.
The mean square error was calculated as follows:
where \(N_\mathrm{{nodes}}\) is the number of nodes of the truss structure, \({\varvec{u}}_i^*\) is the displacement of node i calculated by the proposed method, and \({\varvec{u}}_i\) is the displacement of node i calculated by finite element analysis. In the deformation analysis, increasing the number of qubits tended to approach the exact solution. The mean square error between the analytical results and the exact solution using the proposed method was 0.641 \(\%\) compared to the maximum deformation \(12.5^2\) \(\textrm{mm}^2\). This confirms the validity of the Hamiltonian formulation of elastic energy in Eq. (4)
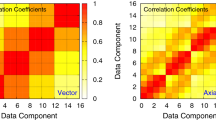
It also became possible to optimize truss structures with quantum annealing by expressing the increasing and decreasing values of the cross-sectional area as a binary variable. Figure 12 depicts a graph plotting the history of the cross-sectional areas of each element of the two-dimensional truss. As the evolution of the cross-sectional areas reached a near-equilibrium state by the 30th step, the structure at that point was considered the optimal solution. Figure 13 also depicts a graph plotting the history of the cross-sectional areas of each element of the three-dimensional truss. As the evolution of the cross-sectional areas reached a near-equilibrium state by the 30th step, the structure at that point was considered the optimal solution. Optimization calculations were performed on a classical computer under the same conditions as the optimization calculations performed in this study and their comparison was made: concerning Reference51, optimization of a two-dimensional truss structure using the optimality criteria method was implemented using Abaqus and Isight. Figure 14 depicts a result of the conventional method. The external shapes of both results show a similar trend. The nodal displacement, cross-sectional area, and strain values for each result were compared. Figure 15a–c to show the correlations. The correlation coefficients calculated for both results were 0.998 for nodal displacement, 0.829 for cross-sectional area, and 0.991 for strain. Note that trusses that are almost completely missing or nodes with no connected trusses are excluded from the comparison. All of the correlations are high, indicating that the structure obtained by the present method is valid.
In the current D-Wave full quantum annealing machine, the Advantage, approximately 5000 qubits are available. If 16 qubits are used per real variable, the machine can treat problems with around 300 degrees of freedom (DOFs). The current D-wave Leap Hybrid Solver can handle up to 1,000,000 bits, which allows problems with approximately 60,000 DOFs under the condition of 16 bits for real variable representation. Fixstars Amplify Annealing Engine, a digital annealer, manages up to 260,000 bits, enabling us to treat problems with up to 16,000 DOFs. Regarding the computation time, each optimization step took approximately 3 seconds using the current D-wave Leap Hybrid Solver in this study. It is expected that the performance of quantum devices will be improved and be able to handle larger-scale problems in the future.
In future work, we are considering extending the method proposed in this study to structural optimization of 2D and 3D continuum elements. In addition, as an extension of truss structure analysis by quantum annealing, we are considering developing a method for structural analysis of trusses with nonlinearities by quantum annealing.
The advantage of this research is that quantum annealing is expected to be able to search for the global optimal solution faster than conventional methods when the problem size is large.
An important aspect of solving large-scale problems is how to develop the method to effectively combine the classical computation and quantum computation. In nonlinear problems with continuum elements, for example, it is expected that a low-resolution solution obtained by quantum annealing will be used as an initial condition for a high-resolution solution in classical computing. This approach has the potential to accelerate the convergence in complex nonlinear large problems. Moreover, sparse matrices are frequently utilized in the structural analysis. The incorporation of variables that generate the elastic energy into the coupled qubits in quantum annealing machines is anticipated to enhance computational efficiency. Cooperation between hardware and applications is expected.
Data Availibility
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
Code availability
Code for analysis is provided as part of the replication package. It is available in Supplementary Material.
References
Catbas, F. N., Susoy, M. & Frangopol, D. M. Structural health monitoring and reliability estimation: Long span truss bridge application with environmental monitoring data. Eng. Struct. 30, 2347–2359 (2008).
Asadpoure, A., Tootkaboni, M. & Guest, J. K. Robust topology optimization of structures with uncertainties in stiffness - application to truss structures. Comput. Struct. 89, 1131–1141. https://doi.org/10.1016/j.compstruc.2010.11.004 (2011).
Kanno, Y. Robust truss topology optimization via semidefinite programming with complementarity constraints: a difference-of-convex programming approach. Comput. Optim. Appl. 71, 403–433 (2018).
Hughes, T. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. Dover Civil and Mechanical Engineering (Dover Publications, 2012).
Altman, E. et al. Quantum simulators: Architectures and opportunities. PRX Quantum 2, 017003. https://doi.org/10.1103/PRXQuantum.2.017003 (2021).
Olsacher, T. et al. Scalable and parallel tweezer gates for quantum computing with long ion strings. PRX Quantum 1, 020316. https://doi.org/10.1103/PRXQuantum.1.020316 (2020).
Alexeev, Y. et al. Quantum computer systems for scientific discovery. PRX Quantum 2, 017001. https://doi.org/10.1103/PRXQuantum.2.017001 (2021).
Bernhardt, C. Quantum Computing for Everyone (MIT Press, Cambridge, 2020).
Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2, 79. https://doi.org/10.22331/q-2018-08-06-79 (2018).
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).
Messiah, A. Quantum Mechanics (Courier Corporation, New York, 2014).
Landau, L. D. & Lifshitz, E. M. Quantum Mechanics: Non-relativistic Theory Vol. 3 (Elsevier, Amsterdam, 2013).
Nielsen, M. A. & Chuang, I. Quantum computation and quantum information (2002).
Tanaka, S., Tamura, R. & Chakrabarti, B. K. Quantum Spin Glasses, Annealing and Computation (Cambridge University Press, Cambridge, 2017).
Jaksch, D. et al. Fast quantum gates for neutral atoms. Phys. Rev. Lett. 85, 2208–2211. https://doi.org/10.1103/PhysRevLett.85.2208 (2000).
Burkard, G., Loss, D. & DiVincenzo, D. P. Coupled quantum dots as quantum gates. Phys. Rev. B 59, 2070–2078. https://doi.org/10.1103/PhysRevB.59.2070 (1999).
Barenco, A. et al. Elementary gates for quantum computation. Phys. Rev. A 52, 3457–3467. https://doi.org/10.1103/PhysRevA.52.3457 (1995).
Kadowaki, T. & Nishimori, H. Quantum annealing in the transverse ising model. Phys. Rev. E 58, 5355–5363. https://doi.org/10.1103/PhysRevE.58.5355 (1998).
Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473, 194–198 (2011).
Das, A. & Chakrabarti, B. Quantum Annealing and Related Optimization Methods. Lecture Notes in Physics (Springer, Berlin, 2005).
Ohzeki, M. & Nishimori, H. Quantum annealing: An introduction and new developments. J. Comput. Theor. Nanosci. 8, 963–971 (2011).
Abel, S. & Spannowsky, M. Quantum-field-theoretic simulation platform for observing the fate of the false vacuum. PRX Quantum 2, 010349. https://doi.org/10.1103/PRXQuantum.2.010349 (2021).
Callison, A. et al. Energetic perspective on rapid quenches in quantum annealing. PRX Quantum 2, 010338. https://doi.org/10.1103/PRXQuantum.2.010338 (2021).
Kairys, P. et al. Simulating the shastry-sutherland ising model using quantum annealing. PRX Quantum 1, 020320. https://doi.org/10.1103/PRXQuantum.1.020320 (2020).
Vuffray, M., Coffrin, C., Kharkov, Y. A. & Lokhov, A. Y. Programmable quantum annealers as noisy gibbs samplers. PRX Quantum 3, 020317. https://doi.org/10.1103/PRXQuantum.3.020317 (2022).
Sanders, Y. R. et al. Compilation of fault-tolerant quantum heuristics for combinatorial optimization. PRX Quantum 1, 020312. https://doi.org/10.1103/PRXQuantum.1.020312 (2020).
Efthymiou, S. et al. Qibo: A framework for quantum simulation with hardware acceleration. Quantum Sci. Technol. 7, 015018 (2021).
Shnirman, A., Makhlin, Y. & Schön, G. Noise and decoherence in quantum two-level systems. Phys. Scr. 2002, 147 (2002).
Roffe, J. Quantum error correction: an introductory guide. Contemp. Phys. 60, 226–245 (2019).
Aharonov, D. & Ben-Or, M. Fault-tolerant quantum computation with constant error. In Proceedings of the twenty-ninth annual ACM symposium on Theory of computing, 176–188 (1997).
Childs, A. M., Farhi, E. & Preskill, J. Robustness of adiabatic quantum computation. Phys. Rev. A 65, 012322 (2001).
Qiu, X., Zoller, P. & Li, X. Programmable quantum annealing architectures with ising quantum wires. PRX Quantum 1, 020311. https://doi.org/10.1103/PRXQuantum.1.020311 (2020).
Chang, C. C., McElvain, K. S., Rrapaj, E. & Wu, Y. Improving schrödinger equation implementations with gray code for adiabatic quantum computers. PRX Quantum 3, 020356. https://doi.org/10.1103/PRXQuantum.3.020356 (2022).
Könz, M. S., Lechner, W., Katzgraber, H. G. & Troyer, M. Embedding overhead scaling of optimization problems in quantum annealing. PRX Quantum 2, 040322. https://doi.org/10.1103/PRXQuantum.2.040322 (2021).
Glover, F., Kochenberger, G. & Du, Y. A tutorial on formulating and using qubo models, https://doi.org/10.48550/ARXIV.1811.11538 (2018).
Neukart, F. et al. Traffic flow optimization using a quantum annealer. Front. ICT 4, 29 (2017).
Ikeda, K., Nakamura, Y. & Humble, T. S. Application of quantum annealing to nurse scheduling problem. Sci. Rep. 9, 1–10 (2019).
Denchev, V. S. et al. What is the computational value of finite-range tunneling?. Phys. Rev. X 6, 031015 (2016).
Raisuddin, O. M. & De, S. Feqa: Finite element computations on quantum annealers. Comput. Methods Appl. Mech. Eng. 395, 115014. https://doi.org/10.1016/j.cma.2022.115014 (2022).
Harrow, A. W., Hassidim, A. & Lloyd, S. Quantum algorithm for linear systems of equations. Phys. Rev. Lett. 103, 150502 (2009).
Cai, X.-D. et al. Experimental quantum computing to solve systems of linear equations. Phys. Rev. Lett., https://doi.org/10.1103/physrevlett.110.230501 (2013).
Barz, S. et al. A two-qubit photonic quantum processor and its application to solving systems of linear equations. Sci. Rep.https://doi.org/10.1038/srep06115 (2014).
Rogers, M. L. & Singleton, R. L. Jr. Floating-point calculations on a quantum annealer: Division and matrix inversion. Front. Phys. 8, 265 (2020).
Pollachini, G. G., Salazar, J. P., Góes, C. B., Maciel, T. O. & Duzzioni, E. I. Hybrid classical-quantum approach to solve the heat equation using quantum annealers. Phys. Rev. A 104, 032426 (2021).
Dridi, R. & Alghassi, H. Prime factorization using quantum annealing and computational algebraic geometry. Sci. Rep. 7, 1–10 (2017).
Endo, K., Matsuda, Y., Tanaka, S. & Muramatsu, M. Novel real number representations in ising machines and performance evaluation: Combinatorial random number sum and constant division. PloS One (2024).
Ye, Z., Qian, X. & Pan, W. Quantum topology optimization via quantum annealing. IEEE Trans. Quant. Eng. (2023).
Wang, Y., Kim, J. E. & Suresh, K. Opportunities and challenges of quantum computing for engineering optimization. J. Comput. Inf. Sci. Eng. 23, 060817 (2023).
Key, F. & Freinberger, L. A formulation of structural design optimization problems for quantum annealing. Mathematics 12, 482 (2024).
Sigmund, O. A 99 line topology optimization code written in matlab. Struct. Multidiscip. Optim. 21, 120–127 (2001).
Acknowledgements
S. T. was supported in part by JSPS KAKENHI (Grant Numbers JP21K03391, JP23H05447). M. M. was supported in part by the JST FOREST (Grant Numbers JPMJFR212K). S. T. and M. M. were supported in part by JST Grant Number JPMJPF2221. The Human Biology-Microbiome-Quantum Research Center (Bio2Q) is supported by the World Premier International Research Center Initiative (WPI), MEXT, Japan. The authors would like to thank to Mechanical Design & Analysis Corporation for their technical assistance with optimization.
Author information
Authors and Affiliations
Contributions
R.H. conducted data curation, formal analysis, investigation, methodology, software, visualization, validation, writing - original draft, writing - review & editing. K.E. conducted investigation, methodology, software, visualization, validation, writing - review & editing. T.K. conducted investigation, visualization, validation, writing - review & editing. Y.S. conducted investigation, methodology. Y.M. provided methodology, resources, supervision. S.T. performed methodology, funding acquisition, supervision. M.M. conducted conceptualization, funding acquisition, project administration, writing - review & editing, supervision.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Honda, R., Endo, K., Kaji, T. et al. Development of optimization method for truss structure by quantum annealing. Sci Rep 14, 13872 (2024). https://doi.org/10.1038/s41598-024-64588-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-64588-2
This article is cited by
-
An efficient Quantum Approximate Optimization Algorithm with fixed linear ramp schedule for truss structure optimization
Advanced Modeling and Simulation in Engineering Sciences (2025)