Introduction

Bladder cancer accounts for an estimated 500,000 new cases and 200,000 deaths worldwide1. Bladder cancer is a type of urothelial carcinoma, arising from the “umbrella-shaped” cells lining the bladder cavity2. Standard imaging modalities for pre-treatment diagnosis of bladder cancer include magnetic resonance imaging (MRI), positron emission tomography (PET) and computed tomography (CT)3. However, in clinical practice, pathological examination following transurethral resection of bladder tumor (TURBT) and cystoscopy is the gold standard for diagnosing bladder cancer4. Complete initial tumor resection can reduce bladder cancer recurrence and progression, yet multifocal disease precludes comprehensive removal in up to 40% of cases5.

The majority of the current literature6,7,8,9 utilizes deep learning to identify and segment tumors from CT and MRI findings, with little reference to WLC and TURBT. CT scanning primarily utilizes X-ray tomography, where photodetectors capture the signals and convert them into digital input for electronic computers, which subsequently transform the signals into images. MRI is a diagnostic technique based on the principle that atomic nuclei possessing magnetic moments can undergo transitions between energy levels under the influence of a magnetic field. CT and MRI only play a supplementary role in the preoperative diagnosis of bladder cancer. Applying deep learning to cystoscopy and TURBT procedures facilitates diagnosis of bladder cancer and guides subsequent therapeutic management. This also lays the foundation for the application of automated surgical robots in the future. Meanwhile, the resection of bladder tumors has high requirements for the resection area. Resecting more is likely to remove normal bladder tissue, which may affect the patient’s quality of life; incomplete resection is likely to lead to a recurrence of bladder tumors.

The purpose of medical image segmentation is to perform pixel-level classification on medical images. In recent years, medical image segmentation has been applied in multiple fields, such as aneurysm segmentation10, retinal vessel segmentation11, cancer diagnosis, cell counting, assisted surgery, etc. During cystoscopy and TURBT, the use of deep learning-based segmentation networks can assist doctors in localizing bladder tumors. In particular, tumors that are similar to surrounding tissues or smaller can avoid incomplete bladder tumor resection. Recently, the emergence of convolutional neural networks (CNNs)12 has changed people’s reliance on manually extracted features. Due to the high efficiency and good segmentation results, these CNNs-based methods have achieved very good results in many medical image segmentation areas. On CNNs-based architecture, several network models for medical image segmentation have been proposed6,7,8,9. These models have achieved relatively good segmentation results.

Although CNNs-based methods have achieved considerable success, CNNs can only extract local information and cannot capture long-range dependencies between images. In recent years, vision transformer (ViT)13 has greatly improved the accuracy of image analysis in medical image segmentation. ViT can better capture long-range dependencies between images, which is beneficial for image segmentation14. For ViT-based models, it first adds positional information to the input image divided into image blocks. Then, the image blocks are interactively processed through a multi-head self-attention layer. Finally, after normalization, the output is obtained15. The above process constitutes a basic transformer module, and multiple transformer modules can be stacked according to the needs of the model to obtain the most desirable results.

In recent years, boundary information has gradually gained importance in several segmentation tasks16,17. The incorporation of boundary information in the model facilitates the attainment of more refined segmentation results. For medical image segmentation, it is very important to generate good segmentation boundaries18,19,20. For example, during TURBT, if the ___location of the tumor boundary can be accurately identified, it helps young doctors who lack more clinical experience to perform tumor resection successfully. Fig. 1 shows two examples of bladder tumors and skin lesions. From Fig. 1, it can be noticed that the target region often encompasses complex tissues, rendering delineation of ambiguous boundary pixels challenging. Furthermore, poor lesion-to-background contrast and the presence of artefacts and noise on imaging hamper accurate segmentation. It has been shown in the literature21 that when a single basis network is used to optimize both boundary segmentation and target segmentation, the two tasks promote each other, which will lead to better performance.

Inspired by the above analysis, we propose a new network framework for medical image segmentation with boundary guidance, called Boundary Guidance Network (BGDNet). Specifically, the encoder network of BGDNet consists of CNNs backbone and parallel ViT (P-ViT) module skip connections, which can fully learn local features and long-range dependencies. We propose a new boundary extraction module to extract boundary features and then fuse complementary target and boundary features through a one-to-one bootstrap module. In this way, the boundary information not only improves the quality of the boundary segmentation, but also enables more accurate target localization. In the decoder network, we propose a foreground-background dual-channel decoding module. It decodes the fused rich context and boundary feature mappings through a cascade of three modules to obtain the final segmentation prediction sequentially. Finally, we evaluate our BGDNet on one private medical image dataset and three public medical image datasets with consistent performance improvements.

Figure 1
figure 1

Examples of two representative medical images. The first row shows the bladder tumor in cystoscopy images and the second row indicates the skin lesion in the dermoscopy image.

Full size image

In summary, the contributions of this work are four-fold:

  1. 1.

    In the encoder network, we combine CNNs, P-ViT and boundary extracted module to jointly extract complementary target information and boundary information to improve boundary segmentation. Meanwhile, boundary features help to localize the target. In the decoder network, we utilize boundary features to guide the decoder network for two-channel decoding of foreground-background prediction.

  2. 2.

    Our model simultaneously optimizes boundary and interior segmentation jointly to improve segmentation performance.

  3. 3.

    We propose a new loss function with weight decay for boundary loss and target internal segmentation loss.

  4. 4.

    We propose a new cystoscopic bladder tumor dataset and conduct comprehensive experiments for four different tasks: bladder tumor segmentation, breast cancer segmentation, skin lesion segmentation, and lung segmentation. The experimental results validate the effectiveness of our proposed method.

Related works

In the past few years, a number of traditional segmentation methods have been proposed to segment medical images. Earlier methods used manual features to predict significance maps using bottom-up patterns, such as contrast22, histogram statistics23, boundary detection, center prior24, and texture-based methods.

Compared to utilizing handcrafted features for medical image segmentation, CNNs have greater advantages. U-Net25 has gained significant traction in the ___domain of medical image segmentation, and its symmetrical U-shaped encoder-decoder architecture has become one of the benchmark network architectures in the field of medical segmentation. Subsequently, ResUnet26, KiU-Net27, PraNet28, Resunet++29 and other models based on U-Net were proposed. Through enhanced integration of CNNs into a U-shaped architecture, the network achieves stronger recognition capabilities, broader receptive coverage, and multi-scale information aggregation. Moribata et al.6 proposed a modified U-Net automatic segmentation of bladder cancer on two-center, multi-vendor MR images using a CNNs that has proved to have high generalization performance. Ge et al.7 introduced a multi-input extended convolution approach for semantic segmentation of bladder tumors in MRI scans. By leveraging multi-stream input, their method effectively integrated the ___location information of feature maps with high-level semantic information, enhancing the segmentation performance. Hammouda et al.8 developed a CNN architecture termed Pyramid in Pyramid Network (PiPNet) for semantic segmentation of bladder tumors in MRI, built upon a U-Net backbone. The proposed PiPNet incorporates a U-Net-like pyramid design along with an atrous spatial pyramid pooling (ASPP) module, comprising four parallel atrous convolutions with increasing dilation rates. Liu et al.9 developed a deep learning model to segment bladder cancer on MRI. Their framework implements a pyramid design with lateral connections linking the encoder and decoder sections. PraNet28 aggregates multi-scale features, extracts contours according to local features, and refines the segmentation map successively. Isensee et al.31 developed an adaptive segmentation framework comprising 2D U-Net, 3D U-Net and cascaded U-Net architectures. Their approach automatically tunes all hyperparameters without necessitating human input.

The model based on CNNs can capture the local features of two-dimensional space well. However, CNNs have difficulty in depicting the global dependencies of features. In recent years, attention has also been widely used in the field of MISeg to overcome the shortcomings of CNNs’ lack of remote dependence. It can effectively use the information passed by multiple subsequent feature maps to detect significant features. Later, with the proposal of ViT13, attention mechanism has been widely used in the field of medical image segmentation. Swin UNETR32, UNETR33, CTO15, MT U-Net34, MedNeXt35 and other models based on attention mechanism have effectively improved segmentation performance. The Swin Transformer36 adopts a hierarchical structure to produce high-resolution feature maps, mimicking CNNs behavior. This architecture enables efficient dense prediction, conferring distinct advantages for semantic segmentation tasks. Wang et al.37 introduced spatial attention and channel attention in the segmentation task to enhance the model’s focus on the target region.

At the same time, boundary information has gradually been paid attention to in medical image segmentation18,19,20, and has been used to explicitly enhance the learning ability of models. Many attempts have been made to improve the ability of boundary segmentation. Lee et al.38 employed an algorithm to select keypoints along the boundary for predicting the target boundary. Meng et al.39 used attention refinement module (ARM) and graph convolution network (GCN) to extract boundary information. Zhang et al.40 Embed boundary attention representations to guide the segmentation process.

Figure 2
figure 2

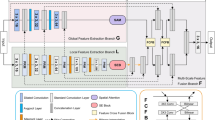
BGDNet architecture. (a) BGDNet uses an encoder-decoder architecture. The encoder network combines CNNs and P-ViT modules, the decoder network utilizes Boundary Extracted Module (BETM) to guide the decoding process, and decodes the foreground and background respectively. BGDNet optimizes boundary segmentation and target segmentation in an end-to-end manner. (b) P-ViT Module. The proposed P-ViT module consists of ViT in parallel, with patches of different sizes. (c) Boundary Integrated Module (BITM). The BITM decodes the foreground and background separately, and then concatenates them together for output.

Full size image

Methods

The overall network architecture of BGDNet is shown in Fig. 2a. The whole model uses an encoder-decoder architecture. For the encoder, we designed a combination of CNNs, P-ViT and boundary extracted module to capture local feature dependencies, remote feature dependencies and boundary features between images respectively. For the decoder, we used the boundary features extracted by the boundary extracted module to guide the decoding process with two-channel decoding prediction for foreground-background. Good boundary detection results can help the segmentation task21 and vice versa. Based on this idea, we propose a BGDNet model to model and fuse complementary boundary and segmentation information in a single network in an end-to-end manner. The BGDNet training process is show in Algorithm 1.

Algorithm 1
figure a

BGDNet training process

Full size image

Encode

CNNs stream

The network we proposed can use different CNNs networks as needed. Convolutional networks are capable of capturing local features from images. Here, we use the powerful ResNeSt41. ResNeSt utilizes a multi-branch architecture and cross-branch channel-wise attention. This integrates complementary benefits from both feature map attention and representation aggregation across multiple pathways. ResNeSt contains five outputs after convolution. For simplicity, these five features can be represented by a backbone feature set C:

$$\begin{aligned} C=\left\{ C^{1}, C^{2},C^{3},C^{4},C^{5}\right\} \end{aligned}$$
(1)

The spatial resolution of the backbone feature set C is respectively: \(H/2^{n}\times W/2^{n}(n=1,2,3,4,5)\).

P-ViT stream

ViT can be used to capture long-range dependencies between images to compensate for the shortcomings of CNN networks that can only extract local information. Specifically, P-ViT consists of parallel ViT modules, each of which is similar and the only difference lies in the size of its feature blocks. P-ViT utilizes feature blocks of different sizes to obtain long-range dependencies between different levels of an image.

As shown in Fig. 2b, for the features extracted after convolution \(C^{*} =\left\{ C^{2}, C^{3},C^{4} \right\} \), and enter it into the P-ViT network. First, we crop \(C^{*}\) to the size of the \(p\times p\) and then spread it to get the vector \(\textbf{v} \in \mathbb {R}^{p\times p\times c}\). Therefore, \(C^{*}\) is divided into \(WH/16p^{2} \), \(WH/64p^{2} \)and \(WH/256p^{2} \) sizes respectively. Here, we use two different sizes of P-ViT modules, \(\mathrm {P-ViT^{4} } \) using \(p=\left\{ 4,8,16,32 \right\} \) feature size blocks and \(\mathrm {P-ViT^{2} }\) using \(p=\left\{ 4,8\right\} \) feature size blocks. Among them, \(\mathrm {P-ViT^{4} } \) is used for \(C^{2} \) and \(C^{3} \), and \(\mathrm {P-ViT^{2} } \) is used for \(C^{4}\). Each vector is then linearly projected and the positional coding information is embedded into the vector. Subsequently, the encoding layer consists of a multi-head self-attention (MSA) layer and a feed-forward network.The MSA receives the truncated query Q, key K, and value V as inputs and then computes the attention score as follows:

$$\begin{aligned} Attention(Q,K,V)=softmax\left( \frac{QK^{T} }{\sqrt{d_{k} } }\right) V \end{aligned}$$
(2)

where \(d_{k} \) is the dimension of key K. Subsequently, the result is reshaped to the same dimension as \(C^{*} \) through the Feed Forward and Norm (FFN) operation. where FFN is a two linear layer feed forward network with ReLU activation function. Then, all the vectors of different sizes cropped by \(C^{*} \) are passed through the P-ViT module, and concatenate the results along the channel dimension. Finally, \(C^{*} \) is skip-connected to the output of the P-ViT module to obtain features that contain both local and global information about the image: \(F=\left\{ F^{2}, F^{3},F^{4} \right\} \).

Decode

Since there is spatial consistency in the tumor image, the boundary information of the tumor can be obtained using the boundary extraction module. Good boundary detection results can help the segmentation task and vice versa. Based on this idea, this subsection extracts and fuses the complementary boundary information and the tumor target information, and then inputs them into the boundary-guided decoding module to improve the model’s segmentation ability for tumors.

Boundary extracted module

In this module, our goal is to extracted boundary features. As mentioned above, \(C^{1}\) is too close to the input and the receptive field is too small. \(C^{2}\) retains better boundary information. Therefore, we extract local boundary information from \(C^{2}\). At the same time, if we add advanced semantic information to the localized information, significant boundary features can be obtained by adding high-level semantic information or ___location information. The top layer has the largest receptive ___domain and the most accurate localization, so we propagate the high-level semantic information from \(C^{5}\) to \(C^{2}\), in order to suppress non-significant boundaries and improve the ability of boundary features extraction. The fused feature \(\bar{C } ^{2}\) can be expressed as:

$$\begin{aligned} \bar{C } ^{2}=C^{2} + Upsample((Conv(C^{5});C^{2} ) \end{aligned}$$
(3)

where \(Conv(*)\) contains three Conv layers. \(Upsample(*,C^{2}) \) is a bilinear interpolation operation designed to upsample * to the same size as \(C^{2} \). The fused feature \(\bar{C}^{2} \) contains rich information about the top and bottom layers, which facilitates the extraction of boundary features. As shown in Figs. 3 and 4, the extracted boundary features \(F_{E} \) can be expressed as:

$$\begin{aligned} F_{E} = f(ExT(C^{2}),ExT(\bar{C}^{2})) \end{aligned}$$
(4)
Figure 3
figure 3

Detailed architecture of the boundary features extraction network. It is an integral part of the Boundary Extracted Module (BETM).

Full size image
Figure 4
figure 4

Detailed architecture of the boundary features fusion network. It is an integral part of the Boundary Extracted Module (BETM).

Full size image
Figure 5
figure 5

Visualization of boundary attention maps in our Boundary Extracted Module (BETM).

Full size image

Among them, \(ExT(*)\) includes two boundary extraction branches, one is an implicit boundary extraction network composed of Conv layer and sigmoid activation function, and the other is an explicit boundary extraction network composed of Sobel operator and sigmoid activation function. The implicit boundary extraction network obtains the implicit boundary features by convolution and sigmoid normalization. The explicit boundary extraction network applies the Sobel operator to the input image in the vertical and horizontal directions, respectively, to capture the spatial derivatives along these orientations and then performs the square root operation to obtain the gradient maps of the input features. Then, the gradient mapping is sigmoid normalized and multiplied with the input features to obtain the explicit boundary features. The implicit boundary features and explicit boundary features of the two inputs are summed and then passed through the convolutional layer respectively, and then concatenated by the channel dimension, the boundary features \(B_{feature} \) before fusion can be obtained. These two boundary extraction branches can promote each other for better extraction of boundary features. The explicit boundary extraction branch can provide rough boundary features for the implicit boundary extraction branch to accelerate the convergence of the implicit boundary extraction model, while the implicit boundary extraction branch can supplement the details of the boundary that the explicit boundary extraction branch does not pay attention to. \(f(*)\) is a boundary feature fusion network consisting of a Conv layer and skip connections, and finally a sigmoid activation function to obtain the fused boundary features \(F_{E} \). As shown in Fig. 5, BETM highlights features around the boundaries to precisely locate the distribution range of the tumor.

In order to explicitly model the boundary features, we add an additional boundary supervision to supervise the boundary features, yielding the boundary enhancement feature \(F_{b} \). See Section Loss Function for a detailed definition.

Boundary integrated module

After obtaining boundary features \(F_{b} \), we propose a foreground-background dual-channel fusion module, the BITM module. This module can decode the foreground and background separately and then stitch them together, which helps to facilitate the representation of features in the foreground and background and improve the accuracy of model segmentation labeling. Before BITM, the features at each level obtained above need to be fused as input to BITM. The fused feature \(F_{D} \) can be represented as:

$$\begin{aligned} F_{D} = PA(F_{d}) + CA(F_{d}) \end{aligned}$$
(5)

Among them, \(PA(*)\) denotes position attention, \(CA(*)\) denotes channel attention, \(F_{d} = concat(Down(F^{2});Down(F^{3});F^{5}) \) denotes the splicing operation of the obtained features, \(Down(*)\) denotes downsampling, and \(concat(*)\) denotes splicing after downsampling \(F^{2} \) and \(F^{3} \) to the same size as \(F^{5} \).

Figure 6
figure 6

Illustration of the weighted block.

Full size image

As shown in Fig. 2c, the BITM requires two inputs: the corresponding \(F^{i} \) and boundary enhancement features \(F^{b} \) in the encoder network fusing the local and global features of the image multiplied bitwise, and the features of the low-level decoder feature \(D^{i-1} \) after up-sampling through the weight module(the first decoder layer uses \(F_{D} \) as input). These two inputs are then spliced by channel to obtain \(F_{ig} \), which is input to the BITM and contains two separate paths for facilitating the representation of features in the foreground and background, respectively. For the foreground path, we go through the three Conv-BN-ReLu layers in turn to obtain the foreground features \(F_{fg} \). For the background path, we focus more on the background information and obtain the background feature \(F_{bg} \) as:

$$\begin{aligned} F_{bg} = Conv(1-sigmoid(F_{ig})) \end{aligned}$$
(6)

where \(Conv(*)\) contains three consecutive Conv-BN-ReLu layers. \(sigmoid(F_{ig}) \) generates the foreground feature map. \(1-sigmoid(F_{ig}) \) is the background feature map. We splice the foreground features \(F_{fg} \), and background features \(F_{bg} \) along the channel dimensions feeding into the corresponding weighted blocks to highlight the valuable information and obtain the output.

Existing methods5,28 aggregate multi-scale outputs across the channel dimension to account for variations in object shape and size. However, not all feature maps from the high-level layers may activate or prove useful in delineating these objects. So we use Weight Block to emphasize the valuable features. The structure of the Weight Block is shown in Fig. 6, which uses four \(3\times 3\) convolutional layers with different non-linearity activation functions. After Weight Block will produce more representative output features.

Loss function

To improve the boundary segmentation effect, we define the binary cross entropy (BCE) loss \(L_{BCE} \) with weight decay and mean intersection-over-union (mIoU) loss \(L_{mIoU} \) to supervise the internal target segmentation effect, and use Dice loss \(L_{Dice} \) to supervise the boundary segmentation effect.

Since the segmentation of the target boundary is more sensitive to the loss function, in order to obtain a higher quality boundary segmentation, we improve the BCE loss and mIoU loss by defining the BCE loss \(L_{BCE} \) with weight decay and the mIoU loss \(L_{mIoU} \) with weight decay:

$$\begin{aligned} L_{BCE}= & {} -\frac{1}{N}\sum _{i=1}^{N}w_{i}(y_{i}log(\hat{y} _{i})+(1-y_{i})log(1-\hat{y}_{i} )) \end{aligned}$$
(7)
$$\begin{aligned} L_{mIoU}= & {} 1- w_{i}\sum _{i=1}^{N}(y_{i} *\hat{y}_{i})/\sum _{i=1}^{N}(y_{i}+\hat{y}_{i}-y_{i}*\hat{y}_{i}) \end{aligned}$$
(8)

Where, \(w_{i}\in [1,5]\) is the asymptotic decay weight of the ith pixel, \(w_{i}\) is calculated based on the Chebyshev distance \(L_{\infty }\), which is calculated by taking the weight value of the boundary to be 5, and \(L_{\infty } =3\) pixels as the decay distance, and the decay coefficient to be 1. For overlapping regions, the largest weight value is retained. \(y_{i} \) and \(\hat{y}_{i}\) are the ground truth and the predicted label of the ith pixel respectively, and N is the total number of image number of pixels.

Dice Loss can alleviate class imbalance issues, therefore we employ the Dice Loss function to optimize the boundary predictions:

$$\begin{aligned} L_{Dice}=1-\frac{2\sum _{i=1}^{N}(y_{i}*\hat{y}_{i})}{\sum _{i=1}^{N}(y_{i}+\hat{y}_{i} )} \end{aligned}$$
(9)

Therefore, the total loss consists of the combination of the above loss functions. Among them, for the boundary loss Dice Loss, we only need to calculate the loss predicted by the BETM, and for the internal target segmentation loss \(L_{BCE} \) and \(L_{mIoU} \), we need to calculate the loss predicted by the BITM of the three decoder modules separately. In summary, the total loss Loss is as follows:

$$\begin{aligned} Loss=\sum _{i=1}^{3}(\alpha L_{BCE} +\beta L_{mIoU}) + \gamma L_{Dice} \end{aligned}$$
(10)

where \(\alpha \) , \(\beta \) and \(\gamma \) is the weighting factor to balance each different loss, and let \(\alpha =1\), \(\beta =1\) and \(\gamma =2\) here.

Experiments

We implemented BGDNet using PyTorch. After 90 training iterations, our model eventually converged. To prevent overfitting, we employed several methods including data augmentation (such as rotation, scaling, cropping, and color variations), incorporation of regularization terms, and batch normalization.

Datasets and evaluation metrics

We evaluated our BGDNet on a private cystoscopic bladder tumor dataset. In order to validate the generalization ability of the model and to evaluate the model’s ability to segment different types of medical image data, we also validated it on three widely used public datasets. The ethical part of this study was reviewed and approved by the Ethics Committee of the First Affiliated Hospital of Anhui Medical University. We obtained endoscopic video data on bladder tumor resection surgeries from the First Affiliated Hospital of Anhui Medical University. This video data is completely anonymized and does not contain any personal information of patients. Our research was granted an exemption from the requirement of obtaining participant consent by the ethics committee. The private dataset Bladder Tumor Dataset (BTD) is a manually curated collection of 1948 bladder tumor images derived from the acquired video data. We removed frames from the video data that were severely blurred, where surgical equipment heavily obscured the tumor site, or where bubbles significantly affected the visibility of the cystoscopic field. This resulted in the final BTD. The sizes of the images include two dimensions: \(1920\times 1080\) and \(720\times 576\). Each image contains bladder tumors of varying numbers and morphologies. We used 1558 images as the training set and the remaining 390 images as the test set. The BTD is annotated by a professional doctor to ensure the accuracy and authority of the annotation. Public datasets include International Skin Imaging Collaboration (ISIC 2017)42, Shenzhen Hospital x-ray sets (X-Ray)43 and Breast Ultrasound Images Dataset (BUSI )44. The ISIC dataset features dermatological images acquired by standard cameras along with matched segmentation maps outlining skin lesion areas. The ISIC 2017 release encompasses 3594 images. 2594 of them were used as a training set and 1000 as a test set.The Shenzhen Hospital x-ray dataset (566 images) was collected as part of the routine care at The Shenzhen Hospital x-ray dataset (566 images) was collected as part of the routine care at Shenzhen No.3 Hospital in Shenzhen, Guangdong providence, China. 426 of them were used as the training set and 140 as the test set. The BUSI dataset includes 780 breast ultrasound images, of which 624 are used as the training set and 156 as the test set. The aforementioned public datasets can all be openly accessed online.

We used four widely used evaluation metrics: Intersection over Union (IoU), Hausdorff Distance (HD), Mean Average Percision (mAP), F measure(\(F_{\beta } \)). HD can be a good measure of the quality of boundary segmentation. The formal definitions are as follows:

$$\begin{aligned} F_{\beta }= & {} \frac{(1+\beta ^{2})Precision*Recall }{\beta ^{2}*Precision*Recall } \end{aligned}$$
(11)
$$\begin{aligned} IoU= & {} \frac{TP}{TP+FP+FN}\end{aligned}$$
(12)
$$\begin{aligned} HD= & {} max(h(\partial A,\partial B),h(\partial B,\partial A)) \end{aligned}$$
(13)

where Precision and Recall are associated with four values i.e., true-positive (TP), true-negative (TN), false-positive (FP), and false-negative (FN): \(Precision=\frac{TP}{TP+FP} \), \(Recall = \frac{TP}{TP+FN} \). We set \(\beta ^{2} \) to 1. A and B are two regions and \(\partial A\) and \(\partial B\) are their boundary curves. \(h(\partial A,\partial B)\) and \(h(\partial B,\partial A)\) are the distance functions between the two curves, which is defined as:

$$\begin{aligned} h(\partial A,\partial B)=\mathop {{max}}\limits _{a\in \partial A} \mathop {{min}}\limits _{b\in \partial B} ||a-b||,h(\partial B,\partial A)=\mathop {{max}}\limits _{b\in \partial B} \mathop {{min}}\limits _{a\in \partial A} ||b-a|| \end{aligned}$$
(14)

Experimental results

We compare BGDNet with methods including U-Net41, CENet45, PraNet28, CaraNet46, HarDNet47, DCRNet48, CTO15, XBound49, H2Former50, ACC-UNet51 and ET-Net52.

Table 1 Quantitative comparison including IoU, HD, mAP and F1 in BTD datasets and the comparison of FLOPs, params and times with state-ofthe-art methods.
Full size table
Table 2 Quantitative comparison including IoU, HD, mAP and F1 in three datasets.
Full size table

Quantitative comparison

We compared BGDNet with above state-of-the-art(SOTA) models, which are shown in Tables 1 and  2. The red represents the best results, blue represents the second best results. On BTD, we can observe that the IoU reaches 91.3%, which is 1.7% higher than the SOTA method, HD reaches 10.43, which is 0.43 lower than the SOTA method, and mAP and F1 reach 0.853, 0.948, which are 3.2% and 1.5% higher than the SOTA method. Our method outperforms the SOTA method on all four metrics compared, especially on boundary segmentation (HD metric). At BUSI, we can see that IoU reaches 0.846, which is 1.8% better than the SOTA method, HD reaches 7.78, which is 0.27 lower than the SOTA method, mAP reaches 0.746 which is 3% better than the SOTA method, and F1 reaches 0.896 which is 1.7% better than the SOTA method. At ISIC 2017, our BGDNet IoU reached 0.862, which is 0.6% higher than the SOTA method, HD reached 15.39, which is 0.09 lower than the SOTA method, and mAP and F1 reached 0.856, 0.917, which are 1.4% and 1.1% higher than the SOTA method, respectively. On X-Ray, we can see that the IoU reaches 0.949, the HD reaches 14.31, the mAP reaches 0.936, and the F1 reaches 0.973, all of which are better than the SOTA. Compared to other methods, BGDNet achieved the best results across various evaluation metrics without a significant increase in params and inference time.

Qualitative Evaluation

We compared the segmentation performance of BGDNet with SOTA models, as shown in Fig. 7. It can be seen that our proposed BGDNet can better segment the boundaries of the target. And the accurate segmentation of the boundary is of great significance for doctors and is one of the conditions that must be met by future automatic surgical robots. Compared with other methods, Our method performs more precise boundary segmentation. It is worth mentioning that Our method can generate coherent and accurate boundaries. For example, for the sample in the fourth row, other methods cannot accurately localize and segment the target due to the complex scene. However, thanks to the significant boundary features, our method performs better, while other models appear to have discontinuous and inaccurate boundaries. Meanwhile, our model also improves and achieves better performance for the problem of segmenting the interior of the target, which is prone to mis-segmentation and generates “voids” with incorrect segmentation labels. This is due to the fact that we use a single base network to optimize both boundary segmentation and target segmentation at the same time, when the two tasks will promote each other, which will bring better performance. And the fact that the BITM module can decode the target and the background separately also helps to produce the correct segmentation labels. For example, in the second row of samples, other models tend to form “voids” inside the tumor. Our model can better solve the problem of missed detection and misdetection. For example, for the sample in the 7th row, CTO, CaraNet and DCRNet all produce false detections. For the sample in the penultimate row, all models except ours produce false detections. For the sample in the penultimate row, most of the models produced missed detections and produced very inaccurate segmentation results.

Figure 7
figure 7

Qualitative comparisons with state-of-the-arts.

Full size image

Ablation study

We conduct ablation studies to explore the effectiveness of each component in BGDNet In Table 3, we compare the performance of BGDNet variants on BTD. Model a contains only the convolution stream; model b adds the P-ViT module on the basis of model a; model c adds the BETM module on the basis of model b; model d adds the BITM module on the basis of model c, which is our final model. Among them, the decoder network of model abc is built with reference to U-Net. All the components improve the performance by 1.5%, 2.7%, 3.2% in IoU respectively, and reduce by 0.11, 0.44, 0.51 in HD respectively. Especially, we observe that the Boundary Extracted Module (BETM) is crucial for MISeg.

We show the segmentation effect of adding different modules to the model in Fig. 8. It can be seen that the segmentation using only the basic CNN network is very poor, with more false segmentations. Adding the P-ViT module can improve the segmentation ability of the model, and most of the regions of the target to be segmented can be recognized and segmented, but it also produces the problem of mis-segmentation and omission. After adding the BETM module, the model’s fine segmentation ability can be improved, and the boundaries of the target to be segmented can be accurately recognized, and the segmentation performance of the target’s interior is also greatly improved, but a small number of small “voids” will also be generated. With the addition of the BITM module, the small “voids” inside the target to be segmented are given correct segmentation labels. In summary, each of the modules proposed in our model contributes to the correct segmentation of the network model.

Figure 8
figure 8

Visual comparison of BGDNet variants on BTD. (A) CNNs, (B) CNNs+P-ViT, (C) CNNs+P-ViT+BETM, (D) CNNs+P-ViT+BETM+BITM.

Full size image
Table 3 Ablation study results on BTD.
Full size table

Conclusion

In order to improve the segmentation performance of bladder tumors and better preserve the target boundary, this paper proposes a medical image segmentation network, BGDNet, with boundary guidance. We combine the local features extracted by CNNs and the long-range dependencies between different layers inscribed by Parallel ViT (P-ViT), which can capture the tumor features more effectively. We designed the Boundary Extracted Module (BETM) to extract boundary features and utilize the boundary features to guide the decoding process. The BETM performs implicit and explicit boundary extraction on the two inputs respectively, and then fuses them. These two boundary extraction branches can enhance each other for better extraction of boundary features. We utilize the Boundary Integrated Module (BITM) for decoding.BITM is a foreground-background dual-channel fusion module that decodes the foreground and background separately, which helps to facilitate the representation of features in the foreground and background and improves the accuracy of the model segmentation labels. The boundary and localization of the target to be segmented can be improved by using boundary features. Experiments show that our model outperforms state-of-the-art methods on the cystoscopic bladder tumor dataset. Also, to validate the model’s transferability, we tested it on three widely used datasets, and the results show that our model outperforms state-of-the-art methods in all cases.