Introduction

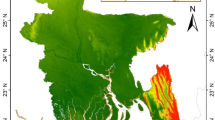
Precipitation is a critical variable for assessing changes in hydrological cycle processes under climate warming1. However, measuring, estimating, and modeling precipitation remains a challenge in the high mountains of Asia (HMA) due to the sparse and uneven distribution of ground-based observation stations2 (Fig. 1). Complex topography makes precipitation highly spatially heterogeneous3,4,5. Thus, the results of different precipitation datasets vary widely in the study of precipitation and associated hydrological processes in HMA. For example, Guan et al. found that differences in precipitation estimates from different precipitation datasets significantly affected the simulation of hydrological models6. Zhang et al. found large differences between different precipitation datasets in runoff volume simulations in southeastern Tibetan Plateau watersheds7. They suggested that the uncertainties should be assessed before using precipitation data sets for hydrological simulations. Therefore, it is crucial to evaluate the accuracy of precipitation retrievals for different source precipitation datasets in HMA and to decompose their spatiotemporal errors.

Figure 1
figure 1

Location map of high mountain Asia with Rain Gauges (Note: The map was generated using ArcMap 10.8, https://www.esri.com).

Full size image

Many studies have assessed the precipitation retrieval ability of multi-source precipitation data sets such as gauge-based, satellite-based, and reanalysis datasets8,9,10,11. Meanwhile, there have been many studies on precipitation assessment in regions with complex terrain, especially in HMA. For example, Ouyang et al. evaluated the precipitation simulation accuracy using the WRF 1.5 model in the Yarlung Tsangpo River Basin12. The results showed that the precipitation simulation accuracy at the monthly scale exceeded that at the hourly and daily scales. Wu et al. evaluated the accuracy of precipitation retrieval for ERA5 and integrated multisatellite retrievals for global precipitation measurement (IMERG) in the Qinghai-Tibet Plateau region13. The study showed a significant increase in error during winter compared with other seasons. Du et al. evaluated the effectiveness of satellite and reanalysis datasets for retrieving daily extreme precipitation from three river source regions and found that summer had the largest deviations compared with the other seasons in the selected datasets14. However, these studies did not investigate the time-varying characteristics of precipitation errors.

From the perspective of precipitation detection capabilities, the most common approach is to consider ground-observed precipitation data as a baseline and use statistical metrics (i.e. Pearson correlation coefficient (CC), bias (BIAS), Kling-Gupta efficiency (KGE), and root mean square error (RMSE)) to evaluate the precipitation errors of different precipitation products15,16. For example, Wang et al. used RMSE, standard deviation, and CC to evaluate the accuracy of precipitation products (i.e. global satellite mapping of precipitation) in the Heihe River Basin16. They found that monthly global satellite mapping of precipitation data were worse than other satellite and reanalysis products. Worqlul et al. used BIAS, CC, and RMSE as evaluation metrics to assess the precipitation errors of three precipitation products (MPEG, CFSR, and TRMM) in the Tana Lake Basin8. The results showed that MPEG and CFSR products had superior RMSE (0.63 to 9.5 mm/day), while TRMM had comparatively poorer RMSE performance (3.8 to 11.8 mm/day).

Some studies have used categorical statistical metrics to assess the detection accuracy of precipitation products in terms of their rainfall detection capabilities. For example, Wu et al. examined the performance of the ERA5 and IMERG precipitation products over the Tibetan Plateau using the probability of detection, false alarm ratio, and critical success index and found that ERA5-Land was better than the IMERG product for monitoring precipitation events13. Nadeem et al. used performance metrics including probability of detection, false alarm ratio, and critical success index to evaluate the retrieval accuracy of two reanalysis products (ERA5 and MEERA2) and seven satellite remote-sensing products (CHIRPS, IMERG, PERSANN-CCS, PERSANN-CDR, PERSANN-PDIR, PERSANN, and TRMM) in Pakistan and found that IMERG was better at detecting daily precipitation events than the other satellite products and reanalysis datasets17. Related studies have performed error decomposition of retrieval data based on indicators of rainfall detection capability. For example, Tian et al. proposed a three-component error decomposition (3CED) method, that decomposed the total error into three components: hit bias, missed precipitation, and false precipitation18. Chaudhary & Dhanya19 and Zhang et al.20, building on the 3CED method, introduced the four-component error decomposition (4CED) method, which further decomposes hit bias into hit overestimation bias (positive) and hit underestimation bias (negative). Li et al. simplified 4CED into a two-component error decomposition (2CED)21. In summary, current research often separates the bias and bias ratio discussion, while precipitation intensity and frequency affect the retrieval errors of precipitation products. Therefore, it is essential to include ratio and magnitude in decomposing retrieval errors in precipitation products.

Therefore, this study investigated the spatiotemporal characteristics of precipitation retrieval accuracy for four precipitation datasets (MSWEP, GPCC, GPM, and soil moisture to rain-advanced scatterometer (SM2RAIN-ASCAT)) based on gauging observations from 76 meteorological stations in HMA and decomposed the errors to identify the sources of error. This study aims to (1) compare spatiotemporal differences in precipitation amounts between rain gauge observations and four precipitation products, (2) assess the spatial characteristics of the daily scale errors in the precipitation products using four error metrics, (3) analyze the variations and differences in monthly scale precipitation errors in the four products using Fourier spectral analysis and seasonal signal decomposition, (4) explain the sources and discrepancies of the errors produced by each precipitation product using multiple linear regression model.

Data sources and methodology

Study area

High Mountain Asia (HMA) lies between 26°–46°N and 66°–105°E and includes the Tianshan, Pamir, and Tibetan Plateaus (Fig. 1). This region has substantial solid water resources (mainly glaciers and snow) that serve as the headwaters of many rivers, such as the Yangtze, Yellow River, Lancang, Yarlung Tsangpo, Ganges, Indus, Amu Darya, and Syr Darya22,23,24, providing water to more than two billion people25,26. The Tibetan Plateau has a typical high-altitude climate1,27, with mean annual temperatures ranging from − 2.57 to 5.75 °C. The annual precipitation varies from approximately 1500 mm in the southeast to less than 100 mm in the northwest, with more than 60% of the precipitation occurring in summer28. The Tianshan Mountains region has a temperate continental climate29,30, with average annual temperatures ranging from − 10 to 10 °C31 and most precipitation occurring in the summer. The escalation of extreme precipitation events in HMA due to global warming32 underscores the criticality of conducting research on precipitation issues in this region.

Data sources

Ground-based precipitation station data

Ground-based observational data from 76 meteorological stations were provided by the Meteorological Data Sharing Centre of the National Meteorological Administration of China (http://ncc.cma.gov.cn), which are mainly located in the southern and eastern parts of the Tibetan Plateau and the eastern part of the Tianshan Mountains (Fig. 1). The elevation distribution of all 76 stations is as follows: less than 1000 m: 4 stations; between 1000 and 2000 m: 9 stations; between 2000 and 3000 m: 22 stations; between 3000 and 4000 m: 29 stations; and above 4000 m: 13 stations. The data accuracy was assessed using strict quality control. Anomalous data values were identified and eliminated to reduce the influence of outliers. Second, the internal logical consistency of the dataset was ensured by verifying the consistency of the data. Finally, potential spatial and temporal errors were identified and corrected by analyzing data from different dates and stations. These procedures were performed to improve the reliability and accuracy of the datasets.

Grid-based precipitation data sets

This study used four grid-based precipitation datasets: Multi-Source Weighted-Ensemble Precipitation (MSWEP) V2.8, Global Precipitation Climatology Centre (GPCC) Full Data Daily Version 2022, Global Precipitation Measurement (GPM) IMERG Final V06, and Soil Moisture to Rain-Advanced Scatterometer (SM2RAIN-ASCAT) Version v1.5. Information about the above products is in Table 1.

Table 1 List of information of four precipitation data sets in this study.
Full size table

The MSWEP data integrated data from over 77,000 rain gauges, satellites, and reanalysis sources33. This study used MSWEP version 2.8, which is a post-real-time corrected daily precipitation product with a spatial resolution of 0.1° × 0.1°. The GPM, calibrates, merges, and interpolates data from all passive microwave instruments in the GPM satellite constellation while combining microwave-calibrated infrared (IR) satellite estimates, rainfall station measurements, and other precipitation sources. Integrated multi-satellite retrieval for the GPM (IMERG) is a GPM-generated tertiary product34. The GPM (IMERG) version 06 final product was used in this study, with a temporal resolution of days and a spatial resolution of 0.1° × 0.1°. The SM2RAIN-ASCAT precipitation product is a global dataset that utilizes satellite-observed soil moisture to infer precipitation amounts35. This study used SM2RAIN-ASCAT version V1.5 with a temporal resolution of days and a spatial resolution of 0.1° × 0.1° for 2007–2020. This dataset version provides quality flags to mask areas with complex terrain, frozen soil, and tropical forests, resulting in a rainfall product after masking. To assess the dataset's comprehensive capability, this study did not use the quality flags to filter it but instead evaluated it as a precipitation product35. GPCC is a high-resolution gridded precipitation dataset for the global landmass (excluding Antarctica), compiled from monthly precipitation records from weather stations around the world. This study used GPCC Full Data Daily Version 2022, a record with a spatial resolution of 1.0° × 1.0°, from 1901 to 202036.

Among the four precipitation datasets, the GPCC data is derived from ground-based precipitation measurement stations, the GPM data is primarily sourced from satellite observations and calibrated with other data, the MSWEP data is integrated from various data sources, and the SM2RAIN-ASCAT data is mainly based on remotely sensed soil moisture observations and adjusted using reanalysis data. The time spans for the accuracy assessment and error decomposition of these datasets are as follows: 2001–2020 for MSWEP, GPCC, and GPM; 2007–2020 for SM2RAIN-ASCAT. These datasets used in this study are total precipitation, including solid and liquid precipitation.

Methodology

Accuracy assessment metrics

This study assesses the discrepancies in accuracy among various precipitation datasets by examining the consistency between meteorological station data and these datasets. Four statistical evaluation metrics were employed to evaluate and compare their reliability, as shown in Table 2. Among them, the correlation coefficient (CC) falls under correlation and similarity metrics, the root mean square error (RMSE) and bias (BIAS) are categorized as Error Metrics, and the Kling-Gupta Efficiency (KGE) is classified under Skill Scores and Efficiency Metrics.

Table 2 Formulae of accuracy assessment metrics.
Full size table

Fourier spectrum analysis

In this paper, the periodicity of the time series of each precipitation dataset was determined using the Fourier transform method37.

First, the error data for the precipitation products were expressed as discrete sequences in the time ___domain. The error series was assumed to be \(e(n)\), where n is the time step. A Fourier transform is then applied to the error sequence to obtain a spectral representation in the frequency ___domain.

The formula for the Fourier transform is given below:

$$F\left(k\right)=\sum e(n)\times \text{exp}\left(\frac{-i\times 2\pi \times k\times n}{N}\right),$$
(5)

where \(F\left(k\right)\) is the spectrum in the frequency ___domain, \(e\left(n\right)\) is the error sequence in the time ___domain, exp is a natural exponential function, \(i\) is an imaginary unit, \(k\) is the frequency index, and \(k\) is the length of the error sequence.

Seasonal decomposition of precipitation errors

In this study, a seasonal decomposition algorithm based on the autoregressive moving average model was used to decompose the series of precipitation errors into trend, seasonal, and stochastic components (Eq. 6) and then to reveal the seasonal characteristics of precipitation errors. The autoregressive moving average method is widely used to analyze and predict a region’s precipitation, temperature, and other climatic elements38,39.

$$Y\left(t\right)=T\left(t\right)+S\left(t\right)+E\left(t\right),$$
(6)

where \(Y(t)\) is the observations of the time series;\(T(t)\) is the trend component and an autoregressive (AR) model is used to capture the long-term trend in the error series, which predicts future trends by linearly combining error values from past time steps;\(S(t)\) is the seasonal component and a moving-average (MA) model was used to fit the seasonal component in the error series, which captures the seasonal patterns repeated over a specific timeframe; and \(E(t)\) is the stochastic component, which represents random fluctuations in the error series that were not captured by the trend and seasonality models.

Multiple linear regression models

In this study, multiple linear regression modeling was used to investigate the extent of the influence of the precipitation amount and number of days on errors in precipitation data sets.

It is assumed that a linear relationship exists between the precipitation product retrieval error \(Y\) and, amount of precipitation (\(X1\)), and number of days of error (\(X2\)), as follows:

$$Y={\beta }_{0}+{\beta }_{1}{X}_{1}+{\beta }_{2}{X}_{2}+\epsilon ,$$
(7)

where \({\beta }_{0}\) is the intercept, \({\beta }_{1}\) and \({\beta }_{2}\) are the regression coefficients, and \(\epsilon\) is the residual.

In a multiple linear regression model, the standard regression coefficient is a dimensionless regression coefficient that eliminates the differences in magnitude and scale between different independent variables, thus allowing for a comparison of the relative degree of influence of different independent variables on the dependent variable. The formula for the standard regression coefficient is,

$${\beta }_{i}={b}_{i}\frac{{S}_{{x}_{i}}}{{S}_{y}},$$
(8)

where \({\beta }_{i}\) is the standard regression coefficient of the \({i}^{th}\) independent variable; \({b}_{i}\) is the original regression coefficient of the \({i}^{th}\) independent variable; \({S}_{{x}_{i}}\) is the standard deviation of the \({i}^{th}\) independent variable; and \({S}_{y}\) is the standard deviation of the dependent variable. The greater the absolute value of the standard regression coefficient, the greater the explanatory power of the independent variable for the dependent variable.

Results

Comparison of precipitation characteristics of different precipitation data sets

The spatial and temporal characteristics of precipitation for the four sets of precipitation products were compared for the period 2001–2020, using precipitation data from rain gauges as a benchmark. Figure 2 shows that the station-observed precipitation was mainly concentrated between May and September, with the highest value occurring in July (99.58 mm) and the lowest in December (2.95 mm), which is consistent with the findings of relevant precipitation studies in the Tibetan Plateau and Tianshan regions of Central Asia40,41,42. Therefore, in this study, the rainy season was determined to be May–September and the dry season was determined to be October–April in the HMA.

Figure 2
figure 2

Monthly averages of precipitation at rainfall stations and four precipitation gridded data in the HMA during 2001–2020.

Full size image

Figure 2 shows that all four sets of precipitation products exhibit seasonal variations similar to those observed at the rain gauges. However, the actual precipitation for each product differed significantly from that observed at rainfall stations. MSWEP overestimated precipitation in the wet (8.17%) and dry seasons (64.68%) (Table 2). GPCC overestimated precipitation in the rainy season (13.45%) and slightly underestimated it in the dry season (− 2.97%). GPM overestimated precipitation in the rainy season (30.07%) and underestimated it in the dry season (− 60.90%). SM2RAIN -ASCAT had the highest wet season overestimation (30.07%) and dry season underestimation of precipitation (− 60.90%) (Table 3). All four datasets overestimated precipitation during the wet season, and three out of the four datasets underestimated precipitation during the dry season.

Table 3 Monthly average rainy and dry seasons deviations and degree of deviation of relative observations for four precipitation datasets.
Full size table

Both site-observed precipitation and corresponding grid-point precipitation showed clear spatial heterogeneity. The daily mean annual precipitation observed at the station gradually decreased from southeast to northwest of the study area (Fig. 3a). The rainy and dry seasons exhibited similar spatial distribution characteristics (Fig. 3f and k). However, there is a large variation in precipitation, with a daily mean of 2.53 mm/day in the rainy season compared to only 0.47 mm/day in the dry season. The spatial distribution of the daily average precipitation for the four precipitation products is similar to that of the field observations. However, there is a general tendency for these products to significantly overestimate precipitation during the rainy season (Fig. 3g–j) and slightly underestimate it during the dry season (Fig. 3l–o). Over the entire year (Fig. 3b–e), the degree of overestimation is lower than during the rainy season. The low-value regions of the SM2RAIN-ASCAT daily mean precipitation had a spatial distribution similar to that of the observed station data. However, there were significant differences in the spatial distribution of the medium- and high-value regions compared with the observed station data (Fig. 3e). Given that the daily mean precipitation for SM2RAIN-ASCAT (1.56 mm/day) is significantly higher than that of the station observations (1.33 mm/day), the error may be due to the error in estimating precipitation in the southeast. In combination with Fig. 3j and o, it can be seen that the area of high values of SM2RAIN-ASCAT in the rainy season is mainly located in the southeast, and the area of low values in the dry season is also located in the southeast of the study area.

Figure 3
figure 3

Spatial distribution of daily mean precipitation values in the HMA from rainfall station observations and precipitation product retrievals (for three time periods: year-round, rainy season, and dry season) (Note: The map was generated using ArcMap 10.8, https://www.esri.com).

Full size image

The results of the probability of precipitation observed at the stations showed that the stations with a high probability of precipitation were mainly located in the Hengduan, Nyaingqentanglha, and Tanggula Mountain regions of HMA (Fig. S1a). Although there was one gauge in the Himalayas with a probability of precipitation greater than 0.4, all other sites in the region had a lower probability of precipitation, between 0.1 and 0.2. Regions with a low probability of precipitation include the Tianshan Mountains and the outer edge of the Qaidam Basin. The precipitation probabilities of all four sets of precipitation products were overestimated to varying degrees relative to the station observations (Figs. S1b–e). Among them, GPCC and SM2RAIN-ASCAT had a lower degree of overestimation, which reflects the spatial distribution characteristics of high values in the southeast and low values in the northwest. Combining Figs. 3 and S1, it can be seen that MSWEP, GPCC, GPM and SM2RAIN-ASCAT overestimated daily mean precipitation and probability of precipitation to different degrees compared with the station observations. The overestimation in the mean sense is reflected in the differences in precipitation frequency identification (Fig. S2), which manifest as the excessive identification of non-precipitation days as precipitation days and the overestimation of precipitation amounts on days with precipitation.

Spatial accuracy of precipitation data sets

Four assessment metrics (CC, Bias, RMSE, and KGE) were used to spatially evaluate the accuracy of daily precipitation for the four sets of precipitation products over the entire year, rainy season, and dry season. The results of the CC metric assessment for the entire year (Fig. 4a–d) showed that GPCC had the best results, with 44 stations having a CC greater than 0.5, and few stations having a CC value less than 0.3. MSWEP followed, with 31 stations with CC above 0.5, which were mostly located in the southeast. The spatial results of the CC values of SM2RAIN-ASCAT were similar to those of MSWEP, with higher CC values in the southeast. The GPM had the worst spatial performance among the four datasets, with all sites having CC less than 0.4. Meanwhile, the spatial pattern of CC for the rainy (Fig. S3a–d) and dry (Fig. S4a–d) seasons was similar to the annual scales, while CC was smaller than the annual CC values. In particular, the CC values of SM2RAIN-ASCAT in the dry season were worse and closer to those of GPM. Therefore, the CC values assessed using the four sets of precipitation products outperformed those of the rainy and dry seasons throughout the year.

Figure 4
figure 4

Spatial distribution of accuracy assessment indices of daily precipitation data for four sets of precipitation products at annual scales relative to station-observed daily precipitation values (Note: The map was generated using ArcMap 10.8, https://www.esri.com).

Full size image

The evaluation of the BIAS metrics for the annual period showed that they were predominantly overestimated for the four sets of precipitation products, with significant spatial variations (Fig. 4e–h). GPCC and MSWEP overestimated precipitation at 55 and 65 stations, respectively. Precipitation was overestimated at fifty stations for SM2RAIN-ASCAT, with stations with BIAS greater than 0.3 mainly distributed along the southern Himalayas and Hengduan Mountains. For GPM, most stations had BIAS between ± 0.15, with stations with BIAS > 0.3 mainly located in the southern part of HMA. During the rainy season (Fig. S3e–h), the BIAS of GPCC (57), MSWEP (52), SM2RAIN-ASCAT (60), and GPM (52) showed overestimation at most sites, with the highest number of sites with BIAS > 0.3 being for SM2RAIN-ASCAT, which were mainly located along the Himalayan–Hengduan Range and in eastern Tianshan. In the dry season (Fig. S4–h), GPCC and MSWEP mainly overestimated precipitation, with as many as 51 stations with BIAS > 0.3 in MSWEP (mean BIAS = 1.18); however, SM2RAIN-ASCAT showed underestimation at 66 stations, with a regional mean BIAS of − 0.28, compared to 0.18 for GPM. However, the number of underestimated stations exceeded that of the overestimated stations, indicating that a larger BIAS value makes the regional mean BIAS positive. Looking at the spatial distribution of stations, the regions where the four precipitation products were overestimated were mainly located in the northern Qilian Mountains, Qaidam Basin–Tianshan belt, and southern Hengduan Mountains-Nyainqentanglha Mountains–Himalayan zone.

The RMSE values for the entire year (Fig. 4i–l), rainy season (Fig. S3i–l), and dry season (Fig. S4i–l) were larger in the east and southeast and smaller in the northwest, which is consistent with the spatial distribution of precipitation. The best precipitation retrieval accuracy throughout the year and during the wet season was obtained for MSWEP, followed by SM2RAIN-ASCAT, GPCC, and GPM. In the dry season, the best precipitation retrieval accuracy was obtained for GPCC, followed by SM2RAIN-ASCAT, MSWEP, and GPM. Comparing the RMSE values with those for the entire year, the RMSE values of each precipitation product were larger during the rainy season and smaller during the dry season. The RMSE of the rainy season was 29.9% higher than the annual RMSE, and 67.2% higher than the dry season RMSE. This is due to the frequent and complex rainfall patterns during the rainy season, which lead to significant spatiotemporal variability in daily rainfall amounts43, resulting in larger absolute errors in the rainfall retrieval for each product during the rainy season.

The results of the KGE assessment for the annual period (Fig. 4m–p) showed that the distribution of stations with lower KGE values was relatively similar for all four precipitation products, with KGE less than 0 being mainly located at the edge of the Qaidam Basin, along the Himalayas to the Nyainqentanglha Mountains, the Hengduan Mountains, and the eastern part of the TianShan Mountains. The areas with high KGE values were mainly located in the central Hengduan Mountains. The highest annual KGE regional mean was found in GPCC (KGE = 0.29), followed by MSWEP (KGE = 0.18), SM2RAIN-ASCAT (KGE = 0.12), and GPM (KGE = 0.07). The spatial distribution characteristics of the rainy season (Fig. S3–p) and dry season (Fig. S4m–p) KGE values were similar to those of the annual KGE values. The regional mean KGE values in the rainy and dry seasons were lower than the regional mean KGE values for the whole year.

Temporal accuracy of precipitation data sets

From the mean values of the error metrics (Table 4), the best accuracy of the monthly precipitation retrieval was achieved by GPCC, which obtained the best values for CC (0.82), BIAS (0.04), and KGE (0.70). GPM achieved the second best CC (0.77), BIAS (− 0.06), and KGE (0.61) and had the smallest RMSE (22.17 mm). MSWEP and SM2TRAIN-ASCAT were relatively less accurate, although MSWEP performed better than SM2RAIN-ASCAT for CC, RMSE, and KGE. However, for BIAS, SM2RAIN-ASCAT was closer to the best value.

Table 4 Mean values of precipitation products in different error metrics on a monthly scale.
Full size table

The monthly precipitation product showed a certain periodicity of error fluctuation pattern in all four error metrics (Figs. S5a–d). In this study, Fourier spectral analysis was used to analyze the periodicity of the precipitation products using four error metrics to test whether this fluctuation pattern was real. The results in Fig. S6 show that the error metrics of MSWEP, GPCC, and GPM have obvious frequency peaks in the 20th cycle, corresponding to the length of the years included in the assessment (2001–2020, 20 years), whereas the SM2RAIN-ASCAT products have obvious frequency peaks in the 14th cycle, corresponding to the length of the years included in the assessment (2007–2020, 14 years). This shows that most precipitation products have a significant annual periodicity in their error indicator results.

The assessment results of the monthly scale error indicators of each precipitation product were seasonally decomposed using an additive model to obtain the seasonal changes in each error indicator. Figure 5a shows that there are two peak periods in the seasonal variation of the CC values for each precipitation product, with the first peak occurring roughly in February–June and the second peak occurring in September–October. However, in terms of the timing of the low CC values, MSWEP, GPCC, and GPM were more consistent (July–August and December–January), whereas SM2RAIN-ASCAT had low CC in April and December–January. Figure 5b shows that the BIAS assessment results for the three precipitation products, GPCC, GPM, and SM2RAIN-ASCAT, have similar seasonal characteristics, being positively biased in May–October and negatively biased in November–April, whereas MSWEP appears to have the opposite change characteristics. This is in line with the results presented in Sect. "Comparison of precipitation characteristics of different precipitation data sets", where the MSWEP significantly overestimated precipitation during the dry season (deviation ratio = 64.68%), while the other three sets of precipitation products underestimated precipitation. Figure 5c shows that the seasonal variation in the RMSE results for each precipitation product was more similar, with a gradual increase in the RMSE values from January to July and a gradual decrease after peaking in July. This is consistent with the intra-annual variation characteristics of precipitation in HMA. For KGE, the precipitation products showed a consistent "peak-low" pattern (Fig. 5d), with two peaks (May–June and September–October) and two lows (July–August and December–January).

Figure 5
figure 5

Seasonal patterns of precipitation products in each error assessment metric, (a–d) for CC, BIAS, RMSE (mm), and KGE, respectively.

Full size image

At the annual scale, precipitation observations and precipitation product retrievals show an increasing trend, as illustrated in Fig. S7e. Across different error metrics, the accuracy of each precipitation product remains relatively stable. Specifically, MSWEP, GPCC, and GPM exhibit similar levels of accuracy, with CC values ranging between 0.8 and 0.9 (Fig. S7a), BIAS values between 0 and 0.2 (Fig. S7b), RMSE values between 100 and 200 mm (Fig. S7c), and KGE values between 0.7 and 0.9 (Fig. S7d). On the other hand, SM2RAIN-ASCAT demonstrates lower overall accuracy across the error metrics compared to other products. Yet, it maintains relatively high precision, with CC values ranging between 0.6 and 0.9, BIAS values between 0 and 0.2, RMSE values between 200 and 300 mm, and KGE values between 0.5 and 0.7.

Decomposition precipitation retrieval error

The results in Table 5 show that the RMSE values of the four sets of precipitation products correlate well with the precipitation amount. To further quantify the influence of precipitation-related error factors on the RMSE, this study constructed a multiple linear regression model to analyze the influencing factors of the RMSE values of each precipitation product, with the RMSE values of each precipitation product as the dependent variable and the six precipitation-related error factors as the independent variables. This study constructed multiple linear regression models, including regional-scale multiple linear regression and station-scale multiple linear regression models.

Table 5 Correlation of RMSE values of each precipitation product with their respective inverse and observed values in spatial and temporal scales.
Full size table

This study draws on the three-component error decomposition (3CED) method18 to propose three scenarios that may affect the RMSE value of each product: precipitation products successfully detecting precipitation events (precipitation detection); precipitation events detected by the precipitation products but not occurring in the rainfall station observations (false alarm); and precipitation events occurring in the rainfall station observations but not detected by the precipitation products (miss alarm). The magnitude of the errors is concurrently influenced by variations in the magnitude and frequency of precipitation events within a given time or spatial ___domain. Therefore, each scenario can be further subdivided into the quantity of precipitation events and the amount of precipitation within each event, resulting in six factors that impact error magnitude: (1) precipitation detected present (PDP): the error between the detected precipitation by the precipitation product and the actual precipitation amount; (2) precipitation detected event (PDE): the number of correctly detected precipitation events by the precipitation product; (3) false alarm precipitation (FAP): the cumulative amount of precipitation erroneously detected by the precipitation product but not observed at rain gauge stations; (4) false alarm events (FAE): the number of precipitation events erroneously detected by the precipitation product but not observed at rain gauge stations; (5) missed alarm precipitation (MAP): the cumulative amount of precipitation present in rain gauge observations but not detected by the precipitation product; and (6) missed alarm events (MAE): the number of precipitation events present in rain gauge observations but not detected by the precipitation product.

Regional-scale multiple linear regression

In the regional-scale multiple linear regression model, 76 daily rainfall stations were counted and the data were also entered into the model over months, with 560–620 sets per month for MSWEP, GPCC, and GPM, and 395–433 sets per month for SM2RAIN-ASCAT. Two rounds of multiple linear regression analyses were conducted on the precipitation products (Table 6). The first round included all four precipitation products, with the coefficient of determination (R2) of each product reaching 0.83 or more, with a maximum of 0.846, indicating that the screened precipitation-related factors had strong explanatory power for the RMSE values of each precipitation product. However, the individual coefficients of the independent variables failed to pass the 95% significance test (t-test) for MSWEP and GPCC; therefore, a second round of multiple linear regression analysis which excluded the independent variables that failed the significance test was performed. The results showed no reduction in R2 for the precipitation products and the remaining independent variables passed the t-test. Figure S8 shows that the independent variable with the highest percentage of standardized coefficients for each precipitation product was PDP, with MSWEP accounting for 68.0%, followed by GPCC (60.7%), SM2RAIN-ASCAT (52.6%), and GPM (47.2%). The second highest overall percentage was observed for FAP, with GPM, GPCC, MSWEP, and SM2RAIN-ASCAT at 32.4%, 26.2%, 18.6%, and 14.2%, respectively. Thus, regional-scale multiple linear regression analysis showed that PDP contributed the most to the RMSE values of each precipitation product (> 50%), followed by FAP, MAP, and PDE. The number of events occurring in the FAE and MAE had negligible effects on the RMSE values of the precipitation products.

Table 6 Results of standardized coefficients in multiple linear regression for RMSE of precipitation products across the entire region.
Full size table

The first round of regression (Table S1) results showed that the R2 of each month for each product was high, reaching 0.74 an average. There were cases where the independent variables failed the 95% significance test for individual months for each product, especially for the independent variables FAE and MAE, which failed the test in high numbers. Therefore, based on the first round of the regression, the corresponding independent variables that did not pass the t-test were excluded. The remaining independent variables were analyzed using multiple linear regression with RMSE, which showed no noticeable decrease in R2 for the precipitation products (0.72), and the remaining independent variables passed the test (Table S2). Figure 6 presents the monthly independent variables for each product during the two regression rounds. It can be seen that changes in the RMSE values for most of the time for MSWEP, GPCC, and GPM are mainly explained by changes in PDP and FAP, and changes in the RMSE values for most of the time for SM2RAIN-ASCAT are mainly explained by changes in PDP and MAP.

Figure 6
figure 6

Results of standardized coefficients in regional-scale monthly RMSE multiple linear regression for precipitation products across the entire region.

Full size image

MSWEP, GPCC, and SM2RAIN-ASCAT showed higher contributions of PDP to the RMSE in the rainy season and lower contributions in the dry season, especially for SM2RAIN-ASCAT. The contributions of PDP to the RMSE in SM2RAIN-ASCAT were highest in July (74.0%) and August (87.2%) and lowest in January (16.2%) and December (7.1%). Conversely, the contributions of MAP and MAE gradually decreased from January to July and then increased, with the highest proportions occurring in January (83.8%) and December (88.0%). However, no statistically significant differences were observed between July and August. The different error contributions of the GPM did not exhibit any obvious monthly variations.

Station-scale multiple linear regression

In the station-scale multiple linear regression model, precipitation product retrieval precipitation and rain gauge observation precipitation have four possible matching situations: precipitation detection, false alarms, miss alarms and observation data are 0. Therefore, this study considered four days as a time unit and counted the RMSE values of each time unit of each rain gauge of the precipitation product as the dependent variable and the corresponding six precipitation-related factors as independent variables, with 1826 sets per site ___location for MSWEP, GPCC, and GPM, and 1278 data sets per site ___location for SM2RAIN-ASCAT.

The station-scale multiple linear regression results showed that the coefficients of the FAE and MAE variables for most stations failed the 95% significance test (Table 7). For example, the percentages of stations failing the significance test were 89.5% and 86.8% for MSWEP, 85.5% and 81.6% for GPCC, 82.9% and 82.9% for GPM, and 65.8% and 88.1% for SM2RAIN-ASCAT. On this basis, the results of the multiple linear regression at the station level, after excluding the two independent variables, FAE and MAE, showed that the standardized coefficients of the remaining four factors for each product passed the 95% significance test in the vast majority of the sites, except for the PDE factor for SM2RAIN-ASCAT, which did not pass the test at 15 sites (Table 7). The regression results of the variables for the sites are shown in Fig. 7. Figure 7a–d show that SM2RAIN-ASCAT has an R2 greater than 0.85 at most sites (56 sites) (mean R2 = 0.87), followed by MSWEP (R2 between 0.75 and 0.85 at most sites), and the spatial distributions of R2 values for GPCC and GPM were similar. In addition, the spatial maps of R2 show that R2 values were relatively low for sites from the central Hengduan Range to the eastern Tanggula Mountains and relatively high for sites in the Tianshan Mountains region and the marginal region of the Qaidam Basin. It is worth noting that the inter-site R2 differences for all precipitation products are small, with a minimum of approximately 0.6 and a maximum of 0.98, suggesting that the four independent variables, FAP, MAP, PDP, and PDE, have strong explanatory power and can explain most of the spatial and temporal variations in the RMSE values of the precipitation products.

Table 7 Number of non-significant stations in station-scale multiple linear regression for precipitation products, based on a 95% significance level.
Full size table
Figure 7
figure 7

Station-scale multiple linear regression R2 and the proportion of standardized coefficients for predictor variables (Note: The map was generated using ArcMap 10.8, https://www.esri.com).

Full size image

The results of the station-specific multiple linear regression analyses for each precipitation product showed that the R2 of each dataset is generally high, averaging between 0.77 and 0.87 (Fig. 7a–d). And the high PDP values for each product were mainly distributed in the central and northern parts of the Hengduan Mountains and along the Nyainqentanglha Mountains to the central Himalayas (Fig. 7e–h). Low PDP values were mainly distributed in the Qaidam Basin area and along the southern Hengduan Mountains to the Himalayas. The spatial distribution of FAP for each product showed some spatial complementarity with the PDP (Fig. 7m–p), with the low-value PDP area (the Qaidam Basin area and the area along the southern part of the Hengduan Mountains to the Himalayas) being the high-value FAP area for each product. The high-value MAP area of each product was in the Tianshan Mountain range. In addition, there was a high-value MAP area for GPM in the Central Hengduan Mountains and SM2RAIN-ASCAT in the Nyainqentanglha mountain region (Fig. 7q–t). The standardized coefficients of the PDE at each station were low in the north (i.e. TianShan Mountain) and high in the south (i.e. from the southern part of the Himalayas to the Hengduan Mountains) (Fig. 7i–l). However, high MSWEP values did not show any apparent regional characteristics. In terms of regional means across stations, the independent variable with the highest influence on RMSE values was PDP (MSWEP 57.6%, SM2RAIN-ASCAT 51.4%, GPCC 49.8%, and GPM 43.1%), followed by FAP, which varied (23 to 29%).

Therefore, based on the results of the regional- and station-scale multiple linear regression analyses, precipitation variability contributed the most to the RMSE error of each product through PDP, with contribution levels ranging from approximately 40 to 60%, and the independent variables PDE, FAP, and MAP to the station-scale RMSE for each product ranged from 10 to 46%. Therefore, precipitation variability primarily contributes to the variability of the “detected precipitation error amount” and consequently affects the accuracy of the different precipitation products. Subsequently, errors are propagated through the effects on the PDE, FAP, and MAP, whereas the propagation of errors through the effects on the FAE and MAE is comparatively less.

The multiple linear regression R2 and standardized coefficient proportions of the respective variables for each station were sorted and linearly fitted according to the daily mean precipitation at the site (Fig. 8). The slopes of the linear fits are presented in Table 8. Figure 8 and Table 8 show a gradual decrease in R2 from low to high precipitation sites, which may be because land-air interactions are more frequent and complex in high-precipitation areas and there are more factors other than precipitation that introduce errors into the retrievals. The contribution of precipitation detection (PD) to the errors gradually increased with increasing precipitation for all four products, with PDP increasing significantly more than PDE, and the average slopes of the two being 0.001955 and 5.36E–04, respectively. FAP and MAP showed a gradual decrease in percentage error contribution with increasing precipitation for most products. MAP showed a weak upward trend in GPM. At the same time, in conjunction with the regional-scale results shown in Fig. 6, PDP for all products had the highest contribution in July, which had the highest precipitation. This trend was particularly evident in the MSWEP and SM2RAIN-ASCAT products, where the influence of precipitation variations was pronounced, whereas other factors contributed less and did not show a clear pattern. The absolute error of the retrieval of each precipitation product increased with the increase in precipitation, which was mainly caused by the error generated by the precipitation detection and the increase in precipitation amplitude.

Figure 8
figure 8

Station-scale multiple linear regression R2 and the proportion of standardized coefficients for each predictor variable, sorted by precipitation amount.

Full size image
Table 8 Slope of the fitted line for four precipitation products in Fig. 8.
Full size table

Discussion

There are two approaches to conducting accuracy assessments of precipitation products: "point-to-grid" comparison and "grid-to-grid" comparison. The fundamental requirement for the dataset used as the evaluation standard must be as reliable and accurate as possible. In recent years, many studies have adopted both comparison methods. Many studies have used gridded data generated based on station measurements as the standard for assessing accuracy. Still, fewer studies have independently evaluated the Tibetan Plateau region44,45,46. Currently, such research primarily employs the CGDPA dataset as the evaluation standard. However, one study identified significant errors in this dataset in western China46. Additionally, some literature employs interpolation methods to interpolate point precipitation observations within the region into gridded data. The interpolated dataset is then used as the standard for assessing the accuracy of various products42. Interpolation methods are suitable for regions with many evenly distributed precipitation observation stations. Similarly, other studies suggest that in certain areas, like the northwest region of the Tibetan Plateau, the distribution of rain gauges is highly sparse, and the nearest rain gauge may not adequately represent the precipitation variability in the interpolation region47. Numerous studies have utilized station measurement data (point-based) as the standard to evaluate the accuracy of precipitation products in the Tibetan Plateau and the Tianshan Mountains. Observations from precipitation stations (such as rain gauges) are considered highly accurate and reliable, making them suitable for validation purposes as ground truth data47,48,49. Comparing station data with corresponding grid data allows for directly assessing of precipitation products in capturing local precipitation patterns. One of the main limitations is the mismatch in spatial resolution between point data (precipitation stations) and grid data (precipitation products). Another limitation is the uneven and sparse distribution of precipitation observation stations in the Asian mountainous regions, with rainfall stations primarily concentrated in the east and less so in the west. This study adopts precipitation observation stations (point data) as the standard to evaluate precipitation products. The rationale is twofold: (1) In the HMA where this research is situated, precipitation observation stations are sparse and unevenly distributed. Interpolating station data onto grids introduces additional errors, and the magnitude of these errors is unclear. When data used for validating the accuracy of precipitation products lacks sufficient reliability, conducting accuracy assessments becomes challenging. (2) The evaluated precipitation products have a high spatial resolution (Table 1). We believe comparing point data with grid data at this spatial resolution is feasible. However, it must be acknowledged that using the "point-to-grid" comparison method for accuracy assessment is currently not entirely justified. In the future, as time progresses, the availability of reference precipitation stations will gradually increase, rendering accuracy assessments more reliable.

CC, BIAS, KGE, and RMSE were used to evaluate the relative and absolute deviations of the four precipitation products in HMA. RMSE was largest during rainy months and smallest during dryer months. The relative deviation of the four precipitation products was small in April–June and September–October (monthly precipitation between 40 and 60 mm) (Fig. 2) and large in July–August (monthly precipitation around 100 mm) and November–February (0–20 mm) (Fig. 2). It has been shown that there is an optimal retrieval interval related to the amount of precipitation during the precipitation retrieval. For example, Chen et al. and Shi et al. found that GPM daily precipitation data have better accuracy in retrieval of "medium rain" intensity precipitation events, while the detection accuracy of "light rain" and "heavy rain" is poorer50,51. In addition, the larger deviation from November to February may have been due to the insufficient retrieval capability of the precipitation products for solid precipitation. For example, Liu et al. and Wu et al. indicated that precipitation products cannot identify solid precipitation13,52. It is worth noting that SM2RAIN-ASCAT overestimated precipitation in the rainy season and underestimated it in the dry season compared to WSMEP, GPCC, and GPM, which may be attributed to the fact that this study area has higher temperatures during the rainy season, which leads to snow and glacier meltwater and thus increases soil moisture, resulting in higher precipitation retrieval values during the rainy season. Meanwhile, the dry season (November to February) is snowy, and snow cover on the ground surface leads to low accuracy of soil moisture retrieval, resulting in lower precipitation retrieval values in the dry season.

Daily precipitation data exhibits high variability, often influenced by short-term weather events, leading to significant fluctuations and extreme values. It is also more susceptible to noise and outliers, which can significantly affect the performance of error metrics for different products. Monthly scale data, through aggregation, smooths out daily variability and extremes, reducing the impact of short-term noise and outliers. Consequently, compared to the daily scale, the monthly scale data for different products performs better in CC, BIAS, and KGE metrics but is worse in RMSE metrics. On the daily scale, the overall best-performing product was GPCC, which achieved the best CC, BIAS, and KGE, followed by MSWEP, which had the second best CC and KGE and best RMSE, the performance of the SM2RAIN-ASCAT product in the CC, KGE, and RMSE metrics is second only to MSWEP, while its performance in the BIAS metric is the worst, and GPM, which had the worst CC, RMSE, and KGE. However, the monthly scale performance of the GPM showed a large improvement (Table 3), coming second only to GPCC, indicating that it is suitable for use in precipitation studies at larger time scales. This result agrees with the findings of Li et al. and Xiao et al.53,54. This situation is likely due to the monthly adjustment correction measures taken by the IMERG Final Run product used in this study before its release. The product combines multi-satellite data with GPCC measurement analysis for the month, adjusting a ratio multiplier every half hour. This ratio multiplier remains constant throughout the month but varies spatially34.

Compared to traditional error decomposition methods18,19,20,21, this study utilizes a multiple linear regression model to consider the magnitude and frequency of errors, evaluating their impact on the accuracy of retrieved data. The results indicate that the contribution of frequency to the error is significantly smaller than that of magnitude (Figs. 6 and 7). Additionally, the R2 of the multiple linear regression model allows us to understand how well the combined factors of "hits", "false alarms", and "misses alarms" explain the errors in precipitation products. The results show a high overall explanatory power, although the R2 decreases as precipitation increases (Figs. 7a–d and 8).

Different precipitation retrieval methods are important factors influencing the accuracy of precipitation product retrieval. The different retrieval methods for four sets of precipitation products: "top-down" for MSWEP, GPCC, and GPM and "bottom-up" for SM2RAIN-ASCAT. The top-down method uses data derived from clouds and atmospheric changes detected by microwaves, infrared, and other sensors55, which are, to some extent, higher in the sky than near the surface and are affected by evaporation before reaching the surface; thus, FAP has a greater influence on the RMSE values. Meanwhile, direct observations of cloud cover and atmospheric changes were less affected by season and errors due to misreporting and omission were only slightly increased by the lower precipitation and number of precipitation events in the dry season. The 'bottom-up' method, which observes soil moisture changes56 in response to retrieval precipitation, is susceptible to the effects of vegetation interception and seasonal snow cover, leading to the under-reporting of precipitation. Thus, MAP had a greater impact on the RMSE values in SM2RAIN-ASCAT than in the other products, especially during winter in HMA.

Following the error decomposition criteria, multiple linear models were used to diagnose the factors contributing to the variation in precipitation retrieval errors for each precipitation product. This provides a new opportunity to improve the accuracy of precipitation retrievals. This study had some limitations. For example, in seasonal characterization, the monthly scale precipitation retrieval of the four precipitation products may have an "optimal interval" in the CC, KGE, and BIAS metrics. Although this may be related to the difference in precipitation intensity in different seasonal months, related studies have reached a similar conclusion40,41. However, no study has yet quantitatively determined the possible "optimal intervals" for precipitation products in CC, KGE, and BIAS or analyzed the reasons leading to this feature. This will be investigated in our future studies.

Summary

At the daily scale, in comparison to station observations, MSWEP, GPCC, GPM, and SM2RAIN-ASCAT tend to overestimate precipitation amount and probability during the rainy season and underestimate these metrics during the dry season (with the exception of MSWEP), but overall, they tend to overestimate.

In terms of the average values of the error metrics, GPCC performed the best, exhibiting the smallest errors for CC, BIAS, and KGE. GPM showed a significant improvement in performance on a monthly scale compared to the daily scale. Simultaneously, there was a clear annual cyclicality in the temporal ___domain of the precipitation product error evaluation metrics. Owing to the significant overestimation of precipitation in the dry season by MSWEP, its performance, particularly for BIAS, exhibited characteristics opposite to those of the other three products (overestimation). In terms of absolute error, the accuracy of the precipitation products was higher in the dry season and lower in the wet season. In terms of relative error, the precipitation product accuracy was lower in the wet and dry seasons, with higher accuracy during transitional periods between the wet and dry seasons.

FAP, MAP, PDP, and PDE explained the spatiotemporal variations in the RMSE values of the precipitation products to a large extent. The influence of each factor on the RMSE values of the precipitation products exhibited seasonal characteristics, with SM2RAIN-ASCAT exhibiting the most pronounced seasonal features. The importance of the PDP in influencing the RMSE at the station scale varied from 50 to 60% for each product. An increase in precipitation contributed to an increase in precipitation retrieval errors for all precipitation products in HMA. This is primarily attributed to an overall increase in daily precipitation, followed by an increase in the number of precipitation days.