Introduction

Coal constitutes 56.2% of China's primary energy consumption structure1. With ongoing advancements in coal production technology, most old mines have transitioned to deep mining phases, where mine water inflow has become a primary factor causing disasters in coal production2. According to incomplete statistics, economic losses caused by mine water inflow over the past 30 years have reached 2.7 billion yuan, with an additional 15 billion yuan in reserves left undeveloped due to this threat3. Furthermore, accurately predicting mine water inflow volumes is crucial for ensuring the safety and ecological balance of mining operations4,5. It is also essential for evaluating the rationality of coal mining schemes and the design of drainage systems, which directly affect mining efficiency and sustainable development6.

Methodologies for predicting mine water inflow typically classify models into dynamics-based and data-driven approaches7,8,9. Dynamics-based models rely on a comprehensive understanding of the mechanisms behind mine water inflow and include mathematical representations and parameterizations of related physical processes, such as the water balance method, analytical method, and numerical methods10,11. Despite their specific applicability and effectiveness, the continuous extraction of coal mines, leading to changes in some geological conditions, complicates accurate data collection and challenges the comprehensive and precise management of mine water inflow volumes12. In contrast, data-driven models offer strong capabilities, low entry barriers, high adaptability, and fewer limitations, providing new avenues for addressing the variability and complexity of mine water inflow volumes. Correlation analysis and time series analysis models are widely used in this context. For instance, Miladinovic et al. utilized a linear correlation regression model to predict and calibrate mine water inflow volume in southwest Serbia, significantly reducing prediction errors due to unknown hydrogeological parameters13. Meanwhile, Yang et al.14 combined SARMA and ARIMA models to achieve a prediction accuracy of 94% for mine water inflow. However, these models primarily reveal linear relationships and fail to adequately address the nonlinear processes involved in mine water inflow, thus showing significant limitations in capturing abrupt changes in trends15.

Deep learning, an innovative data-driven predictive model, demonstrates remarkable resilience to changes in data dimensionality. Research consistently shows that these models can maintain robust predictive performance, even with single-dimensional inputs, provided the data sequence is rich in information16. Among these, Long Short-Term Memory (LSTM) networks, recognized for their effectiveness in time series prediction, excel at managing high-dimensional and nonlinear data relationships17,18. These methods have been widely applied in predicting concentrations of air pollutants, runoff forecasts, and groundwater level predictions. M. Cheng et al. (2020) utilized Artificial Neural Networks (ANN) and LSTM models for daily and monthly runoff predictions in the Nan River Basin (NRB) and the Ping River Basin (PRB), demonstrating that LSTM's unique forget gate feature enhances performance in daily forecasts19. In 2018, Zhang and colleagues assessed the predictive performance of Multilayer Perceptrons, Wavelet Neural Networks, and LSTM, finding that LSTM provided more accurate multi-step time predictions20. Zhang et al.21 developed a recurrent neural network prediction method using LSTM to forecast methane concentrations in coal mine production processes within the mining safety ___domain. Shu et al.22 integrated microseismic monitoring technology with LSTM, showing that LSTM-identified coal fracture microseismic events sequentially respond to gas concentrations, offering potential for early warning of gas accidents. In summary, while LSTM has been primarily focused on predicting methane gas eruptions and seismic activities, research on predictions related to water hazards remains limited23.

Data preprocessing is crucial for enhancing predictive performance. Signal decomposition methods segregate fluctuations and variations at different scales from the original sequence while preserving the inherent characteristics of the data, facilitating better extraction of local features and detailed information24. esearchers commonly use methods such as Singular Spectrum Analysis (SSA), Empirical Mode Decomposition (EMD), Ensemble Empirical Mode Decomposition (EEMD), and Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) to manage the non-stationarity in hydrological time series25,26. Among these, SSA decomposition requires manual selection of windows, risking the loss of essential features or over-decomposition. EMD, which does not require manual intervention, performs better in handling non-stationary and nonlinear data27. However, EMD faces the issue of mode mixing, leading to the development of improvements such as EEMD and CEEMDAN28. Notably, Ji et al.24 showed that CEEMDAN effectively avoids mode mixing and reduces noise in decomposed sequences, thus enabling more accurate trend predictions in models. Additionally, optimization algorithms play a vital role in enhancing model predictive capabilities by automatically adjusting model parameters to find global optima, thus minimizing manual intervention29,30. Among the plethora of optimization algorithms, Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Grey Wolf Optimizer (GWO) have recently garnered significant attention and research31,32. Jian Zhou et al.33 introduced a hybrid model combining the Grey Wolf Optimizer with Random Forest (RF) for predicting tunnel water inflow volumes, demonstrating that this hybrid model predicts tunnel water inflow effectively and exhibits higher accuracy and stability compared to traditional methods.

Despite the significant insights provided by previous studies into the application potential of signal decomposition and optimization algorithms for time series data, researchers have not thoroughly explored critical issues regarding the generalizability of models and their ability to detect abrupt changes in the data. To address the volatility of water inflow data and enhance model precision, we developed robust data-driven models that integrate LSTM, Northern Goshawk Optimization (NGO), and CEEMDAN to predict mine water inflow. A comparative analysis of this model’s performance against traditional data-driven models demonstrates its superior stability and accuracy. The primary contributions of this study are as follows:

  1. 1.

    Investigating the impact of sliding input steps on model prediction outcomes.

  2. 2.

    Developing a new “decomposition-optimization-prediction” coupled model framework for mine water forecasting, suitable for complex and highly variable mine water inflows. This framework integrates CEEMDAN, NGO, and LSTM, enhancing the capture of subtle changes and nonlinear characteristics in mine water inflow data and effectively predicting sudden trend shifts.

  3. 3.

    Analyzing the predictive performance of the coupled model across different forecasting periods (1 day, 3 days, 5 days, and 7 days) to determine the optimal forecasting period. This analysis provides robust support for short-term forecasting in mine water prevention and control.

Study area and methodology

Experiment area and data collection

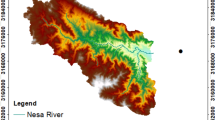
The study area, located in the Gaojiabao mining district of Xianyang, Shaanxi Province, extends approximately 25.7 km east to west and about 16.6 km north to south, covering an area of roughly 219 km2 (Fig. 1). The coal seams within this district are buried at depths ranging from 600 to 1100 m, with a primary focus on exploiting the No. 4 coal seam. We estimate the extractable area for this seam to be 111.29 km2, with an average extractable thickness of 9.33 m. Table 1 presents the hydraulic properties and seepage characteristics of high-pressure aquifers in the overlying strata, along with their distances from the coal seam roof boundary. The stratigraphy, from bottom to top, comprises the Yan'an Formation (J2y), Zhiluo Formation (J2z), Anding Formation (J2a), Luohui Formation (K1l), Huachi Formation (K1h), Neogene System (N), and Quaternary System (Q). The Jurassic Yan'an Formation within the mining area contains coal-bearing strata. The principal aquifers can be categorized as follows: the porous phreatic aquifer of the Quaternary system; the sandstone fissure aquifer of the Lower Cretaceous Huachi Formation; the sandstone porous-fissure confined aquifer of the Lower Cretaceous Luohe Formation; and the sandstone fissure confined aquifer of the Middle Jurassic Zhiluo Formation.

Figure 1
figure 1

Location of the study area.

Full size image
Table 1 Hydraulic properties and seepage characteristics of high-pressure aquifers in overlying strata and their distance from the coal seam roof boundary.
Full size table

Methodology

CEEMDAN method

The CEEMDAN, an advanced decomposition method, builds on the principles of EMD34 and EEMD35. This method adaptively decomposes an original signal into various Intrinsic Mode Functions (IMFs), each incorporating a level-specific white noise to address the mode mixing issues found in EMD and improve upon EEMD's limitations, such as significant reconstruction errors and low computational efficiency36. The main steps involved in the CEEMDAN process are:

  1. 1.

    Initial Decomposition: CEEMDAN utilizes Empirical Mode Decomposition (EMD) to perform n decompositions on the original signal S(t) augmented with Gaussian white noise wi(t) that follows a standard normal distribution (i = 1, 2, …, n). The first modal component derived from this decomposition is expressed as:

$$\begin{array}{c}IM{F}_{1}\left(t\right)=\frac{1}{M}\sum_{1}^{M}IM{F}_{1}^{i}\left(t\right)\end{array}$$
(1)

The first decomposed component, IMF1(t), is then removed from the original time series S(t), resulting in the first residual sequence R1(t):

$$\begin{array}{c}{R}_{1}\left(t\right)=S\left(t\right)-IM{F}_{1}\left(t\right)\end{array}$$
(2)
  1. 2.

    Subsequent Decompositions: This step replicates the initial procedure, where a series of adaptive Gaussian white noises wi(t) (i = 1, 2, …, m) are added to the first residual series. This involves the continued decomposition of the sequence R1(t) + ε1E1[vm(t)] using EMD, resulting in the extraction of the IMF2 mode component:

$$\begin{array}{c}IM{F}_{2}\left(t\right)=\frac{1}{M}\sum_{1}^{M}{E}_{1}\left[{R}_{1}\left(t\right)\right]+{\varepsilon }_{1}{E}_{1}\left[{v}_{m}\left(t\right)\right]\end{array}$$
(3)
  1. 3.

    Continued Decomposition: Repeating the aforementioned steps yields the k-th residual and the (k + 1)-th order modal component. The CEEMDAN decomposition process terminates when the number of extrema in the residual does not exceed two, resulting in k-order modal components. The final residual is denoted as r(t):

$$\begin{array}{c}{R}_{k}\left(t\right)={R}_{k-1}\left(t\right)-IM{F}_{1}\left(n\right)\end{array}$$
(4)
$$\begin{array}{c}IM{F}_{i+1}\left(t\right)=\frac{1}{M}\sum_{1}^{M}{E}_{1}\left({R}_{i}\left(t\right)+{\varepsilon }_{i}{E}_{i}\left[{v}_{m}\left(t\right)\right]\right)\end{array}$$
(5)
$$\begin{array}{c}r\left(t\right)=S\left(t\right)-\sum_{K=1}^{K}IM{F}_{1}\left(t\right)\end{array}$$
(6)

Therefore, the original time series S(t), after undergoing CEEMDAN decomposition, can satisfy:

$$\begin{array}{c}S\left(t\right)=r\left(t\right)+\sum_{K=1}^{K}IM{F}_{K}\left(t\right)\end{array}$$
(7)

LSTM method

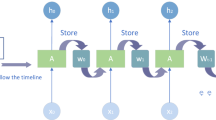
Introduced in 1997 by Hochreiter and Schmidhuber, LSTM37,38 is an enhancement over the existing Recurrent Neural Networks (RNNs) and addresses issues of vanishing and exploding gradients encountered during RNN training. This innovation presents an effective method for modeling complex time series with multiple variables over extended periods39,40. The cell structure41,42 of the LSTM is illustrated in Fig. 2.

Figure 2
figure 2

LSTM memory cell structure. Ct, ht, and xt is the cell state, hidden state, and input of the cell at time t.

Full size image
  1. 1.

    Forget Gate: The forget gate determines, based on a specific formula, which information is retained from the previous time step Ct-1 to the current state Ct:

$$\begin{array}{c}{f}_{t}=\sigma ({W}_{f}\cdot \left[{h}_{t-1},{x}_{t}\right]+{b}_{f}\end{array}$$
(8)

Here, ft denotes the output function value of the forget gate at time t. Wf and bf represent the forget gate's weight matrix and bias vector, respectively. The function σ indicates the sigmoid activation function, and ht-1 is the output value of the hidden layer at time t-1.

  1. 2.

    Input Gate: The input gate determines which new information should be updated to the cell state, which is formulated into the following formula:

$$\begin{array}{c}{i}_{t}=\sigma ({W}_{i}\cdot \left[{h}_{t-1},{x}_{t}\right]+{b}_{i}\end{array}$$
(9)

In this formulation, it represents the activation function value of the input gate at time t. Wi and bi respectively denote the input gate's weight matrix and bias vector.

$$\begin{array}{c}{\widetilde{C}}_{t}=tan\text{h}\left({W}_{C}\cdot \left[{h}_{t-1},{x}_{t}\right]+{b}_{c}\right)\end{array}$$
(10)

Furthermore, C̃t indicates the function value of the candidate cell state at time t, with tanh representing the hyperbolic tangent function. Wc and bc respectively represent the candidate cell state's weight matrix and bias vector.

  1. 3.

    Memory Update: The new cell state is formed by combining the old memory processed through the forget gate and the latest memory processed through the input gate. The cell state is updated from ct-1 to ct using the following formula:

$$\begin{array}{c}{C}_{t}={f}_{t}*{C}_{t-1}+{i}_{t}*{\widetilde{C}}_{t}\end{array}$$
(11)
  1. 4.

    Output Gate: The output gate determines which information will be transferred from the cell state to the hidden state, as calculated by the following equation:

$$\begin{array}{c}{o}_{t}=\sigma ({W}_{o}\cdot \left[{h}_{t-1},{x}_{t}\right]+{b}_{o}\end{array}$$
(12)

In this context, ot represents the function value of the output gate at time t, with Wo and bo denoting the weight matrix and bias vector of the forget gate. The hidden state at time t, denoted as St, is determined by the output gate and the cell state.

$$\begin{array}{c}{S}_{t}=tanh({C}_{t})*{o}_{t}\end{array}$$
(13)

NGO method

The Department introduced the NGO algorithm in 202143. This algorithm models the hunting behaviors of Northern Goshawks, including prey identification, attack, pursuit, and evasion strategies. The NGO algorithm effectively balances global and local searches, allowing it to tackle complex problems characterized by multiple local optima. Its robust adaptability simulates natural optimization processes, making it a powerful, flexible, and efficient tool for solving a variety of complex optimization challenges44,45. The steps are outlined as follows:

  1. 1.

    Algorith Initialiation Process: Mathematically, each goshawk in the population is represented as a vector within a population matrix. Initially, the members of the population are randomly initialized within the search space:

    $$\begin{array}{c}X={\left[\begin{array}{c}{X}_{1}\\ \vdots \\ {X}_{i}\\ \vdots \\ {X}_{N}\end{array}\right]}_{N\times m}={\left[\begin{array}{ccccc}{x}_{\text{1,1}}& \cdots & {x}_{1,j}& \cdots & {x}_{1,m}\\ \vdots & \ddots & \vdots & \ddots & \vdots \\ {x}_{i,1}& \cdots & {x}_{i,j}& \cdots & {x}_{i,m}\\ \vdots & \ddots & \vdots & \cdots & \vdots \\ {x}_{N,1}& \cdots & {x}_{N,j}& \cdots & {x}_{N,m}\end{array}\right]}_{N\times m}\end{array}$$
    (14)

    Here, X denotes the matrix of the Northern Goshawk population; Xi is the initial solution of the i-th goshawk; N and m represent the number of individuals in the population and the dimensions of the problem space, respectively.

    The objective function for the problem is evaluated based on the proposed solutions by each member of the group, and the values of the objective function can be expressed as a vector:

    $$\begin{array}{c}\left(X\right)=\left[\begin{array}{c}{F}_{1}=F\left({X}_{1}\right)\\ \vdots \\ {F}_{i}=F\left({X}_{i}\right)\\ \vdots \\ {F}_{N}=F\left({X}_{N}\right)\end{array}\right]\end{array}$$
    (15)

    Here, F represents the objective function vector of the Northern Goshawk population, with Fi denoting the value of the objective function corresponding to the i-th solution.

  1. 2.

    Prey Identification and Attack: Initially, the goshawk selects prey randomly and rapidly attacks, representing the global search of the search space to identify optimal regions. This random prey selection enhances the exploratory capacity of the algorithm. The mathematical model is:

    $$\begin{array}{c}{P}_{i}={X}_{k},i=\text{1,2},\cdots ,N,k=\text{1,2},\cdots i-1,i+1,\cdots ,N\end{array}$$
    (16)
    $$\begin{array}{c}{x}_{i,j}^{new,P1}=\left\{\begin{array}{c}{x}_{i,j}+r({p}_{i,j}-I {x}_{i,j}), {F}_{Pi}<{F}_{i}\\ {x}_{i,j}+r({x}_{i,j}-{P}_{i,j}), {F}_{Pi}\ge {F}_{i}\end{array}\right.\end{array}$$
    (17)
    $$\begin{array}{*{20}c} {X_{i} = \left\{ {\begin{array}{*{20}c} {X_{i}^{{new,{\kern 1pt} P1}} ,F_{i}^{{new,{\kern 1pt} P1}} < F_{i} } \\ {X_{i} ,F_{i}^{{new,{\kern 1pt} P1}} \ge F_{i} } \\ \end{array} } \right.} \\ \end{array}$$
    (18)

    where, Pi represents the position of the i-th Northern Goshawk's prey, and \({F}_{Pi}\) is its corresponding objective function value. The variable k is a randomly chosen integer within the interval [1, N], distinct from i. The term \({x}_{i,j}^{new,P1}\) denotes the new solution value of the i-th goshawk in the j-th dimension. \({x}_{i,j}\) signifies the position of the i-th Northern Goshawk in the j-th dimension, while \({p}_{i,j}\) refers to the j-th dimensional position of the i-th Northern Goshawk's prey. The parameters r and I are random numbers used for searching and iteration updates; r ranges within [0, 1], and I can be either 1 or 2. \(X_{i}^{new,\;P1}\) represents the updated position of the i-th Northern Goshawk after the first phase, and \(F_{i}^{new,\:P1}\) is the objective function value after the first phase.

  1. 3.

    Chase and Escape Operation: When prey attempts to flee following an attack, the Northern Goshawk, known for its keen responsiveness and exceptional speed, can almost continuously pursue and ultimately capture it under any circumstances. This simulation enhances the algorithm's ability to utilize local search within the search space. Assuming a hunting radius of R, the mathematical model for the chase between the Northern Goshawk and its prey is as follows:

    $$x_{i,j}^{new,P2} = x_{i,j} + R2{\text{r}} - 1x_{i,j}$$
    (19)
    $$\begin{array}{*{20}c} {R = 0.021 - \frac{t}{T}} \\ \end{array}$$
    (20)
    $$X_{i} = \left\{ {\begin{array}{*{20}c} {X_{i}^{{new,{\kern 1pt} P2}} ,F_{i}^{{new,{\kern 1pt} P2}} < F_{i} } \\ {X_{i} ,F_{i}^{{new,{\kern 1pt} P2}} \ge F_{i} } \\ \end{array} } \right.$$
    (21)

    where, \(x_{i,j}^{new,P2}\) represents the value of the i-th goshawk's solution at the new position in the j-th dimension. Here, t and T denote the current iteration and maximum number of iterations, respectively. \(X_{i}^{{new,{\kern 1pt} P2}}\) is the updated position of the i-th Northern Goshawk in the second phase, while \(F_{i}^{{new,{\kern 1pt} P2}}\) denotes the objective function value for the i-th Northern Goshawk after the update in the second phase.

Coupling prediction method

Figure 3 displays the schematic flowchart of the CEEMDAN-NGO-LSTM model. This study introduces a prediction model for mine water inflow utilizing an LSTM network, enhanced by data decomposition and optimization techniques. Initially, the CEEMDAN algorithm decomposes the raw data into multiple IMFs, which capture signal characteristics across various scales and frequencies. These IMFs provide a multi-layered input for the LSTM model. Subsequently, the NGO algorithm optimizes the LSTM parameters for each element. The LSTM utilizes its unique gating mechanism (input gate, forget gate, and output gate) to effectively capture long-term dependencies and filter out irrelevant or noisy information, thereby maintaining efficient memory and state updates during the prediction of mine water inflow. The final step involves using the optimized model to make predictions and aggregating the results from each element into a comprehensive forecast.

Figure 3
figure 3

Flow prediction chart based on ICEEMDAN-NGO-LSTM methods.

Full size image

All models were executed using Matlab R2022b on a computer running Windows 10, equipped with an Intel(R) Core(TM) i5-9300H CPU @ 2.40 GHz and 16 GB of RAM.

Model performance evaluation indicators

To assess the predictive accuracy of the model, we selected the following metrics: Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and the Nash–Sutcliffe Efficiency coefficient (NSE)46,47,48,49. RMSE, which is the square root of the average of squared forecasting errors, measures deviations between observed and predicted values. MAE quantifies the absolute differences between observed and predicted values, providing a direct measure of disparity. MAPE, expressed as a percentage, indicates the proportionate error between observed and actual values and is primarily used to assess data anomalies. Smaller values of RMSE, MAE, and MAPE indicate higher accuracy of the prediction model. NSE, a widely used efficiency metric in hydrology, measures the consistency between model predictions and actual observations. NSE values range from -∞ to 1, with values closer to 1 indicating a higher correspondence between predictions and observations. The theoretical formulas for RMSE, MAE, MAPE, and NSE satisfy:

$$\begin{array}{c}RMSE=\sqrt{\frac{1}{N}\sum_{i=1}^{N}{\left({y}_{i}-{y}_{i}^{*}\right)}^{2}}\end{array}$$
(22)
$$\begin{array}{c}MAE=\frac{1}{N}\sum_{i=1}^{N}\left|{y}_{i}-{y}_{i}^{*}\right|\end{array}$$
(23)
$$\begin{array}{*{20}c} {MAPE = \frac{1}{N}\sum\limits_{{i = 1}}^{N} {\left| {\frac{{y_{i} - y_{i}^{*} }}{{y_{i} }}} \right|} \times 100} \\ \end{array} \%$$
(24)
$$\begin{array}{c}NSE=1-\frac{\sum_{i=1}^{N}{\left({y}_{i}-{y}_{i}^{*}\right)}^{2}}{{\sum }_{i=1}^{N}{\left({y}_{i}-\overline{y }\right)}^{2}}\end{array}$$
(25)

where, yi represents the actual mine water inflow data, \(\overline{y }\) denotes the average value of the actual data, and yi* is the predicted mine water inflow.

Result and discussion

Change characteristics of water inflow

Figure 4a presents the measured data for water inflow volumes at the Gaojiabao mine from 2020 to 2023. As shown in Fig. 4, there are localized abrupt changes in water inflow volumes, exhibiting a gradually increasing trend. Specifically, the minimum inflow volume recorded on June 4, 2020, was 3506 m3/h, while the maximum volume reached 7956 m3/h on September 1, 2022, with an average volume of 5390.83 m3/h over the period. The extreme values differ by a factor of two, and significant fluctuations are observed at specific locations.

Figure 4
figure 4

Time series diagram of water inflow (a) and Box plot for each month (b).

Full size image

Box plots were used to analyze the distribution characteristics of mine water inflow volumes on a monthly scale. As depicted in Fig. 4b, the variations in mine water inflow volumes exceeded 1000 m3/h in March and April of 2020, in March, April, September, and October of 2022, and in January and February of 2023. The most significant disparity was observed in September 2022, reaching 2000 m3/h. This analysis highlights numerous abrupt changes and turning points in mine water inflow volumes over short periods. From March 2022 to March 2023, mine water inflow displayed a trough-like pattern with a skewness of 0.376. The right-skewed distribution with a long tail suggests a higher likelihood of exceptionally high inflows as mining progresses. This pattern indicates an increased probability of exceptional mine water inflow due to ongoing mining activities. The underlying causes are likely related to pervasive joint fractures within the Luohe formation, significant static reserves, and the formation of conductive pathways when mining-induced fractures intersect with pre-existing joints.

Comparison of single prediction models

For the time series prediction, 80% of the historical data on water inflow volume from Fig. 4a was allocated to the training set, while the remaining 20% was used as the validation set50. It is important to note that similar results were observed with other models; however, this study focuses primarily on the LSTM model as a representative example. The detailed results of the evaluation metrics for the LSTM model, including sliding input steps and maximum epoch numbers, are presented in Tables 2 and 3. These tables show that the NSE coefficient initially increases and then decreases as the sliding input steps extends from 1 to 10 days, peaking at 3 days. Conversely, when the sliding input steps exceeds 10 days, the NSE values gradually decline. Other metrics, such as RMSE and MAE, display an opposite trend to NSE, decreasing initially and then increasing. This indicates that increasing the sliding input steps does not improve prediction results; optimal performance is achieved at a 3-day lag. Beyond this, the model may learn unnecessary and potentially noisy patterns, distorting the prediction outcomes. The outcomes of backward-in-time iterations show no direct correlation between increased time step value and enhanced forecast accuracy. Extending the time steps excessively compels the model to process irrelevant information, reducing predictive precision. Therefore, selecting a time step that aligns with the model's capabilities is crucial for achieving accurate predictions. The focus on mine water inflow prediction on short-term fluctuations, rather than on long-term trends or the cumulative impact of historical data, underscores the importance of choosing an appropriate time step.

Table 2 The Impact of LSTM Time Lag Length on Predicting Water Inrush.
Full size table
Table 3 Impact of the Maximum Number of Epochs in LSTM on Water Inrush Prediction.
Full size table

In contrast, increasing the maximum number of epochs has only a minor effect on the prediction outcomes. The NSE coefficient initially increases and then decreases, while RMSE displays the opposite trend. The best results are achieved at 400 epochs. Furthermore, MAE achieves its optimum at 200 epochs, and MAPE reaches its best at 300 epochs. Considering all factors, the performance metrics of the parameters are optimal when the maximum number of training epochs is set to 400. Therefore, to enhance prediction accuracy for predicting the volume of mine water inflows, it is recommended to select a sliding input steps of 3 and a maximum of 400 epochs.

Figure 5 displays the predictive performance of six single-models: Autoregressive Integrated Moving Average (ARIMA), Back Propagation (BP), Convolutional Neural Networks (CNN), Recurrent Neural Network (RNN), Gated Recurrent Unit (GRU), and LSTM. The results show that the computational efficiency of each model is similar. However, except for LSTM, the other models generate relatively conservative predictions and do not achieve the predictive accuracy of LSTM. Specifically, LSTM achieves the following results in key performance metrics: a MAE of 186.468, a MAPE of 2.811%, a RMSE of 252.378, and a NSE coefficient of 0.724. These outcomes confirm LSTM's ability to uncover complex nonlinear relationships within time series data, demonstrating its superior predictive performance. However, LSTM's robustness in sequences with frequent abrupt changes can be compromised by vanishing gradients, leading to slight lags as LSTM struggles to fully capture the peaks of sudden changes, as observed in Fig. 6. This phenomenon reduces the predictive value for early warning of inrush events, indicating that achieving accurate predictions of water inflow volumes without comprehensive data preprocessing remains a significant challenge.

Figure 5
figure 5

Comparison of 4 evaluation indicators for each model prediction (a) NSE (b) TIME (c) MAPE (d) MAE (e) RMSE.

Full size image
Figure 6
figure 6

The validation results of the mine water inrush by LSTM.

Full size image

Decomposition-prediction coupled model

Time series decomposition efficiently extracts local characteristics and hidden information from data, segregating fluctuations and variations in mine water inflow data from the baseline dataset. In this study, we utilized three decomposition methods to analyze mine water inflow time series data: EMD, EEMD, and CEEMDAN as shown in Fig. 7. Due to the adaptive nature of these data-driven methods, the EMD decomposition identified 7 IMFs and one residual component R; EEMD decomposition revealed 8 IMFs and one residual component R; by contrast, CEEMDAN decomposition produced 9 IMFs and one residual component R. From IMF1 to the residual component, there is a progressive decrease in the amplitude of oscillations and an increase in wavelength, reflecting a transition from high to low frequencies and depicting the periodic variation characteristics of each component's time scale. These IMFs, along with the residual component R, enable the complete reconstruction of the original signal, ensuring no loss of information during frequency decomposition.

Figure 7
figure 7

Results of (a) EMD (b) EEMD (c) CEEMDAN for the mine water inflow.

Full size image

Integrating EMD, EEMD, and CEEMDAN with LSTM led to the development of EMD-LSTM, EEMD-LSTM, and CEEMDAN-LSTM coupled predictive models. We determined the model with the highest accuracy by comparing the performance of these three coupled models, as detailed in Fig. 8 and Table 4. Specifically, the EMD-LSTM model exhibited a MAE of 143.306, a MAPE of 2.143%, a RMSE of 199.948, and an NSE coefficient of 0.821. Relative to EMD-LSTM, EEMD-LSTM showed a reduction of 8.185% in MAE, 6.337% in MAPE, 12.273% in RMSE, and an improvement of 4.580% in NSE. However, the CEEMDAN-LSTM model surpassed EEMD-LSTM in prediction accuracy, with further reductions of 2.082% in MAE, 2.880% in MAPE, 10.107% in RMSE, and an increase of 5.903% in NSE. The CEEMDAN model demonstrated the most significant performance improvements compared to EMD-LSTM and EEMD-LSTM, while the computation times for the models were similar. Although the CEEMDAN-LSTM model addressed the lag issue associated with LSTM, it was less effective in predicting abrupt changes in trends, showing a notable discrepancy between expected and actual peak values.

Figure 8
figure 8

The validation results of the mine water inrush by EMD-LSTM (a)、 EEMD-LSTM (b) and CEEMDAN- LSTM (c).

Full size image
Table 4 Metrics MAE, MAPE, RMSE, and NSE for Decomposition-Prediction and Decomposition-Optimization-Prediction models.
Full size table

Decomposition-optimization-prediction coupled model

The NGO algorithm offers several significant advantages in addressing complex optimization challenges. Empirical evaluations across various benchmark tests and real-world engineering design problems have demonstrated that NGO outperforms other established algorithms, such as PSO, GA, and GWO, in terms of convergence speed and optimization accuracy. These outcomes highlight NGO's capability in handling complex and high-dimensional optimization tasks. Moreover, the NGO algorithm exhibits robust adaptability and stability across a range of problem environments, affirming its efficiency and reliability as an optimization tool43. Therefore, as illustrated in Fig. 9 and Table 4, integrating the NGO algorithm into the CEEMDAN-LSTM model significantly enhanced the training performance of the coupled model. It accurately captured and predicted abrupt changes in water inflow volumes, thereby increasing the model's overall reliability in real-world scenarios. The optimized model demonstrated reductions of 25.039% in MAE, 24.525% in MAPE, and 22.536% in RMSE, along with a 5.415% improvement in the NSE coefficient. These key metrics substantiate the feasibility and significant practical application value of the CEEMDAN-NGO-LSTM in enhancing prediction accuracy.

Figure 9
figure 9

The validation results of the mine water inrush by CEEMDAN-NGO-LSTM.

Full size image

To evaluate the model's applicability in various scenarios, the CEEMDAN-NGO-LSTM was used to predict the water inflow of a single working face in a mining area, utilizing data from November 4, 2021, to July 5, 2023. The division of the training and test sets is depicted in Figure S1, with the results presented in Fig. 10 and Table 4. The model achieved an NSE of 0.906, a MAPE of 4.060%, an MAE of 87.760, and an RMSE of 117.410. The accuracy and capability of the CEEMDAN-NGO-LSTM to capture abrupt changes were also validated, confirming its effectiveness in practical applications.

Figure 10
figure 10

The validation results of the working face mine water inrush by CEEMDAN-NGO-LSTM.

Full size image

Short-term forecasting

In our analysis, we selected the three top-performing models: the single prediction model, the decomposition prediction model, and the decomposition optimization prediction model. We applied linear fitting to the predicted versus actual values during the training and validation phases, as illustrated in Fig. 11. The results of this approach are revealing.

Figure 11
figure 11

Scatter plot of the simulation vs the observation of the mine water inrush of (a) training and (b) validation.

Full size image

The linear equations during the training phase are as follows:

$${\text{LSTM training phase}}:{\text{ Y }} = { 1}.00{\text{2X }} - { 1}0.{913 }\left( {{\text{R}}^{{2}} = \, 0.{99}0} \right)$$
$${\text{CEEMDAN}} - {\text{LSTM training phase:Y}} = \, 0.{99}0{\text{X}} - {6}0.{955}\left({{\text{R}}^{{2}} = \, 0.{997}} \right)$$
$${\text{CEEMDAN}} - {\text{NGO}} - {\text{LSTM training phase:Y}} = \, 0.998{\text{X}} + {22}.{376}\left( {{\text{R}}^{{2}} = \, 0.{999}} \right)$$

During the validation phase, the equations shifted:

$${\text{LSTM:Y}} = \, 0.935{\text{X}} + 405.915 {\left( {{\text{R}}^{{2}}} = \, 0.723 \right)}$$
$${\text{CEEMDAN}} - {\text{LSTM}}:{\text{ Y }} = { 1}.0{\text{34X }} - { 292}.{777 }\left( {{\text{R}}^{{2}} = \, 0.{9}0{9}} \right)$$
$${\text{CEEMDAN}} - {\text{NGO}} - {\text{LSTM:Y}} = 1.020{\text{X}} - 206.682 {\left( {\text{R}}^{{2}} = \, 0.958 \right)}$$

These equations demonstrate a strong correlation between the predicted and actual values, with improvement noted in the order presented. However, the scatter plots for the first two models still show some outliers. One potential explanation is that the abrupt changes are intrinsic rather than acquired characteristics, while another posits that the series exhibits a high degree of autocorrelation. These findings support the notion that optimization algorithms can significantly enhance feature extraction and learning within decomposition models, thereby reducing the impact of autocorrelation in the series.

Our study employed the LSTM, CEEMDAN-LSTM, and CEEMDAN-NGO-LSTM models to forecast mine water inflow over future intervals of 1, 3, 5, and 7 days as depicted in Fig. 12. Given the brief duration of forecasts, conventional indices like the NSE are not suitable for assessing accuracy. Instead, we used RMSE and MAPE for this purpose. In single-step forecasts, the MAPE values were 0.0650, 0.0460, and 0.0430, respectively, coupled with RMSE of 412.110, 288.230, and 271.430. The CEEMDAN-NGO-LSTM model yielded predictions closest to actual values. For three-step forecasts, MAPE values improved to 0.0290, 0.0160, and 0.0230, with RMSEs of 247.040, 128.170, and 155.437, indicating enhanced accuracy across all models. Still, only the CEEMDAN-NGO-LSTM model accurately captured the actual trend. In the five-step forecasts, the initial volumes of mine water inflow rose, followed by stable fluctuations. The LSTM model predicted a gentle ascending trend, culminating near the interval's maximum value. The CEEMDAN-LSTM model showed an ascending-descending-ascending pattern, but with notable fluctuations and some predictions not aligning with the actual trend. In contrast, the CEEMDAN-NGO-LSTM model closely matched the natural trend, with predictions slightly higher than actual values, providing a solid foundation for mine water hazard prevention. This model's MAPE values were 0.0270, 0.0290, and 0.0160, with RMSEs of 214.060, 198.020, and 122.790, respectively. For seven-step forecasts, the MAPE values were 0.0510, 0.0460, and 0.0460, with RMSEs of 410.100, 394.370, and 382.370, respectively. Again, the CEEMDAN-NGO-LSTM model outperformed the others. However, predictions for the last two days deviated significantly from the actual trend, impairing forecast accuracy. In conclusion, the CEEMDAN-NGO-LSTM model, utilizing the Northern Goshawk Optimization algorithm, achieves superior accuracy and trend prediction in five-step forecasts. This model effectively navigates the complexities of nonlinear, non-stationary signals such as mine water inflow. Additionally, the predicted water inflow trend for the next five days at the working face is highly consistent with the actual trend (Fig. 13), with RMSE and MAPE values of 236.580 and 9.836%, respectively. These results further substantiate that optimization algorithms can enhance the extraction and learning of features within decomposition models, mitigating the effects of series autocorrelation.

Figure 12
figure 12

Comparison chart of predicted versus actual values of mine water inflow for the future (a) 1 day, (b) 3 days, (c) 5 days, (d) 7 days.

Full size image
Figure 13
figure 13

Comparison chart of predicted versus actual values of working face mine water inflow for the future 5 days.

Full size image

Conclusion

This study introduces and applies a novel "decomposition-optimization-prediction" model to address the complex, nonlinear, and non-stationary challenges inherent in predicting mine water inflow volumes. We employed the newly developed CEEMDAN-NGO-LSTM model, which features exceptional decomposition preprocessing capabilities and sophisticated memory functions. This model effectively tackles the challenges of predicting mine water inflow. The principal conclusions are as follows:

  1. (1)

    The single time series prediction model exhibits optimal performance when employing a sliding input step of 3 steps and a maximum of 400 epochs, achieving MAE, MARE, RMSE, and NSE values of 186.468, 2.825, 255.364, and 0.724, respectively.

  2. (2)

    In comparison to the LSTM and CEEMDAN-LSTM models, the CEEMDAN-NGO-LSTM model demonstrates average performance improvements of 44.950% and 19.400%, respectively. It excels in capturing abrupt changes in data and minimizing lags, underscoring the pivotal role of the CEEMDAN and NGO algorithms in enhancing the accuracy of predictions for mine water inflow.

  3. (3)

    The CEEMDAN-NGO-LSTM model forecasts mine water inflow for the next five days with high accuracy, closely mirroring actual trends and achieving the lowest RMSE value of 122.790. Thus, this model provides a solid foundation for the effective prevention and control of mine water hazards.

Although the current CEEMDAN-NGO-LSTM model is proficient in predicting mine water inflow, it necessitates additional testing across diverse datasets to confirm its robustness. Future research will focus on the potential for real-time implementation and integration of the model into existing systems. By developing interfaces and optimization schemes, the model can be seamlessly integrated with current mine monitoring and management systems. Furthermore, advanced predictive visualization tools will be developed by designing intuitive visualization interfaces. These tools will utilize various methods to display predictive data and trends, enabling users to customize views according to specific needs, thereby providing more targeted predictive insights. These research initiatives aim to further enhance the accuracy and stability of mine water inflow predictions, offering more scientific and precise tools for the field.