Introduction

With the intensification of climate change and increasing environmental pollution1,2,3, global water resources issues are facing great challenges4,5. Freshwater scarcity has become a constraint to agricultural development and global food security6,7,8,9. The majority of the Yellow River Basin in China is located in an arid and semi-arid region, where rainfall is insufficient and evapotranspiration is huge, and thus water resources are extremely scarce10,11. This has become one of the most important factors restricting the development of local agriculture. In order to cope with the problem of water shortage and alleviate the contradiction between supply and demand of agricultural water, water-saving irrigation has become a development strategic in many countries and regions. There have been numerous forms of water saving irrigation technologies in use such as sprinkler irrigation12,13, micro-sprinkler irrigation14,15, drip irrigation16,17, intermittent irrigation18, surge root irrigation19,20, and film hole irrigation21,22. However, in the Yellow River Basin of China, soil erosion is severe and leads to a high sand content in the river. When the sand content in irrigation water is high, pipes and irrigators are prone to clogging and become ineffective, making it difficult to popularize water-saving irrigation technologies on a large scale in the region. Considering the sandy characteristics of the rivers in this area, film hole irrigation technology has been the focus of much attention in order to select the appropriate water-saving irrigation technology according to the local conditions.

Film hole irrigation is a relatively new irrigation method in which a plastic film is placed over a bordered field and water is delivered through crop and irrigation holes23. Compared to traditional surface irrigation, film hole irrigation improves the uniformity and quality of irrigation by wetting only the soil in the vicinity of the crop's root system24. Furthermore, the ground plastic film in film-covered irrigation reduces the evaporation of water from the field, which increases the temperature, retains moisture, and saves water and fertilizer25. In addition, film hole irrigation can also employ a canal system to divert water, whereby the water flow advances in the field and subsequently enters the special irrigation hole. Compared with drip and sprinkler irrigation, this approach is less impacted by the water quality, and is thus also applicable to the irrigation area using muddy water irrigation, where the river has a large amount of sand content.

From a theoretical point of view, film hole irrigation involves three-dimensional point source infiltration at a low pressure head (i.e., irrigation depth). Understanding the infiltration characteristics of film hole irrigation is the basis for determining field film hole irrigation schemes with a high application efficiency and distribution uniformity. The film hole irrigation infiltration characteristics are influenced by numerous factors, including soil texture, soil bulk density, hole diameter, and initial soil water content22,26. Fan et al. investigated the Philip infiltration model for film hole irrigation under different factors and concluded that the adsorption rate is a power function of the film hole diameter for the same soil texture24. Li et al. found that the higher the soil bulk density, the weaker the film hole irrigation infiltration capacity27. Film hole irrigation infiltration capacity decreases gradually as the initial soil water content increases28. Under muddy water conditions, sediment is gradually deposited on the soil surface as infiltration proceeds. The sediment forms a dense layer, which prevents the infiltration of soil29, and thus the muddy water characteristics (e.g. sand content) also affect the infiltration of film hole irrigation. Liu et al. investigated the infiltration characteristics of fertilizer solution under different sand contents of muddy water, and determined the sand content rate to have a significant hindering effect on the infiltration of film hole irrigation30. Currently research focuses on the single-factor aspects of infiltration in film hole irrigation under muddy water conditions. However, actual production practices are faced with the more complex multifactorial influences of infiltration conditions.

The use of numerical simulation methods to explore soil infiltration characteristics has become a research hotspot31,32. For example, by assuming the wetted body produced by drip irrigation to be a sphere, Jiftah et al. investigated the drip irrigation wetted body and its internal water distribution to optimize the layout of the drip irrigation system33. Jie et al. used elliptic equations to model the shape of film hole irrigation wetting fronts and evaluated the effect of initial moisture content on the characteristics of film hole irrigation wetting bodies34. Feng et al. employed a back propagation neural network and support vector machine to establish a soil transfer function for the estimation of the calibration factor by examining the calibration factor and soil property parameters of the Kostiakov model using wavelet and pass path analyses35.

By adopting numerical simulation methods, this paper aims to: (i) investigate the effects of multiple factors on the infiltration characteristics of film hole irrigation under muddy water conditions; and (ii) propose and validate empirical models for the prediction of the cumulative infiltration and transport distance of vertical and horizontal wetting fronts under muddy water conditions for film hole irrigation. The results provide a theoretical basis and technical support for film hole irrigation infiltration under muddy water conditions.

Materials and methods

Experimental equipment

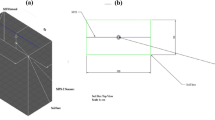
Figure 1 illustrates the laboratory experimental setup. Based on the symmetrical nature of film hole infiltration, the soil box consists of 10 mm thick transparent acrylic material with design dimensions of 30 × 30 × 60 cm (length × width × depth). The bottom of the soil box has numerous parallel ventilation holes for aeration. A Mariotte vessel with an inner diameter of 6 cm and height of 50 cm was used to maintain a constant irrigation head. The Mariotte with the muddy water was placed on the magnetic stirrer and the magnetic field force was used to rotate the stirrer in the Mariotte. This allowed for the continuous stirring of the muddy water to maintain a stable sand content of muddy water.

Figure 1
figure 1

Laboratory infiltration experiment device: (a) is a schematic diagram of the infiltration device; (b) is a physical drawing of the infiltration device.

Full size image

Experimental soil samples

For the experiment, sandy loam soil (based on the US Department of Agriculture Soil Taxonomy System) was obtained from the northern suburbs of Xi'an City, Shaanxi Province, central China. The soil particle size was determined using a Mastersizers-2000 laser particle size analyzer (Malvern Instruments, UK), with a measurement range of 0.02–2000 μm). Table 1 lists the particle size distribution of the experimental soils. Soil samples were collected at a depth of 20–60 cm and the samples were air-dried and sieved through a 2 mm sieve. The sediment contained in the muddy water in the infiltration test was taken from the main canal of Jinghui Canal Irrigation District, Shaanxi Province, and the retrieved sediment was air-dried and passed through a 1 mm sieve. Table 1 reports the composition of each group of sediment particles measured using the Mastersizers-2000 laser particle size analyzer.

Table 1 Properties of test materials.
Full size table

Experimental procedure

The experiment was conducted in August 2023 at the State Key Laboratory of Eco-hydraulic in Northwest Arid Region, Xi’an, China. Given the constraints of film hole irrigation in the field, the diameter of the film hole is usually determined according to the actual situation of the crop, with diameters typically ranging from 3 to 8 cm. The effects of the muddy water sand content, hole diameter, soil bulk density and infiltration time were taken into account in the experiments. We assumed three treatment levels for three of the above factors (the muddy water sand content, hole diameter and soil bulk density), and thus nine test sets were designed according to the orthogonal test table, with three replications for each set of tests. In addition, three experiments were designed for validation. Thus, a total of 12 sets of experiments were designed. Table 2 reports the details of each experimental set.

Table 2 Experimental scheme.
Full size table

At the beginning of the test, soil samples were pressed into the soil box at a predetermined soil bulk density to simulate the original soil bulk densities. The soil was packed into the soil box in 5 cm layers and compacted to obtain a homogeneous soil profile. To prevent evaporation, the soil surface was covered with a polyethylene film. The film hole device was perpendicular to the surface of the soil box to observe the movement of the wetting front. In order to simulate an adequate water supply for film hole irrigation, the bottom of the Mariotte inlet was adjusted to produce a 5 cm pressure head. Once the experiment started, readings were collected from the Mariotte at 5-min intervals and the wetting front curve was plotted once. After a certain duration, the time intervals used to collect the readings and plot the curves were extended based on the infiltration rate and the migration distance of the wetting front. A camera was used to record the ___location of the wetting front at the end of the experiment.

Data processing and analysis

Data were processed and analyzed using Excel 2021 (version 2021, Microsoft Corporation, Redmond, USA) and IBM SPSS Statistics (version 22.0, International Business Machines Corporation, Armonk, USA). Multifactorial analysis of variance (MANOVA) was performed on the cumulative infiltration, horizontal wetting front transport distance, and vertical wetting front transport distance under the influence of different factors. Multiple comparisons of significant differences between factors and levels were performed using the least significant difference (LSD) method. Furthermore, multiple linear regression (MLR) was employed for the regression analysis of the various influencing factors of the model. The Z-score normalization method was employed for normalization of the data to eliminate complications caused by the dimensions and orders of magnitude of the data.

Model evaluation

The mean absolute error (SMAE), root mean square error (SRMSE), and percent bias (SPBIAS) were used to statistically analyze the predicted cumulative infiltration per unit of film hole area and vertical and horizontal wetting front transport distances. These metrics were calculated as follows:

$${\text{S}}_{\text{MAE}}\text{ = }\frac{{\sum }_{\text{r }\text{=} \, {1}}^{\text{n}}\left|{\text{O}}_{\text{r}} \, -{\text{ S}}_{\text{r}}\right|}{\text{n}},$$
(1)
$${\text{S}}_{\text{RMSE}}\text{ = }{\left[\frac{1}{{\text{n}}}{\sum }_{{\text{r}}\text{ = 1}}^{\text{n}}{\text{(}{\text{O}}_{\text{r}} \, -{\text{ S}}_{\text{r}}\text{)}}^{2}\right]}^{\frac{1}{{2}}},$$
(2)
$${\text{S}}_{\text{PBIAS}} = \frac{{\sum }_{{\text{r}} = 1}^{\text{n}}({\text{O}}_{\text{r}} -{\text{S}}_{\text{r}})\cdot {100}}{{\sum }_{{\text{r}}= 1}^{\text{n}}{{\text{O}}}_{\text{r}}},$$
(3)

where n is the number of observations. r is a value ranging from 1 to n, chosen arbitrarily from n measurements. Or and Sr denote the rth experimentally observed and calculated values, respectively. SMAE and SRMSE values close to 0 and SPBIAS ≤  ± 10 indicate a small difference between the calculated and observed values.

Results

Modeling cumulative infiltration per unit film hole area

Figure 2 depicts the curves of cumulative infiltration per unit of film hole area versus infiltration time under muddy water conditions for film hole irrigation infiltration for each group of experimental treatments. The cumulative infiltration was observed to increase with the infiltration time. After 300 min of infiltration, the cumulative infiltration of the various experimental treatments was 14–25 cm. Moreover, the cumulative infiltration was 42.3% and 64.5% higher in treatments 1 and 6 compared to treatment 7, respectively. Variations were observed in the cumulative infiltration among experimental groups, indicating that the cumulative infiltration per unit (I) was influenced by muddy water sand content (S), soil bulk density (γ), and hole diameter (D).

Figure 2
figure 2

Cumulative infiltration per unit film hole area of film hole irrigation (I) against time under different experimental treatments.

Full size image

Table 3 reports the results the MANOVA results. Sand content, hole diameter, soil bulk density and infiltration time exhibited highly significant (p < 0.01) effects on the cumulative infiltration per unit of film hole area.

Table 3 Influence of multiple factors under different levels of cumulative infiltration per unit film hole area.
Full size table

MLR was employed to determine the empirical equations for the relationship between cumulative infiltration and the four influencing factors:

$$\text{I }= \text{ } {\text{a}}{\text{S}}^{\text{b}}{{\text{D}}}^{\text{c}}{\gamma }^{\text{d}}{{\text{t}}}^{\text{e}},$$
(4)

where I is the cumulative infiltration per unit area. S is muddy water sand content, %; D is hole diameter, cm; γ is soil bulk density, g cm-3; a is muddy water sand content the infiltration coefficient; and b, c, d and e are infiltration regression indices.

Equation (4) becomes after taking both logarithms:

$${\text{ln}}\text{I }= \text{ ln} {\text{a}}\text{ + }{\text{b}}{\text{ln}}{\text{S}}\text{ + }{\text{c}}{\text{ln}}{\text{D}}\text{ + }{\text{d}}{\text{ln}}\gamma + \text{ } {\text{e}}\text{lnt.}$$
(5)

Equation (5) represents a linear combination equation with lnI, lnS, lnD, lnγ, and lnt as variables. Here, lna is the constant term, while b, c, d, and e denote the coefficients for each variable in the equation. The values of these parameters (lna, b, c, d, and e) can be determined through regression analysis using the MLR module in SPSS software, applied to the experimental data from each treatment:

$$\text{I }\text{= 5.733}{\text{S}}^{-\text{0.157}}{\text{D}}^{-0.781}{\gamma }^{-2.278}{\text{t}}^{0.574}.$$
(6)

The SRMSE and R2 for Eq. (6) were determined as 0.027 cm and 0.991 (P < 0.01), respectively. The relatively high R2 and relatively low SRMSE indicate the high accuracy of the model in estimating cumulative infiltration.

The empirical model presented in Eq. (6) is a function of four influencing factors of different units and orders of magnitude. Therefore, the significance of their effect on the cumulative infiltration cannot be directly determined based on the infiltration regression indices. By normalizing the data, we determined the standard regression coefficients of − 0.070, − 0.151, − 0.065, and 0.979 for b, c, d, and e, respectively, revealing that infiltration time had the strongest effect on the cumulative infiltration, followed by hole diameter, muddy water sand content, and lastly, soil bulk density. Moreover, the positive standardized regression coefficient for infiltration time indicates a positive correlation between infiltration time and cumulative infiltration, and vice versa for the remaining three variables. More specifically, the cumulative infiltration per unit of film hole area is negatively correlated with the sand content of muddy water, the soil bulk density, and the hole diameter.

In order to verify the applicability of Eq. (6), a validation experiment was conducted using treatments 10–12. The values observed in the experiment were compared with those calculated using the model. Figure 3 depicts the results.

Figure 3
figure 3

Comparison between measured and calculated values of cumulative infiltration.

Full size image

The SMAE between the measured values of treatments 10, 11, and 12 and the calculated values obtained using the empirical model in Eq. (6) were determined as 0.365, 0.345, and 0.196 cm, respectively, while the equivalent values for SRMSE were 0.485, 0.463, and 0.258 cm, respectively. Both the SMAE and the SRMSE were less than 1 cm. Furthermore, the SPBIAS values were calculated as 2.041, 0.257 and 0.900, respectively, all of which are less than 10, and the regression was close to the 1:1 line. These statistical evaluation metrics indicate that the empirical model effectively describes the relationship between cumulative infiltration and the given influencing factors.

Dynamics of soil infiltration rates

By taking the derivative of the cumulative infiltration per unit film hole area with respect to the infiltration time, the infiltration rate was obtained as a function of infiltration time for film hole irrigated soils under muddy water conditions as follows:

$${\text{i}}\text{ = }\frac{{\text{d}}{\text{I}}}{{\text{d}}{\text{t}}} \, \text{= 4.811}{\text{S}}^{-\text{0.157}}{\text{D}}^{-0.781}{\gamma }^{-2.278}{\text{t}}^{-0.426},$$
(7)

where i is the infiltration rate (cm/min). Other symbols have the same physical meaning as above.

Equation (7) demonstrates that the infiltration rate of film hole irrigation soil under muddy water conditions decreases gradually with the prolongation of infiltration time. The soil infiltration rate gradually stabilizes when the infiltration time reaches a certain point. The effect of the factor on the soil infiltration rate varies with the factor type. Thus, the partial derivatives of the factors were taken and their absolute values were used to analyze the sensitivity of the soil infiltration rate to the influence of each factor:

$$\left|\frac{\partial {\text{i}}}{\partial {\text{S}}}\right| \, \text{= -0.755}{\text{S}}^{-\text{1.157}}{\text{D}}^{-0.781}{\gamma }^{-2.278}{\text{t}}^{-0.426},$$
(8)
$$\left|\frac{\partial {\text{i}}}{\partial {\text{D}}}\right| \, \text{= -8.569}{\text{S}}^{-\text{0.157}}{\text{D}}^{-1.781}{\gamma }^{-2.278}{\text{t}}^{-0.426},$$
(9)
$$\left|\frac{\partial {\text{i}}}{\partial \gamma }\right| \, \text{= -15.770}{\text{S}}^{-\text{0.157}}{\text{D}}^{-0.781}{\gamma }^{-3.278}{\text{t}}^{-0.426},$$
(10)

where Eqs. (8)–(10) represent the sensitivity indexes of the muddy water sand content, soil bulk density and hole diameter to the soil infiltration rate, respectively. The larger the sensitivity index, the greater the influence of the changes in the corresponding factor on the soil infiltration rate. Figure 4 presents the change in the sensitivity index of each factor to the soil infiltration rate against the influencing factors, taking treatment 1 as an example. Each sensitivity index decreased with the increase of the corresponding factor. This indicates that the changes in the muddy water sand content, hole diameter and soil bulk density influenced the soil infiltration rate, with sensitivity indexes ranges of 0.0007–0.0070, 0.0049–0.0715 and 0.1007–0.3742, respectively. Based on these values, soil bulk density exerted the strongest influence on the soil infiltration rate, followed by the hole diameter, and lastly, the muddy water sand content. Each sensitivity indicator was also strongly influenced by the infiltration time. At the infiltration time of 30 min, the sensitivity indexes obviously decreased as the corresponding factors increased, while at the 120 min and 240 min infiltration times, the sensitivity indexes decreased at a reduced rate. For example, at 30 min, the sensitivity index of soil weight decreased by 0.1299 as this factor increased, and only decreased by 0.0719 and 0.0536 at 120 min and 240 min, respectively.

Figure 4
figure 4

Relationship between the sensitivity of the soil infiltration rate to each factor and the corresponding factor, taking treatment 1 as an example. (a) Muddy water sediment content; (b) film hole diameter; (c) soil bulk density.

Full size image

Vertical wetting front transport distance model

Based on the infiltration tests of film hole irrigation under different muddy water conditions, the course of vertical wetting front values of the infiltration time was determined for each test group (Fig. 5). The vertical wetting front increased with the infiltration time. Furthermore, differences in the vertical wetting fronts among the test groups were observed at the same infiltration time. For example, at the infiltration moment of 300 min, the vertical wetting front of treatment 5 was 82.7% higher than that of treatment 8. This indicates that the factors have different degrees of influence on the vertical wetting front.

Figure 5
figure 5

Vertical wetting front transport distance of film hole irrigation (Z) against infiltration time under different experimental treatments.

Full size image

In order to further analyze the effects of each factor on the transport distance of vertical moist fronts, MANOVA was employed to analyze the effects of S, D, and γ on the vertical moist fronts (Z) (Table 4). The results reveal that S, D, γ and infiltration time exerted highly significant (P < 0.01) effects on the vertical wetting front.

Table 4 Influence of the four factors under different vertical wetting front transport distances.
Full size table

Based on the MANOVA results of each factor for the transport distance of the vertical moist fronts, the model between the transport distance of vertical moist fronts and each factor is described as:

$$\text{Z }= \text{ } {\text{f}}{\text{S}}^{\text{m}}{{\text{D}}}^{\text{n}}{\gamma }^{\text{p}}{{\text{t}}}^{\text{q}},$$
(11)

where Z is the vertical wetting front transport distance of film hole irrigation; f is the vertical wetting front fitting coefficient; m, n, p and q are the vertical wetting front fitting indices. Using MLR and data from orthogonal tests 1–9, Z is determined as:

$$\text{Z }\text{= 5.490}{\text{S}}^{-\text{0.202}}{\text{D}}^{0.481}{\gamma }^{-4.127}{\text{t}}^{0.275}.$$
(12)

The R2 and SRMSE for Eq. (12) were calculated as 0.982 (P < 0.01) and 1.029 cm, respectively, indicating a good fit between the model and data.

After normalizing the data, the standard regression coefficients for m, n, p, and q were determined as − 0.152, 0.130, − 0.256, and 0.848, respectively. Thus, the infiltration time exerts the greatest influence on the transport distance of the vertical wetting, followed by the infiltration time, soil bulk density, and lastly, the muddy water sand content. Furthermore, the transport distance of the vertical wetting front is positively correlated with the hole diameter and the infiltration time, and negatively correlated with the remaining factors.

The reliability of Eq. (12) was verified using the data from treatments 10–12. Figure 6 compares the measured values of the test with the values calculated using the model.

Figure 6
figure 6

Comparison between measured and modeled values of the vertical wetting front transport distance.

Full size image

The SMAE values between the modeled (from Eq. (12)) and measured results were 0.451, 0.320, and 0.314 (treatments 10, 11, and 12), and the corresponding SRMSE values were 0.549, 0.388, and 0.375 cm/min, respectively, demonstrating a small overall error. Moreover, the SPBIAS values were calculated as 0.786, 0.855, and 2.464, all of which are less than 10. This indicates that the constructed dynamic model can effectively describe the quantitative relationship between hydraulic conductivity and each of the four factors.

Horizontal wetting front transport distance modeling

Figure 7 depicts the horizontal wetting front transport distance versus infiltration time for each group of experimental treatments of film hole irrigation under muddy water conditions. The horizontal wetting front transport distance was observed to increase with infiltration time. At 300 min, the horizontal wetting front transport distance ranged from 5.45 to 12.75 cm. Thus, at the same infiltration time, the transport distance of the horizontal wetting fronts varied amongst each test group. This demonstrates that the factors exert different degrees of influence on the horizontal wetting fronts.

Figure 7
figure 7

Horizontal wetting front transport distance of film hole irrigation (X) against infiltration time under different experimental treatments.

Full size image

MANOVA was used to analyze the relationship between the transport distance of the horizontal wetting fronts and the four factors. Table 5 reports the results. The muddy water sand content, hole diameter, soil bulk density, and infiltration time exhibited highly significant (P < 0.01) effects on the true horizontal wetting front.

Table 5 Influence of the four factors under different horizontal wetting front transport distances.
Full size table

Based on the MANOVA results, the model for the transport distance of the horizontal wetting front (X) under the influence of each factor is described as:

$${\text{X}}= \text{ } {\text{h}}{\text{S}}^{\text{g}}{{\text{D}}}^{\text{j}}{\gamma }^{\text{k}}{{\text{t}}}^{\text{l}},$$
(13)

where X is the h is the horizontal wetting front transport distance of film hole irrigation; horizontal wetting front fitting coefficient; g, j, k and l are the horizontal wetting front fitting indices. Using the MLR and data from tests 1–9, the dynamic empirical formula for X was determined as:

$$\text{X }\text{= 3.251}{\text{S}}^{-0.123}{\text{D}}^{0.504}{\gamma }^{-1.739}{\text{t}}^{0.186}.$$
(14)

The R2 and SRMSE for Eq. (14) were determined as 0.958 (P < 0.01) and 1.003 cm, respectively, indicating that this equation can accurately estimate the transport distance of horizontal moist fronts. In addition, the standardized regression coefficients for g, j, k, and l were determined as − 0.150, 0.208, − 0.175, and 0.927, respectively. Thus, the influence of each factor on the transport distance of the horizontal wetting front was, in descending order of magnitude, infiltration time, film hole diameter, soil bulk density and muddy water sand content. As with the vertical wetting front transport distance, the horizontal wetting front transport distance was negatively correlated with infiltration time and hole diameter, and positively correlated with the remaining factors.

In order to test the reliability of Eq. (14), it was validated using the data from treatments 10–12. Figure 8 compares the experimental and modeled values.

Figure 8
figure 8

Comparison between measured and modeled values of horizontal wetting front transport distance.

Full size image

The SMAE values between the modeled and experimental results were 0.505, 0.419 and 0.468, for treatments 10, 11 and 12, while the corresponding values for SRMSE were 0.639, 0.492 and 0.584 cm, respectively. Moreover, the SPBIAS values were determined as 1.309, 1.105 and 0.018, respectively. These indicators validate the ability of the model to calculate the transport distance of horizontal wetting fronts under different experimental variables.

Discussion

This study investigated the infiltration process of film hole irrigation under muddy water conditions. We adopted three factors (sand content of muddy water, film hole diameter and soil bulk density) under three levels, resulting in nine groups of orthogonal infiltration tests. The MANOVA results concluded that each factor had a significant factor on the cumulative infiltration per unit of film hole area and vertical and horizontal wetting front transport distance. MLR was used to establish dynamic models containing the experimental factors, the simulation values and the measured values of the SMAE, SRMSE and SPBIAS. The models met the error requirements and the numerical simulation performances were satisfactory.

MLR is employed to investigate the functional relationship between multiple influencing factors and dependent variables based on MANOVA. In this study, multifactor regression models were developed to simulate the change patterns of cumulative infiltration and the vertical and horizontal wetting front transport distances of film hole irrigation over time under muddy water conditions. The models exhibited significant fits, with R2 values exceeding 0.99 and SRMSE values less than 1 cm. In the cumulative infiltration model, muddy water sand content, hole diameter and soil bulk density had significant effects on the cumulative infiltration, which is similar to the work of Li et al. and Liu et al.27,30. However, the models in the aforementioned studies only considered the effect of a single factor on the cumulative infiltration. Under muddy water conditions, the sediment in the muddy water during the infiltration process of the film hole irrigation soil is gradually deposited on the surface of the soil near the film hole, forming a dense layer with weak water conductivity36. The greater the sand content of the muddy water, the thicker the dense layer formed by sediment in the surface soil of the film hole, and the greater the impediment to infiltration. This is consistent with the negative correlation between the cumulative infiltration per unit of film hole area of muddy water film hole irrigation and the muddy water sand content, which agrees with the results of Liu et al.30. Soil bulk density reflects the number of soil pores and the degree of soil compactness to a certain extent, and soil pores decrease with increasing bulk density. Thus, the larger the soil bulk density, the smaller the pores, and the greater the obstruction to water transport in the soil. As a consequence, the cumulative infiltration is negatively correlated with the soil bulk density. This is in line with the conclusion of Todisco et al.37.

A suitable combination between different factors can produce a range of wetting body morphologies to satisfy the crop root system water demand while simultaneously reducing the deep leakage of irrigation water. This can play a vital role in saving water and improving the quality of irrigation. In this study, a multifactor regression model of vertical and horizontal wetting front transport distances was developed by considering several influencing factors. Numerous studies have been carried out on the geometry of wetting fronts in drip irrigation38,39, and the shape of wetting fronts in film hole irrigation under muddy water conditions is similar to such conditions. Based on the multifactorial regression models derived from the vertical and horizontal wetting front transport distances, for the design of more rational film hole irrigation system and irrigation quality evaluation provides a convenient condition. The multivariate regression models developed in this paper can be utilized to describe the cumulative infiltration and vertical and horizontal wetting front transport distances of different muddy water sediment contents, soil bulk density and hole diameters of film hole irrigation under muddy water conditions. The models also provide theoretical support for the rational design of film hole irrigation systems, as well as for irrigation systems under muddy water conditions.

Conclusion

The infiltration process of film hole irrigation is influenced by several factors under muddy water conditions. In this study, we conducted nine sets of three-factor, three-level orthogonal experiments and designed three sets of validation experiments to investigate the effects of sediment content of muddy water, soil bulk density, and hole diameter on infiltration characteristics. We utilized multifactorial analysis of variance (MANOVA) and multiple regression analysis (MLR) for analysis. The results revealed significant effects of muddy water sand content, soil bulk density, and hole diameter on cumulative infiltration per unit film hole area, as well as on vertical and horizontal wetting fronts. Regression models were developed for these variables. Comparing standardized regression coefficients, infiltration time emerged as the most influential factor on cumulative infiltration, followed by hole diameter, sediment content of muddy water, and soil bulk density. Vertical wetting front distance was primarily influenced by infiltration time, soil bulk density, muddy water sand content, and hole diameter. Similarly, infiltration time, hole diameter, soil bulk density, and muddy water sand content were the major factors affecting horizontal wetting front distance. Infiltration rate was found to be most sensitive to changes in soil bulk density, followed by hole diameter and sediment content of muddy water. Validation tests demonstrated close agreement between simulated and calculated values, confirming the efficacy of the developed model in describing the infiltration process of film hole irrigation under muddy water conditions.

In conclusion, the model established can effectively provide a suitable and reliable design for film hole irrigation systems. This is of great significance to the development of the agricultural economy in regions of muddy-water irrigation and the realization of water-saving irrigation.