Introduction

Metal plating and mineral extraction industries cause water pollution by releasing huge quantities of water contaminated with toxic metals such as Pb (II), Fe (III) and Cr (III). These metals do not disintegrate easily and are accumulated by the organisms drinking contaminated water or products of the contaminated water like crops etc1. The most widely used method of mitigating water pollution is adsorption2. In recent years, the adsorption of hazardous water by using clays has been increased because of the advantages of clays as compared to other adsorbing materials such as high adsorption, good accessibility, lesser cost, higher surface area, and higher capacity for ionic exchange3. The adsorption of heavy metals using bentonite has also been investigated by many researchers4,5,6. Bentonite is a naturally occurring clay mineral which has found numerous applications in concrete industry due to its special properties. The incorporation of bentonite in concrete results in enhancement of several key properties of concrete and elimination of toxic metals7. The mixture of conventional concrete and bentonite is called bentonite plastic concrete (BPC), and it is widely used to construct cut-off walls for preventing seepage under dams8,9,10. The swift prediction of compressive strength of BPC is important to reduce the time and cost required by concrete testing procedures in constructing dams with BPC due to the modified mix design of BPC as compared to normal concrete. Thus, having accurate value of 28-day compressive strength (\({f}_{c}{\prime}\)) of BPC is important for making key decisions in construction of large dam projects11,12,13,14.

During the construction of dams and other water-tight structures, two important factors to consider include water tightness and seepage control. The construction of cut-off walls is one of the most commonly used methods to prevent seepage from the dams. However, due to the rigid diaphragm of cut-off walls, a slight deformation in earth embankment can lead to the failure of cut-off wall. Also, cracks can develop in cut-off walls due to the deformation of embankment caused by seismic activity or fluctuation in impounded reservoir levels15,16,17. This issue can be resolved by using plastic concrete whose deformation characteristics are similar to as of embankment soils18,19,20. However, this plastic concrete must be water-tight to allow the soil and wall to deform without separation. This plastic concrete has higher formability and lower strength in contrast to normal concrete due to use of clay in concrete21. The mixture composition of BPC generally includes aggregate (coarse and fine), cement, water, bentonite, and clay formed into a mixture of higher water-to-cement ratio than conventional concrete to result into a ductile material21. The researchers have also suggested using a mixture of bentonite and kaolinite for constructing impermeable clay coatings at places where bentonite isn’t readily available. The study conducted by Karunaratne et al.22 reveals that the consolidating and hydraulic conductivity properties of concrete made with equal amounts of bentonite and kaolinite are almost the same as of concrete made with 100% bentonite. Thus, it shows that bentonite is a versatile material that aids in development of plastic concrete to be used in water-tight structures such as dams and also for adsorbing contaminated water. It is worth mentioning that 28-day compressive strength is an important parameter used for quality control of concrete. In case of BPC, there are various factors which can affect \({f}_{c}{\prime}\) like chemical properties of concrete constituents, water-to-cement ratio, and curing time etc. During the use of BPC, the samples taken from various mixtures must be rigorously tested for \({f}_{c}{\prime}\) and other important parameters. However, it is not possible to cast, store, cure, and test a large number of concrete samples of BPC at construction site due to resource, time, and effort limitations23,24,25. Therefore, a tool for accurate and fast prediction of BPC strength is needed to overcome the above-mentioned limitations and foster the widespread use of BPC for water-tight structures and also for adsorption of toxic metal-contaminated water. Thus, this study aims to develop prediction models that makes use of concrete mixture compositions to estimate \({f}_{c}{\prime}\) of BPC accurately.

In recent years, machine learning (ML) techniques have captured the attention of researchers in different fields to predict different properties26,27,28,29,30. Initially, the use of artificial neural networks (ANNs) was preferred due to their impressive accuracy and because they eliminated the need for a pre-determined mathematical model31,32,33. However, with the passage of time, other ML models such as random forest (RF), support vector machine (SVM), and different boosting algorithms were developed to further increase the accuracy of ML models34,35,36. However, the evolutionary algorithm techniques such as GEP and MEP are advantageous in the sense that they represent their output in the form of an empirical equation thus giving more transparency and insight into the prediction process37. The other ML algorithms don’t have this ability and thus are called black-box models38. Also, GEP and MEP does not need optimization of model architecture like ANN etc., thus reducing the time and computing power required to make predictions39. Table 1 summarizes the main advantages of MEP and GEP algorithms.

Table 1 Advantages of MEP and GEP algorithms.
Full size table

Previous studies regarding concrete strength prediction using ML techniques

It has been observed that during past few years, the subject of predicting strength and other properties of different types of concrete has been popular among researchers. To discuss a few studies, Amin et al.40 used different bagging algorithms such as AdaBoost and boosting algorithms like RF to predict strength of concrete containing rice husk ash (RHA) in place of cement. The authors utilized a dataset for RHA-modified concrete from literature and used it to predict strength of concrete. The developed models were checked for their accuracy by using various error metrices such as average error, correlation coefficient and root mean squared error. The study concluded that RF is the most accurate algorithm which predicted strength values having more than 92% accuracy. In the same way, Li et al.41 predicted splitting tensile strength of concrete containing metakaolin using ANN, SVR, RF and gradient boosting decision tree (GBDT). The authors compared the efficiency of algorithms and revealed that GBDT proved to be the most accurate out of all the algorithms having a mere average error of 0.14. Similarly, Nazar et al.42 employed ANN and GEP for the purpose of predicting strength and slump of geopolymer concrete made with fly ash. The authors also conducted sensitivity analysis on the GEP model since it proved to be more accurate than ANN based on the evaluation using different error metrices. Also, Mahmood et al.43 utilized a laboratory dataset of 133 points for Self-compacting concrete made by replacing cement with marble powder and RHA. The authors utilized variety of algorithms including SVM, RF, decision tree, gradient boosting etc. along with different deep learning techniques to predict compressive strength. The authors measured the relative accuracy of algorithms by means of mean absolute percentage error and average error and concluded that deep learning techniques predicted strength with greater accuracy as compared to other ML algorithms with higher accuracy and lesser errors. Iqbal et al.44 applied MEP to predict split tensile strength and modulus of elasticity of concrete which contained waste foundry sand in addition to natural sand. The authors highlight an important advantage of using MEP that it presented its output in the form of empirical equations which can be effectively utilized by professionals and researchers for calculating modulus of elasticity and split tensile strength of sustainable concrete containing waste foundry sand as a replacement of natural sand. The authors also conducted a parametric analysis to determine the relationship between the input variables and the two output variables which provided further insights into the MEP model and enhanced its effectiveness. Furthermore, Shahab et al.45 predicted electrical resistivity and compressive strength of concrete modified with graphene nanoplatelets. The authors used GEP, SVM and RF for this purpose and also developed a graphical user interface that can be used to predict strength of graphene nanoplatelets-based concrete efficiently. As evident from above discussion, significant work has been done on the subject of predicting strength properties of different types of concrete using various ML techniques but there is still a lack of work focusing on strength prediction of concrete containing clay and bentonite. Thus, this research aims to fill the gap in the literature by employing two evolutionary techniques i.e., MEP and GEP and AdaBoost to predict \({f}_{c}{\prime}\) of BPC.

Overview of machine learning in civil engineering

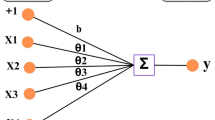
Artificial intelligence (AI) in realm of civil engineering chiefly refers to the use of advanced algorithms and ML techniques for promoting efficient infrastructure design, optimizing construction processes, and increasing overall efficiency and safety of construction projects46,47,48,49,50. ML is a subset of AI by virtue of which machines can learn from the data without explicit human intervention. ML has different types including supervised, unsupervised and reinforcement learning. ANNs are commonly used tool in deep learning (DL), which in turn is a subset of ML as shown in (Fig. 1). ML and DL differ from each other in a way that DL automatically extract features and does classification while in case of ML, the user must identify features on which the algorithm performs classification and calculates predictions. Machine learning essentially refers to the kind of AI in which computers can recognize patterns in the data and use the information from data to make accurate predictions without requiring extensive programming. It has been extensively utilized in civil engineering for structural analysis, materials optimization, construction management and maintenance etc. In particular, different evolutionary techniques, random forests, decision trees, neural networks etc. have been used to predict different properties of concrete and cement composites51,52,53,54,55, soil liquefaction and compaction parameters56,57,58,59, and slope stability60,61,62,63.

Figure 1
figure 1

Artificial intelligence (AI) and its subtypes.

Full size image

Research significance

It is evident from overview of relevant literature that there have been some studies regarding prediction of concrete containing various admixtures like RHA, metakaolin, marble powder, and fly ash etc. However, the subject of prediction of mechanical properties particularly compressive strength is relatively unexplored. Thus, this study is conducted as an attempt to fill this gap in the literature by utilizing evolutionary programming techniques like GEP and MEP and a boosting-based technique known as AdaBoost. The motivation behind using MEP and GEP along with AdaBoost for predicting \({f}_{c}{\prime}\) of BPC stems from the fact that they are widely regarded as grey-box models in contrast to black-box nature of ANN and AdaBoost etc. The MEP and GEP algorithms have the ability to depict the output as an empirical expression. This expression can be seamlessly used by researchers across the globe to calculate the desired value. It also provides transparency to the prediction process and fosters the widespread use of developed models38. Also, the selection of AdaBoost in place of other techniques like SVM and ANNs is due to its increased accuracy, simple algorithm architecture, and efficient implementation64. Moreover, this study is novel in the sense that it compares two evolutionary techniques MEP and GEP with one of the most famous boosting techniques i.e., AdaBoost. Furthermore, to get increased insights into the importance of different variables in predicting \({f}_{c}{\prime}\) of BPC, this study utilizes shapley explanatory analyses on the model of highest accuracy.

Methodology

This study is attributed to predicting \({f}_{c}{\prime}\) of BPC using three soft computing models including GEP, AdaBoost and MEP. The overall methodology followed in the study is given in (Fig. 2). After the identification of the problem, the next step was to collect data from the literature to be used for building the models. A comprehensive literature search was performed, and 246 data points were collected to be used for training the algorithms. Different descriptive statistical analysis techniques were also performed on the data to get useful information about the database on which the models will be constructed. Also, according to the suggestions of previous studies, different statistical evaluation metrices were used to check the performance of developed models. The actual model development process involved finding the appropriate set of hyperparameters which gave maximum accuracy. Furthermore, a comparison was drawn between the developed models and the model proving to be most accurate was selected for further explanatory analysis to gain insight into the model prediction process. This whole process is explained step by step in (Fig. 2).

Figure 2
figure 2

Overall methodology followed in the study.

Full size image

Prediction models

Out of the three ML models employed in current research, two algorithms (MEP and GEP) are subtypes of genetic programming (GP) which is based on the use of evolutionary algorithms. The idea of genetic programming GP was given by John Koza for the first time65 by integrating the concept of genetics with natural selection66. GP is a useful instrument for mathematical modelling due to its parse-trees which are non-linear, rather than binary strings of a fixed length. GP utilizes Darwin’s theory of evolution to solve problems using processes such as mutation, crossover, and reproduction in the same way these processes function inside the genes of human beings65. These processes favour the formation of individuals with good results and thus helps in convergence on the algorithm67. Both MEP and GEP are subtypes of the same parent technique i.e., GP. It uses evolutionary algorithms to create and modify computer programs to solve a problem. The basis of GP lies in Darwin’s theory of natural selection and uses an iterative process to generate increasingly complex programs to improve the accuracy68,69,70. The basic process of GP involves creating random programs according to pre-defined rules and parameters. These programs are evaluated using fitness function and the accurate programs are used to create more programs. This process repeats several times before reaching at the most accurate and efficient program as the solution to the problem71. GP has the advantage that it can discover solutions to the problems which are too difficult to solve for human brain. This ability of GP makes it a useful tool for solving problems that require large computing power. GP has many variants having different ways to represent the individuals in the population, but the basic working principle is same for all variants. This study utilizes the two most common and most accurate variants of GP named as MEP and GEP for modelling strength of bentonite plastic concrete.

Gene expression programming (GEP)

GEP was proposed as an alternative algorithm to GP by Ferreira66 which is based on the evolutionary population theorem. It also utilizes parse trees and fixed-length chromosomes. However, GEP considers fixed length parse trees in contrast to GP which considers parse trees of variable length. It is the same as separating genotype from phenotype66. GEP eliminates the possibility of modifying the whole structure since all mutations are taking place inside a single linear framework. It is because GEP only allows to pass the genotype to the next generations. Also, in the populations made by the GEP algorithm, only one chromosome is responsible for creating populations with many genes.

The overall methodology followed by the GEP algorithm is illustrated in (Fig. 4). The basic methodology of GEP revolves around using genes which represent a smaller segment of the code. These genes are built using mathematical functions known as primitive functions. These primitive functions can range from simple arithmetic functions like addition and subtraction etc. to complex functions like trigonometric and logarithmic functions. Various evolutionary processes such as mutation and recombination72 are used to combine these genes as illustrated in (Fig. 3). The algorithm starts by generating a population of chromosomes and calculates the fitness of these chromosomes on the basis of a pre-determined fitness function. The chromosomes which exhibit good accuracy based on the fitness function are selected to be included in the next generation while the worst performing ones are discarded from the population73,74,75. This whole process of generating chromosomes, evaluating their fitness, and using them to create next generation is repeated for many times which enables the algorithm to converge towards the actual solution76.

Figure 3
figure 3

Visual representation of expression tree and genetic processes.

Full size image

Multi expression programming (MEP)

MEP is a subtype of GP that uses linear chromosomes to make predictions. The basic working principle of MEP is similar to GEP. However, it can encode multiple results in a single chromosome which makes it more accurate than other variants of GP77. The final answer of MEP is derived from the chromosome which performs best according to the fitness function. A binary tournament procedure is used to select two parents and these parents are used to generate an offspring. The offspring is altered using genetic processes and this process repeats over several generations until the most accurate representation of the given problem is discovered as illustrated by (Fig. 4). The prediction process by MEP starts by creating a population of expressions. These expressions are displayed as expressions trees (as illustrated in Fig. 3). The generated expressions are classified according to their ability to solve the problem accurately by means of a fitness function. The expressions having good accuracy are used to generate another population of expressions while others are discarded from the population. The genetic processes of mutation and crossover are used on existing expressions to create new expressions. The visual representation of both these processes is given in (Fig. 3). The process of mutation involves altering the structure of an existing expression while crossover means generating a whole new expression from two parent expressions78.

Figure 4
figure 4

Methodology followed by the genetic programming techniques.

Full size image

AdaBoost regression

In 1990, Schapire argued that a single DT has limited capabilities and thus is a weak learner. He combined several weak learners in series and made a strong learner which laid the groundwork for development of boosting algorithm79. In AdaBoost algorithm, every time the algorithm adds a new tree, the general tree is eliminated and only the strongest tree is added. The repetition of this process over many iterations led to the improvement of algorithmic accuracy80. This algorithm involves a simple weak regression algorithm improvement process, which improves its accuracy by virtue of continuous training. The first weak learner is obtained by learning from the training data81. However, after the creation of first basic tree, some data samples are correctly predicted while some are not. So, the wrong training samples are combined with the untrained data to make a new training sample and the second tree is obtained by training on this newly constructed sample. The wrong samples now are combined again with the untrained data to form yet another training sample, and it is trained to obtain the third weak learner tree. This process is repeated many times until an accurate learner is obtained. The algorithm also gives different weight to the samples to increase the accuracy of learners82. The accurate learners are given less weights while less accurate learners are given more weight so that the algorithm can focus more on the less accurate learners to make them accurate83. The overall process of AdaBoost algorithm is given in (Fig. 5). It is important to mention that while the training process of basic tree model is carried out, the weight distribution of each sample present in the dataset must be adjusted. The training data changes, and hence the training results will also vary, which are summed to get the final result.

Figure 5
figure 5

Methodology followed by AdaBoost regression.

Full size image

Data collection and analysis

Collection of a reliable database to be used for training the algorithms is one of the most important steps in building data-driven models84. Thus, an extensive dataset consisting of 246 instances for BPC strength has been collected from internationally published literature85 given in appendix. The collected dataset has six input parameters that have been identified crucial for predicting \({f}_{c}{\prime}\) of bentonite plastic concrete. These input parameters include cement and water content, quantities of coarse and fine aggregates, bentonite content, and clay content. These six input parameters will be utilized towards the prediction of single output i.e., compressive strength. The input parameters used in this study are measured in kilograms while the output parameter is measured in megapascals (MPa).

Data description and splitting

It has been rigorously suggested that the dataset to be used for model development should be divided into two or three sets and the algorithms should be trained on one set while the other dataset should be used for checking accuracy of the developed algorithms. Thus, the collected data to be used in this study has been divided into training set containing 172 points (70%) and testing set having rest of the 74 points (30%). The ML models were trained using training data then they will be used to make predictions on the unseen test data to make sure that they can perform well when tested against unseen data and are not overfitted to the training data. Moreover, the summary of statistical analysis of the collected data is given in (Table 2). It can be seen from Table 2 that the input and output variables are spread across a wide range and this type of data distribution is imperative for developing widely applicable models.

Table 2 Descriptive analysis of the dataset.
Full size table

Data correlation

It is useful to check the interdependence of selected variables before starting the model development process. This is due to the fact that if the input variables are highly correlated with each other, it might cause a problem during algorithm development known as multi-collinearity86. The interdependence between variables employed in the study can be checked by using a statistical analysis tool known as correlation matrix. It quantifies the regression between different variables in the form of coefficient of correlation (R) and thus can be used to check the effect of explanatory variables on each other. The extent of dependence of one variable on another can be investigated by looking at the value of R between them. This R value can be positive or negative indicating positive and negative correlation between two variables respectively. Generally, R value greater than 0.8 between two variables signifies the presence of a good correlation between them87. Notice from the correlation matrix developed for the data used in current study given in (Fig. 6) that the correlation values between different variables is less than 0.8 for most of the cases. It is an indication that the risk of multi-collinearity will not arise during model development process.

Figure 6
figure 6

Correlation matrix of variables.

Full size image

Data distribution

Another important factor to consider while dealing with data-driven models is the distribution of the data on which the models will be based. The performance of a ML model depends on distribution of the data on which it has been trained88. Thus, the distribution of the data used in current study is shown by contour plots given in (Fig. 7). The frequency distribution density of variables is also shown by density plots shown above and on the right side of the contour plots. The thorough distribution of data is evident from the contour and distribution density plots. These plots provide useful information about the range of each variable involved in the ML model and this type of wide distribution is important for development of robust and accurate models89.

Figure 7
figure 7

Contour plots of input variables.

Full size image

Performance assessment

The performance of ML models should be checked to make sure that the developed models can accurately solve the problem90. Thus, several error metrices suggested by researchers were used for performance assessment of models developed in the current study. These metrices include MAE, RMSE and objective function etc. The metrices MAE and RMSE are the most widely used and are crucial for checking the performance of any ML model91. These two metrices should be kept as close to zero as possible because MAE gives the absolute average difference between experimental and ML predicted values while RMSE is used as an indicator of larger errors. This is because residuals are squared before taking average in RMSE thus giving more weight to larger errors. Also, coefficient of correlation (R) is a commonly used metric for evaluating general accuracy of models. However, it is suggested to never use R as a sole indicator of model’s effectiveness because it is insensitive towards the division or multiplication of output with a constant92. Generally, the correlation value greater than 0.8 is considered satisfactory for a model with good performance90. Similarly, performance index (PI) and objective function (OF) are commonly used metrices for evaluating model’s overall performance. Performance index makes use of relative root mean square error (RRMSE) and correlation coefficient while objective function integrates the relative number of data points in addition to RRMSE and R to predict model’s accuracy. The value of PI and OF being less than 0.2 indicates that the model has superior overall performance93. Moreover, a20-index is another recently developed metric which gives the proportion of predictions deviating more than ± 20% from the actual values94. The summary of the error evaluation metrices used in current study along with the suggested criteria is given in (Table 3).

Table 3 Summary of error evaluation metrics.
Full size table

Results and discussion

Model development

MEP model development

The MEP algorithm was employed with the help of a software developed specifically for this purpose known as MEPX 2021.05.18.0. Before starting the training of the algorithm, there are various parameters that need to be tuned. These parameters should be chosen carefully because they affect the convergence of the algorithm towards the result. These parameters were chosen using a trial-and-error approach and also with the help of recommendations from previous studies95,96,97. The important MEP fitting parameters include subpopulation size and number of subpopulations. The algorithm was started using 10 as subpopulation size and it was varied until the model with highest accuracy was reached at a value of 100. Similar was the case with number of subpopulations. Increase in these two parameters generally increases the accuracy of the model however it also makes the resulting equation complex and increases the computing power of the model. Also, an abnormally high value of these parameters can also lead to overfitting of the model98. Thus, these parameters should be carefully chosen. Code length and crossover probability are another two important parameters. Code length is directly related to the length and complexity of the resulting MEP equation while crossover probability indicates the probability of crossover of two parents to produce an offspring99. In the current study, crossover probability is chosen as 0.9 indicating that 90% of the parents will go under crossover to produce offspring. The combination of MEP parameters used in this study is given in (Table 4).

Table 4 Algorithm fitting parameters used in the study.
Full size table

GEP model development

Similar to the MEP algorithm, GEP was also employed using a special software called GeneXpro Tools100. This software allowed to vary different parameters and monitor the change in algorithm’s accuracy effectively. The GEP fitting parameters were also chosen using a trial-and-error approach. The parameters head size and number of chromosomes control the model’s accuracy and convergence towards the answer. These parameters were varied across a range of possible values until highest model accuracy was reached using number of chromosomes as 30 and number of genes as 10. The variation in these parameters was terminated when there was no considerable change in accuracy with varying these parameters. The combination of parameters that gave the most accurate GEP model presented in this study is given in (Table 4).

AdaBoost model development

The AdaBoost model was implemented with the help of python programming language in the Anaconda software. The optimal combination of AdaBoost hyperparameters used in current study is shown in (Table 4). These parameters were chosen using grid search approach. In this approach, a parameter is selected and varied across a range of possible values while keeping all other parameters constant. In this way, the optimal value of every parameter was found, and the set of values given in (Table 4) resulted in a model with the lowest RMSE and highest R value. The n-estimators and max. depth in AdaBoost algorithm signify with the number of trees constructed and depth of each tree respectively. Learning rate is a factor that is applied to each new prediction of the tree and its value ranges from 0.01 to 0.1101. A smaller learning rate ensures that corrections are made gradually, thus resulting in a larger number of trees. For this reason, the value of learning rate is set to 0.01.

Algorithm results

MEP result

The MEP algorithm provided its output in the form of a C +  + code which was decoded to get the equation to predict \({f}_{c}{\prime}\) given by Eq. (1). Several trials were performed using the MEP software to develop an equation which is simple and accurate. The resultant MEP equation relates \({f}_{c}{\prime}\) of bentonite plastic concrete with six most influential parameters using simple arithmetic functions. Only simple mathematical functions were chosen to be part of the equation in order to keep the resulting equation simple and not computationally challenging. The predictive capabilities of MEP equation are displayed in the form of a curve fitting plot in (Fig. 8). Notice that the MEP equation predicted strength with great accuracy for both training and testing sets except at a few points. Thus, it is evident from Fig. 8 that the developed MEP equation can be used to accurately forecast \({f}_{c}{\prime}\) of BPC.

$${\text{f}}_{{\text{c}}}{\prime} = \left( {{ }\frac{{\frac{{{\text{x}}_{5} }}{{\frac{{{\text{x}}_{3} }}{{{\text{x}}_{1} - {\text{x}}_{4} }}}} - \frac{{\left( {{\text{x}}_{4} } \right)^{2} }}{{\left( {{\text{x}}_{3} } \right)^{3} }}}}{{\frac{{\left( {{\text{x}}_{3} } \right)^{2} }}{{{\text{x}}_{1} }} - {\text{x}}_{2} }}/\frac{{{\text{x}}_{3} }}{{{\text{x}}_{1} - {\text{x}}_{4} }}} \right) + \frac{{{\text{x}}_{0} }}{{\sqrt {{\text{x}}_{3} } }} - \sqrt {\frac{{{\text{x}}_{0} }}{{\sqrt {{\text{x}}_{3} } }}} - \frac{{{\text{x}}_{3} }}{{{\text{x}}_{1} - {\text{x}}_{4} }}$$
(1)
Figure 8
figure 8

Curve fitting plot of MEP model.

Full size image

GEP result

The GEP model was constructed using addition as a linking function. Thus, the subexpression from every gene was added to get the final GEP equation given by Eq. (2). Notice that the GEP equation is also constructed using simple functions for simplification purposes. It is noteworthy that the GEP algorithm expressed the result in the form of four subexpression trees as shown in (Fig. 9). These trees were decoded, and the resulting expressions were added to get the final result. Also, the values of constants used in the expression trees are given in (Table 5).

$${\text{f}}_{{\text{c}}}{\prime} = \left[ {{\text{x}}_{4} - \left\{ {\frac{{{\text{x}}_{4} }}{{\frac{{{\text{x}}_{2} - \left( {{\text{x}}_{1} - {\text{x}}_{3} } \right)}}{{\sqrt {{\text{x}}_{3} } /1.512}}}}} \right\}{ }} \right] + \left[ {\left( {\frac{{\sqrt {2.581{\text{x}}_{1} } }}{{{\text{x}}_{3} }}} \right)\left( {\frac{{{\text{x}}_{5} + \left( {{\text{x}}_{1} /{\text{x}}_{4} } \right)}}{{{\text{x}}_{3} }}} \right)} \right] + \left[ {{\text{x}}_{0} \left\{ {\frac{{\left( { - 38.93{\text{x}}_{5} /{\text{x}}_{2} } \right)}}{{\frac{{{\text{x}}_{1} }}{4.44} - \sqrt {{\text{x}}_{3} } }}} \right\}} \right] + \left[ {\left\{ {\left( {\frac{{\sqrt {{\text{x}}_{5} + {\text{x}}_{0} } }}{{\left( {6.04/{\text{x}}_{0} } \right){\text{x}}_{3} }}} \right)\sqrt {{\text{x}}_{4} } } \right\} - {\text{x}}_{4} } \right]$$
(2)
Figure 9
figure 9

Expression tree representation of GEP equation. The variables \({\text{d}}_{0},{\text{d}}_{1},{\text{d}}_{2},\dots\) etc. in the expression trees correspond to \({\text{x}}_{0},{\text{x}}_{1},{\text{x}}_{2},\dots\) in the equation.

Full size image
Table 5 Values of constants used in GEP expression trees.
Full size table

Moreover, the prediction capacity of the GEP equation is visualized with the help of a curve fitting plot represented in (Fig. 10). It can be seen that GEP also predicted strength with great accuracy in both testing and training phases. There is some difference between actual and predicted values at some points but the overall performance of GEP looks satisfactory from the curve fitting plot.

Figure 10
figure 10

Curve fitting plot of GEP model.

Full size image

AdaBoost result

The results of AdaBoost algorithm to predict BPC strength are shown in (Fig. 11). It can be well understood from curve fitting plot in Fig. 11 that AdaBoost predicted strength values with superior accuracy. The curve of predicted values practically lies above the actual value curve at most of the points. The difference between actual and predicted values at other points is also not as large as in GEP and MEP models. Moreover, from the error evaluation summary given in (Table 5), it can be seen that AdaBoost has the highest correlation with actual values in both training and testing phases and subsequently the lowest values for errors like RMSE and average error. Moreover, the objective function and performance index values are lowest for the AdaBoost model. However, it must be noted that while AdaBoost is more accurate than other two techniques, it failed to express its output in the form of an empirical relation like MEP and GEP algorithms.

Figure 11
figure 11

Curve fitting plot of AdaBoost model.

Full size image

Error assessment of models

It is necessary to evaluate the performance of ML models with the help of error evaluation metrices to validate their performance. Thus, the developed models were tested for their accuracy using previously described error metrices in Sect.  2.3. The summary of this error evaluation is given in Table 6 for both training and testing phases of data-driven models. Notice that the correlation between experimental and predicted values by MEP, GEP, and AdaBoost in both stages is greater than the recommended value of 0.8 and even surpasses 0.9. It indicates the good predictive abilities of all models. Similarly, RMSE and mean absolute error of the models is also very close to zero. Moreover, the values of performance index and objective function are also less than the upper threshold of 0.2, which indicates that the models exhibit overall good performance.

Table 6 Error metrics of developed models.
Full size table

However, it is necessary to evaluate each model’s strengths and weaknesses. To start with, the MEP model exhibited largest absolute error of 1.56 in training phase between actual and predicted values compared to 1.51 for GEP and 0.70 for AdaBoost. Also, the root mean squared error values are highest for MEP training followed by GEP training and lastly AdaBoost. Similarly, the correlation between actual and predicted values is highest for AdaBoost model. Moreover, the value of objective function which indicates the overall performance of a model is lowest for AdaBoost model, then MEP and lastly GEP. Thus, it can be inferred that AdaBoost gave predictions closest to the real values, followed by GEP and MEP gave the least accurate predictions. The two evolutionary techniques expressed their output in the form of empirical equations given by Eqs. (1) and (2). Both of the equations are simple and easy to solve since they involve only basic arithmetic functions.

Although the error evaluation in Table give the values of individual error metrices and reveals that all models are good for prediction purposes according to the evaluation criteria suggested by the literature. However, it is beneficial to test a model by simultaneously considering all of the error metrics employed in the study. Thus, the ability of developed algorithms to predict \({f}_{c}{\prime}\) of BPC is tested using radar plots and given in (Fig. 12). The radar plot for training phase of algorithms is given in Fig. 12a while Fig. 12b represents radar plot of algorithms for testing dataset. Notice from Fig. 12a that AdaBoost exhibits the least values of almost all error metrics. The values of error metrics are same for GEP and MEP except for RMSE. GEP exhibits a lower RMSE in training phase than MEP. But the overall performance of both models is almost same in training phase. However, for the testing phase in (Fig. 12b), the MEP algorithm exhibits lower average error and RMSE than GEP while AdaBoost continues to have the least values of MAE and RMSE than both of the evolutionary techniques. It means that AdaBoost has the lowest values of error metrics in both phases. However, MEP and GEP exhibits same performance in training phase, but MEP performs better than GEP when tested on unseen data.

Figure 12
figure 12

Radar plot-based comparison of algorithms; (a) training phase; (b) testing phase.

Full size image

Comparison of models

The radar plots given in Fig. 12 indicate that AdaBoost algorithm has lesser error values than the other two models in both training and testing phase. However, an interesting way to compare the relative performance of models to predict the given output is by means of a Taylor diagram102. A taylor diagram is a useful technique to compare different ML models on the basis of standard deviation and coefficient of correlation (R). The accuracy of an algorithm can be check by checking its distance from the reference point. An accurate algorithm will lie close to the point of actual data and vice versa. A taylor plot to compare the algorithms deployed in current research is given in (Fig. 13) and it can be seen from (Fig. 13) that the AdaBoost point lies closest to reference point, indicating the superior accuracy of AdaBoost. The MEP and GEP points lie on the same level in regard to correlation with actual values, but since GEP point lies closer to the standard deviation line of actual data than MEP, it can be concluded that GEP values deviate lesser from actual values than MEP. It can also be verified from the a20-index values of algorithms in (Table 6). GEP has higher values of a20-index indicating lesser deviation from actual values than MEP. However, the a20-index values are highest for the AdaBoost model surpassing both its competitors. Thus, from the taylor plot, the overall order of accuracy is AdaBoost > GEP > MEP.

Figure 13
figure 13

Taylor plot-based comparison of developed models.

Full size image

Explanatory analysis

After the development of models and their successful validation using the error metrices, the next step is to carry explanatory analysis to get more information about the model prediction process and relative importance of different input variables. Carrying out this type of analysis on developed models is important for making sure that the model is generalized and can perform well on various data configurations89. Thus, shapley analysis is carried out on AdaBoost model since in Sect.  3.4, we established that it is more robust than other two models for prediction of \({f}_{c}{\prime}\) of bentonite plastic concrete. SHAP is a method that explains how predictions are made by a model and is increasingly catching attention of researchers to enhance the interpretability of soft computing models. It is a reliable method to provide simple and interpretable explanation of ML models to people who are not experts in the field and to different stakeholders. The explanation provided by SHAP analysis can then be used to make informed decisions and further improve the ML models by varying the set of input variables etc. It divides a prediction into sum of contributions offered by each of the input variables. The SHAP analysis results in a dataset having same dimensions as the original training data and it represents each prediction made by the ML model as a sum of these SHAP values and a base value103. With the recent advancements in the field of machine learning to predict various material properties, the need for reliable methods for enhancing interpretability of ML models has also been increased and SHAP successfully caters this need of researchers by providing a reliable method for both overall interpretation of the data-driven model and also the individual explanations for each prediction made by the model104.

SHAP global interpretation

The results of shapley analysis of AdaBoost model to predict BPC strength are given in (Fig. 14). The variables are ranked according to their mean absolute SHAP values for the entire dataset in the bar plot given in (Fig. 14a). Notice from (Fig. 14a) that cement is the most contributing factor to predict strength having absolute shap value of 12.82 followed by coarse aggregate (6.05), fine aggregate (0.43) and the least contributing factor is bentonite (0.12). Although Fig. 14a describes the mean absolute shap values of variables, it does not give an idea about which variables are positively or negatively correlated with the output. To overcome this limitation, the SHAP summary plot is given in (Fig. 14b) in which the SHAP values for input variables considered to develop AdaBoost model for predicting \({f}_{c}{\prime}\) of BPC are given. The values given in SHAP summary plot signify the contribution of each variable in strength prediction and are arranged in the order of decreasing importance from top to bottom. In shapley summary plot, the features having the broadest range of SHAP values are the important ones and vice versa. Each dot on the plot shows contribution of a particular feature with blue showing lower values and red representing higher values105. It can be well visualized from Fig. 14b that cement has the broadest range of red dots, thus it is the most important feature to predict strength followed by coarse aggregate, clay, and fine aggregate while bentonite has the least red dots over a wide range which means it is the least contributing factor. It is depicted by the summary plot that cement, coarse aggregate, and fine aggregate contribute towards an increase in the strength values while clay, water, and bentonite cause a decrease in output values.

Figure 14
figure 14

Shapley analysis of AdaBoost algorithm; (a) mean absolute SHAP values; (b) SHAP summary plot.

Full size image

SHAP local interpretation

After the identifying most important features to predict \({f}_{c}{\prime}\) of BPC by means of global interpretability plots, the next step is to check the combined effect of input variables through partial dependence plots as shown in (Fig. 15). Notice that as coarse aggregate content increases, the cement content also increases along with the increase in corresponding SHAP values of cement. It is because the incorporation of greater quantities of coarse aggregate call for higher cement content so that the cement paste can cover all the aggregate particles and result in a homogeneous concrete matrix. Similarly, the increase in cement content from 80 to 240 kg increases SHAP values of coarse aggregate from -6 to 8. However, the change in SHAP values of fine aggregate with cement content is much more scattered. Same trend is exhibited by water and coarse aggregate. Moreover, the SHAP values of bentonite shows an initial increase with increase in cement content but becomes almost constant when cement content reaches 120 kg. Furthermore, the relation between fine aggregate and SHAP values of clay is much more randomized and does not exhibit a specific trend.

Figure 15
figure 15

SHAP local interpretability; partial dependence plots of variables.

Full size image

Figure 16 depicts three SHAP force plots to show how model generates individual predictions. The force plot tool of shapley additive explanatory analysis is widely used to explain the phenomenon of generating predictions by ML model. The importance of each variable in force plot is proportional to its size in the force plot and the intersection of blue and red arrows show the predicted value by the ML model. The centre point of the plot is base value, which is the average prediction made by the model and each arrow in the force plot represents an input variable which acts as predictor for final output. Each arrowhead represents the direction and magnitude of the effect of a particular input variable on the output. The force plots for predicted strength values of 3.86 and 8.22 MPa are show in (Fig. 16a,b) respectively. Notice from these figures that all variables offer some contribution in the prediction, however cement, coarse aggregate, and fine aggregate are the most contributing factors to BPC strength. The contribution of other variables is relatively small.

Figure 16
figure 16

SHAP force plots for different strength values.

Full size image

While the force plots given in Fig. 16 provide a condensed interpretation of individual predictions, a more detailed explanation can be offered by means of SHAP waterfall plots as shown in (Fig. 17) which depict how different features have significant effect on the AdaBoost predictions. These plots represent a simple yet useful way of explaining local interpretability of ML model plots by providing the contribution of each input variable in yielding output. The predicted values by the model i.e., f(x) are shown at the top of the plot and the base value, which is the average predicted value of the model and same for all predictions is shown at bottom of the plot. The parameters in waterfall plots are arranged according to their impact on the output from top to bottom. The numbers written in grey alongside the names of input variables denote the variable values for the particular instance under consideration. The direction of arrow indicates the direction in which each input affects the prediction. The arrows are colour coded in such a way that red colour corresponds to a push towards higher strength value while blue colour represents a push towards lower strength values. The final prediction of the model is a sum of base value and all shap values from input variables. The waterfall plots for predicted strength values of 8.315 and 12.19 MPa are shown in (Fig. 17a,b) respectively. Notice from Fig. 17a that only water affects strength negatively for this instance while all other inputs positively influence the output. However, the effect of cement, clay, and aggregates is more pronounced than other input variables. Similarly, in Fig. 17b only clay negatively affects the strength. In this way, shapley additive explanatory analysis can be used to check how the algorithm generated individual predictions for more transparency in the model building process.

Figure 17
figure 17

SHAP waterfall plots for different strength values.

Full size image

Notice from the global and local SHAP interpretability that cement, clay, and aggregate content are the most important variables for predicting BPC strength. These findings are also in line with the findings of previous studies. The importance of cement content in BPC has been investigated by Abbaslou et al.106 in which the authors identified that cement is one of the main factors in determining strength of BPC. Similarly, the importance of aggregate content in the BPC has been highlighted in various studies107,108,109. Moreover, the reduction in strength due to incorporation of bentonite and clay minerals in concrete was studied by Guan et al.110 in which the authors highlighted that addition of bentonite and clay minerals results in loss of compressive strength of concrete. This is because the bentonite and clay present in BPC absorbs water due to their excellent absorbative properties which results in less water being available for hydration of cement paste and loss in concrete strength. This is also validation by the results of SHAP analysis where clay and bentonite have the smallest contribution towards concrete strength. Thus, it can be concluded that the AdaBoost is the feasible model for predicting strength of BPC which is robust and accurate and the insights into the prediction process by virtue of shapley analysis reveals that it aligns perfectly with the findings of previous studies.

Graphical user interface (GUI)

As discussed earlier in introduction section, the accurate determination BPC strength is crucial for fostering its widespread adoption in the civil engineering industry. Thus, this study was done to develop predictive models for BPC strength using MEP, GEP, and AdaBoost algorithms. The AdaBoost algorithm predicted the desired outcome with the highest accuracy. However, being a black-box model, its widespread utilization for professionals in the industry is quite challenging. Similarly, the GEP and MEP algorithms yielded equations to predict BPC strength, but both of the equations are computationally challenging. Therefore, a GUI has been developed using python programming language to help compute the BPC strength automatically based on the set of input variables considered in this as shown in Fig. 18. The user can enter desired input values and upon pressing the predict button, result will be obtained instantly in the output box specified in the GUI. This GUI can serve as an invaluable tool for professionals in the civil engineering industry and different stakeholders to effectively predict the BPC strength by entering the mixture composition without requiring extensive technical expertise. Also, with the increasing shift of civil engineering industry towards informed decision making, this GUI is an important tool which reflects the practical application of ML utilization in civil engineering industry.

Figure 18
figure 18

Graphical user interface to predict BPC strength.

Full size image

Conclusions

This study outlines the successful application of ML techniques to foster the use of BPC in construction industry by providing empirical models to predict its 28-day compressive strength by using MEP, AdaBoost and GEP. The dataset of 246 points gathered from published literature was used for this purpose having six important input factors. The gathered dataset was divided into training and testing sets to be used for model training and testing respectively. The main conclusions of this study are:

  • The two evolutionary techniques employed in this study i.e., MEP and GEP offered the advantage of expressing their output in the form of an empirical equation that can be used to effectively calculate \({f}_{c}{\prime}\) of BPC while AdaBoost has no such advantage.

  • The error evaluation revealed that all algorithms satisfied the criteria suggested in literature for good models by exhibiting a correlation coefficient greater than 0.9 between real and predicted values for both training and testing phases.

  • The AdaBoost algorithm proved to be more accurate than GEP and MEP by demonstrating a higher correlation 0f. 0.962 compared to 0.936 of GEP and 0.926 of MEP. Similarly, the value of objective function was 0.10 for AdaBoost, 0.16 for MEP and 0.176 for GEP which indicated that AdaBoost is the most accurate algorithm. Moreover, the performance index values were also lesser for AdaBoost model. However, it doesn’t yield empirical equations like MEP and GEP.

  • Shapley additive explanatory analysis was carried out on AdaBoost model to gain insights into the prediction process and the results indicated that cement, coarse aggregate, and fine aggregate are the most important factors to predict BPC strength.

Recommendations

Although the empirical prediction models developed in current study showcased good performance and can be effectively used for predicting \({f}_{c}{\prime}\) of BPC, but it is important to highlight the limitations of current study and give suggestions for future research endeavours.

  • It should be noted that the models in current study were developed using a dataset of 246 variables as given in Table A. However, it is recommended to consider even larger datasets from variable sources for future studies to develop more generalized models.

  • The input and output variables used in current study had a limited range as given in (Table 1). It is advised to use input and output variables with much wider range in future studies for development of widely applicable and more robust models.

  • Different material properties like nominal diameter of aggregates, type of cement, different properties of bentonite and clay etc. can affect compressive strength of bentonite plastic concrete. This study doesn’t explicitly incorporate the effect of these variables but recommends considering them in future research.

  • Prediction models for other mechanical properties of bentonite plastic concrete like flexural strength, split tensile strength etc. should be developed to foster its widespread use.