Introduction

Graph theory has broad applications in many fields of study, including computer science, chemistry, and biology. It is vital to study the chemical characteristics built into certain molecular structures. In this context, the fundamental representation is a graph, which is defined as an ordered pair consisting of a vertex set and an edge set. The degree of a vertex \({\mathfrak {c}}\) in the chemical graph is denoted by \(\omega (c)\), which is the number of edges incident to that vertex. Let G be a graph consisting of a vertex set and an edge set. A graph invariant is a statistical value that can only be found by the graph itself in the context of chemical graphs, in which atoms and their bonds are represented by vertices and edges, respectively. This characteristic, which is different from a particular graph version, is discussed in the context of chemical graph theory1. Any graphical configuration can be analyzed thanks to graph invariants, which reflect fundamental graph structures. Understanding the network’s topology makes it easier to investigate various chemical properties inherent in the graph structure.

In this investigation, topological connectivity indices, which are graph invariants, are essential for deciphering the intricate details of molecular graphs. The methodology of the whole manuscript is shown in Fig. 1.

Figure 1
figure 1

Methodology

Full size image

A potential catalyst for the oxygen reduction reaction is fe phthalocyanine, or (FePc). The energy effectiveness of metal-air batteries and fuel cells is directly influenced by oxygen reduction. Phthalocyanine molecules with a (FePc) core. These compounds’ interactions with various substrates and their impact on magnetic characteristics have been researched2. The exchange-correlation function is highly dependent on the electronic structure and separation of the molecule from the substrate. Due to weak \(O_{2}\) adsorption and activation, FePc with a plane-symmetric \(F_{e}N_{4}\) site typically exhibits mediocre ORR activity. This hypothesis is realized by coordinating (FePc) with an oxidized carbon. Mössbauer spectra and synchrotron X-ray absorption confirm the Fe–O coordination between carbon and (FePc). Different phthalic acid derivatives, such as phthalonitrile, phthalic anhydride, and phthalimides, are cyclotetramerized to produce phthalocyanine. When FePc was first discovered, dyes and pigments were essentially its only known applications.

Estrada et al.3,4 established the atom bond connectivity index as follows:

$$\begin{aligned} ABC(G)=\sum _{\mathfrak {cd} \in {\mathfrak {E}}(G)}\sqrt{\frac{ \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})-2}{ \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})}} \end{aligned}$$
(1)

Vukic Evic et al.5 presented the geometric arithmetic index as follows:

$$\begin{aligned} GA(G)=\sum _{\mathfrak {cd} \in {\mathfrak {E}}(G)}\frac{2\sqrt{ \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})}}{ \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})} \end{aligned}$$
(2)

Gutman et al6 and Furtula et al.7 presented the forgotten connectivity index as follows:

$$\begin{aligned} F(G)= & {} {\sum _{\mathfrak {cd} \in {\mathfrak {E}}(G)}}{\big ( \omega ({\mathfrak {c}})^{2}+ \omega ({\mathfrak {c}})^{2}\big )} \end{aligned}$$
(3)

Furtula et al.,8,7,9 presented augmented zagreb is as follows:

$$\begin{aligned} AZI(G)= & {} \sum _{\mathfrak {cd} \in {\mathfrak {E}}(G)}\bigg (\frac{{ \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})}}{{ \omega ({\mathfrak {c}})+\omega ({\mathfrak {d}})}-2}\bigg )^{3} \end{aligned}$$
(4)

Gutman et al.10,11 presented Zagreb index as follows:

$$\begin{aligned} M_1(G)=\sum _{\mathfrak {cd} \in {\mathfrak {E}}(G)} ( \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})) \end{aligned}$$
(5)
$$\begin{aligned} M_2(G)=\sum _{\mathfrak {cd} \in {\mathfrak {E}}(G)} ( \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})) \end{aligned}$$
(6)

In 2013, Shirdel et al.9 introduced the Hyper-Zagreb index:

$$\begin{aligned} HM(G)=\sum _{\mathfrak {cd} \in {\mathfrak {E}}(G)}{\bigg ( \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})\bigg )^2} \end{aligned}$$
(7)

The Balaban index12,13 is presented as follows:

$$\begin{aligned} J(G)= & {} \frac{m^{'}}{m^{'}-n^{'}+2}{\sum _{\mathfrak {cd} \in {\mathfrak {E}}(G)}}{\frac{1}{ \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})}} \end{aligned}$$
(8)

Ranjini et al. in14 reformulated versions are as follows:

$$\begin{aligned} ReZG_{1}(G)= & {} \sum _{\mathfrak {cd} \in {\mathfrak {E}}(G)}\frac{ \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})}{ \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})} \end{aligned}$$
(9)
$$\begin{aligned} ReZG_{2}(G)= & {} \sum _{\mathfrak {cd} \in {\mathfrak {E}}(G)}\frac{ \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})}{ \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})} \end{aligned}$$
(10)
$$\begin{aligned} ReZG_{3}(G)= & {} \sum _{\mathfrak {cd} \in {\mathfrak {E}}(G)} ( \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}}))( \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})) \end{aligned}$$
(11)

Structure of phthalocyanine FePc

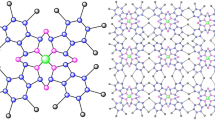
Fe phthalocyanine (FePc) has a typical two-dimensional, plane-symmetric structure that results in a symmetric electron distribution in the described \(F_{e}N_{4}\) compound. The molecule contains two types of nitrogen atoms denoted \(N_{1}\) and \(N_{2}\), whereby the latter one has no direct bond to the Fe center2.

The order and size of the structure of Fe phthalocyanine (FePc) are \(m'=55n+2\) and \(n'=68n\), respectively. It has four types of vertices, of degrees 1, 2, 3, 4 respectively. Table 1 shows the edge partition. The unit structure of FePc(n) is shown in Fig. 2. For more details about this structure of FePc(n) see Figs. 3, 4, and 5. The order and size of Phthalocyanine are \(55n+2\) and 68n, respectively.

Table 1 Edge partition of Fe phthalocyanine \(FePc[{\mathfrak {c}},{\mathfrak {d}}]\).
Full size table
Figure 2
figure 2

The structure of Phthalocyanine FePc(n) for \(n=1\).

Full size image
Figure 3
figure 3

The structure of Phthalocyanine FePc(n) for \(n=2\).

Full size image
Figure 4
figure 4

The structure of Phthalocyanine FePc(n) for \(n=3\).

Full size image
Figure 5
figure 5

The structure of Phthalocyanine FePc(n) for \(n=4\).

Full size image

Main results for Fe phthalocyanine

In this section, the degree-based topological indices have been computed. Using the above-defined formulas of the topological indices and Table 1, we compute the following indices:

  • Atom bond connectivity of FePc

$$\begin{aligned} ABC(FePc)= & {} \sum _{i=1}^{4}\sum _{\mathfrak {cd}\mathfrak {E_{i}}(FePc)}\sqrt{\frac{ \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})-2}{ \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})}}\\= & {} \left( \sqrt{\frac{2}{3}}\right) (12n+4)+\left( \sqrt{\frac{3}{6}}\right) (12n-4) +\left( \sqrt{\frac{4}{9}}\right) (40n)+\left( \sqrt{\frac{5}{12}}\right) (4n)\\= & {} 47.531896n+0.437559. \end{aligned}$$

  • Geometric arithmetic of FePc

$$\begin{aligned} GA(FePc)= & {} \sum _{i=1}^{4}\sum _{\mathfrak {cd}\mathfrak {E_{i}}(FePc)}\frac{2\sqrt{ \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})}}{ \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})}\\= & {} \left( \frac{2\sqrt{3}}{4}\right) (12n+4)+\left( \frac{2\sqrt{6}}{5}\right) (12n-4) +\left( \frac{2\sqrt{9}}{6}\right) (40n)+\left( \frac{2\sqrt{12}}{7}\right) (4n)\\= & {} 66.108829n-0.455082. \end{aligned}$$

  • Forgotten index of FePc

$$\begin{aligned} F(FePc)= & {} \sum _{i=1}^{4}\sum _{\mathfrak {cd}\mathfrak {E_{i}}(FePc)}( \omega ({\mathfrak {c}})^2+ \omega ({\mathfrak {d}})^2)\\= & {} (10)(12n+4)+(13)(12n-4)+(18)(40n)+(25)(4n)\\= & {} 1096n - 12. \end{aligned}$$

  • Augmented Zagreb Index of FePc

$$\begin{aligned} AZI(FePc)= & {} \sum _{i=1}^{4}\sum _{\mathfrak {cd}\mathfrak {E_{i}}(FePc)}\bigg (\frac{ \omega {({\mathfrak {c}})}\times \omega ({\mathfrak {d}})}{ \omega {({\mathfrak {c}})}+ \omega ({\mathfrak {d}})-2}\bigg )^3\\= & {} \left( \frac{4}{3}\right) ^3(12n+4)+\left( \frac{8}{4}\right) ^3(12n-4) +\left( \frac{16}{6}\right) ^3(40n)+\left( \frac{32}{10}\right) ^3(4n)\\= & {} 647.421n-18.5. \end{aligned}$$

  • First Zagreb Index of FePc

$$\begin{aligned} M_1(FePc)= & {} \sum _{i=1}^{4}\sum _{\mathfrak {cd}\mathfrak {E_{i}}(FePc)}{ \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})}\\= & {} (4)(12n+4)+(5)(12n-4) +(6)(40n)+(7)(4n)\\= & {} 496n-4. \end{aligned}$$

  • Second Zagreb Index of FePc

$$\begin{aligned} M_2(FePc)= & {} \sum _{i=1}^{4}\sum _{\mathfrak {cd}\mathfrak {E_{i}}(FePc)}{ \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})}\\= & {} (3)(12n+4)+(6)(12n-4) +(9)(40n)+(12)(4n)\\= & {} 516n-12. \end{aligned}$$

  • Hyper Zagreb Index of FePc

$$\begin{aligned} HM(FePc)= & {} \sum _{i=1}^{4}\sum _{\mathfrak {cd}\mathfrak {E_{i}}(FePc)}({ \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})})^{2}\\= & {} (16)(12n+4)+(25)(12n-4) +(36)(40n)+(49)(4n)\\= & {} 2128n-36. \end{aligned}$$

  • Balban Index of FePc

$$\begin{aligned} J(FePc)= & {} \frac{m^{'}}{m^{'}-n^{'}+2}\sum _{i=1}^{4}{\sum _{\mathfrak {cd}\mathfrak {E_{i}}(FePc)}}{\frac{1}{ \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})}}\\= & {} \left( \frac{68n}{13n-2}\right) \left( \frac{1}{3}(12n+4)+\frac{1}{6}(12n-4) +\left( \frac{1}{9}\right) (40n)+\left( \frac{1}{12}\right) (4n)\right) \\= & {} \left( \frac{68n}{13n-2}\right) (10.78n+0.67). \end{aligned}$$

  • First Redefined Zagreb Index

$$\begin{aligned} ReZG_1(FePc)= & {} \sum _{i=1}^{4}\sum _{\mathfrak {cd}\mathfrak {E_{i}}(FePc)}\frac{ \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})}{ \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})}\\= & {} \left( \frac{4}{3}\right) (12n+4)+\left( \frac{5}{6}\right) (12n-4) +\left( \frac{6}{9}\right) (40n)+\left( \frac{7}{12}\right) (4n)\\= & {} 55n+2. \end{aligned}$$

  • Second Redefined Zagreb Index

$$\begin{aligned} ReZG_2(FePc)= & {} \sum _{i=1}^{4}\sum _{\mathfrak {cd}\mathfrak {E_{i}}(FePc)}\frac{ \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}})}{ \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}})}\\= & {} \left( \frac{4}{5}\right) (12n+4)+\left( \frac{8}{6}\right) (12n-4) +\left( \frac{16}{8}\right) (40n)+\left( \frac{32}{12}\right) (4n)\\= & {} 90.26n-1.8. \end{aligned}$$

  • Third Redefined Zagreb Index

$$\begin{aligned} ReZG_3(FePc)= & {} \sum _{i=1}^{4}\sum _{\mathfrak {cd}\mathfrak {E_{i}}(FePc)}\bigg (( \omega ({\mathfrak {c}})\times \omega ({\mathfrak {d}}))\times ( \omega ({\mathfrak {c}})+ \omega ({\mathfrak {d}}))\bigg )\\= & {} (12)(12n+4)+(30)(12n-4) +(54)(40n)+(84)(4n)\\= & {} 83000n-72. \end{aligned}$$

The numerical comparison of ABC(FePc), GA(FePc), F(FePc), and AZI(FePc) is shown in Table 2, and the graphical representation for each of these indices is shown in Fig. 6. The table and figure that correspond to these indices provide a thorough examination of both the numerical and visual components.

Table 2 Numerical analysis of ABC(FePc), GA(FePc), F(FePc) and AZI(FePc).
Full size table
Figure 6
figure 6

Geometrical analysis of ABC(FePc), GA(FePc), F(FePc) and AZI(FePc).

Full size image

The numerical analysis for \(M_1(FePc)\), \(M_2(FePc)\), HM(FePc), and J(FePc) is shown in Table 3, and Fig. 7a shows a graphical depiction of their behaviours. The numerical and visual properties of these indices are thoroughly explored in both the table and the accompanying graphic.

Table 3 Numerical analysis of \(M_1(FePc)\), \(M_2(FePc)\), HM(FePc), J(FePc).
Full size table
Figure 7
figure 7

Graphical comparison between (a) \(M_1(FePc)\), \(M_2(FePc)\), HM(FePc) and J(FePc); (b) \(ReZG_1(FePc)\), \(ReZG_2(FePc)\), \(ReZG_3(FePc)\).

Full size image

The numerical analysis of each redefined Zagreb index is shown in Table 4, and Fig. 7b provides graphical depictions of these index behaviours. This analysis includes a detailed look at the redesigned Zagreb indices from a numerical and visual standpoint.

Table 4 Numerical analysis of \(ReZG_1(FePc)\), \(ReZG_2(FePc)\) and \(ReZG_3(FePc)\).
Full size table

HOF phthalocyanine

For Fe phthalocyanine, the degree-based topological indices were calculated for the following unit cell configurations: F(FePc), J(FePc), \(M_{1}(FePc)\), and ABC(FePc) etc. These indices show relationships with important Fe phthalocyanine thermodynamic parameters such as heat of formation (HOF). Fe phthalocyanine’s standard molar enthalpy is found to be \(-87.9{\text { kJmol}}^{-1}\). The enthalpy of the cell can be calculated by multiplying this value by the number of formula units in the cell. Notably, the HOF of Fe phthalocyanine inversely decreases with the number of crystal structures and the size of its crystals, as shown in Table 5.

Table 5 Values of HOF for FePc.
Full size table

Standard framework for HOF vs indices

In this section, we develop mathematical models to establish relationships between the Fe phthalocyanine Heat of Formation (HoF), as found in Sect. 2.2, and all the topological indices calculated in Part 2.1. Figures 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18 show graphical representations of the fitted curves for these connections. These curves mean and standard deviations, denoted by \(\Xi\) and \(\Psi\) correspondingly, provide information about the variability and general trends of the established relationships.

Generic framework between ABC(FePc) and HoF

The values of \(p_{i}\) and \(q_{i}\) for various values of i are displayed in Table 6. In the expansion of HoF(x), \(p_{i}\) is the coefficient of the i-th term, and qi is its mean. The confidence intervals (CIs) for \(p_{i}\) and \(q_{i}\) are also displayed in the table. The range of numbers that \(p_{i}\) is most likely to fall inside, given the evidence, is known as the confidence interval (CI). The range of numbers that \(q_{i}\) is most likely to fall inside, given the data, is its confidence interval (CI). Figure 8 plots HoF(x)vsABC(FePc). An additional variable under investigation is ABC(FePc). The plot indicates that HoF(x) and ABC(FePc) have a positive association. This implies that ABC(FePc) increases along with HoF(x).

$$\begin{aligned} HoF(x)=\frac{p_{1}x^3 + p_{2}x^2 + p_{3}x + p_{4}}{x + q1}, \end{aligned}$$

where \(x=ABC(G)\) is classified by \(\Xi =166.8\) and \(\psi =88.92.\)

Table 6 HoF vs ABC(FePc).
Full size table
Figure 8
figure 8

HoF vs ABC(FePc).

Full size image

Generic framework between GA(FePc) and HoF

The values of \(p_{i}\) and \(q_{i}\) for various values of i are displayed in Table 7. In the expansion of HoF(x), \(p_{i}\) is the coefficient of the i-th term and qi is its mean. The confidence intervals (CIs) for \(p_{i}\) and \(q_{i}\) are also displayed in the table. The range of numbers that \(p_{i}\) is most likely to fall inside, given the evidence, is known as the confidence interval (CI). The range of numbers that \(q_{i}\) is most likely to fall inside, given the data, is its confidence interval (CI). Figure 9 plots HoF(x)vsGA(FePc). An additional variable under investigation is GA(FePc). The plot indicates that HoF(x) and GA(FePc) have a positive association. This implies that GA(FePc) increases along with HoF(x).

$$\begin{aligned} HoF(x)=\frac{p_{1}x^3 + p_{2}x^2 + p_{3}x + p_{4}}{x + q1}, \end{aligned}$$

where \(x=GA(FePc)\) is classified by \(\Xi =230.9\) and \(\psi =123.7.\)

Table 7 HoF vs GA(FePc).
Full size table
Figure 9
figure 9

HoF vs GA(FePc).

Full size image

Generic framework between F(FePc) and HoF

The values of \(p_{i}\) and \(q_{i}\) for various values of i are displayed in Table 8. In the expansion of HoF(x), \(p_{i}\) is the coefficient of the i-th term, and qi is its mean. The confidence intervals (CIs) for \(p_{i}\) and \(q_{i}\) are also displayed in the table. The range of numbers that \(p_{i}\) is most likely to fall inside, given the evidence, is known as the confidence interval (CI). The range of numbers that \(q_{i}\) is most likely to fall inside, given the data, is its confidence interval (CI). Figure 10 plots HoF(x)vsF(FePc). An additional variable under investigation is F(FePc). The plot indicates that HoF(x) and F(FePc) have a positive association. This implies that F(FePc) increases along with HoF(x).

$$\begin{aligned} HoF(x)=\frac{(p_{1}x^3 + p_{2}x^2 + p_{3}x + p_{4})}{x + q1}, \end{aligned}$$

where \(x=F(FePc)\) is classified by \(\Xi = 3824\) and \(\psi =2050.\)

Table 8 HoF vs F(FePc).
Full size table
Figure 10
figure 10

HoF vs F(FePc).

Full size image

Generic framework between AZI(FePc) and HoF

The values of \(p_{i}\) and \(q_{i}\) for various values of i are displayed in Table 9. In the expansion of HoF(x), \(p_{i}\) is the coefficient of the i-th term and qi is its mean. The confidence intervals (CIs) for \(p_{i}\) and \(q_{i}\) are also displayed in the table. The range of numbers that \(p_{i}\) is most likely to fall inside, given the evidence, is known as the confidence interval (CI). The range of numbers that \(q_{i}\) is most likely to fall inside, given the data, is its confidence interval (CI). Figure 11 plots HoF(x)vsAZI(FePc) . An additional variable under investigation is AZI(FePc). The plot indicates that HoF(x) and AZI(FePc) have a positive association. This implies that AZI(FePc) increases along with HoF(x).

$$\begin{aligned} HoF(x)=\frac{p_{1}x^3 + p_{2}x^2 + p_{3}x + p_{4}}{x + q1}, \end{aligned}$$

where \(x=AZI(FePc)\) is classified by \(\Xi =2247\) and std \(\psi =1211\)

Table 9 HoF vs AZI(FePc).
Full size table
Figure 11
figure 11

HoF vs AZI(FePc).

Full size image

Generic framework between \(M_1(FePc)\) and HoF

The values of \(p_{i}\) and \(q_{i}\) for various values of i are displayed in Table 10. In the expansion of HoF(x), \(p_{i}\) is the coefficient of the i-th term and qi is its mean. The confidence intervals (CIs) for \(p_{i}\) and \(q_{i}\) are also displayed in the table. The range of numbers that \(p_{i}\) is most likely to fall inside, given the evidence, is known as the confidence interval (CI). The range of numbers that \(q_{i}\) is most likely to fall inside, given the data, is its confidence interval (CI). Figure 12 plots \(HoF(x) vs M_1(FePc)\). An additional variable under investigation is \(M_1(FePc)\). The plot indicates that HoF(x) and \(M_1(FePc)\) have a positive association. This implies that \(M_1(FePc)\) increases along with HoF(x).

$$\begin{aligned} HoF(x)=\frac{p_{1}x^3 + p_{2}x^2 + p_{3}x + p_{4}}{x + q1}, \end{aligned}$$

where \(x=M_{1}(FePc)\) is classified by \(\Xi =1732\) and std \(\psi =927.9.\)

Table 10 HoF vs \(M_1(FePc)\).
Full size table
Figure 12
figure 12

HoF vs \(M_1(FePc)\).

Full size image

Generic framework between \(M_2(FePc)\) and HoF

The values of \(p_{i}\) and \(q_{i}\) for various values of i are displayed in Table 11. In the expansion of HoF(x), \(p_{i}\) is the coefficient of the i-th term and qi is its mean. The confidence intervals (CIs) for \(p_{i}\) and \(q_{i}\) are also displayed in the table. The range of numbers that \(p_{i}\) is most likely to fall inside, given the evidence, is known as the confidence interval (CI). The range of numbers that \(q_{i}\) is most likely to fall inside, given the data, is its confidence interval (CI). Figure 13 plots \(HoF(x) vs M_2(FePc)\). An additional variable under investigation is \(M_2(FePc)\). The plot indicates that HoF(x) and \(M_2(FePc)\) have a positive association. This implies that \(M_2(FePc)\) increases along with HoF(x).

$$\begin{aligned} HoF(x)=\frac{p_{1}x^3 + p_{2}x^2 + p_{3}x + p_{4}}{x + q1}, \end{aligned}$$

where \(x=M_{2}(FePc)\) is classified by \(\Xi =1794\) and \(\psi =965.3.\)

Table 11 HoF vs \(M_2(FePc)\).
Full size table
Figure 13
figure 13

HoF vs \(M_2(FePc)\).

Full size image

Generic framework between HM(FePc) and HoF

The values of \(p_{i}\) and \(q_{i}\) for various values of i are displayed in Table 12. In the expansion of HoF(x), \(p_{i}\) is the coefficient of the i-th term and qi is its mean. The confidence intervals (CIs) for \(p_{i}\) and \(q_{i}\) are also displayed in the table. The range of numbers that \(p_{i}\) is most likely to fall inside, given the evidence, is known as the confidence interval (CI). The range of numbers that \(q_{i}\) is most likely to fall inside, given the data, is its confidence interval (CI). Figure 14 plots HoF(x)vsHM(FePc). An additional variable under investigation is HM(FePc). The plot indicates that HoF(x) and HM(FePc) have a positive association. This implies that HM(FePc) increases along with HoF(x).

$$\begin{aligned} HoF(x)=\frac{p_{1}x^3 + p_{2}x^2 + p_{3}x + p_{4}}{x + q1}, \end{aligned}$$

where \(x=HM(FePc)\) is classified by \(\Xi =7412\) and \(\psi =3981.\)

Table 12 HoF vs HM(FePc).
Full size table
Figure 14
figure 14

HoF vs HM(FePc).

Full size image

Generic framework between J(FePc) and HoF

The values of \(p_{i}\) and \(q_{i}\) for various values of i are displayed in Table 13. In the expansion of HoF(x), \(p_{i}\) is the coefficient of the i-th term and qi is its mean. The confidence intervals (CIs) for \(p_{i}\) and \(q_{i}\) are also displayed in the table. The range of numbers that \(p_{i}\) is most likely to fall inside, given the evidence, is known as the confidence interval (CI). The range of numbers that \(q_{i}\) is most likely to fall inside, given the data, is its confidence interval (CI). Figure 15 plots HoF(x)vsJ(FePc). An additional variable under investigation is J(FePc). The plot indicates that HoF(x) and J(FePc) have a positive association. This implies that J(FePc) increases along with HoF(x).

$$\begin{aligned} HoF(x)=\frac{p_{1}x^3 + p_{2}x^2 + p_{3}x + p_{4}}{x + q1}, \end{aligned}$$

where \(x=J(FePc)\) is classified by \(\Xi =210.4\) and std \(\psi =104.9.\)

Table 13 HoF vs J(FePc).
Full size table
Figure 15
figure 15

HoF vs J(FePc).

Full size image

Generic framework between \(ReZG_1(FePc)\) and HoF

The values of \(p_{i}\) and \(q_{i}\) for various values of i are displayed in Table 14. In the expansion of HoF(x), \(p_{i}\) is the coefficient of the i-th term and qi is its mean. The confidence intervals (CIs) for \(p_{i}\) and \(q_{i}\) are also displayed in the table. The range of numbers that \(p_{i}\) is most likely to fall inside, given the evidence, is known as the confidence interval (CI). The range of numbers that \(q_{i}\) is most likely to fall inside, given the data, is its confidence interval (CI). Figure 16 plots \(HoF(x) vs ReZG_1(FePc)\). An additional variable under investigation is \(ReZG_1(FePc)\). The plot indicates that HoF(x) and \(ReZG_1(FePc)\) have a positive association. This implies that \(ReZG_1(FePc)\) increases along with HoF(x).

$$\begin{aligned} HoF(x)=\frac{(p_{1}x^3 + p_{2}x^2 + p_{3}x + p_{4})}{x + q1}, \end{aligned}$$

where \(x=ReZG_1(FePc)\) is classified by \(\Xi =194.5\) and \(\psi =102.9.\)

Table 14 HoF vs \(ReZG_1(FePc)\).
Full size table
Figure 16
figure 16

HoF vs \(ReZG_1(FePc)\).

Full size image

Generic framework between \(ReZG_2(FePc)\) and HoF

The values of \(p_{i}\) and \(q_{i}\) for various values of i are displayed in Table 15. In the expansion of HoF(x), \(p_{i}\) is the coefficient of the i-th term and qi is its mean. The confidence intervals (CIs) for \(p_{i}\) and \(q_{i}\) are also displayed in the table. The range of numbers that \(p_{i}\) is most likely to fall inside, given the evidence, is known as the confidence interval (CI). The range of numbers that \(q_{i}\) is most likely to fall inside, given the data, is its confidence interval (CI). Figure 17 plots \(HoF(x) vs ReZG_2(FePc)\). An additional variable under investigation is \(ReZG_2(FePc)\). The plot indicates that HoF(x) and \(ReZG_2(FePc)\) have a positive association. This implies that \(ReZG_2(FePc)\) increases along with HoF(x).

$$\begin{aligned} HoF(x)=\frac{(p_{1}x^3 + p_{2}x^2 + p_{3}x + p_{4})}{x + q1}, \end{aligned}$$

where \(x=ReZG_2(FePc)\) is classified by \(\Xi =314.1\) and \(\psi =168.8\)

Table 15 HoF vs \(ReZG_2(FePc)\).
Full size table
Figure 17
figure 17

HoF vs \(ReZG_2(FePc)\).

Full size image

Generic framework between \(ReZG_3(FePc)\) and HoF

The values of \(p_{i}\) and \(q_{i}\) for various values of i are displayed in Table 16. In the expansion of HoF(x), \(p_{i}\) is the coefficient of the i-th term and qi is its mean. The confidence intervals (CIs) for \(p_{i}\) and \(q_{i}\) are also displayed in the table. The range of numbers that \(p_{i}\) is most likely to fall inside, given the evidence, is known as the confidence interval (CI). The range of numbers that \(q_{i}\) is most likely to fall inside, given the data, is its confidence interval (CI). Figure 18 plots \(HoF(x) vs ReZG_3(FePc)\). An additional variable under investigation is \(ReZG_3(FePc)\). The plot indicates that HoF(x) and \(ReZG_3(FePc)\) have a positive association. This implies that \(ReZG_3(FePc)\) increases along with HoF(x).

$$\begin{aligned} HoF(x)=\frac{(p_{1}x^3 + p_{2}x^2 + p_{3}x + p_{4})}{x + q1}, \end{aligned}$$

where \(x=ReZG_3(G)\) is classified by \(\Xi =1.043e+04\) and \(\psi =5612.\)

Table 16 HoF vs \(ReZG_3(FePc)\).
Full size table
Figure 18
figure 18

HoF vs \(ReZG_3(FePc)\).

Full size image

Table 17 provides a quality of fit for the framework fitted between HoF and each index computed in section 2.1. The selection of fits between\(R_{-\frac{1}{2}}(FePc)\), HM(FePc) and J(FePc) has been made considering \(R^2\) etc. and adjusted \(R^{2}\) as well.

Table 17 Quality of Fit for Indices for FePc vs HoF.
Full size table

Conclusion

This work began with a thorough examination of Fe phthalocyanine, first investigating indices based on topological degrees and then calculating thermodynamic characteristics. Strong mathematical models were produced by using fitting curves to find relationships between each topological index and thermodynamic attribute. This analysis covered an important category of thermochemical properties heat of formation (HOF). The application of a curve-fitting strategy carried out via MATLAB software enabled a sophisticated comprehension of the complex connection between the molecular topology and thermodynamic characteristics of Fe phthalocyanine. This coordinated strategy not only improves our understanding of chemical processes but also highlights the value of mathematical modeling in clarifying intricate relationships between molecules.