Introduction

Terahertz (THz) waves, which lie between infrared light and microwaves, are an important subset of electromagnetic (EM) waves with frequencies ranging from 0.1 to 10 THz. In recent years, due to the broad application prospects of THz science and technology in fields such as wireless communications, non-destructive testing, security inspections and optical communications1,2,3,4,5, it has become an important research topic for many scientists. These applications require not only efficient THz sources but high-performance THz devices. However, due to the lack of natural materials that can directly interact with THz waves, researchers have developed artificial materials known as metamaterials (MMs). MMs are made from metal or dielectric materials with dimensions significantly smaller than the operational wavelength, allowing for the modification of EM wave properties such as polarization, phase, amplitude, and frequency through sub-wavelength microstructures. Moreover, with the development of 5G and future 6G technologies, advanced materials that can switch between different states are needed to optimize signal transmission and reception. Therefore, optimizing the performance of switchable MMs plays a key role in improving the efficiency and flexibility of communication systems. To this end, designing optical devices based on switchable MMs to achieve perfect absorption, reflection, transmission, or polarization conversion of EM waves has become a hot topic in recent years6,7,8,9. Since the first metamaterial absorber (MAs) was proposed by Landy et al.10, they have played a significant role in optics and even the THz ___domain, similarly, Grady et al. first introduced a polarization converter based on metallic MMs in 201311. Subsequent reports have described various types of MAs or MMs polarization converters12,13,14,15,16. However, traditional MMs devices, whose performance depending on their intrinsic structural properties, suffer from large size, difficulty in integration, narrow bandwidth, low efficiency, and single functionality, and once designed, their performance cannot be easily altered after production, severely limiting their practical applications17. To address these issues, materials with tunable properties have been introduced into THz MMs devices, such as graphene18,19, vanadium dioxide (VO2)20, diodes21, black phosphorus22, photosensitive silicon23,24,25, liquid crystals26, and Dirac semimetals27.

Despite the capabilities of both graphene and VO2 to create tunable or switchable THz absorbers, they have been limited to single-function applications. Therefore, the development of a high-performance dual-function metamaterial absorber presents a significant challenge. As an excellent candidate for optoelectronic functions, VO2 has demonstrated modulation capacity triggered by electricity, heat, or light characterized by short response times and significant modulation depths28,29,30,31,32. Additionally, when the temperature rises to about 68 °C, it can transition from an insulating to a metallic state, causing its electrical conductivity to change by several orders of magnitude. Therefore, the combination of MMs and VO2 presents a promising approach for designing tunable THz devices. Over the past decade, many THz MMs devices based on VO2 have been reported. In 2021, Zhang et al. proposed a VO2-based tunable wideband THz MAs, with a bandwidth of 4.10 THz and dynamically adjustable peak absorption intensity from 3.6 to 100%33. In 2022, Wang et al. introduced a VO2-based multi-ring structure THz wideband tunable MAs, achieving over 90% absorption in the range of 3.01–7.27 THz34. In 2023, Chang et al. proposed a VO2-based THz switchable wideband linear to cross/circular (LTX/LTC) polarization converter, achieving four large relative bandwidth, high-performance THz polarization devices. Notably, when the device acted as an LTX, its polarization conversion ratio (PCR) was greater than 0.9, with an operational bandwidth of 2.14 THz and a relative bandwidth (RBW) of 99.5%35.

As the application scenarios become increasingly complex, it is evident that integrating multiple functions into a single device based on VO2 aligns with the trend for further development. In 2020, Song et al. designed a dual-functional switchable metasurface that serves as both a wideband absorber and polarization converter, utilizing the insulator-to-metal phase transition of VO2. Within the frequency range of 0.52–1.2 THz, the absorption rate exceeded 90%. Efficient conversion between two orthogonal linear polarizations could be achieved in the range of 0.42–1.04 THz36. In 2022, Li et al. designed a multifunctional MMs structure based on VO2 that could achieve wideband absorption, LTX, LTC polarization conversion and total reflection. The absorption rate exceeded 90% in the range of 2.17–4.94 THz. LTC and LTX polarization conversion was achieved in the range of 0.1–3.5 THz and 3.5–6 THz, respectively. For THz waves incident at a polarization angle of 0°, the metamaterial structure could act as a total reflector37. In 2023, Peng et al. introduced VO2 into metals to isolate the phase transition, obtaining a THz MMs device switchable between wideband absorption and polarization conversion. This device exhibited over 90% wideband absorption in the range of 1.03–2.62 THz, with dual conversion functionalities is LTX and LTC38. However, the design structures are complex, narrow in bandwidth and limited in performance, which significantly restricts their application scope and flexibility. Thus, designing a device with ultra-wideband (UWB) multifunctionality devices an urgent issue to be addressed.

In response to the aforementioned issues, a multifunctional switchable THz MMs device has been proposed. This device can not only achieve ideal UWB absorption in the THz band but perform LTX and LTC conversion functions in UWB. During the design process, with the support of Deep Neural Networks (DNN), the time required for extensive parameter optimization will be significantly reduced. Due to its excellent UWB absorption and polarization conversion performance, stable wide-angle incidence and wide-angle polarization characteristics, it has great application potential in short-range wireless THz communication, ultrafast optical switches, high-temperature resistant switches, transient spectroscopy, and optical polarization control devices.

Design and method

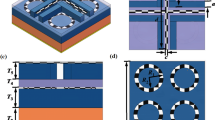
The 3D schematic diagram of the designed switchable THz metamaterial device and its top-down and side views of the x–y–z plane resonance layers are shown in Fig. 1. From top to bottom, the device consists of six layers: the top VO2 resonant layer, a polydimethylsiloxane (PDMS) layer, an Au resonant layer, a VO2 thin film, another PDMS layer, and a bottom Au film reflector layer, as shown in Fig. 1a,b. The VO2 resonant layer, comprising symmetric rings with cruciform openings, effectively responds to incident EM waves to achieve perfect absorption, as shown in Fig. 1c. PDMS serving as an intermediate dielectric layer, causes attenuation of the EM waves entering the material, with a dielectric constant of 2.35. The Au resonant layer consists of two symmetric T-shaped gold films at a 45° tilt, facilitating cross-polarization conversion, as shown in Fig. 1d. The bottom layer uses an Au substrate thicker than the skin depth to prevent EM wave propagation, with a conductivity of σAu = 4.57 × 107 S/m39. By analyzing the impact of geometric parameters on device performance, optimal geometric parameters have been determined, as shown in Table 1. Various methods can be used to optimize structural parameters in the design, such as traditional neural networks, deep learning models, and genetic algorithms. This paper specifically focuses on using DNNs to optimize structural parameters.

Figure 1
figure 1

The THz MMs device (a) 3D schematic. (b) Side views. (c) VO2 resonant layer. (d) Au resonant layer.

Full size image
Table 1 Parameters of the designed THz MMs device.
Full size table

This paper utilizes a software tool, CST Microwave, to numerically simulate the designed switchable THz MMs device. The initial boundary conditions include a magnetic field along the x-direction and an electric field along the y-direction, with the incident THz wave propagating in the opposite direction of the z-axis. The Drude model is employed to describe the relationship between the dielectric constant of VO2 and the angular frequency within the THz range, where the dielectric constant of VO2 can be expressed as40,41.

$$\varepsilon \left( \omega \right) = \varepsilon_{\infty } - \frac{{\omega_{p}^{2} \left( \sigma \right)}}{{\left( {\omega^{2} + i\gamma \omega } \right)}},$$
(1)

where ε∞ = 12 is the dielectric constant at high frequency, γ = 5.75 × 1013 rad/s is the collision frequency, and ωp(σ) is the plasmon frequency dependent on the conductivity (σ), which can be expressed as:

$$\omega_{p}^{2} \left( \sigma \right) = \frac{\sigma }{{\sigma_{0} }}\omega_{p}^{2} \left( {\sigma_{0} } \right),$$
(2)

With σ0 = 3 × 105 S/m, corresponding to ωp(σ0) = 1.4 × 1015 rad/s. When VO2 is in its metallic and insulating states, the σ is respectively 2 × 105 S/m and 10 S/m. The real part [Re(ε)] and imaginary part [Im(ε)] of the dielectric constant of VO2 under different σ are shown in Fig. 2a,b. The results indicate that the real and imaginary parts of the dielectric constant differ by 2–3 orders of magnitude, with the imaginary part significantly larger than the real part. Both the real and imaginary parts of the dielectric constant changes rapidly with the increase in σ, which suggests that VO2 can serve as a tunable material for MMs to design multifunctional switchable devices by controlling σ.

Figure 2
figure 2

(a) Real and (b) imaginary parts of the dielectric constant under varying σ of VO2.

Full size image

When the THz MMs device functions as a UWB absorber, the EM wave is incident on the surface of the structure, and the relationship between the incident electric field and the reflected electric field can be represented by the Jones matrix.

$$\left(\begin{array}{c}{R}_{x}\\ {R}_{y}\end{array}\right)=\left(\begin{array}{cc}{r}_{xx}& {r}_{xy}\\ {r}_{yx}& {r}_{yy}\end{array}\right)\left(\begin{array}{c}{I}_{x}\\ {I}_{x}\end{array}\right),$$
(3)

where Rx and Ry represent the reflected electric field components, Ix and Iy represent the incident electric field components, rxx and ryy are the co-polarized reflection coefficients for x-polarization and y-polarization, and rxy and ryx are the cross-polarized reflection coefficients for y-polarization and x-polarization, respectively. Since the thickness of the VO2 film is much greater than the skin depth typical for THz waves, the transmission rate T(ω) can be considered as 0. Therefore, the absorption rate A(ω) can be calculated as:

$$A\left( \omega \right) = 1 - R\left( \omega \right)$$
(4)

where R(ω) = ryy2. Simultaneously, the impedance matching theory, which determines the values of the reflection coefficients through impedance matching with free space, can be expressed by the following equation42

$$R(\omega ) = \left| {\frac{{Z_{1} - Z_{0} }}{{Z_{1} + Z_{0} }}} \right|^{2} = \left| {\frac{{Z_{r} - 1}}{{Z_{r} + 1}}} \right|^{2}$$
(5)

where Z1 and Z0 = 377 Ω represent the equivalent impedance of the device and the impedance of the free space, respectively, and Zr = Z/Z0 represents the relative impedance between the absorber and free space. This is primarily related to the values of the effective dielectric constant (εeff) and magnetic permeability (μeff), which can be expressed as follows43.

$$Z_{{\text{r}}} = \pm \sqrt {\frac{{\left( {1 + S_{11} } \right)^{2} - S_{21}^{2} }}{{\left( {1 - S_{11} } \right)^{2} - S_{21}^{2} }}} = \sqrt {\frac{{\mu_{{{\text{eff}}}} }}{{\varepsilon_{{{\text{eff}}}} }}}$$
(6)

where S11 and S21 represent the S-parameters of the device. By combining Eqs. (5) and (6), when εeff = μeff and Z1 = Z0, the equivalent impedance matches the impedance of free space.

When the THz MMs device functions as a polarization converter, to estimate the polarization conversion capability of the designed device, taking the incident y-polarized wave as an example, the polarization conversion ratio (PCR) for LTX and the ellipticity (PER) for LTC can be expressed as44

$${\text{PCR}} = \frac{{\left| {r_{xy} } \right|^{2} }}{{\left| {|r_{xy} |} \right|^{2} + \left| {r_{yy} } \right|^{2} }}$$
(7)
$${\text{PER}} = \frac{{2\left| {r_{xy} } \right|\left| {r_{yy} } \right|\sin (\Delta \varphi )}}{{\left| {r_{xy} } \right|^{2} + \left| {r_{yy} } \right|^{2} }}$$
(8)

To accurately describe the reflected electromagnetic waves, we introduce the ellipticity angle (PRA) and the polarization rotation angle (EA) to determine the polarization state. PRA and EA are defined as follows44

$${\text{PRA}} = \frac{1}{2}\tan^{ - 1} \left( {\frac{{2_{{r_{yy} r_{xy} \cos (\Delta \varphi )}} }}{{r_{yy}^{2} - r_{xy}^{2} }}} \right)$$
(9)
$${\text{EA}} = \frac{1}{2}\sin^{ - 1} \left( {\frac{{2r_{yy} r_{xy} \sin (\Delta \varphi )}}{{r_{yy}^{2} + r_{xy}^{2} }}} \right)$$
(10)

where Δφ = φxy − φyy represents the phase difference between rxy and ryy.

For a UWB polarization converter, RBW is commonly used to quantitatively describe its wideband performance. The definition of RBW is as follows.

$${\text{RBW}} = 2\left( {f_{H} - f_{L} } \right)/(f_{H} + f_{L} )$$
(11)

where fH and fL respectively represent the upper and lower limits of the bandwidth where the PCR is near 100%, and fH–fL is the Absolute Bandwidth (ABW).

Results and discussion

In previous work, the optimization of multiple structural parameters and target performances of THz MMs devices was carried out using optimization algorithms and commercial 3D full-wave simulation software, which consumed considerable time and computational resources. Therefore, inspired by traditional neural networks, deep learning models, and genetic algorithms45,46,47, this paper introduces a DNN to optimize the proposed MMs devices to achieve excellent absorption rates (Abr) and PCR under different operational states. The DNN model in this paper consists of three layers: Layers 1 to 3 have 64, 48, and 24 neurons, respectively, as shown in Fig. 3a. All of which are subject to L2 regularization. Since our goal is to achieve a good fit using the minimum amount of training data, we find L2 regularization is necessary to mitigate the network overfitting to the training set, which would be detrimental to the performance of the validation set. The fully connected layer stack handles a large portion of the upsampling task, overall converting the length 26 input vector to a length 170 output vector. These fully connected layers are followed by three transposed-convolution layers and finally a convolution layer smooths out the predicted spectrum48,49,50. These convolution and transposed convolution layers perform the rest of the upsampling task, and allow points of similar frequency to be closely related in a learnable manner via the associated filters. Lastly, in order to mitigate edge effects due to zero-filling in the convolutional operation, we drop 16 points from either end of the output data tensor, producing a spectrum of 320 points. This study obtained a total of 27,328 datasets from CST simulation results, which include combinations of structural parameters (SPs), Abr, and PCR. Of these, 19,130 are used for the training set, 5465 for the validation set, and 2733 for the test set. Python and the PyCharm framework were used to create the model, and the Adam optimizer was used for the optimization algorithm. The training process took a total of 987.53 s, with the Mean Absolute Error (MAE) and Root Mean Square Error (RMSE) being 0.004 and 0.005, respectively. The multifunctional MMs device SPs are described by the following items.

$$SPs = \left[ {\begin{array}{*{20}l} {P,} \hfill & {d_{1} ,} \hfill & {h_{2} ,} \hfill & {d_{2} ,} \hfill & {d_{3} ,} \hfill & {h_{1} ,} \hfill & {d_{4} ,} \hfill & {P_{1} ,} \hfill & {w_{3} ,} \hfill & {L_{1} ,} \hfill & {R,} \hfill & {w_{1} ,} \hfill & {w_{2} ;} \hfill \\ {P^{1} ,} \hfill & {d_{1}^{1} ,} \hfill & {h_{2}^{1} ,} \hfill & {d_{2}^{1} ,} \hfill & {d_{3}^{1} ,} \hfill & {h_{1}^{1} ,} \hfill & {d_{4}^{1} ,} \hfill & {P_{1}^{1} ,} \hfill & {w_{3}^{1} ,} \hfill & {L_{1}^{1} ,} \hfill & {R^{1} ,} \hfill & {w_{1}^{1} ,} \hfill & {w_{2}^{1} ;} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & \cdots \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {P^{n - 1} ,} \hfill & {d_{1}^{n - 1} ,} \hfill & {h_{2}^{n - 1} ,} \hfill & {d_{2}^{n - 1} ,} \hfill & {d_{3}^{n - 1} ,} \hfill & {h_{1}^{n - 1} ,} \hfill & {d_{4}^{n - 1} ,} \hfill & {P_{1}^{n - 1} ,} \hfill & {w_{3}^{n - 1} ,} \hfill & {L_{1}^{n - 1} ,} \hfill & {R^{n - 1} ,} \hfill & {w_{1}^{n - 1} ,} \hfill & {w_{2}^{n - 1} ;} \hfill \\ {P^{n} ,} \hfill & {d_{1}^{n} ,} \hfill & {h_{2}^{n} ,} \hfill & {d_{2}^{n} ,} \hfill & {d_{3}^{n} ,} \hfill & {h_{1}^{n} ,} \hfill & {d_{4}^{n} ,} \hfill & {P_{1}^{n} ,} \hfill & {w_{3}^{n} ,} \hfill & {L_{1}^{n} ,} \hfill & {R^{n} ,} \hfill & {w_{1}^{n} ,} \hfill & {w_{2}^{n} ;} \hfill \\ \end{array} } \right]$$
Figure 3
figure 3

(a) Schematic diagram of the DNN model. Comparison between the predicted curve and the target curve (b) absorption (c) PCR.

Full size image

Within the 1–10 THz range, the absorption rate (Abr) and PCR under different parameter combinations are described by the arrays Abr = [A1, A2, …, An-1, An] and PCR = [C1, C2, …, Cn-1, Cn]. The advantage of DNN is fully demonstrated here, in that after training the DNN with a dataset composed of numerous SPs, Abr, and PCR, when the target performances (Abr and PCR) are input into the DNN, the optimized SPs for MMs devices are effectively outputted for practical design use. Within the 1–10 THz frequency range, we divide the absorption and polarization conversion curves into 90 frequency points with a step of 0.1 THz. By comparing the amplitude of the target curves with the predicted curves at these 90 frequency points, the more alignment points there are, the closer the parameters are to their optimal values. For a clearer comparison, we manually selected three datasets from several predicted output datasets. The structural parameters corresponding to the predicted curves are shown in Table 2. For all three predicted cases, high absorption rates and PCR were achieved within the UWB range, validating the effectiveness of our proposed DNN. Among these, Predicted_2 and Predicted_3 had higher errors than Predicted_1 (Fig. 3b,c). Finally, considering bandwidth, intensity, and manufacturing factors, the Predicted_1 dataset was selected as the optimal structural parameters.

Table 2 Predicted structural parameters of the DNN.
Full size table

When the switchable device is an absorber

When VO2 is in its metallic state (σ = 2 × 105 S/m), the designed THz MMs device switches to a UWB absorber. It mainly consists of the top VO2 resonant layer, the middle PDMS layer, and the bottom VO2 film, while the other three layers can be ignored. Figure 4a shows the absorption and reflection spectra of the UWB absorber under different polarization modes (TE, TM) under normal incidence conditions. Simulation results indicate that when conductivity (σ) of VO2 = 2 × 105 S/m, the absorption rate can exceed 90% within the frequency range of 2.43–10 THz, with an ABW of 7.57 THz and an RBW of 73.8%. There are two ideal absorption peaks at 3 THz and 8.68 THz. Since the transmission energy is nearly 0, the reflection and absorption curves are complementary. It can also be observed that the absorption and reflection curves between TE and TM waves are nearly identical. To understand the reason for the identical curves between TE and TM waves, we extracted the dielectric constant (ε) and magnetic permeability (μ) of the structure through S-parameter inversion. From Fig. 4c, it can be observed that ε and μ are nearly identical for different polarization modes. Additionally, to validate the accuracy of the simulation data, Fig. 4d shows the real and imaginary parts of the relative impedance of TE and TM waves when VO2 is in the metallic state. In the UWB range, the real part approaches 1, and the imaginary part approaches 0. Notably, this frequency range precisely corresponds to the broadband absorption range. Therefore, when the structure operates within the frequency band of 2.43–10 THz, it exhibits good matching with free space. Furthermore, it indicates that impedance consistency is also the reason for the identical behavior between TE and TM waves.

Figure 4
figure 4

(a) Absorption and reflection spectra of the absorber under different polarization modes. (b) The relationship between the σ of VO2 and the ambient temperature. (c) The relationship between ε and μ of the absorber across different polarization modes. (d) The real and imaginary parts of the relative impedance of TE and TM waves when σVO2 = 2 × 105 S/m.

Full size image

Figure 4b illustrates the relationship between σ of VO2 and environmental temperature. At room temperature, VO2 exhibits an insulating state with σ = 10 S/m. As the temperature rises to around 68 °C, σ undergoes a sudden change and stabilizes at 85 °C. At this point, VO2 transitions to a metallic state with σ = 2 × 105 S/m. The entire phase transition process is reversible51. In practice, the following two methods can be used to make the VO2 phase transition 52. The first method is to heat the metal at the bottom of the absorber and convert the VO2 from an insulating to a metallic state by heat transfer, at which point the conductivity gradually increases. When the heating source is removed, the temperature gradually decreases, the conductivity of VO2 gradually decreases, and the metallic state transitions to an insulating state. The second method is to add a metallic patch to the VO2 layer and transfer heat to the VO2 by applying a voltage at the two ends of the metal, thus changing it from an insulating state to a metallic state. When the voltage at both ends is removed, the temperature gradually decreases and the VO2 transitions from a metallic to an insulating state. In addition, there are chemical mixing methods, etc., which can enable the phase transition of VO2 from the insulating to the metallic regime. With the above method, we can change the state of VO2 in practical application, so that the THz MMs device designed in this paper can realize ultra-wideband absorption, enabling multi-functional device applications.

Based on the transition properties of VO2 from an insulating state to a metallic state, the absorption can be dynamically adjusted by changing the σ of VO2. To clearly describe the switchable characteristics of the absorber, simulations demonstrate the change in σ from 10 to 2 × 105 S/m. Fig. 5 shows the 2D and 3D spectral graphs of the absorption curves at different σ values of VO2 under normal incidence. As shown in Fig. 5a, as the σ of VO2 increases, the absorption bandwidth gradually expands, and the absorption at the center frequency of the spectrum gradually decreases, primarily because the impedance matching causes free carriers to reflect the incident waves. When σVO2 = 2 × 105 S/m, the absorption rate at the peak frequency can reach 100%, and the bandwidth is maximized. The 3D absorption spectra shown in Fig. 5b are consistent with the changes in conductivity seen in Fig. 5a. Therefore, the σ of VO2 significantly impacts the absorption performance of the designed absorber, providing additional degrees of freedom for achieving a UWB absorber.

Figure 5
figure 5

2D and 3D spectral graphs of the absorption curves of VO2 at different σ.

Full size image

To further explore the physical mechanism of UWB absorption, Fig. 6 analyzes the electric field (EF) intensity and surface current (SC) distribution at the top and bottom VO2 layers of the UWB absorber at 3 THz and 8.68 THz. At 3 THz, the EF is primarily concentrated in the gaps along the x-axis of the VO2 ring, with almost no resonance occurring in the gaps along the y-axis, indicating that the gaps along the y-axis contribute relatively weakly to absorption. Thus, the absorption peak at this frequency is mainly caused by the electric dipole resonance excited in the gaps of the VO2 ring along the x-axis. At a frequency of 8.68 THz, the EF is mainly distributed in the gaps along the x-axis of the VO2 ring and on both sides of the inner ring, indicating that electrons on the VO2 surface along the x-axis undergo collective coupling oscillations and surface plasmon resonance (Fig. 6a,d)53. Further observation of the SC distribution shows that at 3 THz, an anti-parallel current forms a loop between the top and bottom layers of VO2, effectively transforming the VO2 film into a magnetic dipole and generating a strong magnetic resonance (Fig. 6b,c). At 8.68 THz, the direction of the SC between the top and bottom of VO2 is consistent, producing an electrical resonance (Fig. 6e,f). Therefore, the synergistic effects of magnetic and electric resonances lead to enhanced absorption of the incident EM waves within the resonant cavity, confirming the origin of the UWB absorber.

Figure 6
figure 6

Electric field distribution of the UWB absorber at (a) 3 THz and (b) 8.68 THz. Surface current distribution at the top of VO2 at (c) 3 THz and (d) 8.68 THz, and at the bottom of VO2 at (e) 3 THz and (f) 8.68 THz.

Full size image

Due to the symmetry of the structure, it is necessary to discuss the absorption performance of EM waves at different incident angles to facilitate the practical application of this device in engineering. Figure 7a,b show the absorption performance of TM and TE waves under different polarization angles. As the polarization angle increases from 0° to 90°, the absorption spectra of both TM and TE waves remain essentially unchanged, demonstrating the polarization-insensitive characteristics of the absorber. Furthermore, the effect of different incident angles on the absorption spectrum should also be considered. For TM waves, good UWB absorption performance can be maintained within a large incident angle range of up to 60°. However, the broadband absorption of TE waves can only be maintained at around 40° (Fig. 7c,d). The main reason for this is the inconsistency of the electric fields generated by the top pattern of the structure in the x-axis and y-axis directions, leading to inconsistent stability with respect to the incident angle.

Figure 7
figure 7

(a) Absorption spectra at different polarization angles for TM waves and (b) TE waves. (c) Absorption spectra at different incident angles for TM waves and (d) TE waves.

Full size image

Finally, the effects of structural variations on the absorption spectrum of the designed UWB absorber were studied. It can be seen that for the sandwich structure, the unpatterned VO2 layer contributes almost nothing to the absorption of the entire device, while the cross-shaped open ring achieves more than 90% absorption in the frequency range of 2.62–10 THz. This may be due to the presence of electric dipole resonance in the VO2 ring gap, where the surface electrons undergo collective coupled oscillation and surface plasmon resonance, resulting in broadband absorption within this frequency range, as shown in Fig. 8a,b. Further observations of the patterned three-layer structure and the proposed six-layer structure in the paper reveal that when VO2 is in the metallic state, although the absorption curves of both structures are similar, it is evident that the structure proposed in this paper achieves UWB absorption, as shown in Fig. 8c. This may be due to the electric and magnetic resonances generated between the top and bottom Au of the VO2, whose synergistic effects lead to enhanced absorption of incident EM waves within the resonant cavity. Therefore, the structure proposed in this paper was chosen as the optimized structure, providing the largest working bandwidth for THz MMs devices.

Figure 8
figure 8

The impact of structural variations on the absorption spectrum of the designed UWB absorber. (a) Unpatterned VO2 layer sandwich structure. (b) Cross-shaped open VO2 layer sandwich structure. (c) Cross-shaped open VO2 layer six-layer structure.

Full size image

When the switchable device is a polarization converter

When VO2 is in its insulating state (σ = 10 S/m), the designed THz MMs device switches to a reflective polarization converter, primarily consisting of an Au resonant layer, a bottom Au film, and the PDMS layer between them. To specifically analyze the polarization of the reflected wave, Fig. 9a,b show the cross-polarization reflection coefficients (rxy, ryx), co-polarization reflection coefficients (ryy, rxx), and PCR (PCRy, PCRx) for vertically incident y- and x-polarized waves. It can be seen that the reflection coefficients and PCR for these two polarizations are almost the same. Therefore, this paper focuses on discussing the polarization state of the reflected wave for y-polarized incident waves (Fig. 9a), the reflection coefficients rxy and ryy are similar within the ranges of 1–2.86 THz, 4.16–4.43 THz, and 4.58–10 THz, satisfying one of the conditions for LTC conversion. For the high-frequency band, rxy exceeds 0.9 between 4.58 and 10 THz, and ryy is near 0, meaning that the energy carried by the cross-polarized reflection accounts for over 90% of the incident power. For the low-frequency band, rxy is close to 0 between 1 and 2.86 THz, indicating that the conversion from y-polarized to pure x-polarized waves is well suppressed in this frequency range, ensuring the efficiency of co-polarized y-polarized waves in the low-frequency band. Also, within the high-frequency range, PCR can maintain near 100% with an RBW of 74.3% and an ABW of 5.42 THz, proving its capability to rotate the reflected polarization by 90° with high reflective purity over the UWB. To accurately describe the reflected EM waves, Fig. 9c,d show the PRA and EA of the incident EM waves after passing through the polarization converter in the y-polarization direction. It is observable that between 4.58 and 10 THz, the PRA is close to 90°, and the EA is less than 1°,The data above indicate that the polarization converter has the capability to reflect with high purity, rotating the input linear polarization by 90° within the UWB range. This means that the device can perfectly convert x-linear polarized incident waves into y-cross-polarized waves within the UWB frequency band in the high-frequency segment.

Figure 9
figure 9

Polarization converter showing (a) y-polarized reflection parameters, (b) x-polarized reflection parameters, (c) PRA, and (d) EA.

Full size image

Additionally, Fig. 10a,b show the phases of rxy and ryy (φxy, φyy), and the phase difference between them (Δφ1). From Fig. 10b, it can be observed that within the aforementioned three frequency ranges, Δφ1 is approximately − 90 Ω and 270 Ω, fulfilling another condition for LTC polarization conversion. Based on this, further analysis of the circular polarization conversion effect is shown in Fig. 10c. Within the range of 4.16–4.43 THz, the ellipticity is greater than 0.9 and close to 1, PRA and Δφ1 are close to 90°, and EA is close to 45°, as shown in Fig. 9c,d. This indicates that the reflected waves in this frequency range are circularly polarized, completing the LTC conversion.

Figure 10
figure 10

Polarization converter showing (a) φxy, φyy, (b) Δφ1, (c) PER.

Full size image

To understand the working principle of the reflective polarization converter, the incident y-polarized wave is orthogonally decomposed into two components along the u-axis and v-axis, as shown in Fig. 11a. The reflection coefficients of the reflected wave are shown in Fig. 11b. Here, ruu is the reflection coefficient from u to u, rvu is from u to v, rvv is from v to v, and ruv is from v to u. Due to the asymmetry of the resonant units along the x-axis and y-axis directions, the surface structure has different responses to electromagnetic waves along the u-axis and v-axis. It can be seen that both ruu and rvv are close to 1 and maintain good bandwidth, while rvu and ruv are close to 0. Therefore, we analyzed only the phases of ruu and rvv, and their phase difference Δφ2 = φuu − φvv. As shown in Fig. 12a,b, within the 4.58–10 THz range, there is a phase difference of ±180°, which means that the composite wave of ruu and rvv is deflected by 90° relative to the incident wave. In the 4.16–4.43 THz range, the phase difference is about 270°, indicating that the reflected wave within this band is circularly polarized.

Figure 11
figure 11

(a) Schematic of the polarization converter, (b) reflection coefficients of the reflected wave.

Full size image
Figure 12
figure 12

(a) φuu, φvv, (b) Δφ2.

Full size image

To further elucidate the physical mechanism of the reflection polarization converter, we observed the equivalent current distribution of the top and bottom gold at three resonance frequency points. At 4.58 THz, the equivalent current components of the top and bottom gold are the same, so they form electric dipoles and produce electromagnetic resonance (Fig. 13a,d). These electric dipoles generate electric dipole moments that regulate the phase and amplitude of the EM wave, achieving cross-polarization conversion. At 7.5 THz, the equivalent current components of the bottom and top gold are nearly perpendicular, causing the x-axis and y-axis components above to be vertical and parallel to the x-axis and y-axis components of the top equivalent current, respectively. This means that this frequency point can be considered as the superposition of electric and magnetic resonance (Fig. 13b,e). At 10 THz, the equivalent currents of the top and bottom gold are the same and opposite, forming magnetic dipoles and electric dipoles. The magnetic or electric dipole moments thus generated regulate the EM wave (Fig. 13c,f). Therefore, different types of resonance phenomena will occur at different frequency points when the incident wave passes through the polarization converter, and the magnetic or electric field formed regulates the EM wave, thereby achieving polarization conversion of the reflected EM wave in the UWB range 54.

Figure 13
figure 13

The surface current distribution on the top Au layer at the resonant frequency points: (a) 4.58 THz, (b) 7.5 THz, (c) 10 THz. The surface current distribution on the bottom Au layer at the resonant frequency points: (d) 4.58 THz, (e) 7.5 THz, (f) 10 THz.

Full size image

In addition, the effects of the angle of incidence and the polarization angle on PCR and PER were analyzed. Fig. 14a shows that the PCR is 0 when the polarization angle is 45°. As the polarization angle increases from 0° to 20° and from 70° to 90°, the overall LTX conversion effect is symmetrical, effectively converting y-polarization to x-polarization. Moreover, when the polarization angle is 0° and 90°, the PCR is the highest. In Fig. 14b, within a 15° angle of incidence, the PCR remains within a wideband, and a significant dip appears in the high frequency range as the angle of incidence increases. When the angle of incidence exceeds 45°, the bandwidth narrows sharply, forming a single peak narrowband absorption at 5.9 THz. This is because, when the structure is used as a polarization converter, only the T-shaped Au participates in the resonance, thus the electric field component decreases with increasing angle of incidence, leading to poor incidence angle sensitivity performance of the structure. Fig. 14c,d show the effects of the angle of incidence and polarization angle on PER. It can be seen that as the polarization angle increases at 0°–20° and 70°–90°, the overall LTC conversion effect is symmetrical, and the PER correspondingly decreases from 1 to 0 can effectively achieving LTC. Within a 45° angle of incidence, the wideband LTC conversion effect is maintained at low frequencies. As the angle of incidence further increases, the polarization conversion splits into two peaks. Overall, the structure has excellent polarization insensitivity and relatively weak incidence angle sensitivity for both PCR and PER.

Figure 14
figure 14

The effect of (a) angle of incidence and (b) polarization angle on PCR. The effect of (c) angle of incidence and (d) polarization angle on PER.

Full size image

Performance comparison

Finally, to demonstrate the advanced nature of our work, we compared the bandwidth and performance with recently published works as shown in Table 3. It is evident that the proposed structure not only functions as an absorber and polarization converter within the UWB range but also achieves dual-function conversion of LTX and LTC in UWB.

Table 3 Comparison between recently published THz MMs device and our work.
Full size table

Potential fabrication process of designed metamaterial

The designed switchable THz MMs devices can be manufactured using techniques such as DC magnetron sputtering (DC MS), plasma-enhanced chemical vapor deposition (PECVD), and photolithography (PLT)59. The specific manufacturing process is illustrated in Fig. 1556. (a) Prepare a clean silicon substrate with a thickness of 300 μm, which can provide good processing flexibility for THz devices while maintaining a certain mechanical strength. (b) Au is evaporated onto a clean silicon substrate using DC MS, forming a 0.2 μm thick Au film on the silicon substrate. (c) An 8 μm thick PDMS film is deposited on the Au film using PECVD. (d) A 0.1 μm thick VOx film is sputtered onto the PDMS film with vanadium (V) metal target using DC MS, followed by annealing in low-pressure O2 atmosphere to transform VOx into a 0.1 μm thick VO2 film. (e) A 0.4 μm thick Au film is further evaporated onto the VO2 film, and photoresist is spin-coated uniformly on the Au film. (f) PLT is employed to expose and develop the photoresist with a symmetrical T-shaped Au film mask, transferring the structural pattern onto the photoresist, which is then etched in etching solution, peeled, delaminated, and cleaned to obtain the patterned Au film structure. (g) Continue to use PECVD technology to deposit a PDMS film with a thickness of 12.8 μm on the two T-shaped Au films. (h) Another VO2 film is prepared on the PDMS film, and photoresist is uniformly coated on the 0.08 μm thick VO2 film. (i) Continue to use PLT technology to place a VO2 thin-film mask with a cross-shaped opening on the photoresist for exposure and development, transferring the structural pattern onto the photoresist. Immerse it in etching solution for etching, followed by stripping, removing the resist, and cleaning to obtain the patterned VO2 thin-film structure. Upon completing these steps, the fabrication of the designed THz MMs devices is achieved. It is worth noting that in the actual manufacturing process, due to current technological limitations, there are significant difficulties in the fabrication of terahertz metamaterial devices. However, the processing method we propose can provide new perspectives and valuable contributions to the related research field.

Figure 15
figure 15

The manufacturing process of the designed switchable THz MMs devices.

Full size image

Conclusion

In summary, a multifunctional switchable THz MMs device is designed and optimized using DNN. This device achieves ideal absorption and dual-function polarization conversion in the THz band within the UWB range. When VO2 is in its metallic state, the device as a UWB absorber with an absorption rate of over 90% within the 2.43–10 THz range, an RBW of 145.2%, and wideband absorption performance that is insensitive to polarization. When VO2 is in its insulating state, for THz waves with a polarization angle of 45°, the device switches to a reflective polarization converter, achieving LTX and LTC conversion functions within the 4.58–10 THz and 4.16–4.43 THz ranges. Specifically, within the 4.58–10 THz range, PCR approaches 100% with an RBW of 74.3%, PRA is near 90°, and EA is less than 1°. Within the 4.16–4.43 THz range, RBW is 6.29%, PER approaches 1, PRA and phase difference are close to 90°, and EA is near 45°. The proposed multifunctional switchable THz MMs device demonstrates excellent UWB absorption and polarization conversion performance within a stable wide-angle incidence and polarization range, offering broad application prospects in stealth technology, antenna engineering, ultrafast optical switches, high-temperature resistant switches, transient spectroscopy, and optical polarization control devices, THz communications, and other fields.