Abstract
In this study, we conduct a comprehensive physical analysis of topological indices for the Iron Disulfide (FeS\(_{2}\)) network using a curve-fitting model. Iron Disulfide is a cubic compound. In metamorphic rock, sedimentary rock, and quartz veins, it is typically found in combination with other sulfides or oxides. The numerical properties of molecular structures are referred to as topological indices. There are several different kinds of topological indices, including those that are based on distance, degree, or counting, among other factors. The real process of creating a topological index involves turning a chemical structure into a numerical value. In this paper, we calculate the iron disulfide network topological indices using the degrees of vertices in a chemical network of Iron Disulfide (FeS\(_{2}\)). Thereafter, we discovered the physical parameters of FeS\(_{2}\) production, such as heat of formation. We then fitted curves between the thermodynamic properties and several indices. Several techniques based on rationality, linearity, and nonlinearity were used to fit curves in MATLAB. These quantitative results imply that a variety of thermodynamic characteristics of semiconducting materials may be accurately predicted by topological indices. These findings have significant ramifications as they provide the groundwork for the application of topological indices in semiconducting network design and optimization, which might result in more effective and economical material creation.
Similar content being viewed by others
Introduction
Graph theory is a branch of the discrete mathematics. Graphs, a mathematical construction used to represent pairwise relationships between things, are the subject of the study of graph theory. A graph is made up of a collection of vertices V joined together with a set of edges E. It is commonly represented as \(G=(V, E)\). In a graph, the total number of vertices is often represented as n, whereas the number of edges is typically represented as m. The point where two edges of a polygon or two rays of an angle meet is called the vertex1. In a graph, an edge is the line connecting vertices \(E=(\varsigma ,\vartheta )\) represents an edge, which is a pair of two vertices. A graph G is said to as simple if it lacks loops and many edges, or parallel edges2,3. A vertex \(\varsigma \) degree is defined as the total number of edges that are incident to it and is denoted by \(\Upsilon (\varsigma )\).
A subfield of graph theory known as chemical graph theory is concerned with the concept of a chemical graph, also known as a molecular, structural, or constitutional graph. These terms all refer to graphs where vertices and edges stand in for atoms and bonds, respectively. In a chemical graph, a vertex’s degree is typically referred to as its valence4,5. Topological indices are numerical representations of a graph’s topology that are employed in the study of chemical substances and their characteristics6. They are a crucial area of study in graph theory and have applications in chemistry and mathematical chemistry, among other disciplines7. Graph theory provides chemists with important tools, one of which is topological indices8. Using the terminology of graph theory, vertices in a molecular graph indicate the atoms, while edges represent chemical bonds. Atom bond connectivity is one of the topological indices used to predict the bioactivity of chemical substances9. The Randic index, the Zagreb index, and the index are all quite helpful10. Xuemin et al.11 show the application of graph theory in security systems as a self-organizing key security management algorithm in socially aware networking.
Ghani et al.12 discuss the topological indices for niobium oxide and metal-organic frameworks. Mondal et al.13 talked about the topological indices of a few chemical structures used in COVID-19 patient treatment. QSPR analysis and degree-based topological indices of antituberculosis drugs were computed by Adnan et al.14. Comparative analysis of topological indices for capped and uncapped carbon nanotubes was computed by Nadeem et al.15. Zhang et al.16 used topological indices to do a physical investigation of heat for the production and entropy of cerium oxide. Degree-based topological features of two carbon nanotubes are studied by Zhang et al.17. Wang et al.18 discussed about the relationships between different degree-based indices and Sombor indices. Degree-based topological indices using a geometric approach are computed by Gutman et al.19. Regression models and degree-based topological indices were utilized by Zaman et al.20 to conduct a QSPR analysis of a few new medications utilized in the treatment of blood cancer. Chen et al.21 analyzed the shortest Path in LEO satellite constellation networks: An explicit analytic approach. Bokhary et al.22 provided QSPR analysis and topological indices of medications used in breast cancer treatment. Topological indices and QSPR/QSAR analyses of some antiviral medications under investigation for the treatment of COVID-19 patients are presented by Kirmani et al.23.
The generalized Randi\(\acute{c}\) index was defined as follows by Amic et al.24 and Bollob\(\acute{a}\)s et al.25 in 1998, working independently.
The aforementioned index provides information on the arrangement and numerical representation of atoms within the molecule26,27. Biological activity and physicochemical features are among the indexes that add value to the analysis28,29.
The atom bond connectivity index was created by Estrada et al.30,31 and is defined as follows:
The Geometric-Arithmetic (GA) index, introduced by Vukicevic et al.32, is another topological index that is used in the study of chemical graph theory that represents the properties and structure of molecular graphs. It is defined as follows:
Chemical graph theory has seen a significant amount of interest from Gutman33,34, who introduced the first and second Zagreb indices, which are defined as:
Shirdal et al.35 defined the Hyper-Zagreb index. It is an extension of the Zagreb indices that offers more details about the topology of the molecular graph which is defined as:
In 2012, Ghorbani and Azimi36 introduced the first and second Multiple Zegrab indices which are defined as:
The forgotten topological index was introduced by Furtula and Gutman37 and is defined as follows:
Rajini38 introduced the redefined Zagreb-type indices, which are defined as:
Balaban index is introduced by Balaban39 which is defined as:
Where \(\acute{r}\) represents the order of the graph and \(\acute{s}\) represents the size of the graph.
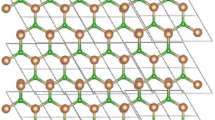
Structure of Iron Disulfide FeS\(_{2}\)
FeS\(_{2}\) is the formula for iron disulfide, a cubic chemical molecule40. Wang et al.41 discussed the Output synchronization of wide-area heterogeneous multi-agent systems over intermittent clustered networks. In quartz veins, sedimentary rock, and metamorphic rock, it is typically found in combination with other sulfides or oxides. It has a strong smell and a metallic sheen42. A dark grey powder known as iron disulfide (FeS\(_{2}\)) powder, chunk, and lumps has garnered a lot of attention as a potential material for lithium-ion battery cathodes and photovoltaics. FeS\(_{2}\) has a great ability to destroy both organic compounds and dyes, making it a viable semiconductor photocatalyst43. In this study, the hydrothermal method which is more efficient and less expensive was effectively used to synthesize FeS\(_{2}\). X-ray diffraction, transmission electron microscopy, and UV-visible spectrophotometry were used to confirm the various characteristics of the synthesized FeS\(_{2}\) material.
Iron disulfide FeS\(_{2}\) nanostructures with photocatalytic activity efficiently destroyed methyl orange dye and a textile dye, which are important organic pollutants44. Determining the surface structures and products of cadmium sorbed on amorphous FeS\(_{2}\) is the aim of this work. The disulfide surface was examined using electron microscopy, scanning tunneling microscopy, and Raman spectroscopy45. When cadmium sorption occurs, the FeS\(_{2}\) experiences surface reconstruction and disproportionation, resulting in distinct zones of elemental sulfur, cadmium sulfide, and iron hydroxide46. Iron Disulfide is an enzyme that catalyzes the conversion of ketones into esters and lactones by the Baeyer-Villiger oxidation process. It is a flavoprotein monooxygenase that, among other substrates, is important in the biotransformation of phenylacetone to benzyl acetate. It does this by using flavin adenine dinucleotide (FAD) as a cofactor47.
Comprehending the structure of FeS\(_{2}\) bears noteworthy consequences for its utilization in industrial operations. Researchers can improve an enzyme’s stability, substrate selectivity, or catalytic effectiveness for specific applications, like the production of fine chemicals, medicines, and biocatalytic processes, by designing particular amino acid residues. By using the unit structure and its copies as shown in Fig. 1 we obtained the formula for Iron Disulfide FeS\(_{2}\).
The order of FeS\(_{2}\) is \(12mn+2m+2n+1\) and the size of FeS\(_{2}\) is 24mn, respectively. The vertex and edge partition are shown in Tables 1 and 2 respectively.
Results for iron disulfide network FeS\(_{2}\)
Theorem 1
Prove that the General Randic indices for Iron Disulfide Network FeS\(_{2}\) are:
Proof
By utilising Table 2, the General Randic indices are calculated as follows:
Table 3 and Fig. 2 show a numerical and graphical comparison of the Randic indices respectively.
\(\square \)
We show the following thesis in light of Eqs. (2),(3),(4),(5), and Table 2.
Theorem 2
Show that the Iron Disulfide Network FeS\(_{2}\) has the following ABC, GA, \(M_{1}\), and \(M_{2}\) indices:
Proof
By utilizing Table 2, the atom bond connectivity index is derived and calculated as follows:
The GA index is computed as:
The first Zagreb index is computed as:
The second Zagreb index is computed as:
Table 4 and Fig. 3 show a numerical and graphical comparison of \(ABC({\text{FeS}}_{2})\), \(GA({\text{FeS}}_{2})\), \(M_1({\text{FeS}}_{2})\), and \(M_2({\text{FeS}}_{2})\) respectively.
\(\square \)
We show the following thesis in light of Table 2 and Eqs. (6), (7) ,(8), and (9).
Theorem 3
Prove that the HM index, \( PM_{1}\) index, \( PM_{2}\) and F index for Iron Disulfide Network FeS\(_{2}\) are:
Proof
The derivations of Hyper Zagreb index using Table 2 are computed as:
Derivation of first Multiple Zagreb index is computed as:
Derivation of the second Multiple Zagreb index is computed as:
The Forgotten index is derived is computed as:
Table 5 and Fig. 4 show a numerical and graphical comparison of \({HM}({\text{FeS}}_{2})\), \({PM_{1}}({\text{FeS}}_{2})\), \({PM_{2}}({\text{FeS}}_{2})\), and \(F({\text{FeS}}_{2})\) respectively.
\(\square \)
We show the following thesis in light of Table 2 and Eqs. (10), (11), (12), (13).
Theorem 4
Prove that the \(ReZG_{1}\) index, \( ReZG_{2}\) index, \( ReZG_{3}\) and J index for Iron Disulfide Network FeS\(_{2}\) are:
Proof
The 1st, 2nd, and 3rd Redefined Zagreb index is using Table 2 are computed as:
The calculation of the Balaban index is:
A numerical and graphical comparison of \(ReZG_{1}({\text{FeS}}_{2})\), \(ReZG_{2}({\text{FeS}}_{2})\), \(ReZG_{3}({\text{FeS}}_{2})\), and \(J({\text{FeS}}_{2})\) is presented in Table 6 and Fig. 5, respectively.
\(\square \)
Comparison of Results via Rational Curve Fitting
A statistical method called curve fitting is used to design a curve that most accurately depicts the relationship between a collection of data points. A method known as rational curve fitting can be used to mathematically estimate a set of data points using a curve that is represented by a rational function. In this paper, we represent the rational curve fitting by \(\textit{r}_{c}{f}\). The concept of the illumination of the heat (Enthalpy) HOF of iron disulfide FeS\(_{2}\) is presented in this section of the article. The enthalpy of formation, sometimes referred to as the heat of formation, is a thermodynamic quantity that indicates the change in enthalpy when one mole of a compound is produced from its constituent elements in their standard states under standard conditions typically 298.15 K and 1 atm pressure48. To calculate the formation of heat (HOF) multiply the molar standard Enthalpy of FeS\(_{2}\)’s, which is approximately 523 (kJ/mol) at temperature 298.15K, by the number of formula units in the cell and then divide the obtained values by the Avogadro’s number.
Where, \(Avogadro's \,\ Number = 6.02214076 \times 10^{23} mol^{-1}\). A mole of a substance such as an atom, molecule, or ion is equivalent to \(6.022 \times 10^{23}\) of that substance.
Finding the rational function that best fits the data points where the indices are the independent variable (x) and the heat of formation values are the dependent variable (y) is the first step in fitting a rational curve between indices and the heat of formation. Next, we collect the data into two lists, one for the indices and another for the heat of formation to fit a rational function. After that determine the polynomials P(x) and Q(x)’s degrees, m and n, respectively. Starting with low degrees (e.g., m=1, n=1) and increasing as needed is a popular option. Fit the rational function to the data using numerical techniques. Evaluate the fit quality by utilizing both visual examination and statistical measurements. The accuracy measures used are \(R^2\), the sum of squared errors (SSE), and the mean squared error (RMSE) which is shown in Tables 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 and graphical behavior presented in Figs. 6, 7, 8, 9, 10, 11, 12 and 13.
-
HOF using \(R_1({\text{FeS}}_{2})\)
where the mean \(1.904e+04\) and standard deviation \(1.75e+04\) normalise \(R_1\). These are the Coefficients:
\(p_1=5.747(3.222, 8.271)\), \(p_2=2.1 (1.392, 2.807)\), \(p_3=-3.354 (-5.219, -1.49)\), \(q_1=-1.529 (-2.107, -0.9511)\), \(q_2=-1.952 (-2.258, -1.645)\), \(q_3=-0.4058 (-0.7617, -0.04992)\), \(q_4=-0.4694 (-0.8079, -0.1309)\), \(q_5=0.4747 (0.2299, 0.7195)\).
The confidence bound in each curve fitting is \(95 \%\).
-
HOF using \(R_{-1}({\text{FeS}}_{2})\)
This normalizes \(R_{-1}\) using the mean (102.7) and standard deviation (90.9. The following are the coefficients:
-
HOF using \({R_{\frac{1}{2}}({\text{FeS}}_{2})}\)
This normalizes \(R_\frac{1}{2}\) using the mean 4947 and standard deviation 4516. The following are the coefficients:
-
HOF using \(R_{\frac{-1}{2}}({\text{FeS}}_{2})\)
This normalizes \(R_\frac{-1}{2}\) using mean 362.6 and standard deviation 324.9. The following are the coefficients:
-
HOF using \(ABC ({\text{FeS}}_{2})\)
In which ABC is normalized by mean 845.8 and std 764.1. The Coefficients:
-
HOF using\(GA({\text{FeS}}_{2})\)
In which GA is normalized by mean 1273 and std 1151. The Coefficients are:
-
HOF using \(M_{1}({\text{FeS}}_{2})\)
where mean \(1.031e+04 \) and standard \(1.031e+04 \) are used to normalise \(M_1\). The following are the coefficients:
-
HOF using \(M_{2}({\text{FeS}}_{2})\)
where mean \(1.904e+04\) and standard \(1.75e+04\) are used to normalise \(M_2\). The following are the coefficients:
-
HOF using \(HM({\text{FeS}}_{2})\)
In which HM is normalized by mean \(8.331e+04 \) and std \(7.671e+04\). The Coefficients are:
-
HOF using \(PM_{{1}}({\text{FeS}}_{2})\)
which uses the mean \(1.031e+04\) and standard deviation 9418 to normalise \(PM_1\). The following are the coefficients:
-
HOF using \(PM_{2}({\text{FeS}}_{2})\)
where mean \(1.661e+11\) and standard deviation \(2.243e+11\) are used to normalise \(PM_2\). The following are the coefficients:
-
HOF using \(F({\text{FeS}}_{2})\)
where mean \(4.527e+04\) and standard deviation \(4.174e+04\) are used to normalise F. The following are the coefficients:
-
HOF using \(J({\text{FeS}}_{2})\)
This normalizes J using the mean 362.6 and standard deviation 324.9. The following are the coefficients:
-
HOF using \(ReZG_{1}({\text{FeS}}_{2})\)
where the mean 749 and standard deviation 671.7 are used to normalise \(ReZG_1\).These are the coefficients:
-
HOF using \(ReZG_2({\text{FeS}}_{2})\)
In which \(ReZG_2\) is normalized by mean 2376 and standard deviation 2167. The coefficients are:
-
HOF using \(ReZG_3({\text{FeS}}_{2})\)
In which \(ReZG_3\) is normalized by mean \(1.573e+05 \) and standard deviation \(1.455e+05\). The coefficients are:
Conclusion
This paper provides a thorough examination of the relationship, via a curve-fitting model, between topological indices and the heat of production for the Iron Disulfide (\(FeS_2\)) network. We first compute the topological indices for (\(FeS_2\)) using a degree-based edge partitioning approach. After that, we compute the heat of formation (HOF) for iron disulfide. We used MATLAB to do the numerical calculations using these computed indices, and Excel was used to build the graph. After that, we fit a plausible model to our data using MATLAB and investigate the relationship between the heat of formation and topological indices for (\(FeS_2\)) networks. Since the rational models fit better than the simple linear or polynomial models, we employ them. These developed correlations were shown graphically together with the values of the indices at which the (HOF) measures changed. A substantial correlation was found between the heat of formation in the (\(FeS_2\)) network and certain topological metrics. The accuracy with which thermodynamic parameters in enzyme networks may be precisely predicted according to topological indices is demonstrated by this finding.
Data availibility
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
References
Bonchev D., Rouvray D.H., Chemical Graph Theory: Introduction and Fundamentals. ISBN 0-85626-454-7 (1991).
Gao, W., Wang, W. & Farahani, M. R. Topological indices study of molecular structure in anticancer drugs. J. Chem. 2016(1), 1–12 (2016).
Wang, Z., Chen, M., Xi, X., Tian, H. & Yang, R. Multi-chimera states in a higher order network of FitzHugh–Nagumo oscillators. Eur. Phys. J. Spec. Top. 233(4), 779–786 (2024).
Zhang, X., Rauf, Abdul, Ishtiaq, Muhammad, Siddiqui, Muhammad Kamran & Muhammad, Mehwish Hussain. On degree based topological properties of two carbon nanotubes. Polycycl. Aromat. Compd. 10(4), 22–35 (2020).
Wu, Z. et al. Real-time stereo matching with high accuracy via spatial attention-guided upsampling. Appl. Intell. 53(20), 24253–24274 (2023).
Lal, S., Staples, R. J. & Jean’ne, M. S. FOX-7 based nitrogen rich green energetic salts: Synthesis, characterization, propulsive and detonation performance. Chem. Eng. J. 452(3), 139–155 (2023).
Sharma, S., Bhat, V. K. & Lal, S. Multiplicative topological indices of the crystal cubic carbon structure. Cryst. Res. Technol. 58(3), 22–32 (2023).
Ghani, M. U. et al. Characterizations of chemical networks entropies by K-Banhatii topological indices. Symmetry 15(1), 143–153 (2023).
Das, K. C. & Mondal, S. On neighborhood inverse sum indeg index of molecular graphs with chemical significance. Inf. Sci. 623(2), 112–131 (2023).
Naz, K., Ahmad, S., Siddiqui, M. K., Bilal, H. M. & Imran, M. On some bounds of multiplicative K Banhatti indices for polycyclic random chains. Polycycl. Aromat. Compd. 44(4), 2270–2291 (2024).
Xuemin, Z. et al. Self-organizing key security management algorithm in socially aware networking. J. Signal Process. Syst. 96(6), 369–383 (2024).
Ghani, M. U. et al. A paradigmatic approach to find the valency-based K-Banhatti and redefined Zagreb entropy for niobium oxide and a metal-organic framework. Molecules 27(20), 6975–6975 (2022).
Mondal, S., De, N. & Pal, A. Topological indices of some chemical structures applied for the treatment of COVID-19 patients. Polycycl. Aromat. Compd. 42(4), 1220–1234 (2022).
Adnan, M., Bokhary, S. A. U. H., Abbas, G. & Iqbal, T. Degree-based topological indices and QSPR analysis of antituberculosis drugs. J. Chem. 2022(1), 5748626–5748642 (2022).
Nadeem, M. F., Azeem, M. & Farman, I. Comparative study of topological indices for capped and uncapped carbon nanotubes. Polycycl. Aromat. Compd. 42(7), 4666–4683 (2022).
Zhang, X. et al. Physical analysis of heat for formation and entropy of Ceria Oxide using topological indices. Comb. Chem. High Throughput Screen. 25(3), 441–450 (2022).
Zhang, X., Rauf, A., Ishtiaq, M., Siddiqui, M. K. & Muhammad, M. H. On degree based topological properties of two carbon nanotubes. Polycycl. Aromat. Compd. 42(3), 866–884 (2022).
Wang, Z., Mao, Y., Li, Y. & Furtula, B. On relations between Sombor and other degree based indices. J. Appl. Math. Comput. 51(4), 1–17 (2022).
Gutman, I. Geometric approach to degree-based topological indices: Sombor indices. MATCH Commun. Math. Comput. Chem. 86(1), 11–16 (2021).
Zaman, S., Yaqoob, H. S. A., Ullah, A. & Sheikh, M. QSPR analysis of some novel drugs used in blood cancer treatment via degree based topological indices and regression models. Polycycl. Aromat. Compd. 44(4), 2458–2474 (2024).
Chen, Q. et al. Shortest path in LEO satellite constellation networks: An explicit analytic approach. IEEE J. Sel. Areas Commun. 42(5), 1175–1187 (2024).
Bokhary, S. A. U. H., Adnan, Siddiqui, M. K. & Cancan, M. On topological indices and QSPR analysis of drugs used for the treatment of breast cancer. Polycycl. Aromat. Compd. 42(9), 6233–6253 (2022).
Kirmani, S. A. K., Ali, P. & Azam, F. Topological indices and QSPR/QSAR analysis of some antiviral drugs being investigated for the treatment of COVID-19 patients. Int. J. Quantum Chem. 121(9), 1–12 (2021).
Amic, D., Bešlo, D., Lucic, B., Nikolic, S. & Trinajstic, N. The vertex-connectivity index revisited. J. Chem. Inf. Comput. Sci. 36(5), 619–622 (1996).
Bollobas, B. & Erdos, P. Graphs of extremal weights. Ars Comb. 50(2), 225–233 (1996).
Al-Dayel, I., Nadeem, M. F. & Khan, M. A. Topological analysis of tetracyanobenzene metal-organic framework. Sci. Rep. 14(1), 1789–1799 (2024).
Zhang, X. et al. Physical analysis of heat for formation and entropy of Ceria Oiotade using topological indices. Comb. Chem. High Throughput Screen. 25(3), 441–450 (2022).
Lal, S., Bhat, V. K. & Sharma, S. Topological indices and graph entropies for carbon nanotube Y-junctions. J. Math. Chem. 62(1), 73–108 (2024).
Sharma, S., Bhat, V. K. & Lal, S. Multiplicative topological indices of the crystal cubic carbon structure. Cryst. Res. Technol. 58(3), 2200222–2200238 (2023).
Estrada, E., Torres, L., Rodriguez, L. & Gutman, I. An atom-bond connectivity index: Modelling the enthalpy of formation of alkanes. Indian J. Chem. 37A, 649–655 (1996).
Gao, W., Wang, W. F., Jamil, M. K., Farooq, R. & Farahani, M. R. Generalized atom-bond connectivity analysis of several chemical molecular graphs. Bul. Chem. Commun. 46(3), 543–549 (2016).
Vukicevic, D. & Furtula, B. Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges. J. Math. Chem. 46(4), 1369–1376 (2009).
Gutman, I. & Trinajstic, N. Graph theory and molecular orbitals. Total electron energy of alternant hydrocarbons. Chem. Phys. Lett. 17(4), 535–536 (1972).
Gutman, I. & Das, K. C. The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem. 50(1), 63–92 (2004).
Shirdel, G. H., Rezapour, H. & Sayadi, A. M. The hyper Zagreb index of graph operations. Iran. J. Math. Chem. 4(2), 213–220 (2013).
Ghorbani, M. & Azimi, N. Note on multiple Zagreb indices. Iran. J. Math. Chem. 3(2), 137–143 (2012).
Furtula, B. & Gutman, I. A forgotten topological index. J. Math. Chem. 53(4), 1184–1190 (2015).
Ranjini, P. S., Lokesha, V. & Usha, A. Relation between phenylene and hexagonal squeeze using harmonic index. Int. J. Graph Theory 1(4), 116–121 (2013).
Balaban, A. T. Highly discriminating distance-based topological index. Chem. Phys. Lett. 69(5), 399–404 (1962).
Kaur, G. et al. Iron disulfide (\({\text{FeS}}_{2}\)): a promising material for removal of industrial pollutants. ChemistrySelect 2(6), 2166–2173 (2017).
Wang, Q., Hu, J., Wu, Y. & Zhao, Y. Output synchronization of wide-area heterogeneous multi-agent systems over intermittent clustered networks. Inf. Sci. 619(4), 263–275 (2023).
Conway, B. E., Ku, J. C. H. & Ho, F. C. The electrochemical surface reactivity of iron sulfide, \({\text{FeS}}_{2}\). J. Colloid Interface Sci. 75(2), 357–372 (1980).
Bostick, B. C., Fendorf, S. & Fendorf, M. Disulfide disproportionation and CdS formation upon cadmium sorption on \({\text{FeS}}_{2}\). Geochim. Cosmochim. Acta 64(2), 247–255 (2000).
Tripathi, J., Chandrawat, G. S., Singh, J., Tripathi, S. & Sharma, Y. A. Correlation among local structure, magnetic, structural and electronic properties in polyol synthesized iron sulfide (\({\text{FeS}}_{2}\)) nanoparticles. J. Alloy. Compd. 861(2), 157–177 (2021).
Kaur, G. et al. Preferentially grown nanostructured iron disulfide (FeS\(_{2}\)) for removal of industrial pollutants. RSC Adv. 6(101), 99120–99128 (2016).
Ennaoui, A. et al. Iron disulfide for solar energy conversion. Sol. Energy Mater. Solar Cells 29(4), 289–370 (1993).
Torres Pazmiño, D. E., Baas, B. J., Janssen, D. B. & Fraaije, M. W. Kinetic mechanism of iron disulfide from Thermobifida fusca. Biochemistry 47(13), 4082–4093 (2008).
Green, D. W. (ed.) Perry’s Chemical Engineers’ Handbook 8th edn, 112–191 (Mcgraw-Hill, 2007).
Author information
Authors and Affiliations
Contributions
Rongbing Huang was employed to conduct investigations, analyse data, create tests, and develop them. Muhammad Farhan Hanif works with financing sources, computation, data analysis, and calculation verification. In addition to supervising the project, Muhammad Kamran Siddiqui organised the approach, organised it, located resources, and penned the paper’s introduction. Muhammad Faisal Hanif approved the paper’s final adumbrate in addition to participating in its computation and analysis. Saba Hanif made contributions to the elevation of the Matlab and Maple graphs. Brima Gegbe works on software development, validation, funding acquisition, and formal analysis of studies. Every author reviews and approves the final report of the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Huang, R., Hanif, M.F., Siddiqui, M.K. et al. On physical analysis of topological indices for iron disulfide network via curve fitting model. Sci Rep 14, 19177 (2024). https://doi.org/10.1038/s41598-024-70006-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-70006-4