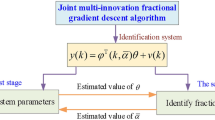
Abstract
This paper proposed the additional fractional gradient descent identification algorithm based on the multi-innovation principle for autoregressive exogenous models. This algorithm incorporates an additional fractional order gradient to the integer order gradient. The two gradients are synchronously used to identify model parameters, thereby accelerating the convergence of the algorithm. Furthermore, to address the limitation of conventional gradient descent algorithms, which only use the information of the current moment to estimate the parameters of the next moment, resulting in low information utilisation, the multi-innovation principle is applied. Specifically, the integer-order gradient and additional fractional-order gradient are expanded into multi-innovation forms, and the parameters of the next moment are simultaneously estimated using multi-innovation matrices, thereby further enhancing the parameter estimation speed and identification accuracy. The convergence of the algorithm is demonstrated, and its effectiveness is verified through simulations and experiments involving the identification of a 3-DOF gyroscope system.
Similar content being viewed by others
Introduction
Autoregressive exogenous (ARX) models are used to describe the dynamic relationship between inputs and outputs in discrete systems1,2,3. These models can effectively capture the characteristics of time-series data and predict future time-series. Consequently, ARX models are widely used in various fields, such as precision machining4, heat conduction5, composite materials6, artificial intelligence7, the petrochemical industry8, and weather prediction9.
Parameter identification is a crucial technique for estimating the unknown parameters of a model by observing output data and input data. Using identification technology to construct models results in high accuracy, and it has thus garnered widespread attention10,11. Various researchers have explored parameter identification methods for ARX models. For example, Dong et al.12 developed a weighted hierarchical stochastic gradient (SG) descent algorithm to improve the parameter convergence accuracy. Li et al.13 studied a decoupled identification scheme based on neural fuzzy network and ARX model. Tu et al.14 proposed a conjugate gradient descent method that resulted in accelerated convergence. Jing et al.15 established an ARX model using a variable step-size SG descent algorithm. A parameter learning scheme using multi-signals was proposed16, which improve the model identification accuracy. Liang et al.17 extended the Nesterov accelerated gradient descent algorithm into a multi-innovation form and used the multi-innovation matrix to accurately identify ARX model parameters. Li et al.18 derived a multi-innovation extended SG descent method to improve the parameter estimation accuracy. Ding et al.19 applied the multi-innovation stochastic gradient (MISG) descent algorithm to the nonlinear ARX systems identification. Chen et al.20 used Kalman filtering to estimate the ARX model output and combined the expectation maximisation algorithm to estimate parameters. Additionally, a Shannon principle-based forgetting factor gradient descent algorithm was proposed21, which improve the parameters convergence speed. Li et al.22 used correlation analysis method and adaptive Kalman filter to estimate the system parameters with measurement noises. Chen et al.23 developed an improved multi-step gradient iteration algorithm based on the Kalman filter to identify ARX models with missing output data, resulting in enhanced parameter identification accuracy. A separation identification algorithm was proposed24, and combined with filtering technology to identify the system parameters with colored noise. Li et al.25 combined with correlation analysis theory and the data filtering technology to estimate the multi-input multi-output system parameters. Stojanovic et al.26 estimated model parameters using the Masreliez–Martin filter. Other researchers27 decomposed the ARX model into two subsystems and establish a two-stage iteration algorithm. Wang et al.28 developed a three-stage subsystem generalised least squares identification algorithm. The SG algorithm was improved by incorporating a convergence index29, resulting in enhanced parameter estimation accuracy. Additionally, Chen et al.30 researched a particle filter based on SG identification algorithm. Li et al.31 developed a long short-term memory networks identification algorithm, and combined with the advantages of SG descent and root mean square propagation algorithms, an adaptive momentum estimation technique is created to optimize the networks parameters.
Notably, among the abovementioned methods for ARX model parameter identification, the gradient descent algorithm has been widely used owing to its broad applicability and ease of implementation in engineering scenarios. However, traditional integer-order SG descent algorithms rely on the convergence speed and direction of the gradient, resulting in low speed and accuracy of parameter identification. Compared with the integer-order gradient, the order selection of fractional-order gradient is arbitrary, which breaks the limitation of integer-order differential. Therefore, the fractional-order gradient has higher flexibility, which can improve the convergence speed and convergence accuracy of the algorithm32,33. In recent years, many scholars have focused on the fractional order gradient. For example, Chen et al.34 ensured that the fractional gradient could converge to the minimum point by changing the initial integration point. Wei et al.35 derived three forms of fractional-order gradients and proved their convergence. Other researchers36 established a fractional order stochastic gradient (FOSG) descent algorithm and an adaptive FOSG descent algorithm. Additionally, the hierarchical principle was used to design a fractional hierarchical gradient algorithm37.
The FOSG directly extends the integer-order gradient into a fractional order. However, because of the significant dependence of a single fractional order gradient on the choice of fractional order, improper order selection might reduce the identification accuracy and speed of the algorithm. Moreover, the fractional gradient typically uses only the current moment information for identifying model parameters of the next moment, resulting in underutilisation of identification information. To address this limitation, this paper proposed the multi-innovation additional fractional gradient descent identification algorithm. The main contributions of this study can be summarized as follows:
-
The proposed algorithm uses an additional fractional-order gradient and the integer-order gradient synchronously to identify model parameters, thereby accelerating the convergence speed of the algorithm.
-
The multi-innovation principle is introduced to expand the integer-order gradient and additional fractional-order gradient into multi-innovation matrices.
-
The proposed method is compared with SG, FOSG and MISG to verify its superiority in convergence speed and convergence accuracy.
-
The proposed algorithm can avoid the inaccurate parameters estimation result caused by improper fractional order selection.
The remainder of this paper is organised as follows: The mathematical model of an ARX system is presented in Section “Autoregressive exogenous models”. Section “Additional fractional gradient descent identification algorithm” outlines the additional fractional gradient descent identification algorithm. Section “Multi-innovation additional fractional gradient descent identification algorithm and convergence analysis” describes the multi-innovation additional fractional gradient identification algorithm and analysis of its convergence. Section “Simulation and experiment” presents details of the simulation and experiment for evaluating the algorithm performance. Section “Conclusion” presents the concluding remarks.
Autoregressive exogenous models
The ARX model is considered
where \(u\left( t \right)\) and \(y\left( t \right)\) are the system input and output, respectively. \(v\left( t \right)\) denotes white noise with finite variance \(\sigma_{v}^{2}\). The polynomials \(A(z^{ - 1} )\) and \(B(z^{ - 1} )\) can be expanded as
where n is a known parameter, and \(z^{ - n}\) denotes the difference operator.
The information vector \(\varphi (t)\) is defined using Eqs. (2) and (3). Combined with \(z^{ - n} y(t) = y(t - n)\) and \(z^{ - n} u(t) = u(t - n)\), \(\varphi (t)\) can be expressed as
Next, the parameter vector \(\theta\) is defined, and parameters \(a_{1} ,a_{2} , \cdots ,a_{n} ,b_{1} ,b_{2} , \cdots ,b_{n}\) in Eqs. (2) and (3) are presented in the vector form
Using Eqs. (2), (3), (4), (5), the Eq. (1) can be rewritten as
Additional fractional gradient descent identification algorithm
The additional fractional gradient descent identification algorithm adds an additional fractional gradient based on the integer gradient, and utilize the flexibility of fractional order to improve the convergence speed of the algorithm. The gradient descent algorithm is an iterative method. The unknown model parameters can be identified by minimising the criterion function through step-by-step iteration along the direction of gradient descent. The directions of the integer order and fractional order gradient correspond to the partial and fractional differentials of the function, respectively.
Fractional differential is an extension of integer differential. The differential order can be any real number or complex number. Compared with integer differential, fractional differential has three different definitions. In this study, the Caputo definition is used, expressed as38
where \(_{{t_{0} }}^{C} D_{{t_{f} }}^{\alpha }\) is the fractional calculus operator; \(\alpha\) is the order of the operator; \(m - 1 < \alpha < m,m \in {\mathbb{Z}}_{ + }\); \(t_{0}\) and \(t_{f}\) represent the low and high integral terminals, respectively; and \(\Gamma (\alpha )\) represents the gamma function.
The Taylor series expansion form of the Caputo differential is
where \(\left( \begin{gathered} p \hfill \\ q \hfill \\ \end{gathered} \right) = \frac{\Gamma (p + 1)}{{\Gamma (q + 1)\Gamma (p - q + 1)}},p \in {\mathbb{R}},q \in {\mathbb{N}}\).
The fractional-order gradient \(\nabla^{\alpha } f(x)\) can be expressed as
where \(0 < \alpha < 1\), and \(\mu\) is the step-size factor. To avoid complex numbers or a zero denominator, Eq. (9) can be rewritten as
where \(\varepsilon\) is a small non-negative number. Equation (10) can be extended to the case of \(1 < \alpha < 2\)39.
Then, the criterion function can be expressed as
The additional fractional gradient descent algorithm, which incorporates both the fractional order and integer order gradients to identify \(\theta\), can be expressed as
where \(\hat{\theta }\) is the estimate of parameter vector \(\theta\), and \(\gamma\) denotes the step-size factor of the integer-order gradient. Substituting Eq. (11) into Eq. (12) yields
where \(\mu \frac{{\varphi (t)[y(t) - \varphi^{{\text{T}}} (t)\hat{\theta }(t - 1)]\Xi (\hat{\theta },\alpha ,t)}}{\Gamma (2 - \alpha )}\) is the additional fractional gradient,\(\Xi (\hat{\theta },\alpha ,t) = {\text{diag}}\left\{ {\left[ {\left| {\hat{\theta }_{1} (t - 1) - \hat{\theta }_{1} (t - 2)} \right| + \varepsilon } \right]^{1 - \alpha } ,\left[ {\left| {\hat{\theta }_{2} (t - 1) - \hat{\theta }_{2} (t - 2)} \right| + \varepsilon } \right]^{1 - \alpha } , \cdots ,\left[ {\left| {\hat{\theta }_{l} (t - 1) - \hat{\theta }_{l} (t - 2)} \right| + \varepsilon } \right]^{1 - \alpha } } \right\}\), and l is the number of identification parameters.\(\gamma\) and \(\mu\) can be expanded into the following form
The output error is defined as in Eq. (13)
Combining Eqs. (13)-(16), we can obtain the iterative formula of the additional fractional gradient descent algorithm, as follows
Equation (17) shows that the two gradients jointly identify the model parameters, which can avoid the algorithm not converging due to improper order selection of a single fractional gradient. Compared with a single integer gradient, the additional fractional gradient can make the parameters converge to the true value faster, even if the fractional order is small.
Multi-innovation additional fractional gradient descent identification algorithm and convergence analysis
Multi-innovation additional fractional gradient descent identification algorithm
The additional fractional gradient descent identification algorithm leverages the flexibility of fractional calculus to simultaneously identify unknown parameters through integer and fractional gradients. By simultaneously treating these two gradients, the convergence accuracy and speed of the algorithm can be improved. However, both these gradients use only the data at the current moment, resulting in underutilisation of the available information, thereby limiting the ability to improve the accuracy of parameter identifies during each iteration. Therefore, to further enhance the speed and accuracy of parameter identification, the multi-innovation principle is introduced, and a multi-innovation additional fractional gradient descent algorithm is established.
The multi-innovation principle involves combining current and past data to form a multi-innovation matrix, which is then used to estimate the current parameters40,41. In this context,\(y(t),\varphi^{{\text{T}}} (t),e(t)\), and \(v(t)\) are termed single innovations, which are then extended to the multi-innovation matrices \(Y(p,t),\Phi (p,t),E(p,t)\), and \(V(p,t)\), respectively.
where p denotes the multi-innovation length. Combining Eqs. (16), (18), and (19), Eq. (21) can be rewritten as
The multi-innovation additional fractional gradient descent algorithm criterion function is defined as
Substituting the single innovations with the multi-innovation matrix from Eqs. (18), (19), and (21), respectively, the multi-innovation additional fractional gradient descent algorithm can be formulated as
Compared with Eq. (17), Eq. (24) uses more observation data in the parameter identification process and has a higher data utilization rate.
Convergence analysis
The analysis of convergence is crucial for the gradient descent algorithm, which determines the reliability and stability of the algorithm. It is a prerequisite for theoretical simulation and practical application. For clarity, the following lemmas are defined.
Lemma 1
Reference42 For the ARX model in Eq. (6) and multi-innovation additional fractional gradient descent algorithm presented in Eqs. (24), (25), (26), there exists a constant \(0 < \overline{\alpha } \le \beta < \infty\) and an integer \(N \ge n\) such that the following strong persistent excitation condition holds.
Then \(\overline{r}(t)\) in Eq. (25) satisfies the inequality
Lemma 2
Reference43 The following inequality holds
where a real numbers.
Lemma 3
Reference43 Suppose the non-negative sequences \(\left\{ {\kappa (t)} \right\},\left\{ {\psi_{t} } \right\}\) and \(\left\{ {\beta_{t} } \right\}\) satisfy \(\kappa (t + 1) \le (1 - \psi_{t} )\kappa (t) + \beta_{t}\),\(\psi_{t} \in [0,1),\sum\limits_{t = 1}^{\infty } {\psi_{t} } = \infty ,\kappa (0) < \infty\). Then
Proof
Let the parameter estimation error be defined as
According Eqs. (6) and (18), (19), (20), we obtain
Subtracting \(\theta\) from both sides of Eq. (24) and combining Eqs. (22) and (32), we can obtain the iterative equation for the \(\tilde{\theta }\).
By taking the norm on both sides of Eq. (33), the following expression is obtained.
According to the discussion in Ref.44 and the definition of \(\Xi (\hat{\theta },\alpha ,t)\) in Eq. (8), \(0 < \hat{\theta }_{i} (t - 1) - \hat{\theta }_{i} (t - 2) < 1,{\kern 1pt}\) \(i = 1,2, \cdots ,l\) holds. Then
Moreover, \(\Xi (\hat{\theta },\alpha ,t) = \max \left\{ {\varepsilon^{1 - \alpha } ,\left( {1 + \varepsilon } \right)^{1 - \alpha } } \right\}\) with \(0 < \alpha < 2\).According to Lemma 1
where \(\overline{\alpha } > 0\), N > 0, within the range of \(0 < \alpha < 2\),\(\Gamma (2 - \alpha ) > 0\). Given that \(r(t) = \overline{r}(t - 1) + \left\| {\Xi (\hat{\theta },\alpha ,t)\Phi (p,t)} \right\|^{2}\), it can be found that \(0 \le \overline{r}(m) - \overline{r}(0) \le r(m + 1)\) and \(0 \le \left\| {\Xi (\theta ,\alpha ,t)\Phi (p,t)} \right\|^{2} \le r(m + 1)\) for \(m = 1,2, \cdots ,t - 1\). Then,\(r(t) > 0\). Thus, Eq. (36) is greater than 0, and the following expression is obtained from Eq. (34).
According to Lemma 1, as p = N, we obtain
Combining Eqs. (36)–(38) and Lemma 1, we obtain the expectation of Eq. (34)
where
\(Q_{4} = 2{\text{E}}\left\{ {\frac{\Phi (p,t)V(p,t)}{{\overline{r}(t)}}\frac{{\Xi (\hat{\theta },\alpha ,t)\Phi (p,t)V(p,t)}}{r(t)\Gamma (2 - \alpha )}} \right\}\), \(Q_{5} = \frac{{E\left[ {\left\| {\Xi (\hat{\theta },\alpha ,t)\Phi (p,t)V(p,t)} \right\|^{2} } \right]}}{{(r(t)\Gamma (2 - \alpha ))^{2} }}\).
According to Lemma 1 and Eq. (35), the following inequality is obtained
Substituting Eqs. (39) and (28) into \(Q_{1}\) yields
We take the limit of \(Q_{1}\) according to Lemma 3
When \(t \to \infty\), \(Q_{1} \to 0\). Now, we use Lemma 2 and Eqs. (38) and (40) to prove the convergence of \(Q_{2}\).
Similarly, according to Lemma 3, Eq. (44) can be rewritten as
When \(t \to \infty\), \(Q_{2} \to 0\). Because \(r(t) = \overline{r}(t - 1) + \left\| {\Xi (\hat{\theta },\alpha ,t)\Phi (p,t)} \right\|^{2}\), it follows that \(r(t) > \overline{r}(t - 1)\). We integrate Lemma 2 and Eqs. (40), (41) to prove the convergence of \(Q_{{_{3} }}\).
According to Lemma 3, Eq. (46) can be rewritten as
When \(t \to \infty\), \(Q_{3} \to 0\). Similarly, we combine Lemmas 1 and 3 as well as Eqs. (40)-(41) to prove the convergence of Q4.
When \(t \to \infty\), \(Q_{4} \to 0\). Lastly, we integrate Lemmas 1 and 3 and Eq. (40) to prove the convergence of Q5.
Based on this analysis along with Eqs. (39), (43), (45), and (47), (48), (49), we conclude that the expectation of the parameter identification error \({\text{E}}\left[ {\left\| {\tilde{\theta }} \right\|^{2} } \right]\) converges to 0, thereby proving the algorithm convergence.
The multi-innovation additional fractional gradient descent identification algorithm steps are summarized below.
Algorithm | Multi-innovation additional fractional gradient descent identification algorithm |
|---|---|
Step 1 | Obtain model input data u(t) and output data y(t). Determine the ARX model unknown parameters \(\theta\) |
Step 2 | Determine the multi-innovation length p. According to Eq. (18)and Eq. (19) to Construct multi-innovation matrix \(Y(p,t)\) and \(\Phi (p,t)\) |
Step 3 | Determine the number of iterations and the fractional gradient order \(\alpha\) |
Step 4 | Use integer order and fractional order gradient in Eq. (24) to estimate model parameters \(\hat{\theta }\) synchronously |
Step 5 | The identification results are used to update the estimate parameter \(\hat{\theta }(t)\) in Eq. (24) |
Step 6 | Repeat steps 4–5. When the algorithm is iterated to the set number, obtain the final identification result |
Simulation and experiment
To verify the effectiveness of the algorithm, we use a simulation example and conduct a three degree-of-freedom (3-DOF) gyroscope model identification experiment. The proposed algorithm is compared with the SG, FOSG36 and MISG19 algorithms. The contributions of the additional fractional orders and multi-innovation lengths to the performance of the algorithm are examined. The model identification accuracy is evaluated using the following index
Numerical simulation
Consider the ARX model as follow
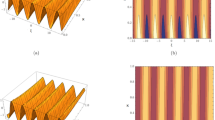
The parameters to be identified are \(\theta = \left[ {a_{1} ,a_{2} ,b_{1} ,b_{2} } \right]^{{\text{T}}} = \left[ {1.5, - 0.65,1.25,0.85} \right]^{{\text{T}}}\), the \(u\left( t \right)\) is a persistent excitation signal, and \(v(t)\) is a white noise with variance \(\sigma_{v}^{2} = 0.6^{2}\). The proposed algorithm is compared with the SG, FOSG, and MISG methods. In the proposed algorithm and FOSG method, the fractional order is set as \(\alpha = 1.2\). The multi-innovation length for the MISG method and proposed algorithm is set as p = 3. The identification results are shown in Figs. 1, 2 and summarised in Table 1.
As indicated in Fig. 1 and Table 1, compared with the existing approaches, the proposed algorithm introduces an additional fractional gradient term. The integer order and fractional order gradient simultaneously identify the model parameters, resulting in higher convergence speed and accuracy, smaller the identified parameter error. Figure 2 shows that the multi-innovation additional fractional-order gradient descent algorithm can promptly and accurately identify four different unknown parameters, highlighting its effectiveness.
Subsequently, we examine the influence of multi-innovation length p on the algorithm performance. To this end, p is set as 1, 3, 5, and 7, with the fractional order being \(\alpha = 1.2\). The identification results are shown in Figs. 3, 4 and outlined in Table 2.
Figures 3, 4 and Table 2 show that with increasing length, the proposed algorithm exhibits enhanced convergence speed and parameter identification accuracy. This improvement is attributable to the additional fractional gradient descent algorithm synchronously extending the single innovations of the fractional and integer gradients into a multi-innovation matrix, thereby enhancing the data utilisation. When a single innovation (p = 1) is transformed to a multi-innovation matrix (p = 7), the evaluation index \(\delta\) decreases from 0.1550 to 0.0196 after 2000 iterations.
Next, we examine the influence of different fractional orders on the identification speed and accuracy of the proposed algorithm. To this end, we set the p = 3 and fractional orders as \(\alpha = 0.5,0.8,1.2,1.5\). The identification results are shown in Figs. 5, 6 and summarised in Table 3.
It can be seen from Figs. 5, 6 and Table 3 that as the fractional order increases, the parameter identification error gradually decreases. Moreover, owing to the presence of both the integer order and fractional order gradients, the proposed algorithm maintains superior convergence speed and accuracy compared with the integer-order gradient descent algorithm, especially because of the small fractional order. Even when \(\alpha = 0.5\), the identification error (\(\delta = 0.0286\)) is still smaller than the SG algorithm (\(\delta = 0.2241\) in Table 1). This outcome further verifies the effectiveness of the proposed algorithm.
Experiment
The experimental analysis is conducted using a 3-DOF gyroscope system, which shown in Fig. 7. It contains a gyroscope, motor, data acquisition card, and power amplifier. The computer controls the input motor torque and transmits the signal to the data acquisition card through the Quarc 2020 real-time control software. The power amplifier amplifies the signal and applies it to the motor to precisely control the attitude angle of the gyroscope.
The 3-DOF gyroscope model can be expressed as follows
The model error is evaluated using the following index
where \(y_{id} (t)\) is identified system output, \(T_{f}\) is the termination time of the system operation.
To determine the system input and output, the Quarc database module in MATLAB/Simulink is used to build the system input and output measurement units. The data collection step length is 0.004 s, and the collection period is 50 s. The proposed algorithm is compared with the SG, FOSG36, and MISG19 methods, we set the p = 5 and fractional order as \(\alpha = 1.2\). The experiment data and identified result are shown in Figs. 8, 9, 10, summarised in Tables 4 and 5.
Figure 8 shows that the proposed algorithm can accurately identify the parameters of the 3-DOF gyroscope system. It can be seen from Fig. 9 and Table 4 that compared with the SG, FOSG and MISG algorithms, the proposed algorithm has the smallest identification error and can more accurately describe the dynamic characteristics of the gyroscope system. Figure 10 and Table 5 show that when \(\alpha\) takes different orders, the identification results are basically consistent, which further verifies that the proposed algorithm has high flexibility in engineering applications.
Conclusion
This paper introduces an additional fractional gradient descent identification algorithm based on the multi-innovation principle for ARX systems. The proposed algorithm incorporates a fractional order gradient along with the integer-order gradient and leverages the flexibility of fractional order calculus to improve the convergence speed. Additionally, it extends single innovations to multi-innovation matrices, enabling further enhanced data utilisation and parameter identification accuracy. The convergence of the algorithm is analysed, and its effectiveness is verified through simulations and experiment. The results show that the proposed approach outperforms the SG, FOSG, and MISG algorithms in terms of the convergence speed and accuracy. With increasing multi-innovation length and fractional order, the parameter identification accuracy and convergence speed improve. In terms of limitations, the fractional order \(\alpha\) of the current algorithm is fixed. Our future work will consider adaptive fractional order selection, and extend the adaptive multi-innovation additional fractional gradient descent identification algorithm to nonlinear systems and time-delay systems.
Data availability
This paper completely describes the theoretical research. The collection of data set is random according to different readers, but some codes can be provided by contacting the corresponding author.
References
Bouzrara, K., Garna, T., Ragot, J. & Messaoud, H. Decomposition of an ARX model on Laguerre orthonormal bases. ISA Trans. 51, 848–860 (2012).
Jin, J. J. et al. Model identification and analysis for parallel permanent magnetic suspension system based on ARX model. Int. J. Appl. Electromagn. Mech. 52, 145–152 (2016).
Ikeda, A., Fujita, K. & Takewaki, I. Story-wise system identification of actual shear building using ambient vibration data and ARX model. Eearthq. Struct. 7, 1093–1118 (2014).
Saxena, A., Dubey, Y. M. & Kumar, M. ARX and ARMAX modelling of SBCNC-60 machine for surface roughness and MRR with optimization of system response using PSO. J. Comb. Optim. 45, 56 (2023).
Pohjoranta, A., Halinen, M., Pennanen, J. & Kiviaho, J. Solid oxide fuel cell stack temperature estimation with data-based modeling-designed experiments and parameter identification. J. Power Sources 277, 464–473 (2015).
Wu, H. J., Yuan, S. F., Zhang, X., Yin, C. L. & Ma, X. R. Model parameter estimation approach based on incremental analysis for lithium-ion batteries without using open circuit voltage. J. Power Sources 287, 108–118 (2015).
Zardian, M. G. & Ayob, A. Intelligent modelling and active vibration control of flexible manipulator system. J. Vibroeng. 17, 1879–1897 (2015).
Xu, W. Q., Peng, H., Tian, X. Y. & Peng, X. Y. DBN based SD-ARX model for nonlinear time series prediction and analysis. Appl. Intell. 50, 4586–4601 (2020).
Ouyang, H. T., Shih, S. S. & Wu, C. S. Optimal combinations of non-sequential regressors for ARX-Based typhoon inundation forecast models considering multiple objectives. Water 9, 519 (2017).
Wang, Z. S., Wang, C. Y., Ding, L. H., Wang, Z. & Liang, S. N. Parameter identification of fractional-order time delay system based on Legendre wavelet. Mech. Syst. Signal Process. 163, 108141 (2021).
Li, J. P., Hua, C. C., Tang, Y. G. & Guan, X. P. A time varying forgetting factor stochastic gradient combined with kalman filter algorithm for parameter identification of dynamic systems. Nonlinear Dyn. 78, 1943–1952 (2014).
Dong, R. Q., Zhang, Y. & Wu, A. G. Weighted hierarchical stochastic gradient identification algorithms for ARX models. Int. J. Syst. Sci. 52, 363–373 (2021).
Li, F., Zheng, T., He, N. B. & Cao, Q. F. Data-driven hybrid neural fuzzy network and ARX modeling approach to practical industrial process identification. IEEE/CAA J. Autom. Sin. 9, 1702–1705 (2022).
Tu, Q., Rong, Y. J. & Chen, J. Parameter identification of ARX Models based on modified momentum gradient descent algorithm. Complexity 2020, 9537075 (2020).
Jing, S. X. Identification of an ARX model with impulse noise using a variable step size information gradient algorithm based on the kurtosis and minimum Renyi error entropy. Int. J. Robust Nonlinear Control 32, 1672–1686 (2022).
Li, F., Zhu, X. J. & Cao, Q. F. Parameter learning for the nonlinear system described by a class of Hammerstein models. Circuits Syst. Signal Process. 42, 2635–2653 (2023).
Liang, S. N., Xiao, B., Wang, C. Y., Wang, Z. S. & Wang, L. Multi-Innovation nesterov accelerated gradient parameter identification method for autoregressive exogenous models. J. Vibr. Control https://doi.org/10.1177/10775463231207117 (2023).
Li, F., Li, J. & Peng, D. G. Identification method of neuro-fuzzy-based Hammerstein model with coloured noise. IET Control Theor. Appl. 11, 3026–3037 (2017).
Ding, J., Cao, Z. X., Chen, J. Z. & Jiang, G. P. Weighted parameter estimation for Hammerstein nonlinear ARX systems. Circuits Syst. Signal Process. 39, 2178–2192 (2020).
Chen, J., Huang, B., Zhu, Q. M., Liu, Y. J. & Li, L. Global convergence of the EM algorithm for ARX models with uncertain communication channels. Syst. Control Lett. 136, 104614 (2020).
Jing, S. X. Identification of the ARX model with random impulse noise based on forgetting factor multi-error Information Entropy. Circuits Syst. Signal Process. 41, 915–932 (2022).
Li, F., Qian, S. Y., He, N. B. & Li, B. Estimation of Wiener nonlinear systems with measurement noises utilizing correlation analysis and Kalman filter. Int. J. Robust Nonlinear Control 34, 4706–4718 (2024).
Chen, J., Zhu, Q. M. & Liu, Y. J. Modified kalman filtering based multi-step-length gradient iterative algorithm for ARX models with random missing outputs. Automatica 118, 109034 (2020).
Li, F., Liang, M. J., He, N. B. & Cao, Q. F. Separation identification approach for the Hammerstein-Wiener nonlinear systems with process noise using correlation analysis. Int. J. Robust Nonlinear Control 33, 8105–8123 (2023).
Li, F., Sun, X. Q. & Cao, Q. F. Parameter learning of multi-input multi-output Hammerstein system with measurement noises utilizing combined signals. Int. J. Adapt. Control Signal Process. https://doi.org/10.1002/acs.3857 (2024).
Stojanovic, V., Nedic, N., Prsic, D. & Dubonjic, L. Optimal experiment design for identification of ARX models with constrained output in non-Gaussian noise. Appl. Math. Model. 40, 6676–6689 (2016).
Ding, F., Lv, L., Pan, J., Wan, X. K. & Jin, X. B. Two-stage gradient based iterative estimation methods for controlled autoregressive systems using the measurement data. Int. J. Control Autom. Syst. 18, 886–896 (2020).
Wang, S. J. & Ding, R. Three-stage recursive least squares parameter estimation for controlled autoregressive autoregressive systems. Appl. Math. Model. 37, 7489–7497 (2013).
Chen, J. & Ding, F. Modified stochastic gradient identification algorithms with fast convergence rates. J. Vibr. Control 17, 1281–1286 (2011).
Chen, J., Liu, Y. J., Ding, F. & Zhu, Q. M. Gradient-based particle filter algorithm for an ARX model with nonlinear communication output. IEEE Trans. Syst. Man Cybern.-Syst. 50, 2198–2207 (2020).
Li, F., Yang, Y. S. & Xia, Y. Q. Identification for nonlinear systems modelled by deep long short-term memory networks based Wiener model. Mech. Syst. Signal Process. 220, 111631 (2024).
Jia, T. Fractional gradient descent algorithm for switching models using self-organizing maps: One set data or all the collected data. Chaos Solitons Fractals 172, 113460 (2023).
Cao, Y. & Su, S. Fractional gradient descent algorithms for systems with outliers: A matrix fractional derivative or a scalar fractional derivative. Chaos Solitons Fractals 174, 113881 (2023).
Chen, Y. Q., Gao, Q., Wei, Y. H. & Wang, Y. Study on fractional order gradient methods. Appl. Math. Computat. 314, 310–321 (2017).
Wei, Y. H., Kang, Y., Yin, W. D. & Wang, Y. Generalization of the gradient method with fractional order gradient direction. J. Franklin Inst. 357, 2514–2532 (2020).
Xu, T. Y., Chen, J., Pu, Y. & Guo, L. X. Fractional-based stochastic gradient algorithms for time-delayed ARX models. Circuits Syst. Signal Process. 41, 1895–1912 (2022).
Chaudhary, N. I., Raja, M., Khan, Z., Mehmood, A. & Shah, S. M. Design of fractional hierarchical gradient descent algorithm for parameter estimation of nonlinear control autoregressive systems. Chaos Solitons Fractals 157, 111913 (2022).
Fernandez, A. & Fahad, H. M. Weighted fractional calculus: A general class of operators. Fractal Fract. 6, 208 (2022).
Yang, Y., Mo, L., Hu, Y. & Long, F. The improved stochastic fractional order gradient descent algorithm. Fractal Fract. 7, 631 (2023).
Liu, L. J., Ding, F., Wang, C., Alsaedi, A. & Hayat, T. Maximum likelihood multi-innovation stochastic gradient estimation for multivariate equation-error systems. Int. J. Control Autom. Syst. 16, 2528–2537 (2018).
Ding, F. Several multi-innovation identification methods. Digit. Signal Process. 20, 1027–1039 (2010).
Zhang, Q., Wang, H. W. & Liu, C. L. Hybrid identification method for fractional-order nonlinear systems based on the multi-innovation principle. Appl. Intell. 53, 15711–15726 (2023).
Ding, F. & Chen, T. W. Performance analysis of multi–innovation gradient type identification methods. Automatica 43, 1–14 (2007).
Cheng, S. S., Wei, Y. H., Chen, Y. Q., Li, Y. & Wang, Y. An innovative fractional order LMS based on variable initial value and gradient order. Signal Process. 133, 260–269 (2017).
Acknowledgements
The manuscript was supported by the Education Department of Jilin Province (Grant No. JJKH20240314KJ) and Information Perception and Intelligent Control Laboratory.
Author information
Authors and Affiliations
Contributions
Zishuo Wang: Conceptualization, Methodology, Writing—Original Draft, Funding acquisition. Shuning Liang: Analysis of the numerical simulation example. Beichen Chen: Construction of the experimental platform and data acquisition. Hongliang Sun: Supervision. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wang, Z., Liang, S., Chen, B. et al. Additional fractional gradient descent identification algorithm based on multi-innovation principle for autoregressive exogenous models. Sci Rep 14, 19843 (2024). https://doi.org/10.1038/s41598-024-70269-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-70269-x