Abstract
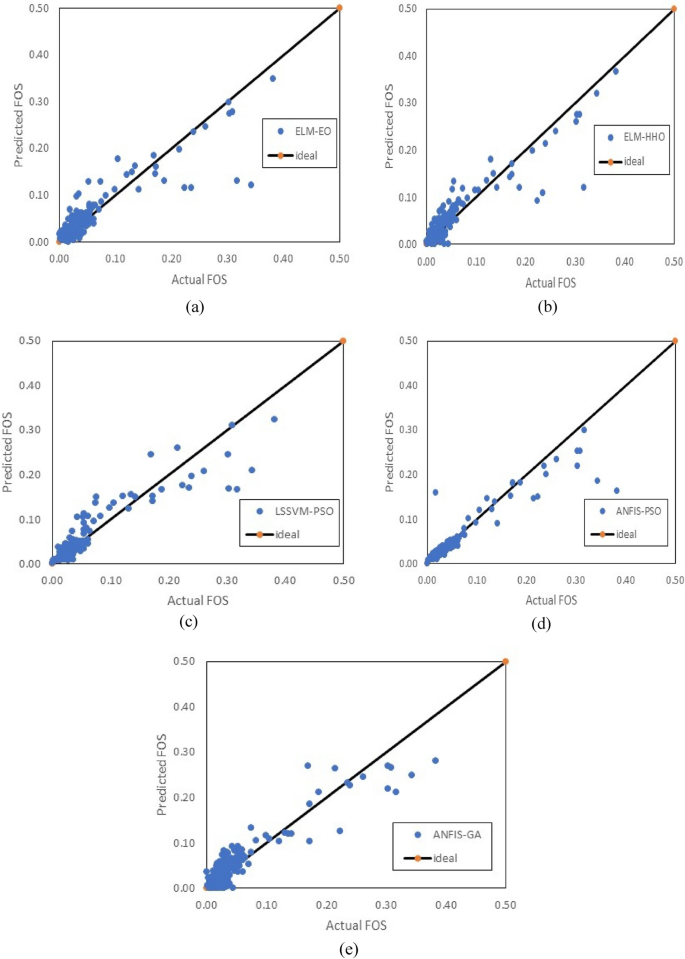
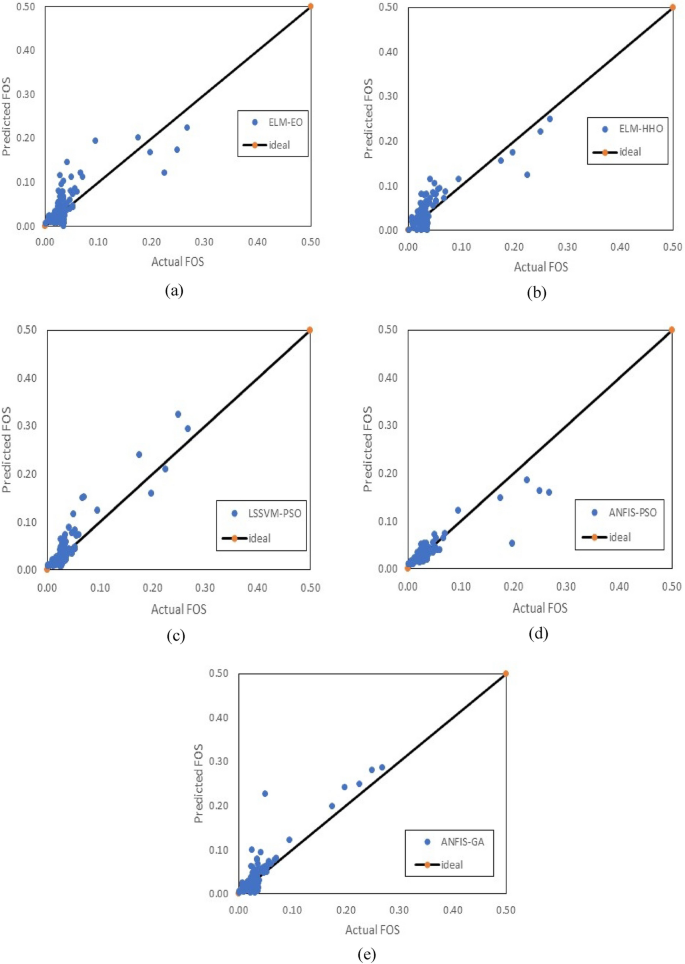
In this work, intelligent numerical models for the prediction of debris flow susceptibility using slope stability failure factor of safety (FOS) machine learning predictions have been developed. These machine learning techniques were trained using novel metaheuristic methods. The application of these training mechanisms was necessitated by the need to enhance the robustness and performance of the three main machine learning methods. It was necessary to develop intelligent models for the prediction of the FOS of debris flow down a slope with measured geometry due to the sophisticated equipment required for regular field studies on slopes prone to debris flow and the associated high project budgets and contingencies. With the development of smart models, the design and monitoring of the behavior of the slopes can be achieved at a reduced cost and time. Furthermore, multiple performance evaluation indices were utilized to ensure the model’s accuracy was maintained. The adaptive neuro-fuzzy inference system, combined with the particle swarm optimization algorithm, outperformed other techniques. It achieved an FOS of debris flow down a slope performance of over 85%, consistently surpassing other methods.
Similar content being viewed by others
Introduction
Analytical studies on debris flow susceptibility typically involve the use of various methods to assess and predict the potential for debris flow in a given area1,2. These studies aim to understand the factors that contribute to the initiation, magnitude, and runout of debris flows, as well as the susceptibility of specific locations to these hazardous events3. Several analytical methods and approaches are commonly used in these studies, including geomorphological mapping (GM), which involves the identification and analysis of landforms, surface materials, and landscape features associated with previous debris flows4. This approach helps in understanding the spatial distribution of potential debris flow source areas and their associated susceptibility factors5. Hydrological and hydraulic modeling (HHM): Analytical studies often utilize hydrological and hydraulic modeling to simulate rainfall-runoff processes and the behavior of flowing debris6. These models can help identify areas at risk of debris flow initiation and estimate potential flow paths and runout areas7. Geotechnical and geophysical investigations (GGI) involve the assessment of soil properties, subsurface conditions, and the mechanical behavior of materials in potential debris flow source areas8. This can include laboratory testing, in situ measurements, and geophysical surveys to evaluate the susceptibility of slopes to failure and debris flow initiation9. Statistical and probabilistic approaches are used to quantify the relationships between debris flow occurrence and various influencing factors, such as rainfall intensity, land cover, slope gradient, and geological characteristics10. Probabilistic models may be developed to assess the likelihood of debris flow events under different conditions11. Remote sensing and geographic information systems (RSGIS): Remote sensing data, including aerial and satellite imagery, as well as GIS-based analyses, are often employed to identify and map terrain characteristics, land cover, and hydrological features associated with debris flow susceptibility12. Field surveys and case studies (FSCS) provide valuable data on past debris flow events, including their triggers, characteristics, and impacts13. These studies contribute to the development of empirical relationships and the validation of predictive models14. By integrating these analytical approaches, researchers and practitioners can develop comprehensive assessments of debris flow susceptibility, leading to improved hazard mapping, risk management strategies, and early warning systems15. These studies are essential for understanding the complex interactions between geological, hydrological, and environmental factors that influence debris flow occurrence and for guiding land use planning and disaster risk reduction efforts16.
Numerical simulation of debris flow susceptibility involves the use of computational models and simulations to assess and predict the potential for debris flows in specific areas17. These simulations aim to capture the complex interactions between various factors that influence debris flow initiation, propagation, and runout18. Several numerical modeling techniques are commonly used for simulating debris flow susceptibility, including HHM, which utilizes numerical models to simulate rainfall-runoff processes and the behavior of flowing debris. This approach is essential for assessing debris flow susceptibility7. These models typically consider factors such as rainfall intensity, soil moisture, topography, and channel characteristics to predict the likelihood and magnitude of debris flow events3. Geotechnical modeling: Numerical simulations can be used to model the mechanical behavior of slopes and the initiation of debris flows under different conditions. These models consider factors such as soil properties, slope stability, and the influence of pore water pressure on slope failure, providing insights into the susceptibility of specific areas to debris flows11. Coupled hydromechanical models (CHMs) integrate the hydraulic and mechanical aspects of debris flows, accounting for the interactions between water, sediment, and the surrounding terrain. They simulate the transient behavior of debris flows, including their initiation, flow dynamics, and deposition, considering the influence of slope geometry and soil properties15. Particle-based models: Some numerical simulations use particle-based methods to represent the behavior of individual sediment particles and the flow of debris9. These models can capture the granular nature of debris flows and their interactions with the surrounding terrain, providing insights into susceptibility factors such as flow velocity, inundation area, and impact forces. Probabilistic and statistical models (PSM): Numerical simulations can incorporate probabilistic and statistical approaches to assess debris flow susceptibility16. These models consider uncertainties in input parameters and help quantify the likelihood of debris flow occurrence under different scenarios, aiding in risk assessment and hazard mapping. Three-dimensional (3D) geomorphic modeling (TDGM): Advanced numerical simulations can utilize 3D geomorphic models to simulate the complex topography and terrain features that influence debris flow susceptibility17. These models can capture the spatial distribution of susceptibility factors and provide detailed simulations of debris flow behavior in complex landscapes18. By employing these numerical modeling techniques, researchers and practitioners can gain insights into the factors that contribute to debris flow susceptibility and develop predictive tools to assess the potential impact of debris flows in specific areas17. These simulations are valuable for informing land use planning, disaster risk reduction strategies, and the development of early warning systems for debris flow hazards.
The mathematics of debris flows down a slope involves the application of the fundamental principles of fluid mechanics, solid mechanics, and granular flow to describe the behavior of the mixture of water, soil, and rock as it moves downslope3. While the specific mathematical models can be quite complex, it is useful to consider a simplified overview of the key mathematical aspects involved in understanding debris flows down a slope. Conservation laws: The conservation of mass and momentum are fundamental principles that underlie the mathematical modeling of debris flows7. These laws are expressed through partial differential equations (PDEs). For example, the continuity equation represents the conservation of mass, and the Navier–Stokes equations describe the conservation of momentum for the fluid phase8. Constitutive relationships: Debris flows are typically non-Newtonian fluids due to the presence of solid particles10. The constitutive relationships describe the rheological behavior of the debris flow material, including the interaction between the fluid phase and the solid particles11. These relationships can be quite complex and may involve empirical or semi-empirical models to capture the behavior of the mixture. Granular flow modeling: Due to the presence of solid particles, the debris flow may exhibit characteristics of granular flow12. Models such as the Coulomb-Mohr yield criterion and the Drucker-Prager model are often used to capture the behavior of granular materials and their interaction with the fluid phase. Slope stability analysis: The mathematics of debris flows down a slope often involves considerations of slope stability and the initiation of the flow13. This can include the application of soil mechanics principles, such as the Mohr–Coulomb criterion, to assess the stability of the slope and predict the conditions under which debris flows may occur. Runout modeling: Debris flows exhibit complex runout behavior as they travel downslope19. Mathematical models, such as depth-averaged models or more detailed computational fluid dynamics (CFD) simulations, can be used to predict the runout distance and behavior of the debris flow based on the properties of the material and the slope geometry6. Numerical simulations: Advanced numerical methods, including the finite element method (FEM), finite volume method (FVM), or discrete element method (DEM), can be used to simulate the behavior of debris flows down a slope17. These simulations involve discretizing the governing equations and solving them numerically to predict the flow behavior5. It is important to note that the mathematical modeling of debris flows down a slope is a highly interdisciplinary field, drawing on principles from fluid mechanics, solid mechanics, and geotechnical engineering19. The actual mathematical models used to describe debris flows can vary in complexity, ranging from simple empirical relationships to sophisticated multiphase flow models, and are often tailored to specific site conditions and phenomena.
Finite element modeling can be a valuable tool for assessing debris flow susceptibility, particularly in the context of understanding the mechanical behavior of the underlying terrain and the potential for debris flow initiation19,20. When using finite element modeling to assess debris flow susceptibility, several aspects are considered. Geotechnical properties: Finite element modeling allows for the incorporation of geotechnical properties of soil and rock masses, including factors such as shear strength, cohesion, internal friction angle, and permeability21. These properties play a critical role in determining the stability of slopes and the potential for debris flow initiation. Slope stability analysis: Finite element models can be used to perform slope stability analyses, considering the influence of various factors, such as slope geometry, soil properties, groundwater conditions, and seismic loading5,22. These analyses can help identify areas of potential instability and assess the susceptibility of slopes to failure and subsequent debris flow generation. Coupled hydromechanical modeling: Finite element models can be coupled with hydraulic analyses to simulate the interactions between water and soil within the slope23. This allows for the assessment of pore water pressure development, the influence of rainfall or rapid snowmelt on slope stability, and the potential for liquefaction and debris flow initiation. Debris flow initiation: Finite element modeling can be used to simulate the conditions under which debris flow initiation may occur24. This includes evaluating the influence of rainfall, pore water pressure changes, and other triggering factors on the mechanical stability of slopes and the potential for mass movement. Material failure and runout analysis: Finite element modeling can be employed to simulate the failure and movement of soil and debris masses, including the mechanics of mass movement, runout distances, and impact forces13. This can provide insights into the potential extent and impact of debris flows in susceptible areas14. Sensitivity analyses: Finite element models can be used to conduct sensitivity analyses to assess the influence of different parameters on debris flow susceptibility15. This can help identify critical factors that contribute to the potential for debris flow initiation and propagation4. By utilizing finite element modeling techniques to assess debris flow susceptibility, researchers and practitioners can gain a better understanding of the geotechnical and hydraulic factors that influence the potential for debris flows10. These models can aid in the identification of high-risk areas, the development of mitigation strategies, and the implementation of measures to reduce the impact of debris flows on human settlements and infrastructure.
The mathematical formulation of a debris flow problem using the FEM involves the description of the governing equations, boundary conditions, and material properties in a way that can be discretized and solved using finite element techniques19. Debris flows are complex phenomena involving the interaction of solid particles and fluid, and their mathematical modeling often requires the use of advanced numerical methods, such as the FEM22. The governing equations for a debris flow problem typically include the conservation of mass, momentum, and possibly energy24. In the case of a two-phase flow involving solid particles and fluid, the governing equations may include the Navier–Stokes equations for the fluid phase, coupled with equations describing the motion of the solid particles25. Constitutive equations are used to describe the behavior of the debris flow material, including the rheological properties of the fluid phase and the interaction between the solid particles and the fluid6. These constitutive equations may include models for viscosity, granular flow, and other relevant material properties26. Boundary conditions define the conditions at the boundaries of the computational ___domain, including inlet and outlet conditions for the flow, as well as any solid boundaries that may affect the flow behavior26,27,28. Discretization: The next step is to discretize the governing equations and boundary conditions using the FEM27. This involves subdividing the computational ___domain into a mesh of elements, defining the basis functions for representing the solution within each element, and then assembling the governing equations into a system of algebraic equations24. Solution: The system of algebraic equations is then solved numerically to obtain the solution for the debris flow problem5,11,18. This may involve the use of iterative solution techniques and time-stepping methods for transient problems5. Validation and post-processing: Finally, the computed solution is validated against experimental or observational data, and post-processing techniques are used to analyze the results and extract relevant information about the debris flow behavior, such as flow velocities, pressures, and particle trajectories12. It is important to note that the specific mathematical formulation for a debris flow problem using the FEM will depend on the particular characteristics of the problem, such as the properties of the debris flow material, the geometry of the flow ___domain, and the boundary conditions15. Additionally, advanced modeling techniques, including multiphase flow and fluid–structure interaction, may be necessary to accurately capture the behavior of debris flows.
Moreno, Dialami, and Cervera27 specifically examined the numerical modeling of spillage and debris floods. The flows are classified as either Newtonian or viscoplastic Bingham flows, and they involve a free surface. The modeling approach utilized mixed stabilized finite elements. This study introduced a Bingham model with double viscosity regularization and presented a simplified Eulerian approach for monitoring the movement of the free surface. The numerical solutions were compared to analytical, experimental, and results from the literature, as well as field data obtained from a genuine case study. Quan Luna et al.28 developed physical vulnerability curves for debris flows by utilizing a dynamic run-out model. The model computed tangible results and identified areas where vulnerable components may experience an adverse effect. The study used the Selvetta debris flow event from 2008, which was rebuilt following thorough fieldwork and interviews. This study measured the extent of physical harm to impacted buildings in relation to their susceptibility to damage, which is determined by comparing the cost of damage with the value of reconstruction. Three distinct empirical vulnerability curves were acquired, showcasing a quantitative method to assess the susceptibility of an exposed building to debris flow, regardless of when the hazardous event takes place. According to Nguyen, Tien, and Do29, landslides in Vietnam frequently transpire on excavated slopes during the rainy season, necessitating a comprehensive understanding of influential elements and initiating processes. This study investigates the most significant deep-seated landslide that occurred because of intense precipitation on July 21, 2018 and the subsequent sliding of the Halong-Vandon expressway. The results indicated that heavy rainfall is the primary component that triggers landslides, while slope cutting is identified as the key causative cause. The investigation also uncovered human-induced impacts, such as inaccurate safety calculations for road construction and quarrying activities, which led to the reactivation of the landslide body on the lower slope due to the dynamic effect of subsequent sliding. Bašić et al.30 presented Lagrangian differencing dynamics (LDD), a method that utilized a meshless and Lagrangian technique to simulate non-Newtonian flows. The method employed spatial operators that are second-order consistent to solve the generalized Navier–Stokes equations in a strong formulation. The solution was derived using a split-step approach, which involved separating the pressure and velocity solutions. The approach is completely parallelized on both CPU and GPU, guaranteeing efficient computational time and allowing for huge time steps. The simulation results are consistent with the experimental data and will undergo validation for non-Newtonian models. Ming-de31 described a finite element analysis of the flow of a non-Newtonian fluid in a two-dimensional (2D) branching channel. The Galerkin method and mixed FEM were employed. In this case, the fluid is regarded as an incompressible, non-Newtonian fluid with an Oldroyd differential-type constitutive equation. The non-linear algebraic equation system, defined using the finite element approach, was solved using the continuous differential method. The results demonstrated that the FEM is appropriate for analyzing the flow of non-Newtonian fluids with intricate geometries. Lee et al.32 analyzed the effects of erosion on debris flow and impact area using the Deb2D model, developed in Korea. The research was conducted on the Mt. Umyeon landslide in 2011, comparing the impacted area, total debris flow volume, maximum velocity, and inundated depth from the erosion model with field survey data. The study also examined the effect of entrainment changing parameters through erosion shape and depth. The results showed the necessity of parameter estimation in addressing the risks posed by shallow landslide-triggered debris flows. Kwan, Sze, and Lam33 employed numerical models to simulate rigid and flexible barriers aimed at reducing the risks associated with boulder falls and debris flows in landslide-prone areas. The performance of cushioning materials, such as rock-filled gabions, recycled glass cullet, cellular glass aggregates, and EVA foam, was evaluated. Finite element models were created to replicate the interaction between debris and barriers. These models showed a reduced hydrodynamic pressure coefficient and negligible transfer of debris energy to the barrier. Martinez34 developed a 3D numerical model for the simulation of stony debris flows. The model considered a fluid phase consisting of water and fine sediments, as well as a non-continuum phase consisting of big particles. The model replicated interactions between particles and between particles and walls, incorporating Bingham and Cross rheological models to represent the behavior of the continuous phase. It exhibited stability even under low shear rates and is capable of handling flows with high particle density. It is useful for strategizing and overseeing regions susceptible to debris movement. Martinez, Miralles-Wilhelm, and Garcia-Martinez35 presented a 2D debris flow model that utilized non-Newtonian Bingham and Cross rheological formulations. This model considered variations in fluid viscosity and internal friction losses. The model underwent testing for dam break scenarios and demonstrated strong concurrence with empirical data and analytical solutions. The model yielded consistent outcomes even when subjected to low shear rates, thus preventing any instability in non-continuous constitutive relationships.
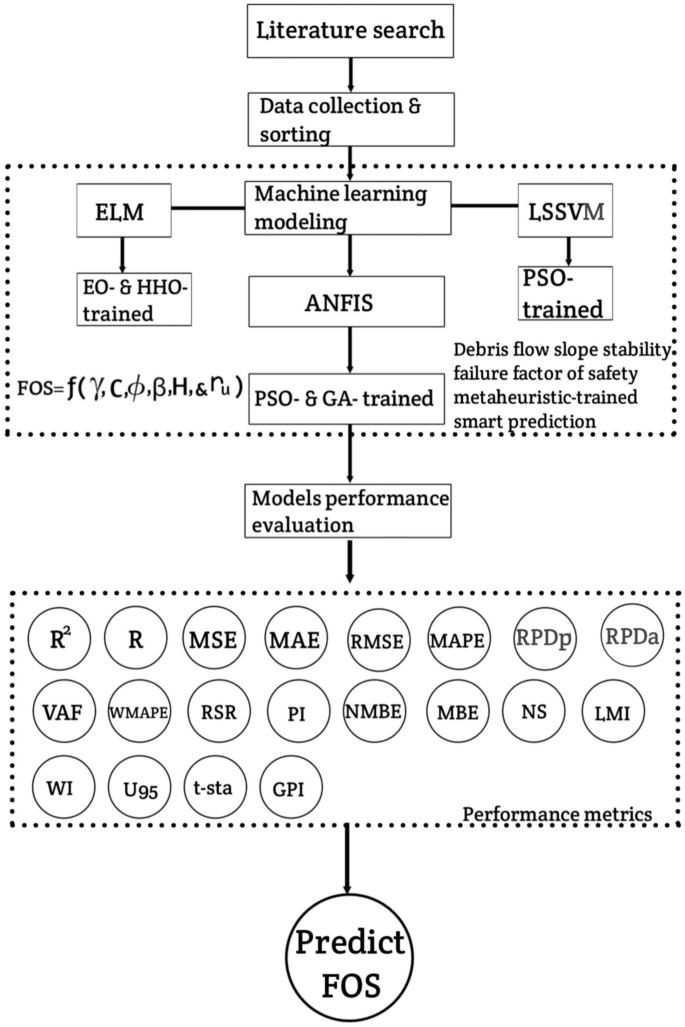
According to Nguyen, Do, and Nguyen36, landslides present a worldwide risk, especially in areas with high elevation. A profound landslide transpired close to the Mong Sen bridge in Sapa town, located in the Laocai province of Vietnam. The fissures were a result of incisions made during the process of road construction. The investigation determined that cutting operations were a contributing factor to the sliding of the sloped soil mass. The rehabilitation efforts involved excavating the soil above the original slope and building a retaining structure to stabilize the slope. According to Negishi et al.37, the Bingham fluid simulation model was formulated using the moving particle hydrodynamics (MPH) technique, which is characterized by physical consistency and adherence to fundamental rules of physics. The model accurately simulated the halting and solid-like characteristics of Bingham fluids, while also accounting for the preservation of linear and angular momentum. The method was confirmed and authenticated by doing calculations on 2D Poiseuille flow and 3D dam-break flow and then comparing the obtained results with theoretical predictions and experimental data. Kondo et al.38 introduced a particle method that is physically consistent and specifically designed for high-viscosity free-surface flows, aiming to overcome the constraints of current methods. The method is validated through experimentation in a revolving circular pipe, high-viscous Taylor-Couette flights, and offset collision scenarios. This validation assures that the fundamental principles of mass, momentum, and thermodynamics are upheld, preventing any abnormal behavior in high-viscous free-surface flows. Sváček39 focused on the numerical approximation of the flow of non-Newtonian fluids with a free surface, specifically in the context of new concrete flow. This work primarily examined the mathematical formulation and discretization of industrial mixes, which frequently exhibit non-Newtonian fluid behavior with regard to yield stress. This study employed the finite element approach for this purpose. Licata and Benedetto40 introduced a computational method for modeling debris flow, specifically focused on simulating the consistent movement of heterogeneous debris flow that is constrained laterally. The proposed computational scheme utilized geological data and methodological ideas derived from simulations using cellular automata and grid systems. This scheme aimed to achieve a balance between global forecasting capabilities and computational resources. Qingyun, Mingxin, and Dan41 examined the influence of debris flow and its ability to carry and incorporate silt in the beds of gullies located in hilly regions. The work used elastic–plastic constitutive equations and numerical simulations to investigate the coupling contact between solid, liquid, and structural components using a coupled analytical method. The model's viability was confirmed by a comparison of simulated results with empirical data. The study also investigated the impact of characteristics linked to the shape of debris on the process of erosion and entrainment in debris flow. Bokharaeian, Naderi, and Csámer42 employed the Herschel-Buckley rheology model and smoothed particle hydrodynamics (SPH) approach to replicate the behavior of a mudflow on a free surface when subjected to a gate. The run-out distance and velocity were determined by numerical simulation and subsequently compared to the findings obtained in the laboratory. The findings indicated that the computer model exhibited a more rapid increase in run-out and viscosity compared to the experimental model, mostly due to the assumption of negligible friction. The use of an abacus is advised for simulating mudflows and protecting against excessive run-out distance and viscosity. Böhme and Rubart43 presented an FEM for solving stable incompressible flow problems in a modified Newtonian fluid. The system employed a variational approach to express the equations of motion, with continuity being treated as a secondary requirement. The inertia term was discretized using finite elements, which led to the emergence of a nonlinear additional stress factor. According to Rendina, Viccione, and Cascini44, flow mass motions are highly destructive events that result in extensive destruction. Examining alterations in motion helps to comprehend the progression phases and construction of control measures. This study utilized numerical algorithms based on a finite volume scheme to examine the behavior of Newtonian and non-Newtonian fluids on inclined surfaces. The Froude number offers a distinct characterization of flow dynamics, encompassing the heights and velocities of propagation. The case studies mostly examined dam breaks in one-dimensional (1D) and 2D scenarios. Melo, van Asch, and Zêzere45 used a simulation model to replicate the movement of debris flow and determine the rheological properties, along with the amount of rainfall beyond what is necessary. A dynamic model was employed, which was validated using 32 instances of debris flows. Under the most unfavorable circumstances, it was projected that 345 buildings might be affected by flooding. We have identified six streams that have been previously affected by debris flow and have suffered harm as a result. Reddy et al.46 presented a finite element model that utilized the Navier–Stokes equations to simulate the behavior of unstable, incompressible, non-isothermal, and non-Newtonian fluids within 3D enclosures. The system employs power-law and Gtrreau constitutive relations, along with Picard's approach to solving non-linear equations. The model was utilized for the analysis of diverse situations and can be adapted for alternative constitutive relationships. Woldesenbet, Arefaine, and Yesuf47 determined the geotechnical conditions and soil type that contribute to the onset of landslides. They also analyzed slope stability and proposed strategies to mitigate the associated risks. The measurement of slope geometry, landslide magnitude, and geophysical resistivity was conducted using fieldwork, laboratory analysis, and software analysis. The results indicated the presence of fine-grained soil, which had an impact on the qualities of the soil. The stability of a slope is influenced by various factors, such as the type of soil, the presence of surface and groundwater, and the steepness of the slope. For the purpose of ensuring stability, it is advisable to make alterations to the shape of the slope, construct retaining walls, improve drainage systems, and cultivate vegetation with deep root systems. Hemeda48 examined the Horemheb tomb (KV57) in Luxor, Egypt, employing the PLAXIS 3D program for analysis. The failure loads were derived from laboratory experiments, and the structure was simulated using finite element code to ensure precise 3D analysis of deformation and stability. The elastic–plastic Mohr–Coulomb model was employed as a material model, incorporating factors such as Young's modulus, Poisson's ratio, friction angle, and cohesion. Numerical engineering analysis includes the assessment of the surrounding rocks, the estimation of elements influencing the stability of a tomb, and the integration of 3D geotechnical models. The study also examined therapeutic and retrofitting strategies and approaches, as well as the necessity for fixed monitoring and control systems to enhance and secure the cemetery. It also examined methods for treating rock pillars and implementing ground support strategies. Böhme and Rubart43 introduced a finite element model for solving stable incompressible flow problems in a modified Newtonian fluid. The method employed a variational version of the equations of motion and utilized a penalty function approach to discretize the inertia term. The program emulated the shift from plug flow to pipe flow and yielded numerical outcomes for different Weissenberg values and constant Reynolds numbers. Whipple49 studied the numerical simulation of open-channel flow of Bingham fluids, providing enhanced capabilities for evaluating muddy debris flows and associated deposits. The findings are only relevant to debris flows that contain a significant amount of mud. The numerical model used (FIDAP) enables the application and expansion of analytical solutions to channels with any cross-sectional shape while maintaining a high level of accuracy. The outcomes restrict the overall equations for discharge and plug velocity, which are appropriate for retroactive computation of viscosity based on field data, engineering analysis, and incorporation into debris-flow routing models in one and two dimensions. Rendina, Viccione, and Cascini44 used numerical methods based on a finite volume framework to compare the behavior of Newtonian and non-Newtonian fluids on inclined surfaces. The Froude number offers a distinct characterization of flow dynamics, encompassing the heights and velocities of propagation. Case studies primarily concentrated on dam breach scenarios. Averweg et al.50 introduced a least-squares FEM (LSFEM) for simulating the steady flow of incompressible non-Newtonian fluids using Navier–Stokes equations. The LSFEM provides benefits compared to the Galerkin technique, including the use of a posteriori error estimator and improved efficiency through adaptive mesh modifications. This approach expands upon the initial first-order LS formulation by incorporating the influence of nonlinear viscosity on fluid shear rate. It explored the Carreau model and used conforming discretization for accurate approximation. The reviewed resources from previous studies presented in Tables 1 and 2 show the current progress in the field, as well as the experimental requirements for the determination of the slope factor of safety (FOS). This requires sophisticated technology, which needs significant funding, technical services, and contingencies to determine the shear parameters (friction and cohesion), unit weight, pore pressure, and geometry of the studied slope. Additionally, previous studies have shown the numerical models applied in the estimation of the FOS; however, this study is focused on field and experimental data collection and sorting. As outlined in the research framework, the collected data is then deployed into intelligent prediction models to determine the FOS. This approach aims to facilitate easier design, construction, and performance monitoring of slope behavior during debris flow or earthquake-induced geohazard events.
Methodology
Governing equations
Eulerian–Lagrangian and the kinematics of flow on inclined surfaces
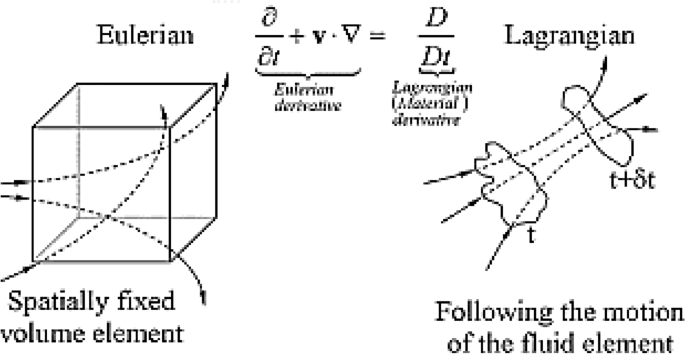
The Eulerian–Lagrangian approach is a mathematical framework used to describe the behavior of fluid–solid mixtures51, which can include debris flows on inclined surfaces and slope stability failures. The coupled interface of this approach is presented in Fig. 1. In this approach, the Eulerian framework describes the behavior of the fluid phase, while the Lagrangian framework describes the behavior of the solid phase51. For the specific case of debris flow on an inclined surface and slope stability failure, the equations can be quite complex and they depend on various factors, such as the properties of the debris, the slope geometry, and the flow conditions51. The governing equations for debris flow and slope stability failure are typically derived from fundamental principles of fluid mechanics and solid mechanics. These equations may include the Navier–Stokes equations for the fluid phase and constitutive models for the solid phase, as well as equations describing the interaction between the two phases51. In the Eulerian framework, the equations governing the behavior of the fluid phase (such as water and sediment mixture in debris flow) can include the continuity equation and the Navier–Stokes equations, which describe the conservation of mass and momentum for the fluid51. These equations can be adapted to account for the specific characteristics of debris flow, including non-Newtonian behavior and solid particle interactions. In the Lagrangian framework, the equations governing the behavior of the solid phase, such as the soil and rock material in slope stability failure, can include constitutive models that describe the stress–strain relationship of the material.
These models can encompass factors such as strain softening, strain rate effects, and failure criteria. The interaction between the fluid and solid phases in the Eulerian–Lagrangian approach is typically described using additional terms that account for the exchange of momentum and mass between the phases51. These terms can include drag forces, buoyancy effects, and fluid-induced stresses on the solid phase. The specific form of the Eulerian–Lagrangian equations for debris flow on inclined surfaces and slope stability failure will depend on the details of the problem being studied, potentially requiring empirical data, numerical simulations, and experimental observations to validate and implement the equations effectively16. Due to the complexity of these equations, they are often solved using numerical methods, such as CFD and the DEM. In practice, researchers and engineers often use specialized software packages to simulate debris flow and slope stability failure, which implement the necessary equations and models within a computational framework to analyze and predict the behavior of these complex phenomena. The Eulerian mathematical equations for debris flow typically involve the conservation equations for mass, momentum, and energy, as well as constitutive relationships that describe the behavior of the debris material. Debris flow is a complex, multiphase flow phenomenon that involves the movement of a mixture of solid particles and fluid (usually water) down a slope51. The Eulerian approach describes the behavior of the mixture as it flows over the inclined surface. The continuity equation describes the conservation of mass for the debris flow mixture. In its Eulerian form, the continuity equation can be written as:
where ρ is the density of the mixture, φ is the volume fraction of the solid phase, t is time, v is the velocity vector of the mixture, and S represents any sources or sinks of the mixture51. The momentum equation describes the conservation of momentum for the debris flow mixture. In its Eulerian form, the momentum equation can be written as:
where v is the velocity vector of the mixture, τ is the stress tensor, g is the gravitational acceleration, and F represents any external forces acting on the mixture. The constitutive relationships describe the stress–strain behavior of the debris material51. These relationships can include models for the viscosity of the mixture, the drag forces between the solid particles and the fluid, and the interaction between the solid particles. Constitutive models for debris flow are often non-Newtonian and may involve empirical parameters based on experimental data. The energy equation describes the conservation of energy for the debris flow mixture. In its Eulerian form, the energy equation can be written as:
where E is the total energy per unit volume, k is the thermal conductivity, T is the temperature, and Q represents any heat sources or sinks. These equations, along with appropriate boundary conditions, form the basis for modeling and simulating debris flow using the Eulerian approach. However, it is important to note that the specific form of these equations may vary depending on the details of the problem being studied and the assumptions made in the modeling approach. Additionally, practical applications often involve numerical methods, such as CFD, to solve these equations and simulate the behavior of debris flow under different conditions51. When considering Lagrangian mathematical equations for debris flow on inclined surfaces, it is important to recognize that the Lagrangian approach focuses on tracking the motion and behavior of individual particles within the flow through space and time51. The equations of motion describe the trajectory and kinematics of individual particles within the debris flow51. These equations account for forces acting on the particles, such as gravity, drag forces, and inter-particle interactions. The equations can be written for each individual particle and may include terms representing the particle's mass, velocity, and acceleration. Constitutive relationships are used to describe the stress–strain behavior of individual particles and their interactions with the surrounding fluid. These models can encompass factors such as particle–particle interactions, particle–fluid interactions, and the rheological properties of the debris material51. Constitutive models for debris flow often consider the non-Newtonian behavior of the mixture and may involve empirical parameters based on experimental data. In the Lagrangian framework, it is important to account for erosion and deposition of particles as the debris flow moves over inclined surfaces. Equations describing erosion and deposition processes can be included to track changes in the particle distribution and the evolution of the flow51. The Lagrangian approach can also involve equations that describe the interaction of individual particles with the surrounding environment, including the boundary conditions of the inclined surface and any obstacles or structures in the flow path. This approach accounts for the interaction between the solid particles and the fluid phase within the debris flow51. Equations can be included to represent the drag forces, buoyancy effects, and fluid-induced stresses acting on the individual particles. The Lagrangian approach for debris flow involves tracking a large number of individual particles, which can be computationally intensive. Numerical simulations using DEMs are often employed to solve the Lagrangian equations and simulate the behavior of debris flow on inclined surfaces. In practice, researchers and engineers use specialized software and numerical methods to simulate debris flow behavior in the Lagrangian framework, taking into account the complexities of particle–fluid interactions, erosion and deposition processes, and the influence of slope geometry on flow dynamics51.
The kinematics of flow on inclined surfaces refers to the study of the motion and deformation of a fluid as it moves over an inclined plane or surface. Understanding the kinematics of flow on inclined surfaces is important in various fields, including fluid mechanics, civil engineering, and geology.
Here are some key concepts related to the kinematics of flow on inclined surfaces: When a fluid flows over an inclined surface, the behavior of the free surface, or the boundary between the fluid and the surrounding air or other media, is of particular interest51. The shape of the free surface and how it deforms as the fluid flows downhill can provide important insights into the flow behavior15. The kinematics of flow on inclined surfaces involves studying how the flow velocity and depth vary along the inclined plane. The flow profiles can be influenced by factors, including gravity, surface roughness, and the viscosity of the fluid. The Reynolds number, which is a dimensionless quantity that characterizes the flow regime, can be used to understand the transition from laminar to turbulent flow on inclined surfaces. This transition affects the flow kinematics and the development of flow structures51. The shear stress exerted by the flow on the inclined surface and the resulting bed shear stress are important parameters that influence the kinematics of the flow. They can affect sediment transport, erosional processes, and the development of boundary layers. Flow separation occurs when the fluid detaches from the inclined surface, leading to distinct flow patterns. Reattachment refers to the subsequent rejoining of the separated flow with the surface. Understanding these phenomena is crucial for predicting the flow kinematics and associated forces. As the fluid moves down an inclined surface, it often experiences changes in velocity, which can result in acceleration or deceleration of the flow. Understanding the spatial and temporal variations in flow velocity is essential for analyzing the kinematics of the flow. The kinematics of flow on inclined surfaces also involves the study of energy dissipation processes, including the conversion of potential energy to kinetic energy and the associated losses due to friction and turbulence. Studying the kinematics of flow on inclined surfaces often involves experimental measurements, theoretical modeling, and numerical simulations51. Researchers and engineers use various techniques, such as flow visualization, particle image velocimetry (PIV), and CFD, to analyze the kinematic behavior of fluid flow on inclined surfaces and to gain insights into the associated transport and geomorphic processes. The mathematical description of flow kinematics on an inclined surface typically involves the characterization of the flow velocity, depth, and other flow-related parameters as a function of position and time. For steady or unsteady flow on an inclined surface, the following equations and concepts are commonly used to describe the flow kinematics. The velocity field of the flow on an inclined surface can be described using components in the direction parallel to the surface and perpendicular to the surface. For example, in Cartesian coordinates, the velocity components can be denoted as u(x, y, z) in the x-direction, v(x, y, z) in the y-direction, and w(x, y, z) in the z-direction. The continuity equation expresses the conservation of mass within the flow and relates the variations in flow velocity to changes in flow depth. In 1D form, the continuity equation for steady, uniform flow on an inclined surface can be expressed as:
where A is the cross-sectional area of flow, V is the average velocity of the flow, and Q is the flow discharge. The flow depth, which represents the vertical distance from the free surface to the bed of the channel, is an essential parameter in the kinematic description of flow51. For uniform flow on an inclined surface, the flow depth can be related to the flow velocity using specific energy concepts. Manning's equation is commonly used to relate flow velocity to flow depth and channel slope in open channel flow, including flow on inclined surfaces51. It is an empirical equation often used in open-channel hydraulics to estimate flow velocity using the flow depth, channel roughness, and slope. The momentum equations describe the conservation of momentum within the flow and account for forces acting on the flow, including gravity, pressure gradients, and viscous forces51. The momentum equations can be expressed using the Navier–Stokes equations for viscous flows or simplified forms of inviscid flows. For viscous flow on an inclined surface, boundary layer theory can be used to analyze the velocity profiles and the development of boundary layers near the surface. This provides insights into the distribution of flow velocity and shear stress close to the boundary51. The energy equations describe the conservation of energy within the flow and relate the flow velocity and depth to the energy state of the flow. In open channel flow, the energy equations can be expressed in terms of specific energy, relating it to flow depth and velocity. These mathematical equations and concepts provide a framework for the analysis of flow kinematics on inclined surfaces. The specific equations used will depend on the nature of the flow (e.g., steady or unsteady, uniform or non-uniform) and the assumptions made regarding flow behavior. In practice, engineers and researchers often apply these equations in conjunction with experimental data and numerical simulations to analyze and predict the kinematic behavior of flow on inclined surfaces.
Viscoplastic-viscoelastic models (bingham model, casson model, and power law)
The study of debris flow down a slope involves complex material behavior, which can be approximated using viscoplastic-viscoelastic models. Debris flows are rapid mass movements of a combination of water, sediment, and debris down a slope, and they exhibit both solid-like and fluid-like behavior51. A viscoplastic-viscoelastic model aims to capture several aspects of debris flow behavior. Debris flows often exhibit solid-like behavior under low strain rates, where the material behaves like a viscoplastic solid. This means that the material deforms and flows plastically under stress, exhibiting a yield stress beyond which it begins to flow. At higher strain rates, debris flows can display fluid-like behavior with viscoelastic properties. This means that the material exhibits a combination of viscous (fluid-like) and elastic (solid-like) responses to applied stress16. Viscoelasticity accounts for the time-dependent deformation and stress relaxation observed in the flow. To model this complex behavior, a viscoplastic-viscoelastic model for debris flow would likely involve a combination of constitutive equations to represent both the solid-like and fluid-like behavior of the material. One possible approach is to use a combination of a viscoplastic model, such as a Bingham or Herschel-Bulkley model, to capture the material's yield stress and plastic behavior, along with a viscoelastic model, such as a Maxwell or Kelvin-Voigt model, to capture the time-dependent deformation and stress relaxation51. Implementing such a model would involve determining the material parameters through laboratory testing and field observations, as well as solving the governing equations of motion for the debris flow, taking into account the complex interactions between the solid and fluid components of the flow. It is important to note that modeling debris flow behavior is a highly complex and multidisciplinary task, involving aspects of fluid mechanics, solid mechanics, and rheology, among others. Therefore, the specific details of the viscoplastic–viscoelastic model would depend on the particular characteristics and behavior of the debris flow being studied. When studying debris flow down a slope, various rheological models can be used to describe the flow behavior of the mixture of water, sediment, and debris51. It is important to understand the Bingham, Casson, and power law models, along with how they can be applied to debris flow. The Bingham model is a simple viscoplastic model that describes the behavior of materials that have a yield stress and exhibit viscous behavior once the yield stress is exceeded. In the context of debris flow, the Bingham model can be used to represent the behavior of the flow when it behaves like a solid, with no deformation occurring until a critical stress, known as the yield stress, is reached. Once the yield stress is exceeded, the material flows like a viscous fluid51. The Bingham model can be expressed mathematically using Eqs. (5)–(7). The Bingham model is characterized by a yield stress (τ_y), which represents the minimum stress required to initiate flow51. This is known as the yield criterion, which can be expressed as:
where τ is the total stress tensor. Viscous flow occurs when the yield stress is exceeded, with the material behaving like a Newtonian fluid with a dynamic viscosity (μ). The relationship between the shear stress (τ) and the shear rate (du/dy) is given by:
Combining these equations, the Bingham model can be summarized as follows:
In the context of debris flow down a slope, these equations can be applied to describe the behavior of the flow when it behaves like a solid (below the yield stress) and when it behaves like a viscous fluid (above the yield stress). It is important to note that in the case of debris flow, the Bingham model may need to be extended or combined with other models to more accurately capture the complex behavior of the flow, especially considering the multiphase nature of debris flow involving water, sediment, and debris2,5,9,51. Additionally, specific boundary conditions and rheological parameters need to be considered and may require calibration based on experimental and field data. The Casson model is another rheological model that accounts for the yield stress of a fluid, while also considering the square root of the shear rate in the relationship between shear stress and shear rate. It is useful for describing the behavior of non-Newtonian fluids with a yield stress, and it can be applied to debris flow to capture the transition from solid-like to fluid-like behavior7. In the context of debris flow down a slope, the Casson model can be used to capture this transition as the yield stress is exceeded16. The Casson model can be expressed mathematically using the following Eqs. (8) and (9). Similar to the Bingham model, the Casson model includes a yield stress (τy), which represents the minimum stress required to initiate flow. The yield criterion can be expressed as:
where τ is the total stress tensor and K is a parameter related to the plastic viscosity of the fluid. Viscous flow occurs once the yield stress is exceeded, with the material behaving like a Casson fluid. The relationship between the shear stress (τ) and the shear rate (du/dy) is given by51:
In the context of debris flow down a slope, these equations can be applied to describe the behavior of the flow when it behaves like a solid (below the yield stress) and when it behaves like a fluid (above the yield stress)51. It is important to note that the Casson model provides a more complex description of non-Newtonian fluids compared to the Bingham model, and it may capture more nuanced rheological behavior exhibited by debris flow. However, as with any rheological model, the specific parameters and boundary conditions for the Casson model need to be carefully considered and may require calibration based on experimental and field data to accurately represent the behavior of debris flow16. The power law model, also known as the Ostwald–de Waele model, describes a non-Newtonian fluid's behavior where the shear stress is proportional to the power of the shear rate. This model is commonly used to describe the behavior of fluids with shear-thinning or shear-thickening properties. In the context of debris flow, the power law model can be used to capture the non-Newtonian behavior of the flow, particularly if the flow exhibits shear-thinning or shear-thickening characteristics51. The power law model can be expressed mathematically using Eq. (10). The viscous flow relationship describes the relationship between shear stress (τ) and shear rate (du/dy) for a non-Newtonian fluid and is expressed as follows:
where τ is the shear stress; du/dy is the shear rate; K is the consistency index, which represents the fluid's resistance to flow; and n is the flow behavior index, which characterizes the degree of shear-thinning or shear-thickening behavior. For n < 1, the fluid exhibits shear-thinning behavior, and for n > 1, the fluid exhibits shear-thickening behavior 51. In the context of debris flow down a slope, these equations can be applied to describe the non-Newtonian behavior of the flow, taking into account the varying shear rates and stress conditions experienced during flow. It is important to note that the power law model provides a simplified but versatile representation of the rheological behavior of non-Newtonian fluids. However, when applying the power law model to debris flow, it is essential to consider the specific characteristics of the flow, such as the mixture of water, sediment, and debris, and the complex interactions between the different phases51. As with any rheological model, calibration and validation based on experimental and field data are crucial for accurately representing the behavior of debris flow. When applying these models to debris flow down a slope, it is important to recognize that debris flow is a complex, multiphase flow involving interactions between water, sediment, and debris5. Therefore, the choice of rheological model should be based on the specific characteristics of the debris flow being studied, as well as the available data and observations1. It is also worth noting that these models provide a simplified representation of the complex behavior of debris flow, and more sophisticated models, such as viscoelastic-viscoplastic models, may be necessary to capture the full range of behaviors observed in debris flows. Additionally, field and laboratory data are crucial for calibrating and validating any rheological model used to describe debris flow behavior37. The Navier–Stokes equations are a set of partial differential equations that describe the motion of fluid substances. When applied to debris flow down a slope, the Navier–Stokes equations can be used to model the conservation of momentum and mass for the generalized flow of the mixture of water, sediment, and debris51. The Navier–Stokes equations are typically written in vector form to describe the conservation of momentum and mass in three dimensions. The conservation of momentum for the generalized flow model of debris flow down a slope is governed by the Navier–Stokes equations, which can be written in vector form as follows:
where \(\frac{{D_{u} }}{{D_{t} }}\) represents the velocity vector of the debris flow; t is time; \(\rho\) is the density of the mixture; \(\nabla\) is the deviatoric stress tensor, which accounts for the shear stress within the flow; and \(\otimes\) denotes the dot product. The terms on the right-hand side of the equation represent, from left to right, the pressure gradient, the viscous effects (stress), and the gravitational force51. The conservation of mass is described by the continuity equation. The continuity equation represents the conservation of mass within the flow, stating that the rate of change of mass within a control volume is equal to the net flow of mass into or out of the control volume51. When modeling debris flows down a slope using the Navier–Stokes equations, it is important to consider the complex nature of the flow, including the interactions between water, sediment, and debris, as well as the influence of the slope geometry, boundary conditions, and other relevant factors. Additionally, the rheological behavior of the debris flow, such as its viscosity and yield stress, can be incorporated into the stress terms in the momentum equation to model the non-Newtonian behavior of the flow.
Theory of the model techniques
Extreme learning machines (ELMs)
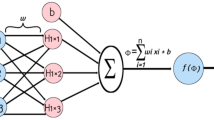
Extreme learning machines (ELMs), depicted in Fig. 2, are machine learning algorithms that belong to the family of neural networks. They were introduced by Guang-Bin Huang, Qin-Yu Zhu, and Chee-Kheong Siew in 2006. ELMs are known for their simple and efficient training process, particularly when compared to traditional neural networks, such as multi-layer perceptrons (MLPs). The key idea behind ELMs is to randomly initialize the input weights and analytically determine the output weights, rather than using iterative techniques like backpropagation. This approach allows ELMs to achieve fast training times, making them particularly suitable for large-scale learning problems52. ELMs have been applied to various tasks, including classification, regression, feature learning, and clustering. They have found use in fields such as pattern recognition, image and signal processing, and bioinformatics. Despite their advantages, it is worth noting that ELMs may not always outperform traditional neural networks, especially on complex tasks that require fine-tuning and iterative learning. Additionally, ELMs’ random weight initialization can lead to some variability in performance, which may require careful consideration when using the algorithm in practical applications53. The theoretical framework of ELMs is based on the concept of single-hidden-layer feedforward neural networks. There are several key components of the theoretical framework. Random hidden layer feature mapping: ELMs start by randomly initializing the input weights and the biases of the hidden neurons. These random weights are typically drawn from a uniform or Gaussian distribution54. The random feature mapping of the input data to the hidden layer means ELMs can avoid the iterative training process used in traditional neural networks. Analytical output weight calculation: After random feature mapping, ELMs analytically calculate the output weights by solving a system of linear equations. This step does not involve an iterative optimization process, which contributes to the computational efficiency of ELMs. Universal approximation theorem: The theoretical foundation of ELMs is grounded in the universal approximation theorem, which states that a single-hidden-layer feedforward neural network with a sufficiently large number of hidden neurons can approximate any continuous function to arbitrary accuracy55. ELMs leverage this theorem to achieve high learning capacity and generalization performance. Regularization and generalization: ELMs’ theoretical framework includes considerations for regularization techniques to prevent overfitting and improve generalization performance. Common regularization methods used in ELMs include Tikhonov regularization (also known as ridge regression) and pruning of irrelevant hidden neurons. Computational efficiency: ELMs’ theoretical framework emphasizes computational efficiency by reducing the training time and computational cost associated with traditional iterative learning algorithms. This efficiency is achieved through the combination of random feature mapping and analytical output weight calculations. Overall, the theoretical framework of ELMs is characterized by its unique approach to training single-hidden-layer feedforward neural networks, leveraging randomization and analytical solutions to achieve fast learning and good generalization performance. Basic notations are required to formulate the prediction output of ELMs. Each input feature vector is denoted as \(x_{i} \epsilon R^{d}\), where i = 1, 2, …, N number of features, with N being the number of samples or data points. The corresponding output for each input is denoted as \(y_{i}\). The model representation considers a single-hidden-layer feedforward neural network with L hidden nodes (neurons). The input–output relationship of the network can be represented as:
where \(w_{j}\) is the weight vector for the j-th hidden node, \(b_{j}\) is the bias term for the j-th hidden node, \(g\left( . \right)\) is the activation function applied element-wise, and \(\beta_{j}\) is the weight associated with the output of the j-th hidden node. To initialize training, weights (\(w_{j}\)) and biases (\(b_{j}\)) are randomly assigned for each hidden node and an activation function, \(g\left( . \right)\), is chosen. Then, the output of the hidden layer for all input samples is computed, thus:
To compute the output weight, the output weight vector (\(\beta\)) is solved using the least squares method:
where Y is the matrix of the target values. Once the output weights are computed, the model can predict new outputs using the learned parameters.
Least squares support vector machine (LSSVM)
LSSVM stands for least squares support vector machine, which is a supervised learning algorithm used for regression, classification, and time-series prediction tasks. LSSVM, the framework of which is illustrated in Fig. 3, is a modification of the traditional support vector machine (SVM) algorithm, and it was introduced by Suykens and Vandewalle in the late 1990s. The LSSVM is formulated as a set of linear equations, whereas the traditional SVM is formulated as a convex optimization problem53. This allows the LSSVM to be solved using linear algebra techniques, which can be computationally efficient, especially for large datasets. Similar to the SVM, the LSSVM can benefit from the kernel trick, which allows it to implicitly map input data into a higher-dimensional space, enabling the algorithm to handle non-linear relationships between input features and the target variable. The LSSVM incorporates a regularization parameter that helps to control the trade-off between fitting the training data and maintaining a smooth decision boundary or regression function55. Regularization is important for preventing overfitting. The LSSVM is often expressed in a dual formulation, similar to SVM. This formulation allows the algorithm to operate in a high-dimensional feature space without explicitly computing the transformed feature vectors. The LSSVM transforms the original optimization problem into a system of linear equations, which can be efficiently solved using matrix methods, such as the Moore–Penrose pseudoinverse or other numerical techniques. The LSSVM has been applied to various real-world problems, including regression tasks in finance, time-series prediction in engineering, and classification tasks in bioinformatics52. Its ability to handle non-linear relationships and its computational efficiency makes it a popular choice for many machine learning applications. Overall, the LSSVM is a versatile algorithm that combines the principles of support vector machines with the computational advantages of solving linear equations, making it a valuable tool for a wide range of supervised learning tasks. The theoretical framework of the LSSVM is grounded in the principles of statistical learning theory and convex optimization. It is useful to understand the key components of the theoretical framework of the LSSVM. Formulation as a linear system: The LSSVM is formulated as a set of linear equations, in contrast to the quadratic programming problem formulation of traditional SVM. This linear equation formulation allows LSSVM to be solved using linear algebra techniques, such as the computation of the Moore–Penrose pseudoinverse, which can lead to computational efficiency, especially for large datasets52. Kernel trick: Similar to the traditional SVM, the LSSVM can benefit from the kernel trick, which enables it to implicitly map the input data into a higher-dimensional feature space. This allows the LSSVM to capture non-linear relationships between input features and the target variable without explicitly transforming the input data. Regularization: The LSSVM incorporates a regularization parameter (often denoted as \(\gamma \)) that controls the trade-off between fitting the training data and controlling the complexity of the model55. Regularization is essential for preventing overfitting and improving the generalization performance of the model. Dual Formulation: The LSSVM is often expressed in a dual formulation, similar to the traditional SVM. The dual formulation allows the LSSVM to operate in a high-dimensional feature space without explicitly computing the transformed feature vectors, leading to computational advantages. Convex optimization: The theoretical framework of the LSSVM involves solving a convex optimization problem, which ensures that the training algorithm converges to the global minimum and guarantees the optimality of the solution. Statistical learning theory: The LSSVM is founded on the principles of statistical learning theory, which provides a theoretical framework for understanding the generalization performance of learning algorithms and the trade-offs between bias and variance in model fitting54. Overall, the theoretical framework of the LSSVM integrates principles from convex optimization, statistical learning theory, and kernel methods. By leveraging these principles, the LSSVM aims to achieve a balance between model complexity and data fitting while providing computational efficiency and the ability to capture non-linear patterns in the data. Basic notations are required to formulate the output for the LSSVM prediction. Each input feature vector is denoted as \(x_{i} \epsilon R^{d}\), where i = 1, 2, …, N number of features, with N being the number of training samples. The corresponding output for each input is denoted as \(y_{i} \epsilon \left\{ { - 1, 1} \right\}\) for binary classifications. The standard SVM aims to find a hyperplane characterized by a weight vector (w) and a bias term (b) that separates the data into two classes with a maximal margin. The optimization problem is given by:
where C is a regularization parameter that controls the trade-off between achieving a small margin and allowing some training points to be misclassified. The LSSVM replaces the hinge loss with a least squares loss, resulting in the following optimization problem:
Subject to the constraints:
where \(e_{i}\) represents the slack variables, allowing for soft-margin classification, \(\gamma\) is a regularization parameter controlling the trade-off between fitting the data well and keeping the model simple. The constraints ensure that each data point lies on or inside the margin. In the dual form, the Lagrangian for the LSSVM dual problem is:
where \(\alpha_{i}\) are the Lagrange multipliers, and \(K\left( {x_{i} x_{j} } \right)\) is the kernel function, capturing the inner product of the input vectors. Once the Lagrange multipliers (\(\alpha_{i}\)) are obtained, the decision function for a new input, x is given by:
where b is determined during training.
Adaptive neuro-fuzzy inference system (ANFIS)
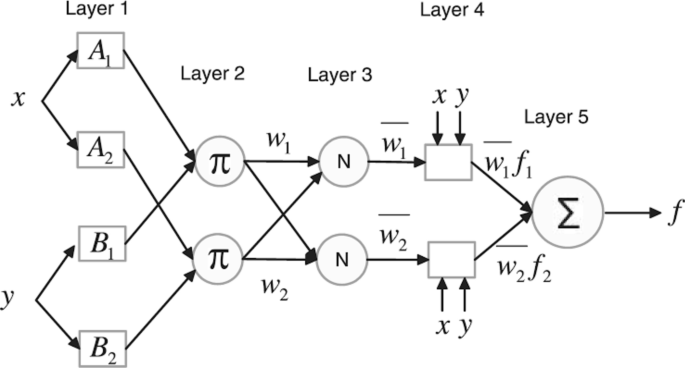
ANFIS stands for adaptive neuro-fuzzy inference system, the framework of which is shown in Fig. 4. It is a hybrid intelligent system that combines the adaptive capabilities of neural networks with the human-like reasoning of fuzzy logic. ANFIS models are particularly well-suited for tasks that involve complex, non-linear relationships and uncertain or imprecise information51. Fuzzy inference system (FIS): The ANFIS is based on the principles of fuzzy logic, which allows for the representation and processing of uncertain or vague information. Fuzzy logic uses linguistic variables, fuzzy sets, and fuzzy rules to capture human expert knowledge and reasoning. These fuzzy rules are often expressed in the form of ‘‘if–then’’ statements. Neural network learning: The ANFIS incorporates the learning capabilities of neural networks to adapt and optimize its parameters based on input–output training data. This learning process enables the ANFIS to model complex non-linear relationships between input variables and the output, similar to traditional neural network models52. Hybrid learning algorithm: The learning algorithm used in the ANFIS is a hybrid of gradient descent and least squares estimation. This hybrid approach allows the ANFIS to optimize its parameters by leveraging both the error backpropagation commonly used in neural networks and the least squares method used in statistical modeling. Membership function adaptation: The ANFIS includes a mechanism for adapting the membership functions and fuzzy rules based on the input data55. This adaptation process allows the ANFIS to capture the nuances and variations in the input–output relationships, leading to improved model accuracy. Rule-based reasoning: The ANFIS employs rule-based reasoning to combine the fuzzy inference system and neural network learning. This integration enables the ANFIS to benefit from the interpretability and knowledge representation capabilities of fuzzy logic while leveraging the learning and generalization capabilities of neural networks. Applications: The ANFIS has been applied to various real-world problems in areas such as control systems, pattern recognition, time-series prediction, and decision support51. Its ability to handle complex, non-linear relationships and uncertain data makes it a valuable tool for a wide range of applications. In summary, the theoretical framework of the ANFIS is rooted in the integration of fuzzy logic and neural network learning, allowing it to effectively model complex systems and uncertain information by combining the strengths of both paradigms. The theoretical framework of the ANFIS can be understood through several key components. Fuzzy logic: The ANFIS is built upon the principles of fuzzy logic, which provides a framework for representing and processing uncertain or vague information. Fuzzy logic allows for the modeling of linguistic variables, fuzzy sets, and fuzzy rules, which capture the imprecision and uncertainty present in many real-world problems52. FIS: The ANFIS incorporates the structure of a FIS, which consists of linguistic variables, fuzzy sets, membership functions, and fuzzy rules. These elements are used to represent expert knowledge and reasoning in a human-interpretable form. Neural network learning: The ANFIS integrates the learning capabilities of neural networks to adapt and optimize its parameters based on training data. The use of neural network learning allows the ANFIS to model complex, non-linear relationships between input variables and the output, similar to traditional neural network models. Hybrid learning algorithm: The ANFIS uses a hybrid learning algorithm that combines the principles of gradient descent and least squares estimation54. This hybrid approach enables the ANFIS to optimize its parameters by leveraging both the error backpropagation commonly used in neural networks and the least squares method used in statistical modeling. Membership function adaptation: The ANFIS includes mechanisms for adapting the membership functions and fuzzy rules based on the input data. This adaptation process allows the ANFIS to capture the nuances and variations in the input–output relationships, leading to improved model accuracy. Rule-based reasoning: The ANFIS employs rule-based reasoning to combine the FIS and neural network learning. This integration enables the ANFIS to benefit from the interpretability and knowledge representation capabilities of fuzzy logic while leveraging the learning and generalization capabilities of neural networks. Parameter optimization: The ANFIS aims to optimize its parameters, including the parameters of the membership functions and the rule consequent parameters, to minimize the difference between the actual and predicted outputs. Applications: The ANFIS has been applied to various real-world problems in areas such as control systems, pattern recognition, time-series prediction, and decision support. Its ability to handle complex, non-linear relationships and uncertain data makes it a valuable tool for a wide range of applications. In summary, the theoretical framework of the ANFIS is rooted in the integration of fuzzy logic and neural network learning, allowing it to effectively model complex systems and uncertain information by combining the strengths of both paradigms. In the formulation of the output for the ANFIS prediction of engineering problems, the following basic notations are used: Each input feature vector is denoted as xi = (xi1, xi2,…, xim), where i = 1, 2, …, N, with N being the number of training samples and m is the number of input variables. The corresponding output or target for each input is denoted as yi and the f(x) represents the overall ANFIS output for a given input x. Hence, the ANFIS output f(x) can be expressed as a weighted sum of the rule consequents:
where J is the number of fuzzy rules, wj is the weight associated with the j-th rule, and yi is the output of the j-th rule.
Eagle optimization (EO)
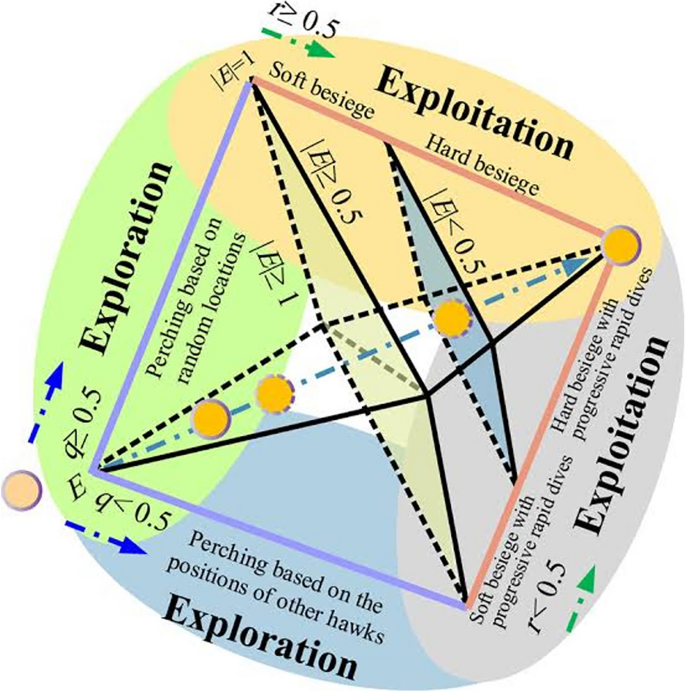
The eagle optimization (EO) algorithm (see framework in Fig. 5) is a metaheuristic optimization algorithm inspired by the hunting behavior of eagles. Like other metaheuristic algorithms, the EO algorithm is designed to solve optimization problems by iteratively improving solutions to find the best possible solution within a search space55. It is useful to have an understanding of the EO metaheuristic algorithm. Inspiration from eagle behavior: The EO algorithm is based on the hunting behavior of eagles in nature. Eagles are known for their keen vision and hunting strategies, which involve searching for prey and making decisions about the best approach to capture it. Population-based approach: Similar to other metaheuristic algorithms, the EO algorithm operates using a population of candidate solutions53. These candidate solutions are represented as individuals within the population, and the algorithm iteratively improves these solutions to find the optimal or near-optimal solution to the given optimization problem. Exploration and exploitation: The EO algorithm balances exploration of the search space (similar to the hunting behavior of eagles searching for prey) and exploitation of promising regions to refine and improve solutions. Solution representation: Candidate solutions in the EO algorithm are typically represented in a manner suitable for the specific optimization problem being solved. This representation could be binary, real-valued, or discrete, depending on the problem ___domain. Objective function evaluation: The fitness or objective function evaluation is an essential component of the EO algorithm. The objective function quantifies the quality of a solution within the search space, which is used to guide the search towards better solutions. Search and optimization process: The EO algorithm iteratively performs search and optimization by simulating the movement of eagles hunting for prey55. The algorithm uses various operators, such as crossover, mutation, and selection, to explore and exploit the search space. Parameter settings: Like most metaheuristic algorithms, the EO algorithm involves setting parameters that control its behavior, such as population size, mutation rate, crossover rate, and other algorithm-specific parameters. Convergence and termination: The algorithm continues to iterate until a termination criterion is met, such as reaching a maximum number of iterations, achieving a satisfactory solution, or other stopping criteria. Metaheuristic algorithms like the EO algorithm are widely used for solving complex optimization problems in various domains, including engineering, operations research, and machine learning. They provide a flexible and efficient approach for finding near-optimal solutions in situations where traditional exact optimization methods may be impractical due to the complexity of the problem or the computational cost of exact solutions.
Particle swarm optimization (PSO)
The framework of particle swarm optimization (PSO), as illustrated in Fig. 6, is a population-based metaheuristic optimization algorithm inspired by the social behavior of bird flocking or fish schooling. It was originally proposed by Kennedy and Eberhart in 199555. PSO is commonly used to solve optimization problems, including continuous and discrete optimization, as well as in training the parameters of machine learning models. Particle representation: In PSO, a potential solution to an optimization problem is represented as a ‘‘particle.’’ Each particle has a position and a velocity in the search space55. These positions and velocities are updated iteratively as the algorithm searches for the optimal solution. Fitness evaluation: The quality of each particle's position is evaluated using an objective function, which measures how well the particle's position performs in solving the optimization problem. This objective function guides the search for the optimal solution55. Swarm behavior: PSO is based on the concept of swarm intelligence, where the particles collaborate and communicate with each other to explore the search space. The particles adjust their positions and velocities based on their own experience and the experiences of their neighboring particles. Velocity and position update: The velocity and position of each particle are updated using formulas that take into account the particle's previous velocity, its distance to the best solution it has encountered (individual best), and the distance to the best solution found by any particle in the swarm (global best)55. Exploration and exploitation: PSO balances exploration and exploitation of the search space. Initially, particles explore the search space widely to discover promising regions. As the algorithm progresses, they exploit the best regions found so far to converge towards the optimal solution. Convergence and stopping criteria: PSO typically includes stopping criteria to halt the search when certain conditions are met, such as reaching a maximum number of iterations or achieving a satisfactory level of solution quality55. Applications in machine learning: PSO is used in machine learning for tasks such as feature selection, parameter tuning in neural networks and other models, as well as in training the weights of neural networks and other optimization problems related to machine learning. In summary, the theoretical framework of PSO is based on the concept of swarm intelligence and social behavior, where particles in a population collectively explore the search space to find optimal solutions. PSO has been widely applied in various fields, including machine learning, due to its ability to efficiently solve complex optimization problems. PSO is primarily an optimization algorithm rather than a learning algorithm in the traditional sense. However, it possesses certain learning capabilities that enable it to adapt and improve its search behavior as it iteratively explores the solution space53. Adaptation of particle velocity and position: PSO's learning capability is manifested in the way particles adapt their velocities and positions based on their own experience and the experiences of their neighboring particles53. Through this process, particles learn to navigate the solution space in search of better solutions. Social learning: PSO particles learn from the collective knowledge of the swarm. They are influenced by the best solutions found by other particles (global best) and the best solutions they have individually encountered (individual best)55. This social learning aspect allows for the sharing and propagation of good solutions within the swarm. Exploration and exploitation: PSO dynamically balances exploration and exploitation as the algorithm progresses. Initially, particles explore the solution space widely to discover promising regions. As the algorithm continues, they exploit the best regions found so far to converge towards the optimal solution. This adaptive behavior can be considered a form of learning from the search process. Convergence behavior: Through its iterative process, PSO exhibits convergence behavior, where the swarm gradually focuses its search around promising regions of the solution space. This convergence can be seen as a form of learning from the algorithm's experience, as it adjusts its behavior based on the information gathered during the search. While PSO does exhibit learning-like behaviors in terms of adaptation, social information sharing, and convergence, it is important to note that its learning capabilities are fundamentally different from those of supervised learning algorithms used in traditional machine learning. PSO's learning is focused on adapting the behavior of the swarm to efficiently explore and exploit the solution space in the context of optimization problems, rather than on generalizing patterns from data or making predictions.
Harris Hawks optimization (HHO)
The framework of Harris hawks optimization (HHO), as presented in Fig. 7, is a metaheuristic algorithm inspired by the hunting behavior of Harris hawks52. Metaheuristic algorithms are optimization algorithms that can be used to find solutions to difficult optimization problems, particularly in the field of machine learning52. In the context of machine learning, metaheuristic algorithms like HHO can be used for various tasks, such as feature selection, hyperparameter tuning, and even optimizing the structure of neural networks52. These algorithms are particularly useful when the search space is large and complex, where traditional optimization methods might struggle to find good solutions in a reasonable amount of time. When applying HHO or similar metaheuristic algorithms to machine learning problems, it is important to carefully define the optimization problem and the constraints, as well as to properly tune the algorithm's parameters to ensure good performance52. Overall, metaheuristic algorithms like HHO can be valuable tools in the machine learning practitioner's toolbox, particularly for challenging optimization tasks where traditional methods may not be effective. The learning capabilities of the HHO algorithm, as with other metaheuristic algorithms, are based on its ability to efficiently explore and exploit the search space to find near-optimal solutions to complex optimization problems52. It is useful to understand some of the key learning capabilities of HHO. Exploration and exploitation: HHO is designed to balance exploration and exploitation of the search space. During the early stages of the optimization process, HHO explores the search space to discover diverse solutions. As the process continues, it shifts towards exploiting the most promising regions of the search space to refine and improve the solutions52. Adaptive search: HHO is capable of adapting its search behavior based on the characteristics of the problem being optimized. This adaptability allows it to efficiently navigate different types of search spaces, including high-dimensional, non-convex, and multimodal spaces. Global and local search: HHO is able to perform both global and local searches. It can efficiently explore the entire search space to find the global optimum, while also focusing on local regions to fine-tune solutions. Convergence and diversification: HHO aims to converge to high-quality solutions while maintaining diversity in the population of candidate solutions. This balance helps prevent premature convergence to suboptimal solutions and encourages continued exploration of the search space52. Robustness: HHO exhibits robustness in handling noisy or uncertain objective functions. It is able to adapt to noisy environments and continue to improve solutions in the presence of uncertainty. Scalability: HHO can scale to handle large-scale optimization problems, making it suitable for real-world applications with complex, high-dimensional search spaces52. Overall, the learning capabilities of HHO make it well-suited for tackling challenging optimization problems in various domains, including machine learning, engineering, and operations research. When applied to machine learning tasks, HHO can be used for feature selection, hyperparameter optimization, model tuning, and other optimization challenges encountered in the development and deployment of machine learning systems.
HHO framework52.
Genetic algorithms (GA)
Genetic algorithms (GAs), the framework of which is presented in Fig. 8, are a class of metaheuristic algorithms that are inspired by the process of natural selection and genetic evolution54. They are used to find approximate solutions to optimization and search problems. It is important to understand the key aspects and capabilities of these algorithms. Representation of solutions: In GAs, potential solutions to the optimization problem are represented as individuals in a population54. These individuals are typically encoded as strings of symbols, such as binary strings, and are often referred to as chromosomes. Selection: GAs use a selection process to choose individuals from the population for reproduction, typically based on their fitness (i.e., how well they solve the given problem). This process is analogous to the principle of ‘‘survival of the fittest’’ in natural selection54. Crossover: During reproduction, GAs perform crossover or recombination, where pairs of selected individuals exchange genetic information to create new offspring. This is often implemented by swapping or mixing parts of the chromosomes of the selected individuals. Mutation: GAs include a mutation step, which introduces random changes in the genetic information of the offspring54. Mutation helps to maintain genetic diversity in the population and avoid premature convergence to suboptimal solutions. Fitness evaluation: The fitness of individuals in the population is evaluated based on a predefined objective or fitness function. This function quantifies how well a particular solution addresses the optimization problem. Population dynamics: GAs maintain a population of solutions over multiple generations. Through the processes of selection, crossover, and mutation, the population evolves over time, with the hope that better solutions emerge in later generations54. Convergence: GAs aim to converge toward better solutions over successive generations55. They are designed to balance the exploration of the search space with the exploitation of promising regions to find high-quality solutions. Application in machine learning: GAs have been applied in various areas of machine learning, including feature selection, hyperparameter optimization, neural network architecture search, and data preprocessing. They can be particularly useful in problems where the search space is large and complex55. GAs are known for their versatility and have been successfully applied to a wide range of optimization problems in different domains54. When appropriately applied, they can be effective in finding near-optimal solutions to challenging optimization problems. The learning capabilities of GAs stem from their ability to efficiently explore and exploit the search space to find near-optimal solutions to complex optimization problems. It is important to understand the key aspects and capabilities of these algorithms. Exploration and exploitation: GAs are designed to balance exploration and exploitation of the search space. During the early stages of the optimization process, GAs explore the search space to discover diverse solutions54. As the process progresses, they shift towards exploiting the most promising regions of the search space to refine and improve the solutions. Adaptation to problem characteristics: GAs exhibit adaptability, allowing them to efficiently navigate different types of search spaces, including high-dimensional, non-convex, and multimodal spaces54. This adaptability enables GAs to effectively address a wide variety of optimization problems. Global and local search: GAs are capable of performing both global and local searches. They can efficiently explore the entire search space to find the global optimum, while also focusing on local regions to fine-tune solutions. Convergence and diversification: GAs aim to converge to high-quality solutions while maintaining diversity in the population of candidate solutions54. This balance helps prevent premature convergence to suboptimal solutions and encourages continued exploration of the search space. Robustness: GAs are robust in handling noisy or uncertain objective functions. They are able to adapt to noisy environments and continue to improve solutions in the presence of uncertainty. Scalability: GAs can scale to handle large-scale optimization problems, making them suitable for real-world applications with complex, high-dimensional search spaces55. Parallelization: GAs can be parallelized to explore the search space more efficiently, especially when dealing with computationally intensive problems. This parallelization capability can lead to improved learning and convergence speed. Versatility: GAs are versatile and can be applied to a wide range of optimization problems, including those encountered in machine learning, engineering, finance, and other domains52. When applied to machine learning tasks, GAs can be used for feature selection, hyperparameter optimization, model tuning, and other optimization challenges encountered in the development and deployment of machine learning systems. Overall, the learning capabilities of GAs make them well-suited for tackling challenging optimization problems in various domains, and they have proven to be effective tools for finding high-quality solutions in diverse applications.
GA framework54.
Performance evaluation indices of models
The performance evaluation of a machine learning model for predicting the slope FOS in debris flow is a crucial step in assessing the model's accuracy and reliability56. There are some key steps and considerations for evaluating the performance of machine learning models to be considered. Data splitting: Dividing your dataset into training and testing sets. A common split is to use a majority of the data for training (e.g., 80% or 70%) and the rest for testing (e.g., 20% or 30%). Model training: Train your machine learning model using the training dataset. In this case, you would use features related to the debris flow slope FOS as input variables and the actual FOS values as the target variable. Model prediction: Use the trained model to make predictions on the testing dataset56. The model will provide predicted values for the slope FOS based on the input features. Performance metrics: Evaluate the model’s performance using appropriate metrics for regression tasks. In the present research work, a multitude of metrics have been applied, including mean absolute error (MAE), mean squared error (MSE), root mean squared error (RMSE), R-squared (R2), weighted mean absolute percentage error (WMAPE), not significant (NS), variance accounted for (VAF), prediction interval (PI), reparameterized slashed Rayleigh (RSR), normalized mean bias error (NMBE), robust partial discriminant analysis (RPDa), mean bias error (NBE), linear matrix inequality (LMI), confidence level within 95% (U95), standard error (t-sta), and genuine progress indicator (GPI). The mathematical expressions for the utilized metrics in this performance evaluation study can be found in statistical texts56. Visual inspection: Create visualizations such as scatter plots comparing predicted values against actual values. This can help identify patterns, trends, or potential outliers. Cross-validation: Perform k-fold cross-validation to assess the model's robustness and overfitting issues. This involves splitting the dataset into k subsets and training the model k times, each time using a different subset as the test set56. Hyperparameter tuning: Fine-tune the model's hyperparameters to optimize its performance. This can involve adjusting parameters such as the learning rate, tree depth, or regularization. Comparisons: If applicable, compare the performance of your machine learning model with baseline models or other algorithms to ensure that it provides added value56. Interpretability: Depending on the complexity of your model, consider assessing its interpretability. Some models, like decision trees, offer easy interpretability, while others, like ensemble methods, may be more complex. By following these steps and metrics, you can comprehensively evaluate the performance of your machine learning model for predicting the debris flow slope FOS. The overall research framework is presented in Fig. 9.
Presentation and analysis of results
Understanding the influence of various factors on the debris flow slope stability FOS involves conducting a comprehensive analysis. Several soil parameters have been studied in this work. Soil unit weight (SUW): Higher SUW generally increases stability, as it contributes to a higher resisting force. However, excessively high SUW may lead to increased loading and could affect stability adversely. Cohesion: A measure of the soil's internal strength; higher cohesion increases stability by providing additional resistance to shearing forces. However, debris flow in some cases may be cohesionless, relying more on frictional resistance. Frictional angle: An increase in the frictional angle between soil particles contributes to higher stability by increasing the resistance to sliding. This is particularly important for understanding the shearing behavior of the soil. Slope angle: As the slope angle increases, the gravitational force component parallel to the slope also increases. Steeper slopes generally reduce stability due to higher driving forces. There is a critical angle beyond which slope failure is more likely. Slope height: Taller slopes may experience higher gravitational forces, potentially reducing stability. The relationship is complex, as other factors like cohesion and frictional angle also come into play. The geometry of the slope can influence how forces are distributed. Pore pressure: Elevated pore pressure within the slope can reduce effective stress, decreasing the soil's shear strength and stability. This is particularly relevant in saturated or partially saturated conditions. To quantitatively assess the influence of these factors, a slope stability analysis using geotechnical engineering principles and methods can be conducted. Numerical modeling or analytical methods, such as the Bishop or Janbu methods, can help estimate the FOS considering these factors. The relationship between these parameters and the FOS may not always be linear, and interactions between different factors should be considered. Empirical relationships derived from field studies and laboratory testing on similar soils can also be valuable for understanding the specific behavior of the debris flow in question. It is essential to note that site-specific conditions, geological characteristics, and the nature of the debris flow material can significantly impact the stability analysis. A thorough geotechnical investigation, including field measurements and laboratory testing, is crucial for accurate slope stability assessments. Figure 10 represents the internal consistency between the output and the studied parameters affecting debris flow down a slope. It can be shown that the consistency between the pore water pressure and the FOS is more concentrated than distributed, which agrees with the conventional principle that states the effect of pore pressure on soil structure within its flow zone. The consistency is more distributed with the shear parameters (cohesion and friction) and slope geometry (slope angle and height). Figures 11 (training set) and 12 (test set) show the graphs between actual and predicted values for the training and testing dataset, where ELM-EO, ELM-HHO, LSSVM-PSO, ANFIS-PSO, and ANFIS-GA have been applied to predict the behavior of FOS considering the influence of the soil parameters and slope geometry. It can be shown that the PSO- and EO-trained predictions produced the most significant outliers from the line of best fit, as illustrated in Fig. 11a,c,d, while the relationship between the outliers and the line of best fit is more consistent in Fig. 11b,e. These show the results for the training set. In the test/validation set illustrated in Fig. 12, the trend is somewhat different because the data cluster is more concentrated at the bottom of the model’s line of best fit. However, the same trend of the outliers’ distribution in Fig. 11 is repeated in Fig. 12. From the overall performance, as presented in Tables 3 and 4, the PSO-trained ANFIS model produced an R2 of 0.8775 in the training set, demonstrating a decisive position consistent with the other indices of performance. In the testing/validation set, it achieved an R2 of 0.8614, outperforming other techniques. This is because of the ability of the ANFIS-PSO, with its multiple layer configuration, to overcome complex data analysis problems, aligning with the outcomes of previous research exercises52,53,54,55. The superior performance of this technique in the prediction of the debris flow slope stability FOS is that the combination of AFNIS and PSO offers several advantages over other machine learning techniques in certain scenarios. ANFIS inherently captures non-linear relationships through the fuzzy rule base53. When combined with PSO for parameter optimization, it enhances the model's flexibility in capturing complex and non-linear patterns in the data. This is particularly beneficial when dealing with datasets characterized by intricate relationships55. ANFIS provides transparent and interpretable models due to its fuzzy rule base. The linguistic rules in ANFIS are easily understandable, making it suitable for applications where interpretability is crucial, such as in decision support systems or domains where human experts need to comprehend the model's reasoning. ANFIS-PSO is adaptive and capable of self-learning55. The combination allows the model to adjust its parameters and rule base to changing patterns in the data. PSO helps optimize the parameters effectively, while the adaptability of ANFIS enables it to continuously refine its knowledge base as new data becomes available55. PSO is a global optimization algorithm that explores the entire solution space efficiently. This global search capability is beneficial when dealing with complex, multi-dimensional parameter spaces, as it helps the system avoid getting stuck in local optima55. This is particularly advantageous in applications where finding the optimal solution is crucial. Traditional neural networks, especially deep learning models, are often sensitive to the choice of initial parameters55. ANFIS-PSO, with its global optimization approach, is generally less sensitive to initialization, making it easier to set up and train compared to certain other machine learning techniques. ANFIS combines symbolic reasoning through fuzzy rules with numeric optimization through PSO. This integration allows for a more robust representation of knowledge in the model, capturing both explicit rules and data-driven patterns. This combination is especially powerful in applications where a hybrid approach is advantageous. ANFIS-PSO often involves fewer hyperparameters compared to some complex machine learning models. The simplicity in parameter tuning can be advantageous in scenarios where ease of implementation and reduced computational cost are priorities. It is important to conclude that the choice of the most suitable machine learning technique depends on the specific characteristics of the problem at hand, the nature of the data, and the goals of the application. While ANFIS-PSO offers advantages in certain contexts, it may not be universally superior and should be carefully considered based on the specific requirements of the task. It is also important to note that previous studies on the FOS of slopes suffering the effects of debris flow and other geophysical flows27,28,29,30,33,35,36,37,38,39,41,42,44,45,47,48 have not taken the effect of the pore water pressure seriously, neglecting the behavior of the soil water retention characteristics in their exercises. However, in this work, the pore water pressure has been studied as an important factor in the prediction of the debris flow slope FOS.
Conclusions
In this work, an intelligent numerical model of debris flow susceptibility using slope stability failure machine learning FOS prediction with LSSVR, ANFIS, and ELM metaheuristic techniques trained with EO, PSO, HHO, and genetic algorithms has been carried out. The selected input variables were soil unit weight, cohesion, frictional angle, slope angle, slope height, and the pore water pressure of the studied debris flow slope, while the FOS was the target or output. From this study, the following conclusions can be drawn:
-
The soil parameters and slope geometry have been studied, with reflective field data collected, sorted, and used to predict the behavior of the debris flow susceptibility and slope stability failure FOS, aiming for cost-effecitve and time-saving debris flow design and construction.
-
Contributions from SUW, cohesion, friction angle, slope angle, slope height, and pore pressure were considered.
-
The metaheuristic algorithm-trained machine learning techniques showed remarkable performance, exceeding 80%.
-
The ANFIS-PSO combination produced the best model performance, exceeding 85%, and proved decisive in the prediction of the debris flow susceptibility and slope stability failure FOS.
Data availability
The supporting data for this research project is available from the corresponding author on reasonable request.
References
Anderson, S. A. & Sitar, N. Analysis of rainfall-induced debris flows. J. Geotech. Eng. 121(7), 544–552. https://doi.org/10.1061/(asce)0733-9410(1995)121:7(544) (1995).
Kim, H., Lee, S. W., Yune, C.-Y. & Kim, G. Volume estimation of small scale debris flows based on observations of topographic changes using airborne LiDAR DEMs. J. Mountain Sci. 11(3), 578–591. https://doi.org/10.1007/s11629-013-2829-8 (2014).
Wang, X., Morgenstern, N. R. & Chan, D. H. A model for geotechnical analysis of flow slides and debris flows. Can. Geotech. J. 47(12), 1401–1414. https://doi.org/10.1139/t10-039 (2010).
Jakob, M. (n.d.). Debris-flow hazard analysis. Springer Praxis Books, 411–443. https://doi.org/10.1007/3-540-27129-5_17
Luna, B. Q. et al. Methods for debris flow hazard and risk assessment. Adv. Nat. Technol. Hazards Res. https://doi.org/10.1007/978-94-007-6769-0_5 (2013).
Ciurleo, M., Mandaglio, M. C., Moraci, N. & Pitasi, A. A method to evaluate debris flow triggering and propagation by numerical analyses. Geotech. Res. Land Protect. Dev. https://doi.org/10.1007/978-3-030-21359-6_4 (2019).
Zhang, N., Matsushima, T. & Peng, N. Numerical investigation of post-seismic debris flows in the epicentral area of the Wenchuan earthquake. Bull. Eng. Geol. Environ. https://doi.org/10.1007/s10064-018-1359-6 (2018).
Hong, M., Jeong, S. & Kim, J. A combined method for modeling the triggering and propagation of debris flows. Landslides https://doi.org/10.1007/s10346-019-01294-5 (2019).
Liu, W., Yang, Z. & He, S. Modeling the landslide-generated debris flow from formation to propagation and run-out by considering the effect of vegetation. Landslides https://doi.org/10.1007/s10346-020-01478-4 (2020).
Rendina, I., Viccione, G. & Cascini, L. Kinematics of flow mass movements on inclined surfaces. Theor. Comput. Fluid Dynam. https://doi.org/10.1007/s00162-019-00486-y (2019).
Kwan, J. S. H., Sze, E. H. Y. & Lam, C. Finite element analysis for rockfall and debris flow mitigation works. Cana. Geotech. J. https://doi.org/10.1139/cgj-2017-0628 (2018).
Li, Y. et al. Numerical investigation of the flow characteristics of Bingham fluid on a slope with corrected smooth particle hydrodynamics. Front. Environ. Sci. 10, 1060703. https://doi.org/10.3389/fenvs.2022.1060703 (2022).
Moreno, E., Dialami, N. & Cervera, M. Modeling of spillage and debris floods as Newtonian and viscoplastic Bingham flows with free surface with mixed stabilized finite elements. J. Non-Newtonian Fluid Mech. https://doi.org/10.1016/j.jnnfm.2021.104512 (2021).
Qingyun, Z., Mingxin, Z. & Dan, H. Numerical simulation of impact and entrainment behaviors of debris flow by using SPH–DEM–FEM coupling method. Open Geosci. 14(1), 1020–1047. https://doi.org/10.1515/geo-2022-0407 (2022).
Whipple, K. X. Open-channel flow of bingham fluids: Applications in debris-flow research. J. Geol. 105(2), 243–262. https://doi.org/10.1086/515916 (1997).
Averweg, S., Schwarz, A., Nisters, C. & Schröder, J. A least-squares finite element formulation to solve incompressible non-Newtonian fluid flow. Proc. Appl. Math. Mech. 20, e202000169. https://doi.org/10.1002/pamm.202000169 (2021).
Ming-de, S. Finite element analysis of non-Newtonian fluid flow in 2-d branching channel. Appl. Math. Mech. 7(10), 987–994. https://doi.org/10.1007/bf01907601 (1986).
Böhme, G. & Rubart, L. Non-Newtonian flow analysis by finite elements. Fluid Dynam. Res. 5(3), 147–158. https://doi.org/10.1016/0169-5983(89)90018-x (1989).
Sváček, P. On approximation of non-Newtonian fluid flow by the finite element method. J. Comput. Appl. Math. 218(1), 167–174. https://doi.org/10.1016/j.cam.2007.04.040 (2008).
Reddy, M. P. & Reddy, J. N. Finite-element analysis of flows of non-Newtonian fluids in three-dimensional enclosures. Int. J. Non-Linear Mech. 27(1), 9–26. https://doi.org/10.1016/0020-7462(92)90019-4 (1992).
Quan Luna, B. et al. The application of numerical debris flow modelling for the generation of physical vulnerability curves. Nat. Hazards Earth Syst. Sci. 11(7), 2047–2060. https://doi.org/10.5194/nhess-11-2047-2011 (2011).
Hemeda, S. Geotechnical modelling and subsurface analysis of complex underground structures using PLAXIS 3D. Geo-Eng. 13, 9. https://doi.org/10.1186/s40703-022-00174-7 (2022).
Melo, R., van Asch, T. & Zêzere, J. L. Debris flow run-out simulation and analysis using a dynamic model. Nat. Hazards Earth Syst. Sci. 18, 555–570. https://doi.org/10.5194/nhess-18-555-2018 (2018).
Woldesenbet, T. T., Arefaine, H. B. & Yesuf, M. B. Numerical stability analysis and geotechnical investigation of landslide prone area (the case of Gechi district, Western Ethiopia). Environ. Challenges 13, 100762. https://doi.org/10.1016/j.envc.2023.100762 (2023).
Onyelowe, K. C., Sujatha, E. R., Aneke, F. I. & Ebid, A. M. Solving geophysical flow problems in Luxembourg: SPH constitutive review. Cogent Eng. https://doi.org/10.1080/23311916.2022.2122158 (2022).
Onyelowe, K. C. et al. Innovative overview of SWRC application in modeling geotechnical engineering problems. Designs 2022(6), 69. https://doi.org/10.3390/designs6050069 (2022).
Moreno, E., Dialami, N. & Cervera, M. Modeling of spillage and debris floods as Newtonian and viscoplastic bingham flows with free surface with mixed stabilized finite elements. J. Non-Newtonian Fluid Mech. 290, 104512 (2021).
Quan Luna, B. et al. The application of numerical debris flow modelling for the generation of physical vulnerability curves. Nat. Hazards Earth Syst. Sci. 11(7), 2047–2060 (2011).
Nguyen, L. C., Van Tien, P. & Do, T.-N. Deep-seated rainfall-induced landslides on a new expressway: A case study in Vietnam. Landslides 17(2), 395–407 (2020).
Bašić, M., Blagojević, B., Peng, C. & Bašić, J. Lagrangian differencing dynamics for time-independent non-Newtonian materials. Materials 14(20), 6210 (2021).
Ming-de, Su. Finite element analysis of non-newtonian fluid flow in 2-d branching channel. Appl. Math. Mech. 7(10), 987–994 (1986).
Lee, S., An, H., Kim, M. & Lim, H. Analysis of debris flow simulation parameters with entrainment effect: A case study in the Mt. Umyeon. J. Korea Water Resour. Assoc. 53(9), 637–646 (2020).
Kwan, J. S. H., Sze, E. H. Y. & Lam, C. Finite element analysis for rockfall and debris flow mitigation works. Can. Geotech. J. 56(9), 1225–1250 (2019).
Martinez, C., Miralles-Wilhelm, F. & Garcia-Martinez, R. Verification of a 2D finite element debris flow model using bingham and cross rheological formulations. WIT Trans. Eng. Sci. 60, 61–69 (2008).
Martinez, Cora E. 2009. “Eulerian-Lagrangian Two Phase Debris Flow Model.”
Nguyen, Lan Chau, Tuan-Nghia Do, and Quoc Dinh Nguyen. 2023. “Characteristics and Remedy Solutions for a New Mong Sen Deep-Seated Landslide, Sapa Town, Vietnam.” In Progress in Landslide Research and Technology, Volume 1 Issue 2, 2022, Springer, 403–13.
Negishi, H. et al. Bingham fluid simulations using a physically consistent particle method. J. Fluid Sci. Technol 18(4), JFST0035–JFST0035 (2023).
Kondo, M., Fujiwara, T., Masaie, I. & Matsumoto, J. A physically consistent particle method for high-viscous free-surface flow calculation. Comput. Part. Mech. https://doi.org/10.1007/s40571-021-00408-y (2021).
Sváček, P. On approximation of non-newtonian fluid flow by the finite element method. J. Comput. Appl. Math. 218(1), 167–174 (2008).
Licata, I. & Benedetto, E. Navier-Stokes equation and computational scheme for non-newtonian debris flow. J. Comput. Eng. 2014, 1–5. https://doi.org/10.1155/2014/201958 (2014).
Qingyun, Z., Mingxin, Z. & Dan, H. Numerical simulation of impact and entrainment behaviors of debris flow by using SPH–DEM–FEM coupling method. Open Geosci. 14(1), 1020–1047 (2022).
Bokharaeian, M., Naderi, R. & Csámer, Á. Numerical experimental comparison of mudflow by smoothed particle hydrodynamics (SPH). Int. Rev. Appl. Sci. Eng. 13(1), 22–28 (2021).
Böhme, G. & Rubart, L. Non-Newtonian flow analysis by finite elements. Fluid Dynam. Res. 5(3), 147 (1989).
Rendina, I., Viccione, G. & Cascini, L. Kinematics of flow mass movements on inclined surfaces. Theor. Comput. Fluid Dyn. 33, 107–123 (2019).
Melo, R., van Asch, T. & Zêzere, J. L. Debris flow run-out simulation and analysis using a dynamic model. Nat. Hazards Earth Syst. Sci. 18(2), 555–570 (2018).
Reddy, M. P. & Reddy, J. N. Finite-element analysis of flows of non-Newtonian fluids in three-dimensional enclosures. Int. J. Non-linear Mech. 27(1), 9–26 (1992).
Woldesenbet, T. T., Arefaine, H. B. & Yesuf, M. B. Numerical stability analysis and geotechnical investigation of landslide prone area (the Case of Gechi District, Western Ethiopia). Environ. Challenges 13, 100762 (2023).
Hemeda, S. Geotechnical modelling and subsurface analysis of complex underground structures using PLAXIS 3D. Int. J. Geo-Eng. 13(1), 9 (2022).
Whipple, K. X. Open-channel flow of Bingham fluids: Applications in debris-flow research. J. Geol. 105(2), 243–262 (1997).
Averweg, S., Schwarz, A., Nisters, C. & Schröder, J. A least-squares finite element formulation to solve incompressible non-Newtonian fluid flow. PAMM 20(1), e202000169 (2021).
Khochtali, H. et al. Comparison of coupled Eulerian-Lagrangian and coupled smoothed particle hydrodynamics-Lagrangian in fluid-structure interaction applied to metal cutting. Arab. J. Sci. Eng. 46, 11923–11936. https://doi.org/10.1007/s13369-021-05737-x (2021).
Heidari, A. A. et al. Harris hawks optimization: Algorithm and applications. Fut. Gener. Comput. Syst. 97, 849–872. https://doi.org/10.1016/j.future.2019.02.028 (2019).
Sun, Z., Tao, L., Wang, X. & Zhou, Z. Localization algorithm in wireless sensor networks based on multiobjective particle swarm optimization. Int. J. Distrib. Sensor Netw. https://doi.org/10.1155/2015/716291 (2015).
Lee, C. K. M. et al. Design of a genetic algorithm for bi-objective flow shop scheduling problems with re-entrant jobs. Int. J. Adv. Manuf. Technol. 56, 1105–1113. https://doi.org/10.1007/s00170-011-3251-4 (2011).
Dubey, A. K., Kumar, A. & Agrawal, R. An efficient ACO-PSO-based framework for data classification and preprocessing in big data. Evol. Intel. 14, 909–922. https://doi.org/10.1007/s12065-020-00477-7 (2021).
Taylor, S. (2015). Regression analysis; the estimation of relationships between a dependent variable and one or more independent variables, CFI Education Inc.
Acknowledgements
The authors extend their appreciation to the Researchers Supporting Project Number (RSPD2024R701), King Saud University, Riyadh, Saudi Arabia.
Funding
This research is funded by the Researchers Supporting Project Number (RSPD2024R701), King Saud University, Riyadh, Saudi Arabia.
Author information
Authors and Affiliations
Contributions
KCO conceptualized the research work, KCO, AABM, FA, AUR and SH wrote the manuscript, and KCO prepared the figures. All the authors reviewed the manuscript. The consent of the authors is given for the publication of this research paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Onyelowe, K.C., Moghal, A.A.B., Ahmad, F. et al. Numerical model of debris flow susceptibility using slope stability failure machine learning prediction with metaheuristic techniques trained with different algorithms. Sci Rep 14, 19562 (2024). https://doi.org/10.1038/s41598-024-70634-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-70634-w
Keywords
This article is cited by
-
3d stability modelling of Tutankhamen,s Tomb (Kv62) using Plaxis 3d with jointed rock model
npj Heritage Science (2025)
-
Developing data driven framework to model earthquake induced liquefaction potential of granular terrain by machine learning classification models
Scientific Reports (2025)
-
Random forest-based prediction of shallow slope stability considering spatiotemporal variations in unsaturated soil moisture
Scientific Reports (2025)
-
Using monitoring and simulation to analyze the failure characteristics of multizone landslides controlled by faults: a case study
Scientific Reports (2025)