Introduction

The kitchen is an important hidden danger affecting the indoor environmental quality because it is the main source of indoor pollutant emissions. The exhaust efficiency of the kitchen will seriously affect the quality of indoor air1,2,3. With the development of residential construction, the structure and smoke exhaust mode of kitchens have changed significantly. People’s requirements for the environmental quality of kitchens are also improving4. The exhaust method of the kitchen was changed from original direct emission to chimney emission, which was later replaced by an exhaust fan. Currently, the main method of kitchen exhaust is to suck smoke into the centralized exhaust flue through the range hood and then discharge it. To expel all harmful oil fumes and reduce environmental pollution and energy consumption as much as possible5, installing vertical public smoke exhaust pipes to collect oil fumes and discharge them centrally has become the choice of most residents6. installing vertical public smoke exhaust pipes to collect oil fumes and discharge them centrally has become the choice of most residents7,8. It was discovered that the existing communal flue exhaust system affects the air quality of the entire residence. Therefore, it is necessary to develop a communal flue-exhaust system.

According to the provisions of the “Code for Design of Town Gas”, the kitchen must be equipped with mechanical equipment such as range hoods for ventilation. The exhaust flow of the kitchen range hood must be at least 300 m/h, and the effective air inlet cross-sectional area can be equivalent to an air inlet velocity of 4–7 m/s9. Nowadays, many buildings apply fluid dynamics to the exhaust flow calculation of domestic range hoods and perform parametric modeling to easily modify parameters10. CFD and Fluent software are often used to simulate and verify turbulence models11. For instance, Li A. et al.12 used computational fluid dynamics to analyze the static pressure and velocity distribution of the central exhaust system. Zheng Q. et al.13 applied CFD technology to simulate the velocity and pressure field distribution of exhaust pipes with different cross-sectional sizes. However, the fluid network modeling methods used in existing studies are relatively simple, usually setting the resistance coefficients of equipment components to fixed values and ignoring the complexity of the effects of equipment characteristics on piping, which limits the accuracy and versatility of the models. Averkova O.A.’s team14 created a discrete mathematical model of three-dimensional stationary separated airflow, specifically for rectangular exhaust pipe inlets, to optimize the performance of a local exhaust ventilation system. By accurately simulating the airflow separation, the model helps to reduce the system resistance and improve the exhaust efficiency. Angui Li’s team15 used the OED and SCD methods to optimize the design of a low-resistance guide vane for the resistance of duct elbows in HVAC systems, and verified the effectiveness of the improved dual-guide vane elbows in reducing the resistance through experiments and numerical simulations. Ziganshin A.M.’s team16, on the other hand, investigated the effect of adding extensions to the local exhaust hood on the local drag coefficient using the discrete eddy current method and computational fluid dynamics, providing important data for exhaust system design. These studies demonstrate the potential for optimization of exhaust systems through mathematical modeling and CFD simulations, while also pointing out the limitations of existing research methods and directions for future improvements.

The purpose of this study is to provide an in-depth analysis of the performance of key components in a public flue exhaust system and to develop a C#-based parametric simulation system software to optimize the design and improve the overall performance of the system. Given that most of the existing studies focus on the macroscopic analysis of the system and lack in-depth discussion on the specific effects of components such as branch pipes, check valves, and tee pipes, our work fills this gap. Through a combination of CFD simulation and experimental testing, we not only identify the key parameters affecting the integrated resistance coefficients of these components, but also improve the accuracy and adaptability of the model through parametric design. Through this study, we expect to provide more accurate and efficient solutions for the design and evaluation of public flue exhaust systems, which in turn will contribute to the improvement of indoor air quality and living environment in urban high-rise residential buildings.

Methods

Centralized exhaust flue model

Simplification of the physical model

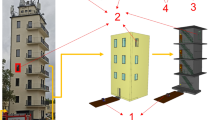
A centralized exhaust system can be divided into branch pipe section and main flue section. The branch pipe section is composed of a range hood, branch pipe, and check valve17,18. The main section is composed of the main flue, hood, roof fan, etc. Figure 1 shows the abstraction of a centralized exhaust system into a two-dimensional physical model.

Fig. 1
figure 1

Simplified model of the public flue exhaust system.

Full size image

Determination of calculation model

The standard k − ε turbulence model was calculated using the flow field, and standard wall functions were used to address the near-wall areas. Because the influence of temperature does not need to be considered, the energy equation is not introduced into the simulation. For a steady incompressible flow, the basic governing equation is as follows:

Continuity equation

$$\frac{{\partial u_{i} }}{{\partial x_{i} }} = 0$$
(1)

Momentum equation

$$\rho \frac{\partial }{{\partial x_{j} }}\left( {u_{i} u_{j} } \right) = - \frac{\partial p}{{\partial x_{i} }} + \mu \frac{\partial }{{\partial x_{j} }}\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) + \rho g_{i}$$
(2)

The turbulent flow energy equation

$$\rho \frac{\partial }{{\partial x_{j} }}\left( {u_{i} k} \right) = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \frac{{\mu_{t} }}{{\sigma_{k} }}} \right)\frac{\partial k}{{\partial x_{i} }}} \right] + \mu_{i} \frac{{\partial u_{j} }}{{\partial x_{i} }}\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) + \rho \varepsilon$$
(3)

Turbulent energy dissipation rate equation

$$\rho \frac{\partial }{{\partial x_{j} }}\left( {u_{i} \varepsilon } \right) = \frac{\partial }{{\partial x_{i} }}\left[ {\left( {\mu + \frac{{\mu_{t} }}{{\sigma_{\varepsilon } }}} \right)\frac{\partial \varepsilon }{{\partial x_{i} }}} \right] + C_{1\varepsilon } \mu_{t} \frac{\varepsilon }{k}\frac{{\partial u_{j} }}{{\partial x_{i} }}\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) - C_{2\varepsilon } \rho \frac{{\varepsilon^{2} }}{k}$$
(4)

where ui and uj are velocity components, i, j are tensor subscripts, and its value range is 1, 2, and 3. Variable ρ is the fluid density, μ is the viscosity coefficient, μt is the viscosity coefficient caused by turbulence, k is turbulent flow energy, and the ε is the energy dissipation rate of turbulent flow. Empirical constant C1ε = 1.44, C2ε = 1.92, Cμ = 0.09, σk = 1.0, σε = 1.3.

For turbulent flow calculation, turbulence parameters need to be specified in the calculation ___domain and give appropriate boundary conditions at the inlet and outlet. When using the k-ε model for calculation, two combined parameters, turbulent flow energy k and turbulent flow energy dissipation rate, are usually used for calculation.

The turbulent flow energy k is calculated according to the following equation.

$$k = \frac{3}{2}\left( {uI} \right)^{2}$$
(5)

where I is the intensity of turbulence.\(I = 0.16\left( {{\text{Re}}_{{D_{u} }} } \right)^{{ - {1 \mathord{\left/ {\vphantom {1 8}} \right. \kern-0pt} 8}}}\), u is the average velocity of turbulence.

The turbulent dissipation rate ε is calculated as follows.

$$\varepsilon { = }C_{u}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}}} \frac{{k^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}{l}$$
(6)

where Cu takes 0.09, l is the turbulent length dimension.

Flue pipe network simulation algorithm

The range hood can absorb the fumes from the kitchen. The sucked oil fume flows through the branch pipe and the check valve in front of the flue and finally discharges into the flue19. The fume at the upper level will be impacted and condensed by the fume from below. After repeating this process several times, the fume will then be discharged into the air outside of the flue. According to the aerodynamics theory, the governing equations of oil smoke velocity and pressure can be obtained.

$$P_{a,n} { = }P_{m} + P_{y,n} \left( {i = n} \right)$$
(7)

First, assume that the number of building layers is n. Then the pressure at the confluence of the nth layer flue can be represented by Pa,n in Eq. (7), and the pressure loss of the roof hood is Pm. The pressure loss along each layer in the concentrated flue is represented by Py,n. In addition, the remaining floors except the top floor have the following equation.

$$P_{a,i} = P_{2 - 3} + P_{y - 3} + P_{a,i + 1} (0 < i < n)$$
(8)

where P2–3 represents the confluence pressure loss between the middle and lower layers of the two adjacent main flue layers relative to the upper layer. Py–3 is the pressure loss along the main flue in each layer. And for all branch pipelines, there is the following equation.

$$P_{c,i} { = }P_{a,i} + P_{1 - 3} + P_{z,i} (0 < i < n)$$
(9)

where P1–3 represents the pressure loss caused by the confluence of the branch flue and the main flue. Pc,i represents the full pressure value of the i-th hood outlet, and the Pz,i is the pressure loss in the i-layer branch pipe. For the pressure loss given in the above eqs. (7–9), there is the following expression.

$$P_{m} { = }\zeta_{m} P_{d,i}$$
(10)
$$P_{2 - 3} { = }\zeta_{2 - 3} P_{d,i}$$
(11)
$$P_{{{1} - 3}} { = }\zeta_{{{1} - 3}} P_{d,i}$$
(12)

If the model of the range hood is known, the P–Q performance curve can be drawn.

$$Q_{i} = f\left( {P_{c,i} } \right)$$
(13)

Among them, Pd,i represents the dynamic pressure in the i-layer concentrated flue. The drag coefficient of the roof hood is ζm. ζ1–3 and ζ2–3 represent the confluence resistance coefficient of branch pipe and low-level flue relative to high-level flue, respectively. The values of dynamic pressure and resistance loss along the way can be determined using the following equations.

$$P_{d} = \rho \frac{{V^{2} }}{2}$$
(14)
$$P_{y} = \lambda \frac{l}{d}\frac{{\rho V^{2} }}{2}$$
(15)
$$\lambda { = }0.11\left( {\frac{K}{d} + \frac{68}{{\text{Re}}}} \right)^{0.25}$$
(16)

where ρ is the air density, V is the gas velocity, λ is the coefficient of frictional resistance of the pipeline, l is the length of the flue, K is the absolute roughness of the pipe wall, and Re is the Reynolds number. Thus, the iterative calculation can be performed by giving the initial values simultaneously eqs. (7–9). The calculation process is shown in Fig. 2.

Fig. 2
figure 2

Calculation process of flue pipe network simulation.

Full size image

Verification of resistance coefficient of key components

Numerical simulation of frictional resistance coefficient

The resistance coefficient of the branch pipe is verified by numerical simulation. After the pipeline modeling, the fluid area was extract by Solidworks, and then the model was imported into Gambit software for meshing. The total length of the branch pipe is 1.8 m, and the numerical simulation was performed after verifying grid independence. When pre-treating the model, the branch pipe was regarded as a smooth surface. When simulating in Fluent, the absolute roughness of the pipe wall should be set according to the experimentally measured value9. The schematic diagram of the three-dimensional model and model grid is shown in Fig. 3.

Fig. 3
figure 3

(a) Model fluid ___domain, and (b) mesh division.

Full size image

The specific settings for numerical simulation are as follows:

  1. (1)

    When starting Fluent, the solver operator is selected as 3ddp double precision;

  2. (2)

    Set the model unit as mm, and then scale;

  3. (3)

    The turbulence model is selected as k-ε model for simulation;

  4. (4)

    The fluid medium is set to air and the density of air;

  5. (5)

    The pressure and velocity are coupled with SIMPLEC algorithm, and the momentum and mass discretization are performed with second-order accuracy;

  6. (6)

    The operating pressure is set to one standard atmospheric pressure;

  7. (7)

    The inlet is a velocity inlet boundary condition and the outlet is a pressure outlet boundary condition;

  8. (8)

    The wall surface uses a no-slip standard wall function with the roughness set to 20 mm;

  9. (9)

    Global parameter initialization;

The influence of computational grids on the accuracy of computer simulation was studied, the results shown as Fig. 4. By comparing the simulation results of three grids pre-divided into 7453, 15,376, and 27,683, it can be seen that the division of the grid is particularly important for simulation. When the mesh density reaches 15,376, the influence of increasing the mesh density on the calculation result is very small. By verifying the grid independence, the final number of selected grids is 15,376.

Fig. 4
figure 4

Mesh-independence study.

Full size image

The pressure difference between the inlet and the outlet can be calculated by intercepting the simulation results on the central axis. Then substitute pressure difference into Eq. (11) to obtain the resistance coefficient of the branch pipe. Figure 5 is the contour map of pressure and speed of the 1.8 m branch pipe under three different working conditions of the range hood. The simulation results indicated that the pressure stratification phenomenon in the pipeline is more obvious due to the influence of the viscous resistance and friction coefficient K in the inner wall of the pipeline. Especially the higher the working range of the range hood, the more obvious the pressure stratification phenomenon. The influence of range hood working gear on flow rate is not obvious.

Fig. 5
figure 5

Simulation results of the smoke machine working in different gears: (a) contour plot of total pressure in third gear, (b) contour plot of velocity in third gear, (c) contour plot of total pressure in second gear, (d) contour plot of velocity in second gear, (e) contour plot of total pressure in first gear, and (f) contour plot of velocity in first gear.

Full size image

The reliability of numerical simulation is verified by building an experimental setup. The field branch pipe resistance coefficient test environment is shown in Fig. 6. Monitoring points were set on both sides of the inlet and outlet of the branch pipe to measure the pressure, thereby obtaining the pressure difference between the inlet and outlet. A flow meter was installed at the outlet of the branch pipe to obtain the airflow of the range hood, so as to calculate the average velocity of the fluid in the branch pipe. The above parameter values were then taken into Eq. (14) to calculate the resistance coefficient of the branch pipe.

Fig. 6
figure 6

Experimental apparatus for testing resistance coefficient of branch pipes.

Full size image

Figure 7 shows the experimental results and numerical simulation results of the branch pipe resistance coefficient. Table 1 demonstrates the results of statistical analysis between measured and simulated data for different branch pipe sizes at different gears. It can be seen from the comparison that the experimental test results are slightly larger than the numerical simulation results, the reason is that the surface roughness of the branch pipe will be slightly different from the actual situation. We compared the measured and simulated data using statistical analysis to determine their consistency. Their Pearson’s correlation coefficient is 0.8929, which indicates that there is a very strong positive linear relationship between the measured data and the simulated data. The very consistent trend of the two sets of data also indicates that the simulation model is able to simulate the actual situation very well. In addition, based on the magnitude and trend of the mean and variance of the resistance coefficients for different factors calculated in the table, it can be seen that the range of hood air volume has little influence on the resistance coefficient of the branch pipe, and the change of the length of the branch pipe will slightly affect the resistance coefficient of the branch pipe. It can be concluded from this that changes in the length and air volume of the branch have little effect on the resistance coefficient of the branch. By analyzing the experimental results, the drag coefficient can be drawn to 2.76.

Fig. 7
figure 7

Comparison of experimental and simulated data for resistance coefficients of branch pipes.

Full size image
Table 1 Table of statistical analysis of measured and simulated data of branch pipe resistance coefficient.
Full size table

Numerical simulation of check valve resistance coefficient

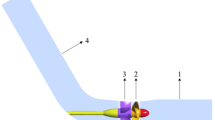
As shown in Fig. 8, a 3D computational model for the non-return valve is established. The non-return valve will be numerically simulated under different opening angles and with the fan set at different volumes of airflow.

Fig. 8
figure 8

Three-dimensional model of check valve.

Full size image

The pressure difference is analyzed in the overall system and the two sections before and after the non-return valve once the fluid flow in the pipe becomes steady. As shown in Fig. 9, Section 1 is the cross-section of the flue axis, and Sections 2 and 3 are the pressure measurement surfaces before and after the non-return valve, respectively.

Fig. 9
figure 9

Cross-section of the flue axis.

Full size image

The opening of the check valve at each interval is 10 degrees, and the resistance coefficient of the check valve at the same air volume is calculated. Select the partial opening angle as a variable to analyze the velocity and pressure contours on the three sections. As shown in Fig. 10, the opening of the check valve is 70 degrees, and the hood air volume in the third gear. In this case, the pressure contour of Section 2 is generally significantly higher than that of Section 3 in Fig. 9.

Fig. 10
figure 10

Check valve at 70 degrees and fan in third gear: (a) pressure contour map in Section 1, (b) velocity contour map in Section 1, (c) pressure contour map in Section 2, and (d) pressure contour map in Section 3.

Full size image

For experimental testing, a check valve measurement platform was built. The experimental test site is shown in Fig. 11, and the model of the check valve is shown in Fig. 12. The check valve was installed at the outlet of the branch pipe, and pressure monitoring points were set at both sides of the inlet and outlet of the check valve.

Fig. 11
figure 11

Test equipment for resistance coefficient of check valve.

Full size image
Fig. 12
figure 12

Photo of check valve.

Full size image

During the experimental test, the opening angle of the check valve is kept constant, and the drag coefficient of the mirror is measured and calculated by changing the wind speed gear of the smoke machine. The experimental data is shown in Table 2. Table 2 contains the mean and variance of the measured and simulated data in three gears at different angles.

Table 2 Test data of the check valve resistance coefficient experiment.
Full size table

During the experimental test, the check valve maintains a constant opening angle, changes the air flow range of the hood for measurement, and calculates the resistance coefficient separately. The comparison between experimental data and numerical simulation is shown in Fig. 13. We statistically analyzed the measured and simulated data to determine their consistency. Their PERSON correlation coefficient is almost 1, indicating that the simulation model can simulate the actual situation well, providing strong evidence for the validity of the simulation model. As can be seen from the figures and tables, when the check valve is opened at a constant angle, the change in the turbine airflow range has almost no effect on the drag coefficient of the check valve. However, the drag coefficient increases as the opening angle of the check valve decreases, which indicates that the opening angle of the check valve has a significant effect on its drag coefficient.

Fig. 13
figure 13

Comparison of resistance coefficient between experimental data and simulated data.

Full size image

Figure 13 shows that the results of the numerical simulation are consistent with the experimental data. Only when the opening Angle is 40° and the turbine air volume is in the 2 gear, there is a deviation, and the 1 gear and 3 gear air volume errors are very small at the same Angle. This may be caused by instability in turbine operation in the second gear. The influence of the change of air volume on the resistance coefficient of the check valve is negligible. By analyzing the data, the mathematical relationship between the resistance coefficient of the check valve and its opening degree is found. Process the data and fit the following relationship.

$$\xi = k_{1} e^{{k_{2} \left( {90 - \theta } \right)}}$$
(17)

where k1 = 0.1154 and k2 = 0.1113.

Numerical simulation of confluence resistance coefficient of tee pipe

The smoke from the residents of each floor first flows through the check valve into the vertical main flue, and then merges with the lower flue gas inside the flue to be discharged upward. Extract the confluence tee part for modeling, and the resistance coefficient is numerically simulated by giving the corresponding inlet velocity. The cross-sectional area of the public flue on different floors is not the same. The specific dimensions are 400*270 (floor number ≤ 18), 430*370 (floor number ≤ 24), and 570*370 (floor number ≤ 33). Model these three sizes of flue separately and define them as size one, size two, and size three respectively. The fluid area model of the tee pipe and the ___location of each cross-section are shown in Fig. 14. The height of each floor is 3 m. Change the wind speed V1 at the inlet of the branch pipe and the wind speed V2 at the inlet of the public flue, and perform numerical simulation on the combined resistance coefficient.

Fig. 14
figure 14

Tee pipe fluid area and section view.

Full size image

Figure 15 shows the results when the number of floors ≤ 18, the branch pipe inlet air velocity, centralized exhaust airway inlet velocity are different values. Figure 16 shows the results of different values of branch pipe inlet air velocity and centralized exhaust air duct inlet velocity when the number of floors ≤ 24. Figure 17 shows the results when the number of floors ≤ 30, the branch pipe inlet air velocity, centralized exhaust air duct inlet speed are different values.

Fig. 15
figure 15

Dimension I Total pressure distribution in local cross section for different flow velocities.

Full size image
Fig. 16
figure 16

Dimension II Total pressure distribution in local cross section for different flow velocities.

Full size image
Fig. 17
figure 17

Dimension III Total pressure distribution in local cross section for different flow velocities.

Full size image

From the above numerical simulation results, it can be seen that, in the connection between the branch pipe and the main pipe in the converging tee, because the gas from the branch pipe enters the public flue by the bottom of the centralized flue gas impact as well as the convergence of this part of the flow field is more turbulent, so it is necessary to calculate its coefficient of merging resistance.

First, calculate the pressure difference between Section 1, 3 and Sections 2, 3 in Fig. 14. Then substitute into eqs. (11) and (12) to get the local resistance coefficient. It can be found in the fluid resistance manual that the resistance coefficient has the following relationship.

$$\xi_{{_{1 - 3} }} = 1 + \left( {\frac{{Q_{1} }}{{Q_{3} }} \cdot \frac{{S_{3} }}{{S_{1} }}} \right)^{2} - 2\left( {1 - \frac{{Q_{1} }}{{Q_{3} }}} \right)^{2}$$
(18)
$$\xi_{{_{2 - 3} }} = 1.55\frac{{Q_{1} }}{{Q_{3} }} - \left( {\frac{{Q_{1} }}{{Q_{3} }}} \right)^{2}$$
(19)

whereζ1–3 refers to the coefficient of confluence resistance from Section 1 to Section 3 relative to Section 3 in Fig. 14, ζ2–3 refers to the confluence resistance coefficient of the fluid from Section 2 to Section 3 and relative to Section 3 in Fig. 14. Q1, Q2, and Q3 represent the flow of the branch pipe of the hood, downstream of the concentrated flue, and upstream of the concentrated flue, respectively. S1 and S3 represent the cross-sectional area of branch pipe and main flue.

To explore the variation law of the local confluence resistance coefficient under different working conditions, the test plan is shown in Fig. 15. In the experimental test, the second and third gears of the range hood are selected for testing.

Equations (18) and (19) are the calculation equations of the local confluence resistance coefficient. But in the experimental test, eqs. (20) and (21) are used to calculate the drag coefficient.

$$\xi_{{{1 - }3}}{\prime} { = }\frac{{\Delta P_{1 - 3} }}{{\rho V^{2} /2}}$$
(20)
$$\xi_{{{2 - }3}}{\prime} { = }\frac{{\Delta P_{2 - 3} }}{{\rho V^{2} /2}}$$
(21)

where ∆P is the pressure difference between import and export \(\xi_{{{1 - }3}}{\prime}\) and \(\xi_{{2{ - }3}}{\prime}\) are the experimental values for \(\xi_{{1{ - }3}}\) and \(\xi_{{2{ - }3}}\). In the experimental part of this study, we chose the frequency of the current flowing through the fan as the control variable for the experiment. This choice allowed us to simulate the effect of smoke evacuation under different conditions of use. We recorded the converging resistance coefficients of the fan at varying flow rates, and the experimental results are detailed in the presentation of Fig. 18. In order to present the experimental environment and equipment more intuitively, Fig. 19 provides an actual photograph of the flue unit, which clearly reflects the structure and layout used in the experiment. Also, to help understand the installation and configuration of the hood, Fig. 20 provides a detailed installation schematic to further elucidate the experimental setup.

Fig. 18
figure 18

Test structure model of flue.

Full size image
Fig. 19
figure 19

Test structure model of flue.

Full size image
Fig. 20
figure 20

Test structure model of flue.

Full size image

The speed of the fan and the airflow before the experiment were linearly related, and the airflow of the fan was changed by changing the frequency of the current of the fan, which was used to simulate the airflow of the lower floors of different layers. The hood was adjusted and the differential pressure at the pressure point was read to calculate the combined resistance coefficient. The size of the experimentally tested flue is the size of the layer ≤ 33, and then compared with the value calculated by the formula.

During the in-depth analysis of the theoretical and simulation data, we used correlation coefficients, especially the Pearson correlation coefficient, to measure the linear relationship between the two. The analysis results show that the Pearson correlation coefficient between the measured and theoretical values of the parameter \(\xi_{1 - 3}\) is as high as 0.9977, and this very high correlation indicates that the measured data are very close to the theoretical predictions, almost in a straight line, thus verifying the very high accuracy of the simulation model in predicting the \(\xi_{1 - 3}\) parameters.

On the other hand, the Pearson’s correlation coefficient between the measured and theoretical values of the parameter \(\xi_{2 - 3}\) is 0.7249.Although this coefficient is lower than the correlation coefficient of the parameter a, it still indicates that there is a strong positive linear relationship between the two. This means that the simulation model also has some accuracy in predicting the \(\xi_{2 - 3}\) parameter, but there may be some influencing factors that lead to some deviation between the model prediction and the actual situation. Figure 21 indicates that the local confluence resistance coefficient obtained by the experimental test is slightly larger than the theoretical calculation value, and the trend of the two confluence resistance coefficients is consistent. In addition, the theoretical results \(\xi_{2 - 3}\) are better than that of \(\xi_{1 - 3}\). This is mainly due to the distance between the two detection points being far apart, and the pressure loss along the way is also introduced during the calculation, which brings a certain error. The resistance coefficient value measured by the experiment is consistent with that calculated by eqs. (20) and (21). Therefore, it can be concluded that the calculation eqs. (20) and (21) of the merge resistance coefficient described in the resistance manual apply to the research of this subject.

Fig. 21
figure 21

Comparison of local drag coefficient in second gear.

Full size image

Experiment

Under the condition of different start-up rates, the experimental tests on the 33-layer vertical flue and 6-layer horizontal flue are shown in Figs. 22 and 23. In the actual test, the vertical test bench relies on Vanke Tower to complete. Before conducting the test, conduct an air volume test to ensure that the smoke machine can work normally. After that, the branch pipe is reinforced to determine the length of the branch pipe and the installation position of the smoke machine. During the experiment, the flow rate of the range hood was measured using an air flow hood, as shown in Fig. 24.

Fig. 22
figure 22

Vertically placed test experiment site: (a) Front view, and (b) Side view.

Full size image
Fig. 23
figure 23

Horizontal test experiment site: (a) Front view, and (b) Rear view.

Full size image
Fig. 24
figure 24

Air volume measurement instruments: (a) The whole figure, and (b) Partial enlarged view.

Full size image

The different working conditions of the 33-layer vertical flue were compared20. The data obtained from the analysis test and calculation program shown in Fig. 25 are taken from the two states of uniform start-up and random start-up. Uniform start-up means that the exhaust hoods on all floors are activated simultaneously. Random start-up refers to the process where a certain proportion of exhaust hoods are selected, and the floors on which they are activated are chosen at random.

Fig. 25
figure 25

The emissions of 2 hood start-up modes: (a) Uniform start-up state, and (b) Random start-up state.

Full size image

According to Fig. 25, we can observe that the trend of the simulation model is consistent with that of the actual experimental data. Specifically, the calculated results not only coincide with the experimental observations under the uniform start-up condition, but also with the experimental data of the range hood under the random start-up condition. Further analysis shows that the Pearson’s correlation coefficient between the simulated data and the experimental data is as high as 0.9768 in the uniform start-up mode, while in the random start-up mode, the coefficient also reaches 0.934. These two significant correlation coefficients reveal that there is a strong positive linear relationship between the simulated and experimental data, and the simulated results are very close to the actual measured values. These findings validate the effectiveness of the simulation methodology and demonstrate that the simulation software is able to accurately predict the airflow distribution observed in the experiment. However, the errors around the 30th layer are relatively large, which may be due to the change of air pressure near the end of the pipe. By analyzing the flow values of different floors under the condition that the floors are evenly turned on, it can be found that the experimental values are mostly distributed near the calculated values of the program, indicating that the calculation program is reliable. From the experimental results, it can be seen that the increase in the start-up rate will reduce the emissions from the power-on floors on the ground floor.

Under the state of 100% start-up rate, where smoke machine on all floors are activated, the bottom user emissions calculated by the calculation program are 185 m3/h, and the top floor is 648 m3/h, which means it is very difficult for the bottom households to emit. As the start-up rate continues to decrease, the emissions of the bottom households gradually increase. When the start-up rate is 69.7%, exhaust hoods in 69.7% of the floors are activated, the calculated value of the bottom emission is 314 m3/h, and the top emission is 686 m3/h. Additionally, the emission is becoming more and more uniform.

Therefore, the higher the start-up rate, the lower the smoke output of the bottom users, and the worse the bottom smoke exhausting ability. With the decrease of the operating rate, the smoke exhaust volume of the bottom floor users increases, and the smoke exhaust volume of all floors tend to be uniform. To improve the uniformity of the smoke exhaust on each floor, the performance of the smoke machine for users on the bottom floor can be appropriately improved to increase its emission.

Conclusion

In this study, we explore the comprehensive resistance coefficient of several common flue structures in centralized flue systems, such as branch pipes, check valves, and tee pipes, through model building and numerical simulations. The comprehensive resistance coefficient is the result of multiple factors in the fluid system, including the tube-wall roughness K, structural parameters, and fluid boundaries. In our research, we found that the comprehensive resistance coefficient of the smoke exhaust branch pipe has a low correlation with the exhaust quantity and length and calculated the comprehensive resistance coefficient of the branch pipe to be 2.76. For check valves, the comprehensive resistance coefficient has only a weak relationship with the airflow but has a strong correlation with the valve opening. We further discovered a functional relationship between the valve opening and the comprehensive resistance coefficient. For the tee pipe, we calculated the confluence resistance coefficients of three different flue sizes. In terms of smoke exhaust research, using the established resistance coefficient model, we simulated the exhaust effects of each layer in a 33-layer flue under two start modes (uniform start and random start of the range hood). The results show that the simulated smoke exhaust volume closely aligns with the experimental data and exhibits a consistent trend. This experiment further revealed an important fact: as the startup rate of the range hood increases, the smoke emissions of the bottom users decrease, implying a decreasing exhaust capacity from the bottom. This paper validates the accuracy and feasibility of the built resistance coefficient model through CFD and physical experiments, which paves the way for the application of this model in relevant fields.

In future research, we plan to consider more variable factors, such as the surface roughness of the branching pipe as well as changes in the wall thickness and inner diameter owing to the accumulation of oil and scale. These factors will be fully considered and integrated in the arrangement of specific simulation work. All of the above explorations and research illuminate our research direction in this field, allowing us to propose and implement more practical solutions based on a comprehensive understanding of the operating principles of the flue system, with the aim of improving the efficiency and function of the flue system.