Introduction

In the background of global climate change and the aggravation of human activities, the intensity and frequency of extreme precipitation have increased significantly over the past decades, leading to flood disasters that pose a serious threat to human life, infrastructure, and the socio-economic situation1,2,3,4. Therefore, accurate flood prediction and timely implementation of corresponding protective measures have become crucial5. Flood forecasting is one of the important non-engineering measures for flood prevention and disaster reduction6. How to improve the accuracy of flood forecasting has always been a hot and difficult topic in the field of hydrology7,8.

Flood forecasting mainly relies on hydrological models. Currently, flood forecasting models are mainly divided into two categories: process-driven and data-driven models9,10. Process-driven models estimate runoff based on the physical processes of hydrology, which in some extent summarize complex hydrological phenomena11. However, the construction of the model needs a large amount of data of basin hydrology and underlying surface, and there are also problems such as parameter calibration12,13. The physical processes are complex, and the applicable conditions and regions are different for each model, so practical application is limited to a certain extent14. With the progress of big data and intelligent water conservancy technology, artificial intelligence (AI) and machine learning (ML) are increasingly applied to data-driven models of hydrological simulation and flood forecasting15. Data-driven models do not need to model the basin hydrological processes, but only perform statistical analysis based on linear and nonlinear relationships between input and output data16. It has been proved that they can effectively deal with nonlinear and unstable data sets.

The most commonly used data-driven model in flood forecasting research currently is the Long Short-Term Memory (LSTM) neural network17. By introducing gate mechanisms and memory cells, LSTM overcomes problems such as gradient vanishing or exploding in recurrent neural networks (RNNs)2. LSTM can capture and store temporal dynamics of model inputs and process data sequentially, thus better capturing long-term dependencies and achieving better prediction results in flood forecasting. Kratzert et al.18 used the Sacramento Soil Moisture Accounting Model (SAC-SMA) coupled with Snow-17 snow melting module as a baseline model. Using CAMELS dataset, they compared and analyzed the effect of daily runoff simulation between LSTM and SAC-SMA + Snow-17 for 241 watersheds located in different hydrological partitions, and the results showed that LSTM has better daily runoff prediction capabilities than hydrological models. Yin et al.19 used hydrometeorological data as input models and built LSTM runoff prediction models for different time horizons. In the runoff prediction of the Jinjiang basin in Jiangxi Province of China, the LSTM model showed a better forecasting performance than the Xinanjiang (XAJ) hydrological model. Zhou et al.20 constructed the LSTM flood forecasting model and applied it to the inflow flood forecasting of the Three Gorges Reservoir. The results showed that the overall prediction effect of the LSTM model was better than that of BPNN and dynamic neural network models. Sudriani et al.21 proposed an LSTM based machine learning algorithm to predict irrigation flow during drought periods in advance. By comparing the measured data from water catchment stations, the results showed that the relative error was less than 10%. Kao et al.22 constructed the LSTM multi-step output flood forecasting model, and achieved good forecasting effects in the 1–6 h inflow discharge prediction of Shimen Reservoir in China. Xu et al.23 used LSTM to construct a watershed flood model for different forecast periods, which was used for flood forecasting in the upper reaches of the Yellow River and discussed the impact of hyperparameters on the forecast accuracy. Ding et al.24 constructed an SLA-LSTM flood forecasting model considering the spatiotemporal distribution changes of input feature variables, and achieved better forecast effects than various machine learning models such as Convolutional Neural Networks (CNN) and Graph Convolutional Networks (GCN). Liu et al.25 combined the grid flow generation model (GRGM) with LSTM to construct a GRGM-LSTM hybrid flood forecasting model, which has a better simulation performance than physical mechanism models such as GRGM-SWMM and SWMM.

These studies show that LSTM model has good applicability in flood runoff process prediction. LSTM has a high prediction accuracy for runoff processes, which is mainly reflected in that when the prediction period is within 3 h, the NSE is more than 0.8. However, these studies also have some shortcomings. Which are mainly reflected in the relatively large error of the model for forecasting flood peak, and the overall accuracy also shows a significant negative change with the increase of the prediction period. This is because as the time interval between input and output data increases during the training period, resulting in a weakening of the spatial–temporal dependencies of the sequence data26. At this time, it is difficult for machine learning to learn the potential relationship between Pt, Qt and Qt+i spatial–temporal sequence data in the confluence calculation, leading to a decrease in prediction accuracy.

Therefore, this study proposes a machine learning flood forecasting method based on the vector direction (VD) of flood process. By increasing the input data dimension of LSTM model, it is helpful for LSTM to better explore the change features of rising and receding flood runoff process, and reduce the training gradient error of input–output data of LSTM model, so as to improve the accuracy of flood forecasting. The VD-LSTM model consisting of coupling VD and LSTM model is expected to further improve the accuracy of machine learning models.

Methods

The characteristic equation based on vector direction of flood process

Runoff process vectorization is realized by constructing the characteristic equation based on the vector direction of the flood runoff process. The basic idea is to convert the flood runoff process line into a vector curve with time series. The vector eigenvalue is determined by the time step and the numerical value of discharge at adjacent times, where positive, negative and parallel vector directions correspond to rising, receding and flat flood process respectively27. The principle of the flood process line vectorization method is shown in Fig. 1. The specific calculation process involves dividing the field-level flood runoff processes into several small segments with a given time interval, and then solving for vector values kt for each segment. The definitions of vector direction characteristic equations are as follows.

  1. (1)

    The vector direction is “+” (Rising flood process):

    $$ k_{t} = \tan \theta_{t} = \frac{{Q_{t} - Q_{t - \Delta t} }}{\Delta t} $$
    (1)
  2. (2)

    The vector direction is “−” (Receding flood process):

    $$ k_{t} = \tan \theta_{t} = \frac{{Q_{t - \Delta t} - Q_{t} }}{\Delta t} $$
    (2)
  3. (3)

    The vector direction is “0” (Flat flood process):

    $$ k_{t} = \tan \theta_{t} = 0 $$
    (3)

    where kt is the vector eigenvalue of the flood process line at time t, \(\theta_{t}\) is the value of the angle between the flood discharge process line and the time axis at time t, Qt is the flood discharge at time t, Qt−1 is the flood discharge at time t − 1, and \(\Delta t\) is the time step.

Fig. 1
figure 1

The computational schematic based on the characteristic formula for the vector direction of the flood process.

Full size image

VD-LSTM model

LSTM is a special recurrent neural network (RNN). The difference between LSTM and RNN lies in the fact that the hidden layer in LSTM is composed of internal self-recurrent units, which can overcome the problems of gradient disappearance or explosion that are easy to occur in the Back Propagation Through Time (BPTT) algorithm of RNN. The memory cell unit has been added to the hidden layer of LSTM, replacing the original cell unit in RNN28,29. The structure of memory cell unit in the hidden layer of LSTM is as shown in Fig. 2.

Fig. 2
figure 2

Memory cell unit structure in LSTM hidden layer.

Full size image

The memory cell unit can selectively remember and forget the input data. It is composed of input gate, output gate and forget gate30. ht−1 is the hidden layer state at the previous time step, Ct−1 and Ct are the memory cell state variables at the previous time step and after passing through the memory cell unit, respectively. ft, it and Ot are the forget gate, input gate and output gate, respectively. When the input Xt passes through the memory cell unit, the state variable Ct−1 becomes Ct. The principle is that when the input Xt passes through the memory cell unit, it successively passes through the forget gate, input gate and output gate, and some information is selected to be forgotten by the memory cell, while other information is selected to be added to the memory.

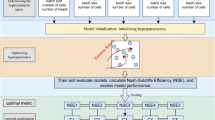
The key steps of constructing the VD-LSTM model include the following components. Firstly, the watershed flood runoff data is reconstructed in a vectorized form. This involves discretizing the runoff process into several smaller segments at a certain time interval, and then solving for the vector characteristic value (kt) segment by segment. Subsequently, in order to accelerate the convergence speed of machine learning calculations and improve prediction accuracy, rainfall, runoff, and vector characteristic values are separately normalized using “minimum–maximum” normalization to the interval [0, 1], forming standardized time series sample data as the input feature variables of the model. Finally, the vectorized runoff process is coupled with the LSTM model to form the VD-LSTM flood forecasting model. The structure of the VD-LSTM model is shown in Fig. 3.

Fig. 3
figure 3

Structure of the VD-LSTM model.

Full size image

Evaluation of model performance

In this study, the Nash Sutcliffe efficiency (NSE), root mean square error (RMSE), and bias as evaluation metrics are adopted to evaluate the model performance. The mathematical expressions for these metrics are as follows:

$$ NSE = 1 - \frac{{\sum\nolimits_{t = 1}^{n} {(Q_{o}^{t} - Q_{s}^{t} )^{2} } }}{{\sum\nolimits_{t = 1}^{n} {(Q_{o}^{t} - \overline{Q}_{o} )^{2} } }} $$
(4)
$$ RMSE = \sqrt {\frac{{\sum\nolimits_{t = 1}^{n} {(Q_{o}^{t} - Q_{s}^{t} )} }}{n}} $$
(5)
$$ bias = \frac{{\sum\nolimits_{t = 1}^{n} {(Q_{o}^{t} - Q_{s}^{t} )} }}{{\sum\nolimits_{t = 1}^{n} {(Q_{o}^{t} )} }} $$
(6)

where \(Q_{o}^{t}\) and \(Q_{s}^{t}\) represent the observed discharge and predicted discharge at time t, respectively. \(\overline{Q}_{o}\) denotes the mean of the observed discharge, and n stands for the number of samples. The Nash Sutcliffe Efficiency (NSE) 31 is used to assess a model's ability to predict deviations from the mean of the variable of interest. It is expressed as a percentage of the initial variance explained by the model, with a value of 1 indicating a perfect fit, and values closer to 1 suggesting more accurate predictions. The root mean square error (RMSE)32 is particularly sensitive to extreme errors and provides a comprehensive evaluation of the overall accuracy of the predictions, and lower values imply higher accuracy. Bias represents the magnitude of the deviation between simulated and observed values and is expressed as a percentage ranging from − 100 to 100%. A bias value close to zero indicates a smaller deviation between the predicted and observed values.

Case study

Study area

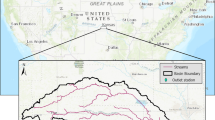
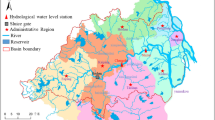
The Yellow River is the fifth largest river in the world and frequently suffers from floods. In recent years, due to human activities (a large number of soil and water conservation measures) and climate change (temperature, rainfall, etc.), there have been significant changes in the underlying surface conditions in the middle and lower reaches of the Yellow River. In this study, the Jingle basin and Lushi basin, which are representative, were selected in the middle reaches of the Yellow River, respectively, and their locations are shown in Fig. 4.

Fig. 4
figure 4

Geographical Location of Jingle and Lushi basins (The map was created using ArcMap 10.1 software, and the drawing boundaries are sourced from https://www.gpsov.com/cn2/).

Full size image

The Jingle basin is located in the upper reaches of the Fen River, with a total length of 83.9 km and a basin area of 2799 km2. It has a warm temperate continental monsoon climate and is situated in the transition zone between semi-humid and semi-arid regions. The average annual precipitation is 503 mm, with significant interannual variability. The historical maximum peak flow recorded was 2267 m3/s, and the multi-year average maximum peak flow was 596 m3/s. Most of the precipitation occurs during the summer months, with June to September accounting for more than 70% of the annual precipitation. The runoff in the Jingle River basin exhibits a clear nonlinear characteristic.

The Lushi basin is located in the middle reaches of the Yellow River, with a total length of 196.3 km and a basin area of 4623 km2. It spans two provinces, Shaanxi and Henan. The basin’s geomorphic types are complex and diverse, belonging to the transition zone between loess edge and mountainous plains. Influenced by the warm temperate continental monsoon climate and altitude, the climate in the basin is cold and dry in winter, and hot and rainy in summer. The multi-year average precipitation in the basin is 692 mm, which is unevenly distributed throughout the year, with the maximum in July and the minimum in December, and the precipitation from June to September accounts for 63% of the whole year.

Data preparation and processing

Rainfall and runoff data are extracted from the Yellow River Basin Hydrological Yearbook. The study collected the flood season rainfall data of 14 rainfall stations in the Jingle basin from 1980 to 2003 and the corresponding flood discharge data of the Jingle hydrological station, with a total of 50 floods, of which 35 floods from 1980 to 1996 were used as training models and 15 floods from 1996 to 2003 were used as validation models. Meanwhile, the flood season rainfall data of 23 rainfall stations in the Lushi basin from 1990 to 2016 and the corresponding flood discharge data of Lushi hydrological station were collected, with a total of 49 floods, of which 35 flood events from 1990 to 2011 were used as the training model, and 14 flood events from 2011 to 2016 were used as the validation model. The dataset is divided into training and validation sets in the ratio of 7:333,8.

The rainfall, discharge, and vector eigenvalue data corresponding to each flood are processed into a temporal feature dataset recognizable by the deep learning model with a time interval of 1 h, as shown in Table 1. Where, m and j respectively represent the number of rainfall stations and the total number of characteristic values. \(P_{t}^{(1)}\), \(P_{t}^{(2)}\), … \(P_{t}^{(m)}\) denote the rainfall from the 1st to the mth rainfall station at time t, respectively. Meanwhile, after dividing the dataset, the constructed dataset is normalized to the interval [0, 1] by the “minimum–maximum” normalization, and the calculation formula is shown in Eq. (7).

$$ x^{\prime} = \frac{{x - min_{x} }}{{max_{x} - min_{x} }} $$
(7)

where \(x^{\prime}\) and x represent the result after normalization and the input original data, respectively, minx and maxx denote the minimum and maximum values of the columns of the input data.

Table 1 The format of input feature data for deep learning models.
Full size table

Parameter selection and model input–output working mechanism

The model parameters mainly refer to the hyperparameters of the LSTM model, with NSE as the objective function, and the trial-and-error method is used to determine the optimal range of parameters. The optimal range for hyperparameters such as the number of cells, number of hidden layers, learning rate, batch size, time step, and number of iterations is 32–256 (with an interval of 16), 1–4 (with an interval of 1), 0.0001–0.1 (with intervals of 0.0001, 0.001, 0.01, 0.1), 16–128 (with an interval of 16), 6 and 300, respectively.

Figure 5 shows the key steps and process of applying the VD-LSTM model in river basins. Firstly, determine the model input and preprocess the data. \(P_{t}^{(1)}\), …, \(P_{t}^{(m)}\) and Qt are traditional feature inputs, while kt is the newly added feature input; Secondly, determine the coupling process and input–output working mechanism of the VD-LSTM model. The sliding window input with a time step of 6 is shown in Fig. 5b. When Qt+1, Qt+3, and Qt+6 are predicted by \(P_{t - 5}^{(1)}\)–\(P_{t}^{(1)}\), …, \(P_{t - 5}^{(m)}\)–\(P_{t}^{(m)}\), kt−5, …, kt and Qt−5, …, Qt, the corresponding output prediction lead time are 1 h, 3 h, and 6 h, respectively. And so on, until the sliding prediction ends.

Fig. 5
figure 5

The input–output working mechanism of VD-LSTM flood forecasting model.

Full size image

Results and discussion

Performance evaluation of VD-LSTM in each basin

Table 2 presents the results of model evaluation metrics for LSTM and VD-LSTM in Jingle basin and Lushi basin. The results show that, both in Jingle and Lushi basins, the average NSE values during training and validation periods of the VD-LSTM model are all above 0.8 with lead time of 1 h, 3 h, and 6 h, and the overall simulation performance is satisfactory. However, the prediction accuracy of VD-LSTM model decreases as the lead time extends, which is a common problem in machine learning models for flood forecasting. Taking the Jingle Watershed as an example, when the lead time is 1 h, the performance of the VD-LSTM model is at its best, with NSE, RMSE, and bias values of 0.97, 24.51 m3/s, 0.82% for the training period, and 0.94, 30.91 m3/s, and 0.92% for the validation period. When the lead time is 6 h, the performance of the VD-LSTM model is at its worst, with NSE, RMSE, and bias values of 0.86, 57.16 m3/s, 12.21% for the training period, and 0.80, 83.44 m3/s, and 12.45% for the validation period, respectively.

Table 2 The evaluation metrics results of LSTM and VD-LSTM models in Jingle and Lushi basins.
Full size table

Whether in the Jingle basin or the Lushi basin, the simulated performance of VD-LSTM models is better than that of LSTM models under the same forecasting periods. In the Jingle basin, the VD-LSTM model achieves NSE values of 0.97, 0.92, and 0.86 during the training period, and 0.94, 0.85, and 0.78 during the validation period, with lead time of 1 h, 3 h, and 6 h, respectively. This is an improvement of 0.02–0.08 over the LSTM model. In the Lushi basin, the VD-LSTM model obtains NSE values of 0.99, 0.96, and 0.90 during the training period, and 0.96, 0.88, and 0.81 during the validation period, with lead time of 1 h, 3 h, and 6 h, respectively. This is an improvement of 0.02–0.06 compared to the LSTM model. Meanwhile, both RMSE and bias are reduced to varying degrees. In addition, as the lead time increases, the accuracy of the VD-LSTM model improves more significantly compared to the LSTM model.

Figures 6 and 7 respectively display scatter plots of the LSTM and VD-LSTM models in the Jingle River and Lushi Basins. It is evident that the scatter plots of the VD-LSTM model are closer to the 1:1 line compared with those of the LSTM model. However, as the prediction time extends, the model’s dispersion gradually increases, indicating a decline in the model's forecasting performance. In the Jingle River Basin, during the validation period, the scattering points of both models were significantly lower than the 1:1 line for flow greater than 1000 m3/s. This could be due to a lack of high flow sample data during training, causing inaccurate simulation of high flow sample points during the validation period. In the Lushi basin, the scatter plot of the VD-LSTM model has the narrowest band at 1 h lead time, with the scatter plot closest to the 1:1 line (Fig. 7d). As the lead time extends, the scattered points of the LSTM model gradually diverge on both sides of the 1:1 line around a flow of 400 m3/s (Fig. 7b,c), with similar situations for the VD-LSTM model. However, at the same lead time, the scatter plot of the VD-LSTM model starts to become scattered after higher flow points, and has better prediction performance for these high flow points (Fig. 7e,f).

Fig. 6
figure 6

Scatter plots of LSTM and VD-LSTM models for the 1h, 3h and 6h lead time in the Jingle basin.

Full size image
Fig. 7
figure 7

Scatter plots of LSTM and VD-LSTM models for the 1h, 3h and 6h lead time in the Lushi basin.

Full size image

Comparison of process simulations for flood events

In order to accurately evaluate the model simulation effects, we selected three flood events during the validation period in two basins, including high peak flow (> 1000 m3/s) and low peak flow (< 300 m3/s), and these events exhibit different flood characteristics, including single-peak flood events and double-peak flood events. Figures 8 and 9 respectively display the simulation results of the three flood events in the Jingle and Lushi basins with a forecast lead time of 1h. The results indicate that the VD-LSTM model has a good fit between the simulated flow and the observed flow process in both basins, reflecting the actual flood process. There is a slight lag in the rising stage of flow in some flood events, but the recession process after the peak is very suitable. Moreover, when simulating high-flow flood events, there is an underestimation of the peak flow. Another situation leading to underestimation of the peak flow occurs when simulating flood events with a double-peak shape, with poorer performance in simulating higher peak flows (Fig. 8b). This may be due to the complex non-linear and spatiotemporal variations involved in the rainfall-runoff process. For flood events with a double-peak shape and higher peak discharge, their formation mechanisms may involve more environmental factors and hydrological processes, introducing more uncertainty and randomness, making their characteristics more difficult to capture by current models.

Fig. 8
figure 8

Observed and simulated hydrographs of LSTM and VD-LSTM during the validation period of three flood events in the Jingle basin.

Full size image
Fig. 9
figure 9

Observed and simulated hydrographs of LSTM and VD-LSTM during the validation period of three flood events in the Lushi basin.

Full size image

In terms of the flood process line simulated by LSTM alone, it also has a good simulation effect, but VD-LSTM has a more accurate prediction of the flood peak in the simulation of high flow events (Fig. 8a,c). From the perspective of lag, LSTM has more significant lag, and VD-LSTM improves this lag (Fig. 9a–c), indicating that the VD-LSTM model combining the vector direction of flood process can more accurately capture the vector characteristic information of flood process line in the stages of flow rising and flow receding, and reduce the uncertainty of input of machine learning model to a certain extent. In addition, as shown in Figs. 8c and 9b, the LSTM model has slight fluctuations in the low flow stage before the flood flow rises, compared with VD-LSTM, which performs better.

The iterative loss variation of models

Under the same task and dataset, with identical hyperparameters, we have plotted the iterative loss function change curves of the LSTM and VD-LSTM models during the training period, as shown in Fig. 10. In polar coordinate form, the curve from inner to outer means that the loss gradually becomes smaller from larger. Firstly, in terms of the magnitude of loss accuracy, at the same epochs, the VD-LSTM has a smaller loss accuracy than the LSTM. This suggests that the model is more effective in learning the characteristic information of the training data. Secondly, in terms of the model fitting speed, we can observe the trend of the loss curves decreasing for the LSTM and VD-LSTM models. The VD-LSTM model can achieve the same or lower loss values with fewer epochs, indicating that the model has a faster convergence speed and fitting capability. This might be attributed to the fact that VD-LSTM model is able to capture long-term dependencies and long-sequence context information more fully through the optimization of input structure design, which accelerates the learning process of effective features for the model. This mutual verification aligns with the previous discussions.

Fig. 10
figure 10

Iterative loss function variation curves for different models.

Full size image

Conclusion

In this study, a machine learning flood forecasting model based on the vector direction of flood flow process was proposed. By vectorizing the flood flow method to increase the input data dimension of LSTM model, it is beneficial for LSTM to better learn the rising and receding flood change characteristics of flood runoff process, reducing the training gradient error of input–output data of LSTM model, thereby improving the accuracy of flood forecasting. The specific conclusions are as follows.

  1. 1.

    By comparing and evaluating the prediction performance of LSTM and VD-LSTM models, it is found that under the same prediction period, VD-LSTM has better simulation effect, NSE is improved, and RMSE and bias are reduced to different degrees.

  2. 2.

    From the perspective of flood process simulation, the flow simulation results of VD-LSTM are in good agreement with the observed flow process line, which can reflect the measured flood process. Compared with LSTM, the model's problem of underestimating the flood peak and lag has been improved.

  3. 3.

    Under the same task and dataset, with the same hyperparameter settings, we observe the change of iterative loss function of the two models. It is found that VD-LSTM can reduce the loss function value more quickly and reach the fitting state faster than LSTM.

Overall, the VD-LSTM model has achieved relatively ideal results in flood forecasting. However, there are still some issues worth exploring in this research model. The ability to improve model accuracy through vectorization methods is limited, and it still has not completely overcome the problem of decreasing model accuracy as the prediction period increases. In order to further reduce the uncertainty and improve the model accuracy in flood forecasting, we need to conduct more in-depth research. A potential solution is to combine the physically-based hydrological model with the deep learning model, incorporating more hydrological influencing factors such as soil moisture, evaporation, temperature, etc. In addition, future research could explore about how in deep learning models by selecting appropriate samples, the model can learn the regularities present in historical data more quickly. The issue of how to improve the interpretability of machine learning models is also worth being explored in order to better understand the predictions of the models.