Introduction

Science is confronted with environmental issues and energy challenges brought on by the exploitation of fossil resources. The development of technology capable of reducing the consumption of fossil fuels is the solution to these problems. We squander a lot of energy in our daily lives as waste heat. Materials which have the capacity to convert waste heat into electrical energy are classified as thermoelectric1,2. By employing these resources, we can lessen our need on fossil fuels and find solutions to energy and environmental issues. In the modern period, thermoelectric materials have gained immense recognition and have had a significant influence on addressing the problems possessed by rising energy stresses. Due to their ability to transform waste heat into electrical energy, these materials are also viewed as potentially promising renewable energy sources in the future3,4. Thermoelectric material conversion efficiency is typically expressed as a figure of merit (ZT), which is defined as:

$$ ZT = {\frac{{{S^{2}} {\sigma}T}}{\kappa } }$$
(1)

where S, σ, κ, and T stand for the Seebeck coefficient, electrical conductivity, total thermal conductivity, and absolute temperature respectively. A high-power factor and low overall thermal conductivity (κ) values is a characteristic of efficient thermoelectric materials. A variety of thermoelectric materials, including Heusler alloys and skutterudites, have been used so far. Heusler alloys have garnered a lot of attention lately because of their potential use as smart materials5. Heusler alloys are essential to a wide range of applications, including spintronics, thermoelectric, superconductors, and topological insulators6, as well as energy and information storage. Back in 1983, de Groot et al.7,8 identified the half-Heusler alloy NiMnSb as the first half-metallic ferromagnet. Despite a relatively slow research pace, magnetic Heusler alloys have gained increasing attention in the last few years due to their potential application in magnetoelectronic devices9. Heusler-type materials crystallize with the space groups Fm-3m or F-43m10, where Z is a p-block elements and X and Y are two distinct transition metals. These materials constitute a broad class of ternary intermetallic compounds with the formula X2YZ. In weak applied magnetic fields, most Heusler alloys saturate and order ferromagnetically. With time, Heusler has developed into a significant collection of materials utilized in magneto resistive, thermoelectric, and spintronics11. One of the rapidly developing areas for the next generation of nano electronic devices is spintronics12,13, which aims to boost processing and memory capacity while lowering power consumption. It makes use of the spin degrees of freedom of electrons and/or holes, which interact with their orbital moments. Fritz Heusler developed some materials14,15, and these materials have garnered a lot of interest since they are utilized in spintronic devices, like spin-resonant tunneling diodes, light-emitting diodes, and spintronic transistors. The half-metallicity, spin-dependent charge transport characteristics, and electronic energy band gap around the Fermi level of Heusler materials16 have been frequently established.

Recent studies on a variety of transition metal compounds have shown half-metallic ferromagnetism. Shakeel et al.17 investigated the cobalt full Heusler alloy family for both Co2ScSb and Co2TiSb compounds under high pressure–temperature effects, and an indirect energy gap was used to demonstrate the half-metallic behavior. The half metallic characteristics of V2YSb (Y = Cr, Mn, Fe, Co) in a Hg2CuTi-type structure were recently predicted by Xing et.al.18. Sharma et.al.19 predicted the physical properties of Vanadium based Heusler alloys. Currently, Hafnium alloys are of great interest because they are less toxic than conventional metals, but they can also withstand structural and electronic transitions. Due to their light weight, static strength, stiffness, and oxidation resistance, these materials find wide application in aerospace industry. Recent work by Zhang et.al. determined the electronic structure and magnetism of Hf2VAl20. It would therefore be worthwhile to investigate the electronic structure and hence the transport properties of Hf-based Heusler compounds, which may act as a guide for experimentalists for synthesizing these ferromagnetic compounds21,22. Their non-toxicity, thermal stability, abundance in nature, environmental friendliness, and mechanical stability make them a good choice for application23,24. In a similar way, when it comes to thermoelectric materials, mechanical properties are crucial both from an application and operation perspective. However, the current compounds are ductile and could be potential candidates for thermoelectric technology25,26.

An outline of the paper is shown below: “Introduction” provides a brief introduction to the materials. “Computational methods” describes the research methodology used on the materials. A review of the structural properties, mechanical stability, electronic structure, magnetism, thermodynamic, thermoelectric, and optical properties is covered in “Structure and stability” (separated into sub-sections). The last “Conclusion” presents the summary and conclusions.

Computational methods

First principle full potential linear augmented plane wave (FP-LAPW) method embedded in WEIN2k code27,28 based on density functional theory (DFT)29 was used to investigate structural, electro-magnetic, thermodynamic and transport properties of Hf-based inverse Heusler alloys. Different approximations like generalized gradient approximation (PBE-GGA)30 which has been used to determine the optimized lattice parameter of the crystal and Tran–Blaha-modified-Becke–Johnson potential (mBJ)31is used to calcite the exchange–correlation potential. The plane wave cutoff parameter RMT KMAX is set to 7, where RMT is the smallest muffin tin radii while KMAX is the magnitude of the largest k-vector. The Brillouin zone is integrated over 1500-k points in the unit cell of k-space to achieve convergence of results. Gibbs2 modified32 code is used to determine various thermodynamic parameters like heat capacity, entropy, Grüneisen parameter, and Debye temperature. Elastic constants and other mechanical parameters were also calculated using cubic elastic package33. The Boltztrap code34 is used to investigate the thermoelectric properties of the alloys.

Structure and stability

Structural optimization

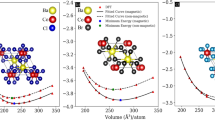
Hafnium based Heusler alloys are categorized under Inverse full Heusler alloy35 which are symbolized with structure formula Y2XZ where X and Y belongs to transition elements and Z belongs to p-block elements and have Hg2CuTi-prototype structure. These type of Heusler alloys crystallize with C1b structure having space group F-43m. The Wycoff’s positions occupied by individual element are Hf-I (0, 0, 0), Hf-II (0.25, 0.25, 0.25), V (0.50, 0.50, 0.50) and (Z = Ga, In, Tl) (0.75, 0.75, 0.75) respectively. Energy versus volume optimization curve of Hf2VZ (Z = Ga, In, Tl) alloys is shown in Fig. 1a–c. Pictorial representation of Hf2VZ (Z = Ga, In, Tl) is shown in Fig. 1d. Results shows that ferromagnetic state has minimum energy than non-magnetic state indicating the stability in FM state. Using Birch Murnaghan equation36, the optimized values of lattice parameter, volume (nm)3, bulk modulus (B), derivative of bulk modulus (BP), are indicated in Table 1.

Fig. 1
figure 1

(a–c) Energy versus volume optimization plot of Hf2VZ (Z = Ga, In, Tl) Heusler alloys, (d) Pictorial representation of crystal structure of Hafnium based Heusler alloys.

Full size image
Table 1 The computed values of Lattice constant (a0), Volume (V0), Bulk modulus (B0), derivative of bulk modulus (BP). ground state energy (E0) and the number of valence electrons of Hf2VZ (Z = Ga, In, Tl) Heusler alloys.
Full size table
$${E}_{\left(V\right)}={E}_{O}+\frac{9{B}_{0}{V}_{0}}{16}\left\{\left[{\left(\frac{{V}_{0}}{V}\right)}^{2/3}-1\right]{B}_{0}{\prime}+{\left[{\left(\frac{{V}_{0}}{V}\right)}^{2/3}-1\right]}^{2}\left[6-4{\left(\frac{{V}_{0}}{V}\right)}^{2/3}\right]\right\}$$
(2)

Cohesive and formation energies

Theoretically, the stability of a material can be ascertained using the factors cohesive energy (ECoh), mechanical stability, and formation energy. The ECoh, which measures an alloy's binding strength, is defined as the energy required to split a material into its component parts. It evaluates the stability of a material39. Therefore, the cohesive energy is employed in the measurement of a substance's intermolecular energy. The following formula, which may be used to calculate the ECoh values of the alloys under consideration, involves adding together all of the atomic energies and deducting them from the alloy's total energy.

$${\text{E}}_{\text{Coh}}=\frac{\left({2E}_{Hf}+{E}_{V}+{E}_{(Ga,In,Tl}\right)-{\text{E}}_{\text{Total}}}{4}$$
(3)

where, ETotal is the total energy of the Hf2VZ (Z = Ga, In, Tl) Heusler alloy, EHf, EV and E (Ga, In, Tl) are the energies of Hf, In and Z (Ga, In, Tl) atoms in free space. A free energy can be calculated from the ground state lattices of all individual atoms. The calculated values of Hf2VZ (Z = Ga, In, Tl) is listed in Table 2

Table 2 Computed values of cohesive energy (eV per atom), Formation energy (eV per atom) and energy difference between in FM and NM states.
Full size table

An enthalpy of formation energy (ΔHF) represents the energy change that occurs when a single mole of a compound is formed from its component elements in their normal states. The following formula can be used to compute it:

$$\Delta {H}_{F}={E}_{Total}-{2E}_{Hf}-{E}_{V}-{E}_{Z(Ga,In,Tl)}$$
(4)

where, ETotal is the total energy of the alloy, EHf, Ev and E(Ga, In, Tl) are the energies of the constituent element while a, b and d are the coefficients of the constituent elements. The computed values are reported in Table 2. The compound is stable if the enthalpy of formation energy is negative. This is due to the fact that the compound's synthesis causes an energy release.

Electronic and magnetic property

The study of electronic structures40,41 focuses on the electronic behavior of the material around the Fermi energy (EF) level. These electronic characteristics are explained by the electronic band structure and density of electronic states. Band structure and densities of states (DOS and PDOS) are the fundamental components of electronic properties; they describe the individual and the correlative interactions among the constituent atoms of a system. For the current materials, the spin-resolved band structure as displayed were predicted using the GGA-PBE functional and mBJ potential. Galanakis et al.42 used d-d hybridization to explain the presence of a band gap in full-Heusler compounds with 18 valence electrons. The band gap known as the d–d band gap is caused by the participation of d-orbitals in full-Heusler compounds. Since the band structure has a significant influence on the thermoelectric properties, it is widely known that the band structure is essential for determining these properties. It is crucial to determine the band gap (Eg) precisely, the generalized gradient approximation and the mBJ potential were employed to predict the band gaps of Hf2VZ (Z = Ga, In, Tl) Heusler alloys. The band structure represents the electronic energy levels of the materials, while DOS represents the number of states per unit volume. The density of the state also reveals whether the material is a conductor, semi-conductor, or insulator. The partial density of states (pDOS) is determined in order to acquire further information about the contribution of each energy state.

Figures 2, 3 and 4 represents the intended spin-polarized band structures of the Hf2VZ (Z = Ga, In, Tl) compounds at the equilibrium lattice constant. A semiconductor or an insulator is produced when there is a prohibited gap between the valence band (VB) and conduction band (CB) and when the electronic states between these two bands overlap at the fermi level, it indicates the metallic nature of the alloys. It demonstrates that the majority spin (spin-up) band around the Fermi level (EF) exhibited semiconducting behavior, and that the minority spin (spin-dn) band was metallic in these hafnium-based alloys where the energy bands crossed the EF at different symmetry points. The d–d hybridization of transition metal atoms is the source of the apparent band gap in the minority spin state and half-metallicity in Heusler compounds. These materials are all indirect bandgap semiconductors in the up spin with band gap values (Eg) 0.64, 0.60 and 0.71 eV respectively as evidenced by the ___location of the valence band maximum (VBM) at the W point and the conduction band minimum (CBM) at the L point.

Fig. 2
figure 2

Band profile of Hf2VGa Heusler alloys in spin-up and spin-dn via. GGA and mBJ approximation.

Full size image
Fig. 3
figure 3

Band profile of Hf2VIn Heusler alloys in spin-up and spin-dn via. GGA and mBJ approximation.

Full size image
Fig. 4
figure 4

Band profile of Hf2VTl Heusler alloys in spin-up and spin-dn via. GGA and mBJ approximation.

Full size image

Figures 5, 6 and 7 represents the total density of states (TDOS) for Hf2VGa, Hf2VIn and Hf2VTl alloys. Subsequently, we have endeavored to comprehend the elemental contribution and visibility of atomic states in these alloys, which were extensively examined by the (mBJ) functional scheme; thus, partial densities of states (pDOS) are plotted as illustrated in Fig. 8, 9 and 10. The activeness of d-states of Hafnium and Vanadium atoms are more populated because of the presence of d-states, which leads a sufficient quantity of magnetism toward the cell structure. The p-states of Ga, In and Tl are deep, low-lying states with minimal visibility, hence the contribution toward magnetic structure in these alloys is modest. Nevertheless, it is evident from the pDOS graphical plots that substantial d–d hybridization is maintained in these kinds of C1b structured alloys, as the Fermi level in both alloys is mostly assembled by these d-states. The band channels, along with their interpretation based on the corresponding DOS, indicate a strong half-metallic characteristic in these alloys, which is responsible for the projected 100% spin polarization effect. Therefore, the ability of high-performance electronic devices to have a necessary tunable band-gap provides a supporting stand to satisfy the needs of modern technology.

Fig. 5
figure 5

Graphical representation of Total density of state (TDOS) in spin-up and spin-down channel of Hf2VGa alloy.

Full size image
Fig. 6
figure 6

Graphical representation of Total density of state (TDOS) in spin-up and spin-down channel of Hf2VIn alloy.

Full size image
Fig. 7
figure 7

Graphical representation of Total density of state (TDOS) in spin-up and spin-down channel of Hf2VTl alloy.

Full size image
Fig. 8
figure 8

Graphical representation of PDOS of Hf2VGa alloy in spin-up and spin-down state.

Full size image
Fig. 9
figure 9

Graphical representation of PDOS of Hf2VIn alloy in spin-up and spin-down state.

Full size image
Fig. 10
figure 10

Graphical representation of PDOS of Hf2VTl alloy in spin-up and spin-down state.

Full size image

Additionally, the report highlights the magnetism as a crucial and noteworthy property of these alloys. The description of these alloys' magnetic characteristics justifies their potential use as an application feature in spin-based disciplines such as spintronics. In order to determine the magnetic moment for these alloys, as indicated in Table 3, the current computation makes full use of the GGA and mBJ methods. According to the Table 3, the Hf-atom in various approximations serves as a demonstration of how to maintain enough magnetism in matching magnetic structures. The overall magnetism in both alloys is attributed to the cell structure, which is also influenced by the magnetic moment of the remaining atoms. Therefore, it is clear from the magnetic analysis of these advantageous alloys that these substances have the potential to be strong contenders for multiferroic and magnetoresistive materials in spintronics and.

Table 3 The total and atomic magnetic moment of individual atom of Hf2VZ (Z = Ga, In, Tl) Heusler alloy.
Full size table

In this section we have also studied about the magnetic properties of the materials. The calculated magnetic moments of Hf2VZ (Z = Ga, In, Tl) are shown in Table 3. The magnetic moment can be calculated using the Slater-Pauling rule43. The Hf2VZ (Z = Ga, In, Tl) inverse Heusler alloys follow Mt = Zt − 18 SP-rule to determine the magnetic moments of these alloys, where Mt stands for total magnetic moment and Zt stands for the total number of valence electrons. Using the GGA and mBJ functions, it is observed that these inverse Heusler alloys are half-metallic ferromagnets. The manuscript provides an overview of the total magnetic moment calculation, which includes contributions from both atomic and interstitial regions. It is discovered that the interstitial region, Hf atoms, V atoms, and (Z = Ga, In, Tl) atoms all contribute to the total magnetic moment (Mt). The information presented in Table 3 indicates that the V atom (with the Hg2CuTi structure) is the primary source of the total magnetic moment (Mt). The contributions to the magnetic moment from the (Z = Ga, In, Tl) atoms and interstitial regions are insignificant, and the atomic magnetic moments of Hf-I and Hf-II are anti-parallel to those of the Cr atoms in the Hg2CuTi type structures44. The half-metallic ferrimagnet nature of Hf2VZ (Z = Ga, In and Tl) is confirmed by its magnetic moment of 2.0 μB (spin polarization 100%). This is a type of magnetic ordering where there are two or more sublattices with different magnetic moments. The moments in different sublattices are aligned anti-parallel to each other, but their magnitudes are not necessarily equal This information is noteworthy that Hf2VZ (Z = Ga, In and Tl) exhibits approximately ferrimagnetic half-metallic behavior. Hf2VZ (Z = Ga, In and Tl) has 16 total valence electrons per unit cell ((2 × 4) + 5 + 3 = 16). As a result, the Hf2VZ compounds, where (Z = Ga, In and Tl) are half-metallic and actually follow the Slater-Pauling equation, which reads Mt = 18 − Zt. Thus, we can say that these compounds have potential to be used as spintronic materials.

Mechanical stability

Elastic constants are used to define mechanical stability45,46. Due to their firmly correlation to several fundamental solid-state phenomena, including interatomic bonding, equations of state, and phonon spectra, these constants are fundamental and essential for explaining the mechanical properties of materials. Additionally, specific heat, thermal expansion, Debye temperature, and Grüneisen parameter are thermodynamically related to elastic characteristics. Most significantly, understanding elastic constants is necessary for a wide range of real-world applications involving a solid's mechanical properties, including sound velocities, internal strain, load deflection, thermoelastic stress, and fracture toughness. The elastic constants Cij are the coefficients of proportionality that relate the stress and applied strain. Thus, the Cij ascertain the crystal's reaction to outside factors. There are twenty-one independent elastic constants Cij, although cubic symmetry number have just three elastic constants namely C11, C12, and C44. The elastic constants Cij are found by adding up all of the energy as a function of strains that break the volume conservation balance47. For Hf2VZ (Z = Ga, In, Tl), the cubic structure is unquestionably supported by structural optimization. Only C11, C12, and C44 are required for cubic structure in order to examine the mechanical behavior of these alloys. Using the Tetra-elastic package48, the elastic constants of our compounds are computed at their equilibrium lattice constants.

The ground state structure is deformed to acquire them, and the computed values are presented in Table 4. The mechanical properties of a material indicate its capability to regain its initial shape after deforming. In terms of technological and industrial applications, these properties provide decent information about the material. Materials' elastic constants are important because they are closely related to their behavior, including their hardness, durability, strength, and performance. The cubic lattice has three elastic constants, C11, C12, and C44. Due to the known mechanical stability of cubic compounds, Born Haung gave the following criteria C11 > 0, C44 > 0, and (C11-C12) > 049,50. The Heusler alloy Hf2VZ (Z = Ga, In, Tl) meets all the conditions outlined above, demonstrating that they are mechanically stable. We have calculated elastic constants and their derived mechanical parameters like shear modulus (G), bulk modulus (B), Voigt shear (GV), Reuss shear (GR), isotropic shear (GH), and Young’s (Y) moduli, and Zener isotropy factor (A), Cauchy pressure (C12 − C44), Pugh’s index of ductility (B/G), Poisson’s ratio (γ), and Kleinman parameter (ξ).

Table 4 Representation of Elastic constants and their derived mechanical parameters of Hf2VZ (Z = Ga, In, Tl) inverse Heusler alloys.
Full size table

The bulk modulus which depends on the value of C11, C12 and C44 is determine by the following equation:

$$B=\frac{{C}_{11}+{2C}_{12}}{3}$$
(5)

The shear modulus (G) is defined as the ratio of shear stress to the shear strain:

$$G=\frac{{G}_{V}+{G}_{R}}{2}\text{where}, {G}_{V}=\frac{{C}_{11}-{C}_{12}+{3C}_{44}}{5}; {G}_{R}=\frac{{5C}_{44}\left({C}_{11}-{C}_{12}\right)}{3\left({C}_{11}-{C}_{12}\right)+{C}_{44}}$$
(6)

The Young's module (Y) is an indicator of material hardness derived from the bulk module (B) and shear module (G). Material with a higher Y value has a stiffer structure than material with a lower Y value.

$$Y=\frac{9BG}{3B+G}$$
(7)

When the material is completely isotropic, elastic anisotropy factor (A) is 1. Otherwise, the material is anisotropic. Based on the calculated values of A, we can conclude that these three materials have anisotropic nature. The calculated value of A is 16.80, 4.01, 2.15 for Hf2VZ (Z = Ga, In, Tl), respectively. The anisotropy factor(A) is determined by the following relation:

$$A=\frac{{2C}_{44}}{{C}_{11}-{C}_{12}}$$
(8)

Another important parameter is Cauchy pressure, if the value of Cauchy It is concluded that these alloys are characterized by a large anisotropy. They can exhibit ductile or brittle nature. Another mechanical feature which determines the brittle and ductile nature of the material is Pugh’s Ratio (B/G)51. If B/G > 1.75, it indicates ductile nature while if B/G < 1.75, it indicates brittle nature. The calculated value of Pugh’s ratio is greater than 1.75, so these alloys represent a ductile behavior. Another parameter is Poisson’s ratio (ʋ) which describes the bonding quality of material by following relation:

$$ \upsilon = \frac{3B - Y}{{6B}} $$
(9)

The Poisson's ratio52 for a typical covalently bound compound is less than 0.25, whereas for a typical ionic compound, it is close to or greater than 0.25. Thus, these materials have value greater than 0.25, it shows ionic bonding. The relative ease of bond bending versus bond elongating is shown by the Kleinman parameter (ξ), which calculates internal strain. Reduced bond bending in a structure shows ξ = 0, while increasing bond stretching indicates ξ = 1. For Hf2VGa, the ξ parameter is 0.94, for Hf2VIn, the ξ parameter is 0.84 and for Hf2VTl, the value of parameter is 0.92. Hence, Hf2VGa reflects slightly more resistance to bond bending in comparison to Hf2VIn and Hf2VTl.The parameter is determined by following relation:

$$\upxi =\frac{{C}_{11}+{8C}_{12}}{{7C}_{11}+{2C}_{12}}$$
(10)

Furthermore, melting temperature is another thermodynamic property that may be computed using the following empirical expression53, which is defined as:

$${T}_{m}\left(K\right)=\left[553\left(K\right)+\left(5.911\right){C}_{11}\right]GPa\pm 300(K)$$
(11)

For Hf2VGa, Hf2VIn and Hf2VTl, the measured Tm values are 1295.53 ± 300, 1240.98 ± 300 and, 1986.77 ± 300 respectively. Since the value of Tm for Hf2VZ (Z = Ga, In, Tl) is very high, therefore these alloys can maintain its ground state structure over a broad range of temperatures. The average velocity (vm) can be estimated utilizing longitudinal velocity (vl) and transverse velocity (vt).

$$ v_{m} = \left[ {\frac{1}{3}\left( {\frac{2}{{v_{l}^{3} }} + \frac{1}{{v_{t}^{3} }}} \right)} \right]^{{ - \frac{1}{3}}} $$
(12)

vl and vt were calculate using Navier’s equation54:

$${v}_{l}=\sqrt{\frac{\left(3B+4G\right)}{3\rho }}; {v}_{t}=\sqrt{\frac{G}{\rho }}$$
(13)

Table 5 displays the pure modes of longitudinal and transverse velocities that were determined in three different directions ([100], [110], and [111]) using Brugger's relation. Calculating the mechanical characteristics is primarily necessary since they need to be able to survive deformations and find appropriate applications in a variety of industries.

Table 5 The calculated longitudinal and transverse velocities of Hf2VZ (Z = Ga, In, Tl) Heusler alloys along [100], [110] and [111] direction.
Full size table

Thermodynamic property

We have determined various thermodynamic properties of these alloy using a modified version of quasi-harmonic approximation (QHA)32 to understand the effect of pressure and temperature variation on the various structural aspects. In this study, we examined the variation for various thermodynamic parameters including heat capacity (CV), Grüensien parameter (γ), Thermal expansion coefficient (α) and Debye temperature (θD). The Hafnium-based alloy shows the effect of temperature ranging from 0 to 500 K and pressure ranging from 0 to 20 GPa.

Heat capacity or the specific heat (CV) is defined as the ability to absorb heat from its surrounding. Figure 11 shows the variation of heat capacity with temperature at different pressure. It is clear from graph that when pressure is applied specific heat decreases, although the decrease is much smaller when temperature is applied. As the temperature rises, Cv tends towards the constant value, confirming Dulong and Petit’s law55 According to Debye T3 law, an exponential increase in heat capacity is shown at low temperature. The obtained value of heat capacity at 0 GPa and 300 K for Hf2VGa is 93.09 J mol−1 K−1, Hf2VIn is 92.76 J mol−1 K−1, Hf2VTl is 89.43 J mol−1 K−1.

Fig. 11
figure 11

Graphical representation of Heat capacity as a function of temperature for Hf2VZ (Z = Ga, In, Tl).

Full size image

Grünesien parameter is a dimensionless parameter used to determine the thermal stability56. Figure 12 represents the variation in grünesien parameter in the pressure range 0–20 GPa and temperature ranging from 0 to 500 K. It is clearly observed from the figure that with increase in temperature it shows a smooth increasing trend while decreasing trend with increase in pressure. The observed value of Grüneisen parameter at room temperature are 3.02 for Hf2VGa, 1.74 for Hf2VIn and 1.75 for Hf2VTl respectively.

Fig. 12
figure 12

Graphical representation of Grünesien parameter as a function of temperature for Hf2VZ (Z = Ga, In, Tl).

Full size image

The Fig. 13 represents thermal expansion coefficient (α) of the materials for the pressure range from 0 to 20 GPa and temperature ranging from 0 to 500 K. With an increase in temperature, a sharp increasing trend is observed in thermal coefficient57 but a declining trend is observed, when pressure is applied, indicating the lattice compression plays an important role. The observed value of thermal coefficient at 300 K and 0 GPa are 4.14 for Hf2VGa, 2.02 for Hf2Vin and 1.11 for Hf2VTl respectively, which follows the trend Ga > In > Tl.

Fig. 13
figure 13

Graphical representation of Thermal Coefficient as a function of temperature for Hf2VZ (Z = Ga, In, Tl).

Full size image

In Fig. 14 we have plotted Debye temperature(θD) with temperature at variable pressure ranging from 0 to 20 GPa and temperature ranging from 0 to 500 K. Debye temperature refers to the behavior of specific heat and provide a wealth of information about the characteristics of solid materials under the influence of temperature. With increase in temperature, θD shows a decreasing trend while increasing trend is seen with pressure. The corresponding value of θD are 356.23 for Hf2VGa, 368.23 for Hf2VIn and 454.49 for Hf2VTl.

Fig. 14
figure 14

Graphical representation of Deby Temperature as a function of temperature for Hf2VZ (Z = Ga, In, Tl).

Full size image

Thermoelectric property

We are searching for alternate ways to address the energy issue we are currently facing. Thermoelectric materials are those that are useful in managing these energy unforeseen circumstances. Thermoelectric materials58 are an efficient way to use waste heat since they can immediately transform heat into useful energy and vice versa. It has been demonstrated that waste heat produced by many sources (such as vehicle heat, industrial heat, or solar heat) can be converted into useable energy by thermoelectric materials. A thermoelectric device59,60 is a solid-state device that has numerous benefits, such as being extremely adaptable, mechanically stable, silent, compatible, and consistent. These qualities also make them ideal for long-term commercial applications. The figure of merit, a dimensionless parameter, can be used to determine the thermoelectric material's performance. Thermoelectric materials are actually an alternative to other power-producing materials since they can transform thermal energy into electrical energy. The conversion of efficiency of thermoelectric is entirely dependent on transport coefficients i.e., σ and S. For a material to be thermoelectric it should have a high electrical conductivity, large seebeck coefficient and a low thermal conductivity. The thermoelectric parameter like seebeck coefficient (S), thermal conductivity (κtotal), electrical conductivity(σ) in the temperature range 0–900 K. Figure 15a–c displays the variation of seebeck coefficient as a function of temperature.

Fig. 15
figure 15

(a–c) Graphical representation of Seebeck Coefficient and (d) represents Total Seebeck coefficient as a function of temperature for Hf2VZ (Z = Ga, In, Tl).

Full size image

The Seebeck coefficient is defined by the following relation:

$$S=\frac{8{\pi }^{2}{K}_{B}^{2}}{3{e}^{2}}{m}^{*}T{\left(\frac{\pi }{3n}\right)}^{2/3}$$
(14)

Here, m is the effective mass and n designates carrier concentration. The positive value of seebeck coefficient indicates that holes are highly dominant in both the spin channels, whereas the variation of seebeck coefficient with temperature shows decreasing trend from 2215.22 to 77.92 μV/K in the spin-up channel revealing the semiconducting nature while increasing trend from 3.20 to 27.78 μV/K in spin-down channel revealing the metallic nature. The total seebeck coefficient is configured by the two current model61:

$$S=\frac{{S}^{\uparrow }{\sigma }^{\uparrow }+{S}^{\downarrow }{\sigma }^{\downarrow }}{{\sigma }^{\uparrow }+{\sigma }^{\downarrow }}$$
(15)

The product of S↑σ↑ and S↓σ↓ are the values of seebeck coefficient in spin up and spin-down channels. The total Seebeck is also represented in Figure 15d. The value of STotal increases from 3.20 μV/K at 50 K to 30.2 μV/K at 900 K for Hf2VGa, from 5.27 μV/Kat 50 K to 40.7 μV/K at 900 K for Hf2VIn and from 3.25 μV/K at 50 K to 39.8 μV/K at 900 K for Hf2VTl respectively. Electronic equipment relies heavily on their electrical conductivity. Materials are classified into metals, ceramics, and semiconductors. Electrical conductivity in these materials differs from each other. The changes are due to the width of the Fermi level. Metals have unbound electrons and a narrow band-gap, whereas semiconductors have a small band-gap. A material's electrical conductivity is characterized by its ability to conduct electric current, and by the mobility and concentration of its carriers (holes and electrons). For high thermoelectric efficiency, the material should have high electrical conductivity. In addition to the increase in carrier concentration, the σ also increases at higher temperatures. A mathematical equation relating carrier concentration and electrical conductivity is σ = neμ, where μ is the mobility. Figure 16 displays the variation of electrical conductivity as a function of temperature for Hf2VZ (Z = Ga, In, Tl) Heusler alloys. From the given plots σ/τ increases with rise in temperature in the up spin for all alloys. The increasing trend lies for Hf2VGa lies from 0.001 × 1020 Ω−1 m−1 s−1 to 0.125 × 1020 Ω−1 m−1 s−1, for Hf2VIn increasing trend lies from 0.00012 × 1020 Ω−1 m−1 s−1 to 0.1444 × 1020 Ω−1 m−1 s−1 and for Hf2VTl lies from 0.00015 × 1020 Ω−1 m−1 s−1 to 1.91 × 1020 Ω−1 m−1 s−1.The thermal conductivity is determined by two processes: (a) drift of electrons and holes (\({\kappa }_{e}\)) and (b) by phonons (\({\kappa }_{l}\)). As a result, thermal conductivity is defined as:

Fig. 16
figure 16

Graphical representation of electrical conductivity as a function of temperature of Hf2VZ (Z = Ga, In, Tl).

Full size image
$$\kappa ={\kappa }_{e}+{\kappa }_{l}$$
(16)

To evaluate the total thermal conductivity of these alloys, consider both the lattice (κl) and electronic (κe) components. Figure 17 shows the variation of total thermal conductivity (both electrical and lattice thermal conductivity) of Hf2VZ (Z = Ga, In, Tl) Heusler alloy. The electrical component shows a linear increase as temperature increases from 0.31 W/mk at 50 K to 6.13 W/mk at 900 K for Hf2VGa, 0.26 W/mk to 4.94 W/mk for Hf2VIn and 0.22 W/mk to 5.21 W/mk for Hf2VTl. In addition, the lattice component in Fig. 17 is assessed using Slack's equation62 approach which is expressed as: -

$${\kappa }_{l}=\frac{A{\theta }_{D}m{V}^{1/3}}{{\gamma }^{2}{n}^{2/3}T}$$
(17)

where A is a constant with a value of 3.0 × 10−8, m is molar mass, V is volume, γ is the Grüneisen parameter, and "n" is the number of atoms in a unit cell. Taking into account the fact that lattice thermal conductivity exhibits an inverse relationship with temperature, indicating a decreasing trend with increasing temperature. Since lattice conductivity is evaluated using thermodynamic parameters, which are mostly temperature independent, κl is dictated by the number of atoms in a unit cell. The band gap depicted in Figs. 2, 3 and 4 makes it clear that the lattice thermal conductivity virtually tends to zero and that electronic conductivity is the only source of total thermal conductivity, with the lattice component being essentially inconsequential. The decreasing trend is as follows: for Hf2VGa 5.37 W/mk at 50 K to 0.25 W/mk at 900 K, while for Hf2VIn 17.77 W/mk to 1.63 W/mk and for Hf2VTl 38.52 W/mk to 3.12 W/mk. To determine the thermoelectric efficiency, we further analyze the dimensionless parameter figure of merit. Figure 18 shows the variation of Figure of merit (ZT) as a function of temperature. The figure of merit determines the efficiency of the alloys, The obtained value of ZT for Hf2VGa is 0.25, Hf2Vin is 0.26, Hf2VTl is 0.12 respectively at room temperature. Conclusive observations show this series of full Heusler alloys have appropriate Seebeck coefficients, making them useful for thermoelectric devices. Hence, these materials in terms of performance have potential for thermoelectric application due to their efficient characteristics. They thus turn into a practical choice for green energy and sustainable development applications.

Fig. 17
figure 17

Graphical representation of Electrical Thermal conductivity (κe) and Lattice thermal conductivity (\({\kappa }_{l}\)) Hf2VZ (Z = Ga, In, Tl) Heusler alloys.

Full size image
Fig. 18
figure 18

Graphical representation of Figure of merit (ZT) as a function of temperature of Hf2VZ (Z = Ga, In, Tl).

Full size image

Optical property

To ascertain whether the materials is appropriate for an opto-electronic applications, its essential to explore various optical parameters like dielectric constants, absorption coefficient, conductivity and reflectivity etc.63. The electronic band structures of semiconductor materials are closely associated with their optical properties, which are often evaluated from the dielectric function using the formula:64,65

$$ \varepsilon \left( \omega \right) = \varepsilon_{{1}} \left( \omega \right) \, + {\text{ i}}\varepsilon_{{2}} \left( \omega \right) $$
(18)

where, (ω) representing the angular frequency and ε1(ω) and ε2(ω) denoting the real and imaginary parts of the complex dielectric function, correspondingly. The Kramers–Kronig66,67 relation serves as an expression for the real dielectric tensor, which specifies the polarization and dispersion of light entering the compound.

$${\varepsilon }_{1}\left(\omega \right)=1+\frac{2}{\pi }P{\int }_{0}^{\infty }\frac{{\omega }{\prime}{\epsilon }_{2}\left({\omega }{\prime}\right)}{{\omega }^{{\prime}2}-{\omega }^{2}}{d\omega }{\prime}$$
(19)

Here, P is the principal value of integration, whereas ε2 (ω)imaginary dielectric tensor describe the attenuation of incident radiations, respectively and the matrix of momentum elements and joint critical points are used to express ε2 (ω)68.

$${\varepsilon }_{2}\left(\omega \right)=\frac{{e}^{2}{h}{\prime}}{\pi {m}^{2}{\omega }^{2}}{\sum }_{V,C}{M}_{i}\delta \left({E}_{c}-{E}_{v}-\omega \hslash \right)$$
(20)

In this equation, m and e represent an electron's mass and electronic charge. ω is the frequency of the photon that excites it from valence to conduction state. Figure 19a,b illustrates the real and imaginary part of the dielectric constant Heusler alloys' main qualities are their capacity to serve as materials that absorb light and can be for a range of optoelectronic applications. Therefore, the main goal was to determine how these materials may be used in the visible and ultraviolet light absorption spectrum, which is crucial for optoelectronic applications. Usually, to do this, the absorption coefficients are assessed and their energy gaps are determined. According to the complex dielectric function, the frequency-dependent absorption coefficient (α) is as follows:

Fig. 19
figure 19

Variation of the dielectric constant (a) Real part (ε1) and (b) Imaginary part (ε2) as a function of energy of Hf2VZ (Z = Ga, In, Tl).

Full size image
$$\alpha \left(\omega \right)=\sqrt{2{\omega }^{2}\left({\varepsilon }_{1}^{2}+{\varepsilon }_{2}^{2}\right)}-\sqrt{2\omega {\varepsilon }_{1}}$$
(21)

The absorption coefficient of the entire Heusler alloys Hf2VZ (Z = Ga, In, Tl) is displayed in Fig. 20. The absorbance coefficient sharply increases in the energy range of 4–10 eV, suggesting that more transitions between the conduction and valence bands take place in this region. Furthermore, a broad range of energy is shown to be absorbed, suggesting that these materials have potential use as optical devices as well as electromagnetic wave shielding materials. Electromagnetic waves are reflected and absorbed by materials that act as shields against electromagnetic waves.

Fig. 20
figure 20

Variation of the absorption coefficient as a function of energy of Hf2VZ (Z = Ga, In, Tl).

Full size image

Materials that conduct electrons when exposed to photons of a certain frequency are said to be optically conducting. Figure 21 shows the variation in optical conductivity (σ) in spin-up and spin-dn channels for Hf2VZ (Z = Ga, In, Tl). It is characterized as the electrical transmission's amplification to high spectral frequencies (ω). Hence, based on their optical characteristics, these materials exhibit absorption in the UV and visible regions and have a propensity to be employed in opto-electronic systems. Our data clearly show that Hf2VZ (Z = Ga, In, Tl) has a substantial value, which makes it a suitable option for solar systems. Refraction is the phenomenon that happens when a change in the propagation speed causes a light beam to rotate while it is passing through an optical medium. This phenomenon has a refractive index of ƞ(ω). The refractive index, or ƞ(ω), as indicated in Fig. 22a,b, quantifies the amount of deformation or refractive index that occurs when light enters an element. Complex refractive index can be expressed in terms of dielectric coefficient as:

Fig. 21
figure 21

Variation of optical conductivity (σ) as a function of energy of Hf2VZ (Z = Ga, In, Tl).

Full size image
Fig. 22
figure 22

Variation of Refractive Index (ƞ) as a function of energy of Hf2VZ (Z = Ga, In, Tl).

Full size image
$$N=\sqrt{\varepsilon (\omega )}$$
(22)

Complex refractive index can be expressed as the sum of real and imaginary parts,

$$N=n(\omega )+ik(\omega )$$
(23)

As a result, the real and imaginary parts of the complex refractive index are expressed as follows:

$$n\left(\omega \right)={\left(\frac{\sqrt{{\varepsilon }_{1}^{2}+{\varepsilon }_{2}^{2}}+{\varepsilon }_{1}}{2}\right)}^{1/2}$$
(24)
$$k\left(\omega \right)={\left(\frac{\sqrt{{\varepsilon }_{1}^{2}+{\varepsilon }_{2}^{2}}-{\varepsilon }_{1}}{2}\right)}^{1/2}$$
(25)

It also shows the phase velocity of an electromagnetic wave as it passes through a substance. The linked energy and wavelength have a big impact on penetration. Since all of the light will be absorbed here, where the wavelength is short, there won't be any transmittance at higher energies. There will be a relatively strong transmittance at lower energy with longer wavelengths since there are no notable electronic transitions at a range of low energies. For the three compounds under research, Hf2VZ (Z = Ga, In, Tl), the static refractive index is 4.93, 4.74, and 5.06 in this instance, as indicated in Fig. 19a. The potential transmission of electromagnetic waves through any material is commonly quantified by the extinction coefficient, a complicated component of the refractive index. The ability of a substance to absorb or reflect radiation or light at a specific wavelength is measured by a parameter called the extinction coefficient. As seen in Fig. 19b, all compounds reflect their maximum extinction coefficients in the UV region. From the perspective of applications, the refractive index and extinction coefficient are used in optical devices like photonic crystals, wave guides, and solar cells, as well as the amount of light that will be reflected upon reaching the interface.

Conclusion

By using the FP-LAPW method of WEIN2k, we investigated the electronic, magnetic, and thermoelectric properties of the Hf2VZ (Z = Ga, In, Tl) compound with Hg2CuTi structure in detail. The ground state properties of these alloys are obtained by optimizing in FM and NM state showing stability in ferromagnetic state. In addition to being half-metallic, the compound is predicted to be 100% spin polarized, making it an excellent candidate for spintronic devices. With increasing Z atomic number, the lattice constant increases. We found the alloys to be ferromagnetic with half-metallic behavior. Slater-Pauling's generalized rule Zt = Mt − 18 of magnetism determines the total magnetic moment within a unit cell. and vanadium atom contribute the largest amount of magnetism in these alloys. Due to the presence of band gaps in spin-up channels, two approximations, GGA and mBJ, depict the half metallic nature of the alloys. In addition to their mechanical properties, thermoelectric properties have demonstrated their stability, durability and suitability for energy conversion devices. The exceptional optical characteristics of these alloys, which exhibit absorption in the visible and ultraviolet spectrum, make them popular choices for opto-electronic systems. These results suggest that these alloys can be utilized to thermoelectric devices and spintronics applications successfully. The examined materials' band gap allows for applications in the infrared spectrum beyond fiber communication, astronomy, chemical industries, and medical.