Introduction

The paradigm of unmanned aerial vehicle (UAV)-assisted communication is poised to play a crucial role in future wireless communication systems, offering ubiquitous communication connections with wider and deeper coverage1. In particular, utilizing UAVs as aerial base stations (BSs) to assist ground devices (GDs) in data transmission tasks is anticipated to be a promising technology for green communication. The data transmission system based on UAV-BS offers several advantages over terrestrial BS-based. For instance, it leverages the UAVs’ high mobility to enable long-distance data transmission and the high probability of a Line-of-Sight (LoS) channel to quickly accomplish transmission tasks2. Additionally, the deployment of UAVs and their versatility provide assistance to ground communication equipment in complex environments (such as earthquakes, tsunamis, fires, etc.), enabling seamless completion of data transmission tasks3.

Additionally, UAVs can efficiently move towards selected GDs and establish reliable communication connections with low time costs. Thus, the UAVs’ trajectory design and GDs’ communication scheduling are essential for UAV-assisted communication networks. In particular, several recent studies have validated the significant gain of the UAVs’ trajectory design and GDs’ communication scheduling in UAV-assisted data transmission system4,5,6,7,8,9. The authors maximize the system throughput by optimizing the trajectory of the UAVs in the UAV-assisted communication system4,5. In addition, a block coordinate descent (BCD) algorithm is proposed6 to solve the non-convex trajectory design issue. For the scenario of UAV equipped with an intelligent reflecting surface (IRS), the authors7 jointly optimize communication scheduling, the phase shift of RIS, and the trajectory of UAV to maximize the minimum average transmission rate. In addition, the works8,9 propose UAV-assisted schemes to optimize the energy-efficient of the whole operation system by designing the three-dimensional (3D) trajectory of the UAV and communication scheduling. However, the above literature does not consider more practical scenarios. For instance, the works4,5,6,7,9 only consider the simplified LoS-dominant channel. In addition, the mobility of GDs and NFZs are also ignored in4,5,6,7,8,9, i.e., GDs are fixed in one ___location. On the one hand, the trajectory of UAV is restricted more by the detailed characteristics of the environment, which requires the design carefully taking into consideration environmental factors such as altitude variation, multi-dimensional propagation characteristics, and the effects of obstacles and blockages on the channel. On the other hand, in practical scenarios, GDs are often in a mobile state, and there are areas such as schools, shopping malls, etc., where UAVs are prohibited from flying.

Nevertheless, due to the non-convex nature of the problem, the dynamic changes system caused by mobile GDs, the difficulty in obtaining accurate channel state information (CSI), and other factors, traditional methods like convex optimization10 and game theory11 are difficult to address the 3D trajectory and resource scheduling problems in practical scenarios12. To address these challenges, recent researches have made significant progress by leveraging artificial intelligence (AI) techniques (e.g., deep reinforcement learning (DRL), federated learning (FL), and machine learning (ML)) to intelligently manage resources or design UAVs trajectories. In particular, this AI-based approach can achieve long-term gains by optimizing the system’s strategy in situations where precise information about the system is not available13,14. For instance, an efficient federated distillation learning system is proposed to solve the problem of multitasking time series classification15. Additionally, an evolutionary multi-objective RL (EMORL) algorithm is proposed to solve the multi-objective trajectory control and task offloading16. Furthermore, DRL-based approaches are utilized to design UAVs’ trajectories and scheduling17,18. In addition, the authors propose a DRL-based method for constructing radio mapping and navigation cellular-connected UAV19. Moreover, multi-UAV trajectory design is considered based on deep Q-networks (DQNs) method in the sensing and coverage scenarios20,21,22. Nevertheless, most of the literature mentioned above is based on centralized learning methods, which require the collection of state information from all agents, resulting in an increased communication overload. Additionally, centralized training has a high time complexity and requires excessively long training time. Moreover, ensuring data privacy is also a critical concern for centralized learning methods.

Fortunately, multi-agent federated reinforcement learning (MAFRL) approaches, which leverage the benefits of distributed multi-agent training (e.g. federated learning (FL)) and the decision-making capabilities of reinforcement learning (RL), have emerged as a promising solution to address the challenges of distributed learning and multi-UAV trajectory design. In particular, the MAFRL method has many advantages over the traditional centralized multiple-agent reinforcement learning (MARL) method for designing UAVs’ trajectories. On the one hand, the centralized MARL method requires each agent to share its states and actions with the central controller while searching for optimal strategies. In the training of MAFRL method, the local UAVs only need to upload their model parameters to the service center, which reduces the communication delay and improves the communication efficiency. Furthermore, because the MAFRL method does not upload local data during the training process, only the model parameters are exchanged, which also protects data privacy. In addition, as a distributed method, the MAFRL method allows multiple agents to train locally instead of in a centralized training server, which can enhance training efficiency and reduce training time. Several works have investigated UAV communication based on the MAFRL approach. The work23 proposes an adaptive and flexible joint multi-UAV deployment and resource allocation scheme by exploiting a personalized MAFRL framework. In addition, the federated multi-agent deep deterministic policy gradient (F-MADDPG) based trajectory optimization algorithm is proposed for optimizing the air-ground cooperative emergency networks24. Furthermore, the trajectories of UAVs and communication resources are designed based MAFRL approach for NOMA system25,26. Moreover, the MAFRL method is utilized to optimize the resource allocation in the UAV-assisted multi-access edge computing (MEC) systems27. However, the research27 assumes that the UAVs fly around a fixed circle, while without optimization of UAV trajectories the corresponding performance achievements are restricted in some degree.

To the best of our knowledge, for practical multiple UAV-assisted data collection system with multiple mobile GDs, considering the NFZs, efficient distributed 3D trajectory design and communication scheduling are still open issues. Compared with the above works, we consider a UAV-assisted distributed data collection system with practical assumptions, e.g., considering the mobility of GDs, NFZs constraints, and probabilistic LoS channel. In the proposed practical scenario, our aim is to minimize the whole operation time by jointly optimizing the 3D trajectory of UAVs and the GDs’ scheduling. However, due to the non-convex nature of the formulated problem, the complexity of modeling the motion of GDs, as well as the existence of NFZs, traditional analytical methods (such as convex optimization or matching theory) have met huge difficulties in addressing such issues. In addition, compared to 2D trajectory design, the expanded exploration space of 3D trajectory design results in slower convergence of the algorithm. Consequently, it is essential to design algorithms that accelerate convergence and enhance overall performance. To address such issues, we propose a modified MAFRL approach to efficiently solve the optimization problem. The main contributions of this paper are summarized below:

  • Practical system design To minimize the whole operation time in the multiple UAV-assisted data collection system, we have developed a model to address the joint design problem that incorporates UAVs’ 3D trajectory design and communication scheduling of GDs, while taking into consideration the mobility of GDs, NFZs, and collision avoidance among UAVs.

  • Modified MAFRL based approach The formulated problem poses challenges due to its non-convex, as well as the analytically difficult nature of GDs’ random mobility and a large number of coupled variables. To address these issues, a MAFRL-based approach is utilized to jointly design the UAVs’ 3D trajectory and GDs’ communication scheduling. In particular, the proposed approach as a distributed learning method only requires UAVs to share model parameters, which reduces communication overload, preserves UAVs’ privacy, and reduces training time. Then we reformulate the established problem as a Markov decision process (MDP), treating each UAV as an independent agent, and design the state space, action space, state transition strategy, and reward function accordingly. Moreover, the multi-step dueling double deep Q-network (DDQN) algorithm is utilized for training each agent. Compared with the traditional DDQN method21,22, the proposed method with dueling network boosts the performance of the system, and multi-step bootstrapping technology with a suitable step makes the algorithm converge faster.

  • System performance evaluation We conduct numerical experiments to show the superiority of the proposed MAFRL method. Compared with the centralized MAFRL methods, the proposed method is more robust to the dynamic multi-GD and with NFZs environment. In addition, the performance of the system is comparable to that of the centralized MARL method and the ideal environment without NFZs, and outperforms the baseline methods. Moreover, the proposed 3D trajectory design is verified to be capable of improving the system performance by exploring vertical space, compared to the 2D trajectory design cases.

System model

System description

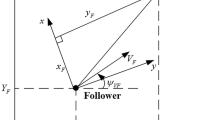
We consider a UAV-assisted data collection system with M UAVs and K GDs, where all the GDs are randomly moving on the ground, as illustrated in Fig. 1. The sets of GDs and UAVs are denoted by \({\mathscr {K}} \buildrel \Delta \over = \left\{ {1,2,...,K} \right\}\) and \({\mathscr {M}} \buildrel \Delta \over = \left\{ {1,2,...,M} \right\}\), respectively. In addition, these UAVs serve as aerial base stations (BSs) that are dispatched to collect data sent by GDs in 3D space with NFZs, and all the UAVs jointly train a global trajectory optimization model utilizing distributed learning method. Moreover, one of the UAVs acts as a parameter server to process parameters sent from other UAVs, as shown in Fig. 1. For a period \(T>0\), the time-varying 3D ___location of the UAV \(m\in {\mathscr {M}}\) can be denoted as \({\mathbf{{q}}_{m}}(t) = \left[ {{x_{m}}(t),{y_{m}}(t),{z_{m}}(t)} \right]\) with \(t \in [0,T]\). For convenience, we discretize the period time T into N small equal-size time slots by length of \(\sigma\), i.e., \(T=N\sigma\), which are indexed by \(n \in {\mathscr {N}} = \left\{ {1,2,...,N} \right\}\). Note that the slot length \(\sigma\) is small enough, such that the channel can be regarded as an approximate constant in each time slot. Then we can assume the ___location change within the current time slot is negligible and the channel state is stable. Therefore, the ___location of UAV m in time slot n can be denoted by \({\mathbf{{q}}_{m,n}} = [{x_{m,n}},{y_{m,n}},{z_{m,n}}]\), satisfying \({\mathbf{{q}}_m}(t) = {\mathbf{{q}}_m}(\sigma n) = {\mathbf{{q}}_{m,n}}\). The coordinate of the k-th GD at time slot n is denoted as \({\mathbf{{w}}_{k,n}} = [{x_{k,n}},{y_{k,n}},0]\). For the sake of flight safety, we assume that the minimum flying altitude of the UAVs is greater than the maximum height of buildings, i.e., \({z_{\min }} \le {z_{m,n}} \le {z_{\max }},\forall\), where \({z_{\min }}\) and \({z_{\max }}\) represent the minimum and maximum flying altitudes of the UAVs, respectively. In addition, we let \({\alpha _{m,k,n}}\) be the data sending decision variable from the k-th GD to the m-th UAV at the time slot n, which can be expressed as

$$\begin{aligned} {\alpha _{m,k,n}} = \left\{ {0,1} \right\} ,\forall m \in {\mathscr {M}}, k \in {\mathscr {K}}, n \in {\mathscr {N}}. \end{aligned}$$
(1)

In particular, the case \({\alpha _{m,k,n}}=1\) represents that the k-th GD decides sending its data to the UAV m at time slot n, otherwise \({\alpha _{m,k,n}}=0\). In this paper, the communication mode between the UAVs and GDs adopts time division multiple access (TDMA) scheme, that is, each UAV could only receive one GD’s signal in each time slot, i.e., \(\sum \limits _{k = 1}^K {{\alpha _{m,k,n}}} \le 1,\forall m \in {\mathscr {M}},n \in {\mathscr {N}}\). In particular, to avoid collisions between any two UAVs and avoid UAVs entering the NFZs, the safety distance constraints are considered, given by

$$\begin{aligned} \left\| {{\mathbf{{q}}_{m,n}} - {\mathbf{{q}}_{m *,n}}} \right\| \ge {d_{\min }},\forall m,{m^ * } \in {\mathscr {M}}, m \ne {m^ * }, n \in {\mathscr {N}}, \end{aligned}$$
(2)
$$\begin{aligned} \left\| {{\mathbf{{q}}_{m,n}} - \mathbf{{u}}_{j,l}} \right\| \ge {d_{\min }},\forall m \in {\mathscr {M}}, n \in {\mathscr {N}}, \end{aligned}$$
(3)

where \({d_{\min }}\) denotes the safe distance and \(\mathbf{{u}}_{j,l}\) denotes the coordinate of the vertical line of UAV m mapped to the l-th side of the j-th NFZ. Constraint (2) means that the distance between any two UAVs at time slot n should be greater than \(d_{\min }\). On the other hand, constraint (3) specifies that the minimum horizontal distance from UAVs to NFZs, i.e., the horizontal distance between UAVs and the closest boundary points of NFZs, should also be greater than \({d_{\min }}\) at any time slot.

Fig. 1
figure 1

UAVs-assisted multi-GDs data collection system in probabilistic LoS channel.

Full size image

System operation

As depicted in Fig. 1, the whole operating system operates by continuously iterating through three stages. First, each local UAV collects data from GDs as part of its task. Next, at regular intervals, the local UAVs upload their respective model parameters to the server UAV. Finally, the server UAV calculates the received local model parameters and then distributes global model parameters to all the local UAVs. This iterative process continues until all the GDs’ data is collected. In this paper, we assume that the server UAV is sufficiently capable of calculating the received local model parameters, such that the time required to perform these calculations is negligible. Consequently, the operation time can be divided into three stages: data collection time, local FL model update time, and global FL model broadcast time. The duration of each stage is expressed as follows:

  • Data Collection Time Let \(D_{k}\) denote the total date size in bits needed for GD k to send to UAVs. In particular, the data transmission constraint needs to satisfy when the UAV m completes its data collection task from GD k, i.e.,

    $$\begin{aligned} \sum \limits _{m = 1}^M {\sum \limits _{n = 1}^{N_m^C} {{\alpha _{m,k,n}}{R_{m,k,n}}} \ge {D_k}}, \forall m \in {\mathscr {M}}, k \in {\mathscr {K}}, n \in {\mathscr {N}}, \end{aligned}$$
    (4)

    where \(N_m^C\) denotes the total number of time slots that UAV m has consumed for the data collection task from GD k. Then the total data collection time \(T^C\) of all UAVs data collection tasks can be expressed as

    $$\begin{aligned} {T^C} = N^C\sigma = \sum \limits _{m = 1}^M {N_m^C}\sigma , \forall m \in {\mathscr {M}}, \end{aligned}$$
    (5)

    where \(N^C\) is the total number of time slots that all the UAVs complete the whole data collection task.

  • Local FL Model Update Time The total data size of local model parameters needed for UAV m transmit to the server UAV \({\bar{m}}\) is represented by \(D_m\) in bits. Moreover, assuming that the UAVs remain stationary while transferring model parameters, the time taken for UAV m to upload its local model parameters to the server UAV \({\bar{m}}\) can be represented as:

    $$\begin{aligned} {T^U} = {N^U}\sigma = \varsigma {D_m}/R_{m, {{\bar{m}}},n}^U, \forall m \in {\mathscr {M}}, k \in {\mathscr {K}}, n \in {\mathscr {N}}, \end{aligned}$$
    (6)

    where \(\varsigma\) represents the total number of interactions of model parameters after collecting the data task, and \(R_{m, {{\bar{m}}} ,n}^U\) is the model parameters transmission rate from the server UAV \({{\bar{m}}}\) to the UAV m.

  • Global FL Model Broadcast Time Let \({D_{{{\bar{m}}}}}\) denote the total data size of the global model parameters required for the server UAV \({{\bar{m}}}\) to broadcast to other UAVs in bits. Then the global model parameters broadcast time from the serve \(\bar{m}\) to the UAV m can be expressed as

    $$\begin{aligned} {T^D}={N^D}\sigma = \varsigma {D_{{{\bar{m}}}}}/R_{m, {{\bar{m}}},n}^D, \forall m \in {\mathscr {M}}, k \in {\mathscr {K}}, n \in {\mathscr {N}}. \end{aligned}$$
    (7)

    where \(R_{m, {{\bar{m}}},n}^D\) is the model parameters transmission rate from the UAV m to the server UAV \({{\bar{m}}}\).

Communication model

Air-ground communication model

In general, the LoS channel28,29 cannot accurately represent the channel environment between UAVs and GDs in complex urban environments. In this paper, we consider the probabilistic Air-to-Ground (AtG) channel30,31, where both the LoS link and NLoS link between UAVs and GDs are considered. The quality of the AtG channel model is mainly determined by the elevation angle between the UAVs and the GDs, and the flying height of the UAVs32. In time slot n, let \(c_{m,k,n}\) denote the binary channel state between the m-th UAV and the k-th GD, where \(c_{m,k,n}=1\) and \(c_{m,k,n}=0\) represent the LoS and NLoS states, respectively. In addition, the LoS probability, denoted by \({{{\mathbb {P}}_{m,k,n}^L}}\left( {{c_{m,k,n}} = 1} \right)\), is mainly determined by the elevation angle between the UAV m and the GD k. In particular, a widely adopted probability LoS model32 is based on a logistic function with the following form of

$$\begin{aligned} {{\mathbb {P}}_{m,k,n}^L}\left( {{c_{m,k,n}} = 1} \right) = \frac{1}{{1 + a{e^{ - b({\theta _{m,k,n}} - a)}}}}, \end{aligned}$$
(8)

where \({\theta _{m,k,n}}\) denotes the elevation angle between UAV m and GT k in time slot n. The elevation angle can be expressed as

$$\begin{aligned} {\theta _{m,k,n}} = \frac{{180}}{\pi }\arctan \left( {\frac{{{z_{m,n}}}}{{\left\| {\mathbf{{q}}_{m,n}^\lambda - \mathbf{{w}}_{k,n}^\lambda } \right\| }}} \right) , \end{aligned}$$
(9)

where \(\mathbf{{q}}_{m,n}^\lambda\) and \(\mathbf{{w}}_{k,n}^\lambda\) represent the horizontal coordinates of UAV m and GD k mapped to the ground. Additionally, a and b are model parameters that describe environmental factors, such as the distribution and height of buildings. For convenience, we re-denoted the LoS probability by \(P_{m,k,n}^L \buildrel \Delta \over = {\mathbb {P}}\left( {{c_{m,k,n}} = 1} \right)\). In addition, to improve the accuracy of the probabilistic LoS channel model, a more precise approximation of the LoS probability can be achieved by utilizing the following generalized logistic function32:

$$\begin{aligned} P_{m,k,n}^L = {B_3} + \frac{{{B_4}}}{{1 + {e^{ - \left( {{B_1} + {B_2}{\theta _{m,k,n}}} \right) }}}}, \end{aligned}$$
(10)

where \({B_1} < 0,{B_2}> 0,{B_4} > 0\), and \(B_4\) are constants with \({B_3} + {B_4} = 1\). Among them, \(B_1\), \(B_2\), \(B_3\), and \(B_4\) are constants that depend on the environment. The corresponding NLoS probability can be represented as \(P_{m,k,n}^L \buildrel \Delta \over = {\mathbb {P}}\left( {{c_{m,k,n}} = 0} \right) = 1-P_{m,k,n}^N\). The large-scale channel gain between UAV m and GD k at time slot n considers both path loss and shadowing effects and can be approximated by the following model:

$$\begin{aligned} {h_{m,k,n}} = {c_{m,k,n}}h_{m,k,n}^L + \left( {1 - {c_{m,k,n}}} \right) h_{m,k,n}^N, \end{aligned}$$
(11)

where \(h_{m,k,n}^L\) and \(h_{m,k,n}^N\) denote the channel power gain in the state of LoS and NLoS, respectively. To elaborate, \(h_{m,k,n}^L\) and \(h_{m,k,n}^N\) are expressed as

$$\begin{aligned} h_{m,k,n}^L = {\beta _0}d_{m,k,n}^{ - \alpha _L},~h_{m,k,n}^N = \mu {\beta _0}d_{m,k,n}^{ - \alpha _N}. \end{aligned}$$
(12)

Here, \({\beta _0}\) represents the average channel power gain in LoS state when the reference distance is 1m, \(\mu <1\) denotes the additional attenuation factor, and \({\alpha _L}\) and \({\alpha _N}\) represent the average path loss exponents in LoS and NLoS states, respectively, with \(2 \le \alpha _L \le \alpha _N\le 6\). The Euclidean distance between UAV m and the GD k in time slot n is denoted by \({d_{m,k,n}} = \sqrt{{{\left\| {{\mathbf{{q}}_{m,n}} - {\mathbf{{w}}_{k,n}}} \right\| }^2}}\). The real-time achievable rate \({R_{m,k,n}}\) in Mbps when the UAV m collects data from the GD k can be expressed as:

$$\begin{aligned} {R_{m,k,n}} = c _{m,k,n}R_{m,k,n}^L + \left( {1 - {c_{m,k,n}}} \right) R_{m,k,n}^N, \end{aligned}$$
(13)

where \(R_{m,k,n}^L = B{\log _2}( {1 + \frac{{{\gamma _k}}}{{d_{m,k,n}^{{\alpha _L}}}}} )\), \(R_{m,k,n}^N = B{\log _2}( {1 + \frac{{\mu {\gamma _k}}}{{d_{m,k,n}^{{\alpha _N}}}}})\) represent the achievable rates in the LoS and NLoS states. Here, B is the transmission bandwidth of the GD k, \({\gamma _k} = \frac{{{\beta _0}{P_k}}}{{{N_0}\Gamma }}\), where \({{P_k}}\) is the transmit power of the GD k, \({{N_0}}\) represents the receiver noise power, and \(\Gamma > 1\) is the SNR gap between the practical modulation-and-coding scheme and the theoretical Gaussian signaling. Not that the channel power gain \(h_{m,k,n}\) is subject to two sources of randomness: the occurrence of random LoS and NLoS links, and random small-scale fading. By averaging these two randomness sources, the expected achievable rate can be expressed as follows:

$$\begin{aligned} {\mathbb {E}}[{R_{m,k,n}}] = P_{m,k,n}^LR_{m,k,n}^L + P_{m,k,n}^NR_{m,k,n}^N. \end{aligned}$$
(14)

Air-to-air communication model

In this work, we can reasonably assume that the channel between the serving UAV and the local UAV for transmitting the task model parameters is a LoS connection as the flight altitude is higher than the buildings. As a result, the time-varying channel power gain can be expressed separately during the process of uploading and distributing the model parameters as follows

$$\begin{aligned} {h_{m,{{\bar{m}}},n}^U} = \frac{{{\beta _0}}}{{{{\left\| {{z_{m,n}} - {z_{{{\bar{m}}},n}}} \right\| }^2} + {{\left\| {\mathbf{{q}}_{m,n}^\gamma - \mathbf{{q}}_{{{\bar{m}}},n}^\gamma } \right\| }^2}}},\forall {m,{{\bar{m}}}} \in {\mathscr {M}}, n \in {\mathscr {N}}, \end{aligned}$$
(15)
$$\begin{aligned} {h_{m,{{\bar{m}}},n}^D} = \frac{{{\beta _0}}}{{{{\left\| {{z_{m,n}} - {z_{{{\bar{m}}},n}}} \right\| }^2} + {{\left\| {\mathbf{{q}}_{m,n}^\gamma - \mathbf{{q}}_{{{\bar{m}}},n}^\gamma } \right\| }^2}}},\forall {m,{{\bar{m}}}} \in {\mathscr {M}}, n \in {\mathscr {N}}, \end{aligned}$$
(16)

where \({\mathbf{{q}}_{m,n}^\gamma }\) and \({\mathbf{{q}}_{{{\bar{m}}},n}^\gamma }\) represent the horizontal coordinate positions of UAV m and server UAV \({{\bar{m}}}\) at time slot n, respectively. Then the instantaneous transmission rate in the uplink in Mbits per second (Mbps) between the UAV m and the server UAV \({{\bar{m}}}\) at time slot n can be expressed as

$$\begin{aligned} {R_{m, {{\bar{m}}},n}^U} = B{\log _2}\left( {1 + \frac{{{P_m}{h_{m,\bar{m},n}^U}}}{{{N_0}B}}} \right) = B{\log _2}\left( {1 + \frac{{\zeta {P_m}}}{{{{\left\| {{z_{m,n}} - {z_{{{\bar{m}}},n}}} \right\| }^2} + {{\left\| {\mathbf{{q}}_{m,n}^\gamma - \mathbf{{q}}_{\bar{m},n}^\gamma } \right\| }^2}}}} \right) , \end{aligned}$$
(17)

where \(P_m\) is the transmit power of the UAV m, the white Gaussian noise power spectral density is denoted as \({N_0}\) in watts/Hz at the server UAV \({{\bar{m}}}\), the total channel bandwidth for supporting communication is denoted as B in hertz (MHz), and the reference signal-to-noise ratio (SNR) is denoted as \(\zeta = \frac{\beta _0 }{{{N_0}B}}\) at the reference distance. Let \(P_ {{{\bar{m}}}}\) represent the transmit power of the server UAV \(\bar{m}\). Similarly, the transmission rate of model parameters from the server UAV \({{\bar{m}}}\) to the UAV m can be represented as

$$\begin{aligned} {R_{m, {{\bar{m}}},n}^D} = B{\log _2}\left( {1 + \frac{{{P_{\bar{m}}}{h_{m,{{\bar{m}}},n}^D}}}{{{N_0}B}}} \right) = B{\log _2}\left( {1 + \frac{{\zeta {P_ {{{\bar{m}}}}}}}{{{{\left\| {{z_{m,n}} - {z_{{{\bar{m}}},n}}} \right\| }^2} + {{\left\| {\mathbf{{q}}_{m,n}^\gamma - \mathbf{{q}}_{{{\bar{m}}},n}^\gamma } \right\| }^2}}}} \right) . \end{aligned}$$
(18)

Problem formulation

The time-varying communication channel conditions in UAV-assisted networks hold significant importance for the data collection system. To optimize the channel gains for communication service, it becomes crucial to strategize the trajectories of UAVs. In particular, the objective of this study is to minimize the overall operation time \(N_{total}\sigma\) by jointly optimizing the trajectory of UAVs and communication scheduling among GDs. Recall that the whole operation time \(N_{total}\sigma\) encompasses the data collection time \(N^C\sigma\), local FL model update time \(N^U\sigma\), and global FL model broadcast time \(N^D\sigma\), i.e., \(N_{total}\sigma = {N^C}\sigma + {N^U}\sigma + {N^D}\sigma\). Thus, the considered optimization problem can be formulated as

$$\begin{aligned} {\mathscr {P}} 1:&\mathop {\min }\limits _{\{ {\mathbf{{q}}_{m,n}}, {\textbf{v}_{m,n}},{\alpha _{m,k,n}}\} } N_{total}{\sigma } \end{aligned}$$
(19)
$$\begin{aligned} & s.t. {\alpha _{m,k,n}} \in \left\{ {0,1} \right\} ,\forall m \in {\mathscr {M}}, k \in {\mathscr {K}}, n \in {\mathscr {M}}, \end{aligned}$$
(19a)
$$\begin{aligned} & \sum \limits _{k = 1}^K {{\alpha _{m,k,n}}} \le 1,\forall m \in {\mathscr {M}}, k \in {\mathscr {K}}, n \in {\mathscr {N}}, \end{aligned}$$
(19b)
$$\begin{aligned} & {\text{{z}}_{\min }} \le {z_{m,n}} \le {z_{\max }}, \forall n \in {\mathscr {N}}, \end{aligned}$$
(19c)
$$\begin{aligned} & {\sum \limits _{m = 1}^M {\sum \limits _{n = 1}^{N_m^C} {{\alpha _{m,k,n}}{R_{m,k,n}}} } } \ge D_k, \forall m \in {\mathscr {M}}, k \in {\mathscr {K}}, n \in {\mathscr {N}},\end{aligned}$$
(19d)
$$\begin{aligned} & {\mathbf{{q}}_{m,n + 1}} = {\mathbf{{q}}_{m,n}} + {\Delta _s}\mathop {\textbf{v}_{m,n}}, \forall n \in {\mathscr {N}}, \end{aligned}$$
(19e)
$$\begin{aligned} & {\Delta _s} = V\sigma , \end{aligned}$$
(19f)
$$\begin{aligned} & \left\| {{\mathbf{{q}}_{m,n}} - {\mathbf{{q}}_{m^ *,n}}} \right\| \ge {d_{\min }},\forall m,{m^ * } \in {\mathscr {M}}, m \ne {m^ * }, n \in {\mathscr {N}}, \end{aligned}$$
(19g)
$$\begin{aligned} & \left\| {{\mathbf{{q}}_{m,n}} - \mathbf{{u}}_{j,l}} \right\| \ge {d_{\min }},\forall m \in {\mathscr {M}}, n \in {\mathscr {N}}. \end{aligned}$$
(19h)

Constraints (19a) and (19b) specify that one UAV is restricted to establishing communication with only one GD during a given time slot. Constraint (19c) indicates that the UAVs can only move within a specified range of flight altitude. Constraint (19d) represents that the UAVs must finish collecting data from the GD k. In addition, the flight displacement of the UAVs is subject to constraints (19e) and (19f), where \(\Delta _s\) represents the distance traveled by the UAVs per unit time slot, \(\textbf{v}\) denotes the direction of the UAVs’ flight during time slot n and V is the scalar of the speed of UAVs flight. Moreover, equation (19g) means that any two UAVs need to keep a safe distance when flying, and formula (19h) denotes that UAVs need to avoid flying into the NFZs when performing tasks.

Federated reinforcement learning solution

The problem \({\mathscr {P}}\)1 is a non-convex problem due to the nonconvex feasible, i.e., the presence of NFZs. In addition, the mobility of GDs and NFZs results in system dynamics and uncertainty. These issues increase the difficulty of addressing the optimization problem by using traditional algorithms33,34,35. In order to tackle this challenge, we convert it into a Markov Decision Process (MDP) problem and then develop a solution method based on MAFRL, as shown in Fig. 2.

Fig. 2
figure 2

Trajectory design framework of the proposed method.

Full size image

Primarily of reinforcement learning

RL involves an agent interacting with its environment with the goal of improving its policy \(\pi\), which maximizes its long-term return \({\mathbb {E}}[G_{m,n}]\). The return is defined as the sum of discounted rewards from time step n onwards, where the discount factor \(\lambda\) is between 0 and 1. In particular, RL is well-suited to solve Markov Decision Process (MDP) problems represented by a 4-tuple \(<{\mathscr {S}},{\mathscr {A}},{\mathscr {P}},{\mathscr {R}}>\), where \({\mathscr {S}}\) is the state space, \({\mathscr {A}}\) is the action space, \({\mathscr {P}}\) is the state transition probability, and \({\mathscr {R}}\) is the reward function. At each discrete time step n, the agent selects an action \(a_n\) from the action space \({\mathscr {A}}\) based on its policy \(\pi\), receives a reward \(r_n\), and transitions to a new state \(s_{n+1}\) based on the state transition probability \({\mathscr {P}}\).

Deep Reinforcement Learning (DRL) is an extension of Reinforcement Learning (RL) that utilizes deep neural networks (DNNs) to approximate the Q-value function, which represents the expected return of performing an action \(a_n\) in state \(s_n\). In the Double Deep Q-Network (DDQN) algorithm36, the Q-value approximator \(Q({s_n},{a_n}|w_{m,n})\) with parameters \(w_{m,n}\) is updated by minimizing the following loss function:

$$\begin{aligned} \begin{aligned}({r_{n + 1}} + \gamma Q({s_{n + 1}},\mathop {\arg \max }\limits _{{a_n^*}} Q({s_{n + 1}},{a_n^* }|w_{m,n} )|{ w_{m,n}^ *}) - Q({s_n},{a_n}|w_{m,n} ))^2. \end{aligned} \end{aligned}$$
(20)

Here, \(w_{m,n}\) and \(w_{m,n}^*\) represent the parameters of the on-line Q network and target Q network, respectively. In particular, the DDQN algorithm updates the on-line Q network using the loss function to approximate the target Q network, which is updated periodically.

The DDQN network predicts the state \(s_{n+1}\) solely based on the value \(Q(s_n,a_n)\) of the current action \(a_n\) under the current state \(s_n\). However, if the relationship between the action \(a_n\) and the state \(s_n\) is weak, this prediction can be inaccurate. In contrast, the dueling network architecture separates the state and action, allowing for individual judgment of each. This reduces the dependence of the state on the value of the action throughout the calculation process, leading to higher stability of the algorithm. As a result, compared with the traditional DDQN architecture, the proposed method with dueling networks enhances the performance and stability of the system. Additionally, we also employ multi-step bootstrapping to accelerate convergence, by considering the return of future \(\wp\) steps. By selecting an appropriate \(\wp\), the algorithm converges faster and better. The following modifications have been made to the neural network:

  • Dueling network The dueling network architecture features two distinct streams for evaluating the action value. The state value function stream predicts the value of the current state, while the state-dependent action advantage function evaluates the quality of the available actions. Unlike traditional Q-networks, the dueling network can determine the validity of states without requiring a full evaluation of all possible actions. This makes it more stable and less prone to overestimating the values of certain actions37. The Q-function for the dueling network architecture is represented as follows:

    $$\begin{aligned} \begin{aligned} Q(s,a|\theta ,\phi ,\beta ) = V(s|\theta ,\beta ) + A(s,a|\theta ,\phi ) - \frac{1}{{\left| A \right| }}\sum \limits _{{a^ \bullet }} {A(s,{a^ \bullet }|\theta ,\phi )}, \end{aligned} \end{aligned}$$
    (21)

    where \(V(s|\theta ,\beta )\) denotes the state value, \(A(s,a|\theta ,\phi )\) is the action advantage value, \(\beta\) and \(\phi\) are the parameters of the state value stream and the state-dependent action advantage stream, and |A| represents the size of the action space.

  • Multi-step approach This approach differs from Monte Carlo (MC) and temporal difference (TD) methods in that it considers the return of the future \(\wp\) steps. By selecting an appropriate value for \(\wp\), the algorithm is able to converge faster and more effectively than traditional methods38. The truncated \(\wp\)-step return is defined by the following equation:

    $$\begin{aligned} {R_{m,n:n + \wp }} = \sum \limits _{i = 0}^{\wp - 1} {{\gamma ^i}{R_{m,n + i + 1}}}, \end{aligned}$$
    (22)

Then the loss function of the improved method can be expressed as

$$\begin{aligned} {\left( {{R_{m,n:n + \wp }} + {\gamma ^\wp }{Q^ * }({\mathbf{{q}}_{m,n + \wp }},\textbf{v}_{m,n}^ *;w_{m,n}^ * ) - {Q^ * }({\mathbf{{q}}_{m,n}},{{\textbf{v}}_{m,n}};{w_{m,n}})} \right) ^2}, \end{aligned}$$
(23)

where \(\textbf{v}_{m,n}^ * = \mathop {\arg \max }\limits _{\textbf{v}_{m,n}^ \bullet \in {A_{m,n}}} {Q^ * }({\mathbf{{q}}_{m,n + \wp }},\textbf{v}_{m,n}^ \bullet ;{w_{m,n}}).\)

Algorithm 1
figure a

Proposed MAFRL Method

Full size image
Algorithm 2
figure b

GDs Scheduling Optimization

Full size image

Markov decision process

In the DRL framework, each UAV acts as an agent that obtains state information through interactions with the environment, and subsequently selects actions from the action space to make decisions. Based on the selected action, each UAV receives a reward that evaluates the effectiveness of its decision. During the process of training the UAV network model, each UAV can gradually update its model-free policy that maps its observations to optimal actions. The MDP of a local transition tuple \(\left\langle {{S_{m}},{A_{m}},{\pi _m},{r_{m}}} \right\rangle\) contains the essential elements for the m-th UAV, which is defined as follows:

  • State Space\(S_{m}\): At each time slot n, the state \({s_{m,n} \in S_{m}}\) of each UAV m characterizing the environment is comprised of its 3D coordinates \([x_{m,n},y_{m,n},z_{m,n}]\). In particular, the state space \(S_{m}\) encompasses all locations within the region of interest.

  • Action Space \(A_m\): All agents have the same action space \(A_{m}, \forall m \in {\mathscr {M}}\). At each time slot n, each agent (i.e., UAV m) selects its corresponding action \(a_{m,n} \in A_{m}\) according to its observed state \(s_{m,n}\). The action \(a_{m,n}\) corresponds to the flight direction of the UAVs, which can be expressed as \([a_1,a_2,a_3,a_4,a_5,a_6]\), where \({a_1} = [0,1,0]\) means that the UAV m moves to the forward, \({a_2} = [0,-1,0]\) represents the UAV moves to the behind, \({a_3} = [1,0,0]\) denotes the UAV moves to the left, \({a_4} = [-1,0,0]\) means the UAV moves to the right, \({a_5} = [0,0,1]\) means the UAV is flying up, \({a_6} = [0,0,1]\) denotes the UAV is flying down. Moreover, \(a_{m,n}\) is the action of the individual agent m at time slot n and all agents have independent actions.

  • State Transition Function \({\eta _m}\): Let \({\eta _m}({s_{m,n + 1}}|{s_{m,n}},{a_{m,n}})\) denote the transition probability of the UAV m, after executing an action \(a_{m,n}\) at current state \(s_{m,n}\) and transmit to a new state \(s_{m,n+1}\). The state transition function of UAV m is mainly determined by its motion displacement function, i.e., equation (19e).

  • Reward Function\(r_{m}\): To minimize the total time taken to collect data, we define a local reward for each UAV m, denoted as \(r_m\). The value of \(r_m\) can be expressed as:

    $$\begin{aligned} {r_m} = \left\{ \begin{array}{l} \vartheta ,\,\,\,\, \text{{if\,\, outbound/fly\,\, into\,\, NFZs/collision}};\\ \varpi + \xi {R_{m,n}},\,\,\,\text{{else}}; \end{array} \right. \end{aligned}$$
    (24)

    Here, \(\vartheta\) is a negative value used to penalize UAVs for behaviors such as flying out of bounds, entering NFZs, or colliding with other UAVs. Additionally, \(\varpi\) is also a negative value utilized to reduce the number of time slots for UAVs to fly. Conversely, \(\xi\) is a positive value that helps to speed up the data collection process for UAVs.

MAFRL method for solving the problem of \({\mathscr {P}} 1\)

To address the time minimization problem of \({\mathscr {P}} 1\), we propose a MAFR-based solution that jointly optimizes the 3D trajectory of UAVs and scheduling of GDs. Instead of utilizing a centralized learning approach that increases the central dimension as the number of UAVs increases, the proposed solution involves training UAVs locally and then combining their model parameters. This allows each UAV to distribute the training of its own model and communicate with a parameter server UAV to create a global network. In addition, the proposed approach only involves uploading parameters of each device and downloading policy, which significantly reduces communication overload and delays. Moreover, the proposed approach ensures the privacy of the system.

The framework of MA-FRL is illustrated in Fig. 2. The entire process can be divided into four stages: signal UAV local training, uploading local model parameters from each local UAV to the server UAV, aggregating the model parameters at the server UAV, and sending global model parameters to each local UAV. The proposed MA-FDRL algorithm is summarized in Algorithm 1 and Algorithm 2. During the preparation phase of Algorithm 1, various parameters such as the replay buffer and the parameters \(w_{m,0}\) and \(w_{m,0}^*\) of the on-line network and target network are initialized. In particular, the initial locations \({\mathbf{{w}}_{k,0}}, k \in {\mathscr {K}},\) of the GDs and the initial locations \({\mathbf{{q}}_{m,0}}, m \in {\mathscr {M}},\) of the UAVs are randomly generated. The UAVs then interact with the environment and train their neural network using the following process:

Local UAVs training

During the local training stage, each UAV serves as a signal agent and interacts with the environment. At the start of each episode, each UAV executes Algorithm 2 using its current ___location to determine the GDs scheduled for the current time slot. Next, each UAV receives its selected GD’s data with the index \(ID_k\). Once all UAVs have collected the data for the current slot, they select an action from the action space using the \(\epsilon\)-greedy policy. In particular, Let \(\pi _m\) denote the policy function of UAV m, which maps the perceived states to a probability distribution over actions that the agent can select in those states, i.e., \(\pi \left( {a_m|s_m} \right) = {\mathscr {P}}\left( {a_m|s_m} \right)\). The \(\varepsilon\)-greedy action selection policy can be denoted as

$$\begin{aligned} {a_{m,n}} = \left\{ \begin{array}{l} \text{{randomly \, \, selected \, \, from \, \, }}{A_m} \text{{, \, \, with \, \, }}\varepsilon \text{{ \, \, probability; }}\\ \mathop {\arg \max }\limits _{{a_{m,n}} \in {A_m}} Q({s_{m,n}},{a_{m,n}}|w_{m,n} ),\text{{ \, \, with \, \, 1 - }}\varepsilon \text{{ \, \, probability.}} \end{array} \right. \end{aligned}$$

At each time slot n, a decimal number between 0 and 1 is generated randomly. If this number falls below the specified threshold value of \(\varepsilon\), UAV m chooses an action from its action space \(A_m\) at random. If the number exceeds \(\varepsilon\), the UAV selects the action with the highest Q value from \(A_m\). To balance the exploration and exploitation of our design, the value of \(\varepsilon\) gradually increases from a higher value to a lower value as the episode progresses. This approach increases the probability of the UAV selecting the action with the best Q value in the later stages of training. The chosen action is performed by each UAV, and a reward is obtained. The UAVs then move to the next state based on the state transition model of equation (19e). The truncated return of \(\varphi\)-step is calculated, and the tuple \(\left( {{s_\tau },{a_\tau },{R_{\tau :\min \left( {\tau + {\varphi },N} \right) }},{s_{\min \left( {\tau + {\varphi },N} \right) }}} \right)\) is stored in the replay memory C. Then a mini-batch transition is randomly sampled from C, and the gradient descent is utilized to update parameter \(w_{m,n}\) of the on-line network. Specifically, the model parameter \(w_{m,n}\) of the on-line network is copied to the target network every \(N_Q\) step. The calculation of \(n/N_F\) determines whether to enter the model parameter update stage. If \(n/N_F\) is not an integer, each UAV repeats the previous steps until \(n/N_F\) is an integer. Otherwise, the Local Model Parameters Uploaded stage is entered.

Local model parameters uploaded

Once \(n/N_F\) becomes an integer, each local UAV uploads its on-line model parameter \(w_{m,n}\) and target model parameter \(w_{m,n}^*\) to the server UAV.

Federated aggregation

When the server UAV has obtained the model parameters of all local UAVs, it aggregates these parameters to obtain the global model parameter, which is expressed as follows:

$$\begin{aligned} {w_m} = \sum \limits _{m = 1}^M {\frac{{{w_{m,n}}}}{M}}, w_m^ * = \sum \limits _{m = 1}^M {\frac{{w_{m,n}^ * }}{M}}, \forall m \in {\mathscr {M}}, n \in {\mathscr {N}}, \end{aligned}$$
(25)

where \(w_{m,n}\) and \(w_{m,n}^*\) represent the model parameters of on-line Q-network and target Q-network, respectively. In addition, \({w_m}\) and \(w_m^ *\) represent the global model parameters of the aggregated on-line Q-network and the global model parameters of the target Q-network, respectively.

Global model parameters distribution

After processing the model parameters sent by the local UAVs, the server UAV sends the global model parameters to each local UAV. Each local UAV then copies the global model parameters to its networks every \({N^{Agg}}\) time slot, i.e., \(w_{m,n+1} = w_m\) and \(w_{m,n+1}^* = w_m^*\).

Convergence and complexity analysis

Convergence analysis

To prove the convergence of the proposed MAFRL method, we need to prove the convergence of the modified multi-step dueling DDQN and the convergence of FL. In the theorem 1 of39, it has been proved that the DDQN method can converge to the optimal value under certain conditions, such as \(0 \le {a_n} \le 1\), \(\sum \nolimits _n {{a_n} = \infty }\), \(\sum \nolimits _n {{a_n}^2 < \infty }\). In addition, multi-step bootstrapping and dueling networks will only change the method’s stability and convergence speed, but not change the convergence performance of the proposed method40. Thus, the convergence of the modified multi-step dueling DDQN method is guaranteed. On the other hand, the work41 has demonstrated that under certain conditions, FL can converge to an optimized value.As a result, the convergence performance of the proposed method can be guaranteed and theoretically converges to the optimal value. Besides, we also validate the convergence of the proposed algorithm through simulations in the next section.

Complexity analysis

The proposed method consists of an outer MAFRL algorithm and an inner greedy scheduling algorithm. Firstly, we analyze the computation complexity of the MAFRL. We assume that the neural network contains Y fully connected layers, and \(\upsilon\) is the number of neurons in the y-th layer. In addition, we also assume that the dueling layer has \({\upsilon _{dueling}}\) neurons. For a single sample, the computational complexity of each time step can be denoted as \(O(\sum \nolimits _{y = 0}^{Y - 1} {{\upsilon _y}{\upsilon _{y + 1}}} + {\upsilon _Y}{\upsilon _{dueling}})\)21. Thus, for \({Y_{ep}}\) episode, \({Y_{slot}}\) time slots and M UAVs, the computational complexity of the MAFRL algorithm can be expressed as \(O(M{Y_{ep}}{Y_{slot}}\frac{{{Y_{slot}}}}{{{N^{Agg}}}}(\sum \nolimits _{y = 0}^{Y - 1} {{\upsilon _y}{\upsilon _{y + 1}}} + {\upsilon _Y}{\upsilon _{dueling}}))\), where \({{N^{Agg}}}\) is the model parameter aggregation frequency. On the other hand, for the number of K GDs, the computational complexity of the greedy scheduling algorithm is O(K). Therefore, the overall computational complexity of the proposed method is \(O(KM{Y_{ep}}{Y_{slot}}\frac{{{Y_{slot}}}}{{{N^{Agg}}}}(\sum \nolimits _{y = 0}^{Y - 1} {{\upsilon _y}{\upsilon _{y + 1}}} + {\upsilon _Y}{\upsilon _{dueling}}))\). Similarly, the computational complexity of baseline No Dueling MAFR is \(O(KM{Y_{ep}}{Y_{slot}}\frac{{{Y_{slot}}}}{{{N^{Agg}}}}(\sum \nolimits _{y = 0}^{Y - 1} {{\upsilon _y}{\upsilon _{y + 1}}} ))\). Compared to the proposed method, Without NFZs MAFR method only involves a change in the scenario, thus its complexity remains the same as the proposed method. In addition, Random Scheduling MAFRL method randomly schedules GDs, so the computational complexity of the algorithm is \(O(M{Y_{ep}}{Y_{slot}}\frac{{{Y_{slot}}}}{{{N^{Agg}}}}(\sum \nolimits _{y = 0}^{Y - 1} {{\upsilon _y}{\upsilon _{y + 1}}} + {\upsilon _Y}{\upsilon _{dueling}}))\). Moreover, the centralized MARL method does not require local training of agents, so its computational complexity is \(O(K{Y_{ep}}{Y_{slot}}(\sum \nolimits _{y = 0}^{Y - 1} {{\upsilon _y}{\upsilon _{y + 1}}} + {\upsilon _Y}{\upsilon _{dueling}}))\). Based on the above analysis, the computational complexity of the proposed method is equal to the Without NFZs MAFRL method and greater than methods No Dueling MAFRL, Random Scheduling MAFRL, and Centralized MARL.

Simulation results and analysis

In this section, we evaluate the whole operation time cost performance of the proposed MAFRL method for jointly designing the 3D trajectory of UAVs and scheduling of GDs. The network considers two UAV and six GDs and the data size of each GD needs to transmit is 40 Mbit. The GDs are randomly distributed in the 3D urban environment with a ratio of side length 1000 m, and the size of the discrete slot \(\sigma\) is 0.5s. Typically, the mobility of the GDs follow the Random Walk (GDs move in an area randomly and frequently change their directions) with the angle constraint \([0,2\pi ]\) and velocity is 5 m/s, and the speed of all UAVs is set to \(V=20\) m/s. In particular, there are many practical applications of GDs random walk scenario and it is worth studying, such as GDs randomly roaming to sense nearby data. Furthermore, the initial locations of UAVs and GDs are randomly generated and the flight altitude range of UAVs is \(z_n \in [50,100]\) m. In addition, the on-line network and the target network share the same structure consisting of five hidden layers, with 512, 256, 128, and 128 neurons in the first four hidden layers, and a dueling layer with 7 neurons in the last hidden layer. The estimation state-value corresponds to one neuron, while the remaining six neurons represent the action advantage for 6 actions. The activation function for the hidden layers is ReLu, and the optimizer used is Adam. The simulations were conducted in Python 3.7, using TensorFlow 2.0.0 and Keras 2.3.1 as the operating environment. Other parameters are shown in Table 1.

Table 1 Simulation parameters.
Full size table

Performance evaluation

In this section, we compare the proposed MAFRL algorithm with commonly utilized baseline methods in UAV data collection systems. The comparison schemes are as follows:

  • No Dueling MAFRL Proposed MAFRL algorithm without utilizing the dueling architecture.

  • Without NFZs MAFRL To verify the applicability of the proposed algorithm to the area, we make the assumption that there are without NFZs. Namely, the UAVs can perform their tasks everywhere in the given area.

  • Random Scheduling MAFRL During scheduling the GDs, each UAV randomly schedules the GDs to collect its data.

  • Centralized MARL A centralized DRL method generates a policy for all agents in the system, rather than making separate decisions for each agent at every time slot.

Impact of different hyperparameters and convergence validation

In this subsection, we compare the impact of different hyperparameters on the performance of the proposed method and choose the appropriate one. In the following plots, the UAVs and GDs have the same initial locations. In particular, we take the average of every 30 episodes in 1000 episodes as the displayed results. Fig. 3a illustrates the relationship between the learning rate lr and the whole operation time. The plot indicates that a learning rate of 0.0005 achieves faster convergence than rates of 0.005 and 0.00005, while also exhibiting greater stability with less oscillation. This is because of the fact that an appropriate learning rate is critical for successful model training. If the learning rate is too high, the model may skip critical local minima, leading to unstable optimization. Conversely, if the learning rate is too low, the model may get stuck in a local minimum and fail to reach the global minimum. Hence, when the learning rate are 0.005 and 0.00005, the oscillation is more severe and the convergence effect will be worse. So we choose the learning rate as 0.0005 in this paper.

Fig. 3
figure 3

Impact of different hyperparameters for whole operation time (a–d) and accumulated reward (e–h).

Full size image

Figure 3b displays the relationship between the whole operation time and the size of \(\wp\). The plot indicates that when compared to values of \({\wp } = 64\) and \({\wp } = 256\), a value of \({\wp } = 128\) leads to a lower final convergence value, less oscillation, and greater stability throughout the process. This is due to choosing an appropriate value for \(\wp\) is essential for discovering the optimal Q value during network training. If \(\wp\) is too small, only a limited number of states are utilized to update the Q value, resulting in inaccurate predictions. Conversely, if \(\wp\) is too large, the proposed method will converge slowly and may not achieve satisfactory ultimate convergence. To ensure the performance of our proposed method, we selected \({\wp } = 128\) for our simulation trials.

Figure 3c illustrates the relationship between the whole operation time and the mini-batch size. Our simulation results show that a mini-batch size of 512 leads to the fastest convergence and shortest operation time. This is because a larger batch size allows the UAVs to fully exploit the sample data stored in the replay buffer, leading to the identification of optimal action selection strategies during interaction with the environment. Conversely, for smaller batch sizes (128 or 256), we observe stronger oscillations during the initial training phase due to underutilization of the stored samples and sub-optimal action selection strategies. This results in fluctuations in the whole operation time. We have thus selected a batch size of 512 to ensure the optimal performance of our proposed method.

Furthermore, Fig. 3d shows the relationship between the whole operation time and the update frequency \(N_Q\) of the target network. From the simulation results, it can be observed that \(N_Q=20\) achieves better performance compared to update frequencies of 10 and 40, and it also exhibits greater stability. This is mainly because if the target network parameters are updated too frequently (\(N_Q=10\)), it can lead to overestimation of target Q-values, making the training process unstable and difficult to converge to the optimal policy. On the other hand, when the update frequency is too slow (\(N_Q=40\)), the target network cannot accurately acquire network parameter values during the training process, leading to inaccurate predictions. Therefore, the update interval of the target network is set to 20.

Moreover, we verified the convergence performance of the selected parameters through simulation. As shown in Fig. 3e, it is evident that the case with learning rate of 0.0005 converged after 420 episodes, whereas learning rates of 0.00005 and 0.005 required longer training to converge. Similarly, it can be seen from Fig. 3f–h that when \({\wp } = 128\), batch size \(= 512\) and \(N_Q=20\), the reward value is greater, and the convergence is faster. In addition, compared to the baseline schemes, the selected hyperparameters also exhibit greater stability. This demonstrates that the selected hyperparameters contribute to superior performance and convergence of the algorithm.

Finally, we also study the impact of the discount factor on the convergence performance, as shown in Table 2. On the one hand, in terms of convergence performance, when the discount factor is too small (e.g., values between 0.1 and 0.6) or too large (e.g., a value of 1), the algorithm fails to converge. Although the algorithm eventually converges when the discount factor is set to 0.7 and 0.8, the convergence speed is slower compared to the case when the discount factor is set to 0.9. On the other hand, the task completion time is unstable as the discount factor increases from 0.1 to 0.6, and it gradually decreases as the discount factor increases from 0.7 to 0.9. Additionally, when the discount factor is set to 1, the UAVs’ task completion time is unexpectedly higher. The main reasons for the above phenomena are as follows: when the discount factor is too small, the agent may disregard long-term benefits, leading the algorithm to get stuck in local optima and potentially not convergence. Conversely, when the discount factor is too large, there is an overestimation of future rewards, resulting in uncertainty regarding long-term returns. This can lead to issues such as exploding or vanishing gradients during the training process, making it difficult to converge. Therefore, the discount factor is set to 0.9 in our algorithm design.

Table 2 Comparison of performance and convergence of different discount factors.
Full size table

Performance evaluation of the proposed method

Figure 4 displays a comparison of the proposed method’s performance with different baselines. The plot of the whole operation time reveals more pronounced fluctuations in the early stage of training, which subsequently decrease and stabilize with the increase of training episodes. This phenomenon can be attributed to the lack of experience of UAVs in the initial stage of training, which makes it difficult for them to discover the optimal strategy. As the training progresses, the UAVs gradually learn from their experiences and find more effective strategies. Secondly, the performance of our proposed method is comparable to that of centralized MARL and the without NFZs MAFRL method, while outperforming the benchmarks of the no dueling MAFRL approach and the random scheduling MAFRL method. This can be explained by several factors. The centralized MAFRL approach doesn’t require model aggregation and thus has no performance loss, resulting in better performance than our proposed method. Nevertheless, centralized training entails that each UAV must share its position, obtained channel gain, and other data with the server UAV. This process not only increases the communication load but also poses a potential risk of compromising user privacy. Moreover, the method without NFZs allows UAVs to shorten the path to complete the whole operation task. On the other hand, the no dueling MAFRL method doesn’t utilize the dueling architecture, which reduces the stability of the algorithm and leads to worse performance than our proposed method. Lastly, the method of random scheduling MAFRL causes severe curve oscillation due to the random scheduling of GDs.

Fig. 4
figure 4

Performance of the proposed method compared with different baselines.

Full size image

Furthermore, to validate the effects of dueling networks and multi-step techniques on the proposed method, we conducted relevant ablation experiments, as shown in Fig. 5. From Fig. 5, it can be observed that compared to the proposed method, the performance of the method without dueling networks (No Dueling Method) is poorer and unstable. In addition, the method (No Multi-step Method) converges more slowly when the multi-step technique is not utilized. Moreover, when neither the multi-step technique nor dueling networks are used, the algorithm exhibits the most severe oscillations, converges the slowest, and has the poorest performance. Therefore, through simulations, we can conclude that the multi-step technique can accelerate the convergence speed of the method, while dueling networks can enhance the stability and performance of the method. This is consistent with our theoretical analysis.

Fig. 5
figure 5

Ablation study performance analysis.

Full size image

Moreover, Fig.6 illustrates the impact of different combinations of UAVs and GDs speeds on system performance, where (10, 5) denotes a UAV speed of 10m/s and a GD speed of 5m/s. Firstly, it can be observed that with an increase in UAVs’ speed (while GDs’ speed remains constant), the whole operation time initially decreases and then increases. This indicates that both excessively high and excessively low UAV speeds can increase the whole completion time. Additionally, when the UAVs speed remains constant and the GDs’ speed increases from 2.5 m/s to 5 m/s, the whole operation time remains almost the same. However, when the speed increases to 10 m/s, the whole completion time significantly increases. This indicates that excessively high GDs speeds will decrease system performance.

Fig. 6
figure 6

Performance comparison of the proposed method versus different combinations speeds of GDs and UAVs.

Full size image

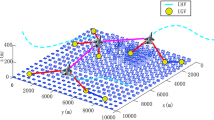
In Fig. 7, we present the 3D trajectories of our proposed method and baselines for the UAVs. These trajectories are represented by 3D curves, with the initial positions of UAV1 and UAV2 depicted as red and blue points ’\(\bullet\)’, respectively. In addition, the starting point of the GDs is marked by an ’x’ on the ground, and the GDs are in a state of random movement. From Fig. 7a–e, we can observe that the UAVs exhibit fluctuations in height while collecting data sent by the GDs. This behavior is due to a trade-off between LoS probability and transmission distance. Specifically, when the UAV is flying at a low altitude and in a NLoS state, it increases its height to establish a LoS state. Conversely, in a LoS state, the UAV reduces its Euclidean distance from the scheduled GD to increase the transmission rate. Furthermore, it can be seen that UAV1 tends to approach GD1, GD3, and GD4 while collecting data, whereas UAV2 is closer to GD2, GD5, and GD6. Additionally, they do not change their flight direction within a certain trajectory. This is primarily because UAVs tend to gradually approach their scheduled GDs to enhance data transmission. In this process, UAVs choose directions that allow them to get closer to the scheduled GDs to save operational time, which also results in UAVs maintaining a consistent direction within a period time. Moreover, Fig. 7d,f demonstrate that the UAV can collect data from a ___location within the NFZs in the absence of any such zone. This can significantly reduce the time required to complete the tasks as compared to the scenario that includes NFZs. This finding also accounts for the observed shorter task completion time in the absence of the NFZs in Fig. 4, as compared to that of our proposed method.

Fig. 7
figure 7

Exhibition UAVs’ 3D trajectories under different methods.

Full size image

Next, we present the percentage of UAVs that do not comply with the space flight constraints when using the proposed method. The space flight constraints are defined as UAVs flying out of a designated area, colliding with each other, or breaching the no-fly zone. A collision between UAVs occurs when the flight space constraints are not met, and the collision percentage for each episode is calculated by dividing the total number of collision slots by the total number of time slots when the UAVs complete their tasks. From Fig. 8, we can observe that the UAV no longer collision after the episode exceeds 630. The reason for this is that the UAVs’ trajectories strategy, which was improved by accumulating environmental experience during the previous training, prevents collisions from occurring. Furthermore, the UAVs trajectories of Fig. 7 also indicate that the UAVs successfully avoided the NFZs and there were no collisions between the UAVs. This demonstrates that the proposed method effectively addresses the issues of NFZs and collisions for UAVs.

Fig. 8
figure 8

The percent of collision per episode versus episodes.

Full size image

Moreover, Fig. 9 presents a comparison of the performance of our proposed method with that of 2D cases, i.e., the UAVs’ flying height is fixed. From Fig. 9, we can observe that as the data size of each GD increases, the whole operation time also increases. In addition, 3D trajectory designing takes less time compared to 2D cases, indicating that adjusting the height of UAVs helps to attain efficient trajectories. Furthermore, from Fig. 9, we notice that for 2D trajectory designs at different heights, the whole operation time first decreases (when \(z_n\) increases from 50m to 100m) and then increases (when \(z_n\) increases from 100m to 150m). The decrease in time is due to the UAV-GD channel being predominantly in the NLoS state at low altitudes, and as the altitude increases, the channel state shifts from NLoS to LoS, resulting in a shorter operation time. However, when the UAV operates in the LoS state, the increase in distance between the UAV and GD causes the whole operation time to increase. Finally, we can observe that the scenario without NFZs requires less time compared to the scenario with NFZs. This is because UAVs need to fly longer path to avoid entering NFZs while collecting data in the scenario of with NFZs, leading to a longer time.

Fig. 9
figure 9

Performance comparison of 3D trajectory design versus 2D cases.

Full size image

At last, to validate the robustness of the proposed method for different scenarios of GDs movement, we also investigated the scenario where GDs move along a longer path on the ground, i.e., GDs move on a ground path and less frequently change their directions. Figure 10 shows the trajectories of UAVs and GDs in the long path movement scenario, and Fig. 11 compares the whole operation time of UAVs in two different scenarios. Firstly, from Fig 10, it can be observed that compared to the trajectories of GDs in Fig. 7a (GDs follow Random Walk), less frequently change the GDs’ direction result in GDs covering longer relative distances. Additionally, the increase in relative distances covered by GDs also results in UAVs flying longer distances. Moreover, from Fig. 11, it can be observed that the whole operation time of UAVs is longer in the long path movement scenario compared to the Random Walk scenario. These are mainly because the data transmission rate is primarily affected by the distance and elevation angle between the UAV and the scheduled GDs. To reduce the whole operation time, UAVs need to gradually approach the scheduled GDs. Thus, the increase in the movement distance of GDs results in the UAV flying longer distances and also requires more time to complete the task.

Fig. 10
figure 10

UAVs’ 3D trajectories exhibition in the scenario of Long Path Movement of GDs.

Full size image
Fig. 11
figure 11

Performance comparison in different GDs’ movement scenarios.

Full size image

Impact of different data size

Figure 12 depicts the whole operation time versus the data size per GD. Figure 12a, c demonstrate that as the data size for each GD increases, the time required for data collection and the whole operation also increases. This is due to the fact that as more data is collected, the UAVs require more time to complete the data collection task. Figure 12b illustrates that as the data size for each GD increases, the model parameters transmission time for the centralized MARL method remains constant at zero, while the model parameters transfer time for other methods increases correspondingly. This is because the centralized MAFRL method does not need to process the model parameters, but other methods lead to an increase in the number of model parameter exchanges. In particular, the method of centralized MARL requires the UAVs to share information such as their current ___location, which cannot ensure privacy protection. In addition, the proposed method consistently demonstrates strong performance as the data size of each GD increases, approaching the ideal environment without NFZs MAFRL method and centralized MAFRL method. Moreover, compared to the random scheduling MAFRL method and no dueling MAFRL method, our approach exhibits increasingly superior performance, providing further evidence of the effectiveness of the proposed method.

Fig. 12
figure 12

Time cost performance comparison with different methods.

Full size image

Comparison of methods with different numbers of NFZs and UAVs

The impact of the number of NFZs on the whole operation time is shown in Fig. 13. It is observed that the baseline method without NFZs MAFRL is not affected by the number of NFZs. In contrast, the other methods experience an increase in the whole operation time with the increase of NFZs. This is due to the increasing complexity of the mission environment, which requires UAVs to take longer paths to complete their mission. Furthermore, the figure also demonstrates that when the number of NFZs is less than 1, the centralized MARL method has a shorter whole operation time than the MAFRL method without NFZs. This is because when the number of NFZs is small, their impact on system performance is small, and the whole operation time is mainly influenced by the method itself. Finally, the advantages of the proposed method become more significant as the size of the NFZs increase, particularly when compared to the comparison methods without NFZs MAFRL and no dueling MAFRL. In addition, Fig. 14 shows the whole operation time versus the number of UAVs. From Fig. 14, we can see that as the number of UAVs increases, the whole operation time gradually reduces. This means that more UAVs can collect the same data in less time. In addition, it can also be seen that as the number of UAVs increases, the slope of the decrease in the whole operation time gradually becomes smaller. This suggests that for limited data sizes, increasing the number of UAVs may not significantly reduce mission completion time. Hence, in practical situations, it is essential to deploy an optimal number of UAVs to fulfill tasks based on varying mission requirements.

Fig. 13
figure 13

Performance comparison of different numbers of NFZs.

Full size image
Fig. 14
figure 14

Performance comparison of different numbers of UAVs.

Full size image

Time complexity analysis

We also compare the time complexity of MARL and MAFRL methods, as shown in Table 3. Within 1000 episodes of training, MAFRL saves nearly 19.4% training time compared to MARL. Therefore, from the perspective of time complexity performance, the proposed MAFRL algorithm is more suitable for multi-UAV data collection system than the centralized one.

Table 3 Time complexity of different methods.
Full size table

Conclusion

This paper proposed a learning-based design for a UAV-assisted data collection system in a 3D urban environment with multiple mobile GDs and NFZs. The aim was to minimize the whole operation time by jointly optimizing the UAVs’ 3D trajectory design together with the communication scheduling of GDs. However, the established problem was nonconvex and the GDs’ motion was difficult to process. Additionally, the UAVs’ privacy issue needs to be considered due to server attacks, fake commands, computational load, and privacy leakage. To tackle these issues, we formulated the problem as an MDP and proposed a MAFRL method where each UAV acted as an agent to learn the policy of 3D trajectory and GDs’ scheduling. In addition, we conducted simulations to select appropriate hyperparameters and compared the proposed method’s performance with baseline methods. Furthermore, the study also investigated the performance improvement of 3D trajectory design compared to 2D cases, and the effect of different numbers of NFZs/UAVs on the whole operation time. Moreover, the proposed method can be extended to other systems, i.e., the motion of GDs in 3D space, and multi-task scenarios. Moreover, the proposed method can be extended to other systems, i.e., the motion of GDs in 3D space, and multi-task scenarios. On the other hand, the design of the reward function has a significant impact on the performance of the system. In our future work, we will investigate how the performance of the proposed algorithm can be enhanced when the reward function is designed as a continuous function to prevent UAVs from entering NFZs or collisions.