Introduction

Conventional energy prices are primarily responsible for the current inflation of the world. The materials researchers are working hard to comfort society by providing an economical alternative to energy. Since the sun is a vast energy source, it can help us to escape conventional energy. The devices that can convert solar energy into useful energy need specific materials with a bandgap between their conduction and valance bands (i.e., CB & VB), known as semiconducting materials. Single perovskite (SP) and double perovskite (DP) are famed for their execution in galore types of practical devices like gas sensors, wireless communication systems, detectors for temperature, lasers, conducting devices having negligible resistance, LEDs, energy storage applications, photovoltaic electrodes, and photovoltaic cells 1,2,3,4,5,6,7,8,9,10,11.

DP materials are known for their high stability both in heat & air, high optical absorption & optical conductivity capability, befitting bandgaps, and nominal defects 12,13,14,15. Nowadays, researchers are avoiding DP materials which contain Pb (i.e., lead) due to their toxicity and instability in open air and heat. Previously, many DP 'K' (i.e., potassium) based halides & oxides have been examined and reported by diverse research groups. Shah et al. reported K2NaBiCl6 material and found that this compound is semiconducting with a bandgap of 3.75 eV. Moreover, owing to the examined absorption peaks in the material’s ultra-violet (UV) region, the researchers claimed that the investigated material best fits the UV detectors and sensors 16.

Similarly, Murtaza et al. examined K2NaGaBr6 & K2RbTlBr6 via DFT. They proclaimed that these two materials are semiconducting and possess high stability. These compounds were suggested for optoelectronic and renewable energy applications based on their maximum absorption behaviour and momentous ZT values 17. Ain et al. reported K2BGaI6 (B = Tl & Rb) DP materials and argued for their experimental synthesis. The authors observed that these investigated materials are ductile, complex, and stable 18. X2YIO6 (X = K, Rb) oxides were studied theoretically and found thermodynamically stable from their acquired Gibbs-free and formation energies 19. A series of halide K2CuSbX6 (where "X" denote Cl, Br, I) DP were reported for the transport and optoelectronic applications by Al-Qaisi et al. 20. Several other researchers also worked on the "K" based DP materials and elaborated their vast behaviours for the intentions of abundant applications 21.

The literature mentioned earlier made it clear that "K" based materials are widely chosen for their study due to their superior exhibiting properties. Our research group also worked on "K" based DP and found that K2MgSiCl6 (i.e., KCl) & K2MgSiBr6 (i.e., KBr) compounds are not been investigated before. So, we thoroughly investigated computationally all the basic behaviors of these materials, hoping that it would facilitate the experimentalists in manufacturing these halides in their labs.

Computational model

For the Kohn Sham equations’ solution, we employed the Full-Potential Linearized Augmented-Plane wave (FP-LAPW), which is coded within the WIEN2k 22,23. First, the lattice parameters of the KBr & KCl were optimized in the cubic structure. Next, with the assistance of Tran & Blaha, modified Becke-Johnson (Tb-mBJ) potential & using the acquired optimized lattice parameters, the band structures of the studied halides were determined 24,25. For the matrix size convergence, we used RMT × Kmax as 7, and the wave function expansion was given as 10 interiors of muffin-tin. For both KCl & KBr materials, the RMT values were presented as 5, K-points chosen for all the calculations were 2000, and to elude the charge outflow from the atomic spheres "–6 Ry" was selected as a valance and core energy gap. After confirming the semiconducting nature of KCl & KBr, we calculated all the optical properties’ primary parameters, and their mechanical properties were elaborated with the assistance of the IRelast Package 26. Moreover, the tolerance factor, AIMD, and formation energy were also calculated for the currently studied KBr & KCl materials.

Results and discussion

Structural properties

Initially, we checked whether the KCl & KBr halides having cubic structures accomplish the stability criteria recommended by Goldschmidt; for this purpose, we use the following formula 27.

$$\tau {\text{f}} = \frac{rA + rH}{{\sqrt 2 \left( {rB + rH} \right)}}$$
(1)

From Eq. (1), it was concluded that the KCl & KBr halides have τf values of structure stability as 0.95 & 0.94, respectively. From these τf values of the studied compounds, it was concluded that they have stable structures because their exhibited values, as presented in Table 1, are in the range recommended for stable cubic structures 27. Goldschmidt suggested that the compounds with cubic structure and tolerance factors values in the range of 0.8 to 1 are the most stable. Moreover, these compounds were also found to have negative formation energy (EFE) values, which were calculated using the below Eq. 2.

$${\text{E}}_{{{\text{FE}}}} {\text{ = E}}_{{{\text{Total}}}} - \, \left( {{\text{2E}}_{{\text{K}}} + {\text{ E}}_{{{\text{Mg}}}} + {\text{ E}}_{{{\text{Si}}}} + {\text{ 6E}}_{{\text{H}}} } \right)$$
(2)
Table 1 Achieved structural parameters values for the K2MgSiH6 (H = Cl & Br) halides.
Full size table

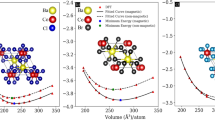
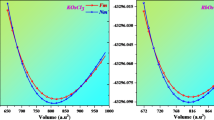
The calculated EFE values of Kcl (i.e., − 2.31) & KBr (i.e., − 1.96) compounds sustained the thermodynamic solidity of these KCl & KBr compounds 28,29,30. The atoms of the KCl & KBr compounds were placed at the positions in their crystalline structure, as presented in Fig. 1. These structures of the KCl & KBr halides were optimized, and their resultant optimized volumes-energy curves are shown in Fig. 2. From their optimized curves, the achieved lattice parameters found were 10.31 & 10.93 for the KCl & KBr compounds, respectively. Since “Br” has larger ionic radii than the “Cl” this feature was accountable for the more significant lattice parameter of KBr than the KCl. As a result of having larger lattice parameters of KBr than the KCl compound, the ground state volume was also observed to be more bigger for the KBr compound than the KCl compound, as presented in Table 2. However, the bulk modulus value was noted to be less for the KBr compound than the KCl compound, which makes it less resistant to compression than the later compound. Furthermore, ground state energy was recorded less for the KBr halide than for the KCl halide. This lower value of ground state energy ensures that the KBr compound’s structure stability is greater than that of the KCl compound. Figure 3 (a,b)/(e,f), represents the geometrical crystal structures of KCl/KBr before and after heating the system at 300 K. Figure 3 (c & d) represents the ab initio molecular dynamic calculations of KCl and KBr, respectively. The analysis of data reveals no evidence of bond dissociation or structural reconstruction following the thermal treatment at 300 K for 195 femtoseconds, thus confirming the thermal stability of KCl and KBr.

Fig. 1
figure 1

Position of the elements in the optimized structures of the K2MgSiH6 (H = Cl & Br) halides.

Full size image
Fig. 2
figure 2

Achieved optimization curves of the Energy verses Volume for the K2MgSiH6 (H = Cl & Br) halides.

Full size image
Table 2 Achieved mechanical parameters values for the K2MgSiH6 (H = Cl & Br) halides.
Full size table
Fig. 3
figure 3

Geometric crystal structure of K2MgSiCl6/K2MgSiBr6 (a/e) before and (b/f) after heating the system at 300 K. Thermal stability of (c) K2MgSiCl6 and (d) K2MgSiBr6.

Full size image

Electronic properties

Band structure calculations were also performed for the recently studied KCl & KBr compounds; their final results are presented in Fig. 4. It is obvious from their respective band structure curves that none of the VB or CB curves of the KCl & KBr compounds cross the Fermi level, and these behaviours authenticate the semiconducting character of both the studied halide materials. The bandgaps for the KCl & KBr halides were noted as: 2.42 eV & 1.88 eV, respectively. The patterns of the band structure show that the KCl compound, having a smaller lattice constant, exhibits a larger bandgap than the KBr compound, which possesses a larger lattice constant and such practice of DP materials bandgaps alteration with the lattice constant has been testified by other researchers as well 27,31,32. The lower bandgaps of these materials make them proper entities for their execution in solar cells & other optoelectronic appliances 33.

Fig. 4
figure 4

Noted behavior of the band structures for the K2MgSiH6 (H = Cl & Br) halides.

Full size image

Moreover, their band structures were also detected as indirect at W & L points, as shown in Fig. 5. Since the minima of CB and maxima of the VB did not coexist at the same point and this behaviour makes them indirect bandgap materials. The TDOS and PDOS of these materials also confirmed the KCl & KBr DP band structure results. From the TDOS plots of the studied DP, neither of the CB or VB curves cross the Zeroth (Fermi) level, and hence the semiconducting characteristic of the KCl & KBr materials was confirmed again from these results. The PDOS plots in Fig. 5 demonstrate the single atom contributions in the VB & CB of the KCl & KBr DP. It is confirmed from the KCl & KBr plots of PDOS that non-metal contributions in the VB and CB bands have been significant.

Fig. 5
figure 5

K2MgSiH6 (H = Cl & Br) halides TDOS and PDOS curves.

Full size image

Mechanical behavior

For the physical behaviour of the studied materials upon the applied external force, we calculated the mechanical properties for the KCl & KBr DP; and for this intention, we initially determined the "3" chief constants of elasticity, namely C44, C12, & C11; which are listed in Table 2. The elastic constants of KCl DP were found to be greater than the KBr DP. Moreover, the elastic constants achieved for both the KCl & KBr DP were found to accomplish the basic requirements (a) C11 > B > C12, (b) C11 + 2C12 greater than 0, (c) C11 & C44 greater than 0, and (d) C11 – C12 greater than 0} 22,23,34. Using these 3 elastic constants in the following equations (i.e., Eqs. 3, 4, 5, 6,7 & 8), we determined the other mechanical parameters for the studied KCl & KBr DP. Their final numerical values are presented in Table 2.

$$B=\frac{{C}_{11}+2{C}_{12}}{3}$$
(3)
$$E=\frac{9BG}{3B+G}$$
(4)
$${G}_{V}=\frac{{C}_{11}-{C}_{12}+3{C}_{44}}{5}$$
(5)
$${G}_{R}=\frac{5{C}_{44}({C}_{11}-{C}_{12})}{4{C}_{44}+3({C}_{11}-{C}_{12})}$$
(6)
$$G=\frac{{G}_{V}+{G}_{R}}{2}$$
(7)
$$A=\frac{2{C}_{44}}{{C}_{11}-{C}_{12}}$$
(8)

It is clear from Table 2 that the KBr compound possesses the values of the Bulk modulus (B), shear modulus (G), and Young modulus (E) lesser than the KCl compound, and this shows that the KBr compound is more compressible under the influence of externally applied stress than the KCl compound. It has been reported that the ductile materials have Pugh’s ratio (B/G) and Poison’s ratio (V) greater than 1.75 & 0.26 27. From the achieved numerical values of both B/G & V ratios, it is apparent that the studied KCl & KBr compounds have a brittle nature. However, both the studied materials have an anisotropic nature because neither of the investigated materials display the calculated value of anisotropic factor (A) precisely as 1 35.

Optical properties

To know about the investigated KCl & KBr DP interaction with the incident electromagnetic radiation, we determined all the essential parameters, i.e., dielectric function ε(ω), optical conductivity σ(ω), refractive index η(ω), absorption α(ω), and reflectivity R(ω) of the optics. The dielectric function of any material is a complex quantity and has two parts, i.e., the real component and the imaginary component. Complex ε(ω) can be expressed mathematically by the subsequent Equation:

$$\upvarepsilon \left(\upomega \right) \, = \,\upvarepsilon _{{1}} \left(\upomega \right) \, + {\text{ i}}\upvarepsilon _{{2}} \left(\upomega \right)$$
(9)

In the above Equation, ε (ω) expresses the total dielectric function, while on the other side of the above Equation, ε1(ω) and iε2(ω) stand for the real & imaginary parts of the ε(ω), respectively. ε(ω) explains the overall perturbation produced by the incident electromagnetic radiations within any material 36. Figure 6 (a) represents the ε1(ω) part in the range of 0–40 eV; the ε1(0) values exhibited by the KCl & KBr were 3.28 & 3.87, respectively. The observed curves of the ε1(ω) parts for the studied compounds showed variations in their values above the zero line in the 0–11 eV range. However, the curves moved towards the zero line after increasing the photons energy range further. Moreover, at 11.15 eV and 12.61 eV, the KCl & KBr DP showed metallic behavior, because their ε1(ω) curves crossed the zeroth level. The iε2(ω) parts of the ε(ω) for the two studied compounds are presented in Fig. 6 (b), and this portion of the ε(ω) is proportional to the absorption of any material. The iε2 (ω) curves showed no response to the incident photons having less energy. Still, as the incident photon’s energy comparable to the bandgaps in between the studied materials, the curves showed initial increments in their peaks. Both the materials showed their preliminary highest values of iε2 (ω) in the visible (Vb) energy range of 2.6–3.2 eV; however, in the ultra-violet (UV) range, KBr compound showed more significant response to the incident photons than the KCl compound.

Fig. 6
figure 6

Real and imaginary parameter of the dielectric functions for the K2MgSiH6 (H = Cl & Br) halides.

Full size image

The incident photons dispersion and their absorption within any material can be entirely described by an optical parameter known as refractive index η(ω). For the currently studied KCl & KBr DP, the η(ω) patterns were calculated in the 0–40 eV energy range and are illustrated in Fig. 7 (a). It is obvious from the η(ω) patterns that the static η(ω) values which were found as 1.81 for KCl and 1.97 for KBr, completely fulfil the fundamental correlation between the static values of ε1(ω) and the observed static values of η(ω) {i.e., η(0)2 = ε1 (0) } 37. Moreover, the patterns of the η(ω) were found to have precisely a similar drift with the photon energy to that of the ε1(ω). Since ε1(ω) and η(ω) are correlated to each other by the following relation.

$$\eta^{{2}} {-}{\text{ k}}^{{2}} = \,\upvarepsilon _{{1}} \left(\upomega \right)$$
(10)
Fig. 7
figure 7

Studied parameters of the optical behavior for the K2MgSiH6 (H = Cl & Br) halides.

Full size image

Both the KCl & KBr DP showed their highest η(ω) peaks in the Vb range of 2 & 2.60 eV, making these materials more superior for their use in practical devices working in the Vb range. However, for the more energetic photons, the η(ω) curves showed a decline in their intensities.

From the absorption α(ω) curves received for the KCl & KBr DP, as illustrated in Fig. 7b, it’s evident that both the materials can absorb Vb and UV ranges of electromagnetic radiation incident on them. Since both the compounds showed their initial enhancement in their α(ω) values for the energy of the photons < 3.26. The KCl material displayed more extraordinary absorption ability of both the Vb and UV electromagnetic photons than the KBr material. The highest α(ω) peaks observed for the investigated materials were 194 × 104/cm for KCl and 168 × 104/cm for the KBr in the UV range. However, in the Vb range, the peak values, 24.67 × 104/cm for KCl & 22.11 × 104/cm for KBr, were noted. This tendency of absorbing the electromagnetic radiations in the Vb and UV range enables the KCl & KBr materials appropriate for the detectors, solar cells, & many other optoelectronic appliances.

The optical conductivities were also calculated for the KCl & KBr materials in a range of 0–40 eV, and their resultant graphs are demonstrated in Fig. 7 (c). Its apparent from the figure that both materials have shown their optical conductivity in both the Vb and UV range. Moreover, their response to the photons’ energy within UV range was quite remarkable. The KBr material first showed its response to the electromagnetic radiations in the Vb range and acquired the value of 1219 (Ω.cm)-1; however, KCl material showed its response to a bit higher energetic photons in the Vb range than KBr but its optical conductivity was higher (i.e., 1270 (Ω.cm)-1) than the KCl material in the Vb range. In the UV range, the utmost peak was also observed for the KCl material, achieving the optical conductivity value of 5303 (Ω.cm)-1 at 12.53 eV.

In comparison, KBr showed optical conductivity as 5222 (Ω.m)-1 at 11.11 eV. The optical conductivity achieved by KBr, particularly in the visible region, significantly enhances its potential for use in solar cells 32. In contrast, KCl exhibits properties that make it well-suited for detectors, LEDs, and various other optoelectronic devices. The last Fig. 7 (d) represents the reflectivity R (ω) of the photons from the surfaces of the KCl & KBr materials. This part of the optical property lets us know how much incident photons bounce back from the surface of any material. The static R (ω) values were found to be 0.08 & 0.11 for the KCl & KBr materials, respectively. However, the utmost peak was found for the KCl material in the investigated range of energy.

Conclusion

During the investigation, the lattice parameters found were 10.31 & 10.93 for the K2MgSiCl6 & K2MgSiBr6 compounds, respectively. It was determined that the K2MgSiCl6 & K2MgSiBr6 halides have τf values of structure stability as 0.95 & 0.94, while the calculated formation energy values of thermodynamic stability were − 2.31 & − 1.96, respectively. Moreover, their band structures were also detected as indirect at W & L points. Additionally, the studied materials have an anisotropic nature; since, neither of the investigated materials display the calculated value of anisotropic factor (A) precisely as 1. The highest α(ω) peaks observed for the investigated materials were: 194 × 104/cm for K2MgSiCl6 and 168 × 104/cm for the K2MgSiBr6 in the UV range. However, in the visible range, the peak values of 24.67 × 104/cm for K2MgSiCl6 & 22.11 × 104/cm for the K2MgSiBr6 were noted. This tendency of absorbing electromagnetic radiations both in the visible and UV range enables the K2MgSiCl6 & K2MgSiBr6 materials to be suitable for detectors, solar cells, & many other optoelectronic appliances. In the UV energy range, the highest conductivity was also observed for the K2MgSiCl6 material by the value of 5303 (Ω.cm)-1 at 12.53 eV, while K2MgSiBr6 showed a high conductivity of 5222 (Ω.m)-1 at 11.11 eV.