Introduction

Studying complex fluid dynamics and heat transfer phenomena becomes imperative for advancing our understanding of real-world applications. This investigation delves into the intricate interplay of Dufour, Soret, and radiation effects on a mixed convective power-law heat and species transfer. The system under scrutiny involves the fluid’s interaction with a continuously stretching surface, introducing further complexity through variable heat conductivity and viscosity. This research aims to unravel the nuanced dynamics of these coupled phenomena, shedding light on their implications for diverse engineering and industrial usages.

Chen1 delved into the intricacies of free convective MHD (magnetohydrodynamics) flow through a vertical medium, scrutinizing the impact of viscous dissipation and heating. Hossain2 extended this exploration by focusing on the interplay between viscous and Joule heating influences on free convective MHD flows characterized by a variable plate temperature. Hong et al.3 ventured into porous media, investigating non-Darcy impacts on natural convective flow, particularly in scenarios featuring high permeabilities. The study by Costesèque et al.4 contributed insights into thermos-diffusion in porous media, unravelling its intricate consequences. Alam et al.5 broadened the scope by considering the free convective of Dufour and Soret influences on the species transport in a vertical semi-infinite permeable sheet and porous media. Chen6 explored mixed convective laminar flow in continuously stretched vertical plates, adding a layer of complexity to the understanding of these processes. Zaimi et al.7 delved into nanofluid dynamics by analyzing the flow through a permeable shrinking plate. Sithole et al.8 introduced numerical simulations to investigate magneto-couple stress nanomaterial flowing fluid in porous media, considering chemical reactions and radiative heat. Lone et al.9 brought in the element of stratification, examining a Casson liquid covering microorganisms past a stretchy surface with Arrhenius kinetics. Pal and Chatterjee10 considered the intricacies effect of Soret and Dufour in thermal and chemical reaction MHD convective power-law flow past an inclined sheet, incorporating variable heat conduction within permeable media. El-Kabeir et al.11 extended their analysis to encompass the complexities of stagnation-point of hydromagnetic thermic and species transport of power-law flow along a stretchy plate, incorporating Dufour, Soret chemical reaction and radiation effects.

Exploring heat and mass transfer phenomena in MHD flows extends further by examining various additional studies. Siddique et al.12 scrutinized the time-dependent second-grade magneto-nanofluid flow with Soret and Dufour effects in an exponential stretchy sheet. Hayat et al.13 investigated the mixed convective viscoelastic fluid flow through a vertically stretched boundary surface layer with permeable media, capturing the effect of Soret and Dufour. Pal and Mondal14 delved into the impact of species reactions and radiative heat on convective thermal and mass distribution past a stretched plate in Darcy porous media with the influence of Soret and Dufour. Alam and Ahammad15 explored variable electrical conduction and chemical reaction effects on convective thermal and species propagation over an inclined stretchy surface with Dufour and Soret impacts, and thermal and mass fluxes. Okedoye and Salawu16 considered nonlinear radiation of MHD heat and mass transport flowing fluid through an elongated sheet with variable properties. Khan et al.17 focused on convective MHD non-Newtonian power-law flowing material past a vertical moving plate with reacting species, heat generation and radiative impacts. Mahmoud18 analyzed radiative heat influences on the micropolar MHD fluid flow along a moving sheet with variable properties. Mohammadi et al.19 investigated the influence of convective and radiative fluid flow across an extending plate. Abel et al.20 explored the thermic fluid of a power-law material along an elongating plate with varying heat source and thermal conductivity. Various researchers have been described on heat and flow transfer over an elongated surface with different non-Newtonian fluid flows such as Carreau tri-hybrid nanofluid flow21.

Likewise, Hamid and Khan22 studied time-dependent MHD thermal dispersion Williamson convective nanofluid flow with varying heat conductivity. Seddeek and Almushigeh23 examined the viscosity and radiation effects on convective hydromagnetic reacting species in a stretchy device. Hamad et al.24 considered stagnation-point and thermal radiation impacts on MHD chemical species flow along a porous flat sheet with boundary convective cooling and heat-dependent fluid properties. Patil25 investigated surface-reacting species transport of convective fluid flow in a stretchy vertical device sheet with a variable thermal wall. Prasad et al.26 investigated thermal convective varying fluid flow properties along a nonlinear moving sheet. Idowu et al.27 delved into convective MHD gravity-driven Casson chemical reacting fluid with viscus heating and varying fluid properties. Sultan et al.28 provided computed results for the viscosity and heat conduction of rheology Carreau convective nanofluid. Sui et al.29 investigated power-law thermal convective fluid flow through an inclined conveyor surface. Lare30 analyzed varying conductivity and viscosity of Casson flowing liquid entrenched in thermal saturated media with an exponential stretchy plate varying thermal source. Ali31 explored heat convection and variable viscosity effects on the thermal dispersion of tiny particles in a moving vertical device. Madhu and Kishan32 studied radiative energy and chemical reaction of convective MHD stagnation-point nanofluid flow over a moving device using finite element analysis. Moreover, the authors25,33,34 studied transient convective parallel stream fluid along a stretchy variable thermal vertical wall and non-Darcy media. The study conducted by35,36 investigates the impact of the Lorentz force on the convective thermal and reacting species propagation in porous vertical media. The research considers the thermophoretic and Brownian movements, meaningfully affecting thermal processes. Sparrow and Yu’s work37 on the temperature boundary layer of local non-similarity solutions provides basic insights. Together, these studies contribute valuable knowledge to understanding the interplay of mass transfer, magnetic fields, and porous media in mixed convection scenarios.

From the aforementioned investigations, it is apparent that no consideration is paid to power-law fluid flows induced by continuously extended surface with varying viscosity and thermal conductivity effects. This study has diverse applications in understanding fluid dynamics in advancing biomimetic fluid transport designs in biomedicine, biological systems etc. The approximate solution is found for governing a system of ordinary differential equations. The system of differential equations is solved with the aid of Local Non-Similarity (LNS) method in MATLAB software. The outcomes are displayed in graphical form. This investigation will be explored by following research questions:

  • How does the power-law fluid impact the thermal and solutal boundary layer with in the fluid medium?

  • What role does Soret and Dufour play in influencing the efficiency of fluid transport in the stretching configuration.

  • How do variations in variable viscosity and variable thermal conductivity conditions affect the heat and mass transfer dynamics of the power-law fluid transport.

By thoroughly understanding these interactions, the research aims to contribute valuable insights that can inform the design and optimization of processes in engineering and industrial applications, ultimately enhancing efficiency and performance.

Governing equations

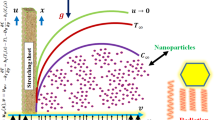
Consider the complex scenario of thermal convective and reacting species propagation of fluid particles over a semi-indefinite vertical device. This intriguing study considers the interplay of radiation, Dufour and Soret influences, introducing a comprehensive understanding of the intricate physical phenomena. Pictorial representation of flow geometry is shown in Fig. 1. The semi-infinite vertical plate is characterized by a surface preserved at a constant, unvarying heat, Tw, and a fluid’s constant, unvarying chemical species, Cw. Importantly, these boundary conditions surpass the equivalent values of T ∞ and C∞, at points satisfactorily distant from the wall. The analysis focuses on the x-axis, aligned upward to the plate, while the y-direction is defined typically. Under these carefully considered assumptions, the encompassing mass conservation, velocity, and heat equations emerge as crucial elements in unravelling the complex dynamics of the system. The continuity equation, a cornerstone in this analytical framework, provides a foundational insight into the mass balance, setting the stage for the subsequent exploration of the intricate energy and species transport processes occurring in this nuanced natural convection scenario following6,7,8.

Fig. 1
figure 1

Pictorial representation of flow geometry.

Full size image

Conservation of mass

$$\:\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$
(1)

Flow momentum rate Eq. 

$$\:\rho\:\left(u\frac{\partial\:u}{\partial\:x}+v\frac{\partial\:u}{\partial\:y}\right)=\frac{\partial\:}{\partial\:y}\left(\mu\:\frac{\partial\:u}{\partial\:y}\right)\pm\:g\beta\:\left(T-{T}_{\infty\:}\right)\pm\:g{\beta\:}^{*}\left(C-{C}_{\infty\:}\right)$$
(2)

Thermal energy Eq. 

$$\:u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=a\frac{{\partial }^{2}T}{\partial {y}^{2}}-\frac{\partial {q}_{r}}{\partial y}+\frac{{D}_{m}{k}_{T}}{{c}_{s}{c}_{p}}\frac{{\partial }^{2}C}{\partial {y}^{2}}$$
(3)

Reacting chemical species Eq. 

$$\:u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}={D}_{m}\frac{{\partial }^{2}C}{\partial {y}^{2}}+\frac{{D}_{m}{k}_{T}}{{T}_{m}}\frac{{\partial }^{2}T}{\partial {y}^{2}}$$
(4)

The boundary constraints can be expressed as

$$\:u={u}_{w}=c{x}^{p},v=0,T={T}_{w}={T}_{8}+A{x}^{n}\:,C={C}_{w}={C}_{8}+B{x}^{n}\:\:\text{at}\:y=0$$
$$\:u=0,\:\:T={T}_{8},C={C}_{8}\:\:\text{as}\:y\rightarrow \infty$$
(5)

Similarity variables for Transformation

Introducing the succeeding dimensionless quantities:

$$\:\eta\:=\frac{y}{x}{\left(\frac{{u}_{w}x}{\upsilon\:}\right)}^{\frac{1}{2}},\hspace{1em}\xi\:=\frac{G{r}_{x}{cos}\beta\:}{{\left(\frac{{u}_{w}x}{\upsilon\:}\right)}^{2}},\hspace{1em}u={u}_{w}{f}^{{\prime\:}}\left(\xi\:,\eta\:\right),\hspace{1em}$$
$$\:v=-\frac{\upsilon}{x}{\left(\frac{{u}_{w}x}{\upsilon}\right)}^{\frac{1}{2}}\left[\frac{p+1}{2}f+\left(n-2p+1\right)\eta\frac{\partial f}{\partial \eta}+\frac{p-1}{2}\eta{f}^{{\prime\:}}\right],$$
$$\:{G}_{rx}=\frac{g\beta\:\left({T}_{w}-{T}_{\infty\:}\right){x}^{3}}{{\upsilon\:}^{2}},$$
$$\:\theta\:\left(\xi\:,\eta\:\right)=\frac{T-{T}_{\infty\:}}{{T}_{w}-{T}_{\infty\:}},\hspace{1em}\phi\:\left(\xi\:,\eta\:\right)=\frac{C-{C}_{\infty\:}}{{C}_{w}-{C}_{\infty\:}},\hspace{1em}\mu\:={\mu\:}_{0}{e}^{-{\beta\:}_{1}\theta\:},\hspace{0.33em}\alpha\:={\alpha\:}_{0}\left(1+{\beta\:}_{2}\theta\:\right)$$
$$\:{q}_{r}=-\frac{4s}{3k}\frac{\partial {T}^{4}}{\partial y},\:{T}^{4}=4T{T}_{8}^{3}-3{T}_{8}^{4}$$
(6)

Introducing Eq. (6) into Eqs. (2)–(4), we respectively have

$$\:{f}^{{\prime\:\prime\:\prime\:}}-{\beta\:}_{1}{f}^{{\prime\:\prime\:}}{\theta\:}^{{\prime\:}}-\left(p{f}^{{\prime\:}2}-\frac{p+1}{2}f{f}^{{\prime\:\prime\:}}\right){e}^{{\beta\:}_{1}\theta\:}\pm\:\xi\:\left(\theta\:+N\phi\:\right){e}^{{\beta\:}_{1}\theta\:}={e}^{{\beta\:}_{1}\theta\:}\xi\:\left(n-2p+1\right)\left({f}^{{\prime\:}}\frac{\partial\:{f}^{{\prime\:}}}{\partial\:\xi\:}-{f}^{{\prime\:\prime\:}}\frac{\partial\:f}{\partial\:\xi\:}\right)$$
(7)
$$\:\frac{1}{Pr}\left(1+\frac{4}{3}N\right){\theta\:}^{{\prime\:\prime\:}}+\frac{1}{\left(1+{\beta\:}_{2}\theta\:\right)}\left[\frac{{\beta\:}_{2}}{Pr}{\theta\:}^{{\prime\:}2}-n{f}^{{\prime\:}}\theta\:+\frac{p+1}{2}f{\theta\:}^{{\prime\:}}+{D}_{f}{\phi\:}^{{\prime\:\prime\:}}\right]=\frac{\xi\:\left(n-2p+1\right)}{\left(1+{\beta\:}_{2}\theta\:\right)}\left({f}^{{\prime\:}}\frac{\partial\:\theta\:}{\partial\:\xi\:}-{\theta\:}^{{\prime\:}}\frac{\partial\:f}{\partial\:\xi\:}\right)$$
(8)
$$\:\frac{1}{Sc}{\varphi}^{\prime \prime}-n{f}^{{\prime\:}}\varphi+\frac{p+1}{2}f{\varphi}^{{\prime}}+{S}_{r}{\theta}^{\prime\prime}=\xi\left(n-2p+1\right)\left({f}^{{\prime\:}}\frac{\partial \varphi}{\partial \xi}-{\varphi}^{{\prime\:}}\frac{\partial f}{\partial \xi}\right)$$
(9)

Here, \(\:N=\frac{{\beta\:}^{*}\left({C}_{w}-{C}_{\infty\:}\right)}{\beta\:\left({T}_{w}-{T}_{\infty\:}\right)}\) is the buoyancy ratio, \(\:Pr=\frac{\upsilon}{a}\) is the Prandtl term, \(\:d=\frac{Qx}{{u}_{w}}\)is the heat generation/absorption, \(\:Sc=\frac{\upsilon}{{D}_{m}}\) is the Schmidt term, \(\:Df=\frac{{D}_{m}{k}_{T}\left({C}_{w}-{C}_{8}\right)}{{c}_{s}{c}_{p}\upsilon \left({T}_{w}-{T}_{8}\right)}\) is the Dufour term and \(\:Sr=\frac{{D}_{m}{k}_{T}\left({T}_{w}-{T}_{8}\right)}{{T}_{m}\upsilon \left({C}_{w}-{C}_{8}\right)}\) is the Soret term.

The corresponding boundary conditions are

$$\:f\left(\xi,0\right)=0,{f}^{{\prime\:}}\left(\xi,0\right)=1,\theta \left(\xi,0\right)=1,\varphi \left(\xi,0\right)=1\:\text{at}\:\eta =0$$
$$\:{f}^{{\prime\:}}\left(\xi,\infty \right)=0,\:\theta \left(\xi,\infty \right)=0,\varphi \left(\xi,\infty \right)=0\:\:\text{as}\:\:\eta \rightarrow \infty$$
(10)

The primary quantities of attention are the coefficient plate-friction, Nusselt number and Sherwood numbers, which are defined as:

$$\:\frac{1}{2}{C}_{f}{\left(\frac{{u}_{w}x}{\upsilon\:}\right)}^{\frac{1}{2}}=-{f}^{{\prime\:\prime\:}}\left(0\right)$$
(11)
$$\:{N}_{u}{\left(\frac{{u}_{w}x}{\upsilon\:}\right)}^{-\raisebox{1ex}{$1$}\!\left/\:\!\raisebox{-1ex}{$2$}\right.}=-{\theta\:}^{{\prime\:}}\left(0\right)$$
(12)
$$\:Sh{\left(\frac{{u}_{w}x}{\upsilon\:}\right)}^{-\raisebox{1ex}{$1$}\!\left/\:\!\raisebox{-1ex}{$2$}\right.}=-{\phi\:}^{{\prime\:}}\left(0\right)$$
(13)

Local non-similarity (LNS) numerical approach

The method employed for a numerical solution involves utilizing the non-similarity local approach to solve a set of coupled ordinary nonlinear derivative models [Matplotlib — Visualization with Python, OpenCV - Open Computer Vision Library and 6–8], which has been transformed to accommodate boundary conditions. This model collectively forms a parabolic system, amenable to various numerical methods, with the non-similarity local method being the chosen approach. Boundary constraints are applied after the interval, constituting a well-known boundary value problem with two points. The Runge-Kutta-Fehlberg approach, coupled with a shooting scheme, is employed to solve problems, a technique widely adopted to resolve diverse boundary layer flow problems. The computational scheme, initially devised by Sparrow and Yu37 and recently implemented by34,35,36, is outlined to elucidate the approach to tackling the aforementioned ordinary differential equations.

A differentiation strategy is employed on the main leading equations with the variable ξ, treating the resulting equations as auxiliary models combined with the main equation. Subsequently, the system is further condensed to an ordinary derivative equation by adopting ξ as a constant in the partial derivative equations.

\(\:\frac{\partial\:f}{\partial\:\xi\:}(\eta\:,\xi\:)=g(\eta\:,\xi\:)\), \(\:\frac{\partial\:\theta\:}{\partial\:\xi\:}(\eta\:,\xi\:)=h(\eta\:,\xi\:)\) and \(\:\frac{\partial\:\varphi\:}{\partial\:\xi\:}(\eta\:,\xi\:)=j(\eta\:,\xi\:)\) are assumed in Eqs. (7)-(9) with the boundary constraints. The equations are changed to,

$$\:{f}^{{\prime\:\prime\:\prime\:}}-{\beta\:}_{1}{f}^{{\prime\:\prime\:}}{\theta\:}^{{\prime\:}}-\left(p{f}^{{\prime\:}2}-\frac{p+1}{2}f{f}^{{\prime\:\prime\:}}\right){e}^{{\beta\:}_{1}\theta\:}\pm\:\xi\:\left(\theta\:+N\phi\:\right){e}^{{\beta\:}_{1}\theta\:}={e}^{{\beta\:}_{1}\theta\:}\xi\:\left(n-2p+1\right)\left({f}^{{\prime\:}}g^{\prime\:}-{f}^{{\prime\:\prime\:}}g\right)$$
(14)
$$\:\frac{1}{Pr}\left(1+\frac{4}{3}N\right){\theta\:}^{{\prime\:\prime\:}}+\frac{1}{\left(1+{\beta\:}_{2}\theta\:\right)}\left[\frac{{\beta\:}_{2}}{Pr}{\theta\:}^{{\prime\:}2}-n{f}^{{\prime\:}}\theta\:+\frac{p+1}{2}f{\theta\:}^{{\prime\:}}+{D}_{f}{\phi\:}^{{\prime\:\prime\:}}\right]=\frac{\xi\:\left(n-2p+1\right)}{\left(1+{\beta\:}_{2}\theta\:\right)}\left({f}^{{\prime\:}}h-{\theta\:}^{{\prime\:}}g\right)$$
(15)
$$\:\frac{1}{Sc}{\varphi}^{\prime\prime}-n{f}^{\prime}\varphi+\frac{p+1}{2}f{\varphi}^{\prime}+{S}_{r}{\theta}^{\prime\prime}=\xi\left(n-2p+1\right)\left({f}^{{\prime\:}}j-{\varphi}^{{\prime\:}}j^{\prime\:}\right)$$
(16)

The equivalent boundary constraints become

$$\:f\left(\xi,0\right)=0,{f}^{{\prime\:}}\left(\xi,0\right)=1,\theta\left(\xi,0\right)=1,\varphi \left(\xi,0\right)=1\:\text{at}\:\eta =0$$
$$\:{f}^{{\prime\:}}\left(\xi,\infty \right)=0,\:\theta\left(\xi,\infty\right)=0,\varphi \left(\eta,\infty \right)=0\:\:\text{as}\:\:\eta \rightarrow \infty$$
(17)

Now to apply the LNS approach to differentiate Eqs. (11) and (12) with boundary constraints in respect to ξ, to have

$$\:g^{\prime \prime\prime}-{\beta\:}_{1}(g^{\prime\prime}{\theta\:}^{{\prime}}+f^{\prime\prime\:}h^{\prime\:})-\left(p2f^{\prime\:}g^{\prime\:}-\frac{p+1}{2}(g{f}^{{\prime \prime\:}}+fg^{\prime \prime\:})+{\beta\:}_{1}h\right){e}^{{\beta\:}_{1}\theta\:}\pm\:\left(\right(\theta\:+N\phi\:)+\xi\:{\beta\:}_{1}h(\theta\:+N\phi\:)+\xi\:(h+Nj\left)\right){e}^{{\beta\:}_{1}\theta\:}$$
$$\:={e}^{{\beta\:}_{1}\theta\:}(\xi\:+{\beta\:}_{1}h)\left(n-2p+1\right)\left({f}^{{\prime\:}}g^{\prime\:}-{f}^{{\prime\:\prime\:}}g\right)$$
(18)
$$\:\frac{1}{Pr}\left(1+\frac{4}{3}N\right)(\left(1+{\beta\:}_{2}\theta\:\right)h^{\prime \prime \:}+\theta^{\prime \prime\:}{\beta\:}_{2})+\left[\frac{{\beta\:}_{2}}{Pr}2{\theta\:}^{{\prime\:}}h^{\prime\:}-n(g^{\prime\:}\theta\:+f^{\prime\:}h)+\frac{p+1}{2}(g\theta^{\prime\:}+fh^{\prime\:})+{D}_{f}j^{\prime \prime \:}\right]$$
$$\:=\left(n-2p+1\right)\left({f}^{{\prime\:}}h-{\theta}^{{\prime\:}}g\right)$$
(19)
$$\:\frac{1}{Sc}j^{\prime \prime\:}-n(g^{\prime\:}\varphi+f^{\prime\:}j)+\frac{p+1}{2}(g {\varphi}^ {\prime\:}+fj^{\prime\:})+{S}_{r}h^{\prime \prime\:}=\left(n-2p+1\right)\left({f}^{{\prime\:}}j-{\varphi}^{{\prime\:}}j^{\prime\:}\right)$$
(20)

Along with the accompanying boundary constraints

$$\:g\left(\xi,0\right)=0,g^{\prime\:}\left(\xi,0\right)=1,h\left(\xi,0\right)=1,j\left(\xi,0\right)=1\:\text{at}\:\eta=0$$
$$\:g^{\prime\:}\left(\xi,\infty\right)=0,\:h\left(\eta,\infty\right)=0,j\left(\xi,\infty \right)=0\:\:\text{as}\:\:\eta \rightarrow \infty$$
(21)

Equations (18)-(21) serve as supplementary equations to the foremost Eqs. (14)-(17), accompanied by their corresponding boundary conditions. As Sparrow and Yu36 have deliberated, it is advised to eliminate terms involving derivatives for the flow-wise coordinate from the right-hand side of the auxiliary Eqs. (14)-(17). Under the previously mentioned hypothesis, the flow rate and thermic boundary-layer model and their associated supporting equations can be amalgamated, incorporating the respective boundary constraints in the following manner:

$$\:{f}^{{\prime\:\prime\:\prime\:}}-{\beta\:}_{1}{f}^{{\prime\:\prime\:}}{\theta\:}^{{\prime\:}}-\left(p{f}^{{\prime\:}2}-\frac{p+1}{2}f{f}^{{\prime\:\prime\:}}\right){e}^{{\beta\:}_{1}\theta\:}\pm\:\xi\:\left(\theta\:+N\phi\:\right){e}^{{\beta\:}_{1}\theta\:}={e}^{{\beta\:}_{1}\theta\:}\xi\:\left(n-2p+1\right)\left({f}^{{\prime\:}}g^{\prime\:}-{f}^{{\prime\:\prime\:}}g\right)$$
(22)
$$\:\frac{1}{Pr}\left(1+\frac{4}{3}N\right){\theta\:}^{{\prime\:\prime\:}}+\frac{1}{\left(1+{\beta\:}_{2}\theta\:\right)}\left[\frac{{\beta\:}_{2}}{Pr}{\theta\:}^{{\prime\:}2}-n{f}^{{\prime\:}}\theta\:+\frac{p+1}{2}f{\theta\:}^{{\prime\:}}+{D}_{f}{\phi\:}^{{\prime\:\prime\:}}\right]=\frac{\xi\:\left(n-2p+1\right)}{\left(1+{\beta\:}_{2}\theta\:\right)}\left({f}^{{\prime\:}}h-{\theta\:}^{{\prime\:}}g\right)$$
(23)
$$\:\frac{1}{Sc}{\varphi}^{\prime\prime}-n{f}^{{\prime\:}}\varphi+\frac{p+1}{2}f{\varphi}^{{\prime\:}}+{S}_{r}{\theta}^{\prime\prime}=\xi \left(n-2p+1\right)\left({f}^{{\prime\:}}j-{\varphi}^{{\prime\:}}j^{\prime\:}\right)$$
(24)
$$\:g{\prime \prime \prime\:}-{\beta\:}_{1}(g{\prime \prime\:}{\theta\:}^{{\prime\:}}+f{\prime \prime\:}h{\prime\:})-\left(p2f{\prime\:}g{\prime\:}-\frac{p+1}{2}(g{f}^{{\prime\:\prime\:}}+fg{\prime \prime\:})+{\beta\:}_{1}h\right){e}^{{\beta\:}_{1}\theta\:}\pm\:\left(\right(\theta\:+N\phi\:)+\xi\:{\beta\:}_{1}h(\theta\:+N\phi\:)+\xi\:(h+Nj\left)\right){e}^{{\beta\:}_{1}\theta\:}$$
$$\:={e}^{{\beta\:}_{1}\theta\:}(\xi\:+{\beta\:}_{1}h)\left(n-2p+1\right)\left({f}^{{\prime\:}}g^{\prime\:}-{f}^{{\prime\:\prime\:}}g\right)$$
(25)
$$\:\frac{1}{Pr}\left(1+\frac{4}{3}N\right)(\left(1+{\beta\:}_{2}\theta\:\right)h^{\prime \prime\:}+\theta^{\prime \prime\:}{\beta\:}_{2})+\left[\frac{{\beta\:}_{2}}{Pr}2{\theta\:}^{{\prime\:}}h^{\prime\:}-n(g^{\prime\:}\theta\:+f^{\prime\:}h)+\frac{p+1}{2}(g\theta^{\prime\:}+fh^{\prime\:})+{D}_{f}j^{\prime \prime\:}\right]$$
$$\:=\left(n-2p+1\right)\left({f}^{{\prime\:}}h-{f}^{{\prime\prime\:}}g\right)$$
(26)
$$\:\frac{1}{Sc}j^{\prime \prime\:}-n(g^{\prime\:}f+f^{\prime\:}j)+\frac{p+1}{2}(gf^{\prime\:}+fj^{\prime\:})+{S}_{r}h^{\prime \prime\:}=\left(n-2p+1\right)\left({f}^{{\prime\:}}j-{f}^{{\prime\:}}j^{\prime\:}\right)$$
(27)

A Runge-Kutta-Fehlberg approach, in combination with a shooting method, has been adopted to provide numerical solutions to the flowing thermal species fluid model due to the lack of a closed solution. This technique was employed due to its stability, convergence, consistency and suitability. Tables 1 and 2 present the numerical results comparison with the works of Chen6, Zaimi7, Sithole8, and Lone et al.9, as respectively demonstrated in each table. The Prandtl number is varied correspondingly with n, m, and p values, respectively. All the fluid model assumptions and conditions remain the same with the specified parameter default values. The variation in the Prandtl number under various conditions is presented in the tables, and a strong agreement of the previous and present computational outcomes is found.

Table 1 Variation for Nusselt number − θ′(0) in respect to Prandtl term (pr) and index term (n).
Full size table
Table 2 Variation for Nusselt number − θ′(0) in respect to Prandtl term (pr).
Full size table

Results and discussion

The obtained graphical outputs from the computational analysis of the governing equations are provided for the velocity, thermal, and concentration fields under various parameter value variations. Thus, the graphical illustration provides better insight into the flow dimensions and implications. Furthermore, the governing wall parameters, namely Nusselt number, skin friction, and Sherwood numbers, were considered to assist in appropriately forecasting the engineering activities. These findings underscore the intricate interplay of various factors in the studied system, providing valuable insights for understanding and optimizing thermic and reacting species processes in practical applications. The observed dependencies and relationships among the fluid terms open ways for further exploration and refinement in engineering and industrial contexts.

Figure 2(a-b) shows the influence of varying viscosity terms on the velocity and thermic fields, while all other term values are fixed. The graphical results of Fig. 2(a) depict that the variable viscosity damped the fluid velocity distribution close to the bounded wall and gradually rose far to the stream due to the increased shear stress. The shear rate measures the degree of the fluid flow velocity and fluid particle deformation; as such, the velocity profile decreases and increases as the shear stress is strengthened. Meanwhile, in Fig. 2(b), the fluid particle thermal dispersion is raised to inspire the temperature profile, as seen in the plot. The fluid viscosity depends on the heat transfer; a reduction in viscosity causes a rise in temperature profile. The particle’s kinetic energy increases and the molecular bond weakens, thereby encouraging the thermal profile. Figure 2(a-b) confirms the impact of nonsimilar terms on the concentration profile and buoyancy influence on the flow rate separately. In Fig. 2(a), the mass transfer decreased to increasing nonsimilar terms. Since the nonsimilar parameter depends on the horizontal distance, a profile decrease is observed for the concentration distribution. Thus, the concentration decreases along the streaming regime as the reaction species is boosted. Figure 2(b) reflects the influence of the buoyancy force on the velocity profile. The fluid experiences an upward force, which opposes the fluid particle weight as the pressure rises to the fluid flow depth. Therefore, the entire flow system is enhanced as the fluid viscosity decreases and internal heating increases. Thus, the dynamical physical term induced heat propagation and encouraged species reaction, consequently encouraging the velocity profile. Figure 4(a) and 4(b) focus on the variation of the nonsimilar parameter for flow velocity and thermic transport. An increase is noted in the velocity profile while the temperature field decreases. This is directly related to the flow characteristics and the d” dimensional effect on the flow rate and thermal distribution. The significance of the nonsimilar parameter is noteworthy as it influences the flow and thermal distribution.

Fig. 2
figure 2

(a-b) Effect of variable viscosity on velocity and temperature profiles.

Full size image
Fig. 3
figure 3

(a-b) Effect of similar term on the species profile and buoyancy term on the velocity field.

Full size image
Fig. 4
figure 4

(a-b) Effect of nonsimilar parameter on the velocity profile and temperature profile.

Full size image

Figure 5 (a-b) illustrates a notable influence on temperature and concentration profiles as the buoyancy parameter value increases. The buoyancy parameter represents the ratio of concentration change to thermal change. As obtained for the temperature profile, an elevated value of N corresponds to a temperature rise, thereby encouraging molecular interaction. The fluid materials bond is discouraged as the internal heating is strengthened; as such, thermic distribution is raised. Meanwhile, the rising buoyancy term decreases the chemical species mixture for the concentration profile. The fluid tiny particle collision does not affect the chemical reaction due to the dominance of the shear rate arising from viscosity. Hence, the chemical concentration field declines. In Fig. 6(a-b), the rising Dufour number significantly influences fluid velocity and thermic distribution. The flow rate and temperature field increase progressively along the far boundless flow regime. The Dufour number illustrates the influence of the mass transfer gradient on the thermic energy flux, which enhances the tiny particle’s random motion and heat transfer within the system. Thus, the enthalpy transport stimulates the activation change of molecule diffusion, resulting in a rising flow velocity field and thermic profile.

Figure 7(a-b) represents the index parameter n determines whether the disparity between wall and free stream properties follows a linear or polynomial pattern. In this context, the thermal and mass distribution properties are discouraged. As we introduce a higher order in the variation, there is an observed decline in the profile distributions. Figure 8(a-b) comprehensively depicts the combined variation of the Soret and Dufour numbers. The visual representation in the figures showcases substantial alterations in the profiles, indicating the influence of these parameters on the observed phenomena. The data used for this analysis was organized in a tabular format, as documented in35. From this tabular data, a detailed profile description was meticulously extracted, offering a thorough understanding of the intricate relationships and patterns arising from the simultaneous variations of the Soret and Dufour numbers. This analytical approach enhances our comprehension of the complex interactions within the system, shedding light on the nuanced effects of these thermophysical parameters on the observed profiles. Figure 9(a-b) clarifies the influence on velocity and concentration profiles, considering variations in the velocity index parameter (p) and Schmidt number (Sc). The transition from negative to positive indexing indicates a significant alteration in the velocity profile, with non-positive values reaching a peak velocity distinct from the wall velocity. Likewise, an increase in the Schmidt number diminishes the concentration profile, as indicated by the corresponding diffusivity ratio. The Schmidt number (Sc) is a fluid dynamics term demonstrating the ratio of momentum and species diffusivities. This characterizes the flowing fluid under the influence of simultaneous convection processes of momentum and chemical reaction diffusivities. Thus, the mass and thermal boundary layers decrease to prompt thermal diffusion, which results in a decreasing concentration profile.

Fig. 5
figure 5

(a-b) Effect of buoyancy parameter on the velocity profile and concentration profile.

Full size image
Fig. 6
figure 6

(a-b) Effect of Dufour number on velocity and temperature profiles.

Full size image
Fig. 7
figure 7

(a-b) Variation of velocity and temperature profiles due to variation of the index parameter.

Full size image
Fig. 8
figure 8

(a-b) Impact of combined Sorret and Dufour numbers on the thermal and species profiles.

Full size image
Fig. 9
figure 9

(a-b) Effect of power index on velocity field and Schmidt number on species field.

Full size image

Variations in both heat transfer and mass transfer gradients were observed due to alterations in the thermal variation coefficient for the nonlinearity term, as depicted in Fig. 10(a-b). The heat gradient (Nusselt number) decreases while the mass gradient (Sherwood number) increases correspondingly to the viscosity of the thermal or concentration boundary layer. The temperature variation coefficient term is an inherent property of materials resulting in thermal conductance-based changes under the varying influence of material composition, pressure and temperature. Therefore, an increase in the values of the term declines the thermic gradient and inspires the mass gradient. In Fig. 11(a-b), the variation of the Nusselt and Sherwood numbers is explored concerning changes in both the buoyancy parameter and the Prandtl number. As noticed, the temperature gradient increases correspondingly with increasing buoyancy term (N) with variation in the Prandtl number, and the concentration gradient reduces for rising buoyancy term (N) with an increasing Prandtl number. These wall effects and behaviour can be linked to the boundary viscidness strength and the dominance of thermal diffusivity over the momentum diffusivity. Meanwhile, Fig. 12(a-b) delves into skin friction variations and Nusselt number variations for the Soret number and buoyancy parameter. This analysis demonstrates a noteworthy alteration in the wall properties, emphasizing the impact of these parameters on the observed changes. The wall friction and heat gradient decline as the Soret number is raised with varying buoyancy term values due to very low boundary layer viscosity that allows ambient thermal diffusion.

Fig. 10
figure 10

(a-b) Variation in Nusselt and Sherwood numbers due to thermal variation coeficient.

Full size image
Fig. 11
figure 11

(a-b) Variation of Nusselt and Sherwood numbers due to buoyancy and Prandtl terms.

Full size image
Fig. 12
figure 12

(a-b) Variation of skin friction term for Sorret number and buoyancy parameter.

Full size image

Conclusion

In this research, we apply scaling transformations to obtain similar solutions, effectively converting the governing equations and their associated boundary conditions into a set of ordinary differential equations. This transformation process greatly simplifies the mathematical model, making it more suitable for analysis and solution. To address these similarity equations, we employ a double-step extrapolation method, specifically utilizing the Runge–Kutta–Fehlberg fourth-fifth order scheme, a highly efficient numerical method known for its accuracy following implementation of the Local non-similarity solution. After acquiring the solutions, we extensively compare them with findings from prior investigations. The alignment between our results and those of earlier studies is remarkable, showcasing the validity and dependability of our computational approach.

The results of our study provide several crucial insights, each contributing to our comprehension of the system’s behaviour under diverse conditions:

  • The presence of mixed convection term accelerates the motion of thermal buoyancy parameter.

  • The motion of the varying viscosity term damped the fluid velocity distribution.

  • Fluid motion and thermal distribution profiles significantly raises by increasing the non-similar parameter.

  • Presence of Soret and Dufour is significant in enhancing both fluid motion and thermal performance of power-law fluid.

  • The thermic gradient experiences an increase with a rise in the non-similarity parameter, yet it demonstrates a decrease with an increase in variable thermal diffusivity. However, the Sherwood number exhibits a different trend in response to these changes.

  • There is a decrease in the temperature gradient as the buoyancy term reduces, while an increase is observed with changes in the Prandtl number.

  • Skin friction variation shows limited impact with variations in the Soret number. Conversely, a rise in the buoyancy term magnifies its influence. Similarly, the Nusselt number experiences a comparable impact due to changes in the Soret number.

  • The local Nusselt number demonstrates an increase with an escalating non-similarity parameter but declines with an increase in variable thermal diffusivity. Meanwhile, the Sherwood number responds differently to these alterations.

  • The Sherwood number rises in response to changes in the buoyancy parameter, but an opposing effect occurs with alterations in the Prandtl term. The impact of these terms on skin friction variation is relatively minor for the Soret number, while the buoyancy parameter amplifies its influence, a pattern similarly observed in the Nusselt number with an additional impact from the Soret term.

In conclusion, investigating Dufour, Soret, and radiation’s coupled influences on a power-law fluid’s mixed convection and mass transfer flow over a continuously stretching surface with variable viscosity and thermal conductivity has yielded significant insights. The study addressed complex phenomena, integrating multiple factors impacting fluid dynamics and transport processes for example between two coaxial cylinders38. The findings underscore the importance of considering these combined effects in practical applications.

Overall, this study enhances our comprehension of the interplay between various parameters in a power-law fluid flow, providing a comprehensive perspective on the system’s behaviour. Future research avenues may explore additional complexities or practical applications of the obtained insights, paving the way for heat and mass transfer advancements.