Introduction

Background

Mineral resources are the basis for scientific and technological development. With the development and utilization of mineral resources, easily mined resources are gradually exhausted1,2,3. To meet the needs of industry development and the sustainable development requirements of the mining industry, research on broken and difficult-to-mine ore bodies is of great significance. The selection of mining methods, as a core aspect of resource extraction, forms the foundational work and critical premise for the construction and development of mining enterprises. A reasonable choice of mining methods is crucial for safe and efficient extraction of resources4,5,6.

In the actual implementation process, due to the complex and variable geological conditions, different mining methods exhibit significant differences in cost-effectiveness, safety risks, and resource utilization efficiency. Decision-makers must comprehensively consider various factors, including geological conditions, technical feasibility, economic benefits, and environmental impacts, to select the optimal mining method. This is recognized as a typical multi-criteria decision-making problem. Moreover, the presence of multiple fuzzy indicators, which are dependent on the decision-makers’ experience, introduces a high degree of subjectivity into the decision-making process.

Therefore, this study proposes a group decision-making method based on IVPFS for optimizing mining methods, with the aim of preserving the maximum amount of information from fuzzy indicators in comprehensive evaluation systems. A combined approach, utilizing entropy measurement principles and the EWM, is employed to determine the weights of decision-makers and evaluation criteria, thereby objectively distinguishing their relative importance. The extended TOPSIS and Grey Relational Analysis (GRA) integration method is then used to rank the alternatives.

Literature review

The optimization of mining methods is a multi-attribute decision-making (MADM) problem that is affected by multiple factors such as economics and safety7. For mines with simple geological conditions, method selection is typically guided by experienced decision-makers. However, for mines with complex geological conditions, numerous influencing factors usually need to be considered, rendering empirical analogy methods insufficient.

Consequently, many researchers have adopted multi-criteria decision-making (MCDM) theories and methods to scientifically select mining methods. Suprakash8 applied the analytic hierarchy process (AHP) to the selection of mining methods. Liu9 used the uncertainty measure theory and the entropy weight method (EWM) to determine the optimal mining method for the Sanshan Island Xinli Gold Mine. Qinqiang7 used the AHP-TOPSIS method to identify the optimal solution for the method selection of difficult ore bodies under soft rock layers. In addition to the above methods, commonly used MCDM methods include CRITIC10, VIKOR11,12, and so on. Both single models and combined models have shown promising results. However, previous research has predominantly focused on determining subjective and objective weights, often neglecting the evaluation of multiple uncertainty indicators in the selection of mining methods. Decision-makers frequently substitute these uncertainties with simple deterministic values, which can compromise the accuracy and reliability of the decision-making process.

Of course, some scholars used fuzzy sets in fuzzy theory to deal with the uncertain information existing in indicators. For example, Mahmut Yavuz13, Karimnia14, and Sanja15 used the fuzzy analytic hierarchy process (FAHP) to overcome the limitations of AHP and determine uncertain information using fuzzy theory, thereby enhancing model accuracy. Liang16 proposed a hybrid model of triangular fuzzy numbers and TODIM for selecting seabed mining methods, considering factors such as safety, technology, and economy, which demonstrated a certain degree of reliability. With the development of fuzzy set theory, Atanassov introduced the concept of the intuitionistic fuzzy set of second type based on the intuitionistic fuzzy set framework17. This concept was later expanded by Yager into what is known as the Pythagorean fuzzy set18. Compared to traditional fuzzy numbers, such as triangular fuzzy numbers and intuitionistic fuzzy numbers19,20,21, the Pythagorean fuzzy set (PFS) offers a more advanced approach to handling uncertainty. Moreover, Shuai22 applied the combined simulation of PFS and TOPSIS to the mining method selection problem, effectively avoiding direct comparisons of various uncertainties in the plans, and achieved favorable results in the Suichang Gold Mine. This further illustrates the advantages of fuzzy sets in dealing with mining method decision-making problems.

Using fuzzy sets to handle uncertain information is a common approach in decision-making, addressing the challenge of preserving the richness of fuzzy linguistic information in multi-criteria decision problems. Traditional fuzzy set-based multi-criteria decision models have been applied in various fields. For example, Khan23 proposed a trapezoidal fuzzy environment for three-way decision-making, introducing operators to resolve real-life decision problems. Ali24,25 leveraged intuitionistic fuzzy sets (IFS) and decision theory rough sets with power aggregation operators, introducing a new three-way decision model. They further enhanced this model by integrating interval values and Bayesian rules, demonstrating strong performance in the medical ___domain. Iftikhar26 utilized Pythagorean fuzzy numbers, applying Aczel–Alsina T-norm and T-conorm operations to propose a novel Pythagorean fuzzy aggregation operator for preference ranking in multi-attribute group decision-making, validating its effectiveness through comparative analysis. Ali27 combined intuitionistic hesitant fuzzy sets (IHFS) with set pair analysis (SPA) theory to propose a new hybrid model for MADM, showing its practicality and efficiency through comparative analysis and graphical interpretation in real-world decision scenarios.

Dealing with uncertainty and preserving fuzzy language information in multi-criteria decision-making is challenging. To address this, Garg28 combined the strengths of PFS and interval-valued intuitionistic fuzzy sets (IVIFS), generalizing PFS into IVPFS. IVPFS not only extends the constraints of IVIFS but also allows membership and non-membership values to be represented as intervals, thus improving its ability to capture uncertain information22,29. Among them, Chunxia30 aimed at the decision-making problem of sustainable supplier groups, using optimism to simplify complex operations under IVPFS, and finally using the extended TOPSIS method to select the optimal solution. Wu31 established a DEA model that can internalize quantitative indicators based on IVPFS, providing a solution for the selection of green suppliers. Wang32 applied IVPFS to three-way conflict analysis and proved its superiority through comparative analysis of multiple models. Given the shortcomings of IVPFS in sorting methods and weight determination, some researchers have improved the scoring function, precision function, and distance measure of IVPFS33,34,35,36,37,38,39, and introduced new aggregation operators, applying them to multi-criteria decision-making problems to verify the method’s correctness.

The newly proposed IVPFS theory is now relatively complete and has been effectively applied in many fields. Based on the characteristics of the data, scholars have also introduced concepts such as complex fuzzy sets (CFS) and linearly ordered fuzzy sets (LDFS) to address decision problems with fuzzy data exhibiting periodic variations. Muhammad40 developed weighted averaging operators and ordered averaging operators for complex linear Diophantine fuzzy sets (CLDFS), proposing a decision method with visual effects that broadens the computational and applicational scope of CLDFS. When facing decision problems with conflicting data, Zhang41 introduced the concept of bipolar fuzzy information. Harish42 used power aggregation operators of Aczel-Alsina type (AAO) and bipolar complex fuzzy sets to establish a MADM method for exploring applications in quantum mechanics. Fuzzy set-based methods demonstrate excellent performance in decision-making problems. Muhammad43 based on bipolar fuzzy sets, introduced aggregation operators (AO) and derived a novel decision method successfully applied in renewable energy decision-making.

Works and contributions of this study

Based on the aforementioned research findings, while many scholars have explored various methods for mining method decision problems, gaps remain in group decision methods that effectively capture uncertain information. Currently, multi-criteria decision theory and fuzzy set theory are relatively mature, offering new perspectives for solving mining method decision problems. Therefore, this study proposes a model that integrates Interval-Valued Pythagorean Fuzzy Sets (IVPFS) and TOPSIS-GRA to select the optimal mining method for fractured ore bodies. The following contributions have been made:

Firstly, a multi-factor comprehensive evaluation system was established, incorporating IVPFS to effectively represent the fuzzy information in the decision-making process. This approach addresses and represents the uncertainties and ambiguities encountered in evaluating mining methods, thus enhancing the accuracy and comprehensiveness of the assessment.

Secondly, this study proposes a method for determining the weights of fuzzy information, combining the principles of fuzzy entropy measurement with the EWM. This innovative approach objectively differentiates the importance of decision-makers and evaluation criteria, improving the scientific and impartial determination of weights.

Thirdly, the integrated TOPSIS-GRA method, which combines distance and similarity measures, was employed to rank the alternative mining methods. This application provides a scientific basis for selecting the optimal mining method for fractured and difficult-to-mine ore bodies.

Fourthly, the stability of the model was validated through sensitivity analysis, and comparisons under different fuzzy environments (PFS and TFS) demonstrated the robustness of IVPFS in handling fuzzy information for mining method optimization.

Interval-valued Pythagorean fuzzy sets

Definition 1

Intuitionistic fuzzy set of second type 17. Let X be a finite non-empty set. A Pythagorean fuzzy set \(\phi\) in the set X can be expressed by Eq. (1). The concept of the intuitionistic fuzzy set of second type was introduced by Atanassov in 1989 and later extended by Yager as the PFS, which has since been widely applied22,28,29,30. Therefore, the subsequent sections of this study will use PFS.

$$\phi = \left\{ { < x,\phi (\mu_{\phi } (x),\nu_{\phi } (x))|x \in X > } \right\}$$
(1)

where \(\mu_{\phi } (x)\) is a membership degree of \(\phi\), \(\mu_{\phi } (x) \in \left[ {0,1} \right]\). \(\nu_{\phi } (x)\) is a non-membership degree of \(\phi\), \(\nu_{\phi } (x) \in \left[ {0,1} \right]\). For any PFS \(\phi\) belonging to upper, \(x\in X\), \((\mu_{\phi } (x))^{2} + (v_{\phi } (x))^{2} \le 1\) is satisfied. At this time, the degree of hesitation is determined as: \(\pi_{\phi } (x) = \sqrt {1 - (\mu_{p} (x))^{2} - (v_{p} (x))^{2} }\). For convenience, let \(\phi = (\mu_{\phi } ,v_{\phi } )\) denote the Pythagorean fuzzy number (PFN). When \(0 \le \mu_{\phi } (x) + v_{\phi } (x) \le 1\) is satisfied, PFNs degenerate into intuitionistic fuzzy numbers.

Definition 2: IVIFS29

Let X be a finite non-empty set. An interval-valued intuitionistic fuzzy set \(\varphi\) in the set X can be expressed by Eq. (2).

$$\varphi = \left\{ { < x,\left[ {\mu_{\varphi }^{L} (x),\mu_{\varphi }^{U} (x)} \right],\left[ {v_{\varphi }^{L} (x),v_{\varphi }^{U} (x)} \right] >^{{}} |x \in X} \right\}$$
(2)

where \(\left[ {\mu_{\varphi }^{L} (x),\mu_{\varphi }^{U} (x)} \right]\) is a membership degree of \(\varphi\), \(0 \le \mu_{\varphi }^{L} (x) \le \mu_{\varphi }^{U} (x) \le 1\) and \(\mu_{\varphi }^{L} (x),\mu_{\varphi }^{U} (x) \in \left[ {0,1} \right]\), \(\left[ {v_{\varphi }^{L} (x),v_{\varphi }^{U} (x)} \right]\) is a non-membership degree of \(\varphi\), \(0 \le \nu_{\varphi }^{L} (x) \le \nu_{\varphi }^{U} (x) \le 1\) and \(\nu_{\varphi }^{L} (x),\nu_{\varphi }^{U} (x) \in \left[ {0,1} \right]\), In particular, when \(\mu_{\varphi }^{L} (x) = \mu_{\varphi }^{U} (x)\),\(v_{\varphi }^{L} (x) = v_{\varphi }^{U} (x)\), the IVIFS degenerates into an intuitionistic fuzzy set. At this time, defined \(\pi_{\varphi } (x) = \left[ {\pi_{\varphi }^{L} (x),\pi_{\varphi }^{U} (x)} \right]\) as the hesitation degree of any element \(x\in X\) for the IVIFS \(\varphi\). And \(\pi_{\varphi }^{L} (x) = 1 - \mu_{\varphi }^{U} (x) - v_{\varphi }^{U} (x)\), \(\pi_{\varphi }^{U} (x) = 1 - \mu_{\varphi }^{L} (x) - \nu_{\varphi }^{L} (x)\).

Definition 3: IVPFS28

Let X be a finite non-empty set. An interval-valued Pythagorean fuzzy set \(\widetilde{\varphi }\) in the set X can be expressed by Eq. (3).

$$\tilde{\varphi } = \left\{ { < x,\left[ {\mu_{{\widetilde{\varphi }}}^{L} (x),\mu_{{\widetilde{\varphi }}}^{U} (x)} \right],\left[ {v_{{\widetilde{\varphi }}}^{L} (x),v_{{\widetilde{\varphi }}}^{U} (x)} \right] > |x \in X} \right\}$$
(3)

where the membership and non-membership degrees are defined the same as IVPFS. The difference is that for any IVPFS \(\widetilde{\varphi }\) belonging to \(x\in X\), it satisfies \((\mu_{{\widetilde{\varphi }}}^{L} (x))^{2} + (v_{{\widetilde{\varphi }}}^{U} (x))^{2} \le 1\). In particular, when \(\mu_{{\widetilde{\varphi }}}^{L} (x) = \mu_{{\widetilde{\varphi }}}^{U} (x)\) and \(v_{{\widetilde{\varphi }}}^{L} (x) = v_{{\widetilde{\varphi }}}^{U} (x)\), the IVPFS degenerates into a PFS. The hesitation degree of any element \(x\in X\) for the IVPFS \(\widetilde{\varphi }\) is \(\pi_{{\widetilde{\varphi }}} (x) = \left[ {\pi_{{\widetilde{\varphi }}}^{L} (x),\pi_{{\widetilde{\varphi }}}^{U} (x)} \right]\), and, \(\pi_{{\widetilde{\varphi }}}^{L} (x) = \sqrt {1 - (\mu_{{\widetilde{\varphi }}}^{U} (x))^{2} - (v_{{\widetilde{\varphi }}}^{U} (x))^{2} }\), \(\pi_{{\widetilde{\varphi }}}^{U} (x) = \sqrt {1 - (\mu_{{\widetilde{\varphi }}}^{L} (x))^{2} - (v_{{\widetilde{\varphi }}}^{L} (x))^{2} }\). For convenience, let \(\tilde{\varphi } = (\left[ {\mu_{{\widetilde{\varphi }}}^{L} ,\mu_{{\widetilde{\varphi }}}^{U} } \right],\left[ {v_{{\widetilde{\varphi }}}^{L} , \cdot v_{{\widetilde{\varphi }}}^{U} } \right])\) be the interval-valued Pythagorean number (IVPFN).

Definition 4: Interval-valued Pythagorean entropy measure44

It is known that there exists an IVPFN \(\tilde{\varphi } = (\left[ {\mu_{{\widetilde{\varphi }}}^{L} ,\mu_{{\widetilde{\varphi }}}^{U} } \right],\left[ {v_{{\widetilde{\varphi }}}^{L} , \cdot v_{{\widetilde{\varphi }}}^{U} } \right])\), The interval-valued Pythagorean entropy \(E(\widetilde{\varphi })\) can be expressed by Eq. (4).

$$E(\widetilde{\varphi }) = 1 - \sqrt[p]{{\frac{1}{2m}\sum\limits_{i = 1}^{m} {\left\{ {|(\mu_{{\widetilde{\varphi }}}^{L} )^{2} - (v_{{\widetilde{\varphi }}}^{L} )^{2} |^{p} + |(\mu_{{\widetilde{\varphi }}}^{U} )^{2} - (v_{{\widetilde{\varphi }}}^{U} )^{2} |^{p} } \right\}} }}$$
(4)

where p is the LP norm. The greater the interval-valued Pythagorean fuzzy entropy, the greater the uncertainty of the IVPFNs.

Definition 5: Distance measure for IVPFS44,45

Suppose there are two IVPFNs \(\widetilde{A} = (\left[ {\mu_{{\widetilde{A}}}^{L} ,\mu_{{\widetilde{A}}}^{U} } \right],\left[ {v_{{\widetilde{A}}}^{L} ,v_{{\widetilde{A}}}^{U} } \right]) \,\) and \(\tilde{B} = (\left[ {\mu_{{\widetilde{B}}}^{L} \, ,\mu_{{\widetilde{B}}}^{U} } \right],\left[ {v_{{\widetilde{B}}}^{L} ,v_{{\widetilde{B}}}^{U} } \right])\). The distance between these two IVPFNs is expressed as:

$$\begin{aligned} d(\overline{A},\overline{B}) & = \frac{1}{2}(|(\mu_{{\widetilde{A}}}^{L} )^{2} - (\mu_{{\widetilde{B}}}^{L} )^{2} | + |(\mu_{{\widetilde{A}}}^{U} )^{2} - (\mu_{{\widetilde{B}}}^{U} )^{2} | + |(v_{{\widetilde{A}}}^{L} )^{2} - (v_{{\widetilde{B}}}^{L} )^{2} | \\ & \quad + |(v_{{\widetilde{A}}}^{U} )^{2} - (v_{{\widetilde{B}}}^{U} )^{2} | + |(\pi_{{\widetilde{A}}}^{L} )^{2} - (\pi_{{\widetilde{B}}}^{L} )^{2} | + |(\pi_{{\widetilde{A}}}^{U} )^{2} - (\pi_{{\widetilde{B}}}^{U} )^{2} |) \\ \end{aligned}$$
(5)

where, \(\pi_{{\widetilde{A}}} (x) = \left[ {\pi_{{\widetilde{A}}}^{L} (x),\pi_{{\widetilde{A}}}^{U} (x)} \right]\) and \(\pi_{{\widetilde{B}}} (x) = \left[ {\pi_{{\widetilde{B}}}^{L} (x),\pi_{{\widetilde{B}}}^{U} (x)} \right]\) are the hesitation degrees of \(\widetilde{A}\) and \(\widetilde{B}\) respectively.

Definition 6: interval-valued Pythagorean fuzzy weighted average (IVPFWA)46

Suppose there exists IVPFNs \(\widetilde{{A_{i} }} = (\left[ {\mu_{{\widetilde{i}}}^{L} ,\mu_{{\widetilde{i}}}^{U} } \right],\left[ {v_{{\widetilde{i}}}^{L} ,v_{{\widetilde{i}}}^{U} } \right]) \,\), i = 1,2,…, n. The weight size \(w_{i}\) corresponding to each \(\widetilde{{A_{i} }}\), and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). IVPFWA is expressed as:

$$\widetilde{A} = IVPFWA(\widetilde{{A_{1} }},\widetilde{{A_{2} }}, \ldots ,\widetilde{{A^{n} }}) = \omega_{1} \widetilde{{A_{1} }} \oplus \omega_{2} \widetilde{{A_{2} }} \oplus \cdots \oplus w_{k} \widetilde{{A^{n} }} = \left( {\left[ {\sum\limits_{i = 1}^{n} {\varpi_{i} } \mu_{{\widetilde{i}}}^{L} ,\sum\limits_{i = 1}^{n} {\varpi_{i} } \mu_{{\widetilde{i}}}^{U} } \right],\left[ {\sum\limits_{i = 1}^{n} {\varpi_{i} } v_{{\widetilde{i}}}^{L} ,\sum\limits_{i = 1}^{n} {\varpi_{i} } v_{{\widetilde{i}}}^{U} } \right]} \right)$$
(6)

Research on integrated model based on IVPFS and TOPSIS-GRA

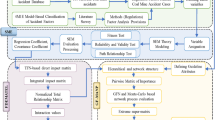
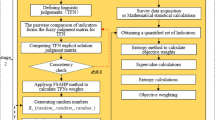
To address the decision-making problem of selecting mining methods more scientifically, This study combined the advantages of IVPFS to construct an integrated model based on IVPFS and TOPSIS-GRA. IVPFS is utilized to handle fuzzy information, employing the TOPSIS method for effective ranking of multiple alternatives. However, the TOPSIS method may encounter the rank reversal paradox in practical applications. To enhance the stability of the model and the reliability of the decision results, GRA is introduced as an effective relational analysis tool. GRA complements TOPSIS by addressing its limitations in ranking, using relational degrees to refine the evaluation process. This combined approach leverages both distance and relational degrees to provide a comprehensive ranking of the alternatives. The flow chart (Fig. 1) and specific framework of this method are as follows:

Fig. 1
figure 1

Flow chart of the integrated method based on IVPFS and TOPSIS-GRA.

Full size image

Suppose there is a MADM problem in which h decision-makers D = {D1, D2, …, Dh} discuss m solutions A = {A1, A2, …, Am} and there are n evaluation indicators C = {C1, C2, …, Cn}. Each decision-maker evaluates the selected alternatives and indicators. Assume the weight corresponding to each decision-maker is \(\varpi\)={\(\varpi\)1, \(\varpi\)2, …, \(\varpi\)h}, and the weight assigned to each evaluation indicator pair is w = {w1, w2, …, wn}. These weights satisfy \(\sum_{i=1}^{h}\varpi =1\) and \(\sum_{i=1}^{n}w=1\).

Step 1: Identify alternatives and decision-makers. Select appropriate evaluation indicators to establish a decision-making evaluation system. Determine the conversion rules for natural language and interval-valued Pythagorean fuzzy numbers.

Step 2: Decision-makers score and determine the IVPFN \(\tilde{a} = (\left[ {\mu_{ij}^{L} ,\mu_{ij}^{U} } \right],\left[ {v_{ij}^{L} ,v_{ij}^{U} } \right])\), i = 0,1,2,…,m, j = 0,1,2,…,n corresponding to each evaluation index. Construct an initial decision matrix \(\widetilde{{A^{k} }} = (\left[ {\mu_{ij}^{kL} ,\mu_{ij}^{kU} } \right],\left[ {v_{ij}^{kL} ,v_{ij}^{kU} } \right])_{mxn}\), k = 0,1,2,…,h corresponding to each decision-maker.

$$\widetilde{{A^{k} }} = \left[ {\begin{array}{*{20}c} {\left( {\left[ {\mu_{11}^{kL} ,\mu_{11}^{kU} } \right],\left[ {v_{11}^{kL} ,v_{11}^{kU} } \right]} \right)} & {\left( {\left[ {\mu_{12}^{kL} ,\mu_{12}^{kU} } \right],\left[ {v_{12}^{kL} , \cdot v_{12}^{kU} } \right]} \right)} & \ldots & {\left( {\left[ {\mu_{1n}^{kL} ,\mu_{1n}^{kU} } \right],\left[ {v_{1n}^{kL} ,v_{1n}^{kU} } \right]} \right)} \\ {\left( {\left[ {\mu_{21}^{kL} ,\mu_{21}^{kU} } \right],\left[ {v_{21}^{kL} ,v_{21}^{kU} } \right]} \right)} & {\left( {\left[ {\mu_{22}^{kL} ,\mu_{22}^{kU} } \right],\left[ {v_{22}^{kL} ,v_{22}^{kU} } \right]} \right)} & \ldots & {\left( {\left[ {\mu_{2n}^{kL} ,\mu_{2n}^{kU} } \right],\left[ {v_{2n}^{kL} ,v_{2n}^{kU} } \right]} \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {\left( {\left[ {\mu_{m1}^{kL} ,\mu_{m1}^{kU} } \right],\left[ {v_{m1}^{kL} ,v_{m1}^{kU} } \right]} \right)} & {\left( {\left[ {\mu_{m2}^{kL} ,\mu_{m2}^{kU} } \right],\left[ {v_{m2}^{kL} ,v_{m2}^{kU} } \right]} \right)} & \ldots & {\left( {\left[ {\mu_{mn}^{kL} ,\mu_{mn}^{kU} } \right],\left[ {v_{mn}^{kL} ,v_{mn}^{kU} } \right]} \right)} \\ \end{array} } \right]$$
(7)

Step 3: Determine the weights of decision-maker and indicator. Due to the differences in experience, expertise, and other factors among decision-makers, their input significantly influences the decision-making results. Simultaneously, the importance of evaluation indicators varies among decision-makers, necessitating careful weight distribution. Entropy measure theory is a widely adopted method for determining weights18,47,48,49. This study determined weights of decision-maker and indicator based on the interval-valued Pythagorean entropy measure and the EWM. The interval-valued Pythagorean fuzzy entropy \({e}_{j}^{k}\) of each decision-makers corresponding index interval value was calculated using Eq. (4). The interval-valued Pythagorean fuzzy entropy matrix \(E\) of the indicator set was established by decision-makers.

$$\overline{E} = \left[ {\begin{array}{*{20}c} {\tilde{e}_{1}^{1} } & {\tilde{e}_{2}^{1} } & \ldots & {\tilde{e}_{n}^{1} } \\ {\tilde{e}_{1}^{2} } & {\tilde{e}_{2}^{2} } & \ldots & {\tilde{e}_{n}^{2} } \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{e}_{1}^{h} } & {\tilde{e}_{2}^{h} } & \ldots & {\tilde{e}_{n}^{h} } \\ \end{array} } \right]$$
(8)

where \(\overline{E }\) is the normalized matrix of the interval-valued Pythagorean fuzzy entropy matrix \(E\)

According to the calculation principle of the EWM50,51,52, the weight of each indicator is expressed as:

$$w_{j} = \frac{{1 - H_{j} }}{{n - \sum\nolimits_{j = 1}^{n} {H_{j} } }}$$
(9)

where \({H}_{j}\) is the information entropy of each indicator in the EWM, and \(H_{j} = - \frac{1}{ln\left( h \right)}\mathop \sum \limits_{k = 1}^{h} \left( {\frac{{e_{j}^{k} }}{{\mathop \sum \nolimits_{k = 1}^{h} e_{j}^{k} }}ln\left( {\frac{{e_{j}^{k} }}{{\mathop \sum \nolimits_{k = 1}^{h} e_{j}^{k} }}} \right)} \right).\)

The weight of each decision-maker is expressed as:

$$\omega_{k} = \sum\limits_{j = 1}^{n} {w_{j} } e_{j}^{k}$$
(10)

Step 4: Weighted decision matrix determination based on decision-maker weights. Aggregate decision matrices from different decision-makers. After assigning weights to the decision-makers, the weighted decision matrix \(\widetilde{R}\) is obtained. This calculation process is implemented using the IVPFWA (Eq. (6)).

$$\begin{aligned} \widetilde{R} & = IVPFWA(\widetilde{{A^{1} }},\widetilde{{A^{2} }}, \ldots ,\widetilde{{A^{n} }}) = \omega_{1} \widetilde{{A^{1} }} \oplus \omega_{2} \widetilde{{A^{2} }} \oplus \cdots \oplus w_{k} \widetilde{{A^{k} }} \\ & = \left[ {\begin{array}{*{20}c} {\left( {\left[ {\mu_{\varpi 11}^{L} ,\mu_{\varpi 11}^{kU} } \right],\left[ {v_{\varpi 11}^{L} ,v_{\varpi 11}^{U} } \right]} \right)} & {\left( {\left[ {\mu_{\varpi 12}^{kL} ,\mu_{\varpi 12}^{kU} } \right],\left[ {v_{\varpi 12}^{L} , \cdot v_{\varpi 12}^{U} } \right]} \right)} & \ldots & {\left( {\left[ {\mu_{\varpi 1n}^{L} ,\mu_{\varpi 1n}^{U} } \right],\left[ {v_{\varpi 1n}^{L} ,v_{\varpi 1n}^{U} } \right]} \right)} \\ {\left( {\left[ {\mu_{\varpi 21}^{L} ,\mu_{\varpi 21}^{kU} } \right],\left[ {v_{\varpi 21}^{L} ,v_{\varpi 21}^{U} } \right]} \right)} & {\left( {\left[ {\mu_{\varpi 22}^{L} , \cdot \mu_{\varpi 22}^{kU} } \right],\left[ {v_{\varpi 22}^{L} ,v_{\varpi 22}^{U} } \right]} \right)} & \ldots & {\left( {\left[ {\mu_{\varpi 2n}^{L} ,\mu_{2n}^{U} } \right],\left[ {v_{\varpi 2n}^{L} ,v_{\varpi 2n}^{U} } \right]} \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {\left( {\left[ {\mu_{\varpi m1}^{L} ,\mu_{\varpi m1}^{U} } \right],\left[ {v_{\varpi m1}^{L} ,v_{\varpi m1}^{U} } \right]} \right)} & {\left( {\left[ {\mu_{\varpi m2}^{L} ,\mu_{\varpi m2}^{U} } \right],\left[ {v_{\varpi m2}^{L} ,v_{\varpi m2}^{U} } \right]} \right)} & \ldots & {\left( {\left[ {\mu_{\varpi mn}^{L} ,\mu_{\varpi mn}^{U} } \right],\left[ {v_{\varpi mn}^{L} ,v_{\varpi mn}^{U} } \right]} \right)} \\ \end{array} } \right] \\ \end{aligned}$$
(11)

Step 5: According to the weighted decision matrix \(\widetilde{R}\), the positive ideal solutions (PIS) and negative ideal solutions (NIS) are determined using Eq. (12) and Eq. (13). TOPSIS, also known as the distance method between superior and inferior solutions, is one of the commonly used decision-making methods in MCDM53,54. When faced with a decision-making problem, TOPSIS chooses the optimal solution that is closest to the positive ideal solution and at the same time, as far away from the negative ideal solution as possible. After extensive development and optimization, TOPSIS and its expanded versions have been applied to many fields such as economics and management, achieving favorable results55,56,57.

$$r_{i}^{ + } = \left\{ {\left( {\left[ {\mu_{\varpi 1}^{ + L} ,\mu_{\varpi 1}^{ + U} } \right],\left[ {\nu_{\varpi 1}^{ + L} ,\nu_{\varpi 1}^{ + U} } \right]} \right),r\left( {\left[ {\mu_{\varpi 2}^{ + L} ,\mu_{\varpi 2}^{ + U} } \right],\left[ {\nu_{\varpi 2}^{ + L} ,v_{\varpi 2}^{ + U} } \right]} \right), \ldots ,\left( {\left[ {\mu_{\varpi n}^{ + L} \cdot \mu_{\varpi n}^{ + U} } \right],\left[ {\nu_{\varpi n}^{ + L} \cdot \nu_{\varpi n}^{ + U} } \right]} \right)} \right\}$$
(12)
$$r_{i}^{ - } = \left\{ {\left( {\left[ {\mu_{\varpi 1}^{ - L} ,\mu_{\varpi 1}^{ - U} } \right],\left[ {\nu_{\varpi 1}^{ - L} ,\nu_{\varpi 1}^{ - U} } \right]} \right),r\left( {\left[ {\mu_{\varpi 2}^{ - L} ,\mu_{\varpi 2}^{ - U} } \right],\left[ {\nu_{\varpi 2}^{ + L} ,v_{\varpi 2}^{ + U} } \right]} \right), \ldots ,\left( {\left[ {\mu_{\varpi n}^{ - L} \cdot \mu_{\varpi n}^{ - U} } \right],\left[ {\nu_{\varpi n}^{ - L} \cdot \nu_{\varpi n}^{ - U} } \right]} \right)} \right\}$$
(13)
$${\text{Where}},.\left\{ \begin{aligned} \mu _{{\varpi j}}^{{ + L}} = \mathop {min}\limits_{i} \mu _{{\varpi ij}}^{L} \hfill \\ \mu _{{\varpi j}}^{{ + U}} = \mathop {min}\limits_{i} \mu _{{\varpi ij}}^{U} \hfill \\ v_{{\varpi j}}^{{ + L}} = \mathop {max}\limits_{i} v_{{\varpi ij}}^{L} \hfill \\ v_{{\varpi j}}^{{ + U}} = \mathop {max}\limits_{i} v_{{\varpi ij}}^{U} \hfill \\ \mu _{{\varpi j}}^{{ - L}} = \mathop {max}\limits_{i} \mu _{{\varpi ij}}^{L} \hfill \\ \mu _{{\varpi j}}^{{ - U}} = \mathop {max}\limits_{i} \mu _{{\varpi ij}}^{U} \hfill \\ v_{{\varpi j}}^{{ - L}} = \mathop {min}\limits_{i} v_{{\varpi ij}}^{L} \hfill \\ v_{{\varpi j}}^{{ - U}} = \mathop {min}\limits_{i} v_{{\varpi ij}}^{U} \hfill \\ \end{aligned} \right.if\,{\text{C}}i \in {\text{M1}}{\text{.}}\left\{ \begin{aligned} \mu _{{\varpi j}}^{{ + L}} = \mathop {max}\limits_{i} \mu _{{\varpi ij}}^{L} \hfill \\ \mu _{{\varpi j}}^{{ + U}} = \mathop {max}\limits_{i} \mu _{{\varpi ij}}^{U} \hfill \\ v_{{\varpi j}}^{{ + L}} = \mathop {min}\limits_{i} v_{{\varpi ij}}^{L} \hfill \\ v_{{\varpi j}}^{{ + U}} = \mathop {min}\limits_{i} v_{{\varpi ij}}^{U} \hfill \\ \mu _{{\varpi j}}^{{ - L}} = \mathop {min}\limits_{i} \mu _{{\varpi ij}}^{L} \hfill \\ \mu _{{\varpi j}}^{{ - U}} = \mathop {min}\limits_{i} \mu _{{\varpi ij}}^{U} \hfill \\ v_{{\varpi j}}^{{ - L}} = \mathop {max}\limits_{i} v_{{\varpi ij}}^{L} \hfill \\ v_{{\varpi j}}^{{ - U}} = \mathop {max}\limits_{i} v_{{\varpi ij}}^{U} \hfill \\ \end{aligned} \right.if\,{\text{C}}i \in {\text{M2}}.$$

M1 and M2 are cost indicators and benefits indicators respectively.

Step 6: According to the TOPSIS principle, the distance measure of the IVPFNs is replaced with the original Euler distance, and the distance between each solution and the ideal solution is calculated. Its distance formula is as follows:

$$\begin{gathered} d_{ij}^{ + } = \frac{1}{2}(|(\mu_{ij}^{L} )^{2} - (\mu_{\varpi i}^{ + L} )^{2} | + |(\mu_{ij}^{U} )^{2} - (\mu_{\varpi i}^{ + U} )^{2} | + |(v_{ij}^{L} )^{2} - (v_{\varpi i}^{ + L} )^{2} | \\ + |(v_{ij}^{U} )^{2} - (v_{\varpi i}^{ + U} )^{2} | + |(\pi_{ij}^{L} )^{2} - (\pi_{\varpi i}^{ + L} )^{2} | + |(\pi_{ij}^{U} )^{2} - (\pi_{\varpi i}^{ + U} )^{2} |) \\ \end{gathered}$$
(14)
$$\begin{gathered} d_{ij}^{ - } = \frac{1}{2}(|(\mu_{ij}^{L} )^{2} - (\mu_{\varpi i}^{ - L} )^{2} | + |(\mu_{ij}^{U} )^{2} - (\mu_{\varpi i}^{ - U} )^{2} | + |(v_{ij}^{L} )^{2} - (v_{\varpi i}^{ - L} )^{2} | \\ + |(v_{ij}^{U} )^{2} - (v_{\varpi i}^{ - U} )^{2} | + |(\pi_{ij}^{L} )^{2} - (\pi_{\varpi i}^{ - L} )^{2} | + |(\pi_{ij}^{U} )^{2} - (\pi_{\varpi i}^{ - U} )^{2} |) \\ \end{gathered}$$
(15)

Step 7: Based on the weight of each evaluation indicator obtained in Step 3, the weighted distance is calculated:

$$D_{i}^{ + } = \sum\limits_{j = 1}^{n} {d_{ij}^{ + } } w_{j}$$
(16)
$$D_{i}^{ - } = \sum\limits_{j = 1}^{n} {d_{ij}^{ - } } w_{j}$$
(17)

Step 8: Use GRA to determine the gray correlation degree of alternatives. GRA is a factor analysis method in gray theory. It is generally used in research on phenomena where the information is partly clear, partly unclear, and contains uncertainty. Determine the optimal solution by calculating the gray correlation between the solution data and the optimal solution data58,59,60. Use Eq. (18) and Eq. (19) to calculate the gray correlation coefficient between each solution and ideal solutions.

$$\xi_{ij}^{ + } = \frac{{\mathop {min}\limits_{i} \mathop {min}\limits_{j} d_{ij}^{ + } + \lambda \cdot \mathop {max}\limits_{i} \mathop {max}\limits_{j} d_{ij}^{ + } }}{{d_{ij}^{ + } + \lambda \cdot \mathop {max}\limits_{i} \mathop {max}\limits_{j} d_{ij}^{ + } }}$$
(18)
$$\xi_{ij}^{ - } = \frac{{\mathop {min}\limits_{i} \mathop {min}\limits_{j} d_{ij}^{ - } + \lambda \cdot \mathop {max}\limits_{i} \mathop {max}\limits_{j} d_{ij}^{ - } }}{{d_{ij}^{ - } + \lambda \cdot \mathop {max}\limits_{i} \mathop {max}\limits_{j} d_{ij}^{ - } }}$$
(19)

According to the weight of each indicator obtained in Step 3, the weighted gray correlation degree GRD is calculated:

$${\text{GRD}}_{i}^{ + } = \frac{1}{n}\sum\limits_{j = 1}^{n} {\xi_{ij}^{ + } } w_{j}$$
(20)
$${\text{GRD}}_{i}^{ - } = \frac{1}{n}\sum\limits_{j = 1}^{n} {\xi_{ij}^{ - } } w_{j}$$
(21)

Step 9: Calculate distance comprehensive closeness and gray comprehensive closeness respectively.

$$D_{i} = \frac{{D_{i}^{ - } }}{{D_{i}^{ + } + D_{i}^{ - } }}$$
(22)
$${\text{GRD}}_{i} = \frac{{{\text{GRD}}_{i}^{ - } }}{{{\text{GRD}}_{i}^{ + } + {\text{GRD}}_{i}^{ - } }}$$
(23)

Step 10: Calculate the overall comprehensive score for each alternative.

$$R_{i} = \gamma D_{i} + (1 - \gamma ){\text{GRD}}_{i}$$
(24)

where \(\gamma\) is the compromise coefficient. \(\gamma \in [\text{0,1}]\) is generally taken as 0.5.

Step 11: Sort solutions based on comprehensive scores and select the best solution.

Application examples

Mine background

The Tanyaokou mining area, located in Wendur Town, Huhe, Wulatehou Banner, Inner Mongolia, mainly engages in the mining of S, Cu, and Zn. Currently, the Tanyaokou mining area is segmented into two regions (south and north), with operations occurring in three mining sections. The 3# ore body in the southern region stands out as the largest and most mineral-rich deposit. This ore body extends 1750 m in length, with an average thickness of 44 m, trending NE70°, dipping northwest with an inclination of approximately 56°, and is distributed in a vein-like formation. It predominantly comprises zinc, copper, and sulfur ores, characteristic of a typical polymetallic deposit. The mineral zone consists of interbedded soft and hard limestone and carbonaceous slate. Copper is predominantly found within the limestone and carbonaceous slate, while zinc is mainly present in the carbonaceous slate. The slate is notably soft, with well-defined lamellae and extensively developed joints and fissures. The ore body’s roof and floor are mainly carbonaceous slate. This study focused on optimizing mining methods for the 3# ore body. The primary mining challenges currently identified are as follows:

  1. 1.

    Geological surveys reveal poor stability of the ore rock, with extensively developed joints and fissures. Excessively large exposure areas and prolonged exposure times are untenable, complicating the mining technology.

  2. 2.

    Despite the ore body’s thickness, the boundary between the ore body and the surrounding rock is indistinct, exhibiting a gradual transition. Early-stage mining methods were suboptimal, leading to significant ore loss and dilution, thereby wasting resources.

  3. 3.

    The initial open stope method resulted in the collapse of the void areas and surface subsidence. Additionally, the safe working conditions for workers and equipment are substandard, failing to meet the essential requirements for sustainable mining practices.

Preliminary selection of mining methods

To achieve comprehensive resource recovery and promote sustainable mining practices, this study was grounded in field investigations and rock mechanics experiments conducted at typical locations representative of mining sites. It integrated geological data from local mines and similar operations. Four mining methods were initially chosen: vertical pre-protected roof downward deep hole mining and subsequent filling mining method (A1), pre-controlled roof continuous segmented and striped filling mining method (A2), mechanized upward horizontal layered filling mining method (A3) and point-pillar upward layered filling mining method (A4). The characteristics of these four mining methods and the standard ore block diagram are summarized as follows:

  1. 1.

    The A1 standard ore block diagram is shown in Fig. 2. This method combines the characteristics of deep hole mining and has a high degree of mechanization, low labor intensity, and elevated labor productivity. It involves relatively modest volumes of mining and cutting engineering, resulting in low costs. However, challenges arise in controlling loss and dilution, necessitating stringent requirements for the blasting process.

  2. 2.

    The A2 standard ore block diagram is shown in Fig. 3. This method represents an advancement over stage mining and stage extraction mining methods. It features significant mechanization, controllable stope parameters, and high safety. The mining and cutting engineering volume is relatively minimal, resulting in cost-effectiveness. However, it requires subsequent filling, hence resulting in relatively lower labor productivity.

  3. 3.

    The A3 standard ore block diagram is shown in Fig. 4. This method is highly mechanized, facilitating easy control over loss and dilution. However, it has a high stope cutting ratio, resulting in lower labor productivity and higher mining costs.

  4. 4.

    The A4 standard ore block diagram is shown in Fig. 5. This method shares similarities with A3 in its advantages. The added point pillars (ore pillars) ensure stope stability when the exposed area is extensive. But the ore pillars are permanent losses and contribute to an overall increase in loss rates.

Fig. 2
figure 2

Vertical pre-protected roof downward deep hole mining and subsequent filling mining method (A1).

Full size image
Fig. 3
figure 3

Pre-controlled roof continuous segmented and striped filling mining method (A2).

Full size image
Fig. 4
figure 4

Mechanized upward horizontal layered filling mining method (A3).

Full size image
Fig. 5
figure 5

Point-pillar upward layered filling mining method (A4).

Full size image

Construction of comprehensive evaluation index system

Optimizing mining methods is affected by various economic and technological factors. By selecting relevant research indicators, this study established a comprehensive evaluation indicator system. Three scholars specializing in mining were chosen as decision-makers: expects from the mine’s technical department (\({D}_{1}\)), university researchers (\({D}_{2}\)) and designers (\({D}_{3}\)). The four alternatives considered are A1, A2, A3 and A4. The evaluation indicators are ore dilution rate (C1), ore loss rate (C2), total cost (C3), construction organization and labor intensity (C4), mining-to-cut ratio (C5), ore recovery rate (C6), stope production capacity (C7), flexibility and adaptability (C8), stope safety conditions (C9). Among these evaluation indicators, C1-C5 are cost indicators (M1), and C6-C9 are benefit indicators (M2). The evaluation index system is shown in Fig. 6.

Fig. 6
figure 6

Evaluation index system.

Full size image

Simultaneously, the corresponding relationship between natural evaluation language and IVPFNs is clarified. Table 1 defines the conversion criteria between the importance of evaluation indicators and IVPFNs.

Table 1 Evaluation index importance and IVPFNs conversion rules.
Full size table

Optimization of broken ore body solutions based on an integrated model

Preferred mining methods are typically grounded in practical mine operations. This study proposed an integrated model to address the decision-making problem regarding mining methods. The specific steps are as follows:

Step 1: Three decision-making decision-makers scored the evaluation indicators corresponding to different options. Table 2 shows the rating results of three decision-makers for different options.

Table 2 Mining method index evaluation system.
Full size table

Step 2: Following to the fuzzy language conversion rules, natural language was converted into IVPFNs. The interval-valued Pythagorean fuzzy decision matrix of the evaluation index was obtained, as shown in Table 3.

Table 3 Interval Pythagorean fuzzy decision matrix corresponding to different decision-makers.
Full size table

Step 3: According to Table 3 and Eq. (4), the interval-valued Pythagorean fuzzy entropy for each evaluation index was calculated, and the interval-valued Pythagorean fuzzy entropy matrix for the evaluation index and decision-makers was established. The decision-maker weight and evaluation index weight were calculated using Eq. (8)–(10). The calculation results are presented in Tables 4, 5, 6.

Table 4 Interval-valued Pythagorean fuzzy entropy.
Full size table
Table 5 The weight value corresponding to each price indicator.
Full size table
Table 6 The weight value corresponding to each decision-maker.
Full size table

Step 4: According to Step 3 and Eq. (11), the weighted decision matrix and the hesitation degree corresponding to the IVPFNs in each interval were calculated. The results are shown in Table 7:

Table 7 Weighted decision matrix.
Full size table

Step 5: PIS and NIS under the weighted decision matrix were calculated from Eq. (12)–(13). The hesitation degree corresponding to the PIS and NIS is shown in Table 8.

$$r^{ + } = \left\{ \begin{gathered} ([0.13,0.31],[0.69,0.84]),([0.09,0.24],[0.76,0.88]),([0.24,0.37],[0.63,0.76]),([0.11,0.26],[0.74,0.87]), \hfill \\ ([0.11,0.26],[0.74,0.87]),([0.76,0.88],[0.07,0.19]),([0.62,0.74],[0.21,0.33]),([0.74,0.87],[0.08,0.21]), \hfill \\ ([0.80,0.95],[0.00,0.15]) \hfill \\ \end{gathered} \right\}$$
$$r^{ - } = \left\{ \begin{gathered} ([0.49,0.62],[0.33,0.48]),([0.34,0.46],[0.52,0.66]),([0.40,0.52],[0.45,0.60]),([0.41,0.53],[0.44,0.59]), \hfill \\ ([0.37,0.47],[0.51,0.66]),([0.54,0.67],[0.29,0.43]),([0.41,0.53],[0.44,0.59]),([0.38,0.51],[0.47,0.62]), \hfill \\ ([0.30,0.45],[0.55,0.70]) \hfill \\ \end{gathered} \right\}$$
Table 8 Hesitation degrees \(\pi\) corresponding to PIS and NIS.
Full size table

Step 6: The distances \({d}_{ij}^{+}\) and \({d}_{ij}^{-}\) between each alternative and ideal solution were calculated from Eq. (14)–(17). The weighted comprehensive distance was obtained. The results are shown in Tables 9, 10, 11.

Table 9 The distance \({d}_{ij}^{+}\) from the alternative to the PIS.
Full size table
Table 10 The distance \({d}_{ij}^{-}\) from the alternative to the NIS.
Full size table
Table 11 The weighted comprehensive distance of alternatives to the ideal solution.
Full size table

Step 7: The gray correlation coefficients \(\xi_{ij}^{ + }\) and \(\xi_{ij}^{ - }\) between each alternative and the ideal solution were calculated using Eq. (18)–(21). The weighted comprehensive gray correlation degree was obtained, and the results are shown in Tables 12, 13, 14.

Table 12 The gray correlation coefficient \(\xi_{ij}^{ + }\) from the alternative to the PIS.
Full size table
Table 13 The gray correlation coefficient \(\xi_{ij}^{ - }\) from the alternative to the NIS.
Full size table
Table 14 Weighted comprehensive gray correlation degree from alternatives to ideal solutions.
Full size table

Step 8: The comprehensive TOPSIS and GRA scores were calculated using Eq. (22)–(24). The compromise coefficient γ was set to 0.5. The calculation results are shown in Table 15:

Table 15 Comprehensive score and ranking of alternatives.
Full size table

The calculation results that the optimal ranking of the four alternative methods is A4 > A3 > A1 > A2. The optimal solution is A4, which is the point-pillar upward horizontal layered filling mining method.

The Point Support Upward Horizontal Layered Filling Mining Method is an optimized version of the traditional upward horizontal layered filling method. Compared to other mining methods, it is particularly effective for fractured ore bodies, as it can control ground pressure, provide filling support, and reduce ore loss and dilution, thereby enhancing mining safety and efficiency. Additionally, this method has successfully addressed the challenges of mining fractured ore bodies at the Xincheng Gold Mine in Shandong, China, offering valuable insights for mining operations under complex geological conditions.

Discussion

Sensitive analysis

This study used an integrated model within an interval-valued Pythagorean fuzzy environment to determine the optimal mining method for the 3# ore body in the Tanyaokou mining area. To avoid errors caused by a single model, a combination of TOPSIS and GRA was used to rank the alternatives. Considering the influence of human subjective factors, variations in the compromise coefficient γ may affect the results. Consequently, sensitivity analysis was performed by altering the compromise coefficient γ to further explore the robustness of the integrated model.

First, increase the compromise coefficient γ from 0 to 1 to simulate different situations. When γ = 0, the model only uses GRA to rank alternatives. When γ = 1, the model only uses extended TOPSIS to rank alternatives. The simulation results of different situations are shown in Fig. 7 and Table 1661. The results reveal that when different values of γ produced different sorting results. When γ ≥ 0.4, the optimal solution among the four alternatives was A4, consistent with the result of this study. When 0 < γ < 0.4, the optimal solution was A3. Notably, when only gray correlation similarity ranking was used, the optimal solution was A2. Despite this, A4 emerged as the optimal solution in a significant proportion of situations, indicating that the γ = 0.5 selected in this study was more reasonable. Moreover, in the actual production process of the 3# ore body in the Tanyaokou mining area, the use of the A1 mining method also achieved ideal results in terms of safety and efficiency. Thus, the combination of models reduces the error caused by a single model. Of course, this also depends on the preferences of decision-makers.

Fig. 7
figure 7

Ranking of alternatives with different γ values.

Full size image
Table 16 Scores and rankings of alternatives for different values of γ.
Full size table

To visually express the differences in rankings for different values of γ, a ranking similarity coefficient is introduced to provide a qualitative measure of the differences between the obtained rankings. Figure 8 shows the weighted Spearman correlation coefficients for various γ values, calculated using the formula provided by Sałabun62.As can be seen from the figure, the rankings for γ = 0.5 and γ = 0.4 are completely identical, exhibiting the same ranking logic. Furthermore, there is a high similarity (correlation coefficient of 0.8) between the rankings for γ = 0.5 and the group with γ values ranging from 0.6 to 1.0. This demonstrates the rationale for selecting γ = 0.5.

Fig. 8
figure 8

Weighted Spearman correlation coefficients for different γ values.

Full size image

Comparison analysis

To illustrate the advantage of IVPFS in handling uncertain information in mining method optimization decision problems, this study conducts comparative analyses with PFS and TFS16,22. Table 17 presents the conversion rules between the natural language of PFSs and TFNs. The evaluation system in the comparative experiments aligns with that of this study. Natural language in the evaluation system is transformed into a fuzzy decision matrix according to the conversion criteria.

Table 17 Conversion rules between natural language.
Full size table
  1. 1.

    Comparative Experiment 1: PFS

Replacing natural language with PFSs in Table 1, the experimental results are shown in Table 18. The calculated weight of the decision-makers was ϖ = (0.64, 0.27, 0.09). The weight of the evaluation index was w = (0.13, 0.16, 0.06, 0.07, 0.15, 0.06, 0.15, 0.16, 0.06). The PIS and NIS of the comparative experiment 1 were:

$$r^{ + } = \left\{ \begin{gathered} (0.28,0.69,0.66),(0.13,0.84,0.52),(0.19,0.77,0.60),(0.13,0.84,0.52),(0.13,0.84,0.52), \hfill \\ (0.92,0.14,0.37),(0.76,0.28,0.59),(0.92,0.14,0.37),(0.86,0.20,0.46) \hfill \\ \end{gathered} \right\}$$
$$r^{ - } = \left\{ \begin{gathered} (0.60,0.37,0.71),(0.45,0.47,0.76),(0.47,0.45,0.76),(0.49,0.41,0.77),(0.45,0.46,0.76), \hfill \\ (0.59,0.37,0.72),(0.49,0.41,0.77),(0.41,0.52,0.75),(0.35,0.60,0.72) \hfill \\ \end{gathered} \right\}$$
Table 18 Experiment comparison analysis table.
Full size table

The Euclidean distance formula is used to calculate the distance between each solution and the positive and negative ideal solutions30. The calculated weighted distance were D +  = {0.2162, 0.3065, 0.3612, 0.3049}, D- = {0.3396, 0.2433, 0.1813, 0.3136}. The weighted gray correlation was GRD +  = {0.0855, 0.0696, 0.0538, 0.0778}, GRD- = {0.0601, 0.0686, 0.1014, 0.0615}. The comparative experiment alternative had a score of R = {0.5119, 0.4695, 0.4938, 0.4753}. The ranking of the alternatives was A1 > A3 > A4 > A2, with the optimal solution under the Pythagorean fuzzy environment in Comparative Experiment 1 identified as A1.

  1. 2.

    Comparative Experiment 2: TFS

Replacing natural language with TFSs in Table 1, the experimental results are shown in Table 18. The calculated weight of decision-makers was ϖ = (0.80, 0.12, 0.08), and for evaluation index was w = (0.15, 0.15, 0.06, 0.07, 0.15, 0.06, 0.15, 0.15, 0.06). The positive and negative ideal solutions for the comparative experiment 2 were:

$$r^{ + } = \left\{ \begin{gathered} (0.067,0.108,0.150),(0.008,0.050,0.092),(0.040,0.082,0.124),(0.008,0.050,0.092), \hfill \\ (0.008,0.050,0.092),(0.242,0.283,0.325),(0.200,0.242,0.283),(0.242,0.283,0.325), \hfill \\ (0.250,0.292,0.333) \hfill \\ \end{gathered} \right\}$$
$$r^{ - } = \left\{ \begin{gathered} (0.158,0.200,0.242),(0.113,0.155,0.196),(0.120,0.162,0.203),(0.121,0.163,0.205), \hfill \\ (0.117,0.158,0.200),(0.137,0.179,0.220),(0.121,0.163,0.205),(0.092,0.133,0.175), \hfill \\ (0.083,0.125,0.167) \hfill \\ \end{gathered} \right\}$$

In Comparative Experiment 2, the Euclidean distance formula was similarly used. The weighted distances were calculated as D +  = {0.0706, 0.1103, 0.1057, 0.0811}, D- = {0.1181, 0.0785, 0.0831, 0.1076}. The weighted gray relational correlation was GRD +  = {0.0857, 0.0708, 0.0736, 0.0746}, GRD- = {0.0648, 0.0791, 0.0855, 0.0694}. The scores for the alternative solutions were R = {0.5286, 0.4717, 0.4888, 0.5261}. The ranking of the alternatives was A1 > A4 > A3 > A2, with the optimal solution under the triangular fuzzy environment in Comparative Experiment 2 identified as A1.

From the results (Table 18 and Fig. 9), the ranking orders vary for each experiment, with the optimal solution under the interval-valued Pythagorean fuzzy environment being A4, while A1 is optimal in both comparative experiments. There are deviations in the decision results between the Pythagorean fuzzy and triangular fuzzy environments because indicators such as construction flexibility and safety conditions in mining method optimization decisions often rely heavily on decision-makers subjective assessments and experience, leading to high fuzziness and subjectivity. The use of IVPFS helps mitigate excessive loss of important linguistic information during conversion and better captures uncertain information. Therefore, handling uncertain information in mining method optimization with IVPFS offers significant advantages, resulting in more reliable decision outcomes.

Fig. 9
figure 9

Experimental comparison analysis chart.

Full size image

Limitations and future work

In this study, the IVPFS effectively handled uncertainty in mining method decision-making. Additionally, entropy measurement and EWM provided objective weight allocation for decisions, making this approach applicable to other fields. However, this method still has limitations. Decision-making inherently involves trade-offs, balancing economic, safety, and technological factors to maximize mining enterprise benefits while considering environmental impacts to meet green mining standards. The fuzzy sets used only consider positive impacts and neglect negative impacts. Reviewing relevant literature41,42,43,63,64,65, bipolar complex fuzzy sets effectively address this limitation by extending fuzzy set definitions from [0,1] to [− 1,0] × [0,1], offering a more comprehensive view of polarity issues40. Bipolar complex fuzzy sets have been successfully applied in medical42,60,61,62 and energy sectors43 and hold potential for mining method decision-making, which is a focus of future research considerations.

Conclusion

The selection of mining methods is fundamental to the sustainable development of mining enterprises. Due to the diverse geological conditions and ore body characteristics, it is necessary to comprehensively evaluate the suitability of mining methods. This study established an integrated multi-criteria decision-making model in the interval-valued Pythagorean fuzzy environment for the optimal selection of mining methods under complex conditions. First, a comprehensive evaluation index system was established, using IVPFS to express indicator information, which better captures uncertainty. Second, the entropy measure and EWM were combined to determine the importance of decision-makers and indicators, avoiding errors caused by subjectivity and different experience values. This approach makes the decision-making process more realistic. Third, an integrated ranking considering distance and similarity was adopted, avoiding the defects of a single model.

Finally, the comprehensive model was applied to the decision-making of mining methods for fragmented ore bodies. The final scores of the four alternatives in the interval-valued Pythagorean fuzzy environment were 0.5172, 0.4683, 0.5192, and 0.5465, with the optimal solution being A4. In the traditional fuzzy sets environment (PFS and TFS), the optimal solution is A1, with scores of 0.5119 and 0.5286, respectively. The results show that traditional fuzzy sets perform poorly in the optimal selection of mining methods under complex environmental conditions. IVPFS are superior in capturing fuzzy information. Additionally, the point-pillar upward horizontal layered filling mining method proves to be better in practical applications than other alternatives, demonstrating the model’s effectiveness. Moreover, sensitivity analysis was conducted by setting preference factors, showing that the stability of the dual-measure integrated ranking is superior to the use of a single-measure method. In summary, this study provides a scientific and reasonable solution for multi-criteria decision-making problems and offers guidance and reference significance for the selection of mining schemes under complex conditions.

In the future, more advanced weight determination methods and the development of decision support systems can be explored to enhance the robustness of decisions. Integrating methods such as bipolar complex fuzzy sets can provide a more comprehensive perspective on polarity problems, potentially improving decision outcomes. In addition, comparing and analyzing with other fuzzy models can provide a deeper understanding of the advantages and disadvantages of different methods, which can contribute to more effective and sustainable mining practices.